Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. In Situ Dataset
2.2.1. Hyperspectral Data
2.2.2. Cchla Measurement
2.3. PRISMA Image
2.4. Denoising Algorithm Description
2.5. Assessment Indices
3. Results
3.1. Effectiveness of Sparse Representing
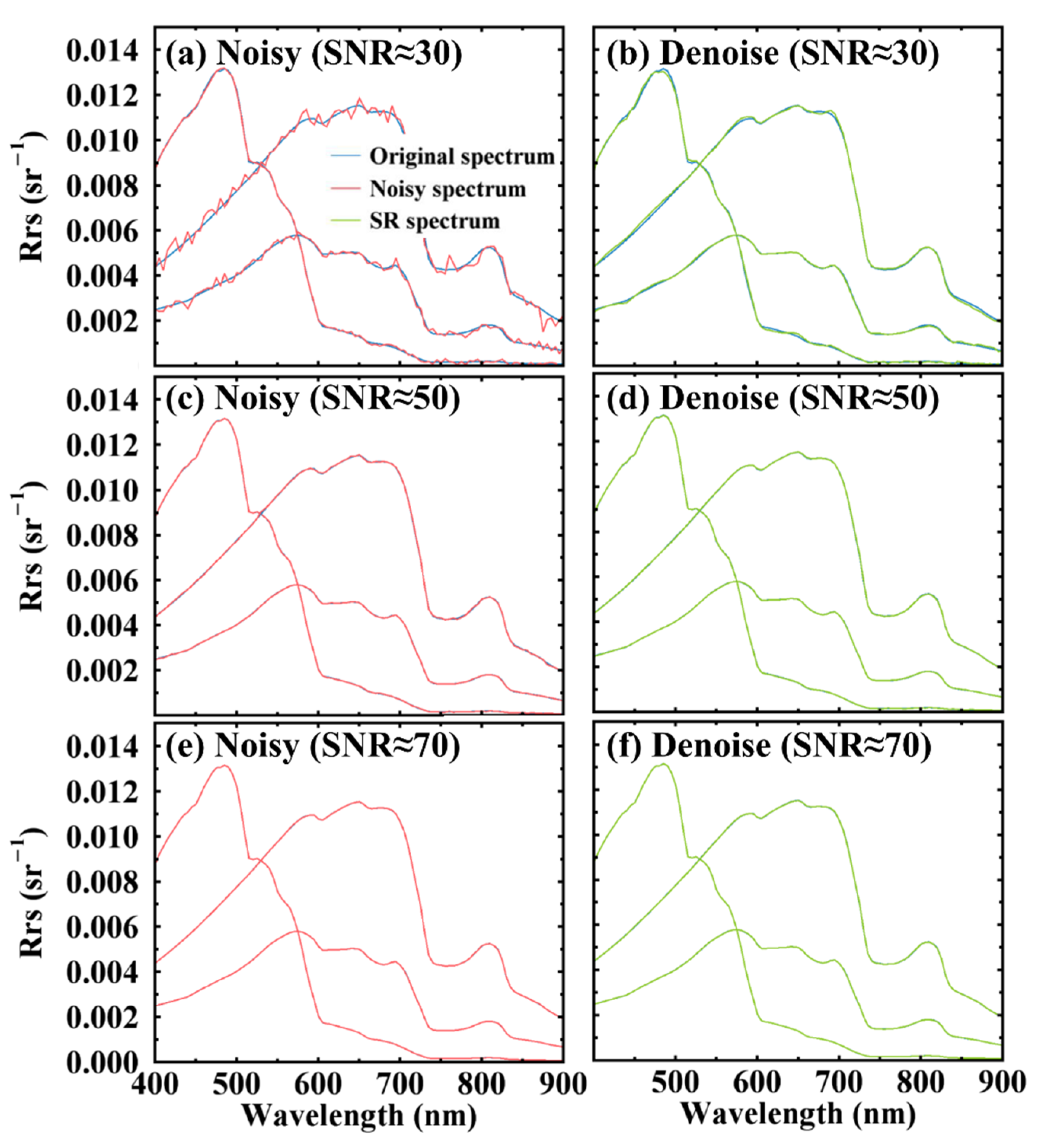
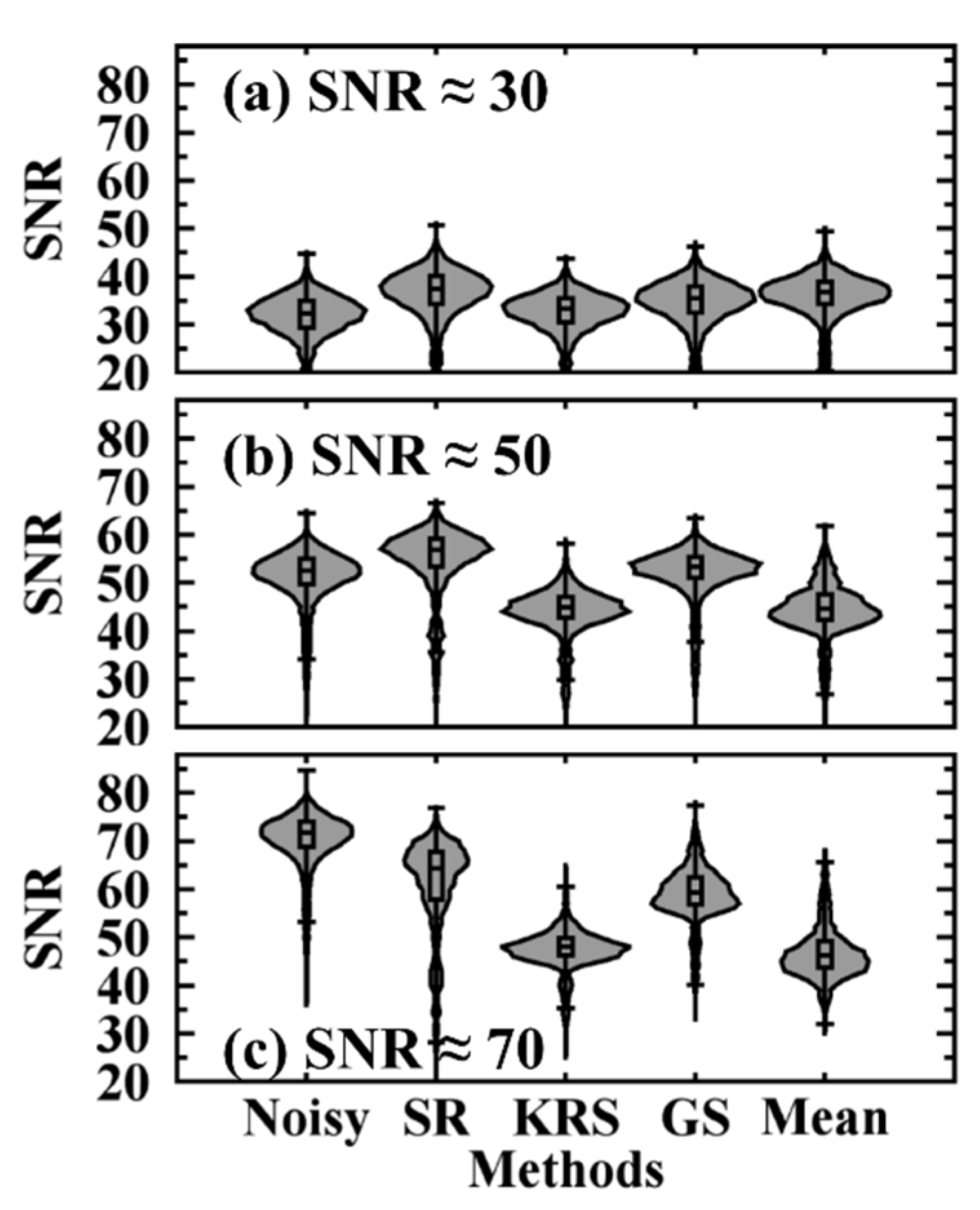
3.2. Denoising Performance in the Simulated Dataset
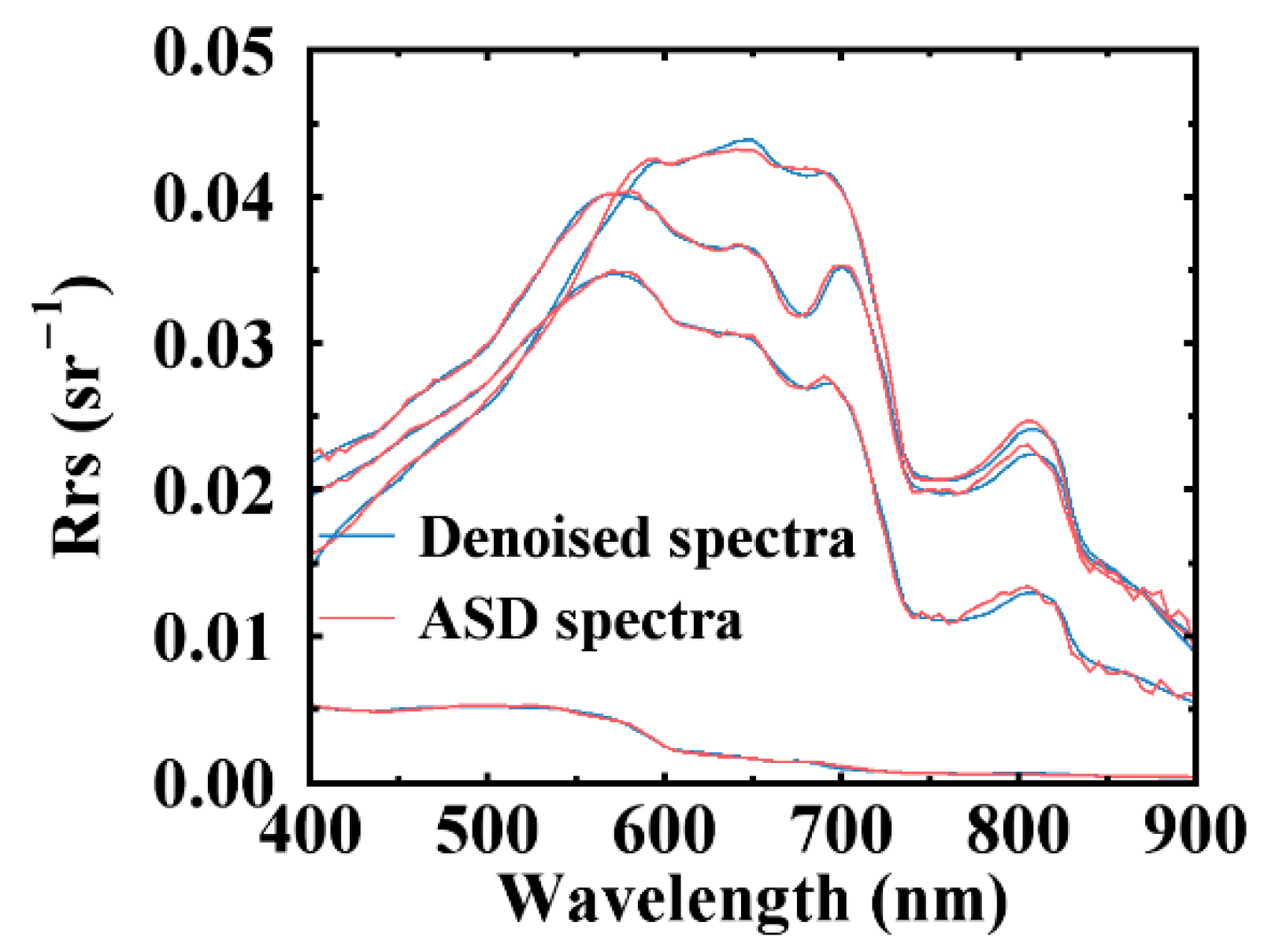
3.3. Denoising Performance in ASD Measured Dataset
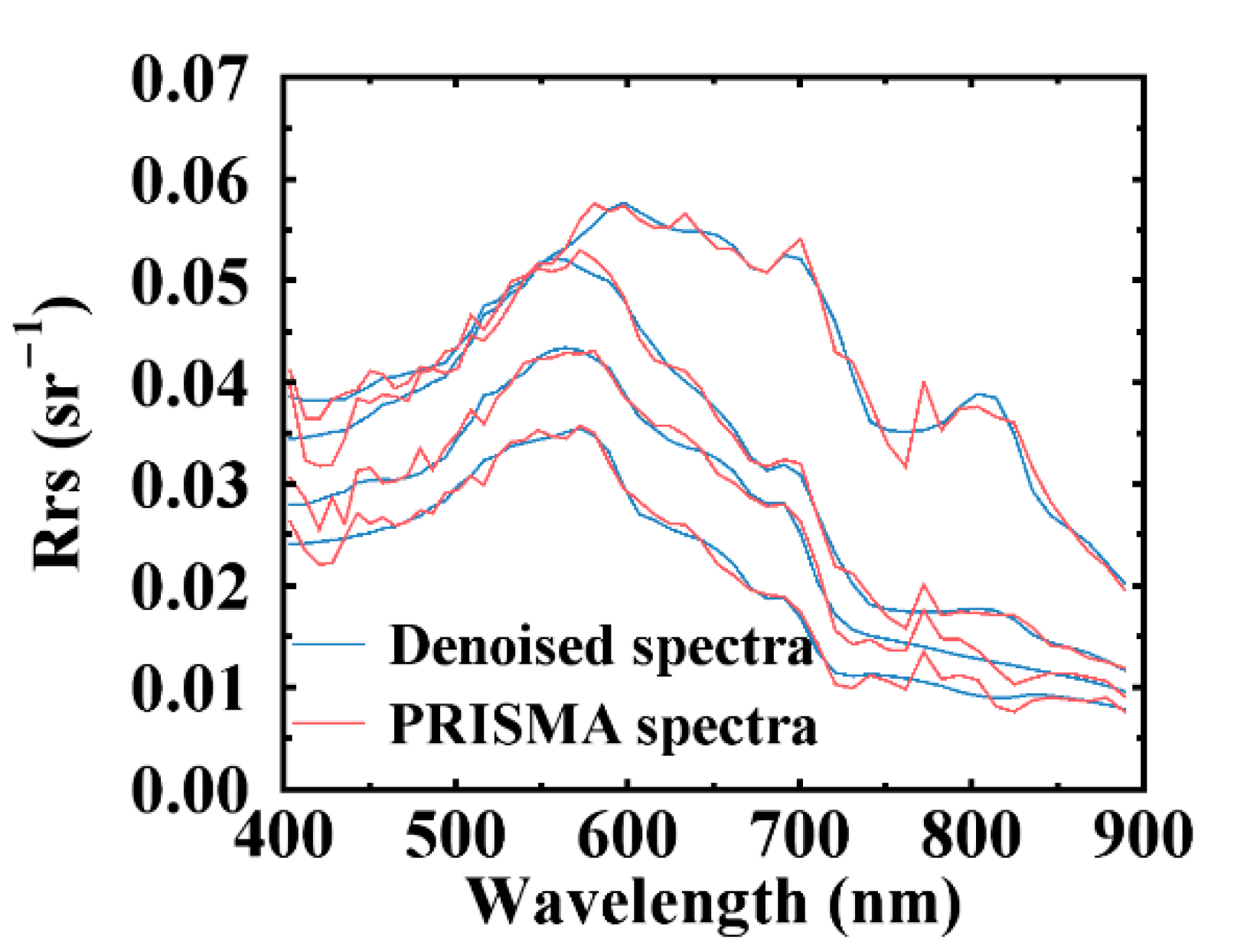
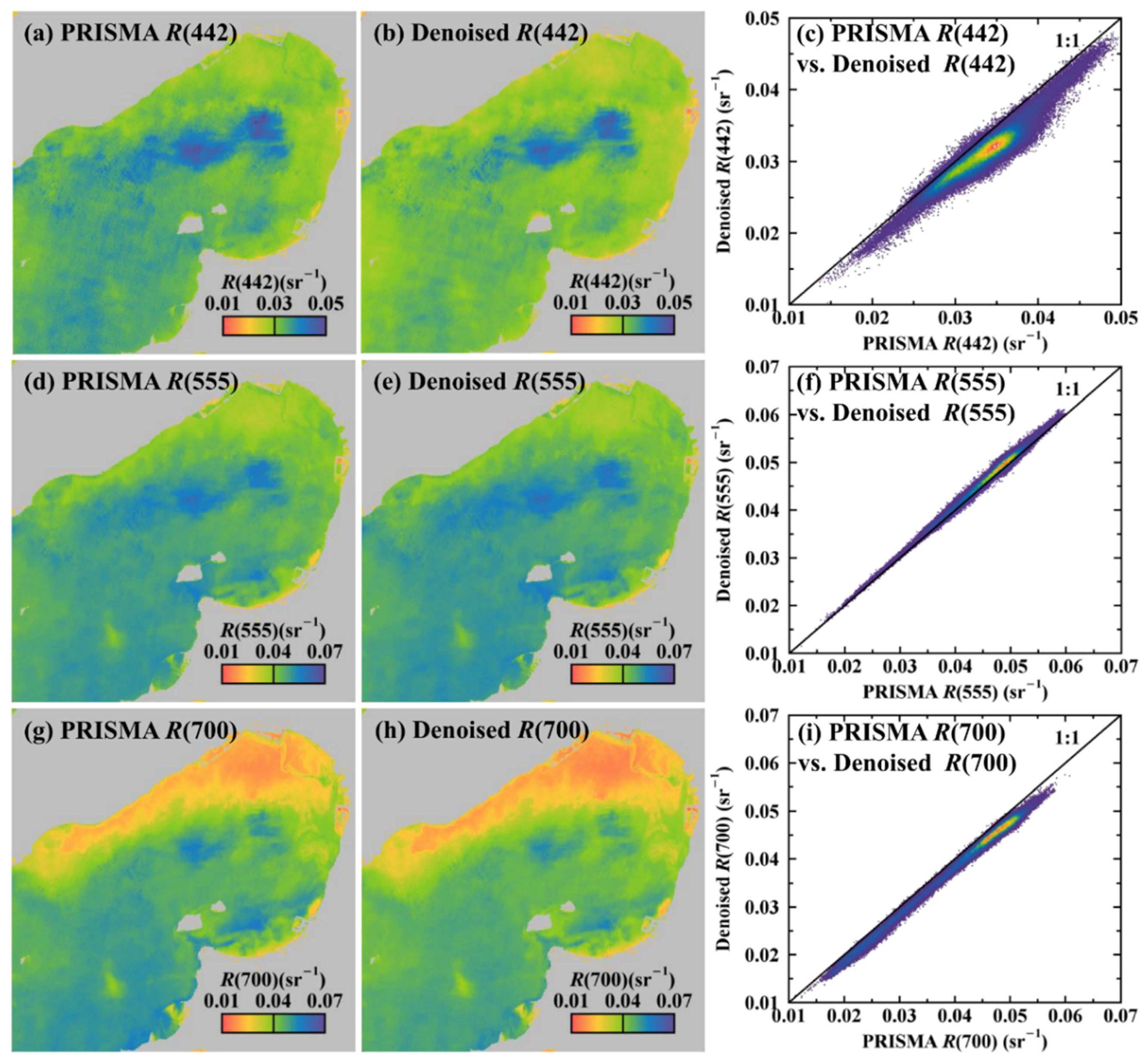
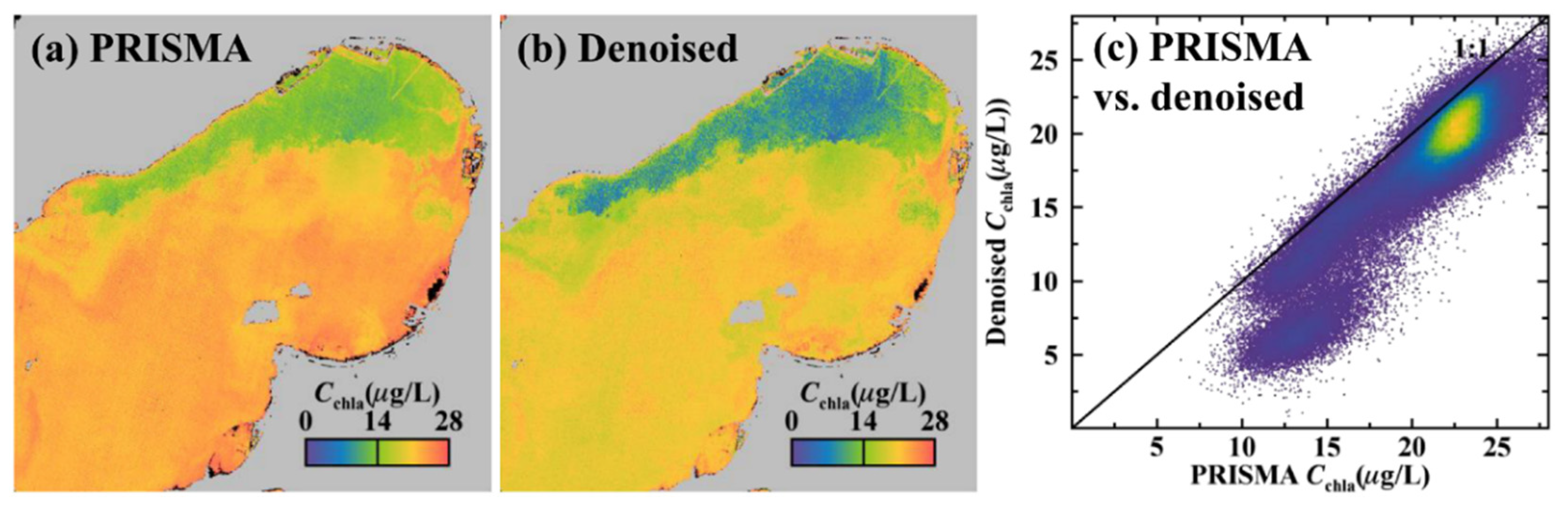
3.4. Denoising Performance in Hyperspectral Image
4. Discussion
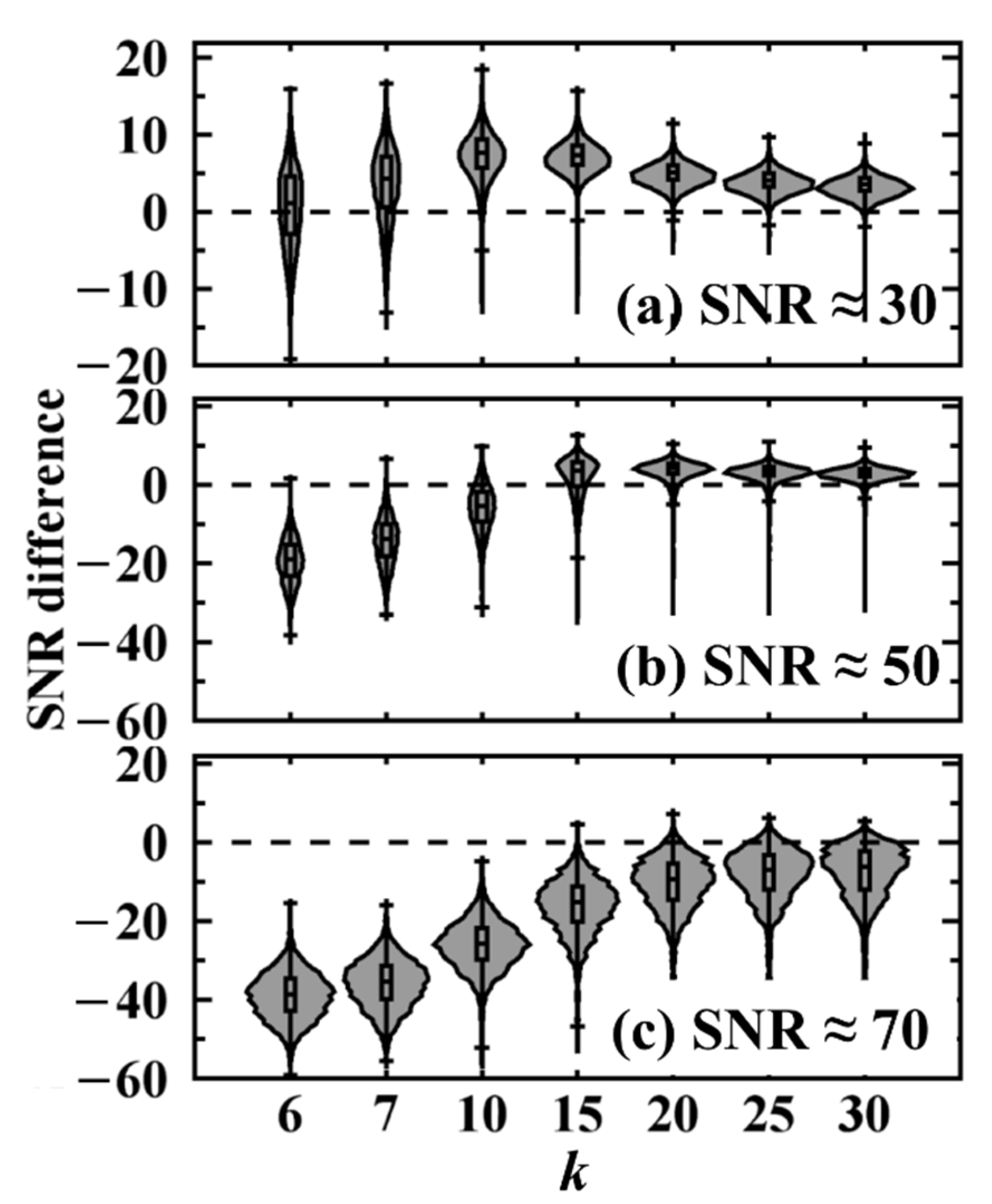
4.1. Influence of K
4.2. Influence of Denoising to Cchla Estimation Models
4.3. Denoised PRISMA Image
4.4. Limitations and Outlooks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, Z.; Kendall, L. Carder Absorption spectrum of phytoplankton pigments derived from hyperspectral remote sensing reflectance. Remote Sens. Environ. 2004, 89, 361–368. [Google Scholar] [CrossRef]
- Garaba, S.P.; Aitken, J.; Slat, B.; Dierssen, H.M.; Lebreton, L.; Zielinski, O.; Reisser, J. Sensing ocean plastics with an airborne hyperspectral shortwave infrared imager. Environ. Sci. Technol. 2018, 52, 11699–11707. [Google Scholar] [CrossRef] [PubMed]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral remote sensing of total phosphorus (TP) in three central Indiana water supply reservoirs. Water. Air. Soil Pollut. 2012, 223, 1481–1502. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, J.; Li, Y.; Guang, J. The Hyperspectral Data Monitoring Model of Chlorophyll-a of Summer in Taihu Lake, China. J. Remote Sens. 2007, 11, 756–762. [Google Scholar]
- Pahlevan, N.; Smith, B.; Binding, C.; Gurlin, D.; Li, L.; Bresciani, M.; Giardino, C. Hyperspectral retrievals of phytoplankton absorption and chlorophyll-a in inland and nearshore coastal waters. Remote Sens. Environ. 2021, 253, 112200. [Google Scholar] [CrossRef]
- Van Der Woerd, H.J.; Pasterkamp, R. HYDROPT: A fast and flexible method to retrieve chlorophyll-a from multispectral satellite observations of optically complex coastal waters. Remote Sens. Environ. 2008, 112, 1795–1807. [Google Scholar] [CrossRef]
- Gege, P. The water color simulator WASI: An integrating software tool for analysis and simulation of optical in situ spectra. Comput. Geosci. 2004, 30, 523–532. [Google Scholar] [CrossRef]
- Schalles, J.F. Optical remote sensing techniques to estimate phytoplankton chlorophyll a concentrations in coastal waters with varying suspended matter and cdom concentrations. In Advances in Water Resources; Springer: Berlin/Heidelberg, Germany, 2002; Volume 25, pp. 8–12. [Google Scholar]
- Lee, Z.; Shang, S.; Hu, C.; Zibordi, G. Spectral interdependence of remote-sensing reflectance and its implications on the design of ocean color satellite sensors. Appl. Opt. 2014, 53, 3301. [Google Scholar] [CrossRef]
- Sun, D.; Hu, C.; Qiu, Z.; Wang, S. Reconstruction of hyperspectral reflectance for optically complex turbid inland lakes: Test of a new scheme and implications for inversion algorithms. Opt. Express 2015, 23, A718. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Schiebe, F.R.; Cooper, C.M.; Harrington Jr, J.A. Chlorophyll measurements in the presence of suspended sediment using broad band spectral sensors aboard satellites. J. Freshw. Ecol. 1994, 9, 197–206. [Google Scholar] [CrossRef]
- Dall’olmo, G.; Gitelson, A.A. Effect of Bio-Optical Parameter Variability and Uncertainties in Reflectance Measurements on the Remote Estimation of Chlorophyll-a Concentration in Turbid Productive Waters: Modeling Results. Appl. Opt. 2006, 15, 3577–3592. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Zheng, Z.; Liu, G.; Du, C.; Du, C.; Lei, S.; Xu, Y.; Xu, J.; Mu, M.; Bi, S.; et al. Simulation and assessment of the capabilities of orbita hyperspectral (OHS) imagery for remotely monitoring chlorophyll-a in eutrophic plateau lakes. Remote Sens. 2021, 13, 2821. [Google Scholar] [CrossRef]
- Liu, G.; Simis, S.G.H.; Li, L.; Wang, Q.; Li, Y.; Song, K.; Lyu, H.; Zheng, Z.; Shi, K. A Four-Band Semi-Analytical Model for Estimating Phycocyanin in Inland Waters from Simulated MERIS and OLCI Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1374–1385. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Bowles, J.H.; Povazhnyi, V.; Saprygin, V.; Wagner, E.J.; Patterson, K.W. HICO-based NIR-red models for estimating chlorophyll-a concentration in productive coastal waters. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1111–1115. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Carder, K.L.; Steward, R.G.; Peacock, T.G.; Davis, C.O.; Mueller, J.L. Remote sensing reflectance and inherent optical properties of oceanic waters derived from above-water measurements. Ocean Opt. XIII 1997, 2963, 160–166. [Google Scholar] [CrossRef]
- Cheng, C.; Wei, Y.; Lv, G.; Yuan, Z. Remote estimation of chlorophyll-a concentration in turbid water using a spectral index: A case study in Taihu Lake, China. J. Appl. Remote Sens. 2013, 7, 073465. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Wang, G.; Cheng, C. Noise Removal in Spectrum Above Water Surface Using Kernel Regression Smoothing. J. Nanjing Norm. Univ. Nat. Sci. Ed. 2010, 33, 97–102. [Google Scholar]
- Cheng, C.; Wei, Y.; Sun, X.; Zhou, Y. Estimation of chlorophyll-a concentration in Turbid Lake using spectral smoothing and derivative analysis. Int. J. Environ. Res. Public Health 2013, 10, 2979–2994. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Qian, S.E. Denoising of hyperspectral imagery using principal component analysis and wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 49, 973–980. [Google Scholar] [CrossRef]
- Strela, V.; Heller, P.N.; Strang, G.; Topiwala, P.; Heil, C.; Heller, P.N. The Application of Multiwavelet Filter Banks to Image Processing. IEEE Trans. Image Process. 1999, 8, 548–563. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.Q.; Yang, J. Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 2015, 53, 296–308. [Google Scholar] [CrossRef]
- Aggarwal, H.K.; Majumdar, A. Hyperspectral Image Denoising Using Spatio-Spectral Total Variation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 442–446. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial-Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef] [Green Version]
- Routray, S.; Ray, A.K.; Mishra, C. An efficient image denoising method based on principal component analysis with learned patch groups. Signal Image Video Process. 2019, 13, 1405–1412. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, W.; Zhang, D.; Shi, G. Two-stage image denoising by principal component analysis with local pixel grouping. Pattern Recognit. 2010, 43, 1531–1549. [Google Scholar] [CrossRef] [Green Version]
- Abderrahim, L.; Salama, M.; Abdelbaki, D. Novel design of a fractional wavelet and its application to image denoising. Bull. Electr. Eng. Inform. 2020, 9, 129–140. [Google Scholar] [CrossRef]
- Li, H.; Wang, S. A new image denoising method using wavelet transform. In Proceedings of the Proceedings—2009 International Forum on Information Technology and Applications, IFITA 2009, Chengdu, China, 15–17 May 2009; Volume 1, pp. 111–114. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear Total Variation Based Noise Removal Algorithms; Elsevier: Amsterdam, The Netherlands, 1992; Volume 60. [Google Scholar]
- Vogelt, C.R.; Oman, M.E. Iterative Methods for Total Variation Denoising. SIAM J. Sci. Comput. 1996, 17, 227–238. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Ma, Y.; Benediktsson, J.A. Spectral-Spatial Adaptive Sparse Representation for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2016, 54, 373–385. [Google Scholar] [CrossRef]
- Elad, M.; Aharon, M. Image Denoising Via Learned Dictionaries and Sparse Representation. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral Image Denoising via Noise-Adjusted Iterative Low-Rank Matrix Approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.-W. Deep Learning on Image Denoising: An overview. Neural Netw. 2019, 131, 251–275. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, B.; Gholamalifard, M.; Kutser, T.; Vignudelli, S.; Kostianoy, A. Spatio-temporal variability in bio-optical properties of the southern caspian sea: A historic analysis of ocean color data. Remote Sens. 2020, 12, 3975. [Google Scholar] [CrossRef]
- El Ouali, A.; El Hafyani, M.; Roubil, A.; Lahrach, A.; Essahlaoui, A.; Hamid, F.E.; Muzirafuti, A.; Paraforos, D.S.; Lanza, S.; Randazzo, G. Modeling and spatiotemporal mapping of water quality through remote sensing techniques: A case study of the hassan addakhil dam. Appl. Sci. 2021, 11, 9297. [Google Scholar] [CrossRef]
- Du, C.; Li, Y.; Lyu, H.; Shi, K.; Liu, N.; Yan, C.; Pan, J.; Guo, Y.; Li, Y. Characteristics of the Total Suspended Matter Concentration in the Hongze Lake during 1984–2019 Based on Landsat Data. Remote Sens. 2022, 14, 2919. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Le, C.; Shi, K.; Huang, C.; Gong, S.; Yin, B. A semi-analytical approach for detecting suspended particulate composition in complex turbid inland waters (China). Remote Sens. Environ. 2013, 134, 92–99. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, C.; Zhang, Y.; Li, Y.; Chen, W. A Novel Multitemporal Image-Fusion Algorithm: Method and Application to GOCI and Himawari Images for Inland Water Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4018–4032. [Google Scholar] [CrossRef]
- Li, Y.; Shi, K.; Zhang, Y.; Zhu, G.; Zhang, Y.; Wu, Z.; Liu, M.; Guo, Y.; Li, N. Analysis of water clarity decrease in Xin’anjiang Reservoir, China, from 30-Year Landsat TM, ETM+, and OLI observations. J. Hydrol. 2020, 590, 125476. [Google Scholar] [CrossRef]
- Xie, D.; Wang, Z.; Gao, S.; De Vriend, H.J. Modeling the tidal channel morphodynamics in a macro-tidal embayment, Hangzhou Bay, China. Cont. Shelf Res. 2009, 29, 1757–1767. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, Q.; Gong, F.; He, X.; Chen, J.; Huang, H. Retrieval of total suspended particulate matter in highly turbid waters of Hangzhou Bay using polarizing spectra data. In Proceedings of the Remote Sensing and Modeling of Ecosystems for Sustainability XI, SPIE, San Diego, CA, USA, 8 October 2014; Volume 9221, p. 92210S. [Google Scholar]
- Mueller, J.L.; Fargion, G.S.; Mcclain, C.R.; Mueller, J.L.; Morel, A.; Frouin, R.; Davis, C.; Arnone, R.; Carder, K.; Lee, Z.P.; et al. NASA/TM-2003-21621/Rev-Vol III Ocean Optics Protocols For Satellite Ocean Color Sensor Validation, Revision 4, Volume III: Radiometric Measurements and Data Analysis Protocols; NASA: Washington, DC, USA, 2003. [Google Scholar]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef] [Green Version]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Water quality retrieval from PRISMA hyperspectral images: First experience in a turbid lake and comparison with sentinel-2. Remote Sens. 2020, 12, 3984. [Google Scholar] [CrossRef]
- Yulong, G.; Changchun, H.; Yunmei, L.; Chenggong, D.; Lingfei, S.; Yuan, L.; Weiqiang, C.; Hejie, W.; Enxiang, C.; Guangxing, J. Hyperspectral reconstruction method for optically complex inland waters based on bio-optical model and sparse representing. Remote Sens. Environ. 2022, 276, 113045. [Google Scholar] [CrossRef]
- Liu, G.; Li, Y.; Lyu, H.; Wang, S.; Du, C.; Huang, C. An Improved Land Target-Based Atmospheric Correction Method for Lake Taihu. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 793–803. [Google Scholar] [CrossRef]
- Bi, S.; Li, Y.; Wang, Q.; Lyu, H.; Liu, G.; Zheng, Z.; Du, C.; Mu, M.; Xu, J.; Lei, S.; et al. Inland water Atmospheric Correction based on Turbidity Classification using OLCI and SLSTR synergistic observations. Remote Sens. 2018, 10, 1002. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Quan, W.; Zhang, M.; Cui, T. A simple atmospheric correction algorithm for MODIS in shallow turbid waters: A case study in taihu lake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1825–1833. [Google Scholar] [CrossRef]
- Wang, M.; Son, S.; Zhang, Y.; Shi, W. Remote sensing of water optical property for China’s inland lake taihu using the SWIR atmospheric correction with 1640 and 2130 nm bands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2505–2516. [Google Scholar] [CrossRef]
- Cheng, C.; Wei, Y.; Wang, G.; Zhang, J.; Xia, X. Using Spectral Smoothing Method to Improve the Validation Precision of the Chlorophyll-a Estimation Model in Turbidity Water. Remote Sens. Technol. Appl. 2013, 28, 941–948. [Google Scholar]
- Li, Y.; Wang, Q.; Wu, C.; Zhao, S.; Xu, X.; Wang, Y.; Huang, C. Estimation of chlorophyll a concentration using NIR/Red bands of MERIS and classification procedure in inland turbid water. IEEE Trans. Geosci. Remote Sens. 2012, 50, 988–997. [Google Scholar] [CrossRef]
- Huang, C.; Zou, J.; Li, Y.; Yang, H.; Shi, K.; Li, J.; Wang, Y.; Chena, X.; Zheng, F. Assessment of NIR-red algorithms for observation of chlorophyll-a in highly turbid inland waters in China. ISPRS J. Photogramm. Remote Sens. 2014, 93, 29–39. [Google Scholar] [CrossRef]
- Augusto-Silva, P.B.; Ogashawara, I.; Barbosa, C.C.F.; de Carvalho, L.A.S.; Jorge, D.S.F.; Fornari, C.I.; Stech, J.L. Analysis of MERIS reflectance algorithms for estimating chlorophyll-a concentration in a Brazilian reservoir. Remote Sens. 2014, 6, 11689–11707. [Google Scholar] [CrossRef] [Green Version]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Li, Y.; Luis, K.; Dai, M.; Wang, Y. Three-Dimensional Variation in Light Quality in the Upper Water Column Revealed With a Single Parameter. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–10. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y.; Zhu, L.; Wang, Q.; Lv, H.; Huang, C.; Li, Y. An Inversion-Based Fusion Method for Inland Water Remote Monitoring. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5599–5611. [Google Scholar] [CrossRef]
- Song, K.; Liu, G.; Wang, Q.; Wen, Z.; Lyu, L.; Du, Y.; Sha, L.; Fang, C. Quantification of lake clarity in China using Landsat OLI imagery data. Remote Sens. Environ. 2020, 243, 111800. [Google Scholar] [CrossRef]
- Cao, B.; Deng, R.; Zhu, S.; Liu, Y.; Liang, Y.; Xiong, L. Bathymetric Retrieval Selectively Using Multiangular High-Spatial-Resolution Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 1060–1074. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Hà, N.; et al. Seamless retrievals of chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in inland and coastal waters: A machine-learning approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Spyrakos, E.; Tyler, A.N.; Shen, Q.; Zhang, F.; Kuster, T.; Lehmann, M.K.; Wu, Y.; et al. Trophic state assessment of global inland waters using a MODIS-derived Forel-Ule index. Remote Sens. Environ. 2018, 217, 444–460. [Google Scholar] [CrossRef] [Green Version]
- Park, E.; Latrubesse, E.M. Modeling suspended sediment distribution patterns of the Amazon River using MODIS data. Remote Sens. Environ. 2014, 147, 232–242. [Google Scholar] [CrossRef]
- Feng, L.; Hu, C.; Li, J. Can MODIS Land Reflectance Products be Used for Estuarine and Inland Waters? Water Resour. Res. 2018, 54, 3583–3601. [Google Scholar] [CrossRef]
- Spyrakos, E.; González Vilas, L.; Torres Palenzuela, J.M.; Barton, E.D. Remote sensing chlorophyll a of optically complex waters (rias Baixas, NW Spain): Application of a regionally specific chlorophyll a algorithm for MERIS full resolution data during an upwelling cycle. Remote Sens. Environ. 2011, 115, 2471–2485. [Google Scholar] [CrossRef] [Green Version]
- Shen, F.; Zhou, Y.X.; Li, D.J.; Zhu, W.J.; Salama, M.H.D.S. Medium resolution imaging spectrometer (MERIS) estimation of chlorophyll-a concentration in the turbid sediment-laden waters of the Changjiang (Yangtze) Estuary. Int. J. Remote Sens. 2010, 31, 4635–4650. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Cannizzaro, J.; Ma, R. A novel MERIS algorithm to derive cyanobacterial phycocyanin pigment concentrations in a eutrophic lake: Theoretical basis and practical considerations. Remote Sens. Environ. 2014, 154, 298–317. [Google Scholar] [CrossRef]
- Huang, C.; Shi, K.; Yang, H.; Li, Y.; Zhu, A.X.; Sun, D.; Xu, L.; Zou, J.; Chen, X. Satellite observation of hourly dynamic characteristics of algae with Geostationary Ocean Color Imager (GOCI) data in Lake Taihu. Remote Sens. Environ. 2015, 159, 278–287. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, C.; Li, Y.; Du, C.; Li, Y.; Chen, W.; Shi, L.; Ji, G. An Expanded Three Band Model to Monitor Inland Optically Complex Water Using Geostationary Ocean Color Imager (GOCI). Front. Remote Sens. 2022, 3, 803884. [Google Scholar] [CrossRef]
- Shi, J.; Shen, Q.; Yao, Y.; Li, J.; Chen, F.; Wang, R.; Xu, W.; Gao, Z.; Wang, L.; Zhou, Y. Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sens. 2022, 14, 229. [Google Scholar] [CrossRef]
- Zhu, L.; Li, Y.; Zhao, S.; Guo, Y. Remote Sensing Monitoring of Taihu Lake water Quality by using GF-1 satellite WFV data. Remote Sens. L. Resour. 2015, 27, 113–120. [Google Scholar]
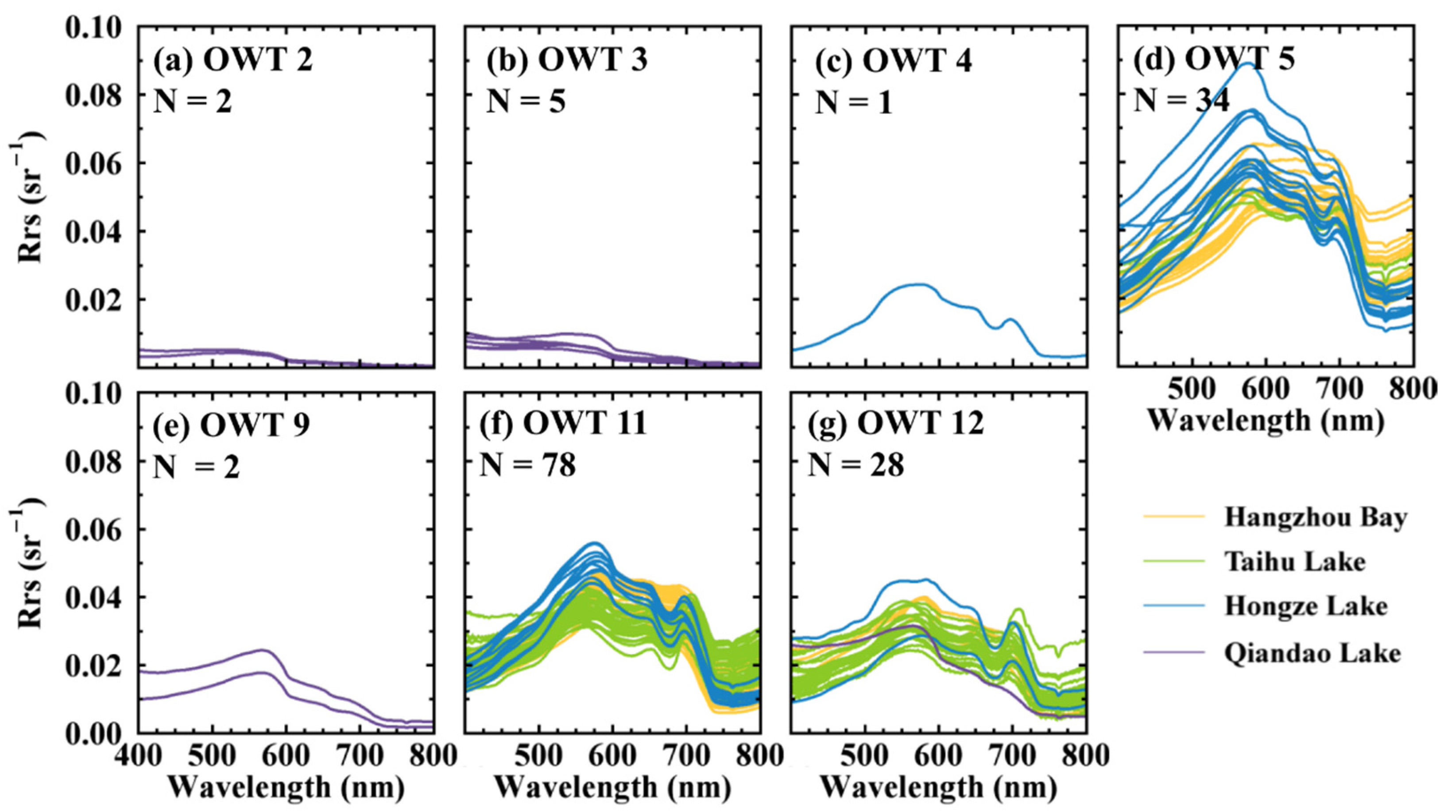
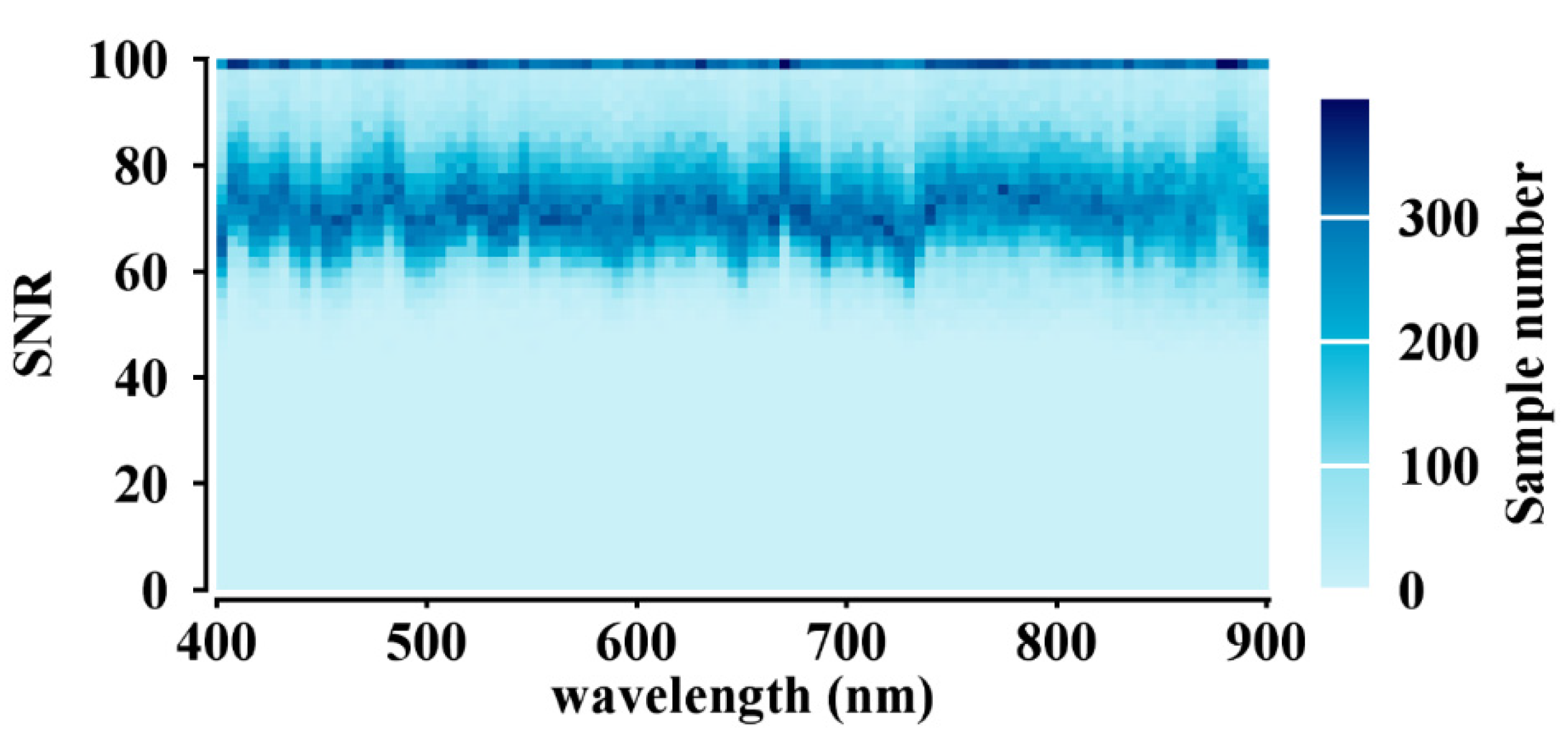
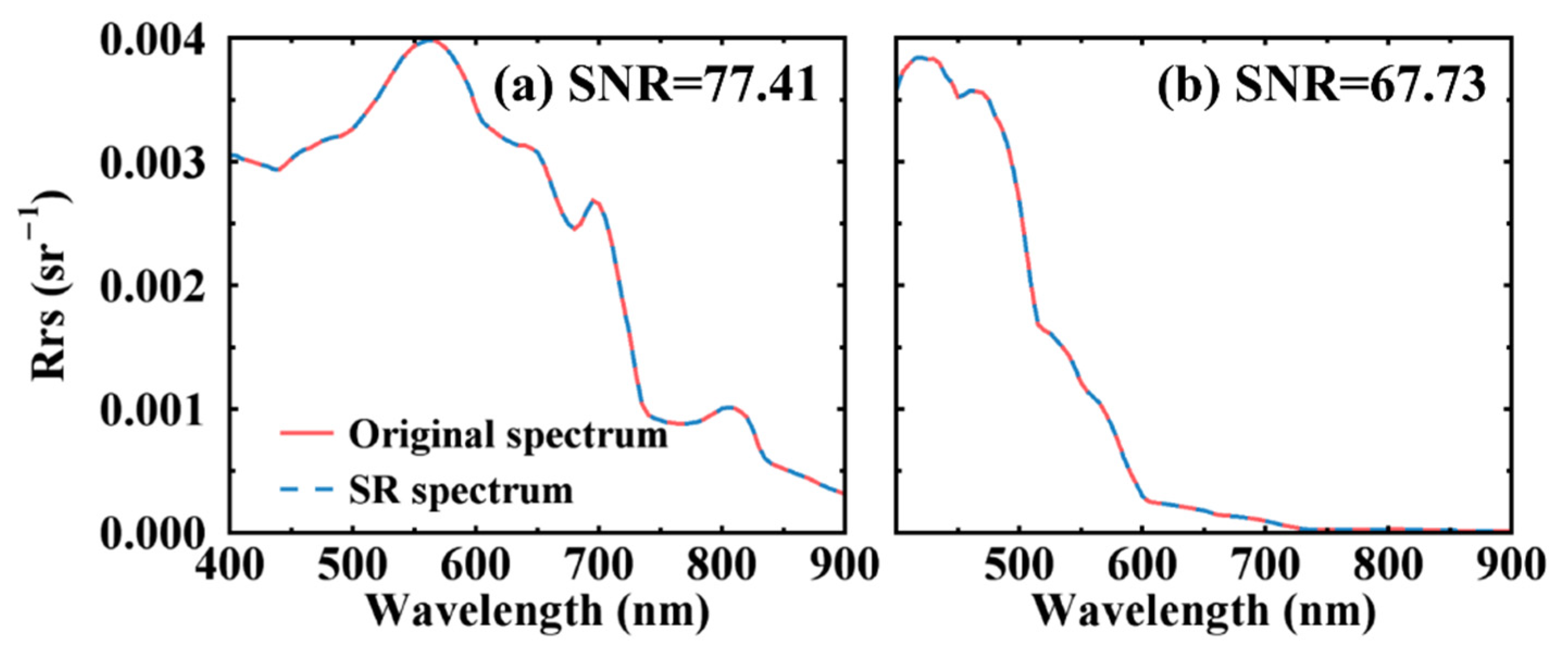
| Sampling Station | Hyperspectral Sample Number | Cchla |
|---|---|---|
| Taihu Lake (1 August 2019) | 60 (OWT5: 3, OWT11: 37, OWT12: 20) | √ |
| Hongze Lake (12 November 2020) | 29 (OWT4: 1, OWT5: 14, OWT11: 13, OWT12: 2) | - |
| Qiandao Lake (1 December 2021) | 10 (OWT2: 2, OWT3: 5, OWT9:2, OWT12: 1) | - |
| Hangzhou Bay (26 July 2017) | 51 (OWT5: 17, OWT11: 30, OWT12: 4) | - |
| Spectral Index | Expression | Original r | Denoised r |
|---|---|---|---|
| Band ratio [54,55] | R710/R680 | 0.719 | 0.721 |
| NDCI [56] | (R710 − R680)/(R710 + R680) | 0.697 | 0.700 |
| Three-band [12] | (1/R680 − 1/R710) × R745 | 0.752 | 0.755 |
| Four-band [57] | (1/R680 − 1/R710)/(1/R745 − 1/R720) | 0.695 | 0.698 |
| Enhanced three-band [58] | (1/R680 − 1/R710)/(1/R745 − 1/R710) | 0.743 | 0.748 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Bi, Q.; Li, Y.; Du, C.; Huang, J.; Chen, W.; Shi, L.; Ji, G. Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing. Appl. Sci. 2022, 12, 7501. https://doi.org/10.3390/app12157501
Guo Y, Bi Q, Li Y, Du C, Huang J, Chen W, Shi L, Ji G. Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing. Applied Sciences. 2022; 12(15):7501. https://doi.org/10.3390/app12157501
Chicago/Turabian StyleGuo, Yulong, Qingsheng Bi, Yuan Li, Chenggong Du, Junchang Huang, Weiqiang Chen, Lingfei Shi, and Guangxing Ji. 2022. "Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing" Applied Sciences 12, no. 15: 7501. https://doi.org/10.3390/app12157501
APA StyleGuo, Y., Bi, Q., Li, Y., Du, C., Huang, J., Chen, W., Shi, L., & Ji, G. (2022). Sparse Representing Denoising of Hyperspectral Data for Water Color Remote Sensing. Applied Sciences, 12(15), 7501. https://doi.org/10.3390/app12157501







