Dynamic Reduction-Based Virtual Models for Digital Twins—A Comparative Study
Abstract
:1. Introduction
- Loaded-Interface [62];
2. Component Modal Synthesis
2.1. Fixed-Interface Modal Synthesis Technique
2.2. Free-Interface Modal Synthesis Techniques
2.3. State-Space Representation of Reduced-Order Model
3. Evaluation Criteria
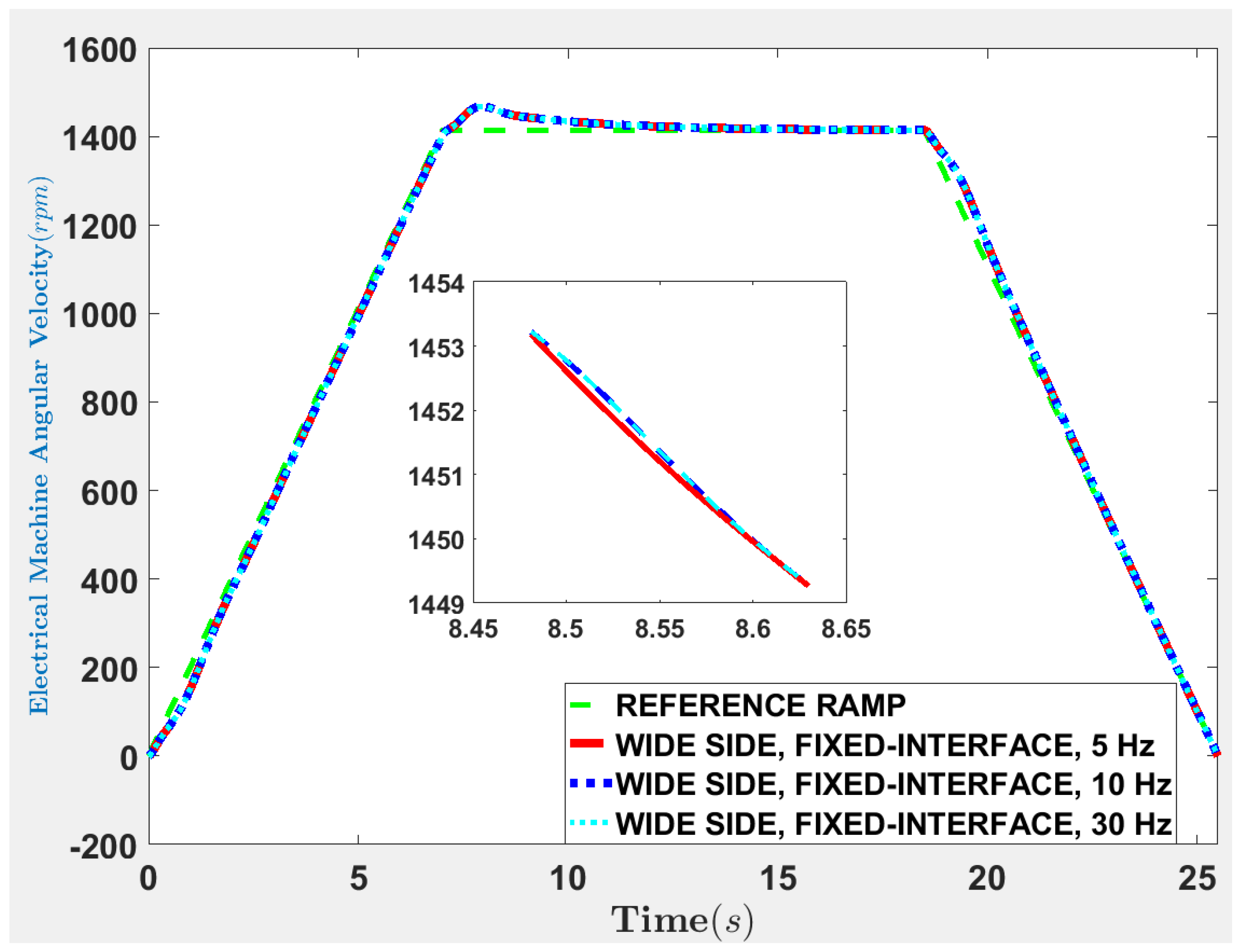
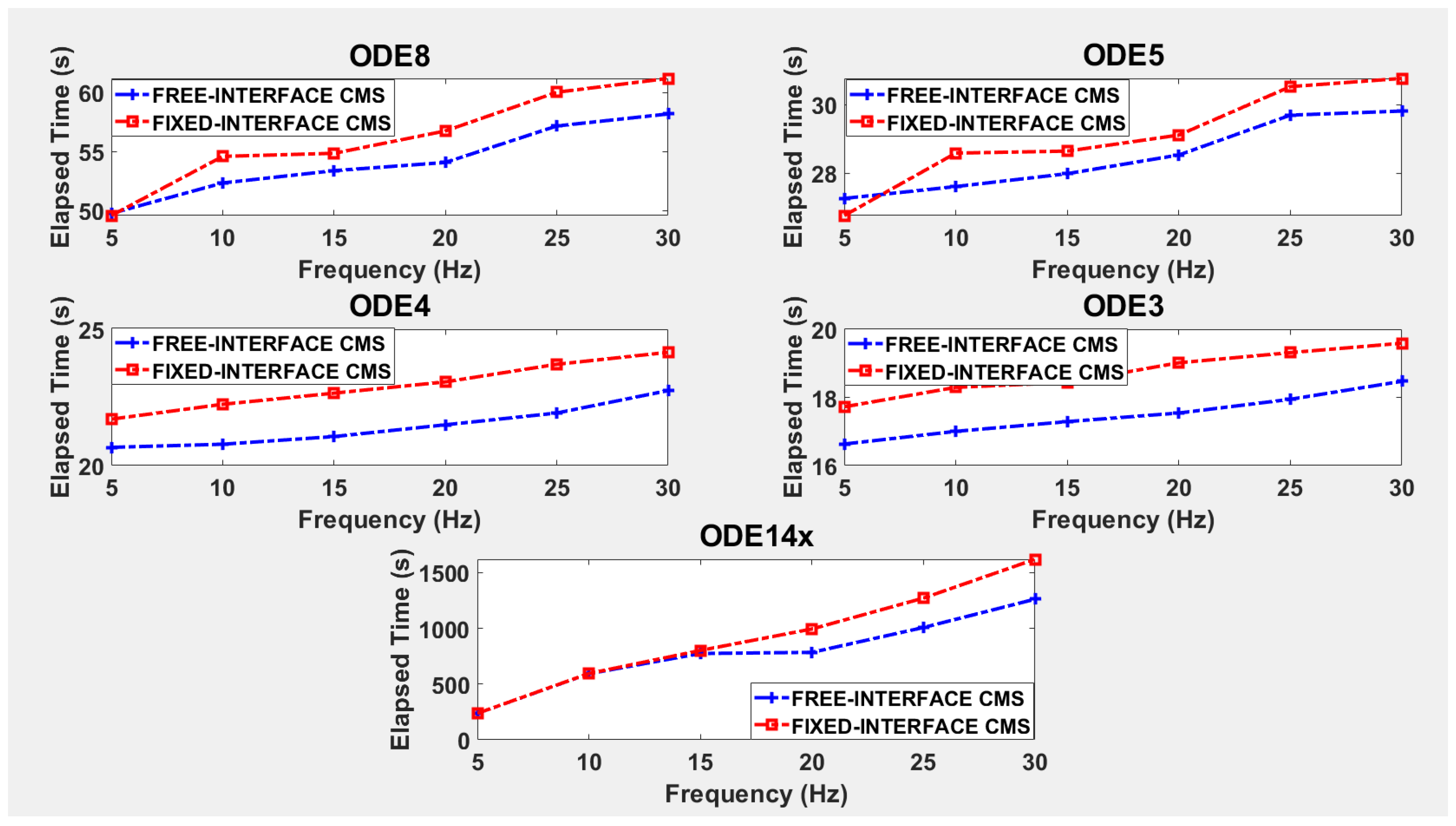
4. Results
5. Conclusions
- A comprehensive review of the dynamic reduction methods, the libraries of which are available as built-in packages on most FEA-based platforms. The dynamic reduction methods eventually facilitate the development of the reduced-order models of the existing and operating structures.
- A mathematical derivation of the state-space representation of the reduced-order models.
- Establishing the performance metrics for evaluating dynamic reduction methods.
- Identifying the most appropriate dynamic reduction approach for developing digital models for off-road vehicles.
- A comparison of the numerical solvers in the problem-solving platforms.
- Selection of the optimal numerical solver to simulate the digital models for off-road vehicles.
- Identifying the lower bound of the frequency range is necessary and sufficient for developing reduced-order models for off-road vehicles.
- Most commercial textual and graphical programming platforms have built-in blocks to represent the state-space models.
- It facilitates the modeling of virtual models based on ROMs incorporating structural damping.
- While performing industrial operations, the configuration of specific components within a structure varies, modifying the full-order finite element model, which subsequently alters the modal characteristics of the overall structure. As a consequence, the reduced-order model changes as well. In these scenarios, the time-varying state-space model can be used on textual and graphical programming platforms to simulate digital models based on changing ROMs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| Matrix of retained fixed-constraint normal modeshapes | |
| Matrix of retained free-interface modeshapes corresponding to boundary degrees of freedom | |
| Matrix of retained free-interface modeshapes corresponding to interior degrees of freedom | |
| Boolean matrix | |
| Stiffness matrix in generalized coordinates | |
| Mass matrix in generalized coordinates | |
| Compatibility matrix | |
| Boolean matrix | |
| Matrix of modeshapes for the reduced-order model | |
| Modified modeshape matrix of reduced system | |
| Matrix of retained attachment modeshapes | |
| Matrix of constraint modeshapes | |
| Matrix of elastic modeshapes | |
| Matrix of fixed-constraint normal modeshapes | |
| Matrix of rigid body modeshapes | |
| Inertia-relief matrix | |
| State matrix | |
| Input matrix | |
| Output matrix | |
| Feed-forward matrix | |
| Stiffness matrix of the ith substructure in physical coordinates | |
| Reduced stiffness matrix in physical coordinates | |
| Mass matrix of the ith substructure in physical coordinates | |
| Reduced mass matrix in physical coordinates | |
| Craig–Bampton transformation matrix | |
| Hintz’s transformation matrix | |
| Percentage error between ith reduced-order and full-order mode | |
| Natural frequencies of full-order system | |
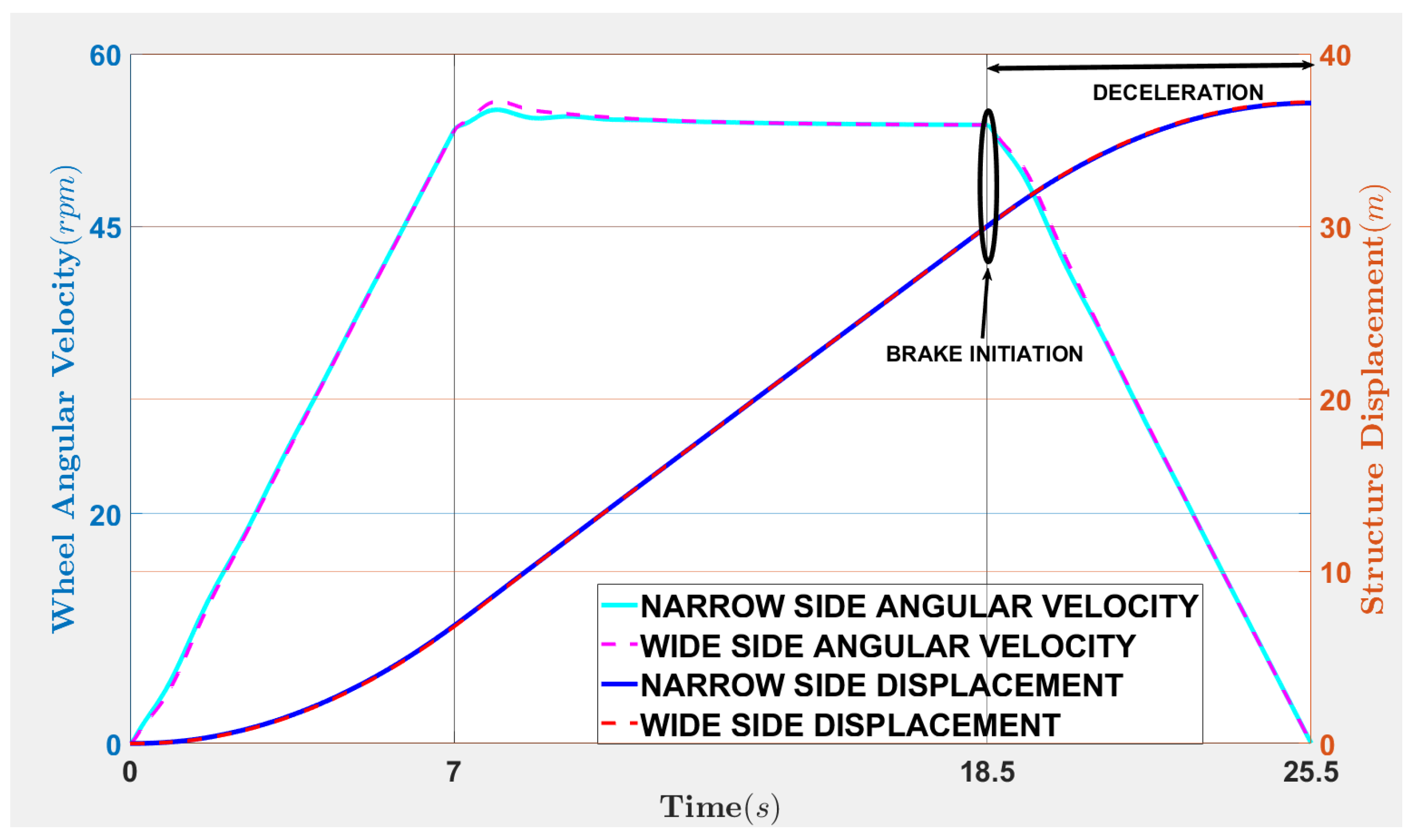
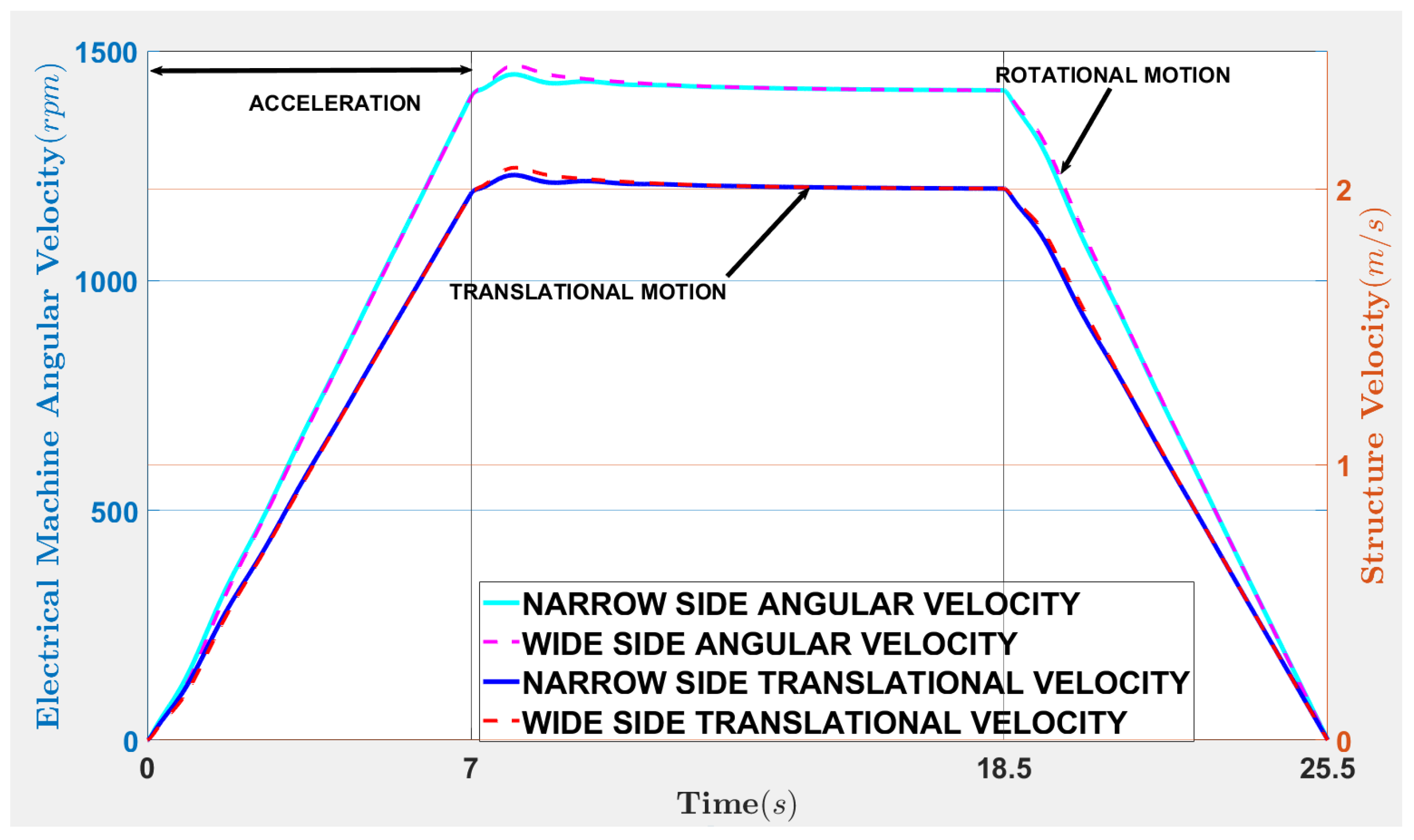
| Reference trajectory at time in the deceleration regime, and where indicates the beginning of the braking of the regime | |
| Reference trajectory at time in the acceleration and steady state regime, and where | |
| indicates the vehicle is commencing travel | |
| Retained modes in reduced system | |
| Fixed-constraint normal modes | |
| Electrical machine rated speed | |
| Free-interface normal modes | |
| Total number of substructures or components | |
| Total number of couplings in the structure | |
| A constant and | |
| A constant and | |
| Global physical displacements | |
| Global physical displacements for uncoupled boundary coordinates | |
| Local acceleration in physical coordinates | |
| Modal coordinates |
| Modal coordinates for reduced-order model | |
| Generalized coordinates | |
| Eigenvectors of free-interface modes corresponding to boundary degrees of freedom | |
| Eigenvectors of free-interface modes corresponding to interior degrees of freedom | |
| External forces in physical coordinates | |
| D’Alembert’s forces or inertial forces | |
| External force at the rth degree of freedom of the reduced-order model | |
| Local displacements in physical coordinates | |
| Elastic deformation vector | |
| Rigid body displacement | |
| State variables | |
| Input vector | |
| B | Boundary degrees of freedom in ith substructure |
| h | Simulation step size |
| I | Interior degrees of freedom in ith substructure |
| N | Total degrees of freedom in full-order system |
| Total degrees of freedom for ith substructure | |
| R | Retained degrees of freedom in reduced system |
| Distance to be traveled | |
| Displacement of the vehicle at time or | |
| Displacement at the narrow side | |
| Displacement at the wide side | |
| t | Simulation epoch |
| Velocity of the vehicle at time or | |
| Maximum allowable velocity for the off-road vehicle |
References
- Lasi, H.; Fettke, P.; Kemper, H.G.; Feld, T.; Hoffmann, M. Industry 4.0. Bus. Inf. Syst. Eng. 2014, 6, 239–242. [Google Scholar] [CrossRef]
- Gilchrist, A. Industry 4.0: The Industrial Internet of Things; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Raj, A.; Dwivedi, G.; Sharma, A.; de Sousa Jabbour, A.B.L.; Rajak, S. Barriers to the adoption of industry 4.0 technologies in the manufacturing sector: An inter-country comparative perspective. Int. J. Prod. Econ. 2020, 224, 107546. [Google Scholar] [CrossRef]
- Ghobakhloo, M. Industry 4.0, digitization, and opportunities for sustainability. J. Clean. Prod. 2020, 252, 119869. [Google Scholar] [CrossRef]
- Bai, C.; Dallasega, P.; Orzes, G.; Sarkis, J. Industry 4.0 technologies assessment: A sustainability perspective. Int. J. Prod. Econ. 2020, 229, 107776. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, R.K.; Dwivedi, Y.K. Application of industry 4.0 technologies in SMEs for ethical and sustainable operations: Analysis of challenges. J. Clean. Prod. 2020, 275, 124063. [Google Scholar] [CrossRef]
- Silvestri, L.; Forcina, A.; Introna, V.; Santolamazza, A.; Cesarotti, V. Maintenance transformation through Industry 4.0 technologies: A systematic literature review. Comput. Ind. 2020, 123, 103335. [Google Scholar] [CrossRef]
- Yadav, G.; Kumar, A.; Luthra, S.; Garza-Reyes, J.A.; Kumar, V.; Batista, L. A framework to achieve sustainability in manufacturing organisations of developing economies using industry 4.0 technologies’ enablers. Comput. Ind. 2020, 122, 103280. [Google Scholar] [CrossRef]
- Benitez, G.B.; Ayala, N.F.; Frank, A.G. Industry 4.0 innovation ecosystems: An evolutionary perspective on value cocreation. Int. J. Prod. Econ. 2020, 228, 107735. [Google Scholar] [CrossRef]
- Culot, G.; Nassimbeni, G.; Orzes, G.; Sartor, M. Behind the definition of Industry 4.0: Analysis and open questions. Int. J. Prod. Econ. 2020, 226, 107617. [Google Scholar] [CrossRef]
- Santos, R.C.; Martinho, J.L. An Industry 4.0 maturity model proposal. J. Manuf. Technol. Manag. 2020, 31, 1023–1043. [Google Scholar] [CrossRef]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Pejic-Bach, M.; Bertoncel, T.; Meško, M.; Krstić, Ž. Text mining of industry 4.0 job advertisements. Int. J. Inf. Manag. 2020, 50, 416–431. [Google Scholar] [CrossRef]
- Furstenau, L.B.; Sott, M.K.; Kipper, L.M.; Machado, E.L.; Lopez-Robles, J.R.; Dohan, M.S.; Cobo, M.J.; Zahid, A.; Abbasi, Q.H.; Imran, M.A. Link between sustainability and industry 4.0: Trends, challenges and new perspectives. IEEE Access 2020, 8, 140079–140096. [Google Scholar] [CrossRef]
- Bag, S.; Gupta, S.; Kumar, S. Industry 4.0 adoption and 10R advance manufacturing capabilities for sustainable development. Int. J. Prod. Econ. 2021, 231, 107844. [Google Scholar] [CrossRef]
- Zheng, T.; Ardolino, M.; Bacchetti, A.; Perona, M. The applications of Industry 4.0 technologies in manufacturing context: A systematic literature review. Int. J. Prod. Res. 2021, 59, 1922–1954. [Google Scholar] [CrossRef]
- Stentoft, J.; Adsbøll Wickstrøm, K.; Philipsen, K.; Haug, A. Drivers and barriers for Industry 4.0 readiness and practice: Empirical evidence from small and medium-sized manufacturers. Prod. Plan. Control. 2021, 32, 811–828. [Google Scholar] [CrossRef]
- Meindl, B.; Ayala, N.F.; Mendonça, J.; Frank, A.G. The four smarts of Industry 4.0: Evolution of ten years of research and future perspectives. Technol. Forecast. Soc. Chang. 2021, 168, 120784. [Google Scholar] [CrossRef]
- Jamwal, A.; Agrawal, R.; Sharma, M.; Giallanza, A. Industry 4.0 technologies for manufacturing sustainability: A systematic review and future research directions. Appl. Sci. 2021, 11, 5725. [Google Scholar] [CrossRef]
- Atzori, L.; Iera, A.; Morabito, G. The internet of things: A survey. Comput. Netw. 2010, 54, 2787–2805. [Google Scholar] [CrossRef]
- Ashton, K. That ‘internet of things’ thing. RFID J. 2009, 22, 97–114. [Google Scholar]
- Deering, S.; Hinden, R. Internet Protocol, Version 6 (IPv6) Specification. 1998. Available online: https://www.rfc-editor.org/rfc/rfc8200 (accessed on 4 April 2022).
- Johnson, D.; Perkins, C.; Arkko, J. Mobility Support in IPv6. 2004. Available online: https://www.rfc-editor.org/rfc/rfc3775 (accessed on 4 April 2022).
- Lee, J.; Bagheri, B.; Kao, H.A. A cyber-physical systems architecture for industry 4.0-based manufacturing systems. Manuf. Lett. 2015, 3, 18–23. [Google Scholar] [CrossRef]
- Glaessgen, E.; Stargel, D. The digital twin paradigm for future NASA and US Air Force vehicles. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC structures, structural dynamics and materials conference 20th AIAA/ASME/AHS adaptive structures conference 14th AIAA, Honolulu, HI, USA, 23–26 April 2012; p. 1818. [Google Scholar]
- Tuegel, E.J.; Ingraffea, A.R.; Eason, T.G.; Spottswood, S.M. Reengineering aircraft structural life prediction using a digital twin. Int. J. Aerosp. Eng. 2011, 2011. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.; Lapira, E.; Bagheri, B.; Kao, H.a. Recent advances and trends in predictive manufacturing systems in big data environment. Manuf. Lett. 2013, 1, 38–41. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Wang, L.; Nee, A. Digital twins and cyber–physical systems toward smart manufacturing and industry 4.0: Correlation and comparison. Engineering 2019, 5, 653–661. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the Digital Twin: A systematic literature review. Cirp J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Errandonea, I.; Beltrán, S.; Arrizabalaga, S. Digital Twin for maintenance: A literature review. Comput. Ind. 2020, 123, 103316. [Google Scholar] [CrossRef]
- Qi, Q.; Tao, F.; Hu, T.; Anwer, N.; Liu, A.; Wei, Y.; Wang, L.; Nee, A. Enabling technologies and tools for digital twin. J. Manuf. Syst. 2021, 58, 3–21. [Google Scholar] [CrossRef]
- Rasheed, A.; San, O.; Kvamsdal, T. Digital twin: Values, challenges and enablers from a modeling perspective. IEEE Access 2020, 8, 21980–22012. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital twin: Enabling technologies, challenges and open research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Sacks, R.; Brilakis, I.; Pikas, E.; Xie, H.S.; Girolami, M. Construction with digital twin information systems. Data-Centric Eng. 2020, 1, E14. [Google Scholar] [CrossRef]
- VanDerHorn, E.; Mahadevan, S. Digital Twin: Generalization, characterization and implementation. Decis. Support Syst. 2021, 145, 113524. [Google Scholar] [CrossRef]
- Boje, C.; Guerriero, A.; Kubicki, S.; Rezgui, Y. Towards a semantic Construction Digital Twin: Directions for future research. Autom. Constr. 2020, 114, 103179. [Google Scholar] [CrossRef]
- Liu, M.; Fang, S.; Dong, H.; Xu, C. Review of digital twin about concepts, technologies, and industrial applications. J. Manuf. Syst. 2021, 58, 346–361. [Google Scholar] [CrossRef]
- Lim, K.Y.H.; Zheng, P.; Chen, C.H. A state-of-the-art survey of Digital Twin: Techniques, engineering product lifecycle management and business innovation perspectives. J. Intell. Manuf. 2020, 31, 1313–1337. [Google Scholar] [CrossRef]
- Kaur, M.J.; Mishra, V.P.; Maheshwari, P. The Convergence of Digital Twin, IoT, And Machine Learning: Transforming Data Into Action. In Digital Twin Technologies and Smart Cities; Springer: Berlin/Heidelberg, Germany, 2020; pp. 3–17. [Google Scholar]
- Glatt, M.; Sinnwell, C.; Yi, L.; Donohoe, S.; Ravani, B.; Aurich, J.C. Modeling and implementation of a digital twin of material flows based on physics simulation. J. Manuf. Syst. 2021, 58, 231–245. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, C.; Kevin, I.; Wang, K.; Huang, H.; Xu, X. Digital Twin-driven smart manufacturing: Connotation, reference model, applications and research issues. Robot. -Comput.-Integr. Manuf. 2020, 61, 101837. [Google Scholar] [CrossRef]
- Lu, Q.; Parlikad, A.K.; Woodall, P.; Don Ranasinghe, G.; Xie, X.; Liang, Z.; Konstantinou, E.; Heaton, J.; Schooling, J. Developing a digital twin at building and city levels: Case study of West Cambridge campus. J. Manag. Eng. 2020, 36, 05020004. [Google Scholar] [CrossRef]
- Cimino, C.; Negri, E.; Fumagalli, L. Review of digital twin applications in manufacturing. Comput. Ind. 2019, 113, 103130. [Google Scholar] [CrossRef]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- He, B.; Bai, K.J. Digital twin-based sustainable intelligent manufacturing: A review. Adv. Manuf. 2021, 9, 1–21. [Google Scholar] [CrossRef]
- Aheleroff, S.; Xu, X.; Zhong, R.Y.; Lu, Y. Digital twin as a service (DTaaS) in industry 4.0: An architecture reference model. Adv. Eng. Inform. 2021, 47, 101225. [Google Scholar] [CrossRef]
- Semeraro, C.; Lezoche, M.; Panetto, H.; Dassisti, M. Digital twin paradigm: A systematic literature review. Comput. Ind. 2021, 130, 103469. [Google Scholar] [CrossRef]
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital twin: Origin to future. Appl. Syst. Innov. 2021, 4, 36. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, K.; Zhang, Y. Digital twin networks: A survey. IEEE Internet Things J. 2021, 8, 13789–13804. [Google Scholar] [CrossRef]
- Bhatti, G.; Mohan, H.; Singh, R.R. Towards the future of smart electric vehicles: Digital twin technology. Renew. Sustain. Energy Rev. 2021, 141, 110801. [Google Scholar] [CrossRef]
- Negri, E.; Fumagalli, L.; Macchi, M. A review of the roles of digital twin in CPS-based production systems. Procedia Manuf. 2017, 11, 939–948. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Paz, M. Structural Dynamics: Theory and Computation; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Soares, R.d.P.; Secchi, A.R. Structural analysis for static and dynamic models. Math. Comput. Model. 2012, 55, 1051–1067. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig, R.R., Jr.; Bampton, M.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef] [Green Version]
- Goldman, R.L. Vibration analysis by dynamic partitioning. AIAA J. 1969, 7, 1152–1154. [Google Scholar] [CrossRef]
- Hou, S. Review of modal synthesis techniques and a new approach. Shock Vib. Bull. 1969, 40, 25–39. [Google Scholar]
- Dowell, E.H. Free vibrations of an arbitrary structure in terms of component modes. J. Appl. Mech. 1972, 39, 727. [Google Scholar] [CrossRef]
- Hintz, R.M. Analytical methods in component modal synthesis. AIAA J. 1975, 13, 1007–1016. [Google Scholar] [CrossRef]
- Benfield, W.; Hruda, R. Vibration analysis of structures by component mode substitution. AIAA J. 1971, 9, 1255–1261. [Google Scholar] [CrossRef]
- MacNeal, R.H. A hybrid method of component mode synthesis. Comput. Struct. 1971, 1, 581–601. [Google Scholar] [CrossRef] [Green Version]
- Rubin, S. Improved component-mode representation for structural dynamic analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- Géradin, M.; Rixen, D.J. Mechanical Vibrations: Theory and Application to Structural Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lee, H.H. Finite Element Simulations with ANSYS Workbench 18; SDC Publications: Mission, KS, USA, 2018. [Google Scholar]
- Helwany, S. Applied Soil Mechanics with ABAQUS Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- MacNeal, R.H. The NASTRAN Theoretical Manual. Scientific and Technical Information Office, National Aeronautics and Space: Washington, DC, USA, 1970; Volume 221. [Google Scholar]
- Thomson, W.T. Theory of Vibration with Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kaszynski, A. pyansys: Python Interface to MAPDL and Associated Binary and ASCII Files. 2020. Available online: https://zenodo.org/record/4009467/export/xd#.YtFQ24RBxPY (accessed on 4 April 2022).
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010; Volume 5. [Google Scholar]
- Stefani, R.T.; Shahian, B.; Savant, C.J.; Hostetter, G.H. Design of Feedback Control Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Nise, N.S. Control Systems Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Allemang, R.J.; Brown, D.L. Experimental Modal Analysis and Dynamic Component Synthesis. Volume 3. Modal Parameter Estimation; Technical Report; College of Engineering and Applied Science (CEAS)|University of Cincinnati: Cincinnati, OH, USA, 1987. [Google Scholar]
- Kuether, R.J.; Allen, M.S.; Hollkamp, J.J. Modal substructuring of geometrically nonlinear finite element models with interface reduction. AIAA J. 2017, 55, 1695–1706. [Google Scholar] [CrossRef]
- Bulirsch, R.; Stoer, J.; Stoer, J. A Theoretical Introduction to Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3. [Google Scholar]
- Calvo, M.; Montijano, J.; Randez, L. A fifth-order interpolant for the Dormand and Prince Runge-Kutta method. J. Comput. Appl. Math. 1990, 29, 91–100. [Google Scholar] [CrossRef] [Green Version]
- Engstler, C.; Lubich, C. MUR8: A multirate extension of the eighth-order Dormand-Prince method. Appl. Numer. Math. 1997, 25, 185–192. [Google Scholar] [CrossRef]
- ANSYS, M.A. Advanced analysis guide, 9. User-Programmable Features SAS, 17th ed.; IP Inc.: Wilmington, DE, USA, 2016. [Google Scholar]
- Ansys, M.A. ANSYS Mechanical APDL Theory Reference; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
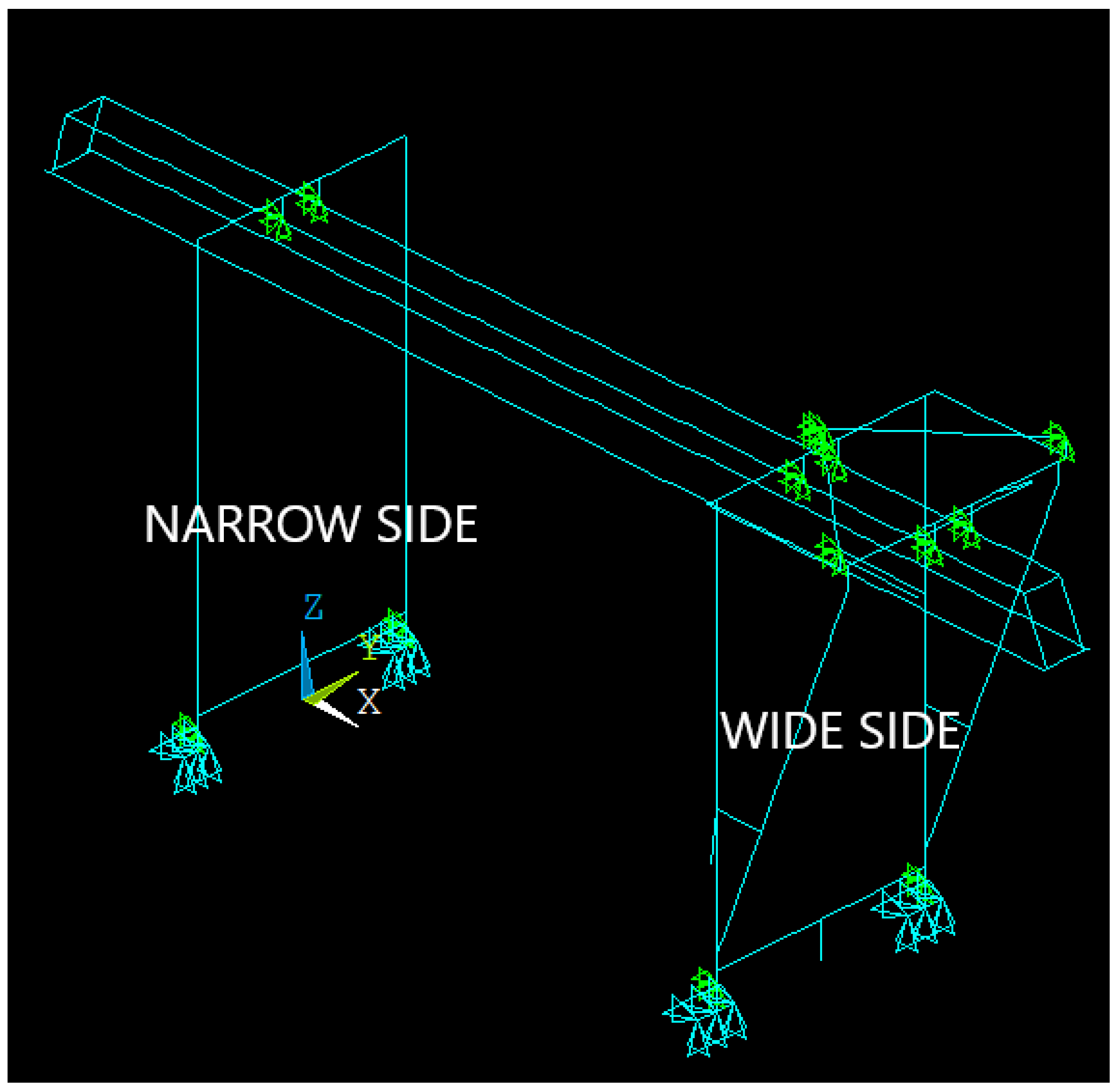
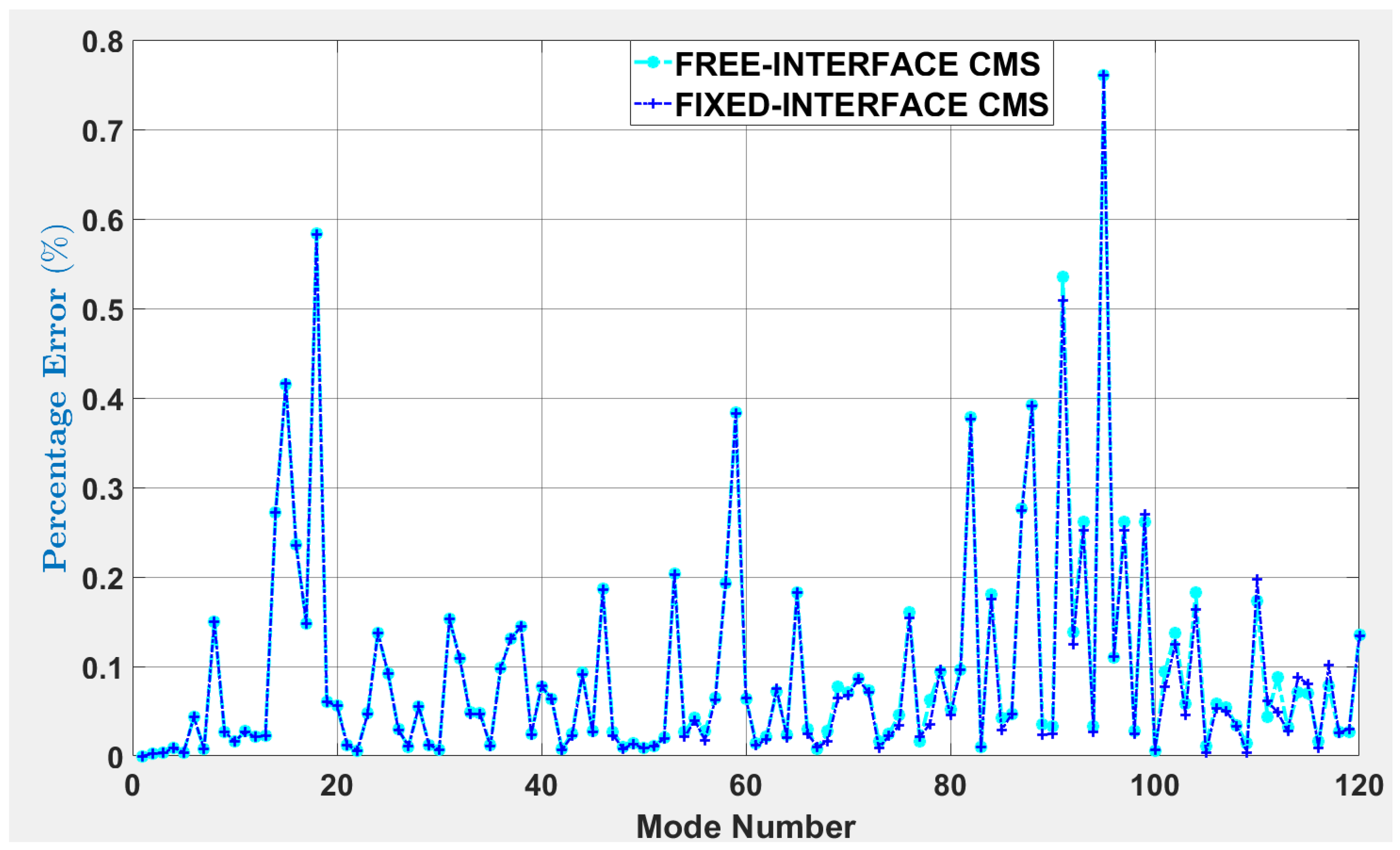
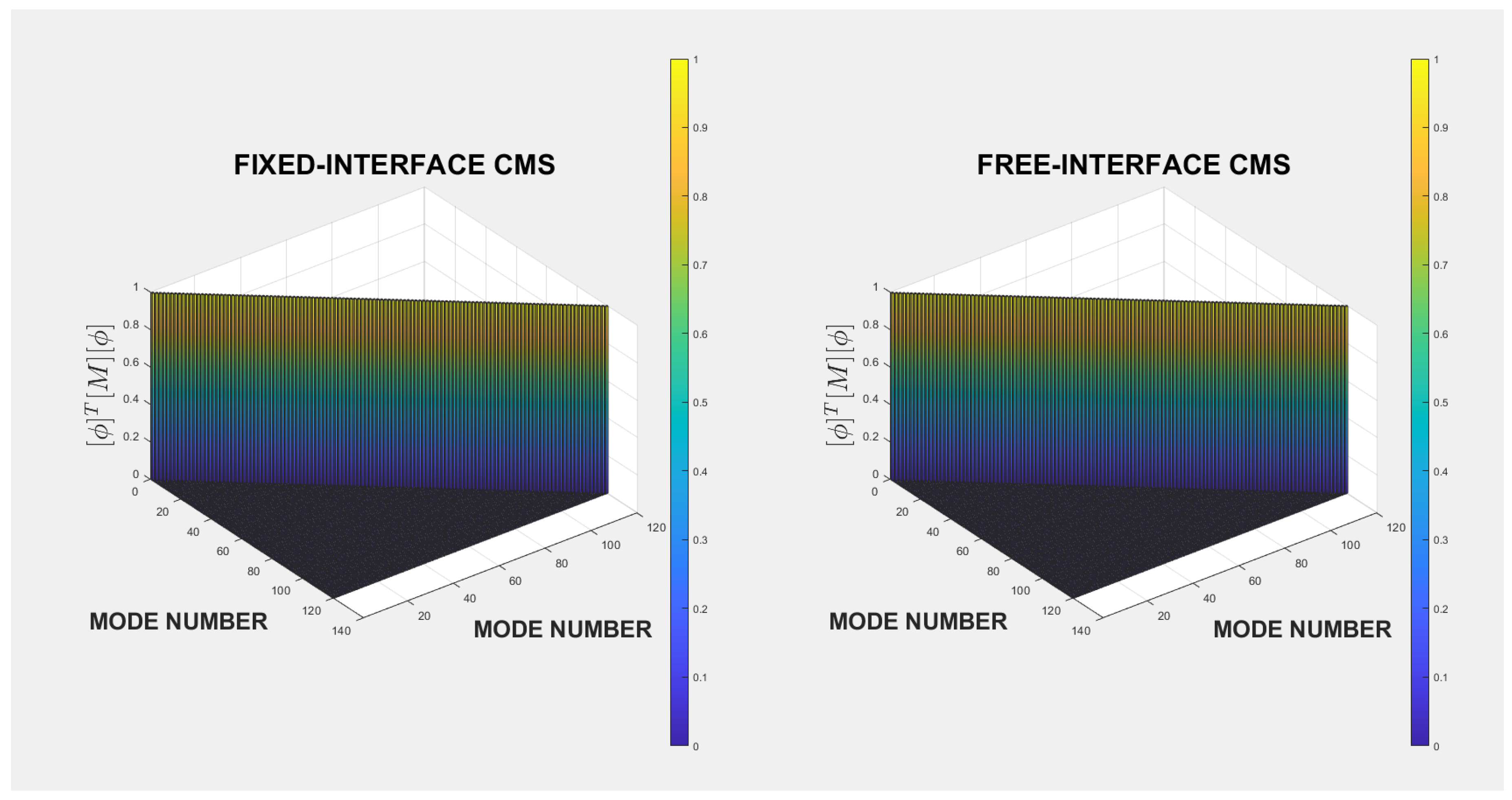
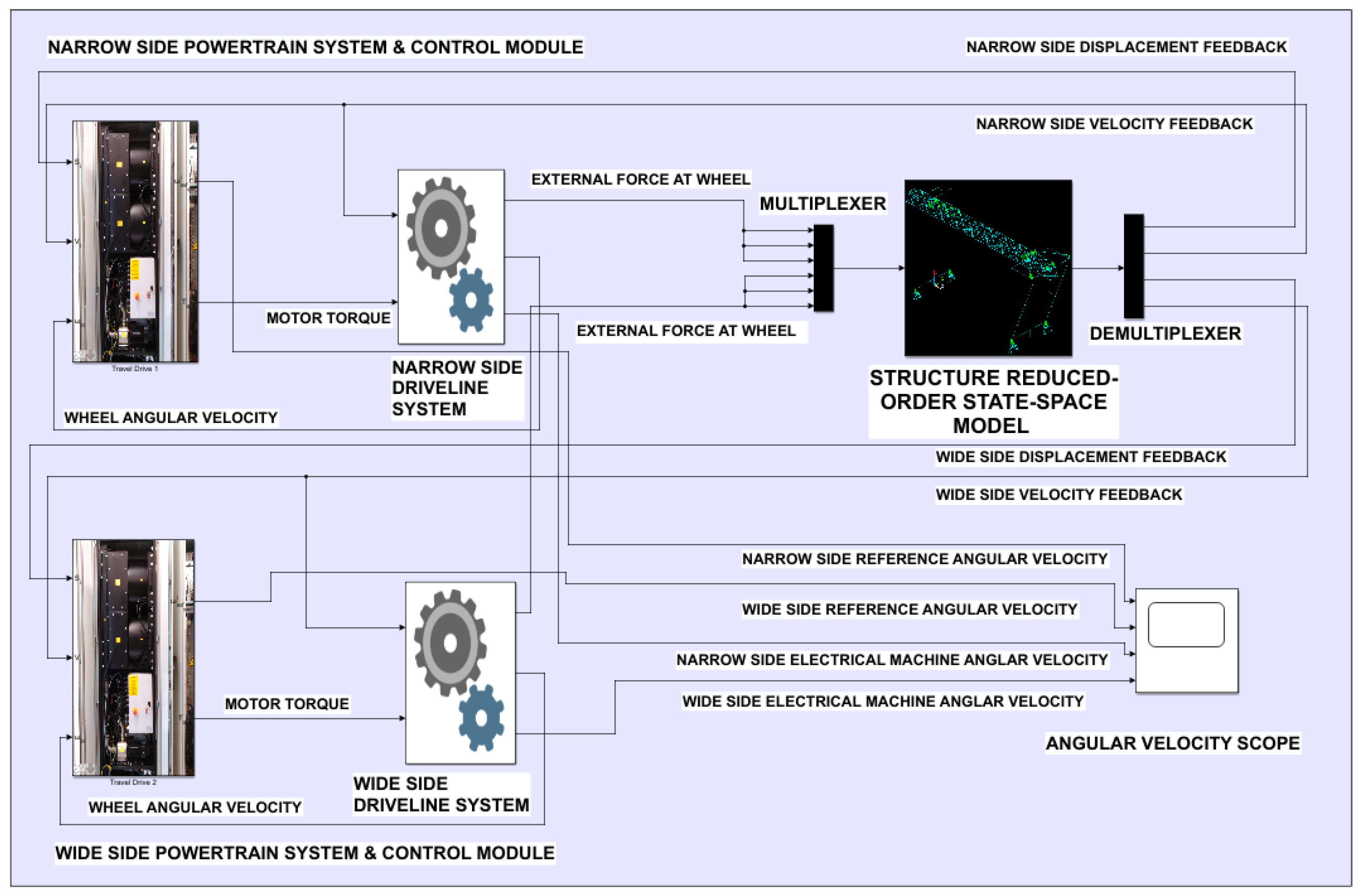


| Mode No. | FULL-ORDER | FREE-INTERFACE CMS | FIXED-INTERFACE CMS |
|---|---|---|---|
| Freq (Hz) | Freq (Hz) | Freq (Hz) | |
| 1 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 0.1857 | 0.1857 | 0.1857 |
| 3 | 0.4302 | 0.4302 | 0.4302 |
| 4 | 1.0493 | 1.0492 | 1.0492 |
| 5 | 1.1142 | 1.1142 | 1.1142 |
| 6 | 1.8422 | 1.8414 | 1.8414 |
| 7 | 2.0013 | 2.0011 | 2.0011 |
| 8 | 2.2746 | 2.2712 | 2.2712 |
| 9 | 2.4619 | 2.4612 | 2.4612 |
| 10 | 2.9458 | 2.9453 | 2.9453 |
| 11 | 3.8005 | 3.7995 | 3.7995 |
| 12 | 4.0081 | 4.0072 | 4.0072 |
| 13 | 4.2623 | 4.2613 | 4.2613 |
| 14 | 4.4271 | 4.4151 | 4.4150 |
| 15 | 4.8720 | 4.8518 | 4.8517 |
| 16 | 5.0604 | 5.0485 | 5.0485 |
| 17 | 5.1830 | 5.1753 | 5.1753 |
| 18 | 5.6314 | 5.5985 | 5.5986 |
| 19 | 5.7793 | 5.7758 | 5.7758 |
| 20 | 5.9551 | 5.9517 | 5.9518 |
| 21 | 6.1300 | 6.1293 | 6.1292 |
| 22 | 6.2820 | 6.2816 | 6.2816 |
| 23 | 6.5562 | 6.5531 | 6.5531 |
| 24 | 6.9902 | 6.9806 | 6.9806 |
| 25 | 7.2392 | 7.2325 | 7.2325 |
| 26 | 7.4208 | 7.4186 | 7.4186 |
| 27 | 7.5028 | 7.5020 | 7.5020 |
| 28 | 7.6217 | 7.6175 | 7.6175 |
| 29 | 7.7598 | 7.7588 | 7.7588 |
| 30 | 7.9304 | 7.9310 | 7.9310 |
| 31 | 7.9935 | 7.9813 | 7.9813 |
| 32 | 8.0515 | 8.0427 | 8.0427 |
| 33 | 8.3542 | 8.3501 | 8.3502 |
| 34 | 8.4016 | 8.3975 | 8.3977 |
| 35 | 8.5372 | 8.5362 | 8.5363 |
| 36 | 8.5915 | 8.5831 | 8.5831 |
| 37 | 8.6763 | 8.6649 | 8.6649 |
| 38 | 8.8309 | 8.8182 | 8.8182 |
| 39 | 9.0159 | 9.0136 | 9.0137 |
| 40 | 9.0726 | 9.0656 | 9.0655 |
| 41 | 9.1020 | 9.1078 | 9.1078 |
| 42 | 9.3330 | 9.3323 | 9.3324 |
| 43 | 9.7096 | 9.7072 | 9.7074 |
| 44 | 9.7463 | 9.7372 | 9.7374 |
| 45 | 10.0290 | 10.0262 | 10.0263 |
| 46 | 10.1870 | 10.1680 | 10.1681 |
| 47 | 10.4320 | 10.4292 | 10.4296 |
| 48 | 11.0240 | 11.0229 | 11.0231 |
| 49 | 11.9730 | 11.9713 | 11.9714 |
| 50 | 11.9930 | 11.9919 | 11.9920 |
| 51 | 12.0290 | 12.0277 | 12.0277 |
| 52 | 12.1350 | 12.1325 | 12.1326 |
| 53 | 12.4540 | 12.4287 | 12.4288 |
| 54 | 13.2190 | 13.2155 | 13.2162 |
| 55 | 13.5810 | 13.5752 | 13.5756 |
| 56 | 13.8690 | 13.8652 | 13.8666 |
| 57 | 14.2990 | 14.2898 | 14.2900 |
| 58 | 14.7240 | 14.6956 | 14.6957 |
| 59 | 14.8700 | 14.8130 | 14.8132 |
| 60 | 15.2040 | 15.1943 | 15.1942 |
| 61 | 15.3810 | 15.3788 | 15.3792 |
| 62 | 16.6140 | 16.6105 | 16.6110 |
| 63 | 16.6540 | 16.6420 | 16.6415 |
| 64 | 16.7850 | 16.7810 | 16.7815 |
| 65 | 17.0350 | 17.0039 | 17.0039 |
| 66 | 17.1120 | 17.1068 | 17.1078 |
| 67 | 17.2230 | 17.2216 | 17.2212 |
| 68 | 17.8190 | 17.8141 | 17.8161 |
| 69 | 18.3840 | 18.3698 | 18.3721 |
| 70 | 18.7200 | 18.7067 | 18.7073 |
| 71 | 18.8380 | 18.8216 | 18.8219 |
| 72 | 18.9780 | 18.9641 | 18.9645 |
| 73 | 19.4900 | 19.4869 | 19.4882 |
| 74 | 19.5310 | 19.5261 | 19.5267 |
| 75 | 19.7960 | 19.7869 | 19.7893 |
| 76 | 19.9100 | 19.8781 | 19.8793 |
| 77 | 20.3080 | 20.3112 | 20.3124 |
| 78 | 20.7510 | 20.7381 | 20.7436 |
| 79 | 21.1300 | 21.1500 | 21.1504 |
| 80 | 21.3580 | 21.3469 | 21.3482 |
| 81 | 21.5700 | 21.5492 | 21.5493 |
| 82 | 21.7170 | 21.6348 | 21.6353 |
| 83 | 21.8040 | 21.8018 | 21.8019 |
| 84 | 22.0530 | 22.0131 | 22.0144 |
| 85 | 22.3150 | 22.3055 | 22.3086 |
| 86 | 22.4830 | 22.4724 | 22.4725 |
| 87 | 22.7500 | 22.6872 | 22.6877 |
| 88 | 23.2110 | 23.1199 | 23.1202 |
| 89 | 23.3010 | 23.2927 | 23.2955 |
| 90 | 23.3880 | 23.3803 | 23.3822 |
| 91 | 24.0510 | 23.9223 | 23.9285 |
| 92 | 24.2010 | 24.1674 | 24.1707 |
| 93 | 24.2800 | 24.2165 | 24.2187 |
| 94 | 24.3390 | 24.3309 | 24.3325 |
| 95 | 24.7000 | 24.5120 | 24.5120 |
| 96 | 25.0620 | 25.0344 | 25.0341 |
| 97 | 25.1270 | 25.0614 | 25.0636 |
| 98 | 25.3970 | 25.3898 | 25.3908 |
| 99 | 25.4890 | 25.5556 | 25.5579 |
| 100 | 25.7190 | 25.7176 | 25.7208 |
| 101 | 25.7810 | 25.7567 | 25.7612 |
| 102 | 26.2300 | 26.1940 | 26.1973 |
| 103 | 26.4390 | 26.4237 | 26.4268 |
| 104 | 26.4940 | 26.4457 | 26.4505 |
| 105 | 26.8210 | 26.8180 | 26.8201 |
| 106 | 26.9660 | 26.9501 | 26.9515 |
| 107 | 27.0410 | 27.0264 | 27.0275 |
| 108 | 27.1310 | 27.1217 | 27.1219 |
| 109 | 27.2620 | 27.2582 | 27.2630 |
| 110 | 27.4920 | 27.5396 | 27.5461 |
| 111 | 27.8520 | 27.8642 | 27.8690 |
| 112 | 28.2750 | 28.2502 | 28.2612 |
| 113 | 28.4250 | 28.4160 | 28.4172 |
| 114 | 28.7100 | 28.7304 | 28.7353 |
| 115 | 28.9110 | 28.9312 | 28.9342 |
| 116 | 29.0080 | 29.0032 | 29.0053 |
| 117 | 29.3980 | 29.4209 | 29.4278 |
| 118 | 29.6380 | 29.6299 | 29.6304 |
| 119 | 29.6620 | 29.6699 | 29.6710 |
| 120 | 29.9190 | 29.8785 | 29.8789 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maulik, S.; Riordan, D.; Walsh, J. Dynamic Reduction-Based Virtual Models for Digital Twins—A Comparative Study. Appl. Sci. 2022, 12, 7154. https://doi.org/10.3390/app12147154
Maulik S, Riordan D, Walsh J. Dynamic Reduction-Based Virtual Models for Digital Twins—A Comparative Study. Applied Sciences. 2022; 12(14):7154. https://doi.org/10.3390/app12147154
Chicago/Turabian StyleMaulik, Soumya, Daniel Riordan, and Joseph Walsh. 2022. "Dynamic Reduction-Based Virtual Models for Digital Twins—A Comparative Study" Applied Sciences 12, no. 14: 7154. https://doi.org/10.3390/app12147154
APA StyleMaulik, S., Riordan, D., & Walsh, J. (2022). Dynamic Reduction-Based Virtual Models for Digital Twins—A Comparative Study. Applied Sciences, 12(14), 7154. https://doi.org/10.3390/app12147154






