Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods
Abstract
:1. Introduction
2. Materials and Methods
3. Results
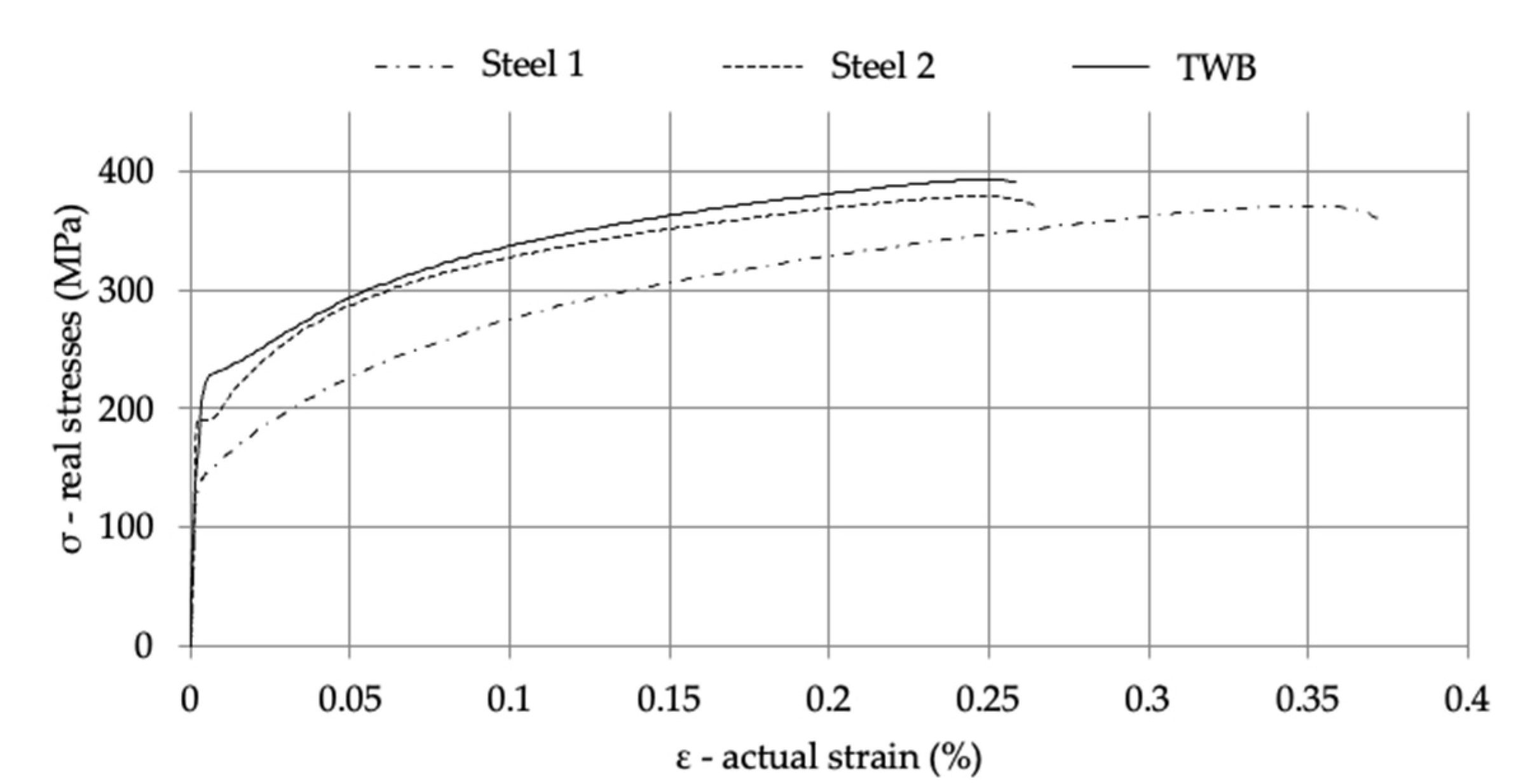
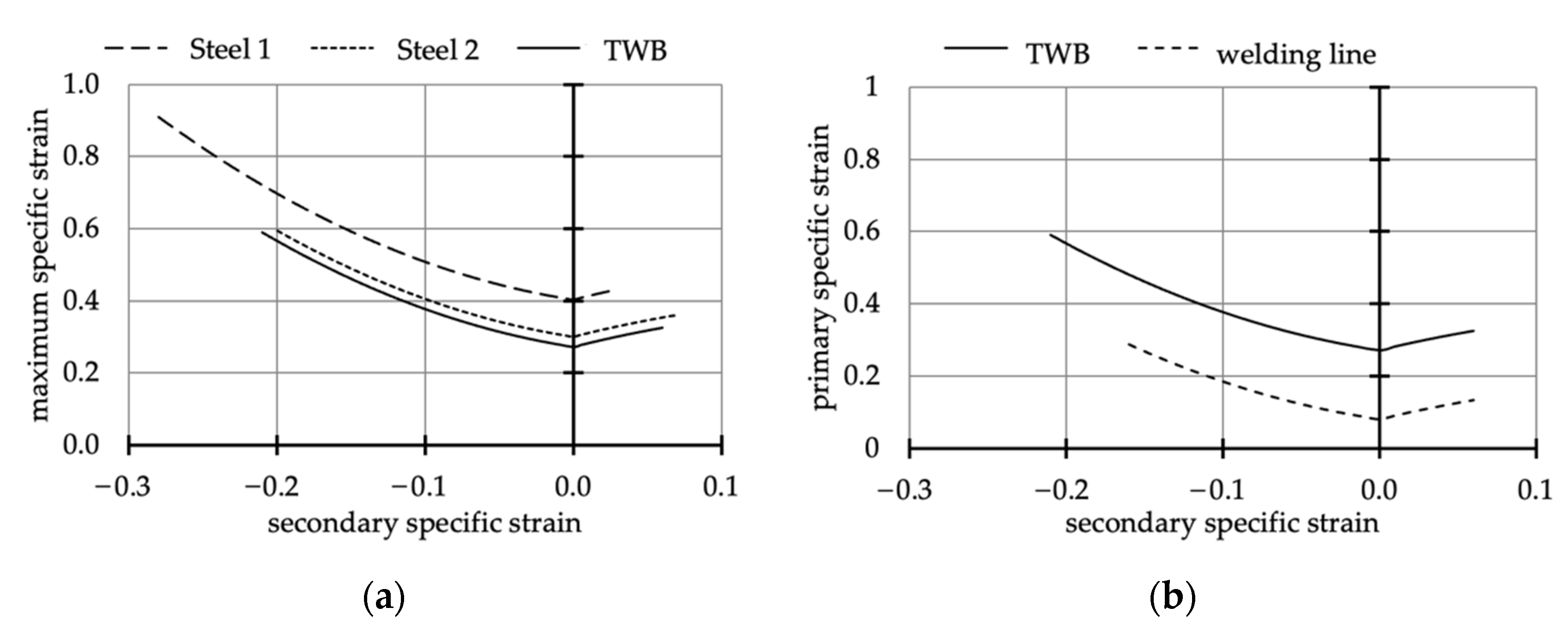
3.1. Forming Limit Curves
3.2. Steps and Conditions in Taguchi Method Application
- establishing the dimensional parameters to be monitored;
- selection of parameters that influence the studied process;
- establishing a range of variation assigning a lower and an upper limit for each of the process parameters;
- establishing the experimental plan;
- performing the simulation of the different forming alternatives established by the experimental plan;
- obtaining a polynomial function that models and estimates the influence of the process parameters, each established function being specific to each desired geometric characteristic;
- global optimization of the forming process parameters so that the geometric characteristics of the part are as close as possible to the desired nominal value;
- proofing the values obtained through the optimization process by finite element analysis and comparing the new values with the part parameters.
3.3. Application of the Taguchi Method with 23 Orthogonal Matrices
3.3.1. Selection of the Forming Process Influencing Factors
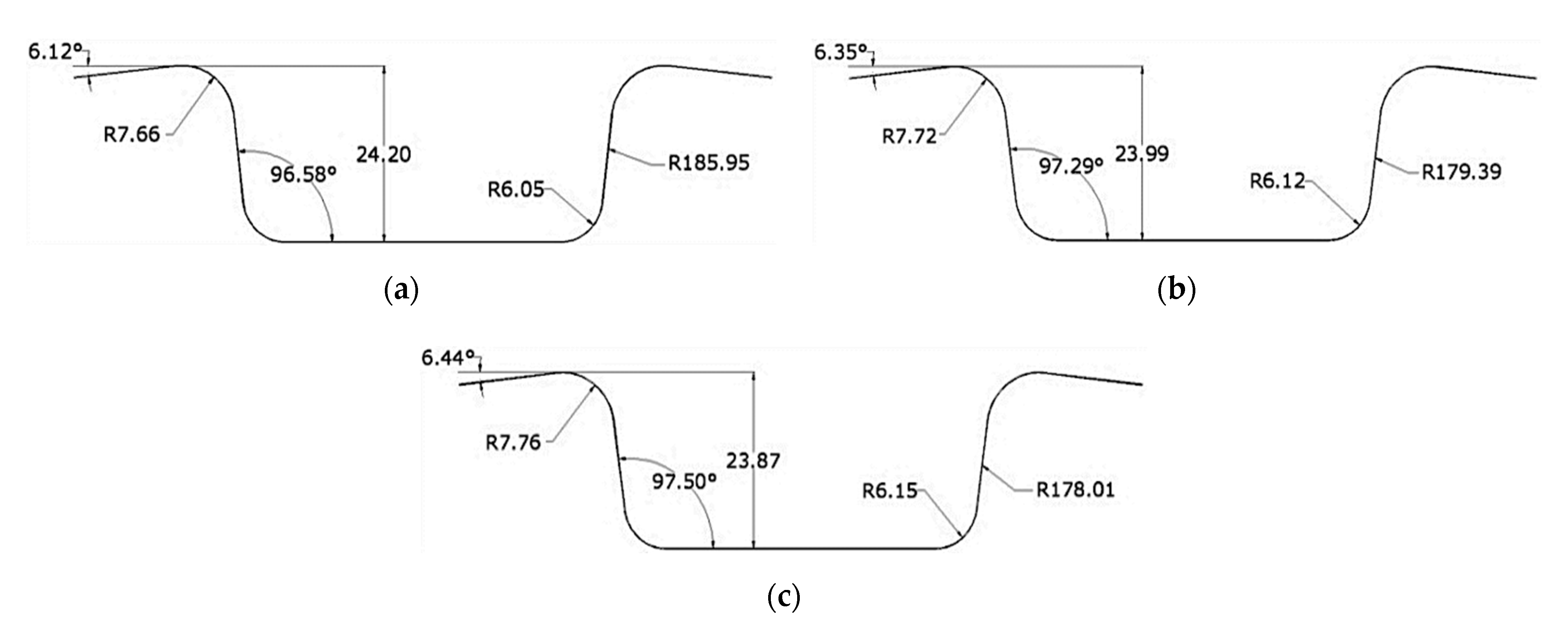
3.3.2. Experimental Plan and Establishment of the Dependency Functions
- Polynomial dependence functions corresponding to steel 1:Rm.o1 = 7.82 − 0.023F′holding − 0.11R′punch + 1.18R′dieRp.o1 = 5.22 − 0.045F′holding + 1.02R′punch − 0.03R′dirRc.o1 = 278.47 − 42.20F′holding + 38.19R′punch + 34.25R′dieθ1.o1 = 94.08 − 0.85F′holding − 0.22R′punch − 0.39R′dieθ2.o1 = 5.97 − 0.04F′holding −1.30R′punch + 0.91R′die
- Polynomial dependence functions corresponding to the weld line:Rm.cs = 7.91 − 0.022F′holding − 0.11R′punch + 1.19R′dieRp.cs = 5.28 − 0.045F′holding + 1.02R′punch − 0.03R′dieRc.cs = 268.64 − 40.72F′holding + 36.84R′punch + 33.04R′dieθ1.cs = 94.77 − 0.86F′holding − 0.23R′punch − 0.39R′dieθ2.cs = 6.18 − 0.043F′holding − 1.34R′punch + 0.94R′die
- Polynomial dependence functions corresponding to steel 2:Rm.o2 = 7.24 − 0.77F′holding + 0.63R′punch + 0.45R′dieRp.02 = 5.30 − 0.045F′holding + 1.03R′punch − 0.03R′dieRc.o2 = 266.55 − 40.4F′holding + 36.56R′punch + 32.79R′dieθ1.o2 = 94.97 − 0.86F′holding − 0.23R′punch − 0.39R′dieθ2.o2 = 6.28 − 0.045F′holding − 1.37R′punch + 0.95R′die
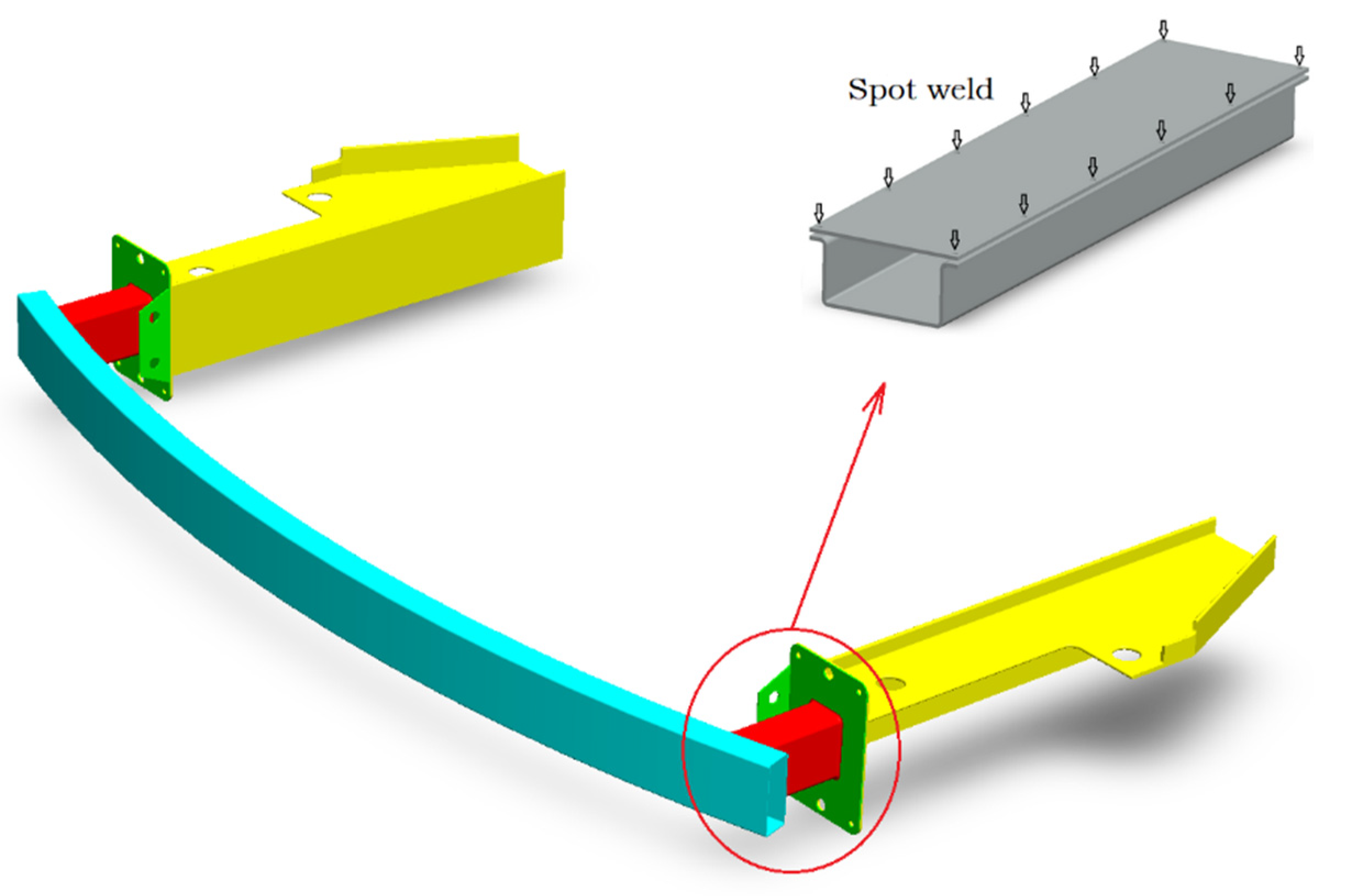
3.4. Testing Methodology of Tubular Structures and Equipment
3.5. Analysis of Thin-Walled Tubular Structures
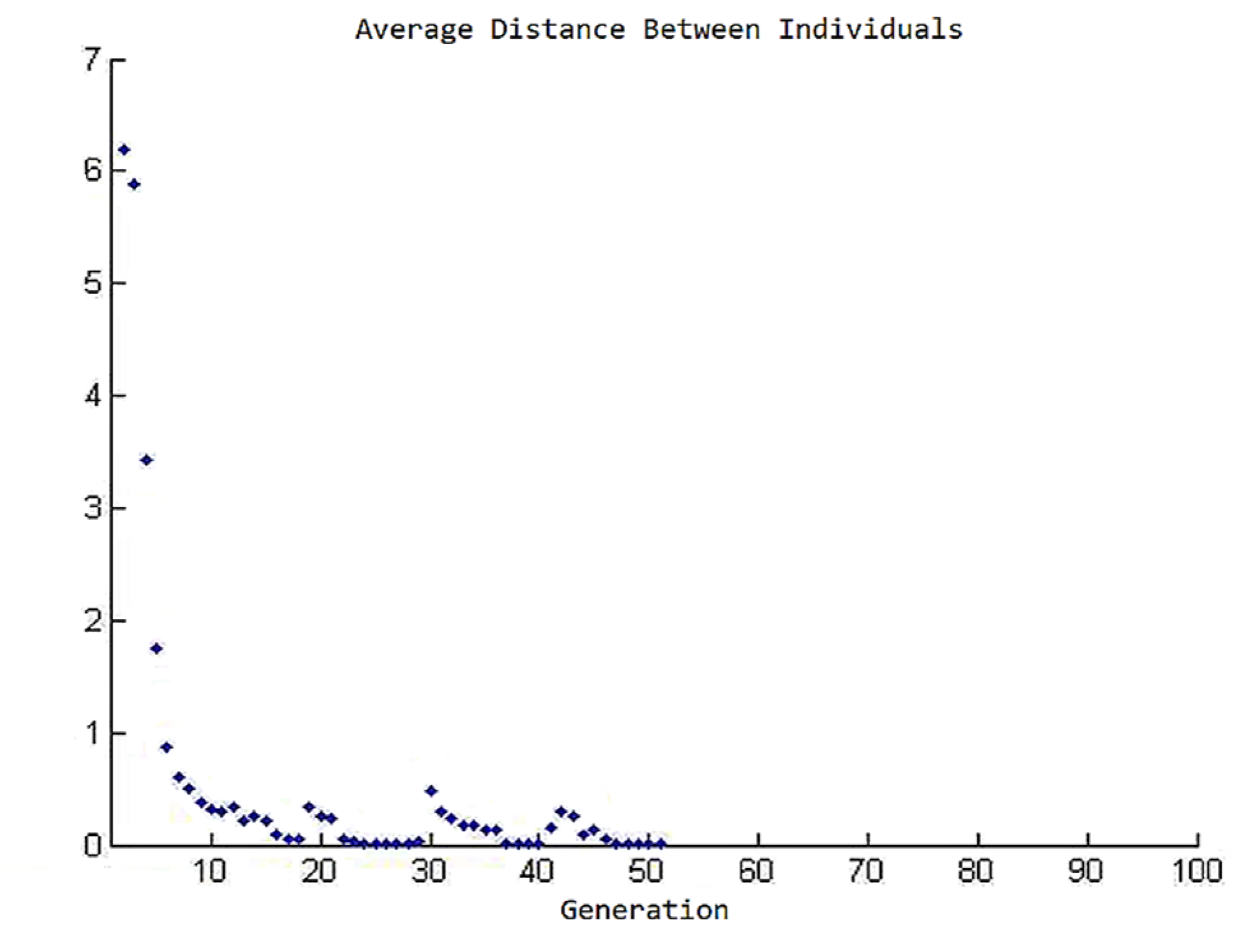
3.6. Use of Genetic Algorithms to Improve the Behavior of TWB Tubular Structures at Dynamic Impact Loading
- Evaluation is when the Genetic Algorithm calculates the value of the adequacy function for each individual of the old population.
- Selection is when the Genetic Algorithm selects individuals from a population-based on their performance. The chosen individuals will represent an intermediate population. Thus, the chromosomes of the intermediate population become the parents of the new generation.
- Recombination and modification: the Genetic Algorithm recombines and modifies selected individuals. For this purpose, the operators’ genetics of crossbreeding (recombination), mutation, and inversion are used. From an algorithmic point of view, genetic operators are methods of locally changing the solutions represented by the parents (conversion or inversion) or combining these solutions (crossover) by a gene transfer between two chromosomes.
- to express the objective function: 1. function y = simple_fitness (x); 2. y = f(x)
- to express the constraint function: 1. function [c, ceq] = simple_constraint (x); 2. c = [constraint 1]; 3. ceq = [].
4. Discussion
5. Conclusions
- the holding force necessary to obtain parts with geometric parameters as close as possible to the nominal value was increased by an average of 52.9%, from an initial value of 45 kN to a final average value of 68.84 kN;
- the connection radius of the die was reduced, depending on each material in the welded assembly subjected to forming, as follows: for steel area 1, the connection radius of the die was decreased by 8.42%, from an initial value of 7 mm to 6.41 mm; for steel area 2, the connection radius of the die was decreased by 10.71%, from an initial value of 7 mm to 6.25 mm; for the weld line area, the connection radius of the die was decreased by 8.85%, from an initial value of 7 mm to 6.38 mm;
- the connection radius of the punch was reduced, depending on each material in the welded assembly subjected to forming, as follows: for steel area 1, the connection radius of the punch was reduced by 5.4%, from an initial value of 5 mm to 4.73 mm; for steel area 2, the connection radius of the punch was reduced by 9%, from an initial value of 5 mm to 4.55 mm; for the weld line area, the connection radius of the punch was reduced by 6.2%, from an initial value of 5 mm to 4.69 mm;
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Auto/Steel PARTNERSHIP. TWB Applications and Manufacturing; Auto/Steel Partnership: Southfield, MI, USA, 2001; pp. 9, 12, 43. [Google Scholar]
- Melbourne, S.; Noel, J.; Baron, J. Tailor Welded Blanks Design and Manufacturing Manual; General Motors: Detroit, MI, USA, 1995. [Google Scholar]
- Kumar, A.; Gautam, V. Formability of tailor welded blanks of high strength steel: A review. Mater. Today Proc. 2021, 46, 6547–6551. [Google Scholar] [CrossRef]
- Lu, R.; Gao, W.; Hu, X.; Liu, W.; Li, Y.; Liu, X. Crushing analysis and crashworthiness optimization of tailor rolled tubes with variation of thickness and material properties. Int. J. Mech. Sci. 2018, 136, 67–84. [Google Scholar] [CrossRef]
- Bartczak, B.; Gierczyzka, D.; Gronostajski, Z.; Polak, S.; Tobota, A. The use of thin-walled sections for energy absorbing components: A review. Arch. Civ. Mech. Eng. 2010, 10, 5–19. [Google Scholar] [CrossRef]
- Peroni, L.; Avalle, M.; Belingardi, G. Comparison of the energy absorption capability of crash boxes assembled by spot-weld and continuous joining techniques. Int. J. Impact Eng. 2009, 36, 498–511. [Google Scholar] [CrossRef]
- Zou, Y.Y.; Zou, K.Z.; Liu, H.H.; Zhou, D.L. Laser-based precise measurement of tailor welded blanks: A case study. Int. J. Adv. Manuf. Technol. 2020, 107, 3795–3805. [Google Scholar] [CrossRef]
- Kim, M.; Bae, G.; Park, N.; Song, J.H. Springback Reduction of Ultra-High-Strength Martensitic Steel Sheet by Electrically Single-Pulsed Current. Materials 2022, 15, 2373. [Google Scholar] [CrossRef]
- Zhang, X.G.; Li, L.Q.; Chen, Y.B.; Zhu, X.C.; Ji, S.J. Numerical Simulation Analysis of Dual-Beam Laser Welding of Tailored Blanks with Different Thicknesses. Metals 2019, 9, 135. [Google Scholar] [CrossRef] [Green Version]
- Gautam, V.; Kumar, D.R. Experimental and numerical investigations on springback in V-bending of tailor-welded blanks of interstitial free steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 2178–2191. [Google Scholar] [CrossRef]
- Zhang, Y.; Lang, L.; Wang, Y.; Chen, H.; Du, J.; Jiao, Z.; Wang, L. Spring Back Behaviour of Large Multi-Feature Thin-Walled Part in Rigid-Flexible Sequential Loading Forming Process. Materials 2022, 15, 2608. [Google Scholar] [CrossRef]
- Liavoli, R.P.; Gorji, H.; Bakhshi-Jooybari, M.; Mirnia, M.J. Investigation on Formability of Tailor-Welded Blanks in Incremental Forming. Int. J. Eng. 2020, 33, 906–915. [Google Scholar] [CrossRef]
- Gautam, V.; Raut, V.M.; Kumar, D.R. Analytical prediction of springback in bending of tailor-welded blanks incorporating effect of anisotropy and weld zone properties. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2018, 232, 294–306. [Google Scholar] [CrossRef]
- Saito, M.; Nakazawa, Y.; Otsuka, K.; Yasuyama, M.; Tokunaga, M.; Yoshida, T.; Hiwatashi, S. Effect of Weld Line Direction on Tensile Deformation Behaviour—Development of Forming Technology for Tailor Welded Blank Application—2nd Report. Mater. Trans. 2020, 61, 1760–1766. [Google Scholar] [CrossRef]
- Sun, G.Y.; Tan, D.D.; Lv, X.J.; Yan, X.L.; Li, Q.; Huang, X.D. Multi-objective topology optimization of a vehicle door using multiple material tailor-welded blank (TWB) technology. Adv. Eng. Softw. 2018, 124, 106029. [Google Scholar] [CrossRef]
- Moayedi, H.; Darabi, R.; Ghabussi, A.; Habibi, M.; Foong, L.K. Weld orientation effects on the formability of tailor welded thin steel sheets. Thin-Walled Struct. 2020, 149, 106669. [Google Scholar] [CrossRef]
- Kahhal, P.; Jung, J.; Hur, Y.C.; Moon, Y.H.; Kim, J.H. Neural Network-Based Multi-Objective Optimization of Adjustable Drawbead Movement for Deep Drawing of Tailor-Welded Blanks. Materials 2022, 15, 1430. [Google Scholar] [CrossRef]
- Kong, X.; Chu, X.; Chen, C.; Wang, Y.; Liu, P.; Wang, Z. Comparative Investigation of the Experimental Determination of AA5086 FLCs under Different Necking Criteria. Materials 2021, 14, 3685. [Google Scholar] [CrossRef]
- Mahalle, G.; Kotkunde, N.; Gupta, A.K.; Singh, S.K. Cowper-Symonds Strain Hardening Model for Flow Behaviour Of Inconel 718 Alloy. Mater. Today-Proceeding 2019, 18, 2796–2801. [Google Scholar] [CrossRef]
- Mennecart, T.; Hassan, H.; Guner, A.; Khalifa, N.; Hosseini, M. Deep Drawing of High-Strength Tailored Blanks by Using Tailored Tools. Materials 2016, 9, 77. [Google Scholar] [CrossRef] [Green Version]
- Mooli, H.; Seeram, S.R.; Goteti, S.; Boggarapu, N.R. Optimal weld bead profiles in the conduction mode LBW of thin Ti-6Al-4V alloy sheets. AIMS Mater. Sci. 2021, 8, 698–715. [Google Scholar] [CrossRef]
- Kondo, M.Y.; Pinheiro, C.; Souza, J.V.C.; Ribeiro, M.V.; Alves, M.C.S. Optimizing cutting parameters for cutting power and roughness in VAT 32(R) turning with an experimental Al2O3-MgO ceramic tool using Taguchi’s method. Procedia CIRP 2018, 77, 610–613. [Google Scholar] [CrossRef]
- Sathishkumar, T.P.; Sathishkumar, S.; Bhuvaneshkumar, K.; Sanjay, M.R.; Siengchin, S. Crashworthiness characterization of jute fibre woven mat reinforced epoxy composite tube for structural application using Taguchi’s method. Int. J. Crashworthiness 2021, 1–17. [Google Scholar] [CrossRef]
- Guo, P.F.; Wang, X.Z.; Han, Y.S. The enhanced genetic algorithms for the optimization design. In Proceedings of the 3rd International Conference on Biomedical Engineering and Informatics, Yantai, China, 16–18 October 2010; pp. 2990–2994. [Google Scholar] [CrossRef]
- Ding, C.C.; Chen, L.; Zhong, B.R. Exploration of intelligent computing based on improved hybrid genetic algorithm. J. Netw. Softw. Tools Appl. 2019, 22, S9037–S9045. [Google Scholar] [CrossRef]
- Zhang, J.M. The application research of genetic algorithm. In Proceedings of the 3rd International Workshop on Materials Engineering & Computer Sciences, Jinan, China, 27–28 January 2018; Volume 78, pp. 138–141. [Google Scholar] [CrossRef]
- Lilinc, M.; Caicedo, J.M. Finding Plausible Optimal Solutions in Engineering Problems Using an Adaptive Genetic Algorithm. Adv. Civ. Eng. 2019, 20, 7475156. [Google Scholar] [CrossRef]
- Nautiyal, L.; Shivach, P.; Ram, M. Optimal designs by means of genetic algorithms. In Soft Computing Techniques and Applications in Mechanical Engineering; IGI Global: Hershey, PA, USA, 2018; pp. 151–161. [Google Scholar] [CrossRef]
- Kusztelak, G.; Lipowski, A.; Kucharski, J. Population Symmetrisation in Genetic Algorithms. Appl. Sci. 2022, 12, 5426. [Google Scholar] [CrossRef]
- Yan, C.; Li, M.X.; Liu, W. Application of Improved Genetic Algorithm in Function Optimization. J. Inf. Sci. Eng. 2019, 35, 1299–1309. [Google Scholar] [CrossRef]






| Chemical Composition wt.% | ||||||||
|---|---|---|---|---|---|---|---|---|
| C | Si | Mn | P | S | Al | Ti | N | |
| Steel 1 | 0.002 | 0.006 | 0.097 | 0.01 | 0.01 | 0.029 | 0.057 | 0.0032 |
| Steel 2 | 0.028 | 0.009 | 0.25 | 0.029 | 0.011 | 0.053 | 0.001 | - |
| Material | Sheet Thickness mm | Welding Type | Welding Line Width mm | Welding Line Average Thickness mm | Section Area of Weld Line mm2 |
|---|---|---|---|---|---|
| Steel 1 | 0.75 | Laser | 1.08 | 0.72 | 0.78 |
| Steel 2 | 0.70 |
| Material | Youngs Modulus ×105 MPa | Ys MPa | UTS MPa | Total Strain % | Resistance Coefficient K | Anisotropy Index r | Hardening Index n |
|---|---|---|---|---|---|---|---|
| Steel 1 | 1.6317 | 140.46 | 370.95 | 37.22 | 490.6 | 1.79 | 0.25 |
| Steel 2 | 2.0417 | 191.43 | 378.47 | 26.51 | 502.9 | 2.21 | 0.19 |
| TWB | 2.1199 | 230.35 | 392.88 | 25.82 | 514 | 2.69 | 0.17 |
| Parameter | Initial Value | Minimum Value (−1) | Maximum Value (+1) |
|---|---|---|---|
| Holding force (Fholding) kN | 45 | 45 | 75 |
| Die radius (Rdie) mm | 7 | 6 | 8 |
| Punch radius (Rpunch) mm | 5 | 4 | 6 |
| 1st Factor Holding Force (kN) | 2nd Factor Punch Radius (mm) | 3rd Factor Die Radius (mm) | |
|---|---|---|---|
| 1 | 1 | 2 | 2 |
| 2 | 2 | 1 | 2 |
| 3 | 1 | 1 | 1 |
| 4 | 2 | 2 | 1 |
| Rm (mm) | Rp (mm) | Rc (mm) | θ1° | θ2° | |
|---|---|---|---|---|---|
| 1 | 6.51 | 6.22 | 240.21 | 93.39 | 3.73 |
| 2 | 9.09 | 4.13 | 232.33 | 93.06 | 8.14 |
| 3 | 8.91 | 6.25 | 393.13 | 94.32 | 5.62 |
| 4 | 6.78 | 4.28 | 248.23 | 95.55 | 6.41 |
| Rm (mm) | Rp (mm) | Rc (mm) | θ1° | θ2° | |
|---|---|---|---|---|---|
| 1 | 6.58 | 6.29 | 231.73 | 94.07 | 3.86 |
| 2 | 9.19 | 4.18 | 224.13 | 93.74 | 8.42 |
| 3 | 9.01 | 6.32 | 379.25 | 95.01 | 5.82 |
| 4 | 6.85 | 4.33 | 239.47 | 96.25 | 6.63 |
| Rm (mm) | Rp (mm) | Rc (mm) | θ1° | θ2° | |
|---|---|---|---|---|---|
| 1 | 6.65 | 6.32 | 229.92 | 94.27 | 3.92 |
| 2 | 9.29 | 4.20 | 222.38 | 93.94 | 8.55 |
| 3 | 9.10 | 6.35 | 376.29 | 95.21 | 5.91 |
| 4 | 6.93 | 4.35 | 237.60 | 96.45 | 6.74 |
| Parameter | R′holding | R′punch | R′die | Calculated Values | Simulation Values | Error (%) |
|---|---|---|---|---|---|---|
| Rd.s1 | 0 | 0 | 0 | 7.55 (mm) | 7.91 (mm) | 4.77 |
| Rp.s1 | 0 | 0 | 0 | 6.16 (mm) | 6.41 (mm) | 4.06 |
| Rc.s1 | 0 | 0 | 0 | 308 (mm) | 323.1 (mm) | 4.90 |
| θ1.s1 | 0 | 0 | 0 | 92.61° | 93.9° | 1.39 |
| θ2.s1 | 0 | 0 | 0 | 5.44° | 5.17° | −4.96 |
| Parameter | R′holding | R′punch | R′die | Calculated Values | Simulation Values | Error (%) |
|---|---|---|---|---|---|---|
| Rd.s1 | 0 | 0 | 0 | 7.86 (mm) | 8.01 (mm) | 1.85 |
| Rp.s1 | 0 | 0 | 0 | 6.23 (mm) | 6.48 (mm) | 4.07 |
| Rc.s1 | 0 | 0 | 0 | 297.82 (mm) | 311.53 (mm) | 4.60 |
| θ1.s1 | 0 | 0 | 0 | 93.28° | 94.59° | 1.40 |
| θ2.s1 | 0 | 0 | 0 | 5.64° | 5.36° | −4.90 |
| Parameter | R′holding | R′punch | R′die | Calculated Values | Simulation Values | Error (%) |
|---|---|---|---|---|---|---|
| Rd.s1 | 0 | 0 | 0 | 7.96 (mm) | 8.09 (mm) | 1.65 |
| Rp.s1 | 0 | 0 | 0 | 6.26 (mm) | 6.52 (mm) | 4.09 |
| Rc.s1 | 0 | 0 | 0 | 295.45 (mm) | 309.27 (mm) | 4.68 |
| θ1.s1 | 0 | 0 | 0 | 93.48° | 94.80° | 1.41 |
| θ2.s1 | 0 | 0 | 0 | 5.72° | 5.44° | −4.84 |
| Objective Function | Minimum Value of ω | R′holding | R′punch | R′die | Rd | Rp | Rc | θ1 | θ2 |
|---|---|---|---|---|---|---|---|---|---|
| ωS1—steel 1 | 106.27 | +1.496 | −0.214 | +3.056 | 7.583 | 5.438 | 458.690 | 92.890 | 1.835 |
| ωwl—welding line | 127.11 | 7.589 | 5.441 | 460.711 | 92.898 | 1.840 | |||
| ωS2—steel 2 | 174.44 | 7.591 | 5.439 | 462.727 | 92.900 | 1.840 |
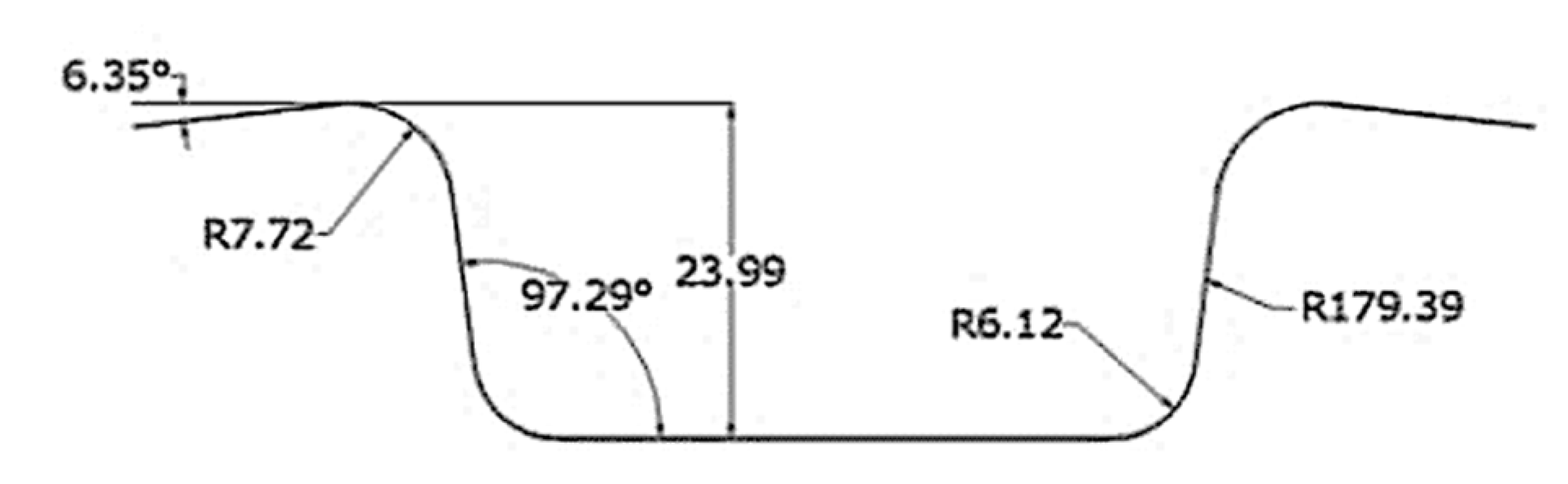
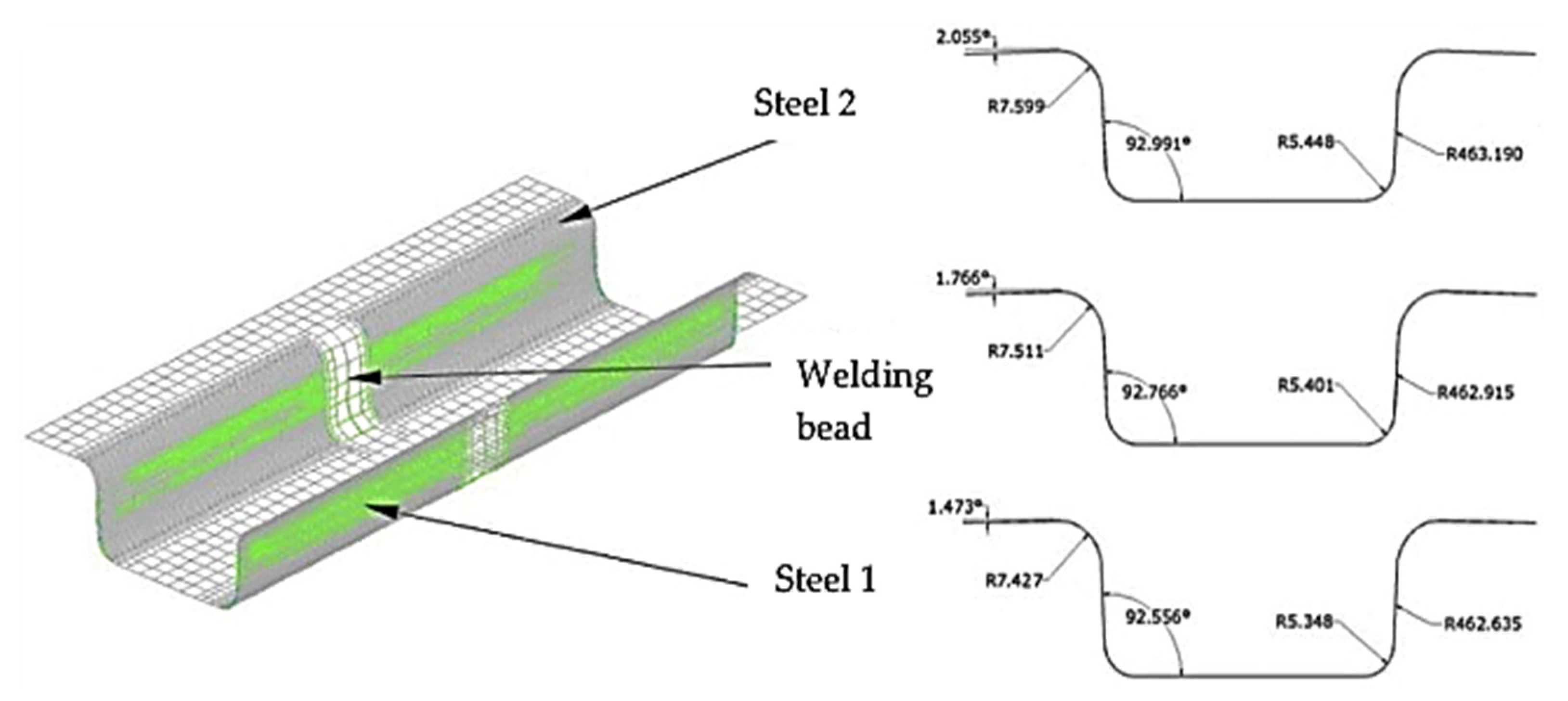
| Material | Optimized Parameters of the Tools | Measured Parameters of the Part | ||||||
|---|---|---|---|---|---|---|---|---|
| Fholding | Rpunch | Rdie | Rd | Rp | Rc | θ1° | θ2° | |
| Steel 1 | 68.21 | 4.73 | 6.41 | 7.427 | 5.348 | 462.635 | 92.556 | 1.473 |
| Welding line | 68.88 | 4.69 | 6.38 | 7.511 | 5.401 | 462.915 | 92.776 | 1.766 |
| Steel 2 | 69.45 | 4.55 | 6.25 | 7.599 | 5.448 | 463.190 | 92.991 | 2.055 |
| Parameter | Value |
|---|---|
| Specific energy absorption—Ase [J/g] | 39.507 |
| The mass of the structure—m [g] | 300.03 |
| Deformation stroke efficiency—Es | 0.5066 |
| Maximum initial force—Fmax [kN] | 17.726 |
| Parameter | Fmax [kN] | Ea [J] | Fm [kN] | Ase [J/g] | EF | Es | Rtwb |
|---|---|---|---|---|---|---|---|
| Value | 17.7260 | 1185.32 | 11.681 | 3.9507 | 0.659 | 0.5066 | 0.5863 |
| Total Height H | Steel 1 Area Height S1 | Steel 2 Area Height S2 | Width L | Section l1 × l2 | |
|---|---|---|---|---|---|
| Value (mm) | 200 | 82 | 117 | 100 | 50 × 50 |
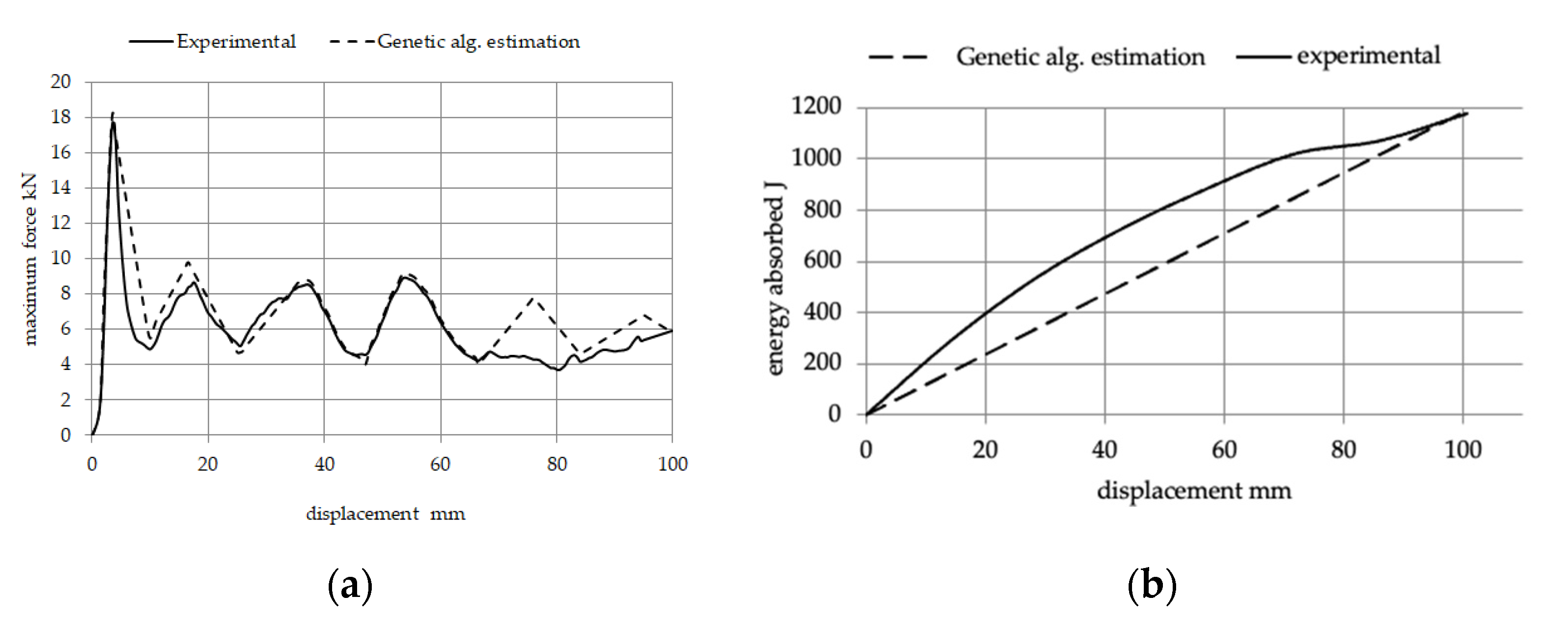
| Parameter | Fmax (kN) | Ea (J) | Fm (kN) | Ase (J/g) | EF | Es |
|---|---|---|---|---|---|---|
| Estimated values | 17.726 | 1185.32 | 11.681 | 3.950 | 0.659 | 0.506 |
| Experimental values | 18.221 | 1177.26 | 11.702 | 3.923 | 0.642 | 0.503 |
| Difference % | 2.97 | −0.68 | 0.18 | −0.68 | −2.54 | −0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ciubotariu, V.A.; Radu, M.C.; Herghelegiu, E.; Zichil, V.; Grigoras, C.C.; Nechita, E. Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods. Appl. Sci. 2022, 12, 6794. https://doi.org/10.3390/app12136794
Ciubotariu VA, Radu MC, Herghelegiu E, Zichil V, Grigoras CC, Nechita E. Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods. Applied Sciences. 2022; 12(13):6794. https://doi.org/10.3390/app12136794
Chicago/Turabian StyleCiubotariu, Vlad Andrei, Maria Crina Radu, Eugen Herghelegiu, Valentin Zichil, Cosmin Constantin Grigoras, and Elena Nechita. 2022. "Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods" Applied Sciences 12, no. 13: 6794. https://doi.org/10.3390/app12136794
APA StyleCiubotariu, V. A., Radu, M. C., Herghelegiu, E., Zichil, V., Grigoras, C. C., & Nechita, E. (2022). Structural and Behaviour Optimization of Tubular Structures Made of Tailor Welded Blanks by Applying Taguchi and Genetic Algorithms Methods. Applied Sciences, 12(13), 6794. https://doi.org/10.3390/app12136794










