Evaluating Effective Dose: A Comparison of Methods Based on Organ Dose Calculations versus Dose-Length Product and Monte Carlo Simulation
Abstract
:1. Introduction
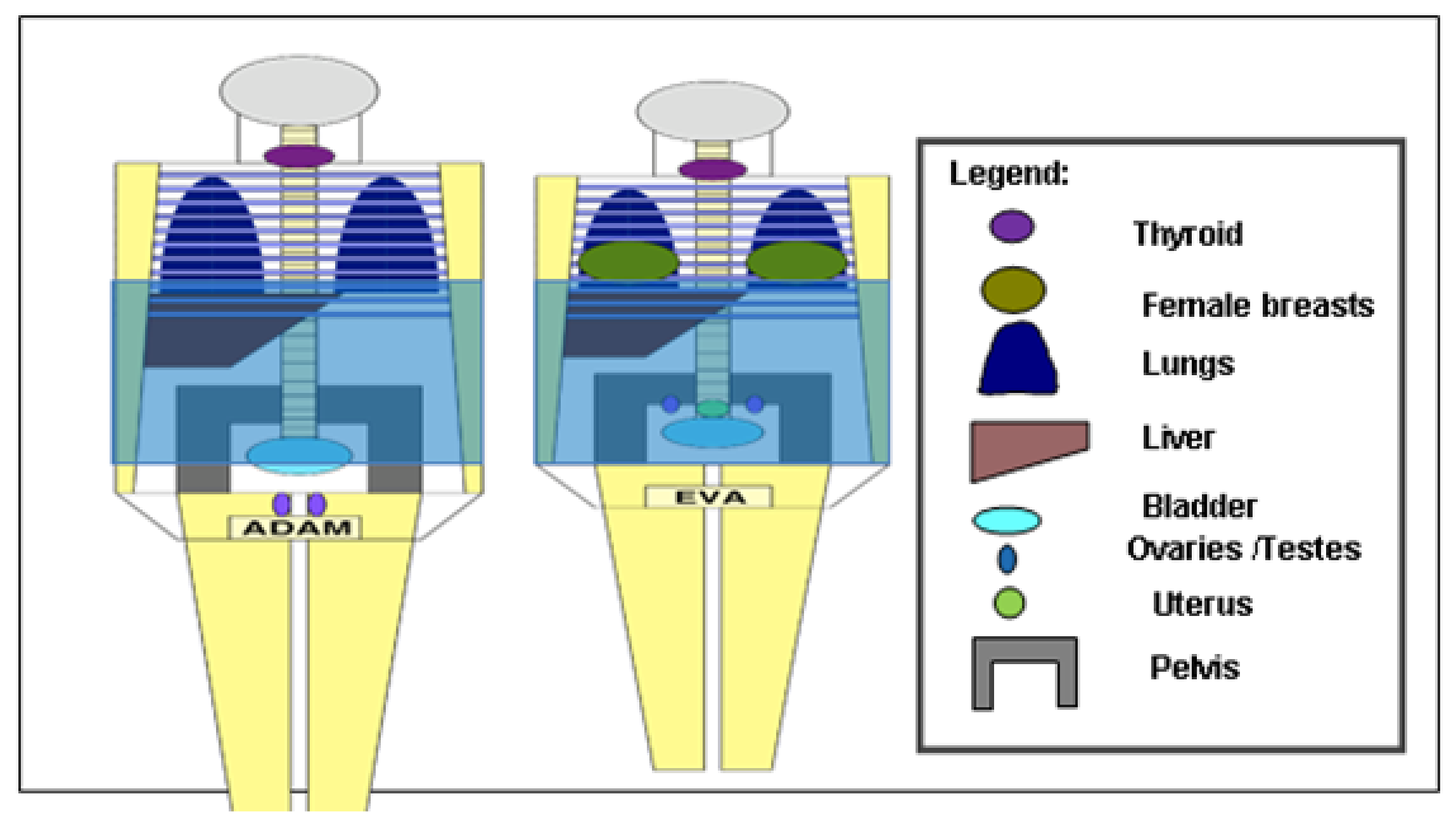
2. Materials and Methods
Calculation of Effective Dose (Ed)
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, R.; Liu, X.; He, L.; Zhou, P.-K. Radiation Exposure Associated With Computed Tomography in Childhood and the Subsequent Risk of Cancer: A Meta-Analysis of Cohort Studies. Dose-Response 2020, 18, 1559325820923828. [Google Scholar] [CrossRef] [PubMed]
- Albert, J.M. Radiation Risk From CT: Implications for Cancer Screening. Am. J. Roentgenol. 2013, 201, W81–W87. [Google Scholar] [CrossRef] [PubMed]
- Abuelhia, E. Awareness of ionizing radiation exposure among junior doctors and senior medical students in radiological investigations. J. Radiol. Prot. 2016, 37, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Abuelhia, E.; Alghamdi, A. Evaluation of arising exposure of ionizing radiation from computed tomography and the associated health concerns. J. Radiat. Res. Appl. Sci. 2020, 13, 295–300. [Google Scholar] [CrossRef] [Green Version]
- International Commission on Radiological Protection. Managing Patients’ Dose in Computer Tomography—International Commission on Radiological Protection Publication 87. In Annals of the ICRP 30; Pergamon: Oxford, UK, 2000; No. 4. [Google Scholar]
- Golding, S.J.; Shrimpton, P.C. Radiation dose in CT: Are we meeting the challenge? Br. J. Radiol. 2002, 75, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Kalender, W. Dose management in multi–slice spiral computed tomography. Eur. Radiol. Suppl. 2004, 14, 40–49. [Google Scholar] [CrossRef]
- Huda, W. Medical radiation dosimetry. In Syllabus: Categorical Course in Diagnostic Radiology: From Invisible to Visible—The Science and Practice of X-ray Imaging and Radiation Dose Optimizatio; Radiological Society of North America: Oak Brook, IL, USA, 2006; pp. 29–40. [Google Scholar]
- Martin, C. Effective dose in medicine. Ann. ICRP 2020, 49 (Suppl. 1), 126–140. [Google Scholar] [CrossRef] [PubMed]
- Newman, B.; Ganguly, A.; Kim, J.-E.; Robinson, T. Comparison of Different Methods of Calculating CT Radiation Effective Dose in Children. Am. J. Roentgenol. 2012, 199, W232–W239. [Google Scholar] [CrossRef] [PubMed]
- Inoue, Y.; Yonekura, Y.; Nagahara, K.; Uehara, A.; Ikuma, H. Conversion from dose-length product to effective dose in computed tomography venography of the lower extremities. J. Radiol. Prot. 2022, 42, 011521. [Google Scholar] [CrossRef] [PubMed]
- De Mattia, C.; Campanaro, F.; Rottoli, F.; Colombo, P.E.; Pola, A.; Vanzulli, A.; Torresin, A. Patient organ and effective dose estimation in CT: Comparison of four software applications. Eur. Radiol. Exp. 2020, 4, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nenot, J.-C.; Brenot, J.; Laurier, D.; Rannou, A.; Thierry, D. ICRP Publication 103 The 2007 Recommendations of the International Commission on Radiological Protection (INIS-FR--18-0662); Institut de Radioprotection et de Surete Nucleaire: Fontenay-aux-Roses, France, 2009. [Google Scholar]
- International Commission on Radiological Protection. Recommendations of the international commission on radiological protection. Ann. ICRP 1991, 21, 60. [Google Scholar]
- International Commission on Radiological Protection. Recommendations of the international commission on radiological protection. Ann. ICRP 2007, 37, 103. [Google Scholar]
- Image Gently. Image Gently Web Site. 2016. Available online: http://www.pedrad.org/associations/5364/ig/ (accessed on 5 March 2022).
- International Commission on Radiation Measurements and Units. Radiation Dose and Image Quality Assessment: In Computer Tomography. J. ICRU 12. ICRU Report No. 87. 2012. Available online: https://cds.cern.ch/record/2307593 (accessed on 8 January 2022).
- McNitt-Gray, M.F. AAPM/RSNA physics tutorial for residents: Topics in CT-radiation dose in CT. Radio Graph. 2002, 22, 1541–1553. [Google Scholar] [CrossRef] [PubMed]
- Crawford, C.R.; King, K.F. Computed tomography scanning with simultaneous patient translation. Med. Phys. 1990, 17, 967–982. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, R.; Fetherston, S. Primary radiation outside the imaged volume of a multislice helical CT scan. Br. J. Radiol. 2002, 75, 518–522. [Google Scholar] [CrossRef] [PubMed]
- Parakh, A.; Kortesniemi, M.; Schindera, S.T. CT Radiation Dose Management: A Comprehensive Optimization Process for Improving Patient Safety. Radiology 2016, 280, 663–673. [Google Scholar] [CrossRef] [PubMed]
- European Guidelines for Quality Criteria for Computed Tomography; European Commission: Luxembourg, 2000.
- McCollough, C.H.; Schueler, B.A. Calculation of effective dose. Med. Phys. 2000, 27, 828–837. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.G.; Shrimpton, P.C. Survey of CT Practice in the UK. Part 3: Normalized Organ Doses Calculated Using Monte Carlo Techniques, NRPB-250; National Radiological Protection Board: Oxon, UK, 1991. [Google Scholar]
- Tang, X.; Geng, C.; Chen, F.; Liu, Y.; Chen, D.; Xie, Q. The Simulation of Effective Dose of Human Body from External Exposure by Monte Carlo Methods. In Proceedings of the 2011 First International Workshop on Complexity and Data Mining, Nanjing, China, 24–28 September 2011; pp. 152–155. [Google Scholar] [CrossRef]
- Stmm, G.; Nagel, H.D. CT-Expo V 2.6. A Tool for Dose Evaluation in Computed Tomography User’s Guide; Buchholz: Hannover, Germany, 2019. [Google Scholar]
- Lewis, M.; Edyvean, S.; Sassi, S.; Kiremidjian, H.; Keat, N.; Britten, A. Estimating patient dose on current CT scanners: Results of the ImPACT CT dose survey. RAD Mag. 2000, 26, 1. [Google Scholar]
- Christner, J.A.; Kofler, J.M.; McCollough, C.H. Estimating Effective Dose for CT Using Dose–Length Product Compared with Using Organ Doses: Consequences of Adopting International Commission On Radiological Protection Publication 103 Or Dual-Energy Scanning. Am. J. Roentgenol. 2010, 194, 881–889. [Google Scholar] [CrossRef] [PubMed]
| Body Organs | Gonads | Lung | Stomach | Breast | Liver | Thyroid | Bladder | Brain | Reminder | |
|---|---|---|---|---|---|---|---|---|---|---|
| Publications | ICRP 60 | 0.20 | 0.12 | 0.12 | 0.05 | 0.05 | 0.05 | 0.05 | - | 0.05 |
| ICRP 103 | 0.08 | 0.12 | 0.12 | 0.12 | 0.04 | 0.04 | 0.04 | 0.01 | 0.12 | |
| Regional Anatomy | Dose Length Product to Ed Conversion Factors (k) [mSv/(mGy × cm)] | Phantom Module (cm) | ||
|---|---|---|---|---|
| Jess. et al. [21] | European Commission Guidelines [22] | European Commission NRPB-W67 (2005) | ||
| Head | 0.0021 | 0.0023 | 0.0021 | 16 |
| Chest | 0.014 | 0.017 | 0.014 | 32 |
| Abdomen | 0.012 | 0.015 | 0.015 | 32 |
| Pelvis | 0.019 | 0.019 | 0.015 | 32 |
| Regional Anatomy | Tube Voltages (kVp) | DLP (mGycm) | K Values (mSv)/ (mGycm) | EDLP (mSv) | EDLP−Es60 | EDLP−E60 | EDLP−E103 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Head | 120 | 634 ± 1.3 | 0.0021 | 1.3 | −1.5 | −1.87 | −5.04 | −54 | −59 | −79 |
| 120 | 334.8 ± 0.4 | 0.0021 | 0.7 | −0.8 | −0.97 | −2.65 | −53 | −58 | −79 | |
| 120 | 265.6 ± 0.1 | 0.0021 | 0.6 | −0.5 | −0.73 | −2.06 | −45 | −55 | −77 | |
| 120 | 657.2 ± 1.2 | 0.0021 | 1.4 | −1.5 | −1.89 | −5.17 | −52 | −57 | −79 | |
| 140 | 428.5 ± 0.3 | 0.0021 | 0.9 | −1.0 | −1.24 | −3.38 | −53 | 58 | −79 | |
| Chest | 120 | 539.7 ± 2.1 | 0.014 | 7.6 | 0.2 | 4.9 | 1.12 | 03 | 181 | 17 |
| 120 | 459.9 ± 0.2 | 0.014 | 6.4 | 0.1 | 4.1 | 0.88 | 02 | 178 | 16 | |
| 100 | 333.8 ± 0.4 | 0.014 | 4.7 | 0.1 | 3.03 | 0.69 | 02 | 181 | 17 | |
| 100 | 380.9 ± 0.2 | 0.014 | 5.3 | 0.1 | 3.4 | 0.73 | 02 | 179 | 16 | |
| 100 | 412.3 ± 1.1 | 0.014 | 5.8 | 0.1 | 3.74 | 0.85 | 02 | 182 | 17 | |
| Abdomen | 120 | 685.5 ± 0.4 | 0.015 | 10.3 | −0.6 | 6.87 | 2.07 | −06 | 200 | 25 |
| 120 | 430.2 ± 3.1 | 0.015 | 6.5 | −0.4 | 4.35 | 1.34 | −06 | 202 | 26 | |
| 120 | 758.3 ± 0.2 | 0.015 | 11.4 | 1.3 | 8.22 | 3.76 | −13 | 258 | 49 | |
| 140 | 636.4 ± 0.1 | 0.015 | 9.6 | −2.5 | 5.81 | 0.5 | −21 | 153 | 5.0 | |
| 140 | 725.8 ± 0.4 | 0.015 | 10.9 | −0.7 | 7.27 | 1.63 | −06 | 200 | 18 |
| Regional Anatomy | Tube Voltages (kVp) | CTDIvol (mGy) | DLP (mGycm) | Es60 (mSv) | Es103 (mSv) | E60 (mSv) | E103 (mSv) | E103−E60 | Scope of Eb (mSv) | Scope of Eb/Es60% (mSv) | Scope of Eb/E60% (mSv) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Head | 120 | 33.43 ± 0.2 | 634 ± 1.3 | 2.8 | 3.2 | 3.17 | 6.34 | 3.17 | 3.54 | 126.43 | 111.67 |
| 120 | 16.28 ± 0.1 | 334.8 ± 0.4 | 1.5 | 1.7 | 1.67 | 3.35 | 1.67 | 1.85 | 123.33 | 110.51 | |
| 120 | 16.08 ± 0.1 | 265.6 ± 0.1 | 1.1 | 1.3 | 1.33 | 2.66 | 1.33 | 1.56 | 141.82 | 117.47 | |
| 120 | 28.85 ± 0.7 | 657.2 ± 1.2 | 2.9 | 3.3 | 3.29 | 6.57 | 3.29 | 3.67 | 126.55 | 111.69 | |
| 140 | 47.3 ± 1.1 | 428.5 ± 0.3 | 1.9 | 2.1 | 2.14 | 4.28 | 2.14 | 2.38 | 125.26 | 111.09 | |
| Chest | 120 | 24.47 ± 0.6 | 539.7 ±2.1 | 7.4 | 7.7 | 2.70 | 6.48 | 3.78 | 5.0 | 67.57 | 185.28 |
| 100 | 11.54 ± 1.2 | 459.9 ± 0.2 | 6.3 | 6.6 | 2.30 | 5.52 | 3.22 | 4.3 | 68.25 | 186.97 | |
| 120 | 5.47 ± 0.03 | 333.8 ± 0.4 | 4.6 | 4.8 | 1.67 | 4.01 | 2.34 | 3.13 | 68.04 | 187.54 | |
| 140 | 13.02 ± 0.07 | 380.9 ± 0.2 | 5.2 | 5.4 | 1.90 | 4.57 | 2.67 | 3.5 | 67.31 | 183.78 | |
| 120 | 12.88 ± 1.0 | 412.3 ± 1.1 | 5.7 | 5.9 | 2.06 | 4.95 | 2.89 | 3.84 | 67.37 | 186.27 | |
| Abdomen | 120 | 13.53 ± 0.09 | 685.5 ± 0.4 | 10.9 | 12.2 | 3.43 | 8.23 | 4.80 | 7.47 | 68.53 | 217.94 |
| 120 | 10.22 ± 1.1 | 430.2 ± 3.1 | 6.9 | 7.7 | 2.15 | 5.16 | 3.01 | 5.55 | 80.43 | 258.02 | |
| 120 | 13.41 ± 0.05 | 758.3 ± 0.2 | 10.1 | 11.4 | 3.18 | 7.64 | 4.45 | 8.22 | 81.39 | 258.35 | |
| 120 | 15.89 ± 0.4 | 636.4 ± 0.1 | 12.1 | 13.5 | 3.79 | 9.10 | 5.31 | 9.71 | 80.25 | 256.10 | |
| 140 | 13.41 ± 1.3 | 725.8 ± 0.4 | 11.6 | 12.9 | 3.63 | 9.27 | 5.08 | 9.27 | 79.91 | 255.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abuelhia, E.; Tajaldeen, A.; Alghamdi, A.; Mabrouk, O.; Aluraik, W.; Msmar, A.; Elsadig, M.; Osman, E.; Al-Othman, A.; Alghamdi, S.; et al. Evaluating Effective Dose: A Comparison of Methods Based on Organ Dose Calculations versus Dose-Length Product and Monte Carlo Simulation. Appl. Sci. 2022, 12, 6691. https://doi.org/10.3390/app12136691
Abuelhia E, Tajaldeen A, Alghamdi A, Mabrouk O, Aluraik W, Msmar A, Elsadig M, Osman E, Al-Othman A, Alghamdi S, et al. Evaluating Effective Dose: A Comparison of Methods Based on Organ Dose Calculations versus Dose-Length Product and Monte Carlo Simulation. Applied Sciences. 2022; 12(13):6691. https://doi.org/10.3390/app12136691
Chicago/Turabian StyleAbuelhia, Elfatih, Abdulrahman Tajaldeen, Ali Alghamdi, Osama Mabrouk, Wejdan Aluraik, Amir Msmar, Muawia Elsadig, Entisar Osman, Abdullah Al-Othman, Salem Alghamdi, and et al. 2022. "Evaluating Effective Dose: A Comparison of Methods Based on Organ Dose Calculations versus Dose-Length Product and Monte Carlo Simulation" Applied Sciences 12, no. 13: 6691. https://doi.org/10.3390/app12136691
APA StyleAbuelhia, E., Tajaldeen, A., Alghamdi, A., Mabrouk, O., Aluraik, W., Msmar, A., Elsadig, M., Osman, E., Al-Othman, A., Alghamdi, S., Albadri, M., & Aljondi, R. (2022). Evaluating Effective Dose: A Comparison of Methods Based on Organ Dose Calculations versus Dose-Length Product and Monte Carlo Simulation. Applied Sciences, 12(13), 6691. https://doi.org/10.3390/app12136691






