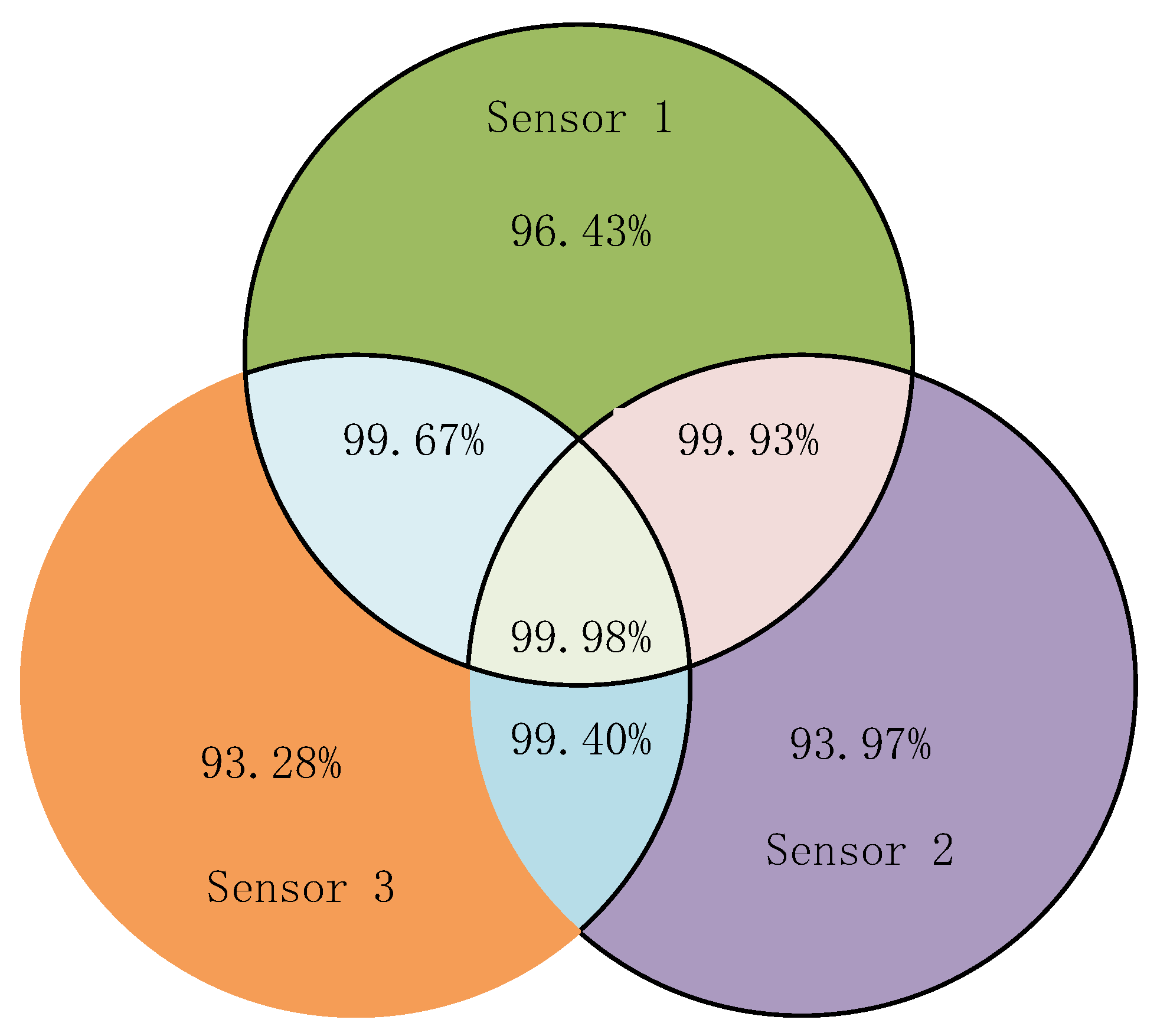Multi-Source Information Fusion Fault Diagnosis for Gearboxes Based on SDP and VGG

Abstract

A decision-level approach using multi-sensor-based symmetry dot pattern (SDP) analysis with a Visual Geometry Group 16 network (VGG16) fault diagnosis model for multi-source information fusion was proposed to realize accurate and comprehensive fault diagnosis of gearbox gear teeth. Firstly, the SDP technique was used to perform a feature-level fusion of the fault states of gearbox gear collected by multiple sensors, which could initially visualize the vibration states of the gear teeth in different states. Secondly, the SDP images obtained were combined with the deep learning VGG16. In this way, the local diagnostic results of each sensor can be easily obtained. Finally, the local diagnostic results of each sensor were combined with the DS evidence theory to achieve decision-level fusion, which can better realize comprehensive fault detection for gearbox gear teeth. Before fusion, the accuracies of the three sensors were 96.43%, 93.97%, and 93.28%, respectively. When sensor 1 and sensor 2 were fused, the accuracy reached 99.93%, which is 3.52% and 6.34% better than when using sensors 1 and 2, respectively, alone. When sensor 1 and sensor 3 were fused, the accuracy reached 99.96%, marking an improvement of 3.36% and 6.85% over individual use of sensors 1 and 3, respectively. When sensor 2 and sensor 3 were fused, the accuracy reached 99.40%, which is 5.78% and 6.56% better than individual use of sensors 2 and 3, respectively. When the three sensors were fused simultaneously, the accuracy reached 99.98%, which is 3.68%, 6.40%, and 7.18% better than individual use of sensors 1, 2, and 3, respectively.

1. Introduction

Gears are widely used in industrial fields [1,2,3], such as in helicopters, underground coal mine equipment, wind turbines, and so on, where mechanical equipment failure can result in major accidents. However, they have a complex structure and operate in confined and harsh environments, making maintenance difficult; therefore, monitoring gear health is a long-standing issue that must be addressed.

Eigen perturbation techniques are widely used in the field of fault diagnosis, and are a key real-time diagnosis method for vibration-based fault detection. Ai et al. [4] proposed an automatic time-convolution network for real-time fault diagnosis, combining wavelet packets with time-convolution networks, which can improve the sensitivity of fault features. This method reduces the time delay and improves the accuracy of real-time fault diagnosis. In the field of fault diagnosis, Soother D.K et al. [5] used a soft real-time fault diagnosis system for edge equipment based on domain adaptive training strategy using long- and short-term memory networks for remote and real-time detection of bearing faults from vibration data in order to reduce faults. Christian V.G et al. [6] made use of a combination of long- and short-term memory networks with multi-level Qtsu threshold segmentation for real-time fault diagnosis of marine machinery, in order to provide intelligent maintenance for the maritime industry. To improve weld quality, Miao et al. [7] established a convolutional neural network combined with 3D laser scanning technology in an imaginative approach to extract weld edge regions for real-time detection of weld defects. When induction motors have multiple faults at the same time, and the faults were difficult to diagnose accurately, Hernandez-Vargas M et al. [8] proposed a composite method incorporating singular value decomposition, statistical analysis, and artificial neural networks to solve this problem; then, the hardware in the FPGA was optimized, making it possible to realize the function of online fault detection.

There are numerous methods for detecting gear faults, including expert experience, machine learning, and deep learning. Hu et al. [9] used an expert system for the health monitoring of rail circuits. Ma D et al. [10] proposed a multi-back propagation (multi-BP) expert system algorithm to resolve power system fault assessment with greater accuracy than a traditional expert system, but it took a lot of time to perform calculations. Lin et al. [11] made use of a probabilistic neural network to address the issue of minimal neural network algorithm accuracy and applied it to gear fault diagnosis. Maamar A et al. [12] used the genetic algorithm (GA-BP) for fault classification of centrifugal pumps. Li et al. [13] established a two-stage attentional recurrent neural network (DA-RNN) combined with a convolutional block attentional module (CBAM) for fault diagnosis. It was able to perform fault diagnosis under conditions of data imbalance. Although machine learning algorithms are very popular in the field of fault diagnosis, deep learning algorithms can obtain more advanced features from the data center, reducing computing time and improving work efficiency. In addition, machine learning algorithms now face the shortcomings of insufficient data processing and over-fitting or under-fitting of training data, but deep learning algorithms can compensate for these shortcomings; therefore, deep learning is widely used in the field of fault diagnosis.

Common deep learning algorithms include deep belief networks (DBNs), long- and short-term memory, and convolutional neural networks. Jin et al. [14] managed to improve the deep confidence network by means of the gray wolf optimization algorithm, thus resolving parameter setting problems. In this case, early bearing faults could be meticulously monitored. Convolutional neural networks (CNNs) can, on the other hand, adopt spatial relativity to reduce the number of parameters and achieve feature extraction from each layer. Alexander E [15] proposed an intelligent method of multi-source signal multi-source thought convolutional neural network combination to detect different levels of frictional faults in response to the inapplicability of early-onset fault handling methods in the industrial field.

Since features in fault states are difficult to extract, Yao et al. [16] proposed an adaptive residual convolutional neural networks (ARCNNs) for small modular reactors (SMRs), and laid the foundation for other fault detection in noisy environments. Moradzadeh A et al. [17] proposed a hybrid diagnostic model using long- and short-term memory with CNN in power systems, where faults have less impact on current and volt-age values, and this method could also be used for fault prediction. In terms of fault diagnosis in gearboxes, Miao et al. [18] used a modified convolutional neural network vibration signal. There are six available CNNs for transfer and classification in convolutional neural networks. These are ShuffleNet, GppgLeNet, ResNet-18, ResNet-50, VGG-16, and DenseNet-201; the various algorithms were compared and analyzed experimentally, and it was determined from the experimental results that VGG16 had the highest accuracy and the best performance [19]. A common fault diagnosis method is the direct processing of time-domain vibration signals, but it is difficult to visually see the fault condition.

SDP image technology converts time-domain vibration signals into images for more intuitive fault diagnosis. Gu et al. [20] proposed the symmetry dot pattern (SDP) for the diagnosis of bearings in response to the difficulty of identifying nonlinear signals in the fault during processing. Xu et al. [21] matched the vibration signals with images through the signals collected by five sensors for detecting wind turbine health monitoring, and although the computation time increased, the accuracy was unexpectedly improved. Sun et al. [22] processed the characteristic components by the SDP method and applied them to the fault diagnosis of rolling bearings, and the proposed method exhibited good stability. Since the source of the fault vibration signal is multi-directional, a sensor installed at a fixed location will not be able to fully capture the fault signal. Using the data from the single direction sensor will not accurately diagnose the fault and obtain accurate diagnosis results.

Since multi-channel sensor extraction data can provide comprehensive data for diagnosis, Guo et al. [23] presented a theoretical DS evidence (Dempster Shafer evidence) fault diagnosis method combining CNN algorithm with multi-linear principal component analysis (MPCA) that was computationally fast and could be used for fault prediction of complex states. He et al. [24] addressed the difficulty of monitoring axial gear pump faults by simultaneously inputting the collected vibration and acoustic signals into the deep learning of migration learning, and the multi-source information fusion of the two signals, and this method was more stable than when using a single signal. Li et al. [25] proposed a novel diagnosis method with an adaptive symmetrized dot pattern and density-based spatial clustering of applications with noise (ASDP-DBSCAN), and applied this for the diagnosis of rolling bearings.

Nowadays, deep learning is very popular in the field of fault identification, and the proposed multi-source information fusion technology can fully reflect the diagnostic data. With traditional fault diagnosis methods, it is not possible to visualize the gear fault conditions, but the SDP technique can transform time series signals into visual representations, which makes it possible to realize direct gear fault diagnosis. In the SDP image processing method, the feature-level fusion of multiple channels can be applied, but decision-level fusion is not considered. Therefore, a fault diagnosis method that combines the SDP image method with CNN for decision-level fusion is proposed in the present study, given current fault diagnosis methods that combine the SDP image method with deep learning methods that only perform feature-level fusion. Firstly, in the selection of a channel with a more obvious state as the experimental data, the sensor acquires data in three directions. Secondly, the experimental data are fused at the feature level based on the SDP image processing method. Ultimately, the fused pictures are fed into the VGG16 fault diagnosis model to realize fault diagnosis using a single sensor. In view of the lack of comprehensiveness and multi-dimensional data signals collected by means of single sensor acquisition, three sensors were used to realize the decision-level fusion of DS evidence theoretically in the present study.

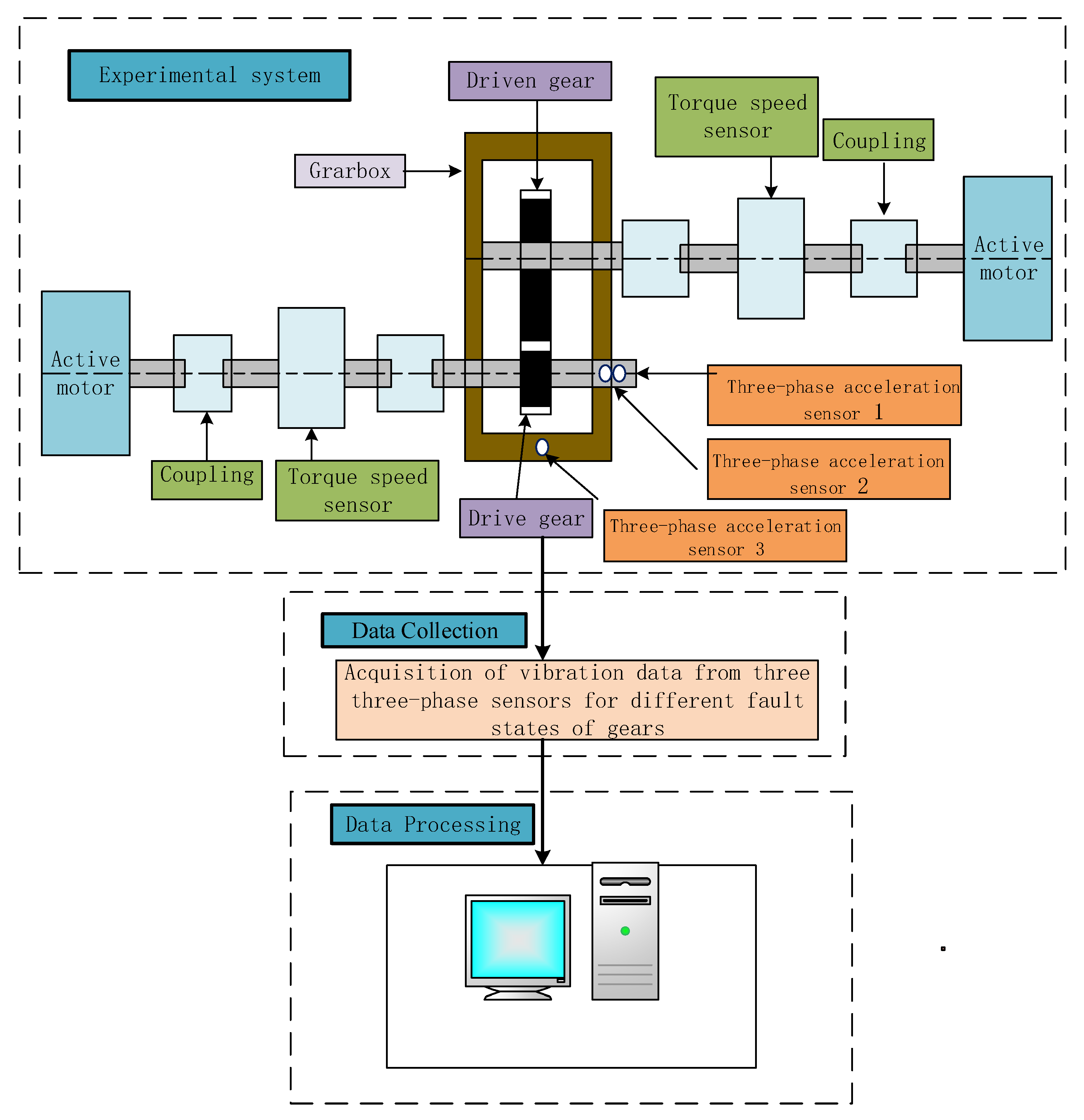
Section 1 provides a background study of the thesis. Section 2 describes the theoretical knowledge on which the proposed method relies. Section 3 verifies the validity of the proposed method using the bearing common dataset from Case Western Reserve University. Section 4 applies the proposed method to an actual fault diagnosis experiment on gear teeth in a gearbox test bench built in the laboratory.

2. Fundamental Theories

2.1. SDP Theory

The point symmetry technique is an approach for converting data on time series into images, which represents the feature information thought to be present in the data and converts the time domain signal into polar coordinates, mainly by using the feature points present in the image. In this way, the characteristics of the fault signal can be visualized; this was first applied for converting speech signals into visual features [26]. The time domain vibration signal X = {x₁, x₂, …, x_i, …, x_n} is converted to point S, S = [r(i), θ(i), ϕ(i)] in the SDP polar coordinate diagram, as shown in Figure 1.

In Figure 1a, the original vibration signals and the corresponding amplitudes at x(i) time and x(i + l) time, respectively, are shown. Their conversion to the polar plot of SDP is shown in Figure 1b. The mapping relationship between the pieces of Figure 1a,b is given by the following equations [27].

$$r(i)=\frac{x_i-x_{\min }}{x_{\max }-x_{\min }}$$

(1)

$$\theta (i)=\theta +\frac{x_{i+l}-x_{\min }}{x_{\max }-x_{\min }}\zeta$$

(2)

$$\varphi (i)=\theta -\frac{x_{i+l}-x_{\min }}{x_{\max }-x_{\min }}\zeta$$

(3)

where r(i) is the radius of the polar coordinates, θ(i) and ϕ(i) are the counterclockwise and clockwise deflection angles, respectively, along the mirror plane of symmetry in the polar coordinates, l is the time lag coefficient, θ is the angle of the mirror plane of symmetry ($\theta =\frac{2\pi m}{n},\zeta \le \theta ,m=1,2,\dots ,n-1$, n is the mirror plane of symmetry), ξ is the angular gain factor, and x_max and x_min are the maximum and minimum amplitudes of the signal, respectively.

2.2. Fault Diagnosis Based on VGG16 Network

CNNs have been proposed to enable accurate recognition of images, and are widely used in areas such as power systems, face recognition, and fault diagnosis [16,28]. CNNs consist of several filter layers and a classifier layer. Of these, the filter layer consists of a convolutional layer and a pooling layer, which are crossed by the filter layer for feature extraction of the input data, respectively. The classifier layer consists of multiple fully connected layers, which is ultimately able to classify and identify faults. The Visual Geometry Group 16 network (VGG16) is a type of convolutional neural network that has a structure with more convolutional layers, more layers, and a regular structure. Its input layer enters the convolutional layer with three channels, passes the activation function ReLU, and then enters the maximum pooling layer. The structure diagram of a typical VGG16 model is shown in Figure 2.

2.3. DS Evidence Theory

Multi-source information fusion, also known as multi-sensor data fusion, processes data from multiple levels and directions to achieve accurate state estimation. The core of DS evidence theory is the construction of a discriminative framework, the assignment of basic probabilities, and the fusion rules. Their selection will directly affect the fusion results.

A discriminative framework consists of various sets belonging to the class, and the sets are mutually exclusive between two sets, which are commonly denoted. The set is denoted as follows [29]:

$$2^{\Theta }=\{\varnothing ,{\theta }_1,{\theta }_2\dots ,{\theta }_N,{\theta }_1\cup {\theta }_2,\dots {\theta }_1\cup {\theta }_2\cup {\theta }_3,\dots ,\Theta \}$$

(4)

As for basic probability assignment, each state has a corresponding probability, generally denoted by m, which is related to the identification framework, as shown in the following Equation (5).

$$\{\begin{array}{l}0\le m(A)\le 1\\ M(\varnothing )=0\\ {\displaystyle \sum _{A\subseteq \Theta }m(A)=1}\end{array}$$

(5)

where A is any subset of the discriminative framework and m(A) is the fundamental probability of A. Since the decision level of multi-source information fusion needs to fuse the basic probabilities generated by multiple sensors to obtain the final diagnosis according to the DS fusion rules, the fusion rules are described in the following Equation (6).

$$\{\begin{array}{l}m(\varnothing )=0\\ m(A)=\frac{1}{1-k}{\displaystyle \sum _{\cap A_i=A}{\displaystyle \prod _{1\le i\le N}{m}_i(A_i)},A\ne \varnothing }\\ k={\displaystyle \sum _{\cap A_i=\varnothing }{\displaystyle \prod _{1\le i\le N}{m}_i(A_i)},k\ne 1}\end{array}$$

(6)

where k is the conflict factor.

3. Public Datasets

Due to the paucity of public datasets on gears and the lack of authoritative sources for published data, they have not yet been fully recognized in academic circles. In the present study, the fault diagnosis considered for the gears is a pitting condition, which tends to take place in both gears and bearings. The validation data for the method were applied to the public bearing dataset of Case Western Reserve University [30], selecting the 6205-2RS JEM SKF deep groove ball bearing, and sensors for detecting the failure of the inner ring of the bearing were located in the drive end (DE) and fan end (FE) of the bearing, referred to as the DE sensor and the FE sensor, respectively. The selected data information on the bearing operating conditions is shown in

Table 1. Bearing public data collection working conditions.

Load (N)	Sampling Frequency (KHz)	Motor Speed (rpm)	Sensors	Fault Diameter (Feet)	Health Status Indication	Sample
0	12	1797	DE	0	0	3 × 117
				0.007	1
				0.021	2
			FE	0	0
				0.007	1
				0.021	2

.

Three classes of states were selected for fault classification, and each class of state data was processed by means of SDP to obtain 117 sets of pictures, with each set consisting of 1024 sample points, of which 27 sets were selected for each state as the test set.

3.1. SDP Image Feature Information Fusion

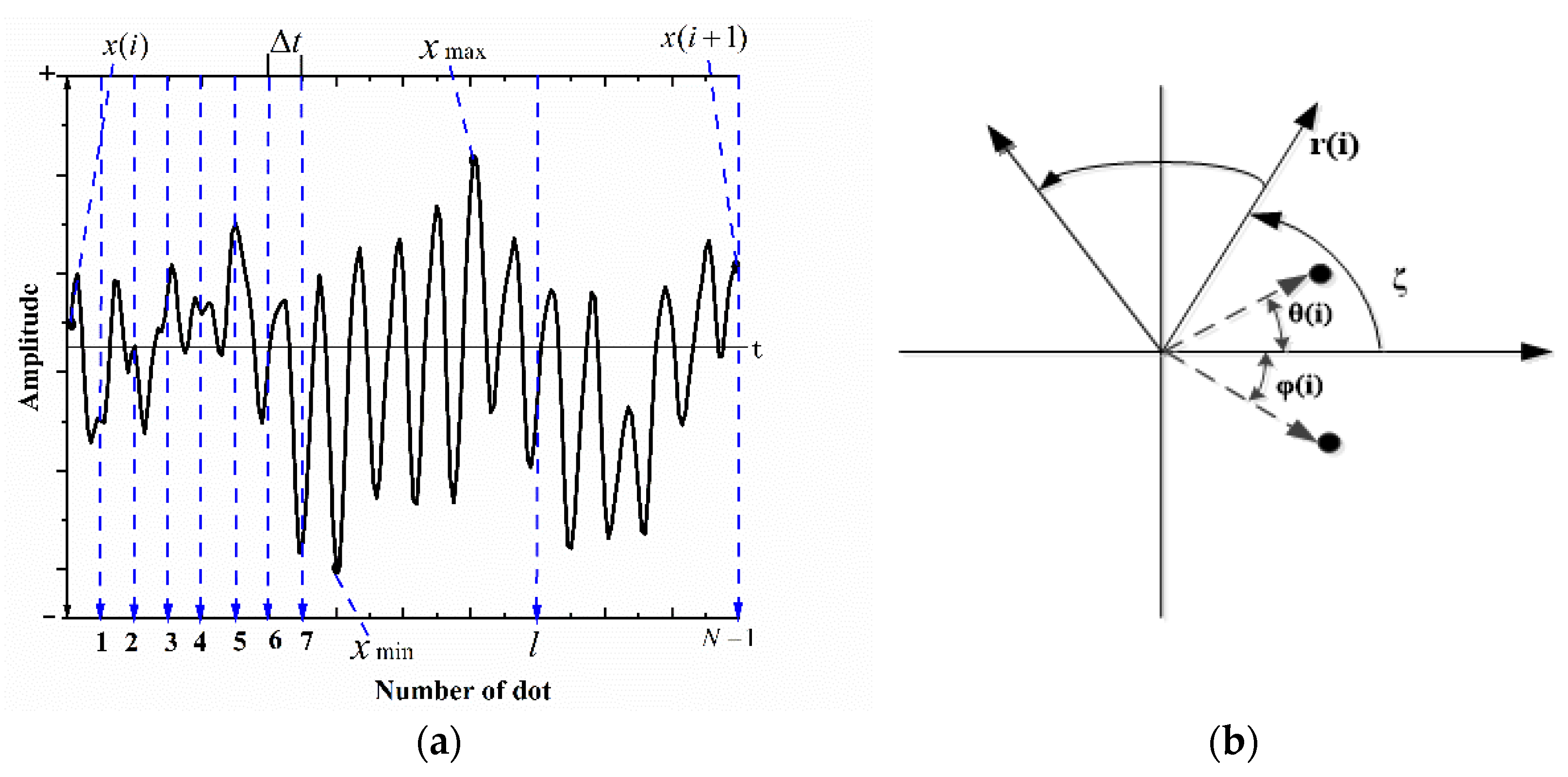
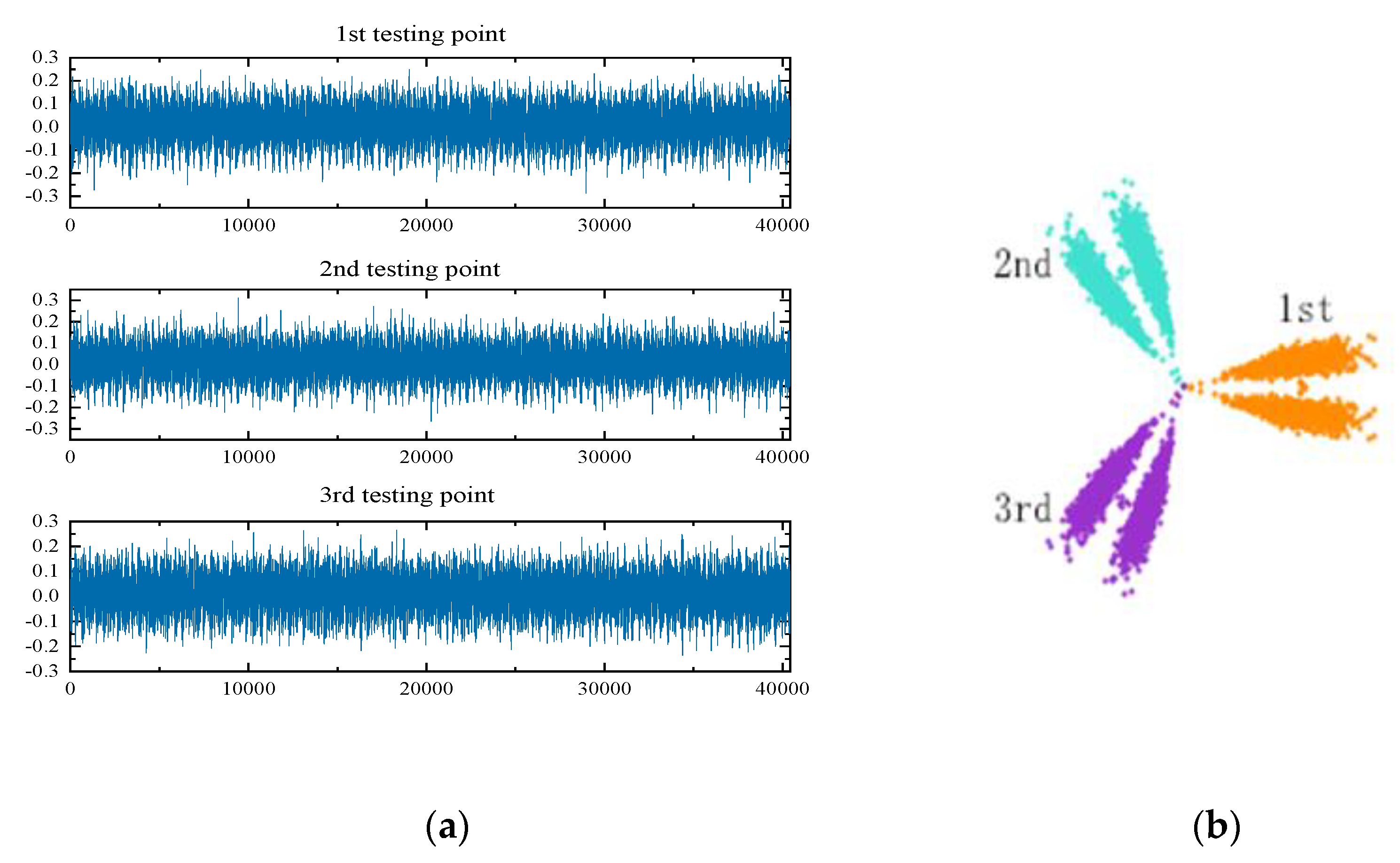
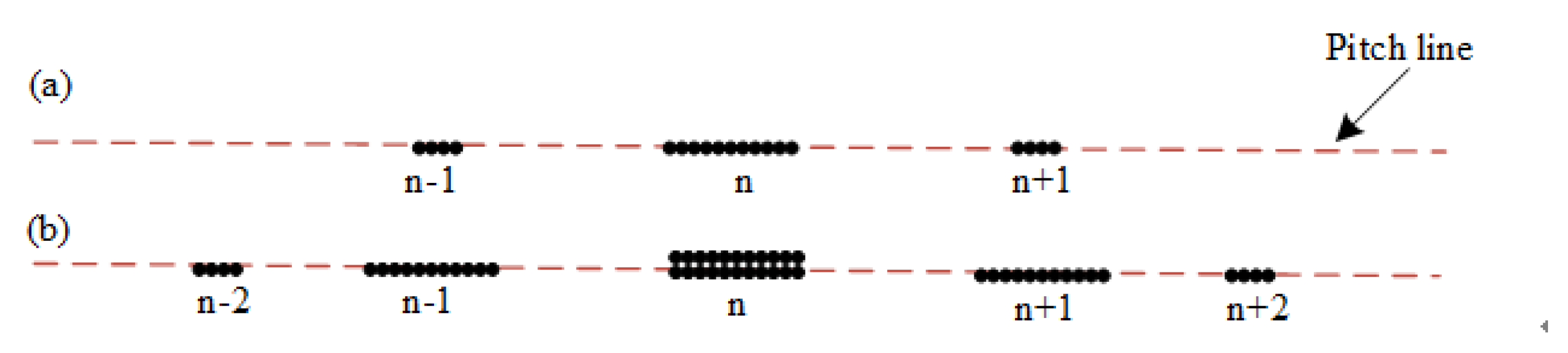
The SDP image conversion method is able to realize the fusion of multiple groups of signals. Each mirror symmetry plane is able to express the characteristic information of a group of signals. Taking the DE sensor as an example to clearly detect the bearing fault status, the bearing data were taken as three test points and the vibration signal was converted into the polar coordinate map of SDP based on SDP technology in the present study. This is shown in Figure 3.

Parameter Setting

When plotting SDP images, deflection angle θ, time lag coefficient l, and angular gain factor ζ are the core parameters of SDP images. Their selection directly affects the final diagnostic results. θ determines the symmetry of the plane; if a value is taken that is too large, there will be no overlap between images, but the image quality will be poor. If it is too small, there will be overlap between the generated images. As a result, it will be difficult to extract features among the sensors. Since there were three measurement points, the deflection angle was set as θ = 120°, in order to form a triangular centrosymmetric pattern and avoid interference with adjacent sensor information. After a lot of experiments, it was determined that [20] 0 < l ≤ 10. By comparing the health of the bearings under l and ζ, a suitable value was selected. The value of the enlargement angle was selected with a step of 1° for 60 sets of comparison experiments, and the time lag coefficient l was taken with a step of 1 for 10 sets of comparison experiments. The results are shown in

Table 2. SDP graph for different states of the bearing with different values of l and ζ.

Time Lag Coefficient l	Magnification Angle ζ	Fault Status
		Normal	Slight Pitting	Severe Pitting
1	10°
	…	…	…	…
	20°
	…	…	…	…
	40°
	…	…	…	…
	60°
…	…	…	…	…
6	10°
	…	…	…	…
	20°
	…	…	…	…
	40°
	…	…	…	…
	60°
…	…	…	…	…
10	10°
	…	…	…	…
	20°
	…	…	…	…
	40°
	…	…	…	…
	60°

.

From Table 2, it can be seen that the degree of difference between the petals representing the three motion states of the bearing was at its greatest when l = 10, ζ = 40°. Specifically, this was mainly reflected in the angle between the petals, concentration, curvature, and so on. Therefore, the optimal time lag coefficient and angular gain factor were initially determined as l = 10, ζ = 40°.

The influence of the deflection angle on the fault state was verified under the condition that the optimal determined time lag coefficient and magnification angle remained unchanged. The data corresponding to the DE sensors in the common dataset data were arrayed into three, four, five, and six mirror symmetry surfaces to take the shape of different deflection angles in order to observe the differences between the faults of the bearings. The results are shown in

Table 3. SDP graphs for different values of deflection angle θ at different bearing states.

Mirror Symmetry Surface	Deflection Angle θ	Fault Condition
		Normal	Slight Pitting	Severe Pitting
3	120°
4	90°
5	72°
6	60°

.

It can be seen from Table 3 that the petals tend to cross when the deflection angles are 72° and 60°. In other words, there is interference between the signals of the sensors, and the fault condition cannot be distinguished. When the deflection angles are 120° and 90°, both can distinguish the gear fault state, and the parameters are determined to require accuracy judgment.

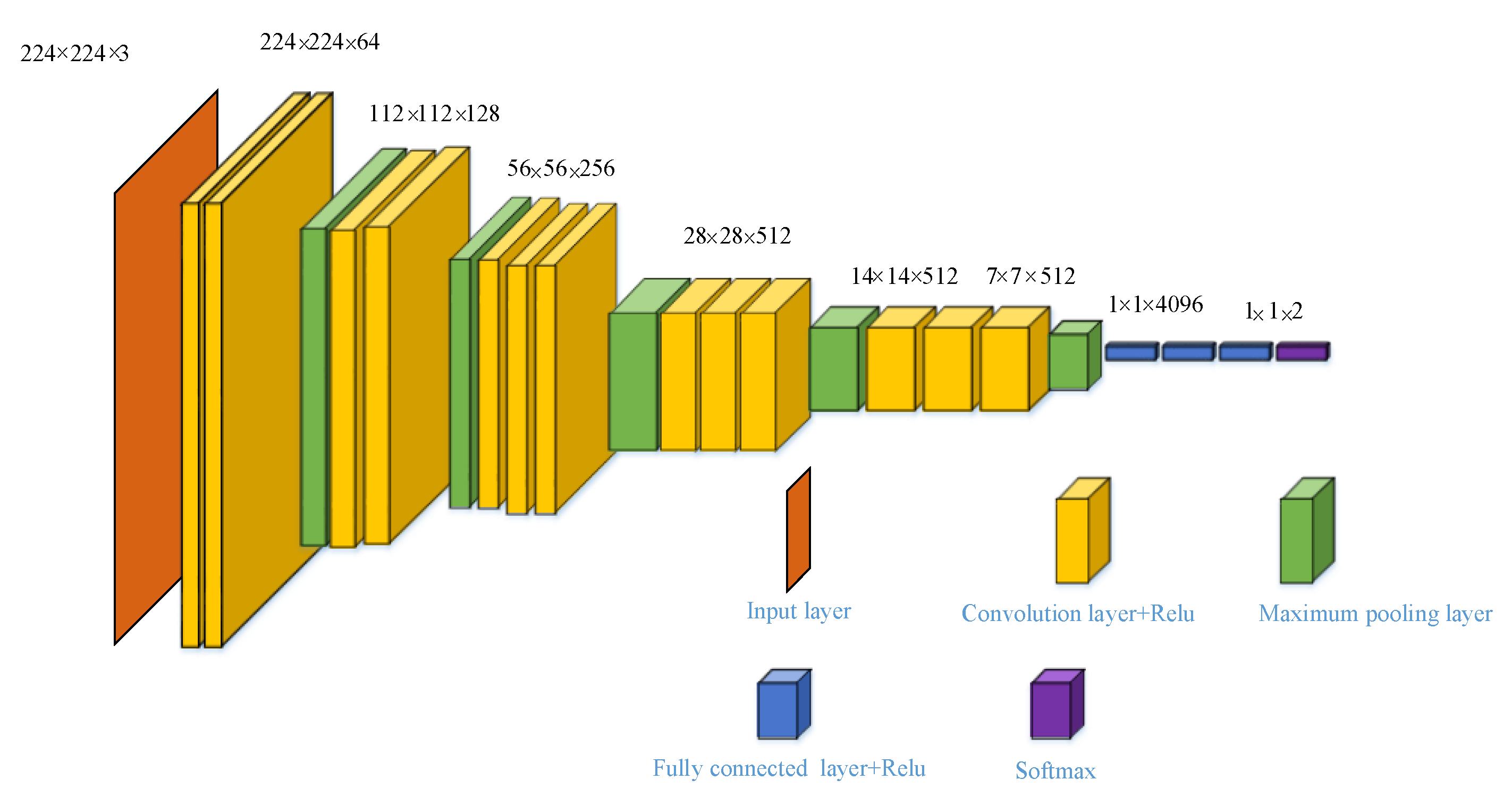
3.2. VGG Fault Diagnosis Model

In the case of θ = 120°, two sets of data were selected for comparison with the optimal data in order to verify that the selected parameters were optimal. The first group of experimental comparisons was used to verify the differences obtained between the thickness and shape characteristics of the petals of the SDP images. The second group of experimental comparisons was used to verify the influence of the degree of concentration of SDP images on the results; the experimental comparisons are shown in

Table 4. Comparison of experimental parameters.

Group	Time Lag Coefficient l	Angular Gain Factor ζ
1	1	10°
2	10	20°
3	10	40°

.

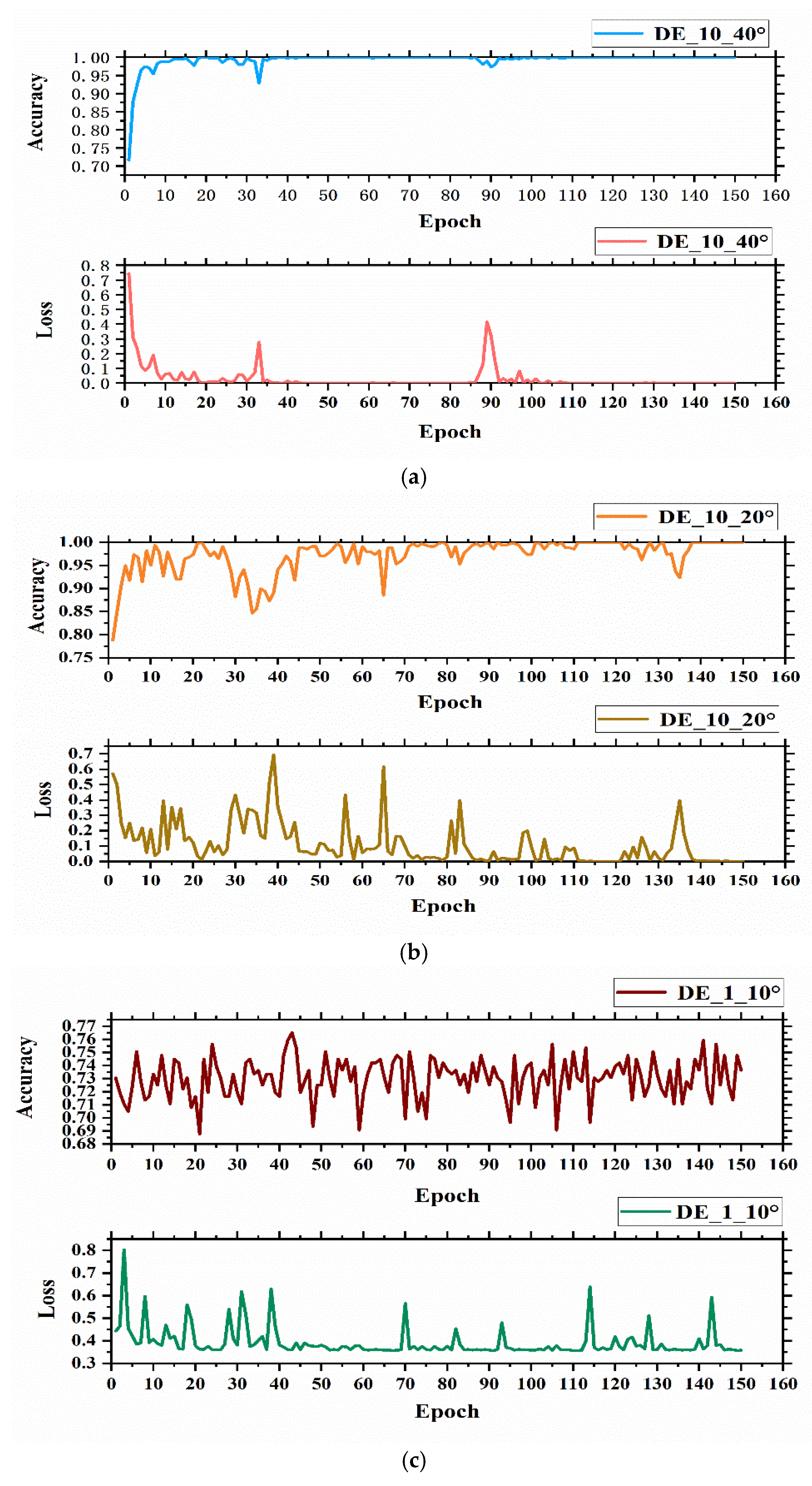
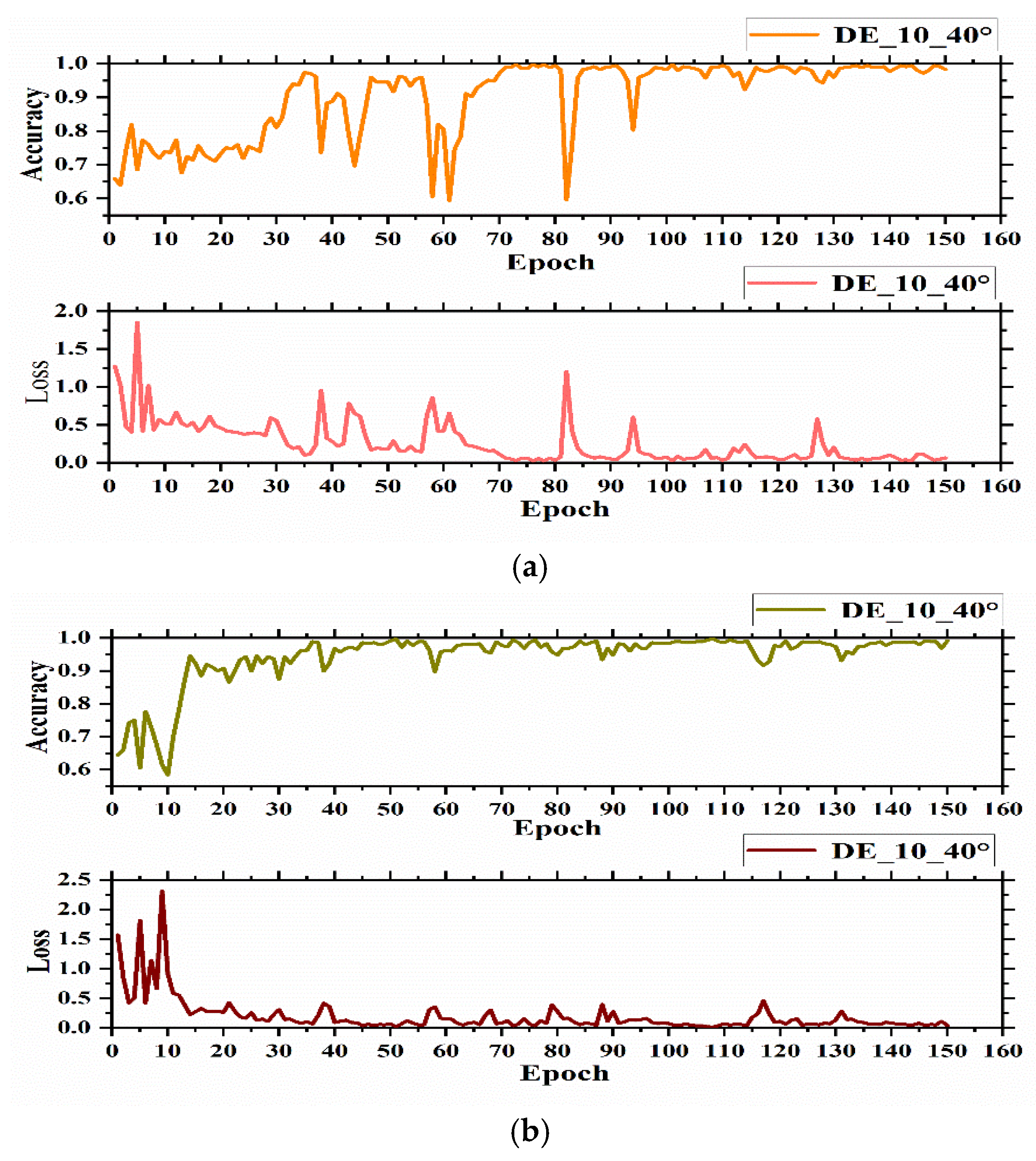
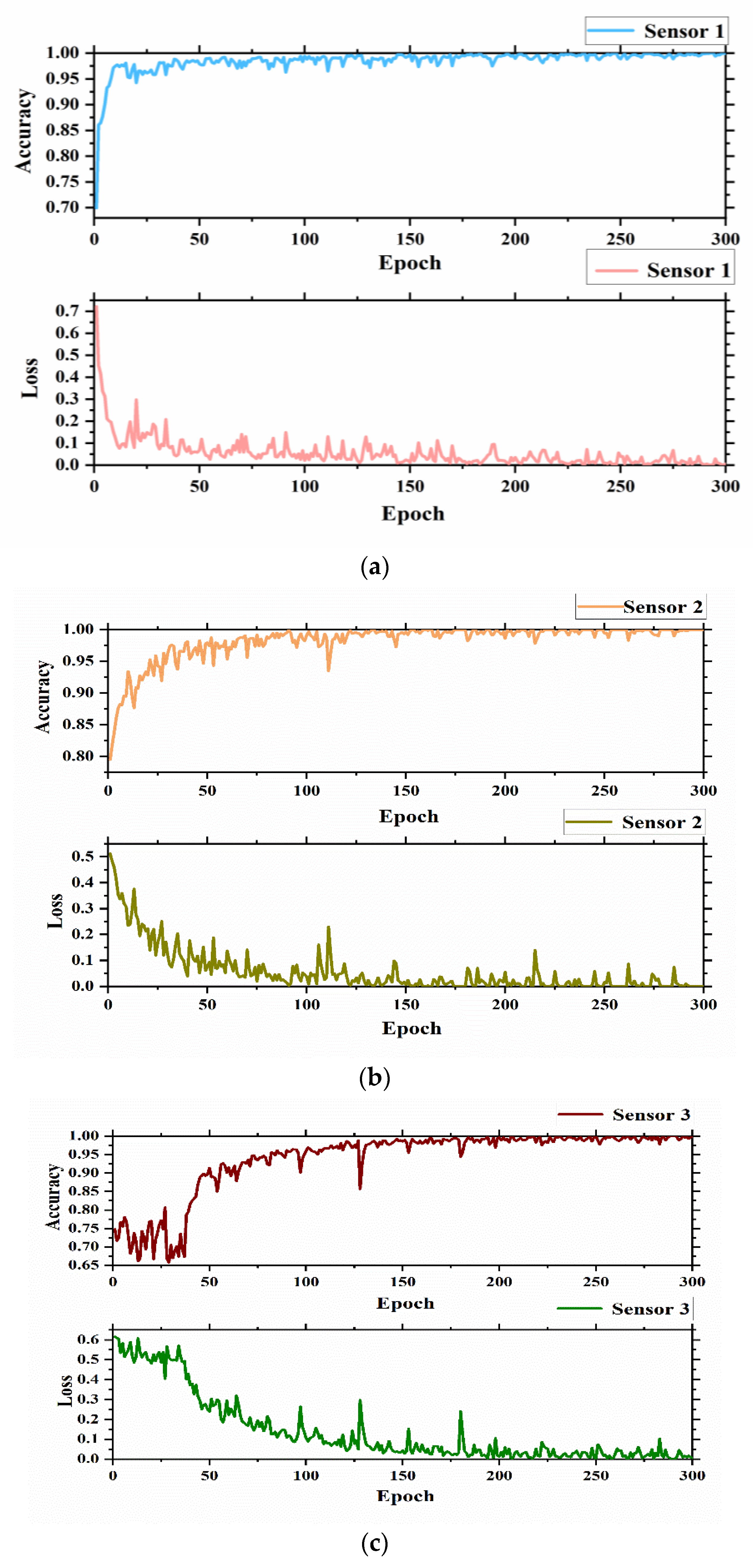
In the VGG16 network structure, the parameter setting matters a great deal. On the basis of several parameter setting experiments, it was concluded that the learning rate set to 0.003, the number of samples per input of 8, and the number of iterations of 1000 were the best settings. When iterating 100 times, the first set of simulation data tends to be stable. Hence, only the first 150 datasets are shown in the figure. The value of sensor accuracy is the sensor name with the time lag factor and the angular gain factor. The training accuracy and loss curve of the VGG16 network structure are shown in Figure 4.

From the experimental results in Figure 4a, the training accuracy of the VGG16 network based on SDP images was close to 100% after 100 iterations of training, with 99.29% accuracy and a 2.86% loss rate. Judging from Figure 4b, the training times were only close to convergence after 140 iterations, with an accuracy of 97.23% and a loss rate of 11.24%; in contrast, in Figure 4c, it can be seen that the accuracy rate keeps fluctuating, with an accuracy rate of 73.02% and a loss rate of 39.27%. Overall, it can be concluded that when θ = 120°, the time lag coefficient and the angular gain factor of l = 10, ζ = 40° were optimal.

On the basis of Figure 4, it was concluded that the diagnosis results based on the SDP method tended to be the best when l = 10, ζ = 40°. Since the deflection angle also affects the diagnosis results, the present study compares the effect of different deflection angles on the fault diagnosis results when l = 10, ζ = 40°, as shown in

Table 5. Comparison of deflection angle parameter settings.

Group	Deflection Angle θ
1	120°
2	90°
3	72°
4	60°

.

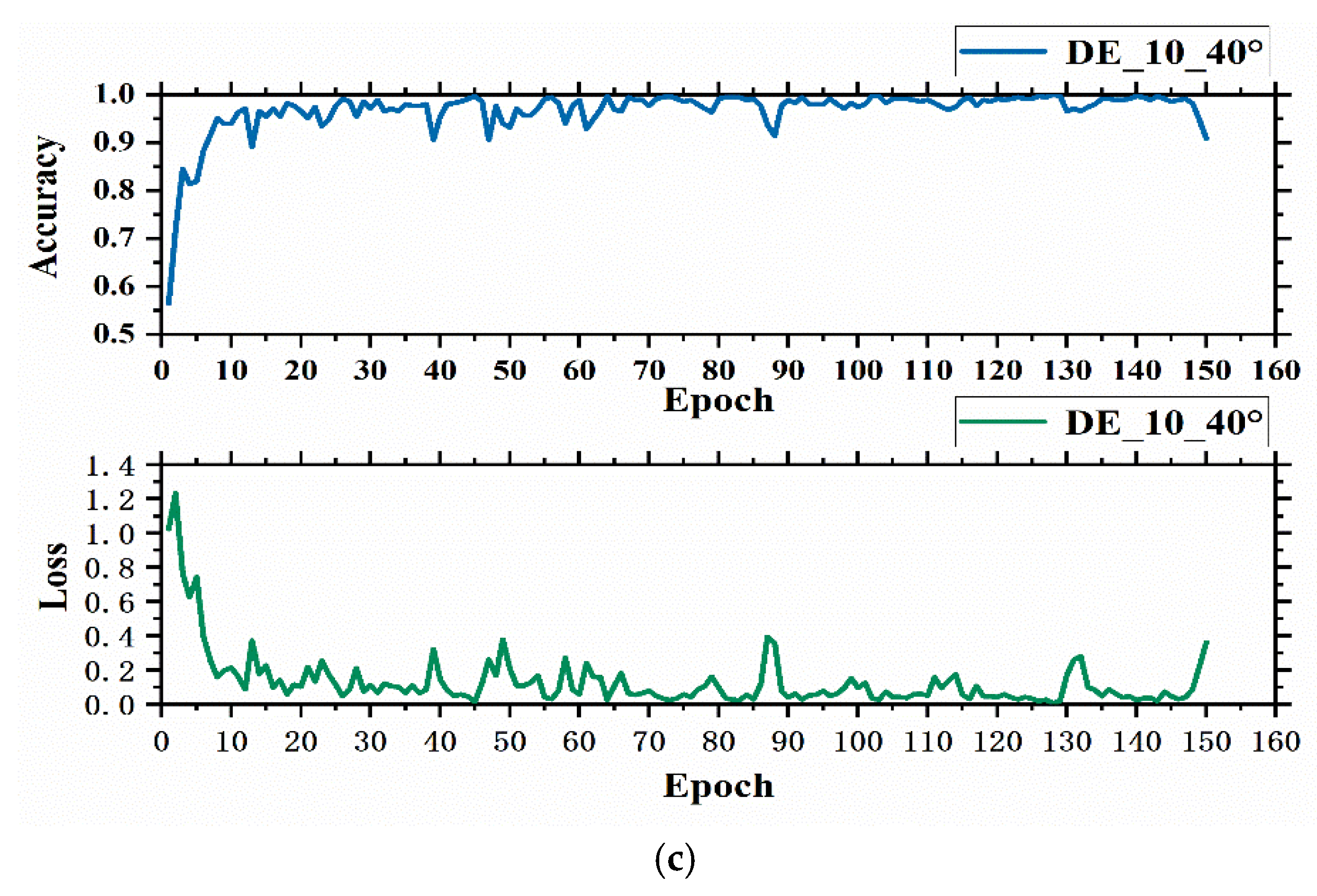
The training accuracy and loss curves of the VGG16 network structure under different values of deflection angle are shown in Figure 5.

From Figure 5a, it can be seen that the accuracy is 90.60% and the loss rate is 25.91%. From Figure 5b, it can be seen that the accuracy is 94.37% and the loss rate is 19.99%. From Figure 5c, it can be seen that the accuracy is 96.75% and the loss rate is 13.12%. However, from Figure 4a it can be concluded that the accuracy is 99.29% and the loss rate is 2.86%. Therefore, the fault diagnosis accuracy reached its maximum value at θ = 120°, l = 10, ζ = 40°.

3.3. Multi-Source Information Fusion Based on DS Evidence Theory

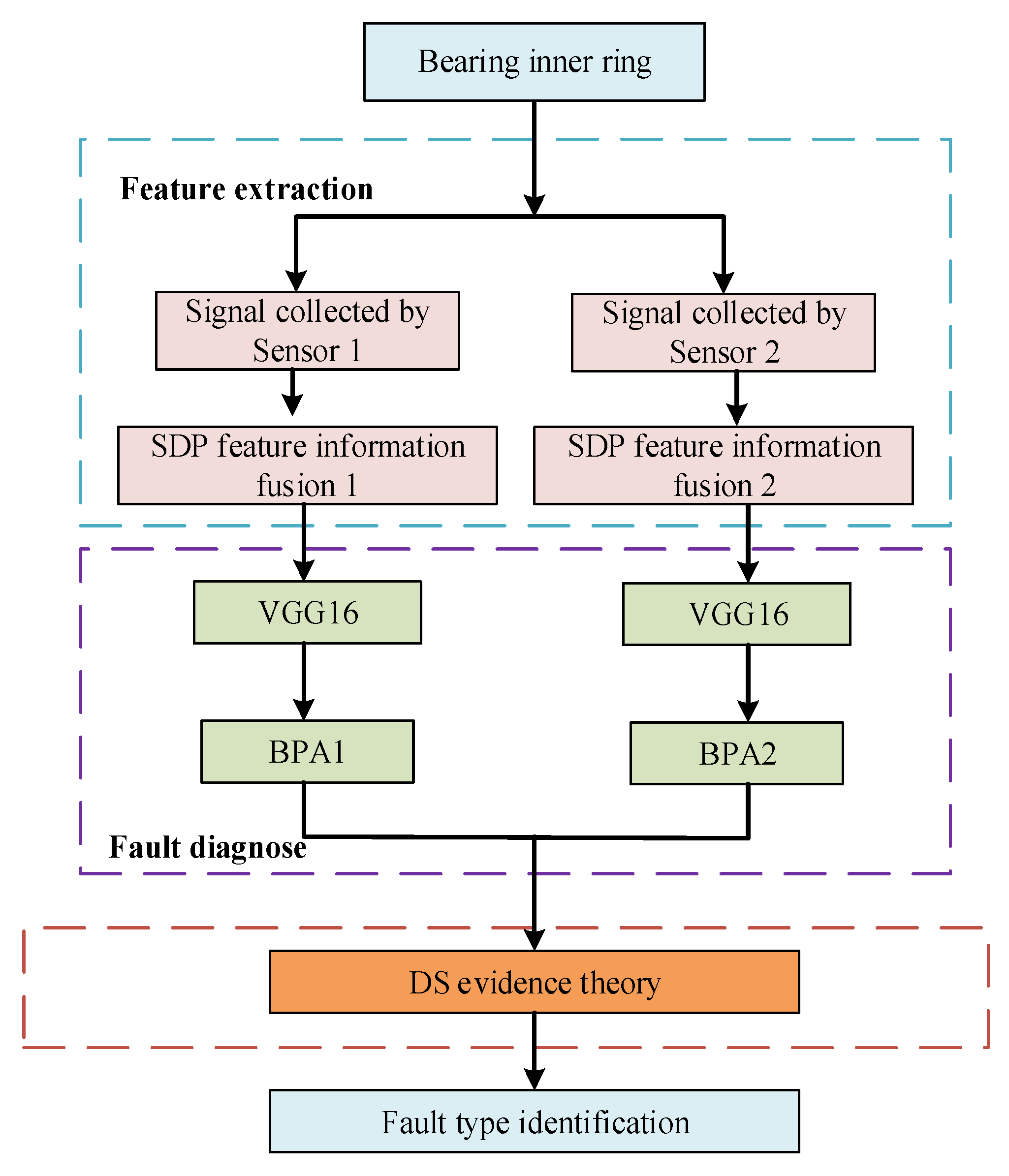
Multi-source information fusion technology can result in greater comprehensiveness of the data sources for diagnostic results, which may help to improve the accuracy of the diagnostic results. It can be divided in terms of hierarchy into data-level fusion, feature-level fusion, and decision-level fusion, where decision-level fusion is located at the highest level. The classification results of each sensor for each state input into the decision-level theory as a body of evidence. Figure 6 shows the technical route of decision-level fusion.

The images obtained using the SDP method were used to perform bearing health diagnosis on the basis of the data acquired by each sensor using the VGG network structure. Ultimately, the decision-level fusion of the local diagnostic results of each sensor obtained by the VGG network was conducted using DS evidence theory. Before fusion, a corresponding recognition framework was established for each sensor. In the presence of three fault states where the conditions were normal, 0.007″, and 0.021″, the corresponding identification frame was $\Theta =\{\mathrm{A},\mathrm{B},\mathrm{C}\}$. Since the fused bodies of evidence were acquired from two sensors, the body of evidence E = {E1, E2}, where E1 represents the bearing base end sensor (DE sensor) and E2 represents the bearing fan end sensor (FE sensor). Then, the fusion rules were used to fuse the bodies of evidence of the two sensors at the decision level. Ultimately, in the present study, fault diagnosis with multi-source information fusion of bearings was realized.

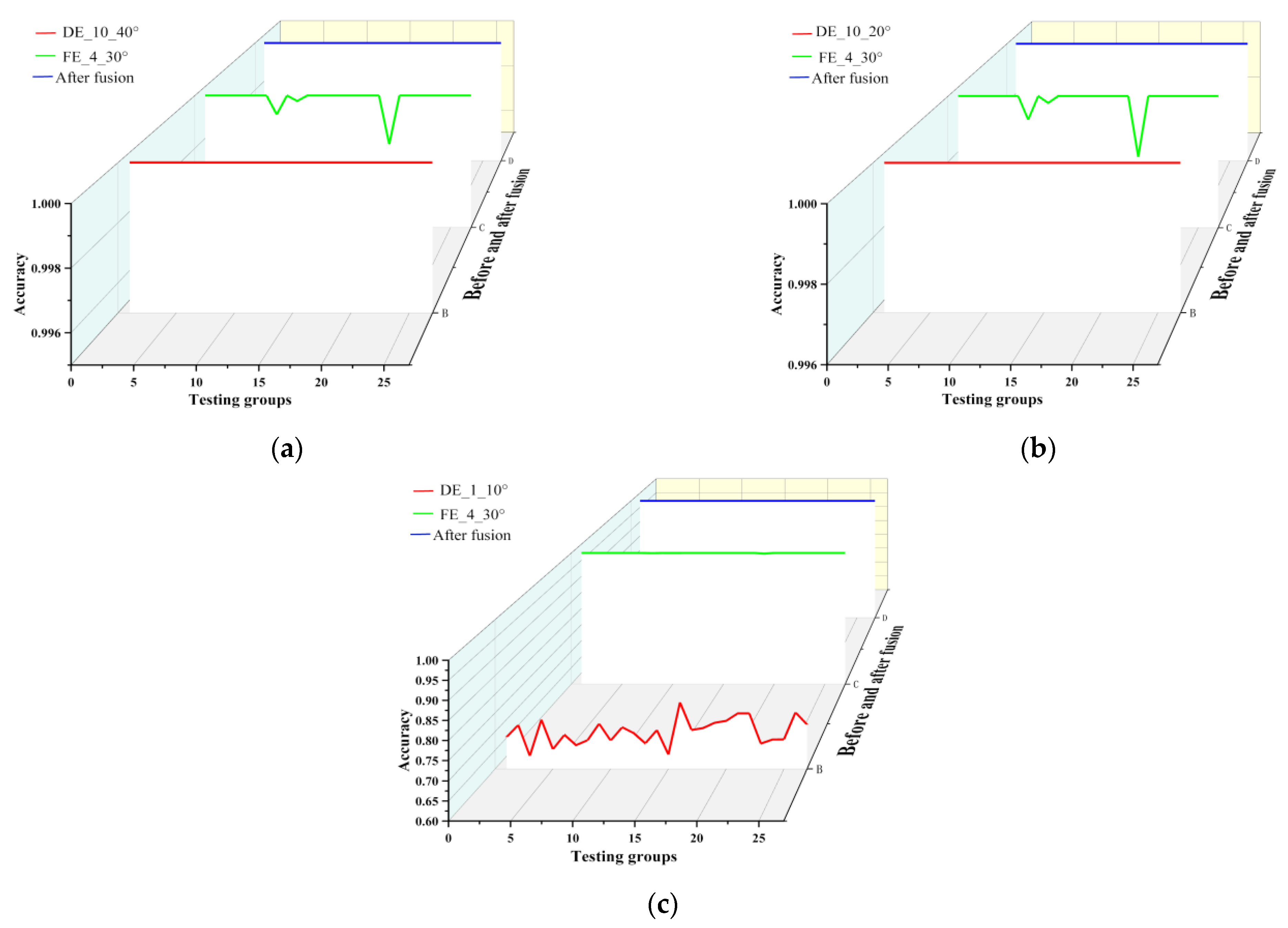
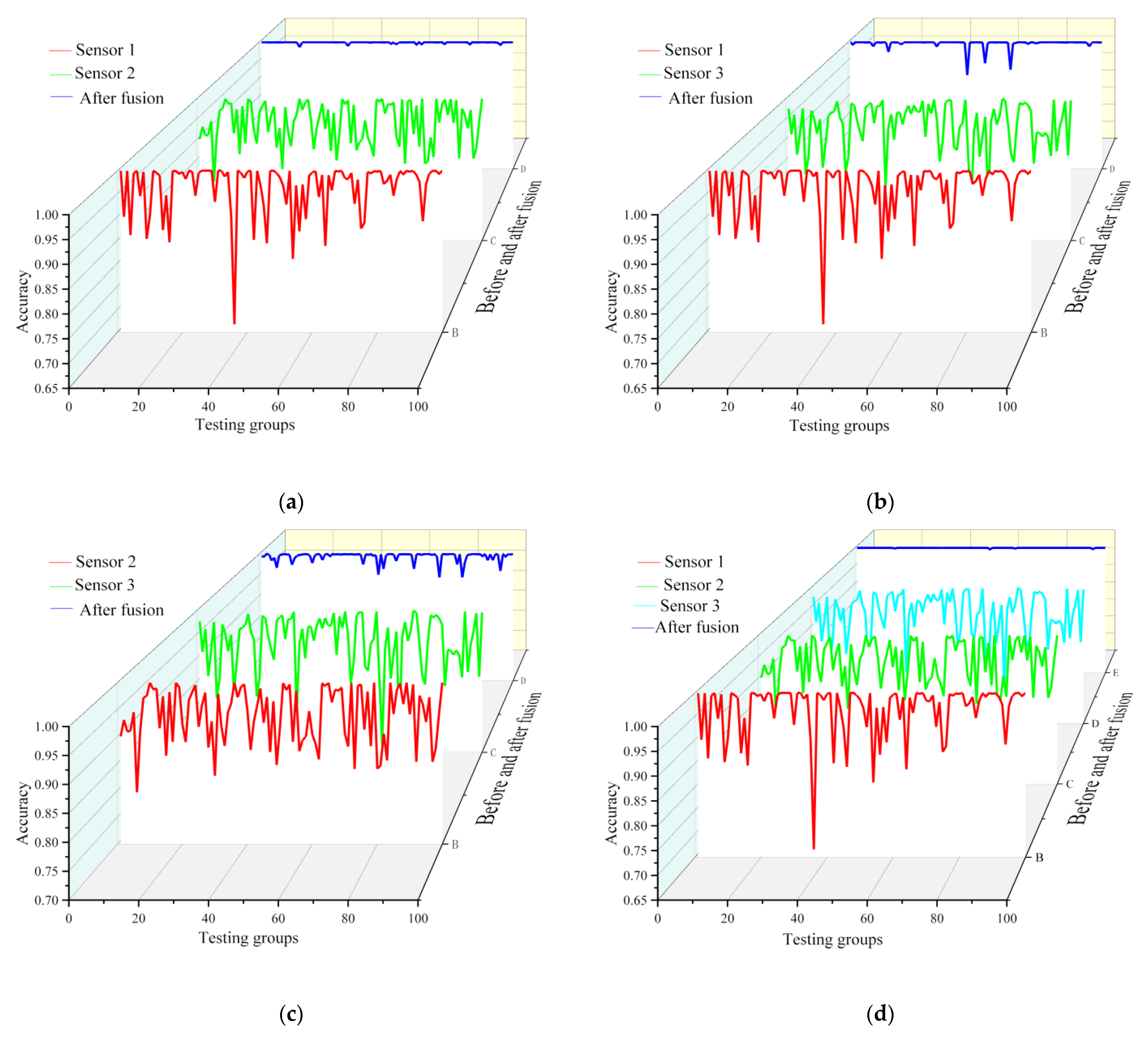
The FE sensor data were extracted in the same way as the data from the DE sensor, and the optimal parameters of the FE sensor were obtained as a time lag coefficient of 4, an angular amplification factor of 30°, and a deflection angle of 120°. 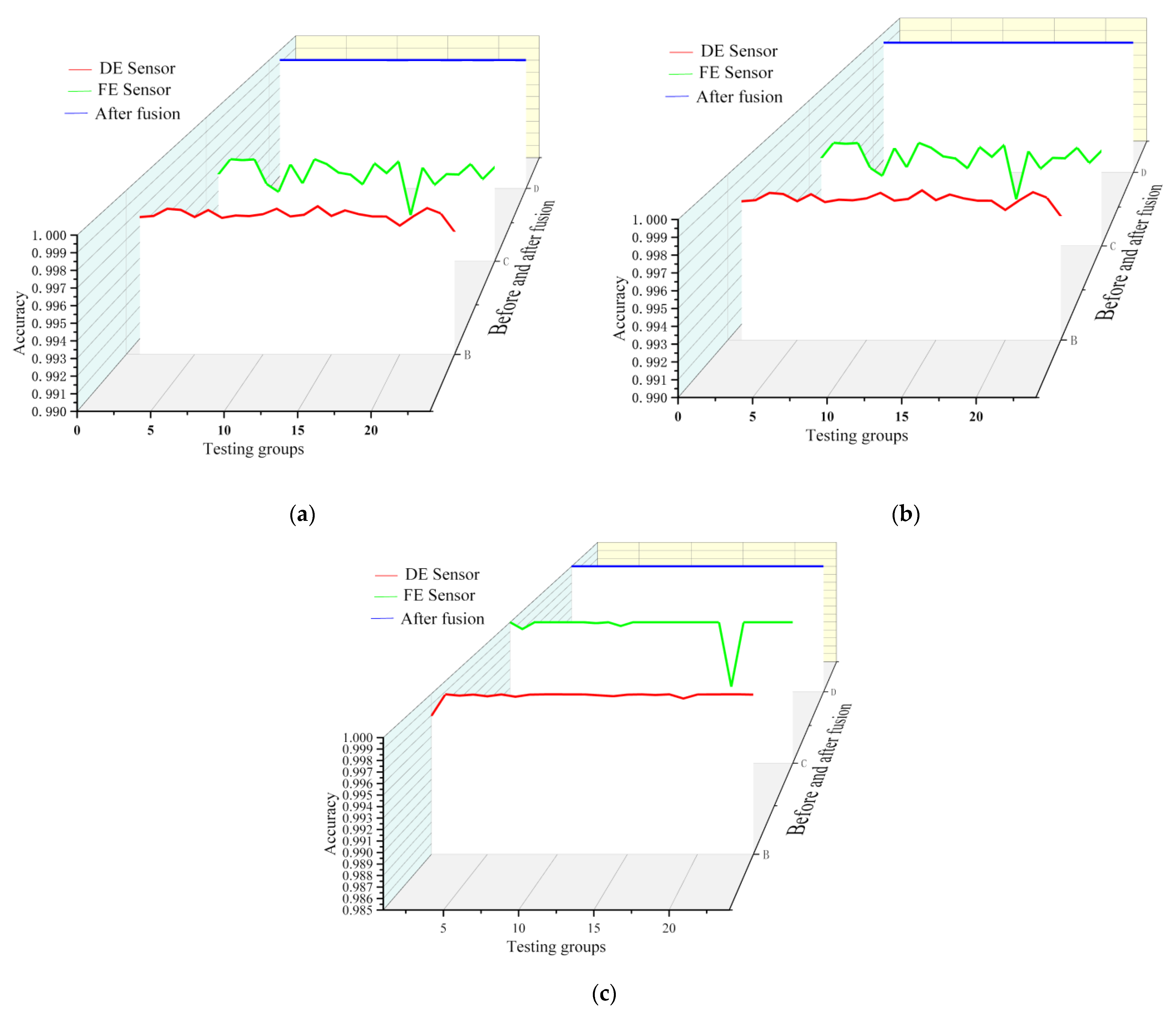When the deflection angles were both 120°, the DE sensors with different values were fused with the FE sensor to provide multi-source information, and the bearing accuracy was obtained before and after the fusion of the two sensors, as shown in Figure 7.

According to Figure 7a, the accuracy of the FE sensor was 99.99% before fusion, the accuracy of the DE sensor was 99.98%, and the accuracy after fusion was 100%. Since the same parameter was used in FE sensor for the purposes of comparison, the accuracy remained the same, while, as can be seen in Figure 7b, the accuracy of the DE sensor before fusion was 99.97%, and the accuracy after fusion was 100%. In Figure 7c, it can be seen that the accuracy of the DE sensor before fusion was 99.98%, and the accuracy after fusion was 100%. Therefore, according to the fusion results, it can be concluded that after using DS fusion technology, the accuracy of failure detection of the bearings was improved.

3.4. Algorithm Comparison

The proposed method was compared with the traditional machine learning-based methods previously studied in order to verify the effectiveness of the proposed method [29]. The BP neural network and GA-BP neural network were used for fault identification, and 118 sets of data were selected for each fault, of which 94 sets were selected as the training set and 24 sets as the test set. The results of the two conventional machine learning algorithms are shown in

Table 6. Comparison of VGG16 with the BP and GA-BP algorithms.

Diagnostic Methods	Features	Accuracy %	DS Theory
BP neural network	Traditional time and frequency-domain	99.85%	100%
GA-BP neural network		99.86%	100%
VGG16	SDP images	99.99%	100%

.

On the basis of the diagnosis results in Table 3, it can be concluded that the inner ring fault diagnosis of the bearing based on SDP images with the VGG16 network can successfully perform the diagnosis function, and the accuracy was higher than that of traditional machine learning diagnosis. Nonetheless, the feature processing of faults was time consuming.

Since a single sensor is not able to fully extract the data from the bearing, DS fusion was used. The accuracies of the traditional machine learning algorithm and the deep learning algorithm of VGG16 before and after multi-sensor fusion are shown in Figure 8.

According to Figure 8, the accuracies of both machine learning algorithms and deep learning algorithms were significantly improved after fusion, and the method proposed in this present study is able to achieve accurate fault diagnosis, reaching accuracies even higher than those of traditional machine learning algorithms.

4. Experiments

4.1. Experimental Data Acquisition

To verify the effectiveness of the proposed method, a gearbox fault detection experiment was set up using an existing gear test bench of the experimental team. The first step was the design of the gearbox experiment, the reasonable selection of sensor positions, and gear selection. The sensor selection for the three three-phase sensors allowed comprehensive monitoring of the gears in the three dimensions of the gearbox. The experimental design is shown in Figure 9. The experimental conditions were established after completion of the design, as shown in Figure 10. This present study aims to make clear the detection of pinion gear teeth under different degrees of pitting, mainly detecting gear teeth in normal condition, and exhibiting slight pitting and medium pitting. The pitting area of the intermediate wheel teeth in the case of slight pitting was 13.09% of the surface area of the wheel teeth, and the pitting area of the two adjacent wheel teeth was 4.36% of the surface area of the wheel teeth. The pitting area of the intermediate wheel teeth in the case of medium pitting was 26.18% of the surface area of the wheel teeth, the pitting area of the two adjacent wheel teeth was 13.09% of the surface area of the wheel teeth, and the pitting area of the two adjacent wheel teeth was 4.36% of the surface area of the wheel teeth [31]. All pitting craters were 1 mm in diameter and 0.5 mm in depth, and the pitting occurred near the pitch line, with a surface area of engagement of 65.70 mm². Thus, for the slight pitting fault, there were 11 pits on one gear teeth and four pits on the two adjacent gear teeth. In terms of the medium pitting fault. There were 22 pits on one gear tooth, 11 pits on the two adjacent gear teeth, and four pits on the two adjacent gear teeth. The pits were located near the knuckle line. The schematic diagram of gear pitting is shown in Figure 11, the actual gear health state is shown in Figure 12, and the experimental data selection is shown in

Table 7. Experimental gear work.

Sampling Frequency (KHz)	Experiment Number of Times	Sampling Time (s)	Load (N · m)	Rotation Speed (r/min)
33.28	60	1	0	500
			…
			10
			…
			30
			0	600
			…
			10
			…
			30

.

A low load was applied to the pinion gear teeth for fault detection at rotational speeds of 500 and 600, as required by the partner company. The gear load varied with the degree of pitting. Under normal conditions, the load was 0 N · m. The load increased in steps of 5 N · m to 30 N · m. According to the experiments, slight pitting took place at a speed of 600 r/min and a load of 10 N · m. On the basis of multiple sets of experiments, it was found that pitting took place at a speed of 600 r/min and a load of 10 N · m. Moderate pitting took place when the rotational speed was 600 r/min and the load was 30 N · m. Therefore, the experimental data are all at 600 r/min, the load of the normal condition is 0 N · m, the load of slight pitting fault is 10 N · m, and the load of medium pitting fault is 30 N · m.

The experimental data for the gear teeth were collected by selecting the experimental data for a certain direction in which the fault state was most obvious from the three sensors. They were then divided into 500 sets of experimental data for each state, with 1024 points for each set of data, and 0, 1, 2 are used to indicate the normal state, light pitting state and medium pitting state of the gear teeth, respectively. After the fault diagnosis model was trained, 100 sets of data were randomly generated to test the accuracy of the model, and the test results were input into the DS fusion theory as evidence to realize multi-sensor decision-level fusion.

4.2. VGG Fault Diagnosis Model with SDP Feature Information Fusion

For each sensor, the experimental data of a certain direction for the gear tooth fault state were selected as the valid data for this experiment. After the analysis of the data, it was found that the changes in the Z-direction were the most obvious for each of the three sensors. Hence, the experimental data in the Z-direction were selected for all three sensors. Using the SDP image processing method, after analyzing the three sensors of the three gear faults at different time lag coefficients, magnification angles, and other important factors, all three sensors had a more obvious fault state when the time lag coefficient l = 7 and angular gain factor ξ = 25°. The gear’s health status is shown in

Table 8. Gears with different levels of pitting.

Sensors	Healthy Condition
	Normal Condition	Normal Condition	Medium Pitting Fault
Sensor 1
Sensor 2
Sensor 3

.

In the VGG16 network structure, the learning rate was set to 0.005, each input sample was 32, and the number of iterations was 1000. When the number of iterations was 300, the accuracy of the experimental data collected by each sensor leveled off. Hence, only the accuracy and loss of the previous 300 sets of experimental data are shown in Figure 13.

According to Figure 13, sensor 1 had an accuracy of 99.42% and a loss of 2.6% in the VGG16 fault diagnosis model. Sensor 2 had an accuracy of 99.36% and a loss degree of 2.38%. Sensor 3 had an accuracy of 97.94% and a loss of 5.21%.

To verify the effectiveness of the VGG16 fault diagnosis model, 100 datasets were randomly generated for each fault state of the gear for detection. In DS evidence theory, the evidence body E = {E1, E2, E3}, where E1, E2, and E3 represent the data collected in the z-direction of sensors 1, 2, 3, respectively. The identification framework $\Theta =\left\{\mathrm{A},\mathrm{B},\mathrm{C}\right\}$, where A, B, and C are the normal condition, slight pitting fault, and medium pitting fault of the gear teeth, respectively. The results obtained by means of inputting 100 sets of randomly generated data into the VGG16 fault diagnosis model were used as the body of evidence for the DS evidence method. After that, decision-level fusion was performed. The accuracy of each sensor before and after fusion is shown in Figure 14 and Figure 15.

From Figure 15, it can be concluded that before fusion, the accuracy of the three sensors was 96.43%, 93.97%, and 93.28%, respectively. When sensor 1 and sensor 2 were fused, the accuracy reached 99.93%, which is 3.52% and 6.34% higher than the accuracies of single sensors 1 and 2, respectively. When sensor 1 and sensor 3 were fused, the accuracy reached 99.96%, demonstrating an improvement of 3.36% and 6.85% compared to single sensors 1 and 3, respectively. When sensor 2 and sensor 3 were fused, the accuracy reached 99.40%, which is 5.78% and 6.56% better than single sensors 2 and 3, respectively. When the three sensors were fused simultaneously, the accuracy reached 99.98%, which is 3.68%, 6.40%, and 7.18% better than the accuracy of single sensors 1, 2, and 3, respectively. Apparently, after applying the DS fusion method, the accuracy became higher than that of the single sensors before fusion. In contrast, when using two sensors fused with each other, the accuracy after fusion was not as high as that of three sensors fused at the same time. In this regard, it is necessary, as far as possible, to collect more comprehensive data signals for gear teeth, in order to greatly improve the accuracy of gear tooth fault diagnosis.

4.3. Analysis of Experimental Results

In this experiment, 500 sets of experimental data were selected, and each set of data consisted of 1024 points. In addition, the experimental results showed that the accuracy of each sensor was improved after the implementation of DS fusion. However, when two sensors were fused with each other, the accuracy was not as high as the accuracy achieved when fusing three sensors at the same time. Additionally, simultaneous fusion of three sensors improved the accuracy by 0.05%, 0.31%, and 0.58% compared to the fusion of sensors 1 and 2, sensors 1 and 3, and sensors 2 and 3, respectively. The experiments showed that the use of the DS fusion method can compensate for the disadvantage of incomplete data collection inherent to using a single sensor and improve the results of gear tooth fault diagnosis. All in all, the fusion algorithm is important for the field of fault diagnosis.

5. Conclusions

To achieve health monitoring for the degree of pitting of gear teeth, since the traditional machine learning algorithm cannot visualize gear fault status, this paper proposes combining SDP images with the VGG16 fault diagnosis algorithm in order to gear tooth fault diagnosis monitoring. Additionally, since the signal collected by single sensors lacks comprehensiveness, and the original signal cannot be obtained from multiple dimensions, it is also proposed to achieve multi-sensor decision-level fusion using DS evidence theory with the local diagnostic results of each sensor obtained using the VGG16 fault diagnosis model algorithm.

In this paper, the proposed method is first compared with the traditional BP algorithm and GABP algorithm through the common bearing dataset of Case Western Reserve University, and the results show that the accuracy of the proposed method is higher than those of the traditional BP algorithm and the GABP algorithm. Then, the proposed method is applied to the experimental data, and the SDP images of each sensor are input into the VGG16 fault diagnosis model, and the obtained local diagnosis results are input into the DS evidence theory as the body of evidence in order to realize the decision fusion level fitting of gear teeth. The results of the simulation and experiment show that the method proposed in this paper, with higher diagnostic accuracy after fusion than before fusion, can compensate for the drawback of poor diagnostic results inherent to using a single sensor. The research results achieved in this paper are as follows: (1) The images generated by the SDP algorithm can detect gear fault diagnosis more intuitively than the time-domain vibration signals. (2) The diagnostic accuracy of the VGG16 algorithm is 0.14% and 0.13% higher than those of the BP algorithm and the GABP algorithm, respectively, in the traditional machine algorithm. (3) The experimental results under the decision-level fusion based on VGG16 show that when three sensors are fused simultaneously, the accuracy can reach 99.98%, which is 3.68%, 6.40%, and 7.18% higher than those of single sensors 1, 2, and 3, respectively. The simultaneous fusion of three sensors improves the accuracy by 0.05%, 0.31%, and 0.58% over sensor 1 and 2 fusion, sensor 1 and 3 fusion, and sensor 2 and 3 fusion, respectively. The use of the DS fusion method can compensate for the disadvantage of incomplete data collection inherent to the use of a single sensor, and can improve the results of gear tooth fault diagnosis, which is important for the fusion algorithm in the field of fault diagnosis.