A Stigmergy-Based Differential Evolution

Abstract

Metaheuristic algorithms are techniques that have been successfully applied to solve complex optimization problems in engineering and science. Many metaheuristic approaches, such as Differential Evolution (DE), use the best individual found so far from the whole population to guide the search process. Although this approach has advantages in the algorithm’s exploitation process, it is not completely in agreement with the swarms found in nature, where communication among individuals is not centralized. This paper proposes the use of stigmergy as an inspiration to modify the original DE operators to simulate a decentralized information exchange, thus avoiding the application of a global best. The Stigmergy-based DE (SDE) approach was tested on a set of benchmark problems to compare its performance with DE. Even though the execution times of DE and SDE are very similar, our proposal has a slight advantage in most of the functions and can converge in fewer iterations in some cases, but its main feature is the capability to maintain a good convergence behavior as the dimensionality grows, so it can be a good alternative to solve complex problems.

1. Introduction

Metaheuristics (MH) are computational algorithms inspired by biological phenomena that solve a great diversity of complex scientific and engineering problems, particularly optimization. Some key features of metaheuristics are: (1) robustness, (2) self-organization, (3) adaptation and (4) decentralized control [1]. Two of the most recognized branches in MH, which group several approaches, are Evolutionary Computation (EC) and Swarm Intelligence (SI) algorithms [2]. Even though different metaphors inspire them, all have a set of parameters that the user must tune in a manual, adaptive, or self-adaptive manner to help the algorithm’s exploration/exploitation balance [3]. However, in several MH, the use of a global best candidate solution to direct the search process toward the real optimum is common.

For instance, Harmony Search [4,5,6] utilizes several individuals from the harmony memory (HM) to improvise a new harmony, and this individual is incorporated into the HM only if it is better than the worst individual in the whole population. Differential Evolution [7] uses in most canonical variants [8] a weighted difference of at least two parents to generate a new individual, which interchanges information with the actual individual and becomes the trial solution. The selection step compares the trial individual’s fitness against both the actual individual’s fitness and the best individual found so far. Another metaheuristic approach is Particle Swarm Optimization [9], which considers the local best and the global best to make a velocity vector added to the actual individual to generate a new individual, whose fitness is compared against the local best and the global best and, if necessary, replaces the global best. The canonical Fireworks algorithm [10,11], whose population is composed of fireworks, modifies the individuals by consecutively applying the explosion, the Gaussian mutation, and the mapping operators. After such alterations, the new candidate solution’s fitness is compared against the best individual so far, and the individual with better fitness value is kept in memory. Based on some plants’ reproduction strategy, the authors in [12] proposed the Flower Pollination Algorithm (FPA). This metaheuristic uses the abiotic, biotic, and switch operators to either locally or globally modify the actual candidate solution. As in the previous algorithms, FPA keeps tracking the best global individual found at each iteration. Another algorithm is the Gravitational Search algorithm [13], in which the movements of the candidate solutions (called objects) consider their masses and accelerations to actualize their velocities and positions. As in other metaheuristics, the algorithm updates the global worst and the global best at each iteration. Other examples of metaheuristics that actualize the best solution found at each iteration are the Firefly Algorithm [14,15], Cuckoo Search [16], Artificial Bee Colony optimization [17,18] and Chicken Swarm optimization [19].

In order to solve high-dimensional problems and evaluate a large amount of data, it is necessary to improve the efficiency and execution times of evolutionary algorithms. Many authors consider parallel and distributed approaches of metaheuristic algorithms as alternatives to overcome the difficulties derived from the increase in data complexity. A recent review of parallel and distributed approaches for evolutionary algorithms is presented in [20]. In addition, much research reports metaheuristics translated to parallel languages, such as CUDA (Compute Unified Device Architecture) [21], which runs on parallel general-purpose graphic processing units (GPGPU). For example, a survey of GPU parallelization strategies for metaheuristics is conducted in [22]. The authors of [23] propose two approaches to parallelize the Gravitational Search algorithm using CUDA: one that modifies the whole population with a single kernel and another that utilizes multiple kernels to operate the complete population. In the multiple kernel version, the least parallelizable is the update mass kernel. At a given moment, all threads could be trying to write the global best to the same memory location.

With respect to DE, several proposals have been made to parallelize this algorithm, such as the one presented in [24], where opposition-based learning and Differential Evolution are programmed with CUDA to optimize 19 benchmark functions. The authors cannot perform the fittest selection in parallel, and they propose a reduction approach to find the best individual at each iteration. A similar approach is found in [25], where only four functions are tested up to 100 dimensions. In this case, the authors propose the use of an adaptive scaling factor and an adaptive crossover probability; even though the authors utilize the DE/rand/1/bin version, they also keep track of the best individual so far. To represent DE variants, a general pattern DE/x/y/z is used, where x describes the base vector selection type, y represents the number of differentials and z is the type of crossover operator, and if there is an asterisk symbol (*) it means that any valid operator can be used for that process. Thus, for DE/rand/1/bin, “rand” indicates that the individuals are randomly chosen, “1” specifies that only one vector difference is used to form the mutated population and “bin” means that a binomial crossover is applied.

A survey of DE parallelized on GPGPU is found in [26], tracking the research efforts to parallelize DE from computer networks since 2004, passing through the use of GPGPU with first (and therefore, with a lack of features) CUDA SDKs and ending with a brief exploration of DE and GPU-based frameworks. It is worth mentioning that, in most of the articles, the original operators are preserved and only the parallel implementation is performed using one kernel for each process. To have a general idea about the implementation of DE on GPUs,

Table 1. GPU differential evolution implementation proposals.

Reference/Year	Version	Modified Operators	Operators Not Modified	Type and Number of Functions	Maximum Dimensionality
[27]/2010	DE/rand/1/bin	None	Mutation, Crossover, Selection	Benchmark functions, 6	100
[28]/2010	DE/rand/1/bin	None	Mutation, Crossover, Selection	Benchmark functions, 12	90
[29]/2011	DE/rand/1/bin	None	Mutation, Crossover, Selection	Task scheduling benchmark, 12	512
[25]/2012	DE/rand/1/bin	None	Mutation, Crossover, Selection	Benchmark functions, 4	100
[30]/2013	DE/rand/1/bin	None	Mutation, Crossover, Selection	Real-world object detection, 2	32, and 9, pertaining to each parametric model
[31]/2012	CDE/rand/1/bin (Coevolution DE)	None	Mutation, Crossover, Selection	Functions with restrictions, 6	10
[32]/2012	EOBDE/rand/1/bin (Elite oppostion-based learning DE)	None	Mutation, Crossover, Selection	Benchmark functions, 10	1000
[24]/2013	GOjDE/rand/1/exp (Generalized opposition j DE)	None	Mutation, Crossover, Selection	Benchmark functions, 19	1000
[33]/2021	DE/*/*/exp	Crossover	Mutation, Selection	Benchmark functions, 3	1000

shows some proposals highlighting the implemented DE version, whether any operator was modified or not, the number and type of test functions and the maximum dimensionality. It can be observed that the idea of proposing modifications to differential evolution operators has not been widely investigated.

Some metaheuristics utilize two methods to update the global best (individual and fitness) by: (a) comparing it against the corresponding values of every individual in the population and (b) sorting the corresponding values of the entire population. In the first approach, parallelization implies that $N_p-1$ individuals will be trying to update the best fitness value in the actual iteration and the best individual to the same memory’s positions: this is the worst-case scenario. This could produce race conditions, which are undesirable because they could produce a loss of information. A better method is the sorting-based approach which can only be partially parallelized, in fact, this DE algorithm version is the one used for comparisons in this research.

This paper considers a modification, based on the stigmergy concept, to Differential Evolution (version best/1/bin, in this case the best individual solution of the DE population is selected as the target vector) to eliminate the global best utilization. For this purpose, the mutation and crossover operators are modified. Such adjustment, which we called Stigmergic Differential Evolution (SDE), has a similar performance to the original DE with a lower computational cost in some cases when programmed into GPGPU; mainly, it preserves a good convergence behavior as the dimensionality grows. Therefore, we consider that other metaheuristics that utilize the global best to guide the optimization process could benefit from the proposed methodology.

The remaining paper is as follows: Section 2 explains the concept of stigmergy and explores some of its applications to solve engineering problems. Section 3 gives an account of our proposal and the benchmark of optimization problems for the comparisons. In contrast, Section 4 explains the experimental setup, shows the results and briefly discusses the results. Section 5 concludes this work and gives some future venues around stigmergic metaheuristics.

2. Stigmergy and Some Stigmergic Applications

Some authors consider insect colonies as complex adaptive systems, with properties of: (1) spatial distribution; (2) decentralized control; (3) hierarchical organization of individuals; (4) adaptation to environmental changes, among others [17,34]. For the second property, this means that there is no global control [34], and therefore the interactions among individuals are distributed. To explain the behavior of insect colonies, researchers proposed the term stigmergy. 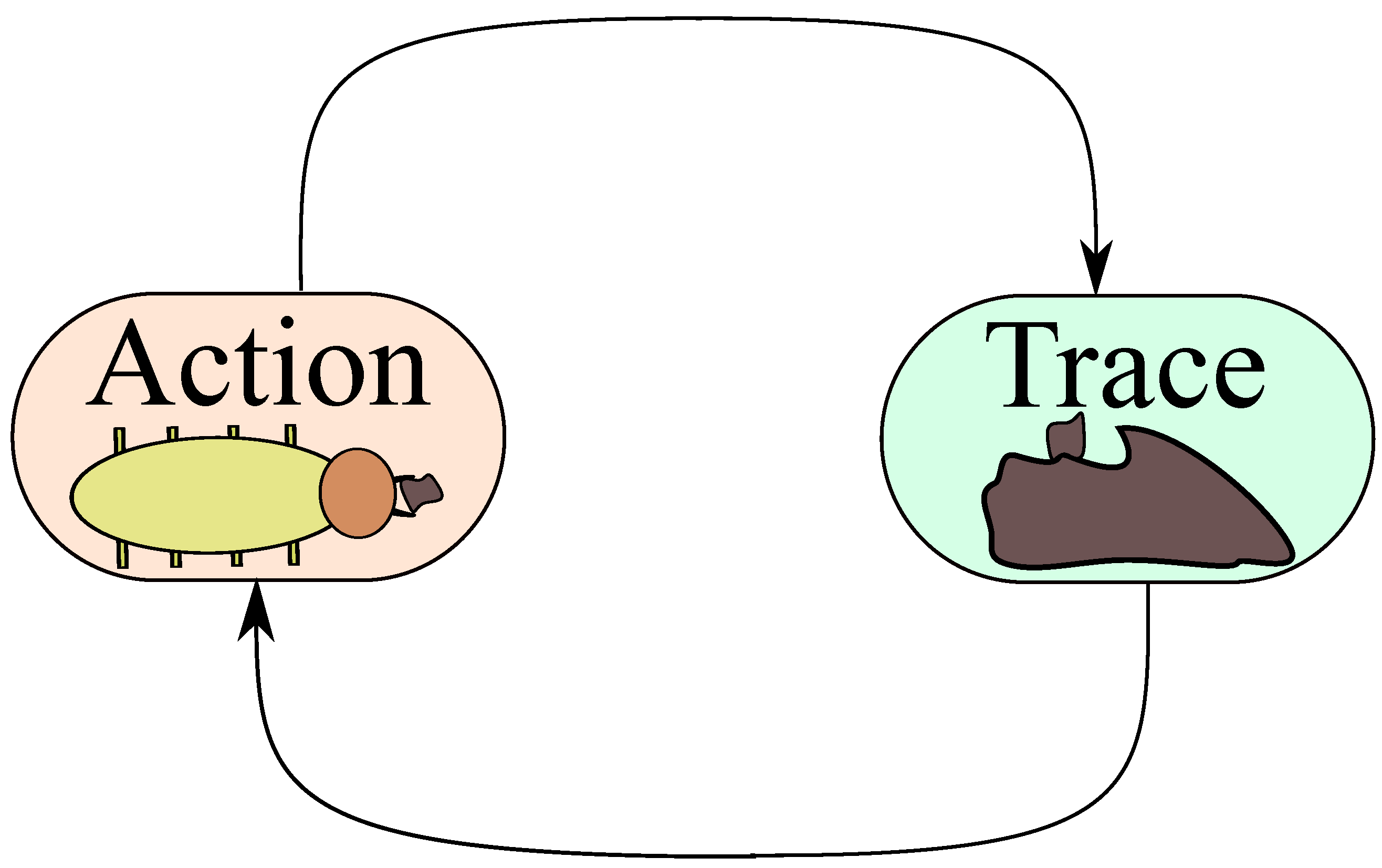Such a concept comes from entomology, and Pierre-Paul Grassé proposed it to explain the coordination and collaboration by the indirect communication [35,36] of social insects (particularly termites and ants) to complete complicated projects [37]. In the original paper, Grassé considers that every individual in a colony that acts (ergon) on the medium leaves a trace (stigma), which at the same time stimulates another action from the same or another individual (Figure 1). Actions and marks occur on the medium, and as mentioned, the latter only stimulate (but not force) the action of either the same or other individuals.

The concept of stigmergy has served as an inspiration to propose algorithms utilized to solve some problems in engineering [38,39,40], and it also was used as an inspiration to propose one of the most known metaheuristic algorithms: Ant System (AS) [41], the predecessor of Ant Colony Optimization (ACO) and its variants. In these approaches, it is the pheromone-based construction of trails that represents the stigmergic mechanism [36,42,43].

ACO considers a population of artificial agents that keep some memory in the form of the pheromone of the best solutions visited so-far; those solutions are paths of a completely connected graph, constructed by selecting every vertex in the path in a probabilistic manner, being that vertices in the graph with the most artificial pheromones are the more likely to be selected. As the algorithm works in the graphs’ space to construct the solutions, it is natural that the first applications of this technique are in combinatorial optimization, such as the Traveling Salesman Problem or job-shop scheduling. The application of ACO to solve numerical optimization problems is not straightforward. Often, the proposals include hybridizations with other techniques, as the continuous ACO (CACO) [44], continuous interacting ant colony (CIAC) [45], or continuous ant colony system (CACS) [42]; however, there are some research efforts using direct modifications to the original ACO. For instance, in his doctoral thesis, Korošec proposed two stigmergy-based modifications of the original ACO to solve numerical problems, including the Differential Ant-Stigmergy Algorithm [36]. In the proposal, the authors present a fine-grained discretization of the continuous search space to construct a directed graph, to which they apply the operators Gaussian pheromone aggregation, pheromone evaporation and parameter precision to build a solution for the continuous optimization problem at hand. Korošec and colleagues later improved the original algorithm to tackle high-complexity problems or even dynamic problems [43,46] by using a pheromone operator based on the Cauchy distribution.

A recently proposed stigmergic algorithm to solve numeric problems is the teaching–learning-based optimization [47]. In the paper, students’ cooperation (ergon/action) through a board (stigma/mark) simulates the stigmergic process. Algorithmically, the authors create a ranking matrix (of the same size as the original population) for every individual, and they use a roulette wheel to select a guide student. Such guiding students serve as the mean to generate new solutions, which utilize as a standard deviation the weighted average of the remaining individuals. Therefore, the guiding student directs the complete exploration–exploitation process, diluting the stigmergic process as it happens in other metaheuristics.

In the next section, we explain our approach, the Stigmergic Differential Evolution, SDE. The algorithm eliminates the use of global best. Thus, the whole population controls the exploration–exploitation process in a coordinated but decentralized manner; moreover, to explore the efficiency of the proposal and its parallelization feasibility, we programmed it on GPGPU using the CUDA language.

3. Stigmergic Differential Evolution

3.1. Differential Evolution

Differential Evolution (DE) is an algorithm proposed in 1995 to solve continuous optimization problems [7]. Even though there are several variants of DE [8], one of the more popular and powerful variants is the DE/best/1/bin, which since its development has solved several problems in science and engineering [48,49,50]. The notation in the next explanations considers lower bold letters as vectors, lower italic letters with subindexes as vector components, upper bold letters as matrices and upper or lower letters without subindexes as single real or integer numbers.

The first step in the algorithm is the initialization of a random population:

$$\begin{array}{c}\hfill \mathit{X}=x_{i,j}^k=l_j+rand\left(\right)\left(u_j-l_j\right)\\ \hfill j=1,\cdots ,D;i=1,\cdots ,N_p;k=0\end{array}$$

(1)

where $N_p$ is the population size, D represents the problem dimensionality, k is the actual iteration, l and u are the lower and upper limits of the search space and $rand\left(\right)$ is a random number drawn from a uniform distribution. In this phase the parameters’ scaling mutation and crossover factor $(F,Cr)$ are also set. The second stage creates a mutant vector:

$${\mathit{v}}^k={\mathit{x}}_{best}^k+F·\left({\mathit{x}}_{r_1}^k-{\mathit{x}}_{r_2}^k\right)$$

(2)

considering $r_1$ and $r_2$ as random integers uniformly distributed in $[1,N_p]$ with the restriction that $r_1\ne r_2\ne i$, and ${\mathit{x}}_{best}^k$ is the best individual found so-far. The next step obtains the trial vector:

$$u_j^k=\left\{\begin{array}{cc}{v}_j^k& ifrand⩽C_{r}orj=j_{rand}\\ x_{i,j}^k& otherwise\end{array}\right.$$

(3)

where $j_{rand}\in \left\{\begin{array}{c}1,2,\cdots ,D\end{array}\right\}$ is a random integer taken from a uniform distribution. In the last phase, the algorithm applies the selection operation by evaluating the trial and the original individual with the objective function f:

$${\mathit{x}}_i^{k+1}=\left\{\begin{array}{cc}{\mathit{u}}^k& iff\left({\mathit{u}}^k\right)<f\left({\mathit{x}}_i^k\right)\\ {\mathit{x}}_i^k& otherwise\end{array}\right.$$

(4)

The previously mentioned steps (mutation, crossover and selection) are repeated until a criterion is met, usually a maximum number of iterations.

3.2. The Proposal–Action, Agent, Medium, Trace and Coordination

As in other bioinspired algorithms, in Stigmergic Differential Evolution, we do not try to precisely copy every aspect of the stigmergy concept but only to use it as an inspiration source. Let us consider a stigmergy process [51,52]: the nesting construction/repairing made by termites. This process is parallel, it needs only local information and it has no apparent global leadership. By considering Figure 1, for a single stigmergic loop, it happens that ${\mathrm{individual}}_i$ (previously stimulated by ${\mathrm{trace}}_i$ or other traces) produces an ${\mathrm{action}}_i$ that leaves a ${\mathrm{trace}}_i$ which probabilistically stimulates either ${\mathrm{individual}}_i$ or near individuals. We also consider that, as in the case of real termites, only a few individuals can share a physical space (Figure 2), and only one of them could leave a trace/mark in the medium at a time. Many termites work in the nest, then, they complete the previous steps in parallel, and they repeat the stigmergic cycle until the mound is complete and functional [37].

As in other metaheuristics, Stigmergic DE considers a population of candidate solutions as the agents, while evaluating the candidate solutions represents the traces. Like its real counterpart, the stigmergic approach considers that few candidate solutions can share consecutive memory spaces with one another. For example, in 

Table 2. Population and fitness arrangement in SDE.

Agent	Trace
${\mathit{x}}_1$	$f\left({\mathit{x}}_1\right)$
⋯	⋯
${\mathit{x}}_{i-1}$	$f\left({\mathit{x}}_{i-1}\right)$
${\mathit{x}}_i$	$f\left({\mathit{x}}_i\right)$
${\mathit{x}}_{i+1}$	$f\left({\mathit{x}}_{i+1}\right)$
⋯	⋯
${\mathit{x}}_{Np}$	$f\left({\mathit{x}}_{Np}\right)$

, candidate solutions ${\mathit{x}}_{i-1}$, ${\mathit{x}}_i$ and ${\mathit{x}}_{i+1}$, and their respective fitness function evaluations, are neighbors, as they share consecutive locations in memory.

As in other algorithms, Equation (1) serves to initialize the population of candidate solutions in SDE. Prior to the action step, we compare the traces of the actual with the next and the previous individuals in the memory:

$${\mathit{x}}_{lead}^k=argmin\left(f\left({\mathit{x}}_{i-1}^k\right),f\left({\mathit{x}}_i^k\right),f\left({\mathit{x}}_{i+1}^k\right)\right)$$

(5)

for $i=2,\dots ,N_{p-1}$; the original index of ${\mathit{x}}_{lead}^k$ is also stored, e.g., $lead=i-1$, $lead=i$, or $lead=i+1$. The remaining two candidate solutions after applying Equation (5) are randomly labeled, with  50% probability, as ${\mathit{x}}_{work1}^k$ and ${\mathit{x}}_{work2}^k$; also, their respective indexes are stored. The action step considers the mutation DE operator with the differential weight F:

$${\mathit{v}}_i^k={\mathit{x}}_{lead}^k+F·\left({\mathit{x}}_{work1}^k-{\mathit{x}}_{work2}^k\right)$$

(6)

together with the original trial DE operator using the crossover rate $C_r$:

$$u_{i,j}^k=\left\{\begin{array}{cc}{v}_{i,j}^k& ifrand\left(\right)<C_{r}orj=j_{rand}\\ x_{i,j}^k& otherwise\end{array}\right.$$

(7)

After the trial vector is complete, the next phase of stigmergic DE is the trace update:

$${\mathit{x}}_{lead}^{k+1}=\left\{\begin{array}{cc}{\mathit{u}}_i^k& iff\left({\mathit{u}}_i^k\right)<f\left({\mathit{x}}_{lead}^k\right)\\ {\mathit{x}}_{lead}^k& otherwise\end{array}\right.$$

(8)

$${\mathit{x}}_{work1}^{k+1}=\left\{\begin{array}{cc}{\mathit{u}}_i^k& iff\left({\mathit{u}}_i^k\right)<f\left({\mathit{x}}_{work1}^k\right)\\ {\mathit{x}}_{work1}^k& otherwise\end{array}\right.$$

(9)

$${\mathit{x}}_{work2}^{k+1}=\left\{\begin{array}{cc}{\mathit{u}}_i^k& iff\left({\mathit{u}}_i^k\right)<f\left({\mathit{x}}_{work2}^k\right)\\ {\mathit{x}}_{work2}^k& otherwise\end{array}\right.$$

(10)

It is essential to clarify that Equations (8)–(10) are mutually exclusive in their application; for example, if the condition is true in Equation (8), then Equations (9) and (10) are not applied in this step of the algorithm. As in other metaheuristics, the algorithm repeats the previous steps until it reaches a specific criterion.

One of the main differences between Differential Evolution and Stigmergic Differential Evolution is the complete elimination of the global optimum. Instead, SDE uses a leader’s concept, which is a local best concerning the actual individual. Another distinction is the tracing step, which involves the previous, actual and posterior candidate solutions. According to their fitness, SDE could update any of the three individuals in this stage, or none in the worst case. This crucial step enables the algorithm to share information among candidate solutions of the whole population via indirect communication. In that sense, we consider that SDE disseminates the improvements in the search for the optimum in a distributed manner.

3.3. Parallel DE and SDE

In the literature, several proposals for parallelization of DE exist to solve plenty of optimization problems, as reported in [24,25,53,54,55,56]. Nevertheless, we utilize a basic CUDA parallelization as mentioned in Section 3.2 of [25] to compare the two algorithms. For the DE version, we programmed three kernels:

1.

Generate mutated and trial vectors and evaluate trial vectors.

2.

Compare and update the fitness of trial vectors and the original population.

3.

Obtain the global best.

This version of DE permits a fine-grained parallelization of the first two kernels. Still, the case is different in the third one, which only can be partially parallelized with reduction steps and using a reduction approach, which is a common way to reduce a search effort in parallel. The complete kernel to obtain the global best is in Algorithm 1; it is essential to notice that this kernel operates only with vector sizes divisible by 2.

In the case of SDE, we programmed only one CUDA kernel containing the steps: comparing previous traces, action and trace updating. In that sense, the nature of Stigmergic DE permits a fine-grained parallelization, meaning all the steps of the stigmergic approach can be applied to every individual in the population in parallel. A pseudocode of the stigmergic kernel is given in Algorithm 2.

Algorithm 1 Kernel of DE to obtain the global best

1: procedure_global_ void getGlobalBest(double* F, double* fbest, double* xbest, double* X, int* indices) 2:     _shared_ double min[Np]; // Declare array in shared memory 3:     _shared_ int indexes[Np]; // Array of indexes in shared memory 4:     int blockId = blockIdx.x + blockIdx.y * gridDim.x; 5:     int arrayIndex = blockId * (blockDim.x * blockDim.y) + (threadIdx.y * blockDim.x) + threadIdx.x, i; 6:     min[threadIdx.x] = F[arrayIndex]; 7:     indexes[threadIdx.x] = indices[arrayIndex]; 8:     _syncthreads(); 9:     int nTotalThreads = blockDim.x; // Total number of active threads 10:     while nTotalThreads > 1 do 11:         int halfPoint = (nTotalThreads >> 1); 12:         // only the first half of the threads will be active. 13:         if (threadIdx.x < halfPoint) then 14:            // Obtain the shared value stored by another thread 15:            double temp = min[threadIdx.x + halfPoint]; 16:            int temp1 = indexes[threadIdx.x + halfPoint]; 17:            if (temp < min[threadIdx.x]) then 18:                min[threadIdx.x] = temp; 19:                indexes[threadIdx.x] = temp1; 20:            end if 21:         end if 22:         _syncthreads(); 23:         nTotalThreads = (nTotalThreads >> 1); 24:     end while 25:     if (threadIdx.x == 0) then 26:         fbest[blockIdx.y + blockIdx.x] = min[0]; 27:         for (i = 0; i < D; i++) xbest[i] = X[(indexes[0]) * D + i]; 28:     end if 29:     _syncthreads(); 30: end procedure

Algorithm 2 Stigmergy-inspired kernel of SDE

1: procedure_global_ void stigmergic(double* X, double* F, double f, double cr, int funcion) 2:     Obtain the thread identity with respect to the block in the grid 3:     Obtain jrand as a uniform integer random number 4:     if (arrayIndex > 0 and arrayIndex < Np − 1) then 5:         // Trace comparison: 6:         Obtain $x_{lead}$, $x_{work1}$, $x_{work2}$ according to their fitness 7:         //Action (Mutant vector, Trial vector): 8:         Calculate mutant vector with Equation (6) 9:         Compose trial vector with Equation (7) 10:         //Trace update: 11:         Compare and update fitness of trial vector against fitness of $x_{lead}$, $x_{work1}$, $x_{work2}$ with Equations (8)–(10) 12:         _syncthreads(); 13:     end if 14: end procedure

A kernel that generates the initial population is the same for both algorithms; also, DE utilizes an extra kernel to evaluate the initial population’s fitness only once.

4. Experimental Results

To perform the experiments, the computer has the next features:

• OS: Windows 10 64 bits
• CPU: i7-4770 running at 3.4 GHz
• RAM: 16 GB
• GPU: GTX 960 with 2 GB of RAM
• Compiler: Visual Studio 2019

Both algorithms are programmed in CUDA C by using the SDK version 11.1, reusing some kernel functions such as creating or evaluating the initial population. Moreover, both implementations utilize global memory, except for the reduction approach, to find the global best in DE, which uses shared memory.

The DE version/best/1/bin is the algorithm programmed in this paper, and the SDE operators are a modified version of DE; also, the parameters are set as: $F=0.8$ and $C_r=0.3$ in the two approaches. Population size is set as 256 and 512 individuals for every experiment, whereas for every problem the dimension is 100 and 500. The reason for these population sizes is because of the requirements of the kernel to obtain the global best used in DE.

4.1. Benchmark Used in the Experiments

The experimental testbed consists of 27 functions. We used 14 multidimensional objective functions (

Table 3. $D>2$ objective functions. The optimum value is denoted as $f^{*}$ and $x^{*}$ is the candidate solution.

Function	$\mathit{f}\left(\mathit{x}\right)$	Limits ${\mathit{x}}_{\mathit{i}}$	${\mathit{f}}^{*};{\mathit{x}}^{*}$
F1: Sphere	${\displaystyle \sum _{i=1}^d}{x}_i^2$	[−5.12, 5.12]	0; 0, …, 0
F2: Step	${\displaystyle \sum _{i=1}^d}{\left(⌊x_i+0.5⌋\right)}^2$	[−100, 100]	0; [−0.5, 0.5)
F3: Sum Powers	${\displaystyle \sum _{i=1}^d}{\left|x_i\right|}^{i+1}$	[−1, 1]	0; 0, …, 0
F4: Sum Squares	${\displaystyle \sum _{i=1}^d}i{x}_i^2$	[−10, 10]	0; 0, …, 0
F5: Dixon and Price	${\left(x_i-1\right)}^2+{\displaystyle \sum _{i=2}^d}i{\left(2x_i^2-x_{i-1}\right)}^2$	[−10, 10]	$0;x_i=2^{-\frac{2^i-2}{2^i}}$
F6: Rosenbrock	${\displaystyle \sum _{i=1}^{d-1}}\left[100{\left(x_{i+1}-x_i^2\right)}^2+{\left(x_i-1\right)}^2\right]$	[−30, 30]	0; 1, …, 1
F7: Schwefel 2.22	${\displaystyle \sum _{i=1}^d}\left|x_i\right|+{\displaystyle \prod _{i=1}^d}\left|x_i\right|$	[−10, 10]	0; 0, …, 0
F8: Trid	${\displaystyle \sum _{i=1}^d}{\left(x_i-1\right)}^2-{\displaystyle \sum _{i=2}^d}{x}_i{x}_{i-1}$	$\left[-d^2,d^2\right]$	$-\frac{d\left(d+4\right)\left(d-1\right)}{6};x_i=i\left(d+1-i\right)$
F9: Zakharov	${\displaystyle \sum _{i=1}^d}{x}_i^2+{\left({\displaystyle \sum _{i=1}^d}0.5i{x}_i\right)}^2+{\left({\displaystyle \sum _{i=1}^d}0.5i{x}_i\right)}^4$	[−5, 10]	0; 0, …, 0
F10: Ackley	$-a\exp \left(-b\sqrt{\frac{1}{d}{\displaystyle \sum _{i=1}^d}{x}_i^2}\right)-\exp \left(\frac{1}{d}{\displaystyle \sum _{i=1}^d}\cos \left(c{x}_i\right)\right)+a+\exp \left(1\right)$ where $a=20,b=0.2$	[−32.768, 32.768]	0; 0, …, 0
F11: Rastrigin	$10d+{\displaystyle \sum _{i=1}^d}\left[x_i^2-10\cos \left(2\pi x_i\right)\right]$	[−5.12, 5.12]	0; 0, …, 0
F12: Schwefel	$418.9829d-{\displaystyle \sum _{i=1}^d}{x}_i\sin \left(\sqrt{\left|x_i\right|}\right)$	[−500, 500]	0; 420.9687, …, 420.9687
F13: Griewank	${\displaystyle \sum _{i=1}^d}\frac{x_i^2}{4000}-{\displaystyle \prod _{i=1}^d}\cos \left(\frac{x_i}{\sqrt{i}}\right)+1$	[−600, 600]	0; 0, …, 0
F14: Levy	${\sin }^2\left(\pi w_i\right)+{\displaystyle \sum _{i=1}^{d-1}}{\left(w_i-1\right)}^2\left[1+10{\sin }^2\left(\pi w_i+1\right)\right]+{\left(w_d-1\right)}^2·\left[1+{\sin }^2\left(2\pi w_d\right)\right]\mathrm{where}{w}_i=1+\frac{x_i-1}{4}$	[−10, 10]	0; 1, …, 1

) that have different search spaces and different complexity levels. For example, the functions: Step, Ackley, Griewank, Levy, Rastrigin, Schwefel and Schwefel 2.22 have many local minima near the global optimum. The functions: Sphere, Sum Powers, Sum Squares and Trid have only one global optimum and are bowl-shaped. The functions Zakharov, Dixon and Price and Rosenbrock have a valley-shaped form, and the Zakharov function has only one global optimum, whereas the other two functions have several optima. Moreover, 13 two-dimensional objective functions (

Table 4. $D=2$ objective functions. The optimum value is denoted as $f^{*}$ and $x^{*}$ is the candidate solution.

Function	$\mathit{f}\left(\mathit{x}\right)$	Limits ${\mathit{x}}_{\mathit{i}}$	${\mathit{f}}^{*};{\mathit{x}}^{*}$
F15: Treccani	$x_1^4+4x_1^3+4x_1^2+x_2^2$	[−5, 5]	0; $\left\{\left(-2,0\right),\left(0,0\right)\right\}$
F16: Beale	${\left(1.5-x_1+x_1{x}_2\right)}^2+{\left(2.25-x_1+x_1{x}_2^2\right)}^2+{\left(2.625-x_1+x_1{x}_2^3\right)}^2$	[−4.5, 4.5]	0; (3,0.5)
F17: Booth	${\left(x_1+2x_2-7\right)}^2+{\left(2x_1+x_2-5\right)}^2$	[−10, 10]	0; (1,3)
F18: Brent	${\left(x_1+10\right)}^2+{\left(x_2+10\right)}^2+exp\left(-x_1^2-x_2^2\right)$	[−10, 10 ]	0; (−10,10)
F19: Cube	$100{\left(x_2-x_1^3\right)}^2+{\left(1-x_1\right)}^2$	[−10, 10]	0; (1,1)
F20: Davis	${\left(x_1^2+x_2^2\right)}^{0.25}\left[{\sin }^2\left(50{(3x_1^2+x_2^2)}^{0.1}\right)+1\right]$	[−100, 100]	0; (0,0)
F21: Matyas	$0.26\left(x_1^2+x_2^2\right)-0.48x_1{x}_2$	[−10, 10]	0; (0,0)
F22: Schaffer	$0.5+\frac{{\sin }^2\left(\sqrt{x_1^2+x_2^2}\right)-0.5}{{\left(1+0.001\left(x_1^2+x_2^2\right)\right)}^2}$	[−100, 100]	0; (0,0)
F23: Bohachevsky1	$x_1^2+2x_2^2-0.3\cos \left(3\pi x_1\right)-0.4\cos \left(4\pi x_2\right)+0.7$	[−100, 100]	0; (0,0)
F24: Egg Crate	$x_1^2+x_2^2+25\left[{\sin }^2\left(x_1\right)+{\sin }^2\left(x_2\right)\right]$	[−5, 5]	0; (0,0)
F25: Bohachevsky2	$x_1^2+2x_2^2-0.3\cos \left(3\pi x_1\right)\cos \left(4\pi x_2\right)+0.3$	[−100, 100]	0; (0,0)
F26: Bohachevsky3	$x_1^2+2x_2^2-0.3\cos \left(3\pi x_1+4\pi x_2\right)+0.3$	[−100, 100]	0; (0,0)
F27: Three-Hump Camel	$2x_1^2-1.05x_1^4+\frac{x_1^6}{6}+x_1{x}_2+x_2^2$	[−5, 5]	0; (0,0)

) were tested. Some of these functions have an optimal value solution outside the vector 0, …, 0. This is useful for testing a bias towards such a value when new metaheuristic approaches are proposed, as suggested by [57].

4.2. Execution Time

To compare the computational time of DE and SDE, we stored the execution time after 5000 iterations of every algorithm and calculated the average and standard deviation after 30 runs. In this case, we measured the execution time since the initial population’s creation until the last iteration; the time counter is reset to zero only after one run is complete. The problem dimensionality has either 100 or 500 dimensions, with 256 and 512 individuals; therefore, this experiment has four instances. The calculus of speedup considers the average time of each function $\left(speedup=\frac{T_{DE}}{T_{SDE}}\right)$. The results are in

Table 5. Mean and averaged execution times in seconds of DE and SDE (D = 100).

	Execution Time $\mathit{\mu }\left(\mathit{\sigma }\right)$ for 256 Individuals			Execution Time $\mathit{\mu }\left(\mathit{\sigma }\right)$ for 512 Individuals
Function	DE	SDE	Speedup	DE	SDE	Speedup
F1: Sphere	9.2106 (0.0782)	8.7910 (0.0708)	1.05	10.3554 (0.0606)	9.2490 (0.0638)	1.12
F2: Step	11.4135 (0.0608)	10.6315 (0.0899)	1.07	12.6158 (0.0.0241)	11.3259 (0.0703)	1.11
F3: Sum Powers	9.2367 (0.0949)	8.8988 (0.0745)	1.04	10.0024 (0.0833)	9.4303 (0.0487)	1.06
F4: Sum Squares	9.2517 (0.1358)	8.7713 (0.0808)	1.05	10.0787 (0.0611)	9.3388 (0.0978)	1.08
F5: Dixon and Price	14.4088 (0.1586)	13.9450 (0.0560)	1.03	15.7625 (0.1041)	14.8474 (0.0390)	1.06
F6: Rosenbrock	19.2443 (0.0919)	18.8281 (0.0662)	1.02	21.1980 (0.1622)	19.9684 (0.0738)	1.06
F7: Schwefel 2.22	6.1812 (0.0072)	5.7724 (0.0417)	1.07	6.3052 (0.0066)	6.0008 (0.0449)	1.05
F8: Trid	9.6917 (0.1798)	8.8270 (0.0528)	1.10	10.3362 (0.0354)	9.4783 (0.0824)	1.09
F9: Zakharov	9.6774 (0.1288)	9.1474 (0.0544)	1.06	10.4172 (0.0930)	9.7241 (0.0509)	1.07
F10: Ackley	12.0315 (0.0585)	11.3902 (0.0685)	1.06	13.4087 (0.1139)	12.1660 (0.0722)	1.10
F11: Rastrigin	11.8263 (0.0988)	11.3737 (0.1139)	1.04	12.7528 (0.0724)	12.1194 (0.1042)	1.05
F12: Schwefel	8.1851 (0.0569)	7.9648 (0.0890)	1.03	8.7612 (0.0524)	8.2109 (0.0296)	1.06
F13: Griewank	13.7655 (0.0846)	14.2824 (0.1054)	0.96	15.3910 (0.0995)	15.6216 (0.0842)	0.98
F14: Levy	17.9642 (0.0813)	16.7896 (0.1229)	1.07	20.6549 (0.1170)	18.4108 (0.0842)	1.12
F15: Treccani	4.6935 (0.1371)	4.2295 (0.0598)	1.11	4.9562 (0.1360)	4.3714 (0.0289)	1.13
F16: Beale	4.8087 (0.0155)	4.6405 (0.0527)	1.04	5.0649 (0.0409)	4.8098 (0.0421)	1.05
F17: Booth	4.4926 (0.0541)	4.4926 (0.0541)	1.00	4.7859 (0.0215)	4.6785 (0.0529)	1.02
F18: Brent	4.5868 (0.0186)	4.7189 (0.0327)	0.97	4.9435 (0.0130)	4.9202 (0.0297)	1.01
F19: Cube	4.6144 (0.0115)	4.1862 (0.0413)	1.10	4.9616 (0.0120)	4.3657 (0.0313)	1.14
F20: Davis	5.0567 (0.0565)	4.4333 (0.0415)	1.14	5.4204 (0.0099)	4.6649 (0.0628)	1.16
F21: Matyas	5.0291 (0.0124)	4.0977 (0.0641)	1.23	5.2439 (0.0023)	4.2874 (0.0416)	1.22
F22: Schaffer	4.8074 (0.0324)	4.4074 (0.0373)	1.09	5.0514 (0.0506)	4.6265 (0.0282)	1.09
F23: Bohachevsky1	4.5953 (0.0241)	4.2020 (0.0644)	1.09	4.8132 (0.0287)	4.3676 (0.0325)	1.10
F24: Egg Crate	4.8835 (0.0081)	4.2803 (0.0422)	1.14	5.2487 (0.0579)	4.4989 (0.0353)	1.17
F25: Bohachevsky2	4.5948 (0.0202)	4.1841 (0.0447)	1.10	4.8038 (0.0175)	4.3554 (0.0375)	1.10
F26: Bohachevsky3	4.6091 (0.0156)	4.1864 (0.0448)	1.10	4.8021 (0.0221)	4.3475 (0.0505)	1.10
F27:Three-Hump Camel	4.8569 (0.0200)	4.1695 (0.0477)	1.16	5.2030 (0.0.0237)	4.3531 (0.0377)	1.20

and

Table 6. Mean and averaged execution times in seconds of DE and SDE (D = 500).

	Execution Time $\mathit{\mu }\left(\mathit{\sigma }\right)$ for 256 Individuals			Execution Time $\mathit{\mu }\left(\mathit{\sigma }\right)$ for 512 Individuals
Function	DE	SDE	Speedup	DE	SDE	Speedup
F1: Sphere	45.1006 (0.1674)	43.5942 (0.1625)	1.03	47.8527 (0.0200)	46.3508 (0.0062)	1.03
F2 Step	55.7603 (0.0492)	55.1497 (0.1864)	1.01	59.7023 (0.0347)	57.5648 (0.2401)	1.04
F3: Sum Powers	47.3859 (0.1270)	44.0992 (0.2072)	1.07	51.0338 (0.0389)	47.4896 (0.0307)	1.07
F4: Sum Squares	45.0150 (0.1787)	43.3325 (0.1482)	1.04	48.2126 (0.0252)	46.6274 (0.0068)	1.03
F5: Dixon and Price	70.2937 (0.2209)	70.2279 (0.1731)	1.00	74.9822 (0.0298)	71.0612 (0.0428)	1.06
F6: Rosenbrock	95.6219 (0.2426)	94.9924 (0.1544)	1.01	101.3595 (0.036)	95.4034 (0.0300)	1.06
F7: Schwefel 2.22	31.7049 (0.0719)	30.0035 (0.1929)	1.06	33.6836 (0.2565)	31.4718 (0.1376)	1.07
F8: Trid	47.2107 (0.1703)	43.6624 (0.1782)	1.08	50.2172 (0.0326)	48.7325 (0.0232)	1.03
F9: Zakharov	46.9736 (0.1404)	45.1113 (0.1838)	1.04	50.1629 (0.0517)	47.0111 (0.0762)	1.07
F10: Ackley	59.2495 (0.1712)	56.5934 (0.1743)	1.05	62.5976 (0.1638)	60.1282 (0.0707)	1.04
F11: Rastrigin	58.9961 (0.0955)	56.4700 (0.1942)	1.04	62.2493 (0.0957)	59.5437 (0.3830)	1.05
F12: Schwefel	39.6069 (0.1385)	39.0363 (0.1085)	1.01	41.7337 (0.0551)	40.8717 (0.0721)	1.02
F13: Griewank	67.4986 (0.1488)	71.4827 (0.1742)	0.94	71.7673 (0.0992)	75.6721 (0.0595)	0.95
F:14 Levy	88.1310 (0.1206)	83.0872 (0.1613)	1.06	93.9297 (0.1430)	89.1134 (0.0781)	1.05
F15: Treccani	23.8224 (0.6603)	21.2687 (0.2196)	1.12	25.3578 (0.6672)	22.4922 (0.2129)	1.13
F16: Beale	23.5141 (0.0369)	23.1105 (0.3537)	1.02	25.1768 (0.0694)	24.5135 (0.2085)	1.03
F17: Booth	23.2668 (0.0490)	23.0368 (0.2329)	1.01	24.8573 (0.0480)	24.4406 (0.1868)	1.02
F18: Brent	23.1873 (0.0809)	23.8490 (0.1661)	0.97	24.7574 (0.0653)	25.2045 (0.1205)	0.98
F19: Cube	23.6192 (0.0523)	21.1600 (0.2700)	1.12	25.1667 (0.0651)	22.5187 (0.2063)	1.12
F20: Davis	24.6654 (0.0647)	21.3285 (0.2838)	1.16	26.2479 (0.0403)	22.7148 (0.1962)	1.16
F21: Matyas	25.3824 (0.0144)	21.1435 (0.1936)	1.20	27.0852 (0.0140)	22.3725 (0.1781)	1.21
F22: Schaffer	23.3038 (0.0899)	21.3305 (0.1633)	1.09	24.9515 (0.0555)	22.7985 (0.2195)	1.09
F23: Bohachevsky1	23.0564 (0.0598)	21.3298 (0.2496)	1.08	24.6339 (0.0576)	22.3473 (0.1723)	1.10
F24: Egg Crate	24.4434 (0.0727)	21.1914 (0.1658)	1.15	26.0469 (0.0843)	22.5681 (0.2205)	1.15
F25: Bohachevsky2	23.0607 (0.1270)	21.1913 (0.2459)	1.09	24.7679 (0.0580)	22.3699 (0.1505)	1.11
F26: Bohachevsky3	23.1568 (0.0570)	21.1915 (0.2585)	1.09	24.8482 (0.0853)	22.3834 (0.2782)	1.11
F27:Three-Hump Camel	24.6552 (0.1462)	21.1373 (0.2239)	1.17	26.3881 (0.2053)	22.2933 (0.2343)	1.18

, with the best ones in bold letters.

SDE has a slightly better averaged execution time in most of the cases, except for the Griewank function and in some experiments for the Brent function. However, a closer review of the speedups reveals that both algorithms have a similar performance regarding the execution time. To further clarify such an issue, we used the Wilcoxon test [58] to probe the null hypothesis that the execution times of both algorithms come from distributions with equal medians. The p-values for DE vs SDE are: (1) $p=0.1215$ for $N_p=256$ and $D=100$; (2) $p=0.09$ for $N_p=512$ and $D=100$; (3) $p=0.1323$ for $N_p=256$ and $D=500$; (4) $p=0.1115$ for $N_p=512$ and $D=500$. According to these results, in every case, the null hypothesis cannot be rejected, suggesting (with 5% certainty) that the execution time of both algorithms is similar for each experimental instance.

4.3. Convergence Speed

For the convergence comparison between DE and SDE, we used the same four instances as in the previous experiment: dimensions of 100 and 500 and populations of 256 and 512 individuals. In this case, the iterations per run are increased to 20,000, with the same number of runs per experimental instance; nevertheless, both algorithms iterate either until the algorithm is near to the optimum (e.g., $f\left(x^{*}\right)=-0.99\frac{d\left(d+4\right)\left(d-1\right)}{6}$ for Trid), or until reaching 20,000 iterations. After either of the two conditions is true, then the best global fitness and the number of iterations are stored, in the case of DE. However, as SDE does not utilizes a global best, we use the fitness of the first individual in the population as the ‘global best’ to demonstrate the capability of the algorithm to distribute the improvements through all the candidate solutions but with decentralized control. Therefore, when either the fitness of the first individual is close to the real global optimum, or 20,000 iterations are achieved, a run is completed in SDE. The results are in

Table 7. Mean and averaged final fitness and iterations of DE and SDE ($N_p=256$; $D=100$).

	Final Fitness $\mathit{\mu }\left(\mathit{\sigma }\right)$		Final Iterations $\mathit{\mu }\left(\mathit{\sigma }\right)$
Function	SDE	DE	SDE	DE
F1: Sphere	0.0096 $(3.5238\times {10}^{-4})$	0.0096 $(3.2083\times {10}^{-4})$	857.26 (21.30)	3832.63 (106.76)
F2: Step	0.00 (0)	0.00 (0)	829.8 (28.91)	4612.2 (143.3675)
F3: Sum Powers	0.0074 (0.0022)	0.0073 (0.0021)	53.16 (9.05)	29.86 (5.96)
F4: Sum Squares	0.0097 ($3.0754\times {10}^{-4}$)	0.0095$(\mathit{4}.\mathit{5164}\times {\mathit{10}}^{-\mathit{4}})$	1266.10 (18.23)	5562.43 (122.29)
F5: Dixon and Price	39.2690 (17.583)	0.6667 $(\mathit{8}.\mathit{0515}\times {\mathit{10}}^{-\mathit{7}})$	20,000.00 (0)	20,000.00 (0)
F6: Rosenbrock	366.7301 (130.1247)	90.1404 (0.1371)	20,000.00 (0)	20,000.00 (0)
F7: Schwefel 2.22	0.0098 ($1.2780\times {10}^{-4}$)	0.0098 ($2.2376\times {10}^{-4}$)	1227.1 (19.36)	6314.47 (136.45)
F8: Trid	$7.889\times {10}^6$ ($9.809\times {10}^6$)	$\mathit{4}.\mathit{821}\times {\mathit{10}}^{\mathit{5}}$$(\mathit{1}.\mathit{97}\times {\mathit{10}}^{\mathit{5}})$	20,000.00 (0)	20,000.00 (0)
F9: Zakharov	0.2932 (0.13712)	262.7573 (19.5592)	20,000.00 (0)	20,000.00 (0)
F10: Ackley	0.0098 ($9.9644\times {10}^{-5}$)	0.0097$(\mathit{1}.\mathit{7791}\times {\mathit{10}}^{-\mathit{4}})$	1367.93 (24.07)	6499.70 (131.53)
F11: Rastrigin	4.3725 (2.6246)	592.3126 (17.7795)	18841.96 (4407.1)	20,000.00 (0)
F12: Schwefel	55.5158 (74.2989)	3723.5101 (5356.9)	10405.80 (9128.0)	20,000.00 (0)
F13: Griewank	0.0097 ($3.3617\times {10}^{-4}$)	0.0095$(\mathit{3}.\mathit{5729}\times {\mathit{10}}^{-\mathit{4}})$	1307.30 (19.59)	5935.20 (107.78)
F14: Levy	0.0097 ($2.7136\times {10}^{-4}$)	0.0095$(\mathit{4}.\mathit{6494}\times {\mathit{10}}^{-\mathit{4}})$	988.06 (18.48)	6339.90 (175.04)
F15: Treccani	0.0062 (0.0032)	0.0048 (0.0032)	32.53 (11.66)	6.53 (3.53)
F16: Beale	0.0058 (0.0034)	0.0058 (0.0025)	92.83 (49.57)	7.73 (4.69)
F17: Booth	0.0071 (0.0032)	0.0044 (0.0032)	89.83 (40.78)	21.4667 (7.64)
F18: Brent	0.0076 (0.0021)	0.0048 (0.0029)	69.4 (22.60)	15.7 (4.66)
F19: Cube	0.0062 (0.0031)	0.0054 (0.0024)	243.23 (179.04)	37 (12.16)
F20: Davis	0.0709 (0.0703)	0.0064 (0.0018)	453.33 (59.00)	153.03 (10.76)
F21: Matyas	0.0065 (0.0032)	0.0050 (0.0034)	47.46 (24.72)	3.16 (2.61)
F22: Schaffer	0.0046 (0.0031)	0.0048 (0.0029)	193.36 (97.32)	19.07 (10.65)
F23: Bohachevsky1	0.0067 (0.0029)	0.0049 (0.0025)	84.83 (40.78)	36.23 (5.48)
F24: Egg Crate	0.0061 (0.0029)	0.0039 (0.0029)	43.86 (11.56)	15.8 (5.67)
F25: Bohachevsky2	0.0060 (0.0033)	0.0058 (0.0026)	126.66 (45.06)	37.1 (5.87)
F26: Bohachevsky3	0.0050 (0.0035)	0.0041 (0.0029)	122.2 (42.91)	33.93 (5.64)
F27: Three-Hump Camel	0.0058 (0.0028)	0.0056 (0.0027)	39.1 (17.82)	7.5 (3.42)

,

Table 8. Mean and averaged final fitness and iterations of DE and SDE ($N_p=512$; $D=100$).

	Final Fitness $\mathit{\mu }\left(\mathit{\sigma }\right)$		Final Iterations $\mathit{\mu }\left(\mathit{\sigma }\right)$
Function	SDE	DE	SDE	DE
F1: Sphere	0.0096 $(3.1580\times {10}^{-4})$	0.0095$(\mathit{4}.\mathit{3491}\times {\mathit{10}}^{-\mathit{4}})$	861.00 (20.67)	4344.16 (114.73)
F2: Step	0.0 (0)	0.0 (0)	828.56 (24.44)	5486.53 (193.96)
F3: Sum Powers	0.0077 (0.0020)	0.0070 (0.0023)	53.00 (8.47)	26.86 (6.14)
F4: Sum Squares	0.0097 ($2.0231\times {10}^{-4}$)	0.0095$(\mathit{4}.\mathit{1157}\times {\mathit{10}}^{-\mathit{4}})$	1263.26 (17.43)	6216.26 (113.12)
F5: Dixon and Price	36.3413 (16.9494)	0.6667 $(\mathit{1}.\mathit{8257}\times {\mathit{10}}^{-\mathit{7}})$	20,000.00 (0)	20,000.00 (0)
F6: Rosenbrock	348.7744 (127.6737)	90.7098 (0.1733)	20,000.00 (0)	20,000.00 (0)
F7: Schwefel 2.22	0.0098 ($1.3374\times {10}^{-4}$)	0.0098 ($2.0745\times {10}^{-4}$)	1227.43 (17.91)	6962.76 (111.36)
F8: Trid	$7.746\times {10}^6$ ($6.448\times {10}^6$)	$\mathit{3}.\mathit{087}\times {\mathit{10}}^{\mathit{6}}$$(\mathit{8}.\mathit{365}\times {\mathit{10}}^{\mathit{5}})$	20,000.00 (0)	20,000.00 (0)
F9: Zakharov	0.2058 (0.0850)	257.4497 (14.3462)	20,000.00 (0)	20,000.00 (0)
F10: Ackley	0.0098 ($2.0868\times {10}^{-4}$)	0.0097$(\mathit{2}.\mathit{2258}\times {\mathit{10}}^{-\mathit{4}})$	1373.53 (21.39)	7401.03 (159.97)
F11: Rastrigin	0.4355 (0.6197)	600.0198 (16.0965)	9035.86 (8486.8)	20,000.00 (0)
F12: Schwefel	52.4709 (65.0721)	5852.3797 (5544.0)	1981.50 (32.62)	20,000.00 (0)
F13: Griewank	0.0097 ($2.8136\times {10}^{-4}$)	0.0095$(\mathit{3}.\mathit{6761}\times {\mathit{10}}^{-\mathit{4}})$	1303.60 (22.27)	6690.20 (152.02)
F14: Levy	0.0097 ($2.1518\times {10}^{-4}$)	0.0096$(\mathit{2}.\mathit{4228}\times {\mathit{10}}^{-\mathit{4}})$	989.70 (25.23)	7744.56 (209.23)
F15: Treccani	0.0059 (0.0031)	0.0049 (0.0028)	33.5 (14.83)	3.8 (3.14)
F16: Beale	0.0066 (0.0032)	0.0048 (0.0031)	76.16 (36.74)	4.73 (2.99)
F17: Booth	0.0068 (0.0029)	0.0051 (0.0031)	82.66 (34.35)	15.86 (6.83)
F18: Brent	0.0068 (0.0025)	0.0044 (0.0026)	61.4 (21.82)	13.63 (4.77)
F19: Cube	0.0051 (0.0040)	0.0048 (0.0028)	329.83 (205.35)	27.47 (11.98)
F20: Davis	0.0038 (0.0346)	0.0065 (0.0017)	587.36 (99.63)	149.76 (9.49)
F21: Matyas	0.0059 (0.0035)	0.0038 (0.0026)	48.13 (23.34)	2.1 (1.56)
F22: Schaffer	0.0048 (0.0033)	0.0048 (0.0027)	258.2 (140.22)	16.56 (8.22)
F23: Bohachevsky1	0.0070 (0.0028)	0.0055 (0.0031)	88.13 (24.36)	33.8 (5.88)
F24: Egg Crate	0.0067 (0.0029)	0.0053 (0.0028)	45.67 (15.39)	13.23 (4.78)
F25: Bohachevsky2	0.0053 (0.0033)	0.0049 (0.0029)	108.23 (61.14)	36.1 (4.79)
F26: Bohachevsky3	0.0059 (0.0032)	0.0039 (0.0026)	102.3 (34.34)	30.86 (3.88)
F27: Three-Hump Camel	0.0053 (0.0033)	0.0070 (0.0023)	53.00 (8.47)	26.86 (6.14)

,

Table 9. Mean and averaged final fitness and iterations of DE and SDE ($N_p=256$; $D=500$).

	Final Fitness $\mathit{\mu }\left(\mathit{\sigma }\right)$		Final Iterations $\mathit{\mu }\left(\mathit{\sigma }\right)$
Function	SDE	DE	SDE	DE
F1: Sphere	0.0099$(\mathit{7}.\mathit{1685}\times {\mathit{10}}^{-\mathit{5}})$	1.5596 (0.1287)	3915.83 (37.75)	20,000.00 (0)
F2: Step	0.00(0)	648.46 (49.02)	3796.33 (208.28)	20,000.00 (0)
F3: Sum Powers	0.0073 (0.0018)	0.0070 (0.0022)	68.66 (14.84)	65.60 (15.11)
F4: Sum Squares	0.0099$(\mathit{6}.\mathit{1043}\times {\mathit{10}}^{-\mathit{5}})$)	1114.1061 (97.5739)	6257.00 (48.87)	20,000.00 (0)
F5: Dixon and Price	1116.7 (411.7089)	$1.1704\times {10}^4$ (2084.0)	20,000.00 (0)	20,000.00 (0)
F6: Rosenbrock	2015.3 (675.7089)	3656.1 (321.2327)	20,000.00 (0)	20,000.00 (0)
F7 Schwefel 2.22	0.0099$(\mathit{5}.\mathit{7235}\times {\mathit{10}}^{-\mathit{5}})$	39.2896 (2.1531)	5416.53 (37.09)	20,000.00 (0)
F8: Trid	$\mathit{1}.\mathit{4111}\times {\mathit{10}}^{\mathit{10}}$$(\mathit{1}.\mathit{662}\times {\mathit{10}}^{\mathit{10}})$	$3.6207\times {10}^{10}$$(4.049\times {10}^9)$	20,000.00 (0)	20,000.00 (0)
F9: Zakharov	3137.0 (397.5563)	4175.8 (112.141)	20,000.00 (0)	20,000.00 (0)
F10: Ackley	0.0099 ($\mathit{4}.\mathit{3961}\times {\mathit{10}}^{-\mathit{5}}$)	3.1094 (0.0798)	5680.50 (117.0)	20,000.00 (0)
F11: Rastrigin	1568.87 (252.57)	4620.0471 (101.5107)	20,000.00 (0)	20,000.00 (0)
F12: Schwefel	$\mathit{5}.\mathit{0077}\times {\mathit{10}}^{\mathit{4}}$ ($\mathit{1}.\mathit{9810}\times {\mathit{10}}^{\mathit{4}})$	$1.7129\times {10}^5$ (776.5318)	20,000.00 (0)	20,000.00 (0)
F13: Griewank	0.0099$(\mathit{7}.\mathit{9325}\times {\mathit{10}}^{-\mathit{5}})$	6.3713 (0.5136)	5270.16 (42.23)	20,000.00 (0)
F14: Levy	0.0247 (0.0811)	17.0589 (1.7703)	5233.73 (2780.0)	20,000.00 (0)
F15: Treccani	0.0049 (0.0034)	0.0039 (0.0026)	33.13 (7.89)	6.86 (3.77)
F16: Beale	0.0057 (0.0032)	0.0052 (0.0029)	67.76 (35.51)	8.26 (4.40)
F17: Booth	0.0064 (0.0036)	0.0051 (0.0030)	80.5 (41.65)	21.63 (10.99)
F18: Brent	0.0074 (0.0021)	0.0049 (0.0029)	63.8 (17.98)	14.43 (5.87)
F19: Cube	0.0049 (0.0038)	0.0048 (0.0031)	271.63 (117.09)	38.03 (15.18)
F20: Davis	0.0069 (0.0033)	0.0065 (0.0018)	584.75 (133.71)	154.3 (9.18)
F21: Matyas	0.0064 (0.0027)	0.0047 (0.0028)	41.63 (19.11)	4 (3.36)
F22: Schaffer	0.0047 (0.0029)	0.0047 (0.0031)	214.08 (107.21)	21.7 (11.65)
F23: Bohachevsky1	0.0074 (0.0025)	0.0047 (0.0028)	94.2 (22.08)	35.93 (5.19)
F24: Egg Crate	0.0057 (0.0026)	0.0060 (0.0027)	48.23 (14.61)	16.36 (3.92)
F25: Bohachevsky2	0.0047 (0.0034)	0.0045 (0.0027)	145.2 (68.44)	37.3 (5.75)
F26: Bohachevsky3	0.0061 (0.0031)	0.0048 (0.0026)	123.07 (42.16)	34.3 (4.06)
F27: Three-Hump Camel	0.0070 (0.0026)	0.0042 (0.0026)	41.03 (21.40)	7.4 (4.61)

and

Table 10. Mean and averaged final fitness and iterations of DE and SDE ($N_p=512$; $D=500$).

	Final Fitness $\mathit{\mu }\left(\mathit{\sigma }\right)$		Final Iterations $\mathit{\mu }\left(\mathit{\sigma }\right)$
Function	SDE	DE	SDE	DE
F1: Sphere	0.0099$(\mathit{6}.\mathit{0612}\times {\mathit{10}}^{-\mathit{5}})$	27.3649 (1.4603)	3685.16 (30.18)	20,000.00 (0)
F2: Step	0.0 (0)	$1.0338\times {10}^4$ (696.03)	3311.96 (107.64)	20,000.00 (0)
F3: Sum Powers	0.0077 (0.0017)	0.0075 (0.0019)	68.86 (13.06)	62.63 (13.32)
F4: Sum Squares	0.0099$(\mathit{1}.\mathit{0435}\times {\mathit{10}}^{-\mathit{4}})$	$1.9638\times {10}^4$ (1214.0749)	5884.63 (30.66)	20,000.00 (0)
F5: Dixon and Price	1186.7 (455.0704)	$1.1704\times {10}^4$ (2084.0)	20,000.00 (0)	20,000.00 (0)
F6: Rosenbrock	2266.0(683.9547)	3656.1 (321.2327)	20,000.00 (0)	20,000.00 (0)
F7: Schwefel 2.22	0.0099$(\mathit{4}.\mathit{9013}\times {\mathit{10}}^{-\mathit{5}})$	202.2585 (8.5413)	5181.37 (27.57)	20,000.00 (0)
F8: Trid	$\mathit{1}.\mathit{4072}\times {\mathit{10}}^{\mathit{10}}(\mathit{1}.\mathit{775}\times {\mathit{10}}^{\mathit{10}})$	$1.8198\times {10}^{11}$$(1.070\times {10}^{10})$	20,000.00 (0)	20,000.00 (0)
F9: Zakharov	3109.1 (348.8842)	4175.8 (112.1416)	20,000.00 (0)	20,000.00 (0)
F10: Ackley	0.0099$(\mathit{3}.\mathit{4051}\times {\mathit{10}}^{-\mathit{5}})$	7.0142 (0.1369)	5229.16 (48.38)	20,000.00 (0)
F11: Rastrigin	1567.5246 (388.10)	4990.5538 (64.7224)	20,000.00 (0)	20,000.00 (0)
F12: Schwefel	$\mathit{4}.\mathit{0269}\times {\mathit{10}}^{\mathit{4}}$$(\mathit{2}.\mathit{1107}\times {\mathit{10}}^{\mathit{4}})$	$1.7120\times {10}^5$ (760.9840)	20,000.00 (0)	20,000.00 (0)
F13: Griewank	0.0098$(\mathit{1}.\mathit{2733}\times {\mathit{10}}^{-\mathit{4}})$	94.8377 (5.1547)	4964.13 (42.25)	20,000.00 (0)
F14: Levy	0.0099$(\mathit{8}.\mathit{3354}\times {\mathit{10}}^{-\mathit{5}})$	96.7644 (6.7583)	4355.60 (48.12)	20,000.00 (0)
F15: Treccani	0.0061 (0.0024)	0.0049 (0.0032)	33.16 (13.69)	4.1 (2.23)
F16: Beale	0.0063 (0.0032)	0.0044 (0.0025)	69.66 (31.39)	7.4 (3.59)
F17: Booth	0.0075 (0.0026)	0.0056 (0.0029)	87.63 (36.26)	16.56 (9.58)
F18: Brent	0.0075 (0.0024)	0.0048 (0.0029)	65.4 (19.48)	14.23 (4.27)
F19: Cube	0.0058 (0.0037)	0.0059 (0.0030)	252.03 (168.68)	26.67 (11.38)
F20: Davis	0.0037(0.0034)	0.0067 (0.0015)	571.11 (133.95)	149.2 (12.54)
F21: Matyas	0.0049 (0.0032)	0.0035 (0.0028)	47 (16.06)	2.13 (1.63)
F22: Schaffer	0.0051 (0.0031)	0.0055 (0.0031)	218.36 (168.65)	14.96 (7.87)
F23: Bohachevsky1	0.0072 (0.0027)	0.0043 (0.0032)	92.13 (27.13)	32.63 (6.32)
F24: Egg Crate	0.0063 (0.0027)	0.0050 (0.0031)	53.67 (17.51)	13.4 (3.63)
F25: Bohachevsky2	0.0058 (0.0034)	0.0043 (0.0031)	120.43 (52.24)	31.83 (6.90)
F26: Bohachevsky3	0.0073 (0.0027)	0.0050 (0.0032)	140.73 (64.64)	30.9 (5.54)
F27: Three-Hump Camel	0.0062 (0.0028)	0.0051 (0.0030)	49.9 (19.74)	4.93 (3.31)

with the best results in bold letters.

It can be seen from the results of these experiments (Table 7, Table 8, Table 9 and Table 10) that the proposed algorithm does not outperform DE on two-dimensional problems. Although SDE reaches the optimum, it performs a higher number of iterations than DE, however, the performance of SDE in high dimensions is remarkable compared with DE.

Table 7 shows the experimental instance when $D=100$ and $N_p=256$. In this case, both algorithms have a good performance with the Sphere, Step, Sum Powers, Sum Squares, Schwefel 2.22, Ackley, Griewank and Levy functions, as they both achieve a good average fitness; however, except for the Sum Powers function where DE converges in fewer iterations (almost in half of the iterations), SDE is faster than DE in all other cases, with a reduction of more than 84% in the number of iterations for the best result (Levy function), as shown in Figure 3. For the functions Trid, Zakharov, Rastrigin and Schwefel, both algorithms have problems finding the global best, but sometimes SDE obtains better fitness values than DE, with fewer iterations on average.

Table 8 shows that the SDE behavior for more individuals ($N_p=512$) is as reported in previous lines.

From Table 9 and Table 10 ($D=500$), it can be seen that DE struggles with high dimensionality, except for the Sum Powers function. In fact, DE no longer reaches the optimum in 20,000 iterations for the Sum Squares, Schwefel 2.22, Ackley, Griewank and Levy functions, whereas SDE has no problems achieving the optimum for these functions. Another important detail is that with a larger number of individuals ($Np=512$), SDE finds the optimum in slightly fewer iterations than when the population is smaller (see Table 9 and Table 10). This highlights the advantage of using the stigmergy concept for the indirect communication among the population.

5. Discussion

Stigmergic DE implements slight modifications to the original DE operators, so the computational time required to complete several iterations is practically the same, as suggested by the results in Table 5 and Table 6 and after applying the Wilcoxon test to such data. Figure 4 shows a comparison between the execution time of DE and SDE for each test function, considering $D=500$ and $N_p=512$. The comparison considers the difference in percentage between the execution times of each algorithm. In most cases (with the exception of the Brent and Griewank functions in these results), the proposal has a better time performance than its DE counterpart of about 17% in the best case. This behavior is similar in all these experiments; however, as already mentioned, SDE has a marginal advantage.

Moreover, both algorithms present similar problems in finding the global optimum in some functions. However, as can be seen from Table 7 and Table 8, in the case of the Rastrigin, Schwefel and Zacharov functions, the difference between the final fitness values obtained for SDE and DE is very large. SDE obtains fitness values lower than DE by an order of magnitude 2, and for the case of the Trid, Dixon and Price and Rosenbrock functions, DE performs better than SDE, but the difference is less significant. If the dimension increases (Table 9 and Table 10), only in the case of the Sum Powers function does DE have a better performance than SDE, but it is minimal, on the order of 0.0001. These results show the advantage of the proposal in high dimensions; empirically, this is due to the intrinsic parallelism of the stigmergy concept that was used as an inspiration to modify the original operators of a metaheuristic (DE, version best/1/bin in this case). The proposal avoids using the global best in the construction of new candidate solutions, thus simulating indirect communication among all individuals in the population.

In summary, under the same conditions for both metaheuristics, our proposal can find a similar result as DE (and better outcomes for some objective functions) but using fewer iterations on average (Table 7, Table 8, Table 9 and Table 10), especially when the problems are high-dimensional. Even if the iterations are insufficient to find the global optimum, SDE performs better than DE, so it can be a good alternative for solving multiple engineering optimization problems. As mentioned in [59], applications can be in industrial engineering for the job-shop scheduling problem [60,61], in image processing to perform a multilevel thresholding process on a 2D histogram to segment images [62,63], in path planning to solve robotics challenges [64], or to solve area coverage problems for wireless sensor networks (WSNs) [65], to mention a few.

6. Conclusions

In this paper, we presented a modification to Differential Evolution that uses the global best to construct new candidate solutions. The adjustment considers stigmergy, a term taken from entomology to explain the indirect communication used by social insects to achieve complex projects. In the proposal, we eliminate the use of global best and instead we employ a local best. Like the real ants or termites, we utilize two neighbors of that local leader in the approach. The new candidate solution uses the leader’s information and two neighbors in conjunction with a crossover operation as in the original DE. The final step in the approach is trace updating, which could modify any of the three individuals and their fitness values, simulating distributed and indirect communication with all the individuals in the artificial colony. We called this changed metaheuristic Stigmergic Differential Evolution (SDE). Due to the elimination of the global best, SDE has features that make it more parallelizable than DE, therefore, both algorithms were programmed in the CUDA-C language.

We compared DE and SDE with 27 objective functions under the same circumstances. The results suggest that SDE achieves faster convergence than DE when the dimensionality increases and there are a larger number of individuals in the population, and it performs similarly to DE for 2D test functions, but DE converges in fewer iterations. It was demonstrated in [66] that canonical DE is adversely altered by increments in dimensionality, which affects in a super-linear fashion the convergence to the global optimum of the metaheuristic. In that sense, even though SDE has average convergence properties (e.g., Table 5 and Table 6), we claim that its main feature is the capability to maintain a good convergence behavior as dimensionality grows.

The proposed modification could apply to other metaheuristics that use a global best to construct a candidate solution. A possible future work would consider the stigmergy-based adaptation of the original operators in other metaheuristic algorithms and their comparison.