Optimizing the Layout of Run-of-River Powerplants Using Cubic Hermite Splines and Genetic Algorithms
Abstract
:1. Introduction
1.1. Electrification in Developing Countries and Mini-Hydropower Plants
1.2. Optimization of MHPP
1.3. Contributions
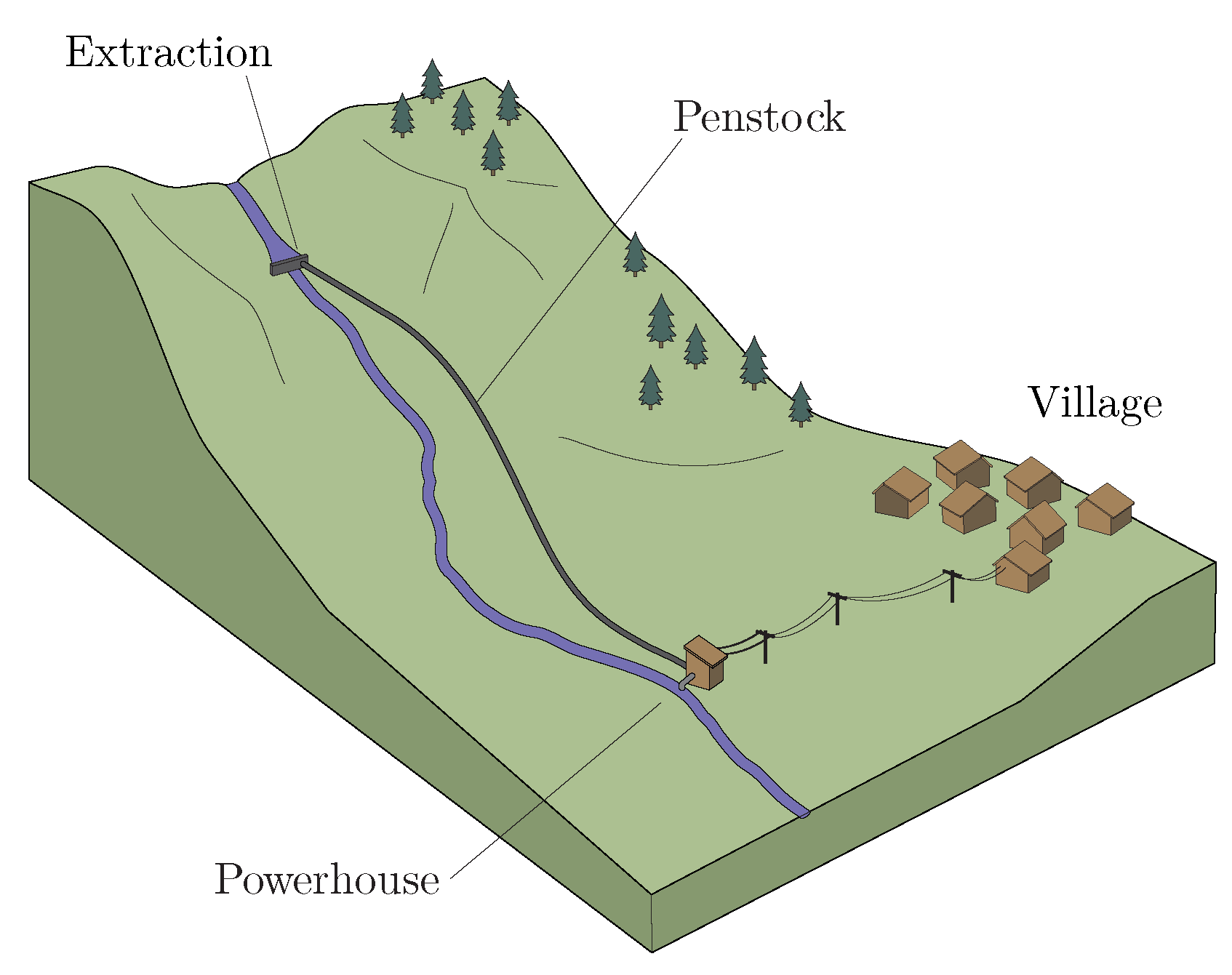
2. Description of the Problem
2.1. Power Generation
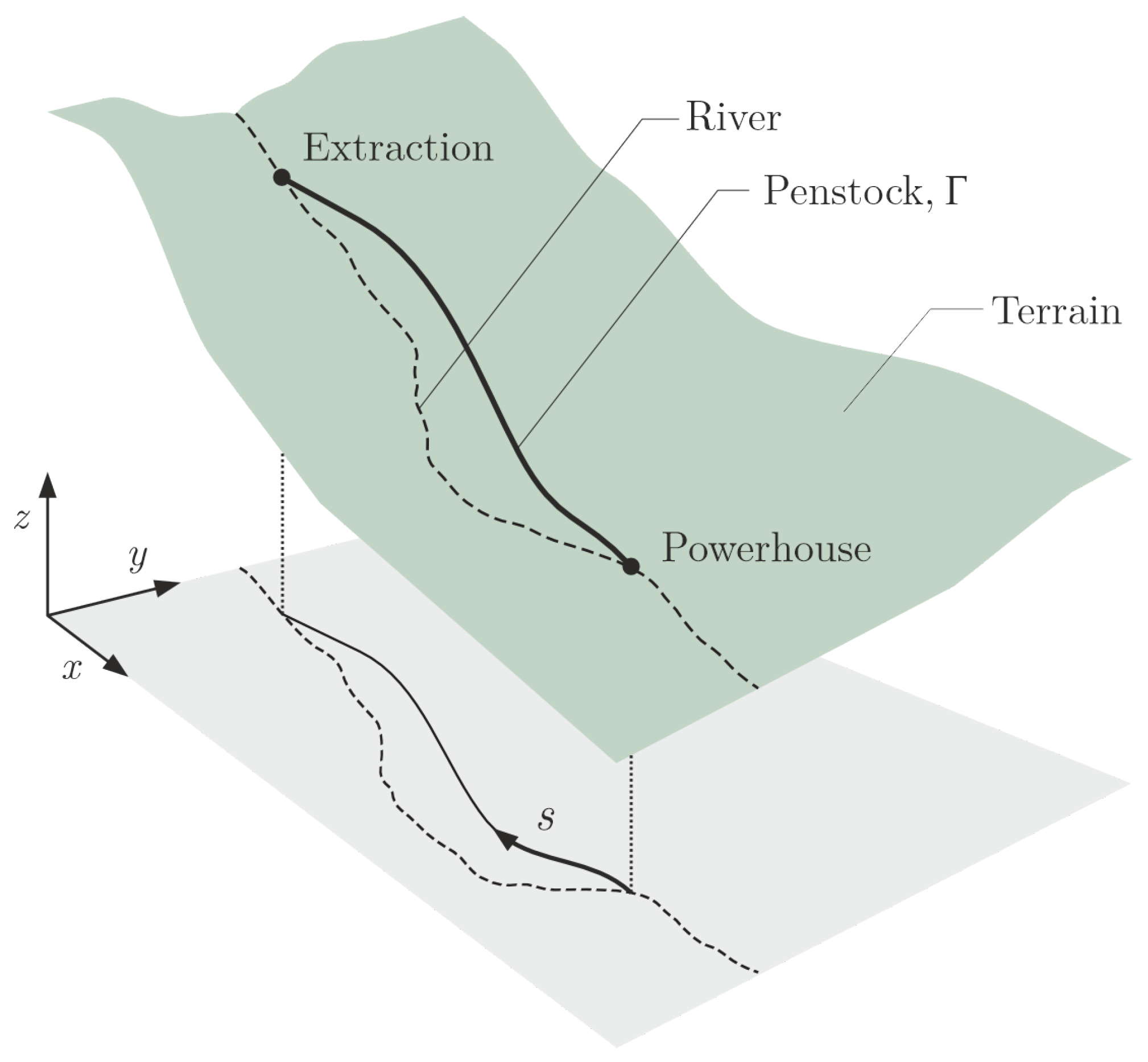
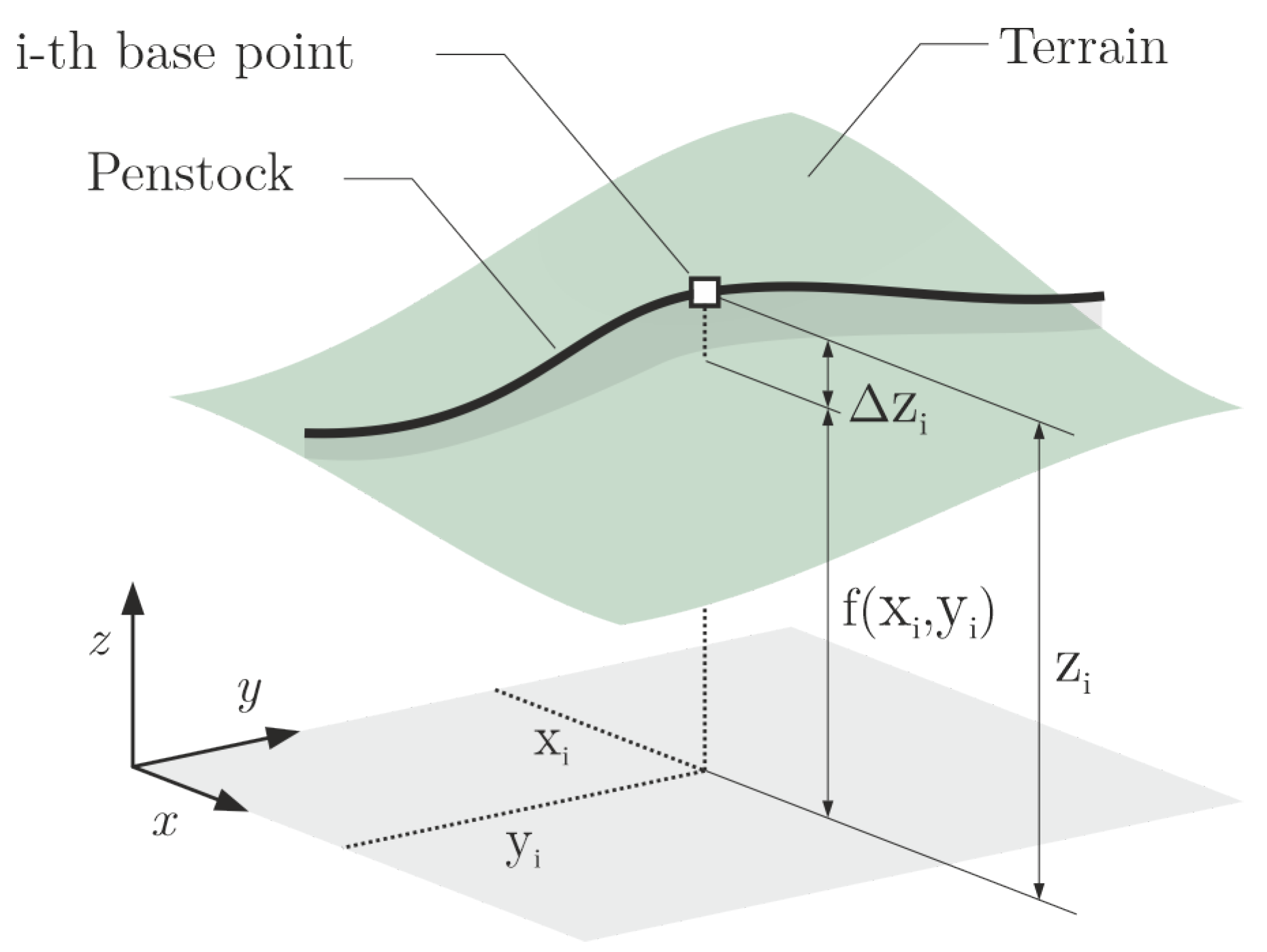
2.2. Terrain
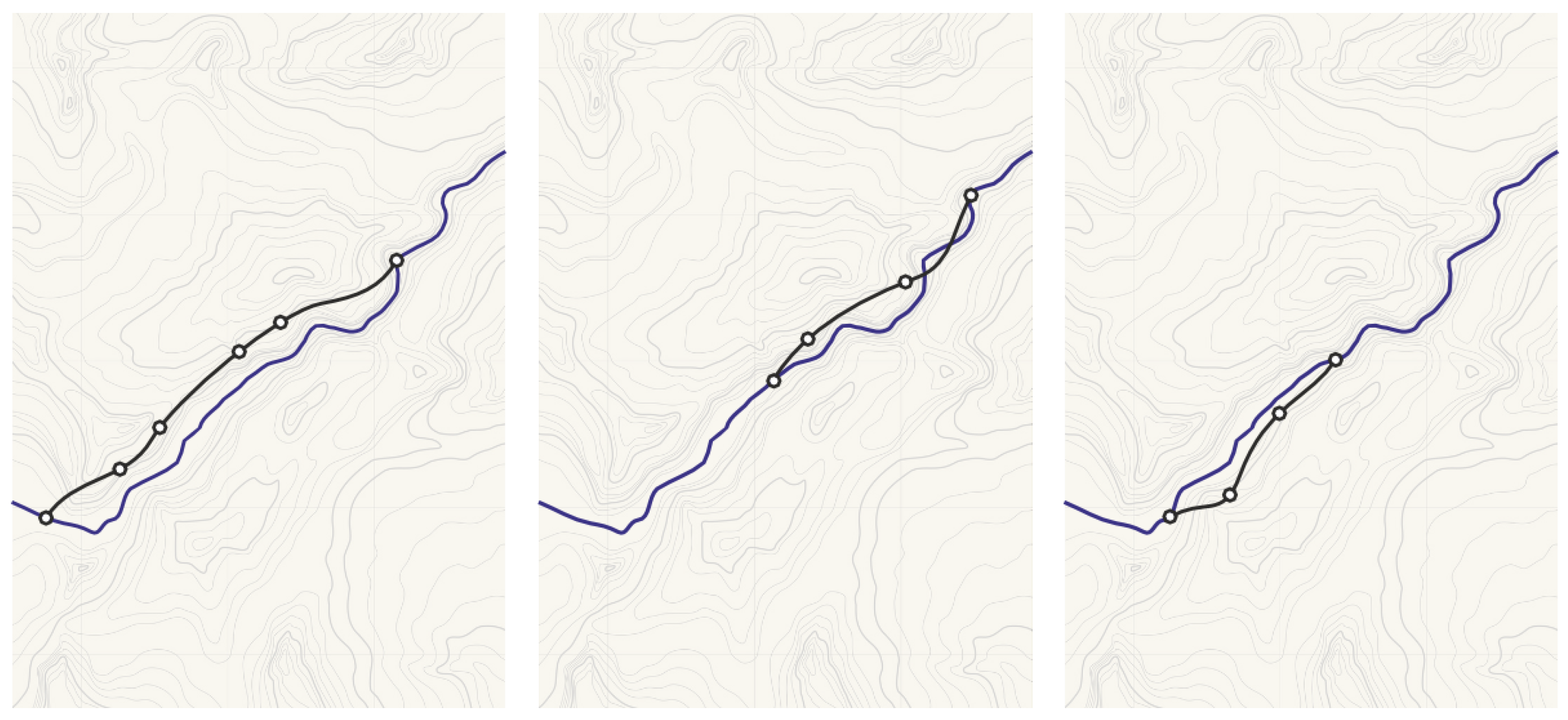
2.3. Spline-Based Penstock Layout
2.4. Pipe Curvature
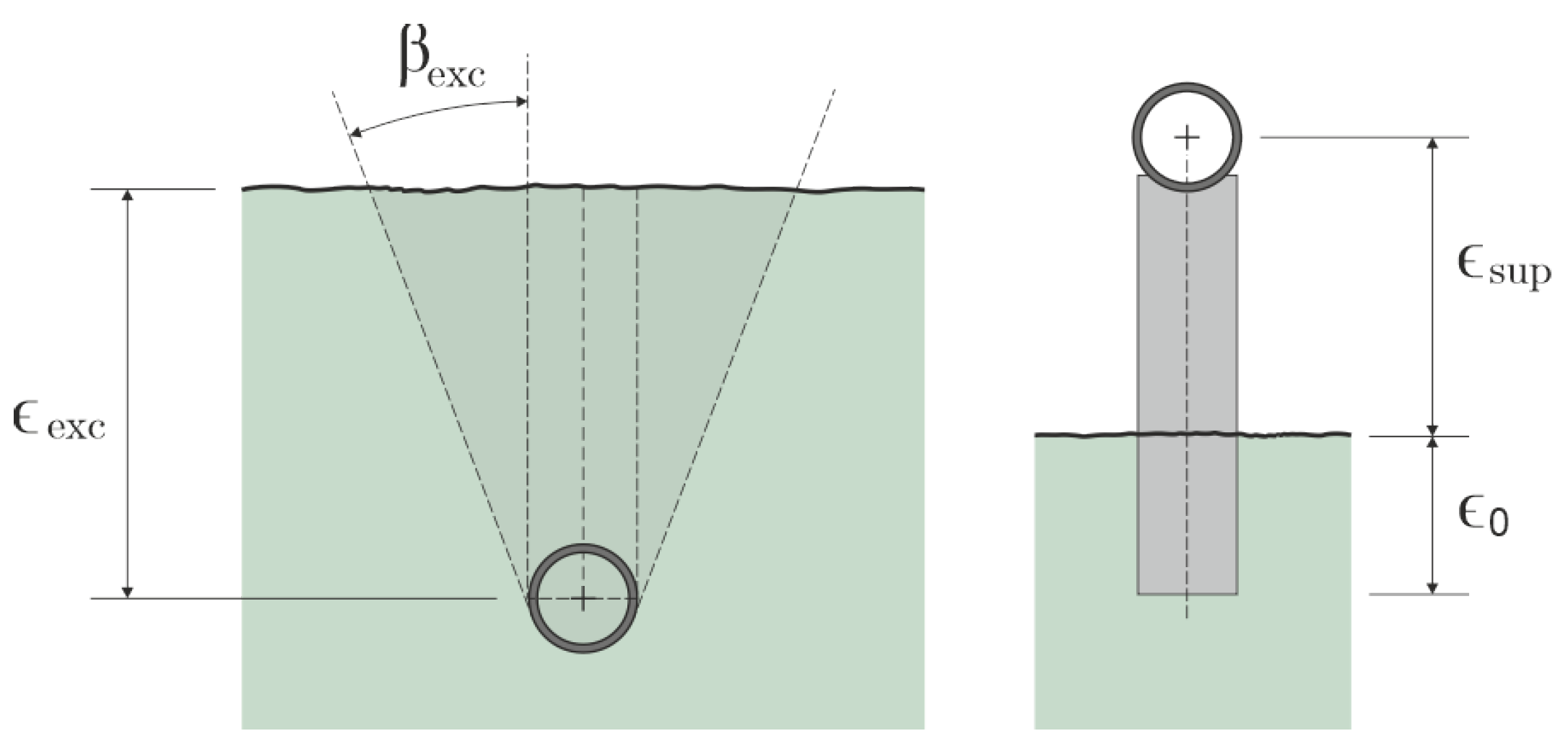
2.5. Cost of the MHPP
2.6. Problem Formulation
2.7. Complexity of the Problem
3. Genetic Algorithm
3.1. Individual Encoding
- The coordinates and corresponding to the end nodes;
- The coordinates of the interior nodes of the penstock, being i the number of each node;
- The height of the nodes relative to the surface of the terrain . Notice that it is a relative value with respect to , which determines the actual height of the terrain;
- The diameter of the penstock .
3.2. Individual Generation
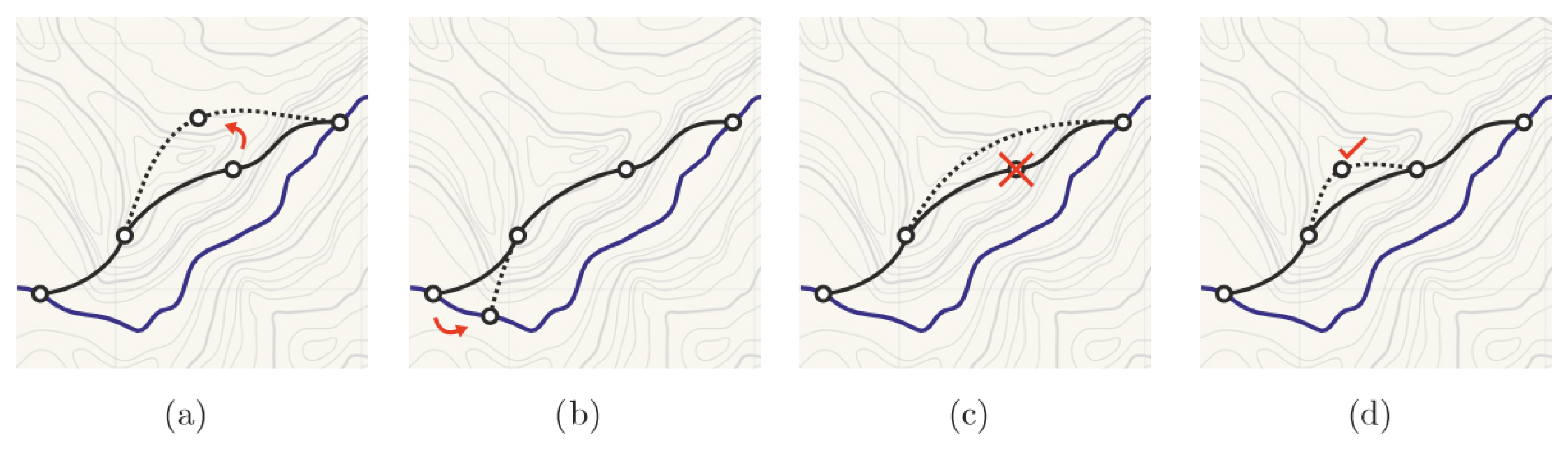
3.3. Mutation Operator
- With a certain probability, , one of the internal nodes can be removed from the individual (see node 4 in Figure 9);
- With a certain probability, , a new node is attached to the individual. This new node is generated through a procedure similar to that in the generation scheme, beginning with the selection of an arbitrary point of the river between the dam and the powerhouse and its later Gaussian displacement (see node 6 in Figure 9).
3.4. Crossover Operator
- 1.
- The offspring is initialized by defining their two end nodes as the lowest and highest nodes contained by the parents;
- 2.
- The interior nodes of both parents are grouped together, and then each of these are being randomly assigned to one offspring;
- 3
- The diameters of the offspring are determined using a simulated binary crossover between the diameters of the parents. This is being and , respectively, the diameter of the two parents, the diameter of the offspring, and are calculated as:where is generated through a random variable as:from where it can be seen that is generated between and . With this approach, the blend crossover of both diameters is not limited to result in values within the range of the diameters of the parents.
3.5. Fitness Function
4. Simulation Examples and Results
4.1. Scenario Parameters
- (1)
- Modified problem 1 is based on reducing the power output constraint. This models the design of a plant for a much smaller village, with a consequently lower power supply requirement. In particular, the required power output, , has been set to 4-kW.
- (2)
- Modified problem 2 is based on (i) increasing the required power output of the plant and (ii) modifying the costs associated with the pipe and its deployment. The first of these modifications represents the application of the method to supply a more populated village. In particular, the required power output, , has been set to 14-kW. The second of these modifications is based on considering a low quality terrain that strongly makes the transport of the pipe difficult, translating into an increase of its cost per unit length, but eases the excavations labor involved. This has been modeled by using a 1.5 multiplier for , on one hand, and reducing the required cut angle of the excavations, , to 10 and the unitary volumetric cost, , to 2 c.u./m, on the other.
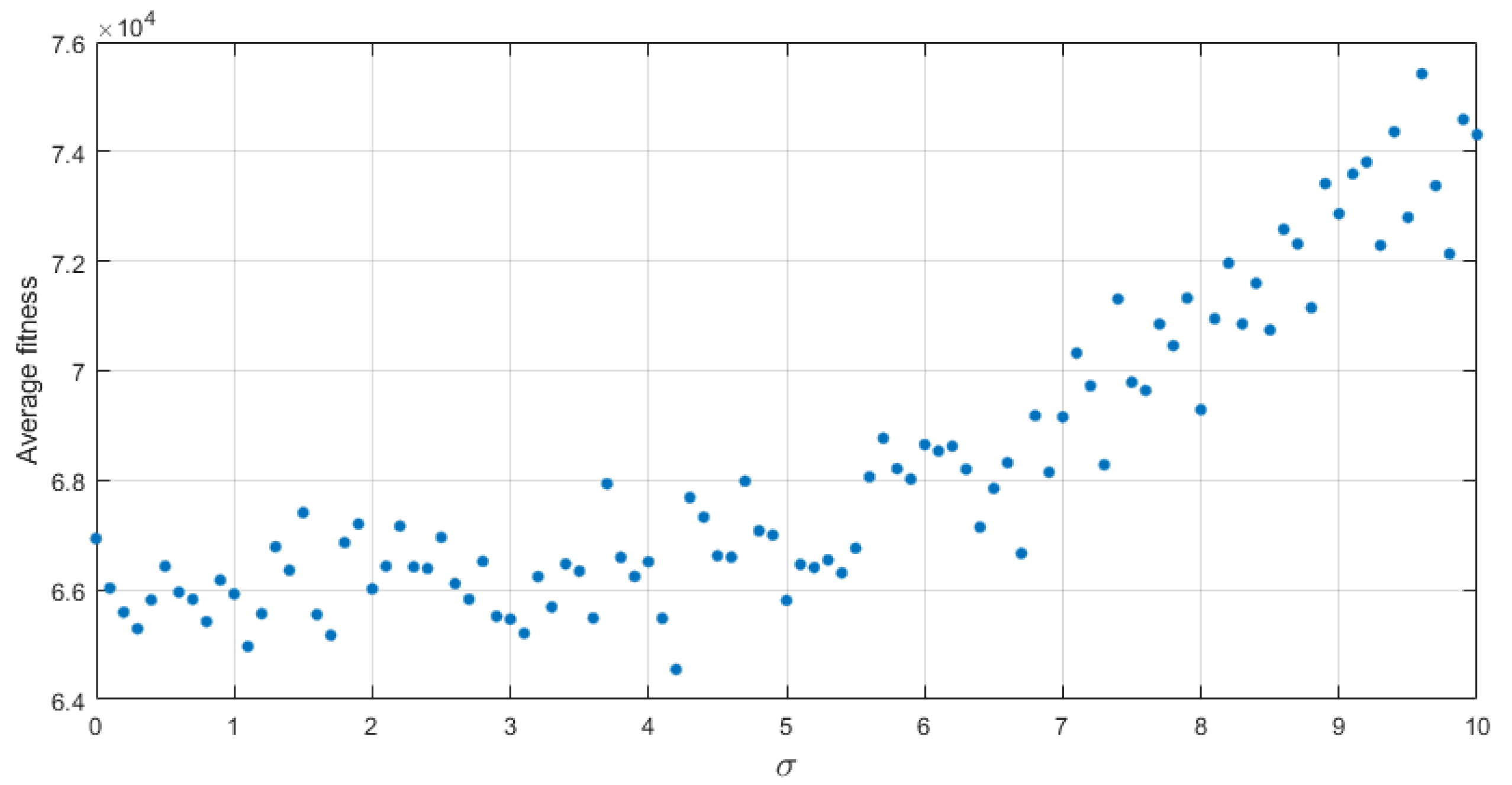
4.2. Algorithm Parameters
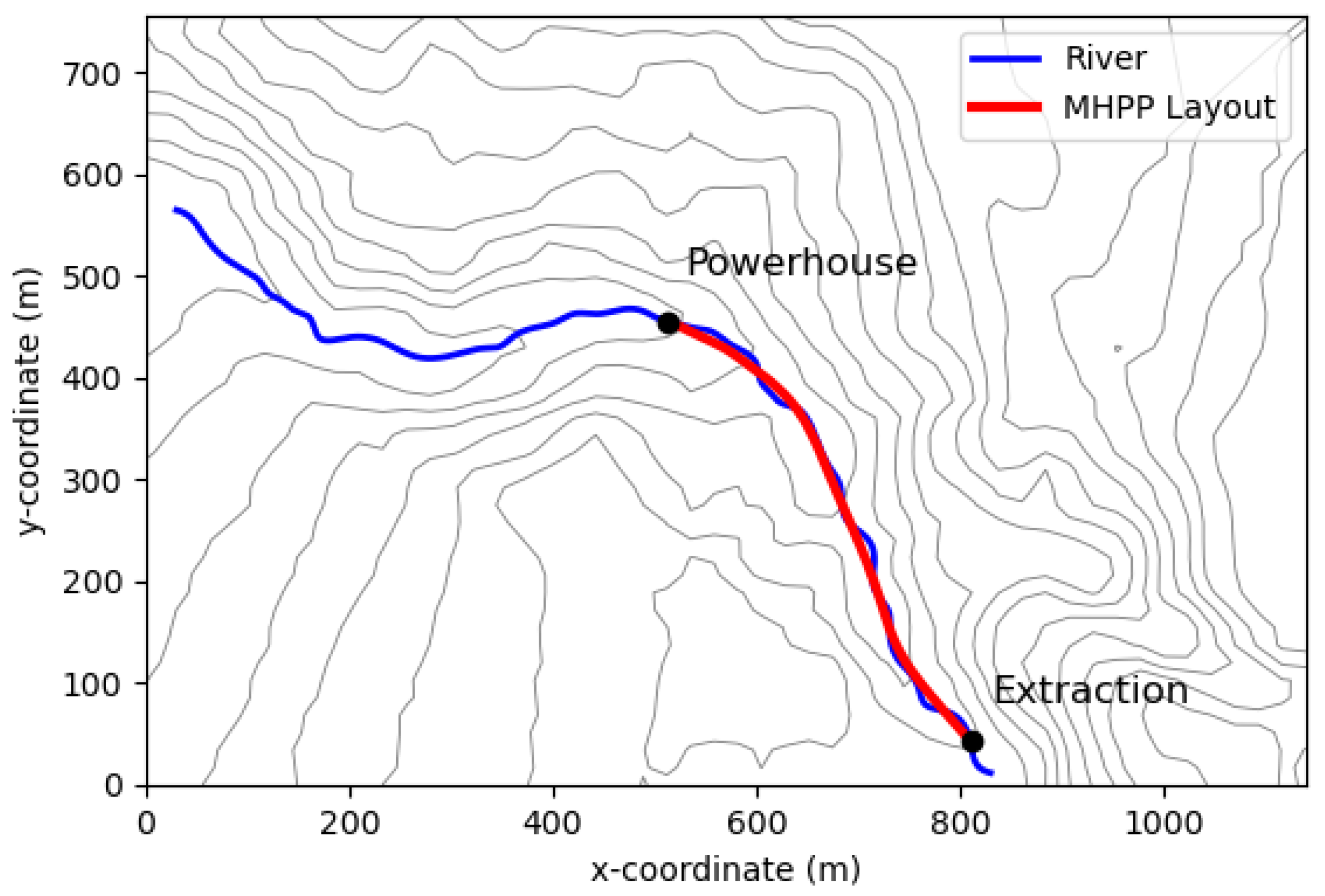
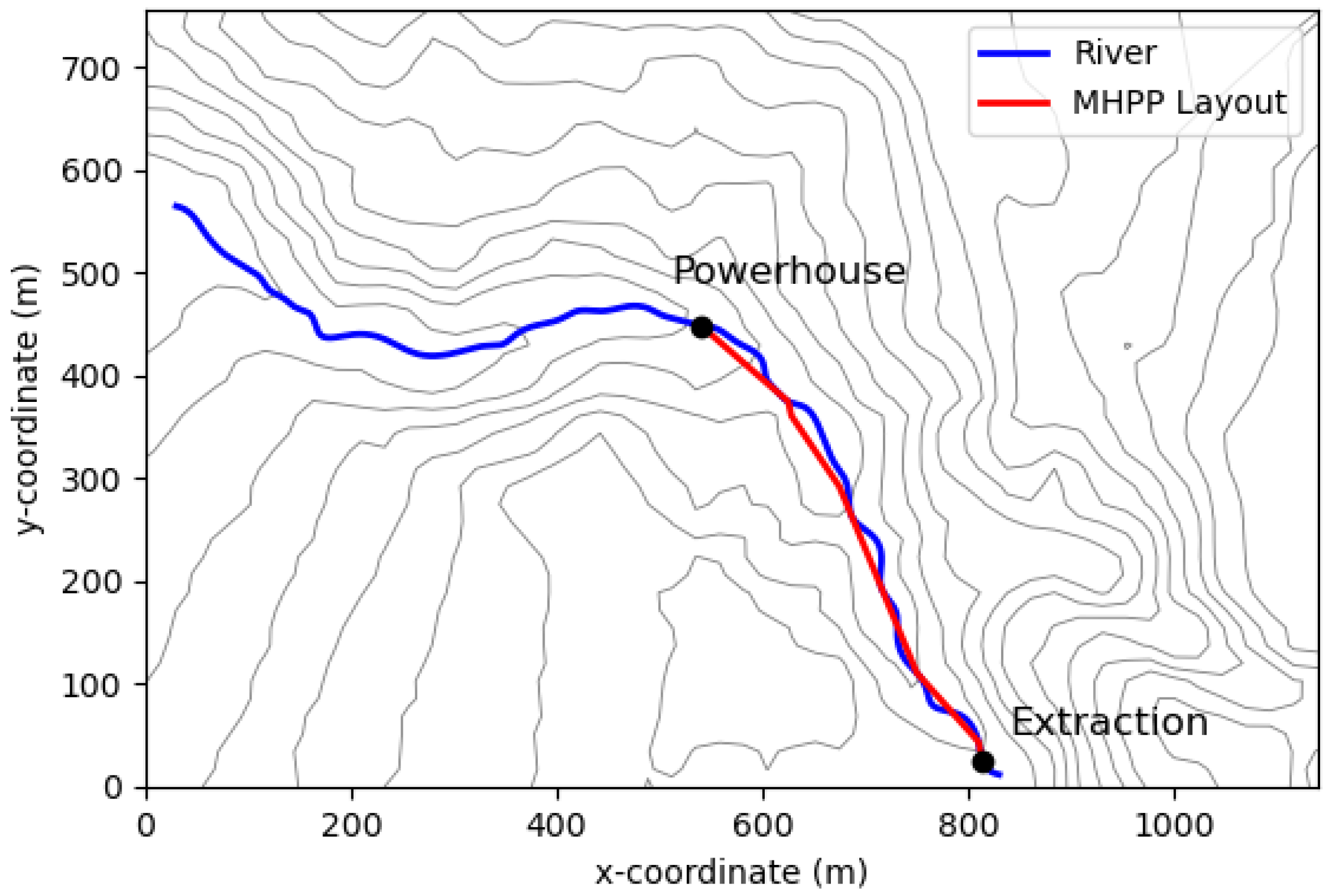
4.3. Results
4.4. Comparison with Previous Approaches
5. Conclusions and Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Couto, T.B.; Olden, J.D. Global proliferation of small hydropower plants-science and policy. Front. Ecol. Environ. 2018, 16, 91–100. [Google Scholar] [CrossRef]
- Apichonnabutr, W.; Tiwary, A. Trade-offs between economic and environmental performance of an autonomous hybrid energy system using micro hydro. Appl. Energy 2018, 226, 891–904. [Google Scholar] [CrossRef]
- Kelly-Richards, S.; Silber-Coats, N.; Crootof, A.; Tecklin, D.; Bauer, C. Governing the transition to renewable energy: A review of impacts and policy issues in the small hydropower boom. Energy Policy 2017, 101, 251–264. [Google Scholar] [CrossRef]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Energy recovery using micro-hydropower technology in water supply systems: The case study of the city of Fribourg. Water 2016, 8, 344. [Google Scholar] [CrossRef]
- Berrada, A.; Bouhssine, Z.; Arechkik, A. Optimisation and economic modeling of micro hydropower plant integrated in water distribution system. J. Clean. Prod. 2019, 232, 877–887. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Flow regime aspects in determining environmental flows and maximising energy production at run-of-river hydropower plants. Appl. Energy 2019, 256, 113980. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Ghasemi, M.H.; Heyns, S. Application of hybrid systems in solution of low power generation at hot seasons for micro hydro systems. Renew. Energy 2020, 160, 323–332. [Google Scholar] [CrossRef]
- Anaza, S.; Abdulazeez, M.; Yisah, Y.; Yusuf, Y.; Salawu, B.; Momoh, S. Micro hydro-electric energy generation—An overview. Am. J. Eng. Res. (AJER) 2017, 6, 5–12. [Google Scholar]
- Jawahar, C.; Michael, P.A. A review on turbines for micro hydro power plant. Renew. Sustain. Energy Rev. 2017, 72, 882–887. [Google Scholar] [CrossRef]
- Hosseini, S.; Forouzbakhsh, F.; Rahimpoor, M. Determination of the optimal installation capacity of small hydro-power plants through the use of technical, economic and reliability indices. Energy Policy 2005, 33, 1948–1956. [Google Scholar] [CrossRef]
- Yildiz, V.; Vrugt, J.A. A toolbox for the optimal design of run-of-river hydropower plants. Environ. Model. Softw. 2019, 111, 134–152. [Google Scholar] [CrossRef]
- Borkowski, D.; Majdak, M. Small Hydropower Plants with Variable Speed Operation—An Optimal Operation Curve Determination. Energies 2020, 13, 6230. [Google Scholar] [CrossRef]
- Payet-burin, R.; Kromann, M.T.; Pereira-Cardenal, S.; Strzepek, K.M.; Bauer-Gottwein, P. Using model predictive control in a water infrastructure planning model for the Zambezi river basin. In Proceedings of the 38th IAHR World Congress: Water–Connecting the World, Panama City, Panama, 1–6 September 2019; CRC Press: Boca Raton, FL, USA, 2019; pp. 4057–4062. [Google Scholar]
- Anagnostopoulos, J.S.; Papantonis, D.E. Flow Modeling and Runner Design Optimization in Turgo Water Turbines. Int. J. Mech. Aerosp. Ind. Mechatron. Eng. 2007, 1, 204–209. [Google Scholar]
- Anagnostopoulos, J.S.; Papantonis, D.E. A fast Lagrangian simulation method for flow analysis and runner design in Pelton turbines. J. Hydrodyn. 2012, 24, 930–941. [Google Scholar] [CrossRef]
- Anagnostopoulos, J.S.; Papantonis, D.E. Optimal sizing of a run-of-river small hydropower plant. Energy Convers. Manag. 2007, 48, 2663–2670. [Google Scholar] [CrossRef]
- Ehteram, M.; Binti Koting, S.; Afan, H.A.; Mohd, N.S.; Malek, M.; Ahmed, A.N.; El-shafie, A.H.; Onn, C.C.; Lai, S.H.; El-Shafie, A. New evolutionary algorithm for optimizing hydropower generation considering multireservoir systems. Appl. Sci. 2019, 9, 2280. [Google Scholar] [CrossRef]
- Alexander, K.V.; Giddens, E.P. Optimum penstocks for low head microhydro schemes. Renew. Energy 2008, 33, 507–519. [Google Scholar] [CrossRef]
- Bozorg Haddad, O.; Moradi-Jalal, M.; Marino, M.A. Design–operation optimisation of run-of-river power plants. In Proceedings of the Institution of Civil Engineers-Water Management; Thomas Telford Ltd.: London, UK, 2011; Volume 164, pp. 463–475. [Google Scholar]
- Hounnou, A.H.; Dubas, F.; Fifatin, F.X.; Chamagne, D.; Vianou, A. Multi-objective optimization of run-of-river small-hydropower plants considering both investment cost and annual energy generation. Int. J. Energy Power Eng. 2019, 13, 17–21. [Google Scholar]
- Tapia, A.; Millán, P.; Gómez-Estern, F. Integer programming to optimize Micro-Hydro Power Plants for generic river profiles. Renew. Energy 2018, 126, 905–914. [Google Scholar] [CrossRef]
- Tapia, A.; Reina, D.G.; Millán, P. An Evolutionary Computational Approach for Designing Micro Hydro Power Plants. Energies 2019, 12, 878. [Google Scholar] [CrossRef]
- Tapia, A.; del Nozal, A.; Reina, D.; Millán, P. Three-dimensional optimization of penstock layouts for micro-hydropower plants using genetic algorithms. Appl. Energy 2021, 301, 117499. [Google Scholar] [CrossRef]
- Abdelhady, H.U.; Imam, Y.E.; Shawwash, Z.; Ghanem, A. Parallelized Bi-level optimization model with continuous search domain for selection of run-of-river hydropower projects. Renew. Energy 2021, 167, 116–131. [Google Scholar] [CrossRef]
- Leon, A.S.; Zhu, L. A dimensional analysis for determining optimal discharge and penstock diameter in impulse and reaction water turbines. Renew. Energy 2014, 71, 609–615. [Google Scholar] [CrossRef]
- Thake, J. Micro-Hydro Pelton Turbine Manual: Design, Manufacture and Installation for Small-Scale Hydropower; ITDG Publishing: Rugby, UK, 2000. [Google Scholar]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli beam theory. In Structural Analysis; Springer: Berlin/Heidelberg, Germany, 2009; pp. 173–221. [Google Scholar]
- Kumar, R.; Singal, S.K. Penstock material selection in small hydropower plants using MADM methods. Renew. Sustain. Energy Rev. 2015, 52, 240–255. [Google Scholar] [CrossRef]
- Reina, D.; Tawfik, H.; Toral, S. Multi-subpopulation evolutionary algorithms for coverage deployment of UAV-networks. Ad. Hoc. Netw. 2018, 68, 16–32. [Google Scholar] [CrossRef]
- Alvarado-Barrios, L.; Rodríguez del Nozal, A.; Tapia, A.; Martínez-Ramos, J.L.; Reina, D. An evolutionary computational approach for the problem of unit commitment and economic dispatch in microgrids under several operation modes. Energies 2019, 12, 2143. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms and Adaptation; Springer US: New York, NY, USA, 1984; pp. 317–333. [Google Scholar] [CrossRef]
- Tapia, A.; Reina, D.; Millán, P. Optimized Micro-Hydro Power Plants Layout Design Using Messy Genetic Algorithms. Expert Syst. Appl. 2020, 159, 113539. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| (KW) | 7 |
| (m) | 0.022 |
| E (GPa) | 200 |
| (MPa) | 250 |
| (c.u.) | 9 |
| (c.u./m) | 8 |
| (1/m) | 0.2 |
| () | 10 |
| (c.u./m) | 13.14 |
| (c.u./m) | 99.76 |
| (c.u./m) | 616.10 |
| Parameter | Value |
|---|---|
| 2000 | |
| 2000 | |
| Generations | 100 |
| Selection | Tournament size = 3 |
| Generation | Custom generation scheme |
| Crossover | Custom crossover scheme |
| = 0.50 | |
| Mutation | Custom mutation scheme |
| Number of trials | 10 |
| Diameter range (m) | 0.01–0.33 |
| Hyper-parameters | |||||
|---|---|---|---|---|---|
| 0.70 | 0.60 | 0.50 | 0.40 | 0.30 | |
| 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | |
| Final population fitness | |||||
| Mean | 22,066.77 | 23,031.35 | 23,397.92 | 22,551.43 | 22,133.37 |
| Std. dev. | 991.25 | 876.34 | 345.59 | 583.70 | 828.1163 |
| Min | 21,193.04 | 21,836.64 | 23,216.90 | 21,787.5 | 20,966.11 |
| Max | 41,083.82 | 48,206.39 | 41,396.83 | 33,011.61 | 25,811.00 |
| Best individual | |||||
| Gross h. (m) | 80.74 | 84.04 | 86.98 | 82.40 | 79.98 |
| Power (W) | 7017.69 | 7000.24 | 7009.17 | 7000.49 | 7003.06 |
| Pens. length (m) | 534.56 | 562.24 | 597.30 | 552.59 | 532.42 |
| Min, bending radius (m) | 80.00 | 67.36 | 60.00 | 58.07 | 58.99 |
| Bending radius allowed (m) | 54.23 | 53.08 | 52.50 | 53.67 | 54.55 |
| Pipe diam. (m) | 0.14 | 0.13 | 0.13 | 0.13 | 0.14 |
| Cost (c.u.) | 21,193.04 | 1836.64 | 23,216.90 | 21,787.50 | 20,966.11 |
| Ref. Problem | Modification 1 | Modification 2 | |
|---|---|---|---|
| Gross height (m) | 79.98 | 48.98 | 109.49 |
| Power (W) | 7003.46 | 4000.19 | 14,000.67 |
| Pens. length (m) | 532.42 | 298.75 | 735.37 |
| Min. bending radius (m) | 58.99 | 127.72 | 100.00 |
| Bending radius allowed (m) | 54.55 | 54.55 | 68.79 |
| Pipe diam. (m) | 0.14 | 0.14 | 0.17 |
| Cost (c.u.) | 20,966.11 | 11,769.02 | 42,191.30 |
| Continuous Approach | Discrete Approach [32] | |
|---|---|---|
| Gross height (m) | 79.98 | 78.56 |
| Power (W) | 7003.06 | 7173.34 |
| Pens. length (m) | 532.42 | 523.78 |
| Pipe diam. (m) | 0.14 | 0.14 |
| Cost (c.u.) | 20,966.11 | 21,590.50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Córdoba, A.T.; Gata, P.M.; Reina, D.G. Optimizing the Layout of Run-of-River Powerplants Using Cubic Hermite Splines and Genetic Algorithms. Appl. Sci. 2022, 12, 8133. https://doi.org/10.3390/app12168133
Córdoba AT, Gata PM, Reina DG. Optimizing the Layout of Run-of-River Powerplants Using Cubic Hermite Splines and Genetic Algorithms. Applied Sciences. 2022; 12(16):8133. https://doi.org/10.3390/app12168133
Chicago/Turabian StyleCórdoba, Alejandro Tapia, Pablo Millán Gata, and Daniel Gutiérrez Reina. 2022. "Optimizing the Layout of Run-of-River Powerplants Using Cubic Hermite Splines and Genetic Algorithms" Applied Sciences 12, no. 16: 8133. https://doi.org/10.3390/app12168133
APA StyleCórdoba, A. T., Gata, P. M., & Reina, D. G. (2022). Optimizing the Layout of Run-of-River Powerplants Using Cubic Hermite Splines and Genetic Algorithms. Applied Sciences, 12(16), 8133. https://doi.org/10.3390/app12168133







