Price Forecast for Mexican Red Spiny Lobster (Panulirus spp.) Using Artificial Neural Networks (ANNs)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Selection of Variables
2.2. Model Development
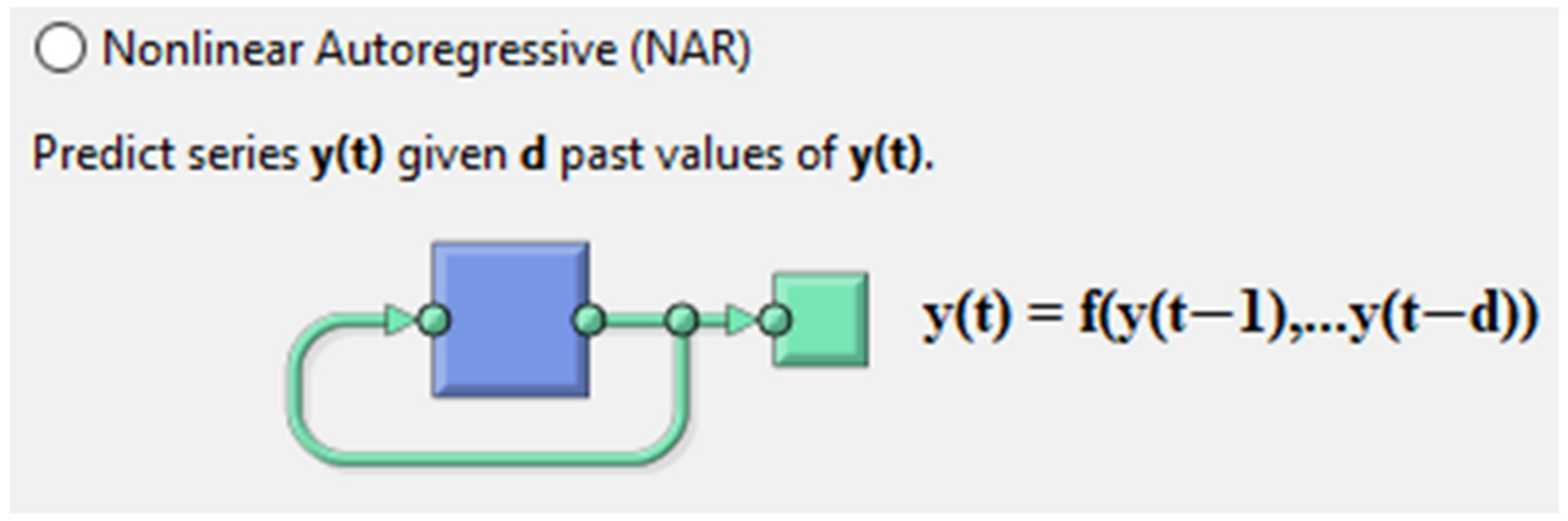
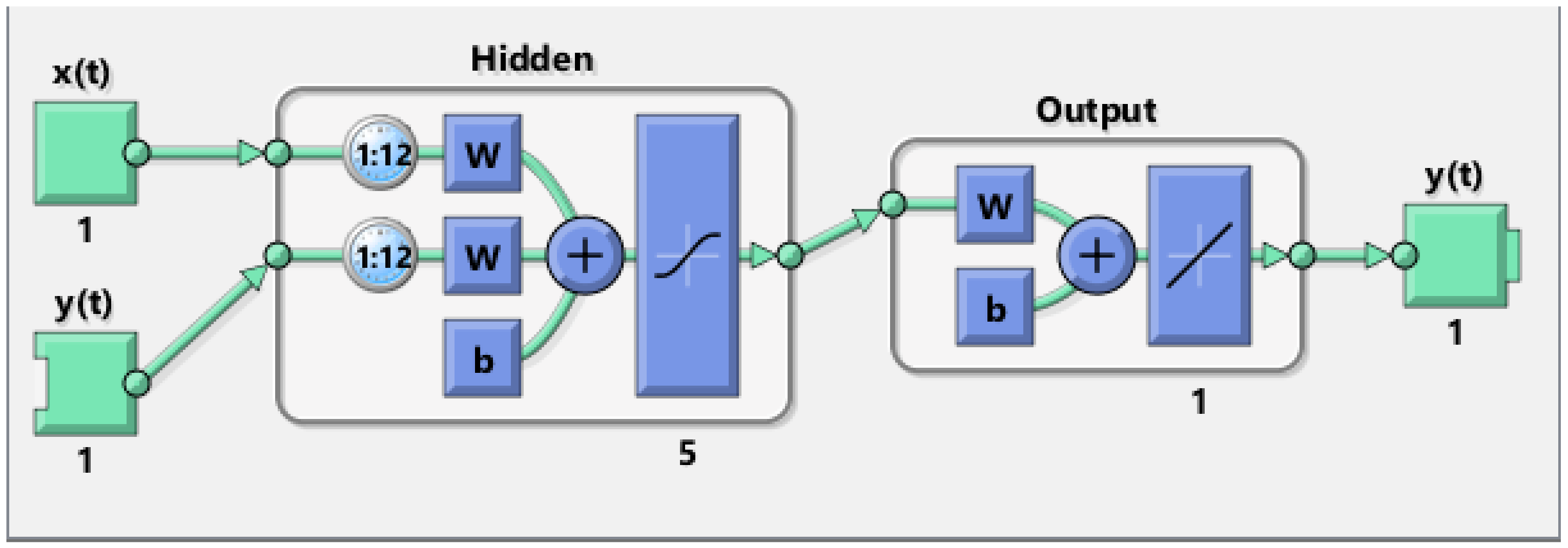
2.2.1. Neural Networks
2.2.2. Autoregressive Integrated Moving Average with an Exogenous Variable
2.2.3. Comparison of ANN and ARIMAX Approach
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- CONAPESCA. Anuario Estadístico de Acuacultura y Pesca 2018; Comisión Nacional de Acuacultura y Pesca: Mazatlán, Mexico, 2018. [Google Scholar]
- Almendárez-Hernández, L.C.; Ponce-Díaz, G.; Urciaga-García, J.I.; Beltrán-Morales, L.F. Mercado externo y desarrollo regional: La importancia de la pesquería de langosta en Baja California Sur. In Recursos Marinos y Servicios Ambientales en el Desarrollo Regional; Urciaga-García, J., Beltrán-Morales, L.F., Daniel Lluch-Belda, D., Eds.; CIBNOR, UABCS, CICIMAR: La Paz, Mexico, 2008; pp. 299–322. [Google Scholar]
- Salas, S.; Ríos-Lara, G.V.; Arce-Ibarra, A.M.; Velázquez-Abunader, I.; Cabrera-Vázquez, M.A.; Cepeda-González, M.F.; Pérez-Cobb, A.U. Integración y asistencia para la concertación del Programa de Ordenamiento de la pesquería de langosta en la Península de Yucatán. Inf. Final CINVESTAV INAPESCA Y ECOSUR 2012, 1, 296. [Google Scholar]
- TradeMap, International Trade Centre. Available online: www.trademap.org (accessed on 18 November 2021).
- DOF. DIARIO OFICIAL DE LA FEDERACION. 2015. Acuerdo Por el que se Modifica el Similar Por el que se Modifican Las Épocas y Zonas de Veda de la Langosta Azul (Panulirus inflatus), Langosta Verde (P. gracilis) y Langosta Roja (P. interruptus), en Aguas de Jurisdicción Federal del Océano Pacífico, Incluyendo el Golfo de California, Publicado en el Diario Oficial de la Federación el 31 de Agosto de 2005. Available online: www.dof.gob.mx (accessed on 2 May 2022).
- Anderson, L.G.; Seijo, J.C. Bioeconomics of Fisheries Management; John Wiley & Sons Ltd., Publication: Iowa, IA, USA, 2010. [Google Scholar]
- Ponce-Díaz, G.; Vergara-Solana, F.J.; Aranceta-Garza, F. Bioeconomic Analysis of Fishery Management Objectives Considering Changes in Selling Price. Econ. Teoría y Práctica 2021, 55, 149–170. [Google Scholar] [CrossRef]
- Pérez-Ramírez, M.; Ponce-Díaz, G.; Lluch-Cota, S. The role of MSC certification in the empowerment of fishing cooperatives in Mexico: The case of red rock lobster co-managed fishery. Ocean Coast. Manag. 2012, 63, 24–29. [Google Scholar] [CrossRef]
- Izumi, K. Complexity of Agents and Complexity of Markets. In New Frontiers in Artificial Intelligence; Terano, T., Ohsawa, Y., Nishida, T., Namatame, A., Tsumoto, S., Washio, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2253, pp. 110–120. [Google Scholar]
- Arthur, W.B. Complexity and the economy. In Handbook of Research on Complexity; Rosser, J., Jr., Ed.; Edward Elgar Publishing: Northampton, MA, USA, 2009; pp. 12–21. [Google Scholar]
- Shafie-khah, M.; Moghaddam, M.P.; Sheikh-El-Eslami, M.K. Price forecasting of day-ahead electricity markets using a hybrid forecast method. Energy Convers. Manag. 2011, 52, 2165–2169. [Google Scholar] [CrossRef]
- Restocchi, V. It takes All Sorts: The Complexity of Prediction Markets. Ph.D. Thesis, University of Southampton, Southampton, UK, 2018; p. 144. [Google Scholar]
- Basulto, C.A.; Medina, J. El precio de exportación. Carta Econ. Reg. 2018, 48, 37–40. [Google Scholar]
- Westerhoff, F.H. Exchange rate dynamics: A nonlinear survey. In Handbook of Research on Complexity; Rosser, J., Jr., Ed.; Edward Elgar Publishing: Northampton, MA, USA, 2009; pp. 235–287. [Google Scholar]
- Sánchez, R.J. La Formación de Precios en el Transporte Marítimo de Contenedores de Exportación y el Rol de Las Expectativas. Ph.D. Thesis, Pontificia Universidad Católica Argentina, Santa María de Buenos Aires, Argentina, 2019; p. 136. Available online: https://repositorio.uca.edu.ar/handle/123456789/11019 (accessed on 3 May 2022).
- Mancini, E.P. Determinación del Precio Mínimo de un Producto Alimenticio Para Exportación. Master’s Thesis, Universidad Nacional de Rosario, Rosario, Argentina, 2022; p. 49. [Google Scholar]
- Dupont, D.P. Price Uncertainty, Expectations Formation and Fishers’ Location Choices. Mar. Resour. Econ. 1993, 8, 219–247. [Google Scholar] [CrossRef]
- Gordon, D.V.; Maurice, S. Vertical and Horizontal Integration in the Uganda Fish Supply Chain: Measuring for Feedback Effects to Fishermen. Aquac. Econ. Manag. 2015, 19, 29–50. [Google Scholar] [CrossRef]
- Rusiman, M.S.; Hau, O.C.; Abdullah, A.W.; Sufahani, S.F.; Azmi, N.A. An analysis of time series for the prediction of barramundi (Ikan siakap) price in malaysia. Far East J. Math. Sci. 2017, 102, 2081–2093. [Google Scholar] [CrossRef]
- Ghiassi, M.; Saidane, H.; Zimbra, D.K. A dynamic artificial neural network model for forecasting time series events. Int. J. Forecast. 2005, 21, 341–362. [Google Scholar]
- Hamzaçebi, C.; Akay, D.; Kutay, F. Comparison of direct and iterative artificial neural network forecast approaches in multi-periodic time series forecasting. Expert Syst. Appl. 2009, 36, 3839–3844. [Google Scholar] [CrossRef]
- Pati, J.; Shukla, K.K. A comparison of ARIMA, neural network and a hybrid technique for Debian bug number prediction. In Proceedings of the 5th International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 26–28 September 2014; pp. 47–53. [Google Scholar]
- Garg, N.; Sharma, M.K.; Parmar, K.S.; Soni, K.; Singh, R.K.; Maji, S. Comparison of ARIMA and ANN approaches in time-series predictions of traffic noise. Noise Control Eng. J. 2016, 64, 522–531. [Google Scholar] [CrossRef]
- Alam, T. Forecasting exports and imports through artificial neural network and autoregressive integrated moving average. Decis. Sci. Lett. 2019, 8, 249–260. [Google Scholar] [CrossRef]
- Adeyinka, D.A.; Muhajarine, N. Time series prediction of under-five mortality rates for Nigeria: Comparative analysis of artificial neural networks, Holt-Winters exponential smoothing and autoregressive integrated moving average models. BMC Med. Res. Methodol. 2020, 20, 292. [Google Scholar] [CrossRef]
- Hilera, J.R.; Martínez, V.J.; Mazo, M. ECG signals processing with neural networks. Int. J. Uncertain. Fuzz. 1995, 03, 419–430. [Google Scholar] [CrossRef]
- Friedman, J. Multivariate adaptive regression splines. Ann. Statis. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Al-Batah, M.S.; MatIsa, N.A.; Zamli, K.Z.; Azizli, K.A. Modified Recursive Least Squares algorithm to train the Hybrid Multilayered Perceptron (HMLP) network. Appl. Soft Comput. 2010, 10, 236–244. [Google Scholar] [CrossRef]
- Vaziri, M. Predicting Caspian Sea Surface Water Level by ANN and ARIMA Models. J. Waterw. Port Coast Eng. 1997, 123, 158–162. [Google Scholar] [CrossRef]
- Jones, A.J. New tools in non-linear modelling and prediction. Comput. Manag. Sci. 2004, 1, 109–149. [Google Scholar] [CrossRef]
- Toriman, M.E.; Juahir, H.; Mokthar, M.; Gazim, M.B.; Abdullah, S.M.S.; Jaafar, O. Predicting for discharge characteristics in langat river, Malaysia using Neural Network application model. Res. J. Earth Sci. 2009, 1, 15–21. [Google Scholar]
- Bildirici, M.; Ersin, O. Forecasting volatility in oil prices with a class of nonlinear volatility models: Smooth transition RBF and MLP neural networks augmented GARCH approach. Pet. Sci. 2015, 12, 534. [Google Scholar] [CrossRef] [Green Version]
- Lim, W.T.; Wang, L.; Wang, Y.; Chang, Q. Housing price prediction using neural networks. In Proceedings of the 12th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Changsha, China, 13–15 August 2016; pp. 518–522. [Google Scholar]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A Deep Neural Network Model for Short-Term Load Forecast Based on Long Short-Term Memory Network and Convolutional Neural Network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef] [Green Version]
- Hainaut, D. A Neural-Network Analyzer for Mortality Forecast. ASTIN Bull. 2018, 48, 481–508. [Google Scholar] [CrossRef] [Green Version]
- Philemon, M.; Ismail, Z.; Dare, J. A Review of Epidemic Forecasting Using Artificial Neural Networks. Int. J. Epidemiol. Res. 2019, 6, 132–143. [Google Scholar]
- Silva, E.S.; Hassani, H.; Heravi, S.; Huang, X. Forecasting tourism demand with denoised neural networks. Ann. Tour. Res. 2019, 74, 134–154. [Google Scholar] [CrossRef]
- Namasudra, S.; Dhamodharavadhani, S.; Rathipriya, R. Nonlinear Neural Network Based Forecasting Model for Predicting COVID-19 Cases. Neural Process. Lett. 2021. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Ho, Q.T. Deep transformers and convolutional neural network in identifying DNA N6-methyladenine sites in cross-species genomes. Methods 2021, 204, 199–206. [Google Scholar] [CrossRef]
- Tng, S.S.; Le, N.Q.K.; Yeh, H.Y.; Chua, M.C.H. Improved Prediction Model of Protein Lysine Crotonylation Sites Using Bidirectional Recurrent Neural Networks. J. Proteome Res. 2021, 21, 265–273. [Google Scholar] [CrossRef]
- Tealab, A. Time Series Forecasting using Artificial Neural Networks Methodologies: A Systematic Review. Future Comput. Informat. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Tran, T.T.K.; Bateni, S.M.; Ki, S.J.; Vosoughifar, H. A Review of Neural Networks for Air Temperature Forecasting. Water 2021, 13, 1294. [Google Scholar] [CrossRef]
- Meng, J.; Shiqian, W.; Juwei, L.; Hock, L.T. Face recognition with radial basis function (RBF) neural networks. IEEE Tran. Neural Netw. 2002, 13, 697–710. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, D.; Choy, M.C.; Cheu, R.L. Neural Networks for Real-Time Traffic Signal Control. IEEE Trans. Intell. Transp. Syst. 2006, 7, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Adebiyi, A.A.; Adewumi, A.O.; Ayo, C.K. Comparison of ARIMA and Artificial Neural Networks Models for Stock Price Prediction. J. Appl. Math. 2014, 2014, 614342. [Google Scholar] [CrossRef] [Green Version]
- Guresen, E.; Kayakutlu, G.; Daim, T. Using artificial neural network models in stock market index prediction. Expert Syst. Appl. 2011, 38, 10389–10397. [Google Scholar] [CrossRef]
- Mombeini, H.; Yazdani-Chamzini, A. Modeling gold price via artificial neural network. J. Econ. Bus. Manag. 2015, 3, 699–703. [Google Scholar] [CrossRef] [Green Version]
- Abidoye, R.B.; Chan, A.P.C.; Abidoye, F.A.; Oshodi, O.S. Predicting property price index using artificial intelligence techniques: Evidence from Hong Kong. Int. J. Hous. Mark. Anal. 2019, 12, 1072–1092. [Google Scholar] [CrossRef]
- Cheng, D.; Yang, F.; Xiang, S.; Liu, J. Financial time series forecasting with multi-modality graph neural network. Pattern Recognit. 2022, 121, 108218. [Google Scholar] [CrossRef]
- Seung, C.K.; Waters, E.C. Evaluating supply-side and demand-side shocks for fisheries: A computable general equilibrium (CGE) model for Alaska. Econ. Syst. Res. 2010, 22, 87–109. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. Fisheries and Aquaculture Statistics. Available online: http://www.fao.org/fishery/statistics/ (accessed on 9 October 2021).
- Restrepo, B.L.; González, L.J. De Pearson a Spearman. Rev. Colom. Cienc. Pecua. 2007, 20, 183–192. [Google Scholar]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Aguado-Behar, A.; Martínez-Iranzo, M. Identificación y Control Adaptativo; Pearson Educación: Madrid, Spain, 2003; p. 285. [Google Scholar]
- Matlab 2021. MATLAB Help (F1), Neural Network Toolbox/Getting Started/Getting Started/Time Series Prediction. Available online: https://la.mathworks.com/help/deeplearning/gs/neural-network-time-series-prediction-and-modeling.html;jsessionid=f29323f88d0fd955e420a6225f35 (accessed on 5 January 2021).
- Gao, Y.; Meng, J.E. NARMAX time series model prediction: Feedforward and recurrent fuzzy neural network approaches. Fuzzy Sets Syst. 2005, 150, 331–350. [Google Scholar] [CrossRef]
- Ortiz de Dios, C.E. Modelos Econométricos y de Redes Neuronales para Predecir la Oferta Maderera en México: ARIMA vs NAR y ARMAX vs NARX. Master’ Thesis, Universidad Autónoma Metropolitana, Ciudad de Mexico, México, 2012; p. 154. [Google Scholar]
- Duch, W.; Korczak, J. Optimization and global minimization methods suitable for neural networks. Neural Comput. Surv. 1998, 2, 163–212. [Google Scholar]
- Wang, Y.; Li, Y.; Song, Y.; Rong, X. The Influence of the Activation Function in a Convolution Neural Network Model of Facial Expression Recognition. Appl. Sci. 2020, 10, 1897. [Google Scholar] [CrossRef] [Green Version]
- Burden, F.; Winkler, D. Bayesian Regularization of Neural Networks. Artif. Neural Netw. 2008, 458, 23–42. [Google Scholar]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Foresee, F.D.; Martin, T.H. Gauss-Newton approximation to Bayesian learning. In Proceedings of the International Joint Conference on Neural Networks, Houston, TX, USA, 12 June 1997; Volume 3, pp. 1930–1935. [Google Scholar]
- MacKay, D.J.C. A practical Bayesian framework for backpropagation networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef]
- Suszynski, M.; Peta, K. Assembly Sequence Planning Using Artificial Neural Networks for Mechanical Parts Based on Selected Criteria. Appl. Sci. 2021, 11, 10414. [Google Scholar] [CrossRef]
- Hanke, J.E.; Wichern, D.W. Pronóstico en Los Negocios, 8th ed.; Pearson Educación de México: Ciudad de México, Mexico, 2006; p. 552. [Google Scholar]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.H. On Mean Absolute Error for Deep Neural Network Based Vector-to-Vector Regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]
- Biscaro, Q. A Price Analysis and Management Model for Adriatic Small Pelagic Fish (Anchovies and Pilchards). New Medit. 2012, 11, 17–26. [Google Scholar]
- Gordon, D.V.; Hannesson, R. The Norwegian Winter Herring Fishery: A Story of Technological Progress and Stock Collapse. Land Econ. 2015, 91, 362–385. [Google Scholar] [CrossRef]
- Hasan, M.R.; Dey, M.M.; Engle, C.R. Forecasting monthly catfish (Ictalurus punctatus) pond bank and feed prices. Aquac. Econ. Manag. 2018, 23, 86–110. [Google Scholar] [CrossRef]
- Vega, V.A.; Espinoza, C.G.; Gómez, R.C. Pesquería de la langosta (Panulirus spp.). In Estudio del Potencial Pesquero y Acuícola de Baja California Sur; Casas-Valdez, M.M., Ponce-Díaz, G., Eds.; SEMARNAP, Gobierno del Estado de Baja California Sur, FAO, Instituto Nacional de la Pesca, UABCS, CIB, CICIMAR, CET del Mar: La Paz, Mexico, 1996; Volume I, pp. 227–261. [Google Scholar]
- Vega, V.A.; Lluch-Belda, D.; Muciño, M.; León, C.G.; Hernández, V.S.; Lluch-Cota, D.; Ramade, V.M.; Espinoza, C.G. Development, perspectives and management of lobster and abalone fisheries, off northwest Mexico, under a limited Access system. In The State of the Science and Management; Proceedings of the 2nd World Fisheries; Hancock, D.A., Smith, D.C., Beumer, J.P., Eds.; CSIRO Publishing: Collingwood, Brisbane, Australia, 1997; pp. 136–142. [Google Scholar]
- Vega-Velázquez, A. Reproductive strategies on the spiny lobster Panulirus interruptus related to the marine environmental variability off central Baja California, Mexico: Mangement implications. Fish. Res. 2003, 65, 123–135. [Google Scholar] [CrossRef]
- Castro-Ortiz, J.L.; Guzmán del Proo, S. Efecto del clima en las pesquerías de abulón y langosta en Baja California, México. Océanides 2018, 33, 13–25. [Google Scholar]
- Ran, T.; Keithly, W.R.; Yue, C. Reference-Dependent Preferences in Gulf of Mexico Shrimpers’ Fishing Effort Decision. J. Agric. Resour. Econ. 2014, 39, 19–33. [Google Scholar]
- Sunoko, R.; Huang, H.W. Indonesia tuna fisheries development and future strategy. Mar. Policy 2014, 43, 174–183. [Google Scholar] [CrossRef]
- Plagányi, É.E.; McGarvey, R.; Gardner, C.; Caputi, N.; Dennis, D.; de Lestang, S.; Villanueva, C. Overview, opportunities and outlook for Australian spiny lobster fisheries. Rev. Fish Biol. Fish. 2017, 28, 57–87. [Google Scholar] [CrossRef]
- Australia Embraces U.S. and Pays Price with China as Trade War Hits Bottom Line. Available online: https://www.nbcnews.com/news/world/australia-embraces-u-s-pays-price-china-trade-war-hits-n1270458 (accessed on 30 April 2022).
- Lawrence, S.; Giles, C.L. Overfitting and neural networks: Conjugate gradient and backpropagation. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, IJCNN 2000, Neural Computing: New Challenges and Perspectives for the New Millennium, Como, Italy, 27 July 2000. [Google Scholar]
- Koehrsen, W. Overfitting vs. Underfitting: A Complete Example. Towards Data Science. 2018. Available online: https://towardsdatascience.com/overfitting-vs-underfitting-a-complete-example-d05dd7e19765 (accessed on 15 May 2022).
- Altman, D.G.; Bland, J.M. Parametric v non-parametric methods for data analysis. BMJ 2009, 338, a3167. [Google Scholar] [CrossRef] [Green Version]
- Malcomson, J.M. Contacts, hold-up, and labor markets. J. Econ. Lit. 1997, 35, 1916–1957. [Google Scholar]
- Marc, I.; Kušar, J.; Berlec, T. Decision-Making Techniques of the Consumer Behaviour Optimisation of the Product Own Price. Appl. Sci. 2022, 12, 2176. [Google Scholar] [CrossRef]
- Samy-Kamal, M.; Forcada, A.; Lizaso, J.L.S. Daily variation of fishing effort and ex-vessel prices in a western Mediterranean multi-species fishery: Implications for sustainable management. Mar. Policy 2015, 61, 187–195. [Google Scholar] [CrossRef] [Green Version]



| Variable | Abbreviation |
|---|---|
| Lobster production in Mexico | PMex |
| Lobster price in Australia | PAus |
| Export price of Mexican lobster in Hong Kong | PMexHK |
| Export price of Mexican lobster in the USA | PMexUsa |
| Export price of Mexican lobster in Taiwan | PMexTC |
| World export price of New Zealand lobster | PNZMun |
| Export price of New Zealand lobster in Hong Kong | PNZHK |
| Export price of New Zealand lobster in the USA | PNZUsa |
| Export price of New Zealand lobster in Taiwan | PNZTC |
| World export price of Australian lobster | PAusMun |
| Export price of Australian lobster in Hong Kong | PAusHK |
| Export price of Australian lobster in the USA | PAusUSA |
| Export price of Australian lobster in Taiwan | PAusTC |
| Price Increase of Australian lobster | VCAus |
| Price increase of New Zealand lobster | VCNZ |
| Price Increase of Mexican lobster | VCMex |
| Export volume of Mexican lobster in Hong Kong | VMexHK |
| Export volume of Mexican lobster in Taiwan | VMexTC |
| Export volume of Mexican lobster in USA | VMexUSA |
| Export volume of Australian lobster in Hong Kong | VAusHK |
| Export volume of Australian lobster in Taiwan | VAusTC |
| World export volume of Australian lobster | VAusMun |
| Export volume of Australian lobster in USA | VAusUsa |
| Volume of lobster imported to the USA from Australia | VUSAAus |
| Volume of lobster imported to the USA from Mexico | VUSAMex |
| Volume of lobster imported to the USA from New Zealand | VUsaNZ |
| Volume of lobster imported to Taiwan from Australia | VTCAus |
| Volume of lobster imported to Taiwan from Mexico | VTCMex |
| Volume of lobster imported to Taiwan from New Zealand | VTCNZ |
| Apparent domestic lobster consumption in Mexico | CNA |
| Per capita lobster consumption in Mexico | CPCMex |
| Export Price from Mexico to Hong Kong | |
|---|---|
| Selected Exogenous Variables | Correlation (rho) |
| PMex | 0.51 |
| PAusMun | 0.46 |
| VMexHK | 0.86 |
| CNAMex | 0.41 |
| R2 | R2 | R2 | R2 | ||||
|---|---|---|---|---|---|---|---|
| NAR, P-R only | 0.92 | NARX2 | 0.96 | NARX1 | 0.94 | NARX3 | 0.95 |
| PAusMun | CNA | PMex | |||||
| VMexHK | PAusMun | ||||||
| CNA | |||||||
| NARX1 | 0.93 | NARX2 | 0.94 | NARX2 | 0.96 | NARX3 | 0.91 |
| PMex | PAusMun | PMex | PMex | ||||
| CNA | PAus | VHK | |||||
| CNA | |||||||
| NARX1 | 0.96 | NARX2 | 0.86 | NARX2 | 0.93 | NARX3 | 0.92 |
| PAus | VMexHK | PMex | PAusMun | ||||
| CNA | VMexHK | VMexHK | |||||
| CNA | |||||||
| NARX1 | 0.91 | NARX3 | 0.91 | NARX2 | 0.96 | NARX4 | 0.96 |
| VHK | PMex | PMex | PMex | ||||
| PAusMun | CNA | VMexHK | |||||
| VMexHK | PAusMun | ||||||
| CNA |
| NAR | NARX | |||||||
| 2017 | P-R | P-R Only | PMex | Paus | VHK | CNA | PMex, Paus | PMex, VHK |
| Month 1 | 39 | 40 | 27 | 30 | 29 | 27.3 | 27.5 | 46.6 |
| Month 2 | 36 | 29 | 40.7 | 33 | 31 | 15.6 | 35 | 22.4 |
| Month 3 | 33 | 17 | 35.3 | 24 | 33 | 31.5 | 40.8 | 38.6 |
| MSE | 42 | 56 | 51.8 | 6.6 | 58.5 | 25.4 | 117 | |
| MAE | 8 | 6.3 | 7 | 5 | 11.2 | 6.7 | 8.9 | |
| NARX | ||||||||
| 2017 | PMex, CNA | PAus, VHK | PAus, CNA | VHK, CNA | PMex, PAus, VHK | PMex, PAus, CNA | PMex, VHK, CNA | |
| Month 1 | 27 | 27 | 27 | 27 | 30.5 | 27 | 30.5 | |
| Month 2 | 46.6 | 38 | 18.5 | 33 | 21.5 | 31.3 | 31.2 | |
| Month 3 | 54.2 | 30 | 44 | 37 | 61.5 | 42.5 | 44.5 | |
| MSE | 228 | 45 | 54 | 11.3 | 231.8 | 19.4 | 28 | |
| MAE | 14.6 | 5.6 | 13.5 | 6.3 | 17 | 8.7 | 8.2 | |
| NARX | ARIMAX | |||||||
| 2017 | PAus, VHK, CNA | PMex, PAus, VHK, CNA | PAus | PMex | VHK | CNA | ||
| Month 1 | 33 | 27 | 47.4 | 47.8 | 49 | 48.4 | ||
| Month 2 | 32.8 | 17.8 | 48.6 | 51.5 | 50.6 | 48.9 | ||
| Month 3 | 42 | 53 | 35.3 | 44.21 | 40.24 | 39.26 | ||
| MSE | 27.8 | 135.5 | 95.6 | 117.8 | 99.5 | 136.1 | ||
| MAE | 6 | 16.7 | 7.7 | 11.8 | 10.6 | 9.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Casas, S.; Beltrán-Morales, L.F.; Vargas-López, V.G.; Vergara-Solana, F.; Seijo, J.C. Price Forecast for Mexican Red Spiny Lobster (Panulirus spp.) Using Artificial Neural Networks (ANNs). Appl. Sci. 2022, 12, 6044. https://doi.org/10.3390/app12126044
Hernández-Casas S, Beltrán-Morales LF, Vargas-López VG, Vergara-Solana F, Seijo JC. Price Forecast for Mexican Red Spiny Lobster (Panulirus spp.) Using Artificial Neural Networks (ANNs). Applied Sciences. 2022; 12(12):6044. https://doi.org/10.3390/app12126044
Chicago/Turabian StyleHernández-Casas, Sergio, Luis Felipe Beltrán-Morales, Victor Gerardo Vargas-López, Francisco Vergara-Solana, and Juan Carlos Seijo. 2022. "Price Forecast for Mexican Red Spiny Lobster (Panulirus spp.) Using Artificial Neural Networks (ANNs)" Applied Sciences 12, no. 12: 6044. https://doi.org/10.3390/app12126044
APA StyleHernández-Casas, S., Beltrán-Morales, L. F., Vargas-López, V. G., Vergara-Solana, F., & Seijo, J. C. (2022). Price Forecast for Mexican Red Spiny Lobster (Panulirus spp.) Using Artificial Neural Networks (ANNs). Applied Sciences, 12(12), 6044. https://doi.org/10.3390/app12126044





