Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography
Abstract
:1. Introduction
2. Theory
2.1. Mathematical Theory
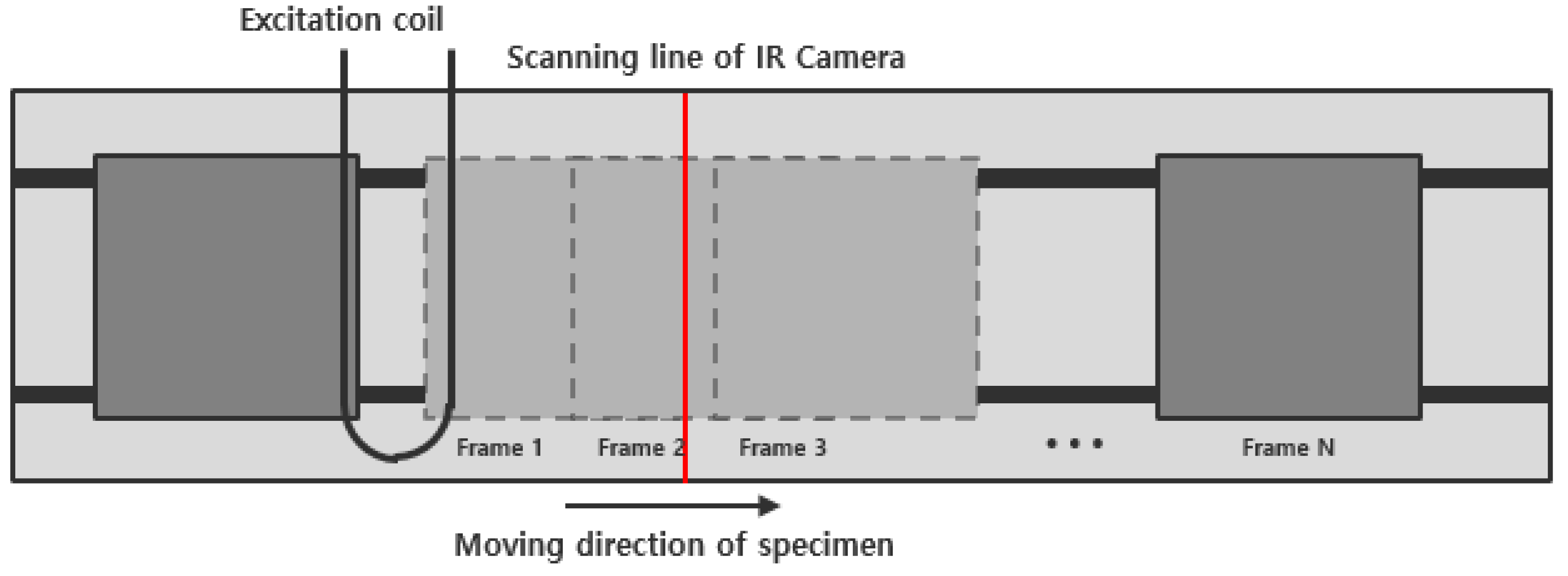
2.2. Line-Scanning Method
3. Experimental Setup
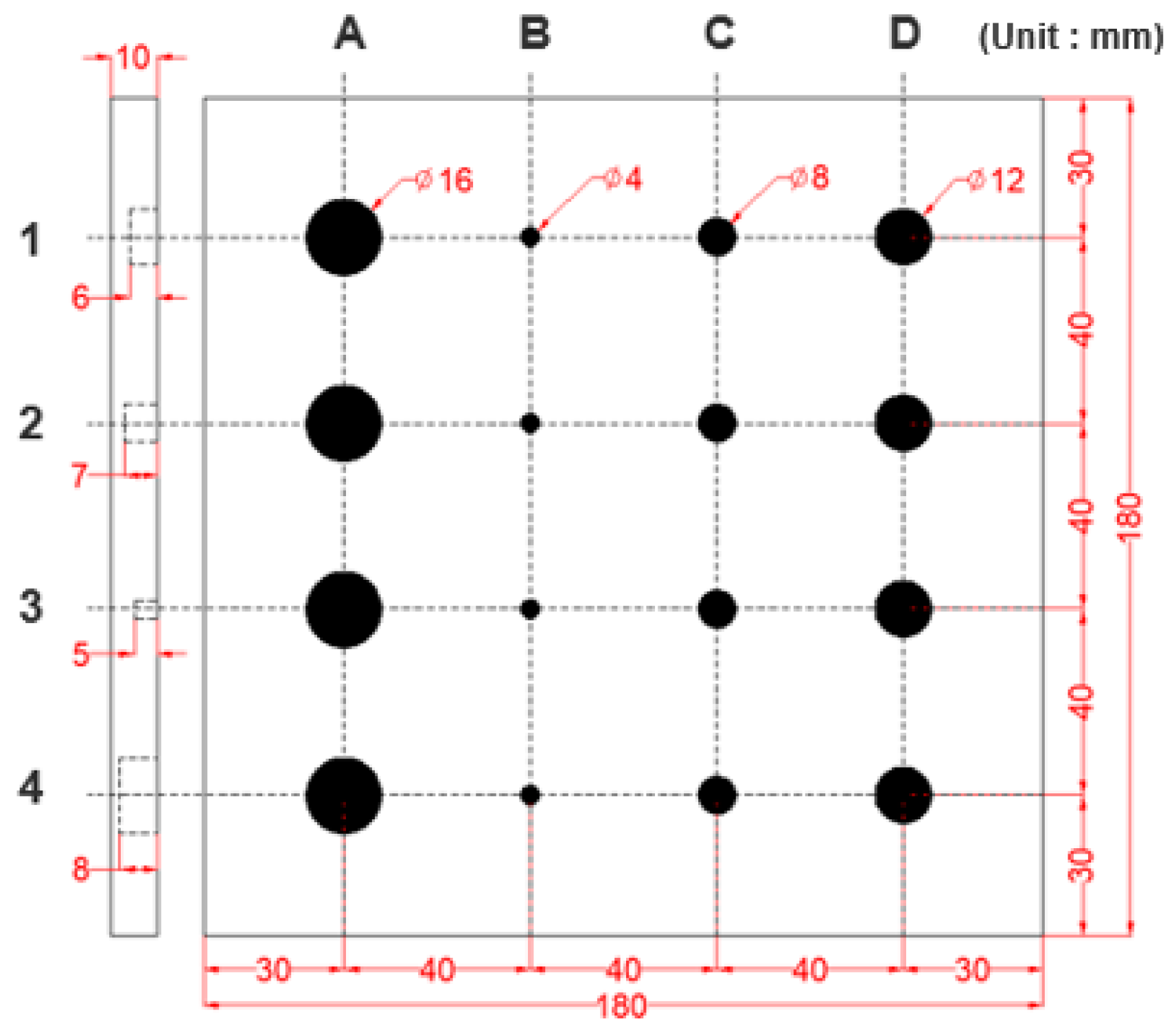
3.1. STS304 Reference Specimen
3.2. LSM Configuration
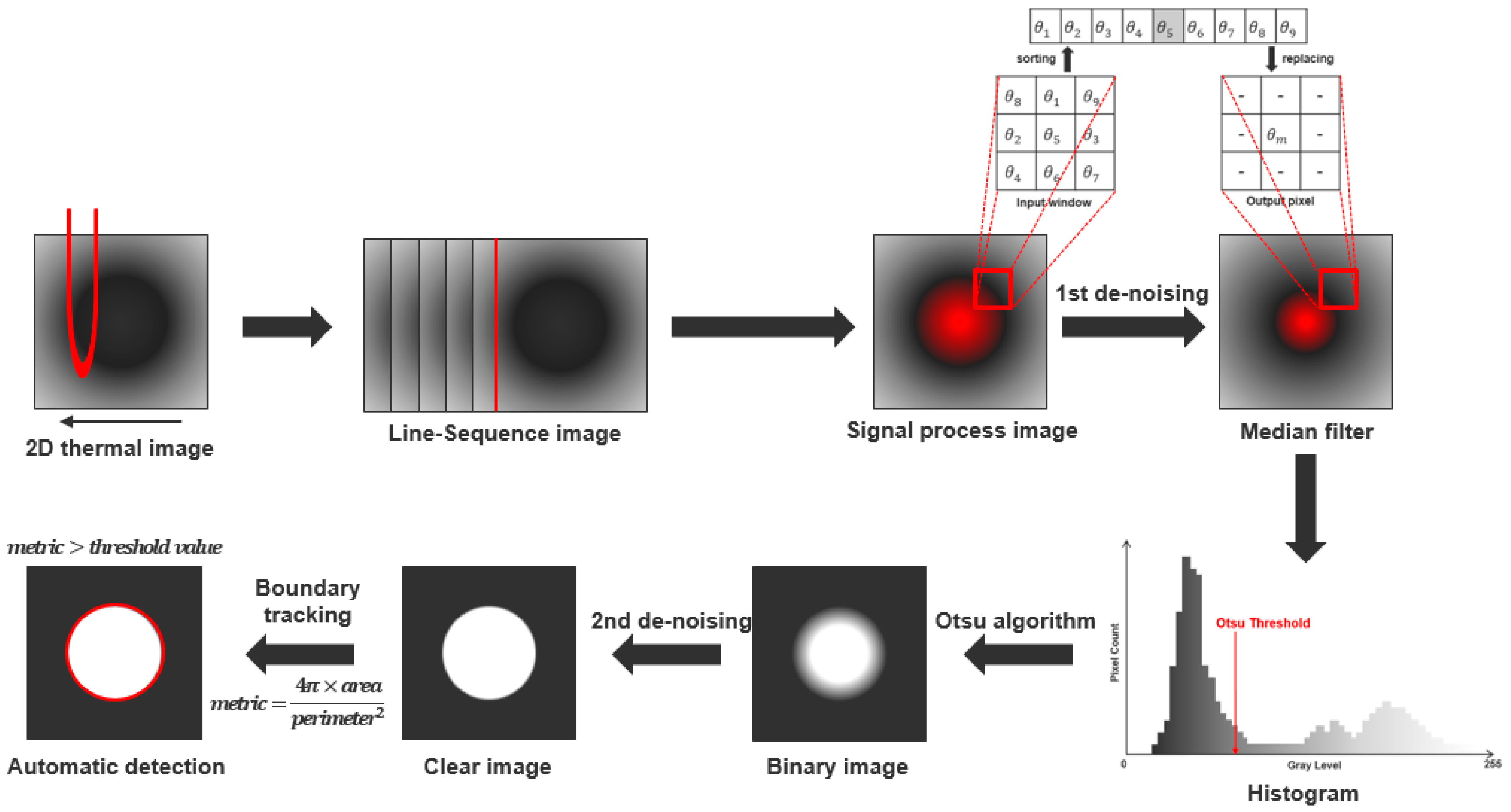
3.3. Image Process
- Step 1:
- In order to provide a uniform heat source to the surface of the specimen, a 2D thermal image was acquired by applying LSM to induction thermography.
- Step 2:
- After calculating the total frame for the 2D scanning image, the thermal image for a specific frame was extracted. In general, the scanning line selected the starting point for the visual identification of the specimen as the infrared camera monitored the moving specimen. After that, a sequence image for a specific frame was acquired based on the scanning line, and the image was cropped using the crop function to analyze the area of the specimen in the entire image.
- Step 3:
- Filtering (mean, median, Gaussian, and NLmeans) was applied to the cropped raw image for the 1st de-noising, and the SNR of the ROI was calculated for a comparative analysis of detectability.
- Step 4:
- In order to classify clear defect objects in the image, binarization was performed using the Otsu algorithm, and the 2nd de-noising was performed.
- Step 5:
- Using the boundary tracking function, the automatic defect recognition in the image was performed based on the threshold value through the roundness equation, and the error rate was analyzed for reliability verification.
4. Results and Discussion
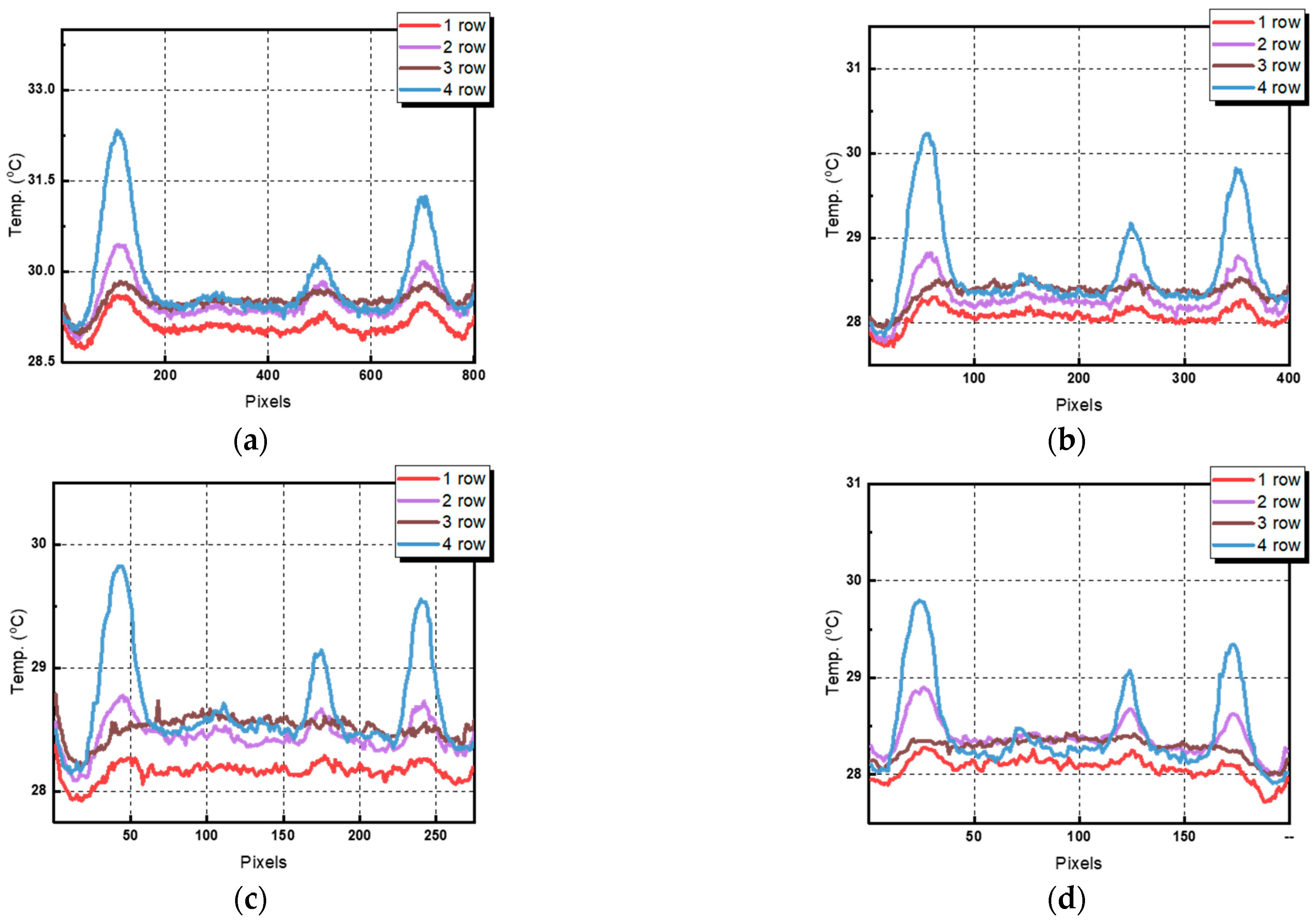
4.1. Two-Dimensional Thermal Image
4.2. Filtering for 1st De-Noising
4.3. Binary Process
4.4. Morphology for 2nd De-Noising
4.5. Automatic Defect Recognition
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maldague, X.P. Nondestructive Testing Handbook. Infrared and Thermal Testing; American Society for Nondestructive Testing: Arlingate Lane, OA, USA, 2001; Volume 3. [Google Scholar]
- Maldague, X.P. Introduction to NDT by Active Infrared Thermography. Mater. Eval. 2002, 60, 1060–1073. [Google Scholar]
- Choi, M.Y.; Kang, K.S.; Park, J.H.; Kim, W.T.; Kim, K.S. Quantitative determination of a subsurface defect of reference specimen by lock-in infrared thermography. NDT E Int. 2008, 41, 119–124. [Google Scholar] [CrossRef]
- Chung, Y.J.; Lee, S.J.; Kim, W.T. Latest Advances in Common signal Processing of Pulsed Thermography for Enhanced Detectability: A Review. Appl. Sci. 2021, 11, 12168. [Google Scholar] [CrossRef]
- Shull, P.J. Nondestructive Evaluation: Theory, Techniques, and Applications; CRC Press: New York, NY, USA, 2002. [Google Scholar]
- Roberts, M.; Wang, K.; Guzas, E.; Lockhart, P.; Tucker, W. Induction infrared thermography for non-destructive evaluation of alloy sensitization. AIP Conf. Proc. 2019, 2102, 120006. [Google Scholar]
- Haneef, T.; Lahiri, B.B.; Bagavathiappan, S.; Mukhopadhyay, C.K.; Philip, J.; Rao, B.P.C.; Jayakumar, T. Study of the tensile behavior of AISI type 316 stainless steel using acoustic emission and infrared thermography techniques. J. Mater. Res. Technol. 2015, 4, 241–253. [Google Scholar] [CrossRef] [Green Version]
- Rodríguez-Martín, M.; Lagüela, S.; González-Aguilera, D.; Martinez, J. Prediction of depth model for cracks in steel using infrared thermography. Infrared Phys. Technol. 2015, 71, 492–500. [Google Scholar] [CrossRef]
- Bagavathiappan, S.; Lahiri, B.B.; Saravanan, T.; Philip, J.; Jayakumar, T. Infrared thermography for condition monitoring—A review. Infrared Phys. Technol. 2013, 60, 35–55. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Venegas, P.; Guerediaga, J.; Vega, L.; Molleda, J.; Bulnes, F.G. Infrared thermography for temperature measurement and non-destructive testing. Sensors 2014, 14, 12305–12348. [Google Scholar] [CrossRef] [Green Version]
- Holland, S.D.; Reusser, R.S. Material evaluation by infrared thermography. Annu. Rev. Mater. Res. 2016, 46, 287–303. [Google Scholar] [CrossRef]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [Green Version]
- Osornio-Rios, R.A.; Antonino-Daviu, J.A.; de Jesus Romero-Troncoso, R. Recent industrial applications of infrared thermography: A review. IEEE Trans. Ind. Inform. 2018, 15, 615–625. [Google Scholar] [CrossRef]
- Qu, Z.; Jiang, P.; Zhang, W. Development and application of infrared thermography non-destructive testing techniques. Sensors 2020, 20, 3851. [Google Scholar] [CrossRef] [PubMed]
- Morozov, M.; Jackson, W.; Pierce, S. Capacitive imaging of impact damage in composite material. Compos. Part B 2017, 113, 65–71. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.; Hutchins, D. Non-destructive evaluation of composite materials using a capacitive imaging technique. Compos. Part B 2012, 43, 1282–1292. [Google Scholar] [CrossRef]
- Kılınç, M.; Gözde, H. Detection of buried anti-personnel mines in thermal images by circular hough transformation supported active thermography method. J. Fac. Eng. Archit. Gazi Univ. 2020, 35, 697–707. [Google Scholar]
- Sec¸kin, A.; Sec¸kin, M. Detection of fabric defects with intertwined frame vector feature extraction. Alex. Eng. J. 2022, 61, 2887–2898. [Google Scholar] [CrossRef]
- Caminero, M.; García-Moreno, I.; Rodríguez, G.; Chacón, J. Internal damage evaluation of composite structures using phased array ultrasonic technique: Impact damage assessment in CFRP and 3D printed reinforced composites. Compos. Part B 2019, 165, 131–142. [Google Scholar] [CrossRef]
- Gao, B.; Li, X.; Woo, W.; Tian, G. Physics-Based Image Segmentation Using First Order Statistical Properties and Genetic Algorithm for Inductive Thermography Imaging. IEEE Trans. Image Process. 2018, 27, 2160–2175. [Google Scholar] [CrossRef]
- Mabrouki, F.; Thomas, M.; Genest, M.; Fahr, A. Frictional heating model for efficient use of vibrothermography. NDT E Int. 2009, 42, 345–352. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Poelman, G.; Segers, J.; Van Paepegem, W.; Kersemans, M. Performance of frequency and/or phase modulated excitation waveforms for optical infrared thermography of CFRPs through thermal wave radar: A simulation study. Compos. Struct. 2019, 225, 111177. [Google Scholar] [CrossRef]
- Renshaw, J.; Chen, J.C.; Holland, S.D.; Thompson, R.B. The sources of heat generation in vibrothermography. NDT E Int. 2011, 44, 736–739. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.J.; Chung, Y.J.; Ranjit, S.; Kim, W.T. Automated Defect Detection Using Threshold Value Classification Based on Thermographic Inspection. Appl. Sci. 2021, 11, 7870. [Google Scholar] [CrossRef]
- Li, X.; Gao, B.; Woo, W.L.; Tian, G.Y.; Qiu, X.; Gu, L. Quantitative Surface Crack Evaluation Based on Eddy Current Pulsed Thermography. IEEE Sens. J. 2017, 17, 412–421. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, X.; Ma, J.; Zhen, D.; Zhang, H. Quantitative Detection of Cracks in Steel Using Eddy Current Pulsed Thermography. Sensors 2018, 18, 1070. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oswald-Tranta, B. Induction thermography for surface crack detection and depth determination. Appl. Sci. 2018, 8, 257. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; He, Y.; Gao, B.; Tian, G.Y.; Peng, J. Lateral heat conduction based eddy current thermography for detection of parallel cracks and rail tread oblique cracks. Measurement 2015, 66, 54–61. [Google Scholar] [CrossRef]
- Abidin, I.Z.; Tian, G.Y.; Wilson, J.; Yang, S.; Almond, D. Quantitative evaluation of angular defects by pulsed eddy current thermography. NDT E Int. 2010, 43, 537–546. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, Z.; Wu, J.; He, S.; Roskosz, M.; Xia, H.; Kang, Y. A Scanning Induction Thermography System for Thread Defects of Drill Pipes. IEEE Trans. Instrum. Meas. 2021, 71, 3502509. [Google Scholar] [CrossRef]
- He, M.; Zhang, L.; Li, J.; Zheng, W. Methods for suppression of the effect of uneven surface emissivity of material in the moving mode of eddy current thermography. Appl. Therm. Eng. 2017, 118, 612–620. [Google Scholar] [CrossRef]
- He, M.; Zhang, L.; Zheng, W.; Feng, W. Crack detection based on a moving mode of eddy current thermography method. Measurement 2017, 109, 119–129. [Google Scholar] [CrossRef]
- He, M.; Zheng, W.; Li, W.; Zhang, Y. Research on temperature distribution law around crack using the moving mode of eddy current thermography. Infrared Phys. Technol. 2019, 102, 102993. [Google Scholar] [CrossRef]
- Zhang, X.; Peng, J.; He, K.; Gao, X. Nondestructive inspection of holes with distinct spacing in plate using the moving mode of Induction Thermography. Infrared Phys. Technol. 2022, 122, 104045. [Google Scholar] [CrossRef]
- Tuschl, C.; Oswald-Tranta, B.; Eck, S. Inductive thermography as non-destructive testing for railway rails. Appl. Sci. 2021, 11, 1003. [Google Scholar] [CrossRef]
- Ranjit, S.; Kim, W.T. Non-destructive testing and evaluation of materials using active thermography and enhancement of signal to noise ratio through data fusion. Infrared Phys. Technol. 2018, 94, 78–84. [Google Scholar]
- Tabatabaei, N. Matched-filter thermography. Appl. Sci. 2018, 8, 581. [Google Scholar] [CrossRef] [Green Version]
- Akram, M.W.; Li, G.; Jin, Y.; Chen, X.; Zhu, C.; Zhao, X.; Aleem, M.; Ahmad, A. Improved outdoor thermography and processing of infrared images for defect detection in PV modules. Sol. Energy 2019, 190, 549–560. [Google Scholar] [CrossRef]
- Forero-Ramírez, J.C.; Restrepo-Girón, A.D.; Nope-Rodríguez, S.E. Detection of internal defects in carbon fiber reinforced plastic slabs using background thermal compensation by filtering and support vector machines. J. Nondestruct. Eval. 2019, 38, 33. [Google Scholar] [CrossRef]
- Venegas, P.; Perán, J.; Usamentiaga, R.; de Ocáriz, I.S. Projected thermal diffusivity analysis for thermographic nondestructive inspections. Int. J. Therm. Sci. 2018, 124, 251–262. [Google Scholar] [CrossRef]
- Dong, X.Y. Review of otsu segmentation algorithm. Adv. Mater. Res. 2014, 989, 1959–1961. [Google Scholar] [CrossRef]
- Manda, M.P.; Kim, H.S. A fast image thresholding algorithm for infrared images based on histogram approximation and circuit theory. Algorithms 2020, 13, 207. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Long, J.; Chen, H. An improved median-based Otsu image thresholding algorithm. AASRI Procedia 2012, 3, 468–473. [Google Scholar] [CrossRef]
- Dong, Y.X. An Improved Otsu Image Segmentation Algorithm. Adv. Mater. Res. 2014, 989, 3751–3754. [Google Scholar] [CrossRef]
- Takashimizu, Y.; Iiyoshi, M. New parameter of roundness R: Circularity corrected by aspect ratio. Prog. Earth Planet. Sci. 2016, 3, 2. [Google Scholar] [CrossRef] [Green Version]
- Chung, Y.J.; Ranjit, S.; Lee, S.J.; Kim, W.T. Thermographic inspection of internal defects in steel structures: Analysis of signal processing techniques in pulsed thermography. Sensors 2020, 20, 6015. [Google Scholar] [CrossRef] [PubMed]










| Reference Citation | Method Used | Target Material | Sensor Used | Calculation Method | Performance Metric | Limitations |
|---|---|---|---|---|---|---|
| [15] | Capacitive Imaging | CFRP | Coplanar capacitive sensor | Serial intensity | Contrast comparative | Local detection of defect, |
| [16] | Intensity analysis | Qualitative Evaluation | Defect detection on surface or thin layers | |||
| [17] | Pulsed active thermography | Buried anti-personnel mines | FLIR T 650 SC thermal camera | Circular Hough transformation | Accuracy | Reduced detectability of binarized images due to low resolution |
| [18] | Feature extraction | Fabric defects | - | Feature extraction, Machine learning | Accuracy, Precision | Low accuracy of surface defects compared to time calculation |
| [19] | Ultrasonic Testing | CFRP | Phased array transducer | Phased array (PA) | Quantitative Evaluation | Requires a lot of data to improve accuracy |
| [20] | Inductive Thermography | Steel | IR camera | Image segmentation | Precision, Recall | Reduced detectability due to noise |
| [21] | Vibrothermography | ASTM E399-05 compact tension specimen | SC3000 IR Camera | Heat capacity by frictional heating | High sensitivity and accuracy inspection for micro-cracks | Inspection of localized surface cracks |
| Thermal Conductivity (k) | 16.2 W/m·K |
| Electrical Conductivity | 106 Siemens/m |
| Density | 8000 kg/m3 |
| Heat Capacity | 500 J/kg·K |
| Initial Temperature | 23 °C |
| Moving Speed | Thermal Contrast |
| 5 mm/s | 2.41 °C |
| 10 mm/s | 1.52 °C |
| 15 mm/s | 1.04 °C |
| 20 mm/s | 0.89 °C |
| Filter Type | SNR | |||
|---|---|---|---|---|
| 5 mm/s | 10 mm/s | 15 mm/s | 20 mm/s | |
| Raw (non-filtering) | 38.5549 | 35.4555 | 25.8822 | 27.1765 |
| Median | 54.6857 | 39.0084 | 29.1514 | 33.3562 |
| Mean | 50.9123 | 38.6698 | 37.7273 | 39.4107 |
| Gaussian | 33.6764 | 36.1395 | 32.6425 | 33.4680 |
| NLmeans | 35.7586 | 36.2160 | 34.7896 | 13.4450 |
| Hole | Optical [24] | Electromagnetic | |
|---|---|---|---|
| Amplitude (0.02 Hz) | Phase (0.01 Hz) | ||
| A1 | - | 88 | - |
| A2 | 87 | 86 | 90 |
| A3 | 81 | 88 | 75 |
| A4 | 86 | 88 | 87 |
| B1 | - | - | - |
| B2 | - | - | - |
| B3 | - | - | - |
| B4 | - | - | 85 |
| C1 | - | 80 | - |
| C2 | 81 | 82 | 81 |
| C3 | 79 | - | - |
| C4 | 83 | 84 | 83 |
| D1 | - | 81 | - |
| D2 | 88 | 84 | 89 |
| D3 | 92 | 86 | 81 |
| D4 | 92 | 89 | 82 |
| RMSE | 23.657 | 23.638 | 24.565 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Chung, Y.; Kim, W. Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography. Appl. Sci. 2022, 12, 6006. https://doi.org/10.3390/app12126006
Lee S, Chung Y, Kim W. Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography. Applied Sciences. 2022; 12(12):6006. https://doi.org/10.3390/app12126006
Chicago/Turabian StyleLee, Seungju, Yoonjae Chung, and Wontae Kim. 2022. "Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography" Applied Sciences 12, no. 12: 6006. https://doi.org/10.3390/app12126006
APA StyleLee, S., Chung, Y., & Kim, W. (2022). Defect Recognition and Morphology Operation in Binary Images Using Line-Scanning-Based Induction Thermography. Applied Sciences, 12(12), 6006. https://doi.org/10.3390/app12126006







