On Hyperbolic Complex Numbers

Abstract

For dimensions two, three and four, we derive hyperbolic complex algebraic structures on the basis of suitably defined vector products and powers which allow in a standard way a series definitions of the hyperbolic vector exponential function. In doing so, we both modify arrow multiplication, which, according to Feynman, is fundamental for quantum electrodynamics, and we give a geometric explanation of why in a certain situation it is natural to define random vector products. Through the interplay of vector algebra, geometry and complex analysis, we extend a systematic approach previously developed for various other complex algebraic structures to the field of hyperbolic complex numbers. We discuss a quadratic vector equation and the property of hyperbolically holomorphic functions of satisfying hyperbolically modified Cauchy–Riemann differential equations and also give a proof of an Euler type formula based on series expansion.

1. Introduction

QED. These three letters are often found at the end of a mathematical proof or even an entire mathematical paper, but what meaning can they have at the beginning of a work, this work? It is the great historical importance that quantum electrodynamics has for the application of complex numbers and vector multiplication outside mathematics. In [1], this connection is presented in a very impressive way for a broad readership. Arrow combination and in particular multiplication form the technical basis there for the mathematical treatment of physical phenomena such as reflection and diffraction and many others. The interactive computer animation programs in [2] make it possible to simulate such physical phenomena on the computer in a fascinating way. The reader is invited to create similar animation programs based on the present mathematical results. For an application of vector multiplication when using photo manipulation programs, we refer to [3].

If complex numbers are not adequate to describe certain mechanical [4], or other physical [5,6,7] or technical [8] processes then their generalizations or modifications may be of interest. Hyperbolic complex numbers which are usually represented as

$$z=x+\mathfrak{j}y,x\in \mathbb{R},y\in \mathbb{R},\mathfrak{j}\notin \mathbb{R},j^2=1$$

(1)

are strictly related to space-time geometry of two dimensional special relativity [9,10,11]. Here, $\mathfrak{j}$ is understood as an abstract or independent quantity taken from somewhere else outside of $\mathbb{R}.$ Hyperbolic complex numbers were developed in [10,12,13,14,15] and are also known by several other names, such as, e.g., perplex numbers [9], split complex numbers [5,9,16,17], space-time numbers [18], dual numbers [6], double numbers [8,10] as well as twocomplex numbers [19], to name just a selection of the numerous possible references.

In this context, the hyperbolic exponential function is defined in [9,15,20] for $\left|x\right|<\left|y\right|$ by

$$x+\mathfrak{j}y=sign\left(y\right)exp(\varrho +\mathfrak{j}\theta )=sign\left(y\right)exp\left(\varrho \right)(sinh(\theta )+\mathfrak{j}cosh(\theta \left)\right)$$

(2)

where $\varrho =\sqrt{|x^2-y^2|}$ and the hyperbolic rotation of an angle $\theta$ transforms a vector $z=x+\mathfrak{j}y$ in the new vector

$$z^{\prime }=zexp\left(\mathfrak{j}\theta \right).$$

(3)

The quantity ${\left|z\right|}^2={\left|z^{\prime }\right|}^2$ is invariant with respect to hyperbolic rotation.

The generalized complex multiplication discussed in [11] includes the ordinary product

$$(x_1+\mathfrak{i}{y}_1)(x_2+\mathfrak{i}{y}_2)=x_1{x}_2-y_1{y}_2+\mathfrak{i}(x_1{y}_2+y_1{x}_2),$$

the Study product

$$(x_1+\mathfrak{i}{y}_1)(x_2+\mathfrak{i}{y}_2)=x_1{x}_2+\mathfrak{i}(x_1{y}_2+y_1{x}_2)$$

and the Clifford product

$$(x_1+\mathfrak{i}{y}_1)(x_2+\mathfrak{i}{y}_2)=x_1{x}_2+y_1{y}_2+\mathfrak{i}(x_1{y}_2+y_1{x}_2)$$

as particular cases. A somewhat different approach to hyperbolic complex numbers is provided in [21] by the use of so called jay-vectors,

$$z=a+\mathfrak{j}b,a\mathrm{and}b\mathrm{are}\mathrm{real}\mathrm{vectors},\mathfrak{j}\notin \mathbb{R},j^2=1.$$

(4)

Does it make things easier to answer the questions of the existence and possible uniqueness of the abstract or formal quantities and operations encountered when having two non-identical approaches, (1) and (4), to the hyperbolic complex unit? How about the true character of this unit? Mathematical quantities are usually defined by positively stating their properties instead of excluding certain properties, as is the case with “$\mathfrak{j}\notin \mathbb{R}$”.

Some new aspects concerning existence and (non-)uniqueness of usual complex numbers as realizations of a general algebraic structure are derived in [22,23,24,25]. There is only briefly mentioned here a property that stands in a certain connection with [1]. There certain probabilities are calculated as length squares of sums of two vectors. If parallel vectors of length 0.2 are oriented in the same direction or in opposite directions, the results are 0.16 and zero, respectively. However, if two such vectors are perpendicular to each other, the value 0.08 results according to the Pythagorean theorem. In [1], reference was made to the fascinating fact that these probabilities are experimentally verified with extremely high accuracy. If one is only interested in obtaining the above three results, any of the vector multiplications from [22] can be used, which might be of some interest for further considerations of physical or other phenomena.

In the present paper, we follow as closely as possible the way taken in [22,23,24,25]. As a result, it becomes possible to generalize hyperbolic complex numbers into different directions. Here, we present multivariate generalizations. We further develop the historically close connection between complex analysis and vector algebra by defining a hyperbolic exponential function using a suitable definition of vector product and power for the definition of the exponential function through a series expansion. While in [22] a vector product based on the ordinary product was introduced, here, to correspondent to Definition 6 of a geometrical hyperbolic vector product, we will introduce a vector product based on the Clifford product.

The paper is organized as follows. We start in Section 2.1, Section 2.2 and Section 2.3 by introducing a hyperbolic vector product, which allows the subsequent introduction of hyperbolic vector powers and a hyperbolic vector exponential function. The latter, as well as the hyperbolic rotation, will therefore be introduced differently than in (2) and (3). In Section 2.4 and Section 2.5, we discuss a quadratic vector equation and modified Cauchy–Riemann differential equations. The slightly modified hyperbolic complex algebraic structure considered in Section 2.6 is based upon a vector product that is a geometrically motivated modification of the vector product being related to the Clifford product. In Section 3, we treat space-time or spherical-hyperbolic complex numbers in dimensions three and four. We close with a discussion in Section 4 and Appendices Appendix A and Appendix B.

We leave it to the reader to choose other basis elements of the underlying event spaces than those chosen here. In [23], it was discussed in detail that changing the basis elements of an event space does not affect the basic properties of the complex algebraic structures considered there. This also applies here.

2. The Basic Hyperbolic Complex Algebraic Structure

2.1. Vector Algebra

Let

$$\mathfrak{X}=\{{(x,y)}^T:x\in \mathbb{R},y\in \mathbb{R},x>0,|y|<x\}$$

denote an event space, that is the set of possible outcomes of an experiment or the light cone in the physical interpretation or just a set of possible observations of interest on which multiplication with positive real numbers is defined to be the function $•:{\mathbb{R}}^{+}\times \mathfrak{X}\to \mathfrak{X}$ where $\lambda •{(x,y)}^T={(\lambda x,\lambda y)}^T,\lambda >0,(x,y)\in \mathfrak{X}$.

Definition 1.

The vector addition $z_1\oplus z_2:\mathfrak{X}\times \mathfrak{X}\to \mathfrak{X}$ is defined componentwise as

$$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)\oplus \left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=\left(\begin{array}{c}{x}_1+x_2\\ y_1+y_2\end{array}\right).$$

If there exists $z_3\in \mathfrak{X}$ such that $z_1\oplus z_3=z_2$, then we say that $z_1$ can be subtracted from $z_2$ or $z_2$ is additively reachable from $z_1$ or event $z_1$ influences event $z_2$. In this case, we write

$$z_2\ominus z_1=\left(\begin{array}{c}{x}_2-x_1\\ y_2-y_1\end{array}\right)=\left(\begin{array}{c}{x}_3\\ y_3\end{array}\right)=z_3$$

and call the operation $\ominus :\mathfrak{X}\times \mathfrak{X}\to \mathfrak{X}$ the operation of constrained vector subtraction.

Let

$$\mathfrak{Y}=\{{(x,y)}^T:x\in \mathbb{R},y\in \mathbb{R},y>0,|x|<y\}$$

and assume that vector addition and constrained vector subtraction are defined analogously on $\mathfrak{Y}\times \mathfrak{Y}.$

Definition 2.

The analytical hyperbolic vector product of $z_1={(x_1,y_1)}^T$ and $z_2={(x_2,y_2)}^T$ is defined as

$$z_1{\odot }_h{z}_2=\left\{\begin{array}{c}{z}_1{\odot }_{h\mathfrak{X}}{z}_2\mathrm{if}{z}_{1}and{z}_{2}arefrom\mathfrak{X}\hfill \\ and\hfill \\ z_1{\odot }_{h\mathfrak{Y}}{z}_2\mathrm{if}{z}_{1}and{z}_{2}arefrom\mathfrak{Y}\hfill \end{array}\right.$$

(5)

where

$$z_1{\odot }_{h\mathfrak{X}}{z}_2=\left(\begin{array}{c}{x}_1{x}_2+y_1{y}_2\\ x_1{y}_2+y_1{x}_2\end{array}\right),and{z}_1{\odot }_{h\mathfrak{Y}}{z}_2=\left(\begin{array}{c}{x}_1{y}_2+y_1{x}_2\\ x_1{x}_2+y_1{y}_2\end{array}\right).$$

The k’th hyperbolic vector power of $z={(x,y)}^T\in \mathfrak{X}\cup \mathfrak{Y}$ and the hyperbolic vector exponential of z are defined by

$$z^k=z^{k-1}{\odot }_{h\mathfrak{X}}z,k\ge 2,z^1=z,z^0={(1,0)}^T$$

and

$$e_{\left[h\right]}\left(z\right)=\sum _{k=0}^{\infty }\frac{z^k}{k!},$$

respectively.

We emphasize that we exclusively use the product ${\odot }_{h\mathfrak{X}}$ for defining the hyperbolic exponential of z. For our motivation for doing so, we refer to Remark 2 below. Vector product and exponential can also be understood as arrow product and exponential in the sense of [1].

Definition 3.

The analytical hyperbolic vector product $z_1{\odot }_h{z}_2$ of $z_1={(x_1,y_1)}^T\in \mathfrak{X}$ and $z_2={(x_2,y_2)}^T\in \mathfrak{Y}$ is defined to be a random variable on an abstract probability space that takes the values $z_1{\odot }_{h\mathfrak{X}}{z}_2$ and $z_1{\odot }_{h\mathfrak{Y}}{z}_2$ accordingly with probabilities $p,p\in (0,1)$ and $1-p$.

Notice that

$$\begin{array}{cc}\hfill z_1& {\odot }_{h\mathfrak{X}}{z}_2\in \mathfrak{X}\mathrm{if}{z}_1\mathrm{and}{z}_2\mathrm{are}\mathrm{from}X\hfill \\ \hfill and& \\ \hfill z_1& {\odot }_{h\mathfrak{Y}}{z}_2\in \mathfrak{Y}\mathrm{if}{z}_1\mathrm{and}{z}_2\mathrm{are}\mathrm{from}\mathfrak{Y}.\hfill \end{array}$$

If you look at Definitions 2 and 3 together, the hyperbolic vector product is a function

$${\odot }_h:(\mathfrak{X}\times \mathfrak{X})\cup (\mathfrak{Y}\times \mathfrak{Y})\cup (\mathfrak{X}\times \mathfrak{Y})\to \mathfrak{X}\cup \mathfrak{Y}.$$

Because the focus of our consideration is $\mathfrak{X}$, we do not consider ${\odot }_h$ on combinations of $-\mathfrak{X}$ and $-\mathfrak{Y}$.

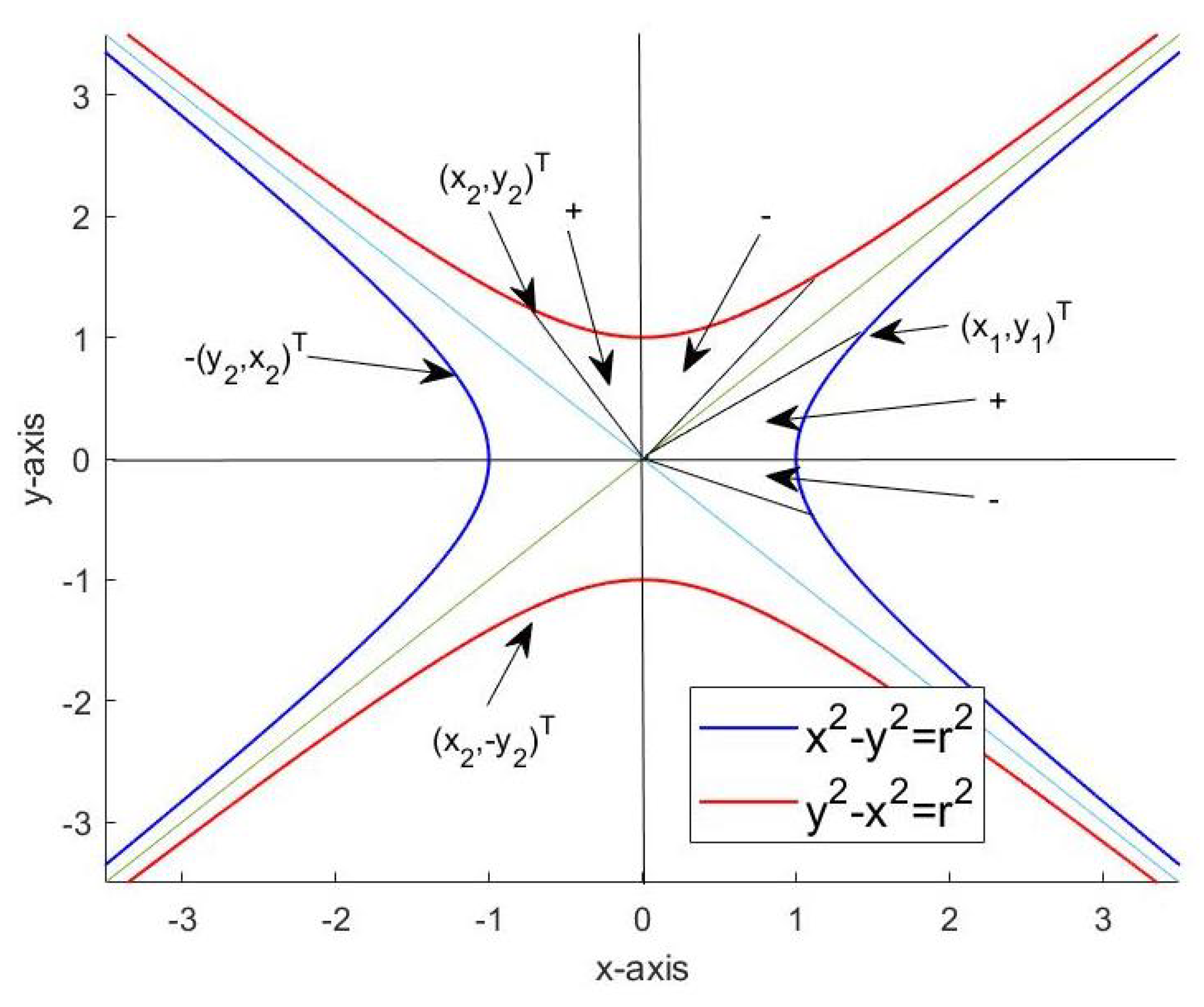
Example 1.

The vector $\mathfrak{o}={(0,0)}^T$ is the additive neutral element. Let $\mathfrak{e}={(1,0)}^T.$ If $z\in \mathfrak{X}$ then

$$z{\odot }_h\mathfrak{e}=z.$$

(6)

That is, within $\mathfrak{X}$ is $\mathfrak{e}$ the multiplicative neutral element. On the other hand, if $z={(x,y)}^T\in \mathfrak{Y}$ then

$$z{\odot }_h\mathfrak{e}=\left\{\begin{array}{c}{(x,y)}^{T}withprobabilityp,p\in (0,1)\hfill \\ \mathrm{and}\hfill \\ {(y,x)}^{T}withprobability1-p.\hfill \end{array}\right.$$

Here $\left(\begin{array}{c}y\\ x\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\in \mathfrak{X}$ is the result of reflecting the point $\left(\begin{array}{c}x\\ y\end{array}\right)$ at the line $y=x.$

Definition 4.

If for $z_1$ and $z_2$ from $\mathfrak{X}$ there exists $z_3\in \mathfrak{X}$ such that $z_1{\odot }_h{z}_3=z_2$, then we say that $z_2$ can be divided by $z_1$ and call the operation $z_2\oslash z_1=z_3$ the operation of constrained vector division. If $\mathfrak{e}$ can be divided by $z={(x,y)}^T$, then we call $\mathfrak{e}\oslash z=z^{-1}$ the inverse of z.

Notice that if $z={(x,y)}^T\in \mathfrak{X}$ has an inverse, then

$$z^{-1}=\frac{1}{x^2-y^2}\left(\begin{array}{c}x\\ -y\end{array}\right).$$

The vector product ${\odot }_h$ is obviously commutative and the second up to the fourth hyperbolic vector powers of $z={(x,y)}^T\in \mathfrak{X}$ are

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^2=\left(\begin{array}{c}{x}^2+y^2\\ 2xy\end{array}\right),{\left(\begin{array}{c}x\\ y\end{array}\right)}^3=\left(\begin{array}{c}{x}^3+3x{y}^2\\ y^3+3y{x}^2\end{array}\right)$$

and

$${\left(\begin{array}{c}x\\ y\end{array}\right)}^4=\left(\begin{array}{c}{x}^4+6x^2{y}^2+y^4\\ 4xy(x^2+y^2)\end{array}\right),$$

respectively.

2.2. Geometry

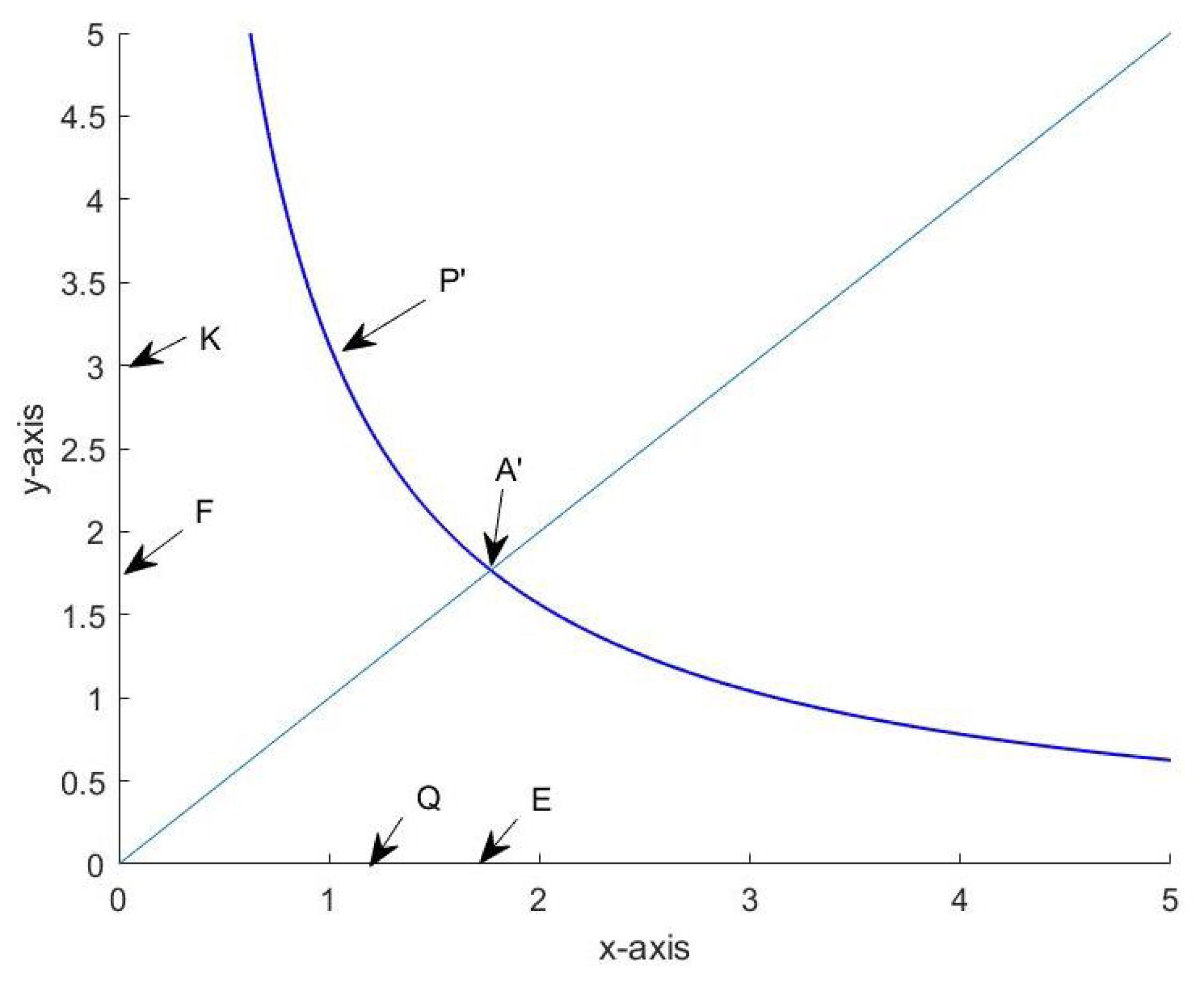
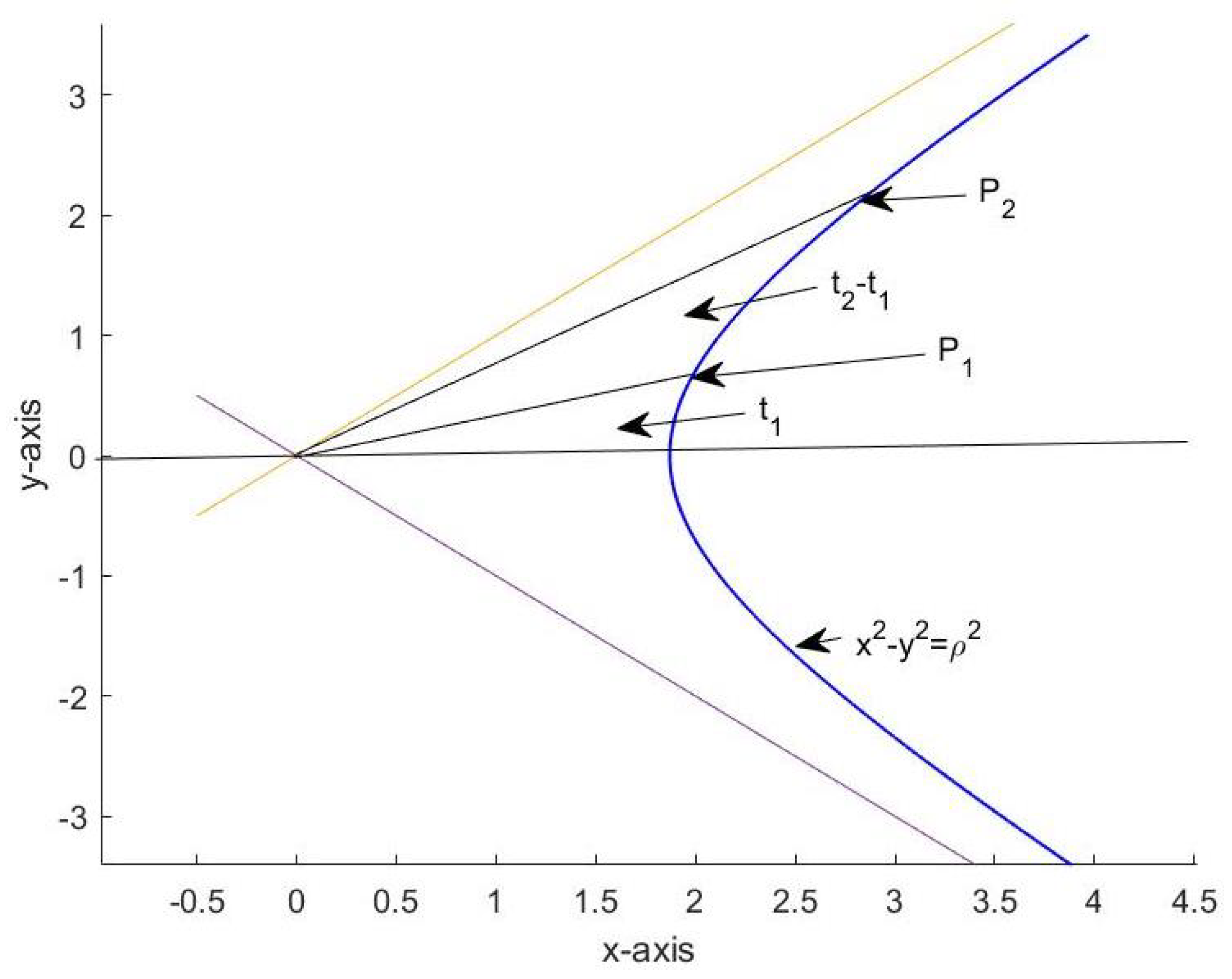
Let us call

$$C_h\left(r\right)=\{{(x,y)}^T\in {\mathbb{R}}^2:x^2-y^2=r^2\}$$

a hyperbolic circle of hyperbolic radius $r>0$ and

$$C_h^{+}\left(r\right)=C_h\left(r\right)\cap \{{(x,y)}^T\in {\mathbb{R}}^2:x>0\}$$

its $\mathfrak{X}$-sector in short, see Figure 1.

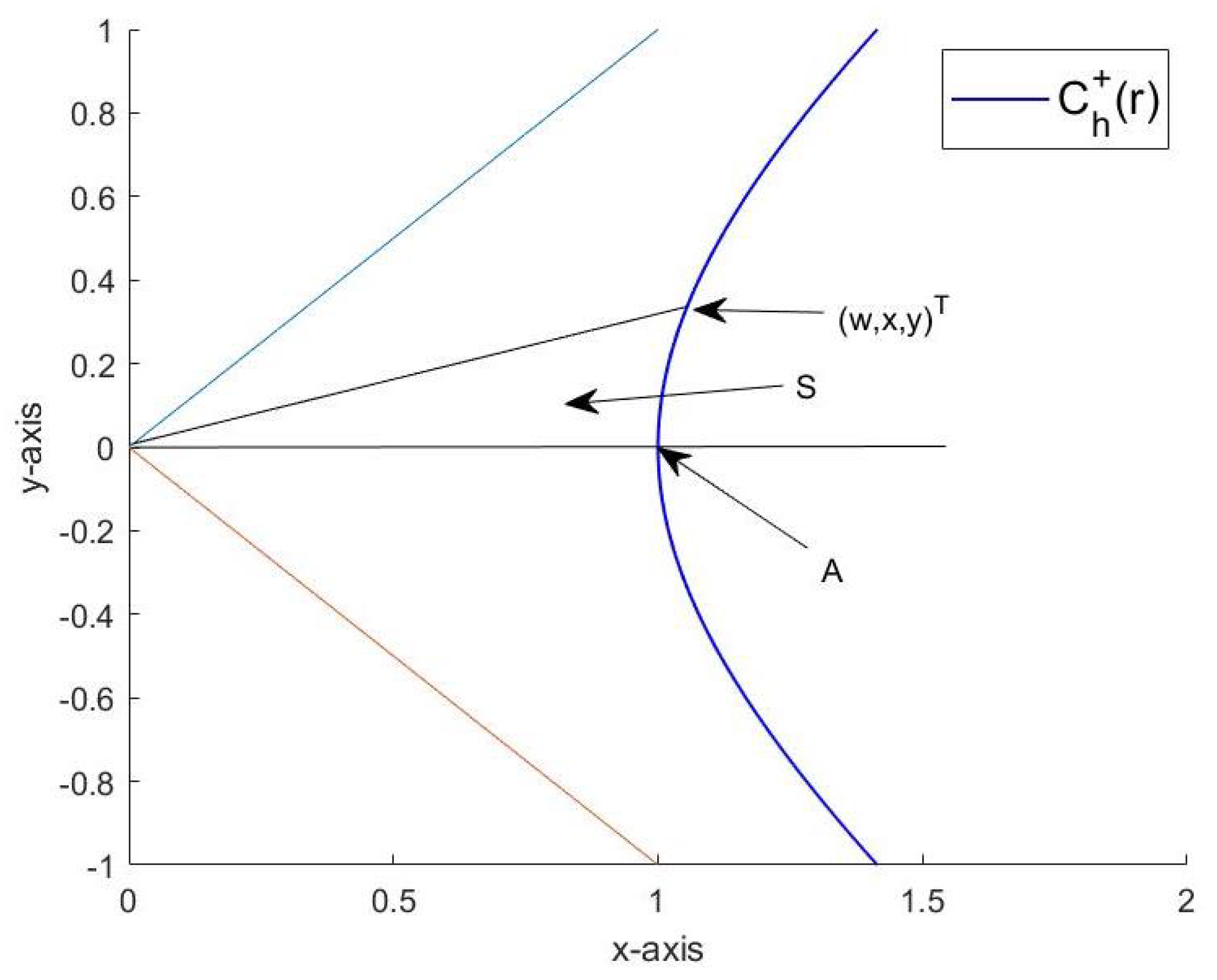
If $z_1\in C_h^{+}\left(r\right)$ and $z_2\in C_h^{+}\left(1\right)$, then $z_1{\odot }_h{z}_2\in C_h^{+}\left(r\right)$. The Lie group on $C_h^{+}\left(r\right)$ is thus generated by the multiplications with the elements from the unit half-circle $C_h^{+}\left(1\right).$ In other words, if the function $Q_h:{\mathbb{R}}^2\to \mathbb{R}$ is defined by $Q_h(x,y)=x^2-y^2$, then multiplication of $z_1={(x,y)}^T$ by any $z_2\in C_h^{+}\left(1\right)$ leaves $Q_h$ invariant.

Definition 5.

The hyperbolic coordinate transformation $Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}:{\mathbb{R}}^{+}\times \mathbb{R}\to \mathfrak{X}\left(\mathfrak{Y}\right)$, ${(x,y)}^T=Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r,\psi )$, is accordingly defined as

$$x=rcosh\psi ,y=rsinh\psi \mathrm{or}x=rsinh\psi ,y=rcosh\psi .$$

(7)

Here, the notation $\mathfrak{X}\left(\mathfrak{Y}\right)$ indicates whether the signed area content ψ is measured counterclockwise between ${(1,0)}^T$ and ${(x,y)}^T\in \mathfrak{X}$ or clockwise between ${(0,1)}^T$ and ${(x,y)}^T\in \mathfrak{Y},$ see Figure 2.

The union of all $\mathfrak{X}$-sectors $C_h^{+}\left(r\right),r>0$ represents a disjoint decomposition of the cone $\mathfrak{X}$, see Figure 2.

The transformation $Hy{p}_{\mathfrak{X}}$ therefore has an a.e. uniquely determined inverse $Hy{p}_{\mathfrak{X}}^{-1}:\mathfrak{X}\to {\mathbb{R}}^{+}\times \mathbb{R}$, which is given by $Hy{p}^{-1}(x,y)=(r,\psi )$ with

$$r=\sqrt{x^2-y^2},\psi =ln\sqrt{\frac{x+y}{x-y}}.$$

(8)

Remark 1.

With $sign\left(\psi \right)=sign\left(y\right),$ the quantity $\psi ·r^2$ equals two times the signed area content of the hyperbolic sector $S(\mathfrak{o},P,A)=r•S(\mathfrak{o},u,\mathfrak{e})$ the boundary of which is marked with the help of the points $\mathfrak{o}={(0,0)}^T,P={(x,y)}^T\in C_h^{+}\left(r\right)$ and $A={(r,0)}^T,$ see Figure 3.

For an elementary geometric proof of this remark, we refer to Appendix A.

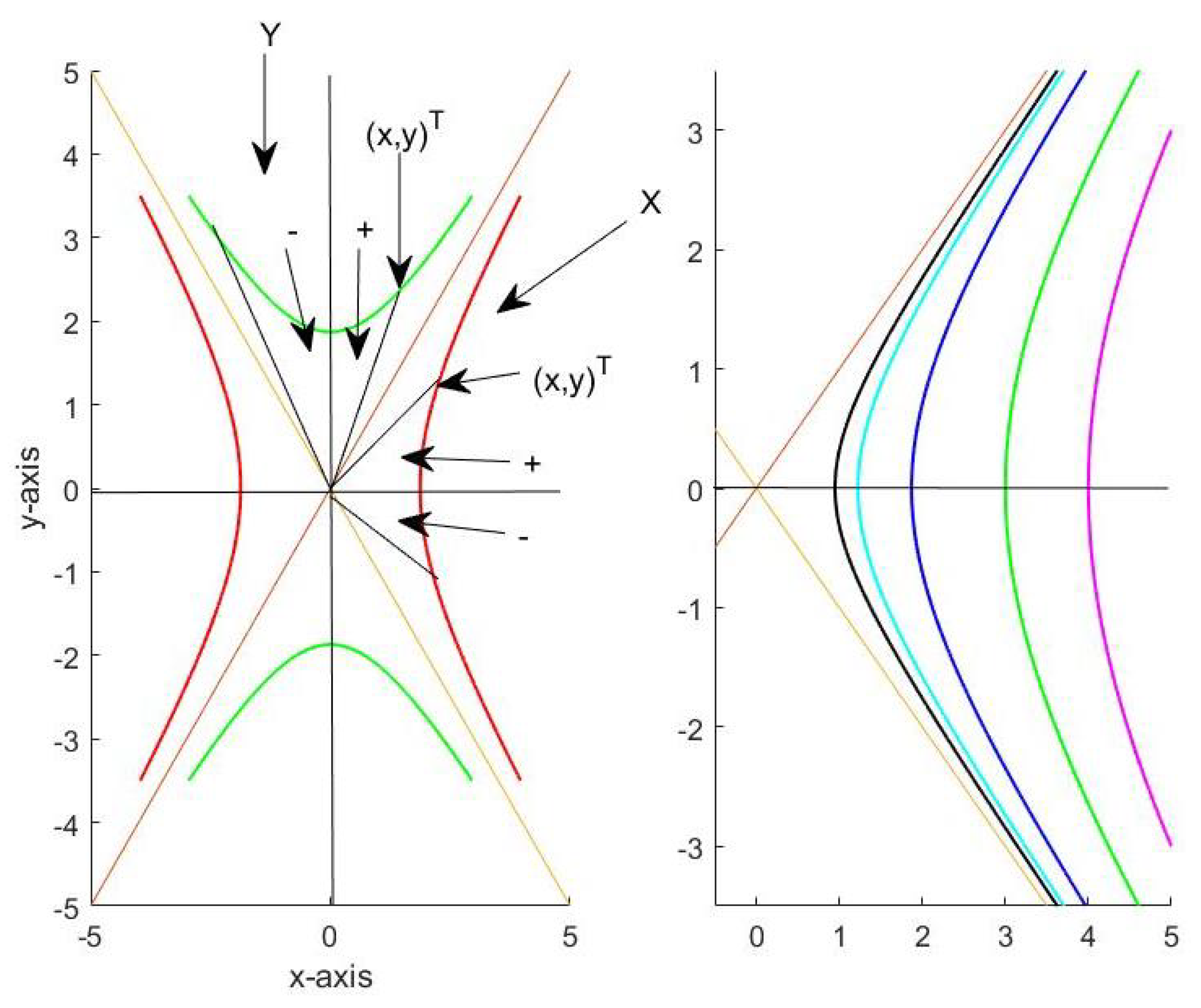
Definition 6.

The geometrical hyperbolic vector product of $z_1=Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r_1,{\psi }_1)$ and $z_2=Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r_2,{\psi }_2)$ being both either from $\mathfrak{X}$ or from $\mathfrak{Y}$ is defined as

$$Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r_1,{\psi }_1){\ast }_{h}Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r_2,{\psi }_2)=Hy{p}_{\mathfrak{X}\left(\mathfrak{Y}\right)}(r_1{r}_2,{\psi }_1+{\psi }_2).$$

The expression on the right side of the last equation is always uniquely defined because due to Remark 1 the sum ${\psi }_1+{\psi }_2$ represents the finite content of a bounded hyperbolic sector (triangle), which itself is a subset of an unbounded set having infinite area content, see Figure 4.

Let $0<t_1<t_2,\varrho >0,P_1=Hy{p}_{\mathfrak{X}}(\varrho ,t_1),P_2=Hy{p}_{\mathfrak{X}}(\varrho ,t_2)$ and let

$$S(\mathfrak{0},P_1,P_2)=\{{(x,y)}^T:x=rcosht,y=rsinht,0<r<\varrho ,t_1<t<t_2\}$$

denote a hyperbolic sector (or hyperbolic triangle) spanned by the points $\mathfrak{0},P_1,P_2,$ see Figure 5. Additionally, let $T_{\psi },\psi >0$ be a transformation defined by

$$\begin{array}{cc}\hfill T_{\psi }S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2))& =Hy{p}_{\mathfrak{X}}(1,\psi ){\ast }_{h}S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2)).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill T_{\psi }S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2))& =\{r\left(\begin{array}{c}cosh\psi \\ sinh\psi \end{array}\right){\ast }_h\left(\begin{array}{c}cosht\\ sinht\end{array}\right),0<r<\varrho ,t_1<t<t_2\}\hfill \\ & =\{r\left(\begin{array}{c}cosh(\psi +t)\\ sinh(\psi +t)\end{array}\right),0<r<\varrho ,t_1+\psi <\psi +t<t_2+\psi \}\hfill \\ & =S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1+\psi ),Hy{p}_{\mathfrak{X}}(\varrho ,t_2+\psi )).\hfill \end{array}$$

Theorem 1.

The transformation $T_{\psi }$ is area-preserving.

Proof. 

We show that $T_{\psi }$ does not change the content of a hyperbolic sector. The area content of such sector $S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2))$ is

$$\begin{array}{cc}\hfill \left|S\right(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2)\left)\right|& =\underset{S(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1),Hy{p}_{\mathfrak{X}}(\varrho ,t_2))}{\int }d(x,y)\hfill \\ & =\underset{0}{\overset{\varrho }{\int }}\underset{t_1}{\overset{t_2}{\int }}\left|det\frac{d(x,y)}{d(r,t)}\right|d(r,t)=\frac{{\varrho }^2}{2}(t_2-t_1)\hfill \\ & =\left|S\right(\mathfrak{0},Hy{p}_{\mathfrak{X}}(\varrho ,t_1+\psi ),Hy{p}_{\mathfrak{X}}(\varrho ,t_2+\psi )\left)\right|\hfill \end{array}$$

□

If $z_1\in \mathfrak{X}$ and $z_2\in \mathfrak{Y}$, then the geometrical hyperbolic vector multiplication may be reflected by sector combinations of two types. Since there is no a priori preferred variant for one of two possibilities of assigning the sum of signed area contents, they can be regarded as occurring randomly. The following definition may thus be considered being well motivated.

Definition 7.

The geometrical hyperbolic vector product of $z_1=Hy{p}_{\mathfrak{X}}(r_1,{\psi }_1)$ and $z_2=Hy{p}_{\mathfrak{Y}}(r_2,{\psi }_2)$ is defined to be a random variable on an abstract probability space, which takes the values $Hy{p}_{\mathfrak{X}}(r_1{r}_2,{\psi }_1+{\psi }_2)$ and $Hy{p}_{\mathfrak{Y}}(r_1{r}_2,{\psi }_1+{\psi }_2)$ accordingly with probabilities $p,p\in (0,1)$ and $1-p$.

Theorem 2.

The geometrical and analytical hyperbolic vector products are equal.

Proof. 

If $z_k=\left(\begin{array}{c}{x}_k\\ y_k\end{array}\right)\in \mathfrak{X},k=1,2,\xi =\sqrt{\frac{(x_1+y_1)(x_2+y_2)}{(x_1-y_1)(x_2-y_2)}}$ then by (8),

$$Hy{p}_{\mathfrak{X}}(r_1{r}_2,{\psi }_1+{\psi }_2)=\sqrt{x_1^2-y_1^2}\sqrt{x_2^2-y_2^2}\left(\begin{array}{c}coshln\xi \\ sinhln\xi \end{array}\right).$$

It follows from this and the definitions of the hyperbolic functions that

$$Hy{p}_{\mathfrak{X}}(r_1{r}_2,{\psi }_1+{\psi }_2)=\frac{r_1{r}_2}{2}\left(\begin{array}{c}\sqrt{\frac{(x_1+y_1)(x_2+y_2)}{(x_1-y_1)(x_2-y_2)}}+\sqrt{\frac{(x_1-y_1)(x_2-y_2)}{(x_1+y_1)(x_2+y_2)}}\\ \sqrt{\frac{(x_1+y_1)(x_2+y_2)}{(x_1-y_1)(x_2-y_2)}}-\sqrt{\frac{(x_1-y_1)(x_2-y_2)}{(x_1+y_1)(x_2+y_2)}}\end{array}\right)=\left(\begin{array}{c}{x}_1{x}_2+y_1{y}_2\\ y_1{x}_2+x_1{y}_2\end{array}\right).$$

If $z_k\in \mathfrak{Y},k=1,2$ or $z_1\in \mathfrak{X}$ and $z_2\in \mathfrak{Y}$ then the proof follows analogously. □

2.3. Complex Analysis

A classical way to introduce complex numbers is to say that they allow the representation $x+\mathfrak{i}y$ where x and y are real numbers and $\mathfrak{i}$ is a formal quantity coming from somewhere other than $\mathbb{R}$ and satisfying ${\mathfrak{i}}^2=-1$. The reader of such a definition is then tacitly asked to believe that the quantity $\mathfrak{i}$ exists in the sense that it can be assigned a strict mathematical meaning and that the operation of squaring this “imaginary unit” agrees or harmonizes with the operation usual in the realm of real numbers. The reader is also left alone with thinking about the possible uniqueness of such a quantity. The answer to this challenge can vary. One can try to take $\mathfrak{i}$ for a vector or a matrix and in each case define a corresponding multiplication rule. However, the usual squaring of vectors and matrixes does not result in the number −1. Therefore people in usual complex number theory sometimes say that they “identify” the vector ${(0,1)}^2=(-1,0)$ with the real number $-1$, without saying, however, what an “identification” is other than an equation. However, obviously $(-1,0)$ does not equal −1. In [26], it is alternatively discussed that a complex number has a dual real value nature, i.e., is capable of two values without being able, however, to fully explain it. We recall that Definition 3 of the present work gives a well motivated explicit definition of a two-valued random hyperbolic vector product.

In [22,23,24,25], algebraic structures are introduced, within which the “imaginary unit” is always explicitly given as a well-defined element from the vector space underlying this structure. Here, we follow this approach as closely as possible and therefore necessarily extend the event space. Just as the imaginary unit $\mathfrak{i}$ does not belong to the real line $\mathbb{R}$ if one describes complex solutions of quadratic equations over $\mathbb{R},$ see Section 2.4 and [24], the vector

$$\mathfrak{j}=\left(\begin{array}{c}0\\ 1\end{array}\right)$$

obviously does not belong to the originally considered event space $\mathfrak{X}$ but belongs to the set $\mathfrak{Y}$. Note that

$$\left(\begin{array}{c}x\\ y\end{array}\right){\odot }_{h\mathfrak{X}}\mathfrak{j}=\left(\begin{array}{c}y\\ x\end{array}\right)$$

and

$$\mathfrak{j}{\odot }_{h\mathfrak{X}}\mathfrak{j}=\mathfrak{e}.$$

(9)

Remark 2.

If one follows usual hyperbolic number notation and writes

$$j^2=1$$

instead of (9), then one is tacitly using the multiplication rule, which is well motivated for elements of $\mathfrak{X}$ for the element $\mathfrak{j}$ of $\mathfrak{Y}$. This motivates our definition of the hyperbolic exponential in Definition 2.

The hyperbolic vector exponential of $x•\mathfrak{j}$ allows a representation that is reminiscent of Euler’s well-known trigonometric representation of usual complex numbers, where, however, the so called imaginary unit $\mathfrak{i}=\sqrt{-1}$ is replaced with vector $\mathfrak{j}$ and the trigonometric functions sine and cosine are replaced with hyperbolic functions.

Theorem 3.

The following hyperbolic Euler-type formula holds true:

$${\mathfrak{e}}_{\left[h\right]}(x•\mathfrak{j})=\left(\begin{array}{c}coshx\\ sinhx\end{array}\right)=(coshx)•\mathfrak{e}+(sinhx)•\mathfrak{j},x\in \mathbb{R}.$$

(10)

Proof. 

The rearrangement of the infinite vector sum

$$\mathfrak{e}+x•\mathfrak{j}+\frac{x^2}{2!}•\mathfrak{e}+\frac{x^3}{3!}•\mathfrak{j}+\dots =(1+\frac{x^2}{2!}+\frac{x^4}{4!}+\dots )•\mathfrak{e}+(x+\frac{x^3}{3!}+\frac{x^4}{4!}\dots )•\mathfrak{j}$$

is allowed due to its convergence properties. Finally, the definitions of the hyperbolic functions apply. □

Note that $\mathfrak{e}$ belongs to the observation set $\mathfrak{X}$, but $\mathfrak{j}$ comes from a well-defined other set and the hyperbolic vector multiplication rule is explained in the extended event space. In contrast to the classical approach to complex numbers, however, $\mathfrak{j}$ is explicitly known, here. The following definition is now well motivated.

Definition 8.

We call $(\mathfrak{X},\oplus ,•,{\odot }_h,\mathfrak{o},\mathfrak{e},\mathfrak{j})$ a hyperbolic complex algebraic structure with $\mathfrak{o}$ and $\mathfrak{e}$ being the additive and multiplicative neutral elements and $\mathfrak{j}$ the hyperbolic element satisfying (9).

We recall from [23] that changing the basis elements of an event space may be very useful and does not affect the basic properties of the complex algebraic structure.

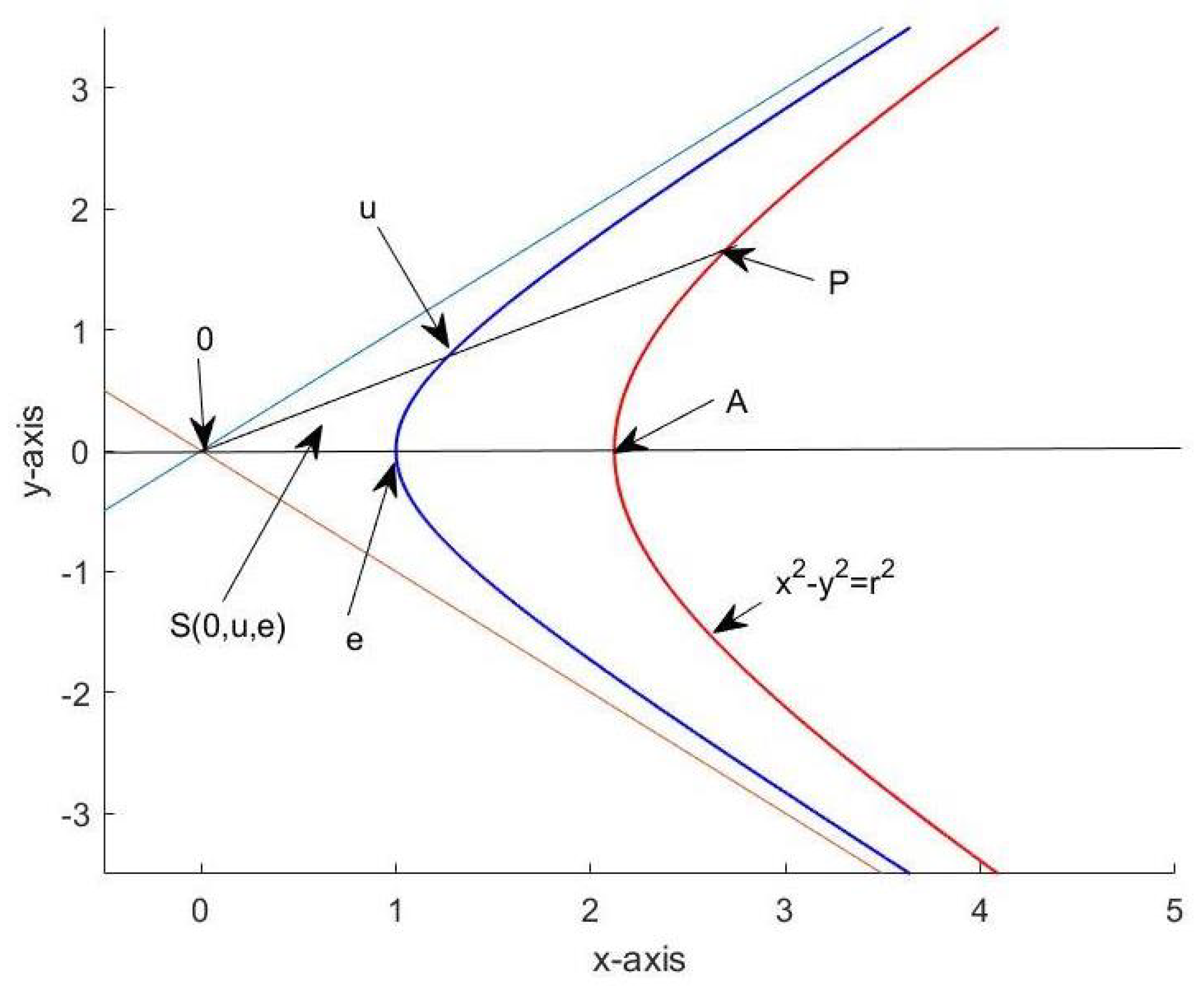
2.4. Solving a Quadratic Vector Equation

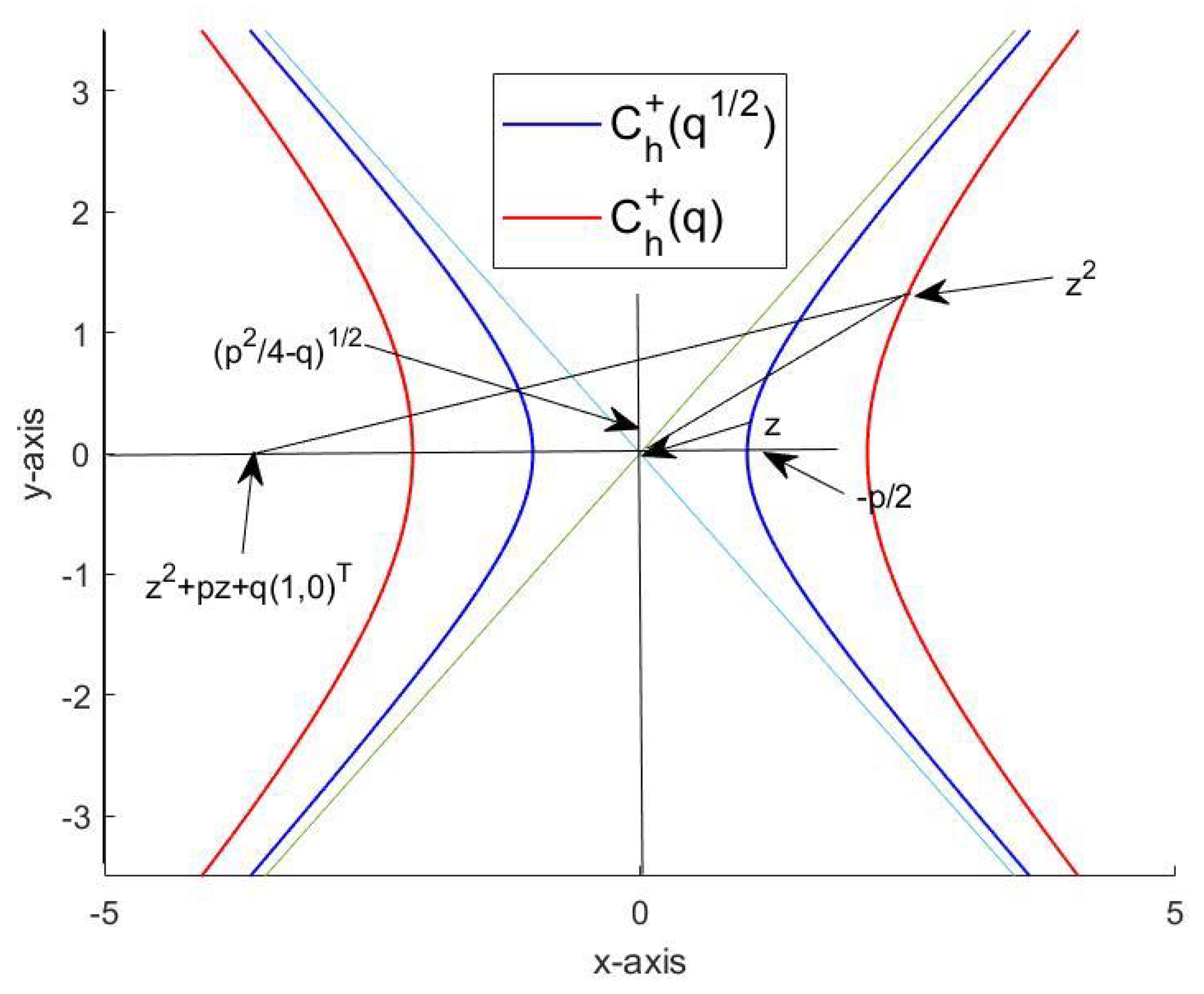
If $p^2/4>q$, then the quadratic equation

$$x^2+px+q=0$$

(11)

has the real solutions $x_{1/2}=-p/2+(-)\sqrt{p^2/4-q}$. The structure of these solutions reproduces if one considers the quadratic vector equation $z{\odot }_{h}z\oplus p•z\oplus q•\mathfrak{e}=\mathfrak{o}$ or

$$\left(\begin{array}{c}{x}^2+y^2\\ 2xy\end{array}\right)+\left(\begin{array}{c}px\\ py\end{array}\right)+\left(\begin{array}{c}q\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right).$$

(12)

The result

$$z=-\frac{p}{2}•\mathfrak{e}+(-)\sqrt{\frac{p^2}{4}-q}•\mathfrak{j}$$

is graphically illustrated in Figure 6. For a closely related geometric discussion of quadratic vector equations with respect to $l_p$-vector multiplication, we refer to [24].

2.5. Hyperbolically Modified Cauchy-Riemann Differential Equations

Let $z_k\in \mathfrak{X},k=1,2.$ According to Definition 4, we call $z_1$ hyperbolic multiplicative reachable from $z_2$ if there exists $z_3\in \mathfrak{X}$ such that $z_1=z_2{\odot }_h{z}_3$. If this is so, then we call $z_3$ the hyperbolic ratio of $z_1$ and $z_2$ and write this as

$$z_3=z_1{\oslash }_h{z}_2.$$

One can check that

$$z_3=\frac{1}{x_2^2-y_2^2}\left(\begin{array}{c}{x}_1{x}_2-y_1{y}_2\\ x_2{y}_1-x_1{y}_2\end{array}\right)$$

(13)

and in particular

$$z_1{\oslash }_h\left(\begin{array}{c}1\\ 0\end{array}\right)=z_1.$$

If we apply (13) also for $z_1=z\in \mathfrak{X}$ and $z_2={(0,1)}^T\in \mathfrak{Y}$, then

$$z{\oslash }_h\left(\begin{array}{c}0\\ 1\end{array}\right)=-\left(\begin{array}{c}y\\ x\end{array}\right).$$

While $z\to z{\oslash }_h\left(\begin{array}{c}1\\ 0\end{array}\right)$ means the identity mapping, the mapping $z\to z{\oslash }_h\left(\begin{array}{c}0\\ 1\end{array}\right)$ means reflection of the point $z=\left(\begin{array}{c}x\\ y\end{array}\right)$ at the line $y=-x$.

Let D be an open subset of $\mathfrak{X}$. A function $f:D\to \mathfrak{X}$ is called hyperbolically differentiable in $z_0\in D$ if the ratio $(f\left(z\right)-f\left(z_0\right)){\oslash }_h(z-z_0)$ converges to a limit point $f^{\prime }\left(z_0\right)$, say, as $z\to z_o$, that is

$$f^{\prime }\left(z_0\right)=\underset{z\to z_0}{lim}(f\left(z\right)-f\left(z_0\right)){\oslash }_h(z-z_0).$$

The function f will be called hyperbolically holomorphic in D if it is differentiable in every $z_0$ from D. If such function is given by

$$f(\left(\begin{array}{c}x\\ y\end{array}\right))=\left(\begin{array}{c}u(x,y)\\ v(x,y)\end{array}\right),\left(\begin{array}{c}x\\ y\end{array}\right)\in D$$

then it follows that hyperbolic modifications of the well known Cauchy–Riemann differential equations hold. To become more specific, we consider points $z_l=z_0+z_{l,h},l=1,2$ with

$$z_{1,h}=\left(\begin{array}{c}h\\ 0\end{array}\right)\mathrm{and}{z}_{2,h}=\left(\begin{array}{c}0\\ h\end{array}\right).$$

Letting now the values of h tending to zero, and, respectively, denoting the partial derivatives with respect to x or y of a function $w(x,y)$ by $w_x$ and $w_y$, we get

$$\begin{array}{cc}\hfill (f\left(z_1\right)-f\left(z_0\right)){\oslash }_h(z_1-z_0)& =\left(\begin{array}{c}u(x_0+h,y_0)-u(x_0,y_0)\\ v(x_0+h,y_0)-v(x_0,y_0)\end{array}\right){\oslash }_h{z}_{1,h}\hfill \\ & =\left(\begin{array}{c}{u}_x(x_0+\delta h,y_0)\\ v_x(x_0+\delta h,y_0)\end{array}\right){\oslash }_h\left(\begin{array}{c}1\\ 0\end{array}\right)\to \left(\begin{array}{c}{u}_x(x_0,y_0)\\ v_x(x_0,y_0)\end{array}\right),h\to 0\hfill \end{array}$$

where $\delta$ is a certain number from the interval $(0,1)$. Similarly,

$$\begin{array}{cc}\hfill (f\left(z_2\right)-f\left(z_0\right)){\oslash }_h(z_2-z_0)& =\left(\begin{array}{c}u(x_0+h,y_0)-u(x_0,y_0)\\ v(x_0+h,y_0)-v(x_0,y_0)\end{array}\right){\oslash }_h{z}_{2,h}\hfill \\ & =\left(\begin{array}{c}{u}_y(x_0+\delta h,y_0)\\ v_y(x_0+\delta h,y_0)\end{array}\right){\oslash }_h{(0,1)}^T\to \left(\begin{array}{c}-v_y(x_0,y_0)\\ -u_y(x_0,y_0)\end{array}\right),h\to 0.\hfill \end{array}$$

The following theorem has thus been proved.

Theorem 4.

The hyperbolically holomorphic function $f:D\to \mathfrak{X}$,$f(\left(\begin{array}{c}x\\ y\end{array}\right))=\left(\begin{array}{c}u(x,y)\\ v(x,y)\end{array}\right),$ satisfies the hyperbolically modified Cauchy–Riemann partial differential equations

$$u_x=-v_y\mathrm{and}{v}_x=-u_y.$$

Consequently, hyperbolically holomorphic functions $f={(u,v)}^T$ have the property

$$u_{xx}-u_{yy}=0.$$

2.6. A Slightly Modified Hyperbolic Complex Algebraic Structure

Let us assume that the definition of the hyperbolic coordinate transformation $Hy{p}_{\mathfrak{Y}}$ is changed so that now the signed area content $\psi$ is measured counterclockwise between ${(0,1)}^T$ and ${(x,y)}^T\in \mathfrak{Y}$, see Figure 7. Then, slightly different from Definition 5, it follows that

$$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right)=r_1\left(\begin{array}{c}cosh{\psi }_1\\ sinh{\psi }_1\end{array}\right)\mathrm{in}\mathfrak{X}\mathrm{and}\left(\begin{array}{c}{y}_2\\ -x_2\end{array}\right)=r_2\left(\begin{array}{c}cosh{\psi }_2\\ sinh{\psi }_2\end{array}\right)\mathrm{in}\mathfrak{Y}.$$

For the geometric definition of the hyperbolic vector product, it then results that, in ${\mathfrak{X}}^2$,

$$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\odot }_{hmod}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=r_1{r}_2\left(\begin{array}{c}cosh{\psi }_{1}cosh{\psi }_2+sinh{\psi }_{1}sinh{\psi }_2\\ sinh{\psi }_{1}cosh{\psi }_2+cosh{\psi }_{1}sinh{\psi }_2\end{array}\right)$$

$$=r_1{r}_2\left(\begin{array}{c}cosh({\psi }_1+{\psi }_2)\\ sinh({\psi }_1+{\psi }_2)\end{array}\right)=\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\odot }_{h\mathfrak{X}}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right).$$

Overall, the analytical and geometric definitions of the hyperbolic vector product are then

$$\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\odot }_{hmod}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=\left\{\begin{array}{c}\left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\odot }_{h\mathfrak{X}}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=r_1{r}_2\left(\begin{array}{c}cosh({\psi }_1+{\psi }_2)\\ sinh({\psi }_1+{\psi }_2)\end{array}\right)\mathrm{in}{\mathfrak{X}}^2,\hfill \\ \left(\begin{array}{c}-x_1{y}_2-y_1{x}_2\\ x_1{x}_2+y_1{y}_2\end{array}\right)=r_1{r}_2\left(\begin{array}{c}-sinh({\psi }_1+{\psi }_2)\\ cosh({\psi }_1+{\psi }_2)\end{array}\right)\mathrm{in}{\mathfrak{Y}}^2\hfill \end{array}\right.$$

and in $\mathfrak{X}\times \mathfrak{Y}$,

$$\begin{array}{cc}\hfill \left(\begin{array}{c}{x}_1\\ y_1\end{array}\right){\odot }_{hmod}\left(\begin{array}{c}{x}_2\\ y_2\end{array}\right)=& \left\{\begin{array}{c}\left(\begin{array}{c}{x}_1{x}_2+y_1{y}_2\\ y_1{x}_2+y_2{x}_1\end{array}\right)\mathrm{with}\mathrm{probability}p,p\in (0,1)\hfill \\ \left(\begin{array}{c}-x_1{y}_2-y_1{x}_2\\ x_1{x}_2+y_1{y}_2\end{array}\right)\mathrm{with}\mathrm{probability}1-p\hfill \end{array}\right.\hfill \\ \hfill =r_1{r}_2& \left\{\begin{array}{c}\left(\begin{array}{c}cosh({\psi }_1+{\psi }_2)\\ sinh({\psi }_1+{\psi }_2)\end{array}\right)\mathrm{with}\mathrm{probability}p,p\in (0,1)\hfill \\ \left(\begin{array}{c}-sinh({\psi }_1+{\psi }_2)\\ cosh({\psi }_1+{\psi }_2)\end{array}\right)\mathrm{with}\mathrm{probability}1-p.\hfill \end{array}\right.\hfill \end{array}$$

The result is a modified hyperbolic complex algebraic structure $(\mathfrak{X},\oplus ,•,{\odot }_{hmod},\mathfrak{o},\mathfrak{e},\mathfrak{j})$ where if $z\in \mathfrak{X}$ and still $\mathfrak{j}=\left(\begin{array}{c}0\\ 1\end{array}\right)$ then

$$z{\odot }_{hmod}\mathfrak{e}=z,$$

(14)

$$\mathfrak{j}{\odot }_{hmod}\mathfrak{j}=\mathfrak{j},$$

(15)

and if $z={(x,y)}^T\in \mathfrak{Y}$ then

$$z{\odot }_{hmod}\mathfrak{e}=\left\{\begin{array}{cc}z\hfill & \mathrm{with}\mathrm{probability}p,p\in (0,1),\hfill \\ \left(\begin{array}{c}-y\\ x\end{array}\right)\hfill & \mathrm{with}\mathrm{probability}1-p.\hfill \end{array}\right.$$

Here, $\left(\begin{array}{c}-y\\ x\end{array}\right)\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)$ is the result of rotating $\left(\begin{array}{c}x\\ y\end{array}\right)$ counterclockwise by ${90}^{\circ }$.

3. Spherical Hyperbolic Complex Numbers

3.1. Three Dimensional Space-Time Structure

Let now

$$C_h^{+}\left(r\right)=\{{(w,x,y)}^T\in {\mathbb{R}}^3:w^2-x^2-y^2=r^2,w>0\},r>0$$

be a hyperbolic half-sphere of hyperbolic radius $r>0$ and assume that the event space is the cone

$$\mathfrak{X}=\bigcup _{r>0}{C}_h^{+}\left(r\right)=\{{(w,x,y)}^T\in {\mathbb{R}}^3:w^2-x^2-y^2>0,w>0\}.$$

We recall that a class of new analytical vector products in ${\mathbb{R}}^3$ is introduced in [23]. Here, we consider a hyperbolic analog as follows.

Let ${\varrho }_k=\sqrt{x_k^2+y_k^2},k=1,2.$ Unless for ${\varrho }_k=0$ for at least one value of $k\in \{1,2\}$ the analytical hyperbolic vector product of ${\mathfrak{x}}_1={(w_1,x_1,y_1)}^T$ and ${\mathfrak{x}}_2={(w_2,x_2,y_2)}^T$ is defined as

$$\left(\begin{array}{c}{w}_1\\ x_1\\ y_1\end{array}\right){\odot }_h\left(\begin{array}{c}{w}_2\\ x_2\\ y_2\end{array}\right)=\left(\begin{array}{c}{w}_1{w}_2+{\varrho }_1{\varrho }_2\\ (\frac{w_1}{{\varrho }_1}+\frac{w_2}{{\varrho }_2})\left(\begin{array}{c}{x}_1{x}_2-y_1{y}_2\\ y_1{x}_2+x_1{y}_2\end{array}\right)\end{array}\right).$$

(16)

Moreover, we put

$${(w,x,y)}^T{\odot }_h{(\lambda ,0,0)}^T={(\lambda w,\lambda x,\lambda y)}^T.$$

(17)

It should be noted that this product differs only slightly from (12) and (13) in [23]. To better understand this vector product, we first introduce a new coordinate system.

Definition 9.

With the notation $\Theta ={\mathbb{R}}^{+}\times [0,2\pi )\times {\mathbb{R}}^{+},$ we define the hyperbolic coordinate transformation $Hyp:\Theta \to \mathfrak{X},{(w,x,y)}^T=Hyp(r,\phi ,\psi ),$ by

$$w=rcosh\psi ,x=rcos\phi sinh\psi \mathrm{and}y=rsin\phi sinh\psi .$$

(18)

With ${\varrho }^2=x^2+y^2$, the a.e. uniquely defined inverse map $Hy{p}^{-1}:\mathfrak{X}\to \Theta$ is given by

$$r=\sqrt{w^2-{\varrho }^2},cos\phi =\frac{x}{\varrho },sin\phi =\frac{y}{\varrho }\mathrm{and}\psi =ln\sqrt{\frac{w+\varrho }{w-\varrho }}.$$

The event space $\mathfrak{X}$ is a subset of the vector space ${\mathbb{R}}^3$. The latter has the set of vectors $\mathfrak{e}={(1,0,0)}^T,{\mathfrak{j}}_1={(0,1,0)}^T$ and ${\mathfrak{j}}_2={(0,0,1)}^T$ as a basis. The subspaces spanned by ${\mathfrak{j}}_1\mathrm{and}{\mathfrak{j}}_2$ or $\mathfrak{e}$ are, respectively, denoted by $\mathfrak{M}$ and $\mathfrak{N}$ and the orthogonal projections of the vector $\mathfrak{x}={(w,x,y)}^T$ onto the spaces $\mathfrak{M}\mathrm{and}\mathfrak{N}$ by ${\Pi }_1$ and ${\Pi }_2$, respectively. It is recalled that in [23], it was discussed what technical implications the choice of a different basis of the vector space ${\mathbb{R}}^3$ or the choice of another three-dimensional space may have. Such a choice obviously depends on the specific application at hand and also applies to the hyperbolic model.

The variable $\phi$ describes the angle between the vectors ${\mathfrak{j}}_1$ and ${\Pi }_1$, which one can imagine in Figure 8.

If the angle $\phi$ runs through the interval $[0,2\pi )$, then the point $\mathfrak{x}$ runs through an Euclidean circle of radius $\varrho$, centered at the point $w•\mathfrak{e}$ and belonging to the two-dimensional plane being parallel to the subspace $\mathfrak{M}.$

If the intersection point of $C_h^{+}\left(r\right)$ and $\mathfrak{N}$ is denoted A and $S=S(\mathfrak{o},\mathfrak{x},A)$ denotes the hyperbolic sector built by the points $\mathfrak{o},\mathfrak{x}={(w,x,y)}^T\in C_h^{+}\left(r\right)$ and A then $\frac{\psi }{2}{r}^2$ equals the area content of S, see Figure 9.

The meaning of r and $\phi$ lacking as a hyperbolic radius and an angle, and $\psi$ as a non-negative area content motivates the following geometric definition of a vector product in ${\mathbb{R}}^3$.

Definition 10.

The geometric hyperbolic vector product of $Hyp(r_1,{\phi }_1,{\psi }_1)$ and $Hyp(r_2,{\phi }_2,{\psi }_2)$ is defined as

$$Hyp(r_1,{\phi }_1,{\psi }_1){\ast }_{h}Hyp(r_2,{\phi }_2,{\psi }_2)=Hyp(r_1{r}_2,{\phi }_1♢{\phi }_2,{\psi }_1+{\psi }_2)$$

(19)

where

$${\phi }_1♢{\phi }_2=({\phi }_1+{\phi }_2)I_{[0,2\pi ]}({\phi }_1+{\phi }_2)+({\phi }_1+{\phi }_2-2\pi )I_{(2\pi ,4\pi )}({\phi }_1+{\phi }_2)={\phi }_1+{\phi }_2.$$

Theorem 5.

The geometric hyperbolic vector product of ${(w_1,x_1,y_1)}^T=Hyp(r_1,{\phi }_1,{\psi }_1)$ and ${(w_2,x_2,y_2)}^T=Hyp(r_2,{\phi }_2,{\psi }_2)$ equals the analytical hyperbolic one.

Proof. 

The proof of this theorem follows the line described in Section 2. □

Example 2.

Since

$$\left(\begin{array}{c}w\\ x\\ y\end{array}\right){\odot }_h\mathfrak{e}=\left(\begin{array}{c}w\\ x\\ y\end{array}\right)$$

(20)

and

$${\mathfrak{j}}_1{\odot }_h{\mathfrak{j}}_1={\mathfrak{j}}_2{\odot }_h{\mathfrak{j}}_2={\mathfrak{j}}_1{\odot }_h{\mathfrak{j}}_2=\mathfrak{e}$$

(21)

the vectors $\mathfrak{e}$ and ${\mathfrak{j}}_1,{\mathfrak{j}}_2$ are called the hyperbolic multiplicative neutral element and the hyperbolic units. Note that (21) is closely related to, but nevertheless different from, (15) in [23].

It is supposed to, respectively, mean ⊕ and • vector addition and scalar multiplication in the usual sense.

Definition 11.

We call $(\mathfrak{X},\oplus ,•,{\odot }_h,\mathfrak{o},\mathfrak{e},{\mathfrak{j}}_1,{\mathfrak{j}}_2)$ with $\mathfrak{e},{\mathfrak{j}}_1,{\mathfrak{j}}_2$ having the properties (20) and (21) a three dimensional hyperbolic complex algebraic structure.

3.2. Four Dimensional Space-Time Structure

Let now a hyperbolic half-sphere of hyperbolic radius $r>0$ be defined as

$$C_h^{+}\left(r\right)=\{{(t,x,y,z)}^T\in {\mathbb{R}}^4:t^2-x^2-y^2-z^2=r^2,t>0\}$$

and the event space or space-time cone as

$$\mathfrak{X}=\bigcup _{r>0}{C}_h^{+}\left(r\right)=\{{(t,x,y,z)}^T\in {\mathbb{R}}^4:t^2-x^2-y^2-z^2>0,t>0\}.$$

We recall that a class of new analytical vector products in ${\mathbb{R}}^4$ is introduced in [25]. Here, we consider a hyperbolic analog as follows.

Definition 12.

Let

$${\zeta }_{1,l}=\sqrt{x_l^2+y_l^2+z_l^2}\mathrm{and}{\zeta }_{2,l}=\sqrt{y_l^2+z_l^2},l=1,2.$$

Unless for ${\zeta }_{1,l}=0$ or ${\zeta }_{2,l}=0$ for at least one value of $l\in \{1,2\}$ the analytical hyperbolic vector product of ${\mathfrak{x}}_1={(t_1,x_1,y_1,z_1)}^T$ and ${\mathfrak{x}}_2={(t_2,x_2,y_2,z_2)}^T$ is defined as

$$\left(\begin{array}{c}{t}_1\\ x_1\\ y_1\\ z_1\end{array}\right){\odot }_h\left(\begin{array}{c}{t}_2\\ x_2\\ y_2\\ z_2\end{array}\right)=\left(\begin{array}{c}{t}_1{t}_2+{\zeta }_{1,1}{\zeta }_{1,2}\\ S({\mathfrak{x}}_1,{\mathfrak{x}}_2)[\frac{t_1}{{\zeta }_{1,1}}+\frac{t_2}{{\zeta }_{1,2}}]\left(\begin{array}{c}{x}_1{x}_2-{\zeta }_{2,1}{\zeta }_{2,2}\\ [\frac{x_1}{{\zeta }_{2,1}}+\frac{x_2}{{\zeta }_{2,2}}]\left(\begin{array}{c}{y}_1{y}_2-z_1{z}_2\\ y_1{z}_2+z_1{y}_2\end{array}\right)\end{array}\right)\end{array}\right).$$

(22)

Moreover, we put

$${(t,x,y,z)}^T{\odot }_h{(\lambda ,0,0,0)}^T={(\lambda t,\lambda x,\lambda y,\lambda z)}^T$$

and

$$\left(\begin{array}{c}t\\ x\\ y\\ z\end{array}\right){\odot }_h\left(\begin{array}{c}u\\ v\\ 0\\ 0\end{array}\right)=u\left(\begin{array}{c}t\\ x\\ y\\ z\end{array}\right)+v\left(\begin{array}{c}\varrho \\ xt/\varrho \\ yt/\varrho \\ zt/\varrho \end{array}\right)$$

(23)

where $\varrho =\sqrt{x^2+y^2+z^2}$.

It should be noted that Formula (16) differs only slightly from Formula (12) in [25], namely with respect to two times the factor $-1$. One of these factors is due to the circumstance that $\mathfrak{X}$ is a one-sided cone and the other factor is caused by the fact that instead of a norm used in [25] we use an antinorm according to [27], here. To better understand this vector product, we first introduce a new coordinate system.

Definition 13.

With the notation $\Theta ={\mathbb{R}}^{+}\times [0,\pi )\times [0,2\pi )\times {\mathbb{R}}^{+},$ we define the hyperbolic coordinate transformation $Hyp:\Theta \to \mathfrak{X},{(t,x,y,z)}^T=Hyp(r,{\phi }_1,{\phi }_2,\psi ),$ by

$$\begin{array}{cc}\hfill t=rcosh\psi ,x& =rcos{\phi }_{1}sinh\psi ,\hfill \\ \hfill y=rsin{\phi }_{1}cos{\phi }_{2}sinh\psi \mathrm{and}z& =rsin{\phi }_{1}sin{\phi }_{2}sinh\psi .\hfill \end{array}$$

(24)

With $\varrho =\sqrt{x^2+y^2+z^2}$, the a.e. uniquely defined inverse map $Hy{p}^{-1}:\mathfrak{X}\to \Theta$ is given by

$$r=\sqrt{t^2-{\varrho }^2},{\phi }_1=arcsin\frac{\sqrt{y^2+z^2}}{\varrho },{\phi }_2=arctan\frac{z}{y},\psi =ln\sqrt{\frac{t+\varrho }{t-\varrho }}.$$

The event space $\mathfrak{X}$ is a subset of the vector space ${\mathbb{R}}^4$. A basis of the latter consists of the vectors $\mathfrak{e}={(1,0,0,0)}^T,{\mathfrak{j}}_1={(0,1,0,0)}^T,{\mathfrak{j}}_2={(0,0,1,0)}^T$ and ${\mathfrak{j}}_3={(0,0,0,1)}^T$. The subspaces spanned by ${\mathfrak{j}}_1,{\mathfrak{j}}_2\mathrm{and}{\mathfrak{j}}_3$ or $\mathfrak{e}$ are, respectively, denoted by $\mathfrak{M}$ and $\mathfrak{N}$ and the orthogonal projections of the vector $\mathfrak{x}={(t,x,y,z)}^T$ onto the spaces $\mathfrak{M}\mathrm{and}\mathfrak{N}$ by ${\Pi }_1$ and ${\Pi }_2$, respectively.

The meaning of r and ${\phi }_1,{\phi }_2$ lacking as a hyperbolic radius and two angles, and $\psi$ as an area content motivates us for the following definition.

Definition 14.

We define the geometric hyperbolic product of the vectors ${\mathfrak{x}}_1=Hyp(r_1,{\phi }_{1,1},{\phi }_{2,1},{\psi }_1)$ and ${\mathfrak{x}}_2=Hyp(r_2,{\phi }_{1,2},{\phi }_{2,2},{\psi }_2)$ as

$${\mathfrak{x}}_1{\ast }_h{\mathfrak{x}}_2=Hyp(r_1{r}_2,{\phi }_{1,1}\circ {\phi }_{1,2},{\phi }_{2,1}♢{\phi }_{2,2},{\psi }_1+{\psi }_2)$$

(25)

where

$${\phi }_1\circ {\phi }_2=({\phi }_1+{\phi }_2)I_{[0,\pi ]}({\phi }_1+{\phi }_2)+({\phi }_1+{\phi }_2-\pi )I_{(\pi ,2\pi )}({\phi }_1+{\phi }_2).$$

Theorem 6.

The analytical hyperbolic vector product of ${(t_1,x_1,y_1,z_1)}^T=Hyp(r_1,{\phi }_{1,1},{\phi }_{2,1},{\psi }_1)$ and ${(t_2,x_2,y_2,z_2)}^T=Hyp(r_2,{\phi }_{1,2},{\phi }_{2,2},{\psi }_2)$ equals the geometric hyperbolic one.

Proof. 

The proof of this theorem follows the line described in Section 2. □

Example 3.

Since

$$\left(\begin{array}{c}t\\ x\\ y\\ z\end{array}\right){\odot }_h\mathfrak{e}=\left(\begin{array}{c}t\\ x\\ y\\ z\end{array}\right)$$

(26)

and

$${\mathfrak{j}}_1{\odot }_h{\mathfrak{j}}_1={\mathfrak{j}}_2{\odot }_h{\mathfrak{j}}_2={\mathfrak{j}}_3{\odot }_h{\mathfrak{j}}_3=\mathfrak{e}$$

(27)

the vectors $\mathfrak{e}$ and ${\mathfrak{j}}_1,{\mathfrak{j}}_2,{\mathfrak{j}}_3$ are called the hyperbolic multiplicative neutral element and the hyperbolic units. Note that (27) is closely related to, but nevertheless different from, (16) in [25].

It is supposed to, respectively, mean ⊕ and • vector addition and scalar multiplication in the usual sense.

Definition 15.

We call $(\mathfrak{X},\oplus ,•,{\odot }_h,\mathfrak{o},\mathfrak{e},{\mathfrak{j}}_1,{\mathfrak{j}}_2,{\mathfrak{j}}_3)$ with $\mathfrak{e},{\mathfrak{j}}_1,{\mathfrak{j}}_2,{\mathfrak{j}}_3$ having the properties (26) and (27) a four dimensional hyperbolic complex algebraic structure.

We recall once again from [23] that changing the basis elements of an event space can be very useful and does not affect the basic properties of the complex algebraic structure under consideration.

4. Discussion

Why do we allow applying the rule in (5) to the extended event space when it is originally defined only for pairs of elements of either $\mathfrak{X}$ or $\mathfrak{Y}$? To approach an answer, let us first recall the situation with usual complex numbers as described at the beginning of Section 2.3. Since there is certainly no explanation for $\mathfrak{i}$ as a “number”, there is no explanation for ${\mathfrak{i}}^2$ in this approach.

However, for centuries, successful applications of complex numbers have provided the motivation to deal with them, even though there is a certain lack of mathematical rigor in their definition. Practical success in using imaginary numbers was taken as proof of their existence, which is rather untypical for pure mathematics. The strict approaches in [22,23,24,25] have overcome this deficit for the usual complex numbers and their certain generalizations by giving explicit vectorial definitions of the imaginary unit.

The meaning of complex numbers has evolved over a historically lengthy process. While complex numbers initially played a formal role in solving quadratic equations, they later became an indispensable tool in many applied sciences, e.g., in electrical engineering where the current I and voltage U in an alternating current circuit satisfy the equation $U{\left(t\right)}^2+I{\left(t\right)}^2=r^2$ in time t. In the event that other quantities $U^{\ast }$ and $I^{\ast }$ satisfy the equation $|U^{\ast }{\left(t\right)|}^p+{\left|I^{\ast }\left(t\right)\right|}^p=r^p$, p-generalized complex numbers were introduced in [22]. Higher dimensional and other generalizations were considered in [23,24,25].

In two-dimensional space-time models, quantities X and T that satisfy the equation $X^2-T^2=r^2$ are of interest. In such a case, ordinary complex numbers do not provide an adequate description, but hyperbolic complex numbers. Such numbers, together with their multidimensional generalizations, have been introduced in the present work. This could pave the way for numerous potential applications of generalized complex analysis. Just as the existence of a verifiable usual imaginary unit was unclear for a long time, so was for the hyperbolic imaginary unit. This gap was closed in the present work and concrete vector representations for the hyperbolic imaginary unit were given. Since the properties of each vector are essentially determined by the properties of the space containing it, the choice of a vector space is of great importance when processing a specific application. In particular, it is of great importance to empirically verify the validity of a vector multiplication or arrow combination in the respective application and to develop corresponding computer animation programs as was mentioned in the Introduction for the QED. A hopefully broad readership from different application areas is invited to follow this path. The creation of interactive computer animation programs in the sense of [2] but for vector multiplication as in the present work can be a building block of such a project.