The Effect of Porous Media on Wave-Induced Sloshing in a Floating Tank
Abstract
:Featured Application
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations and Boundary Conditions
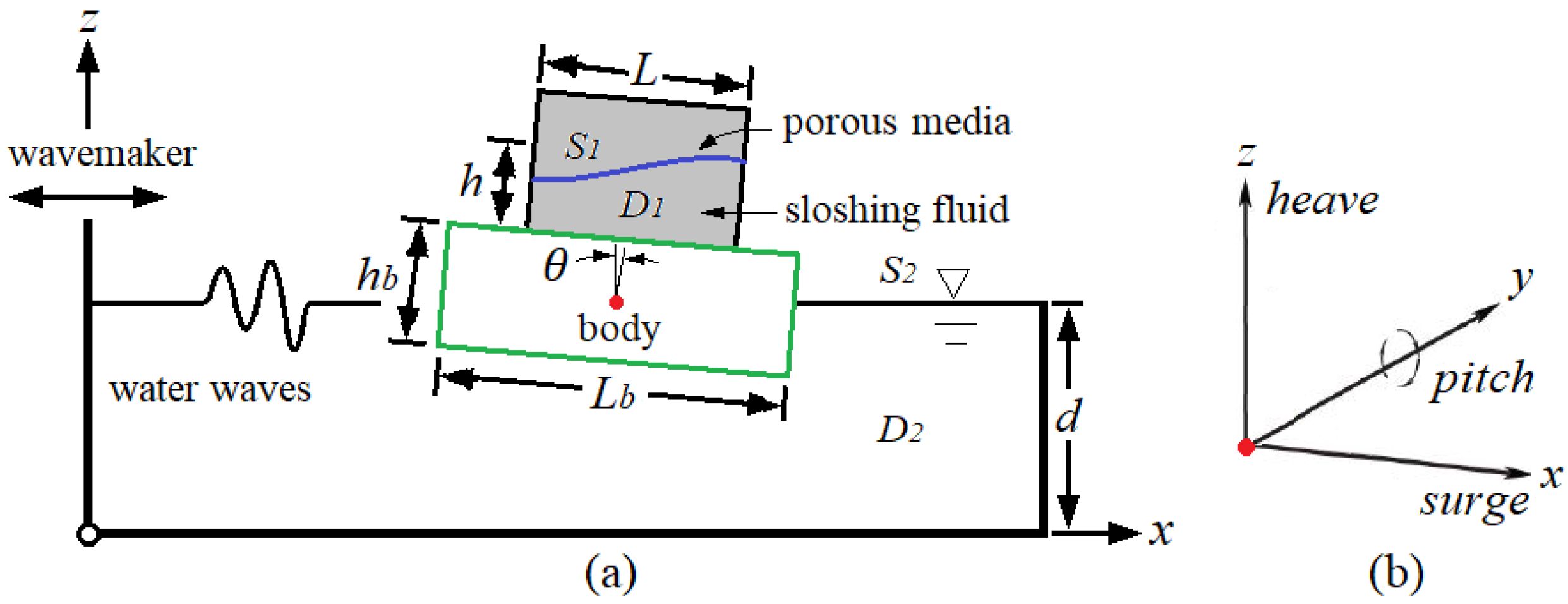
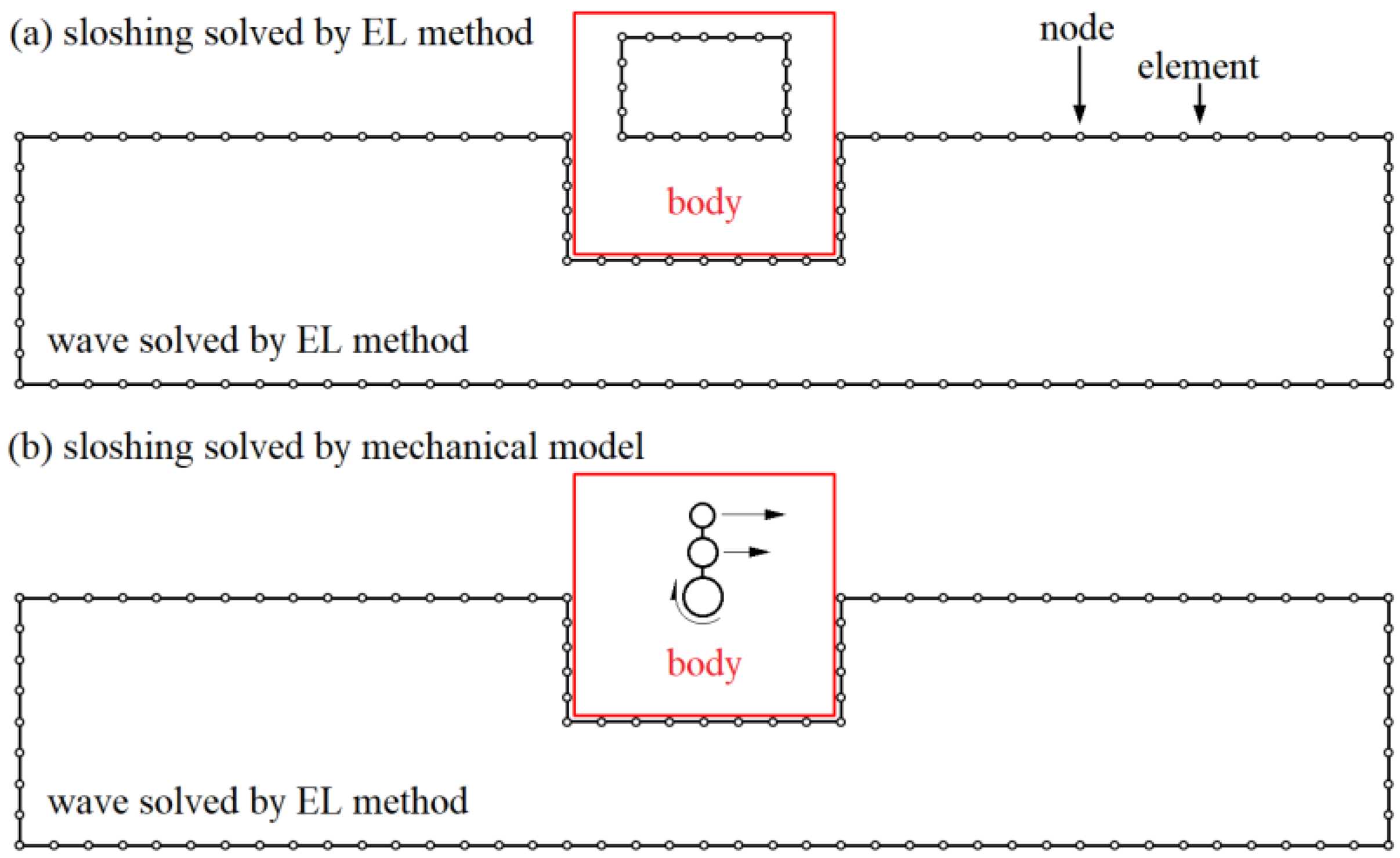
2.2. Eulerian–Lagrangian Method
2.3. Floating Body Dynamics and FSI Coupling
| Algorithm 1: An iterative algorithm for FSI by EL method. |
| do k > 0 Start iterative step with the solution at kth time step as an initial guess do while Solve and (the first BVP) Solve and (the second BVP) Calculate pressure along wetted boundaries Calculate force and moment act on the floating body Define predictor of force and moment: Solve rigid-body motion (Newmark method) Update free surface and body boundary and end do end do |
2.4. Equivalent Mechanical Model
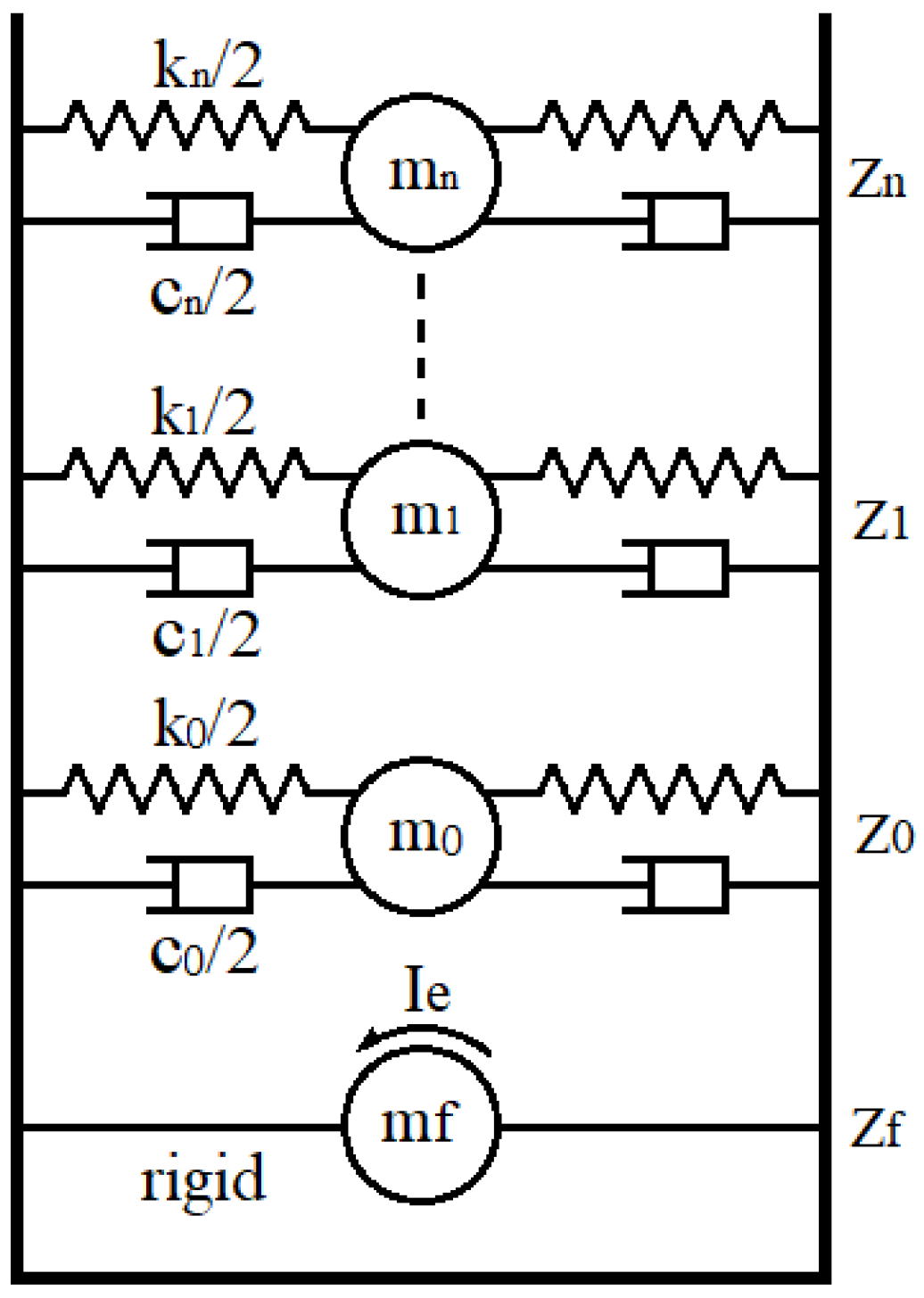
3. Characteristics Analysis for Floating Body
4. Results and Discussion
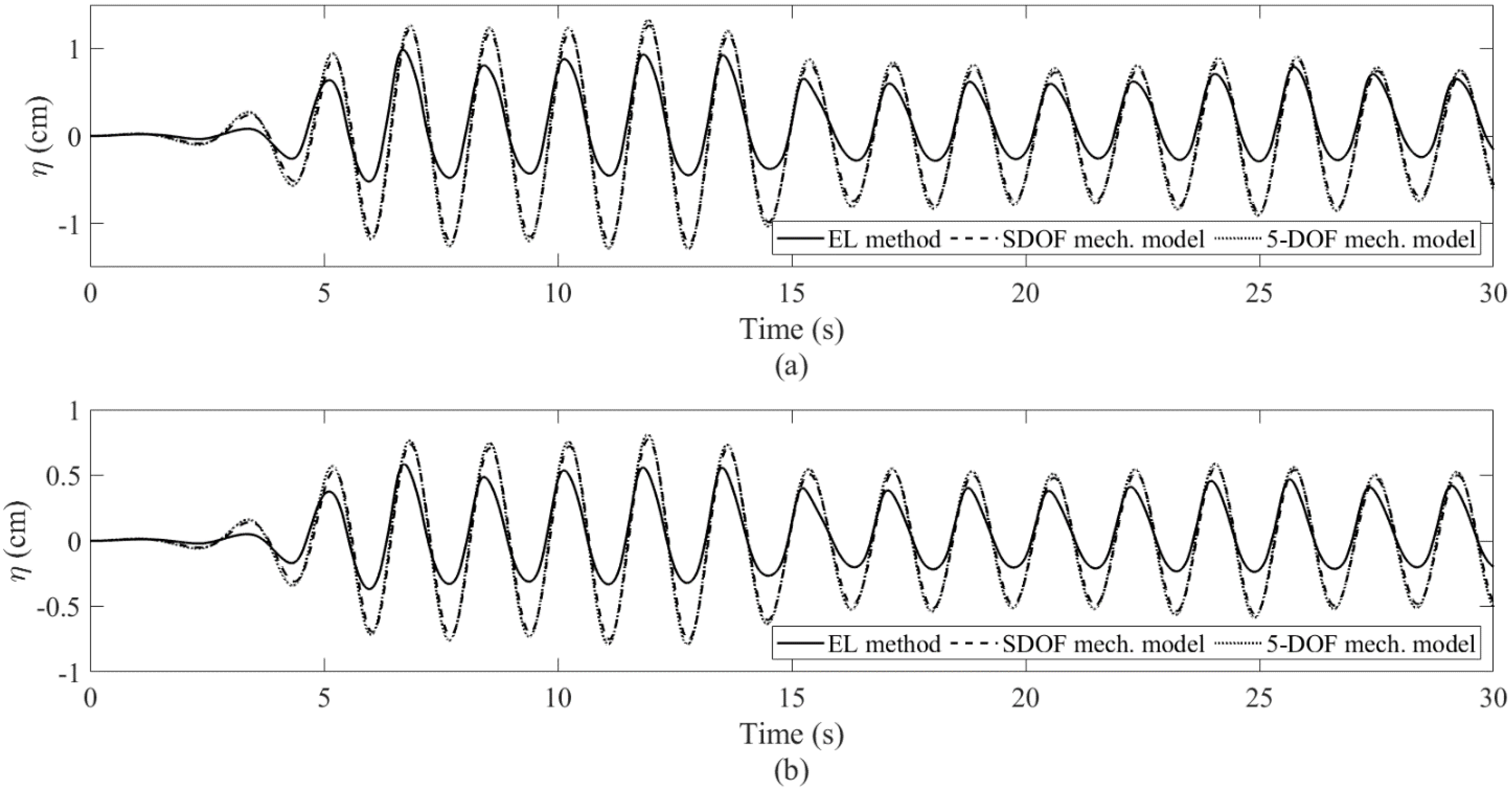
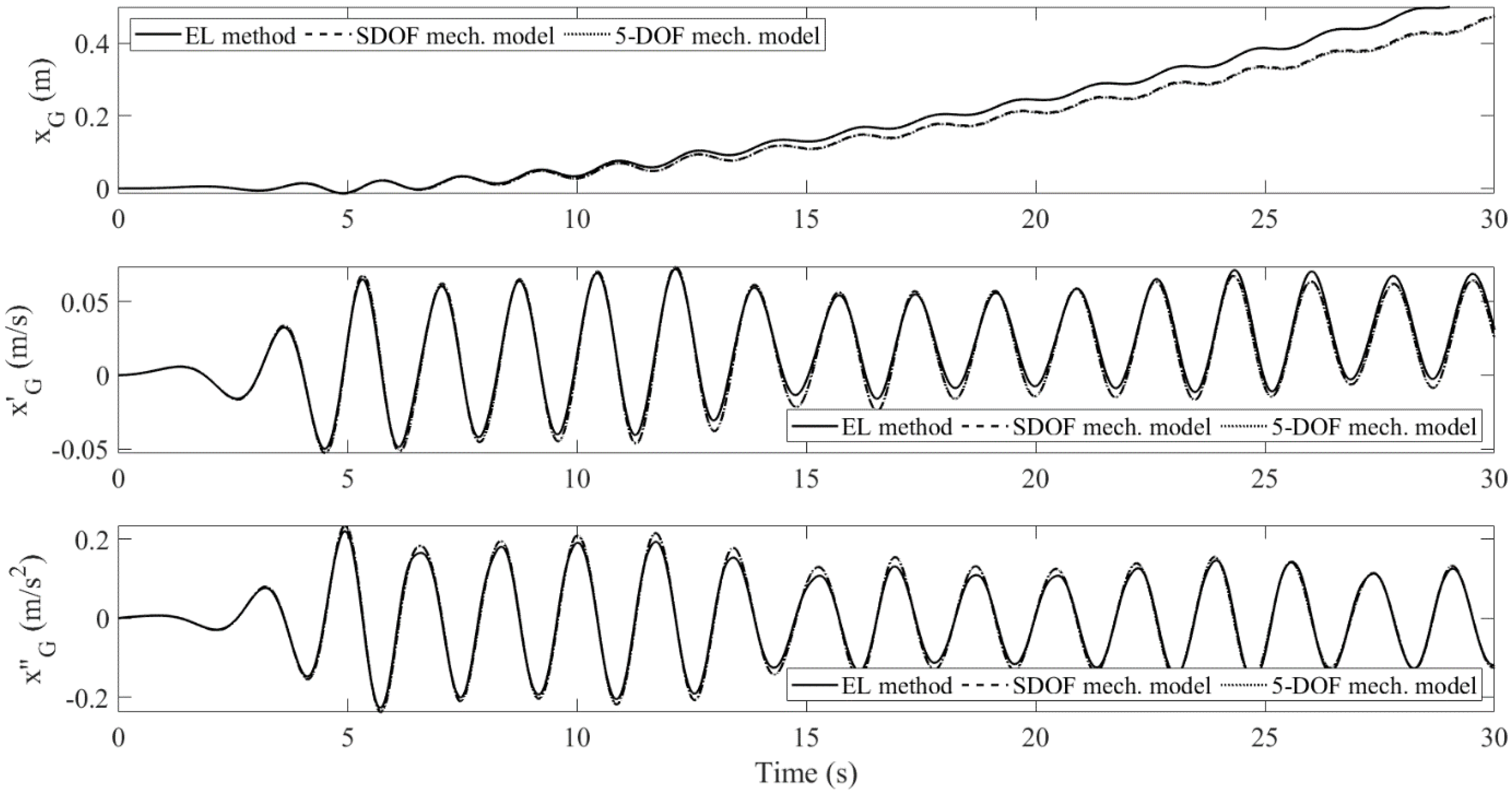
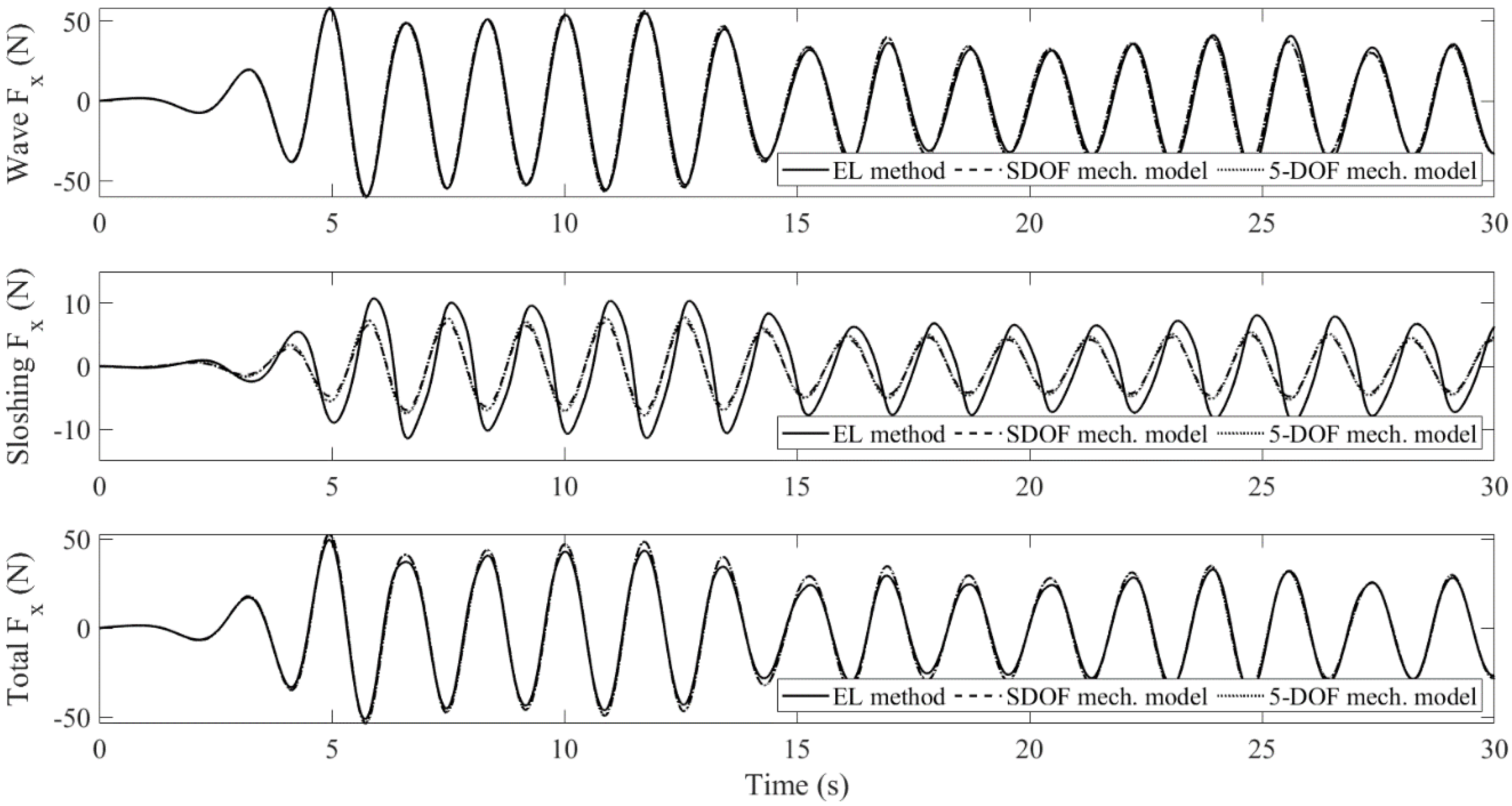
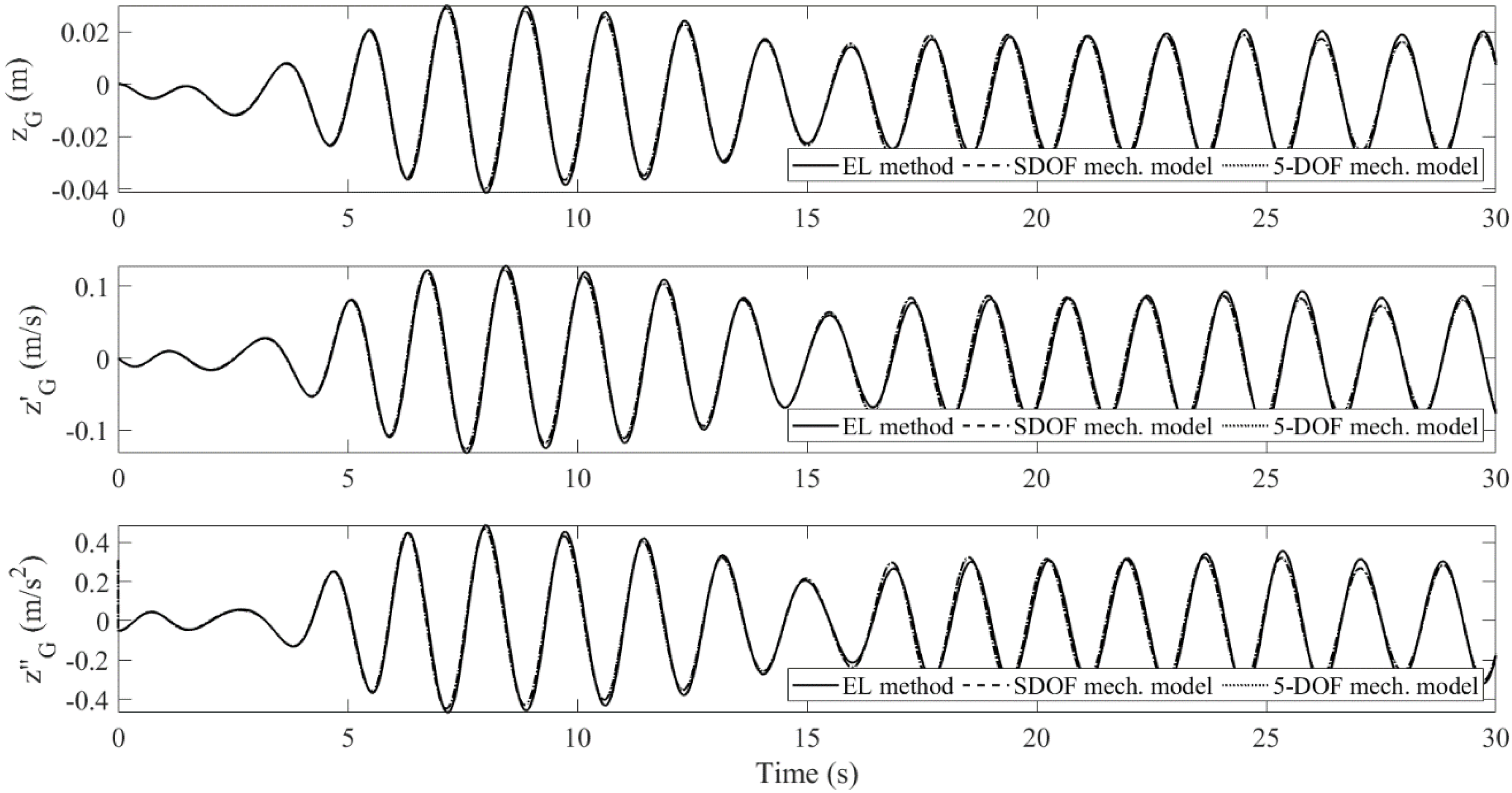
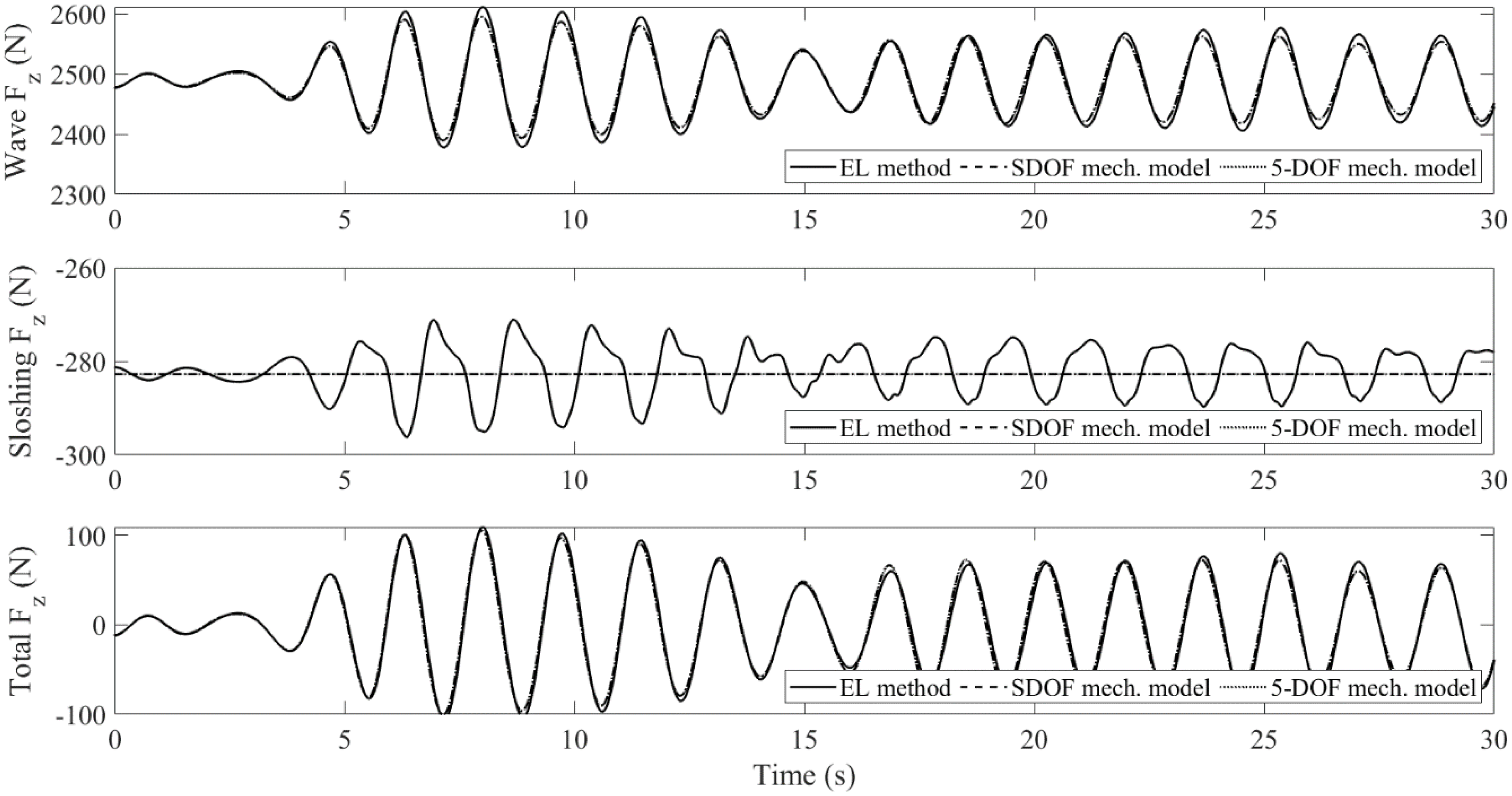
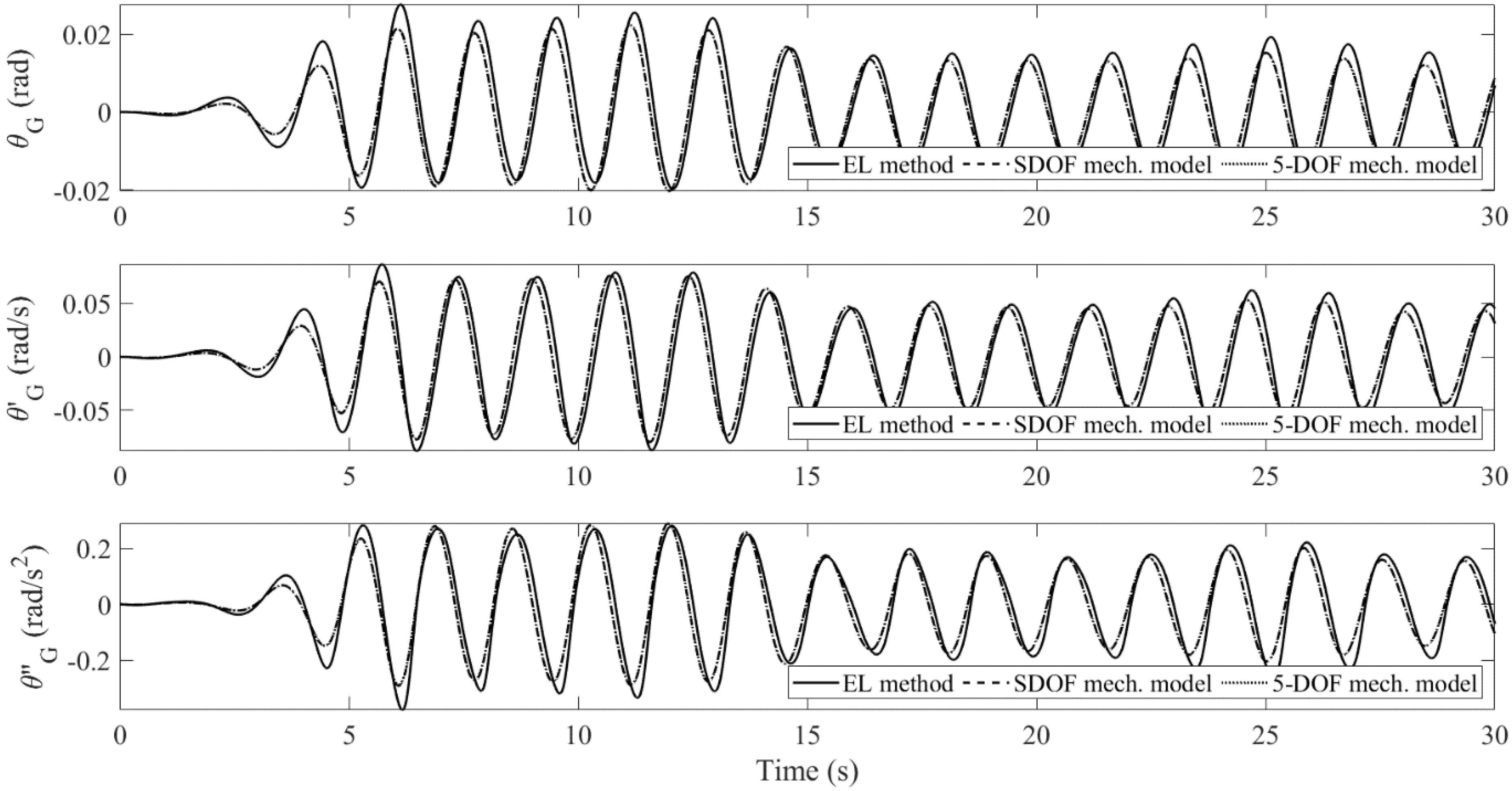
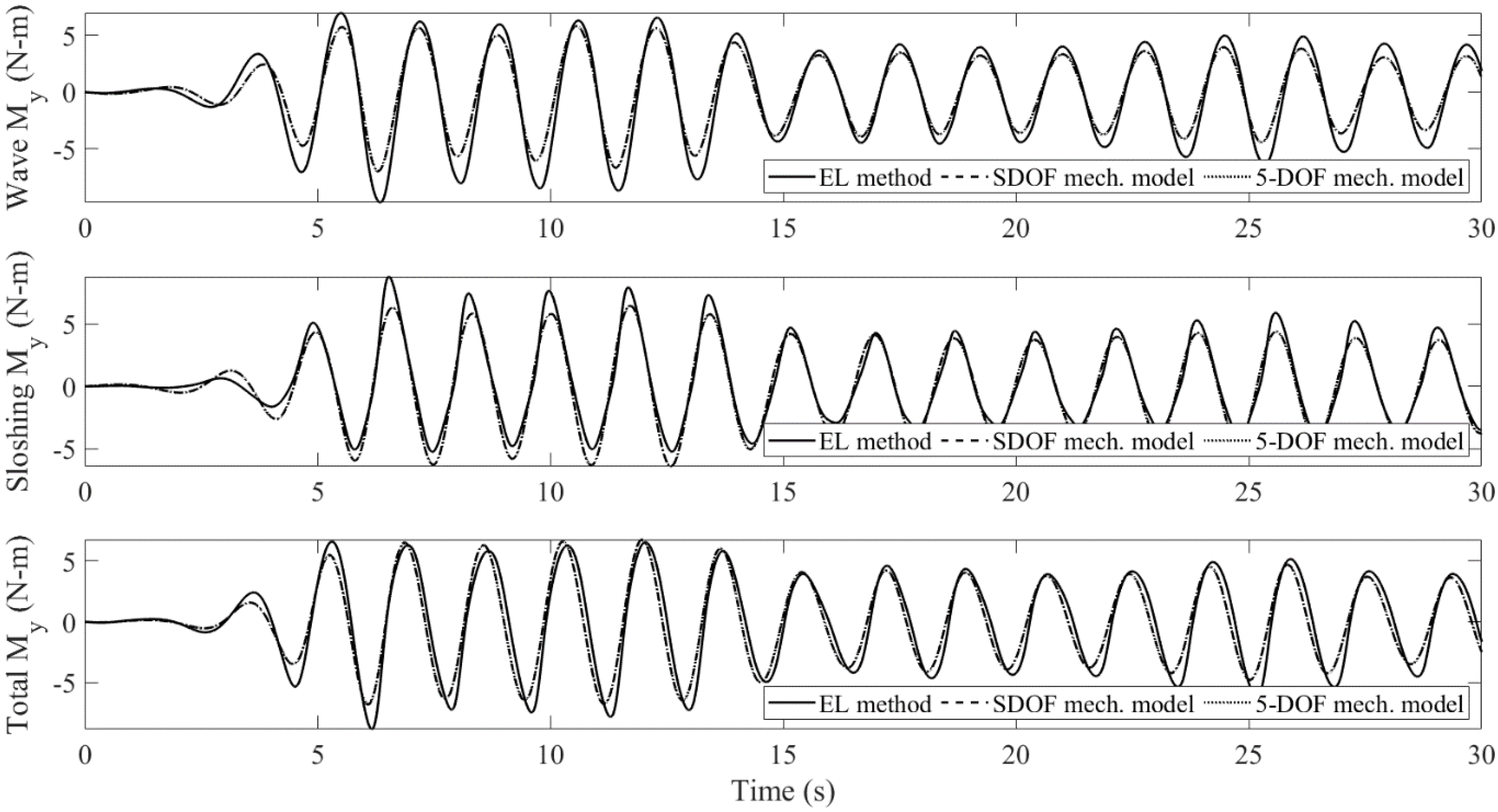
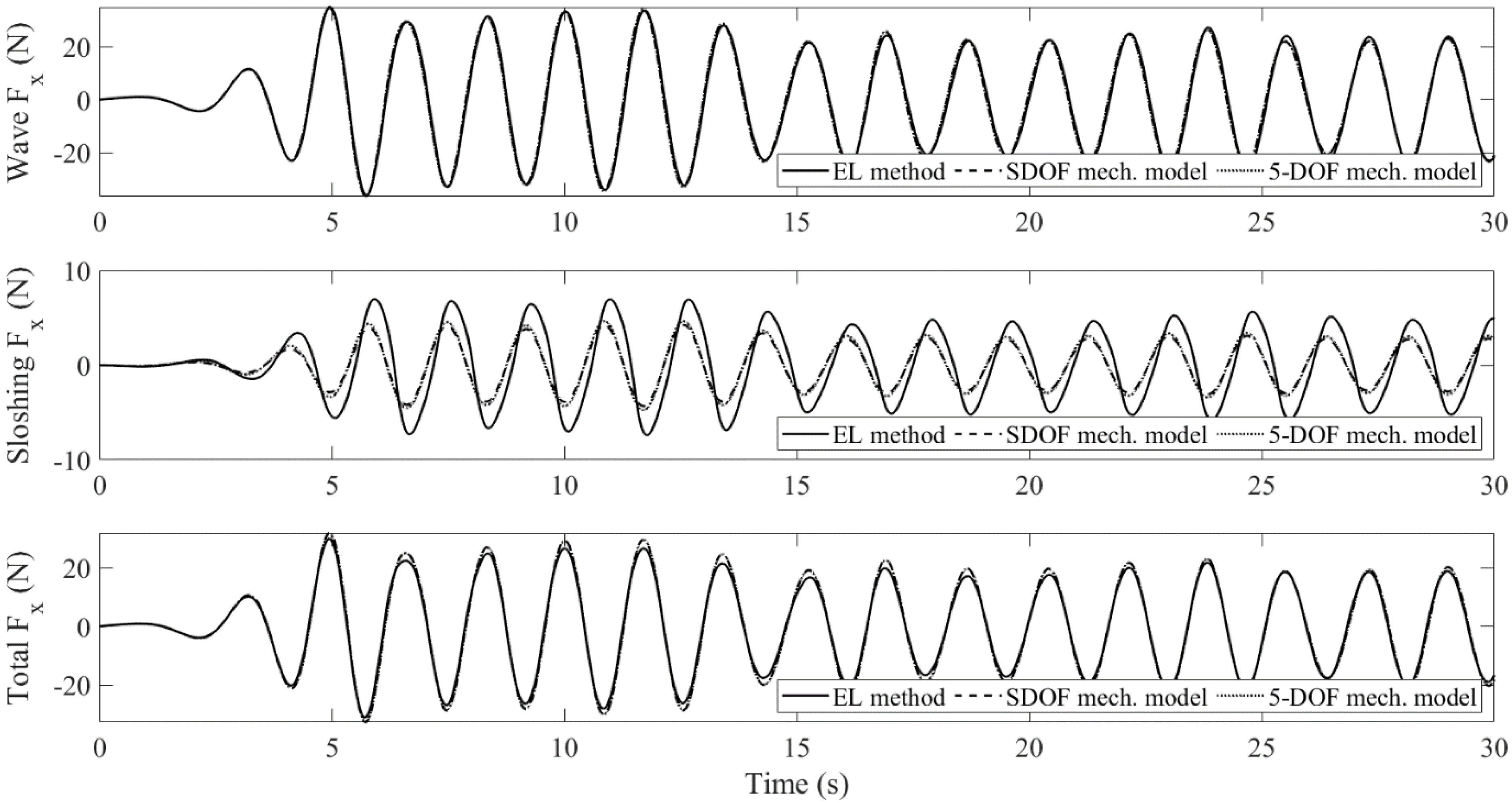
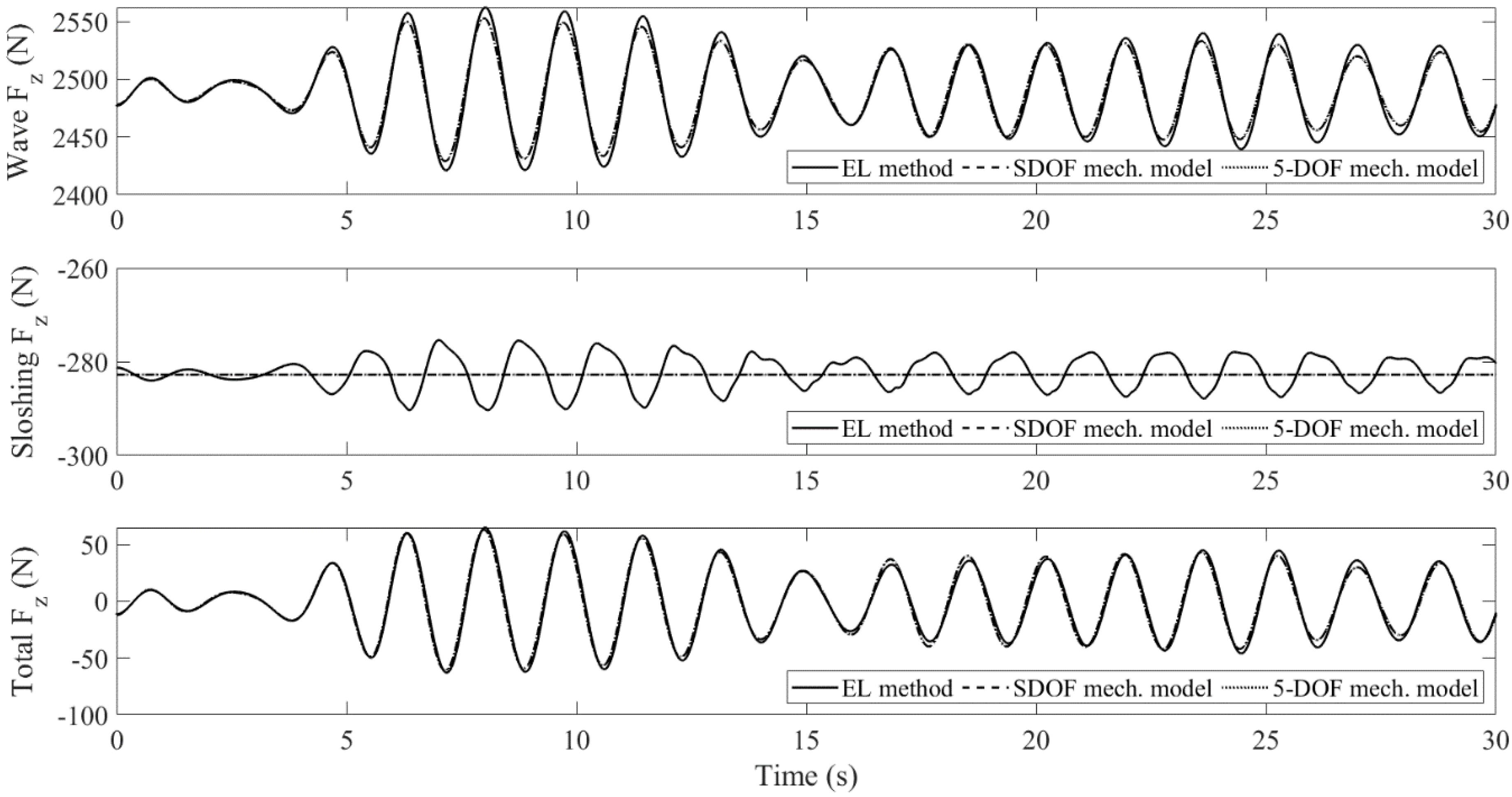
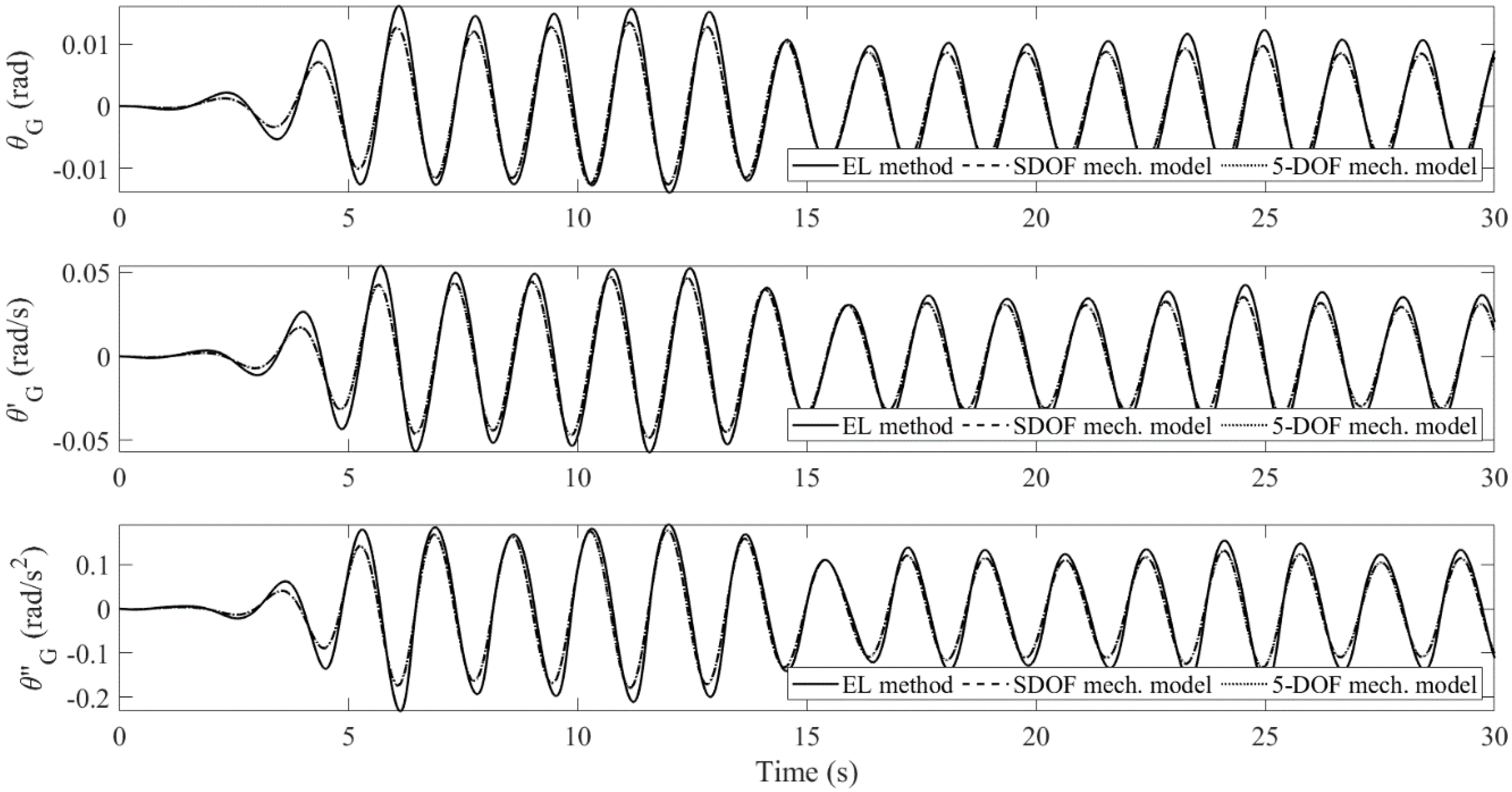
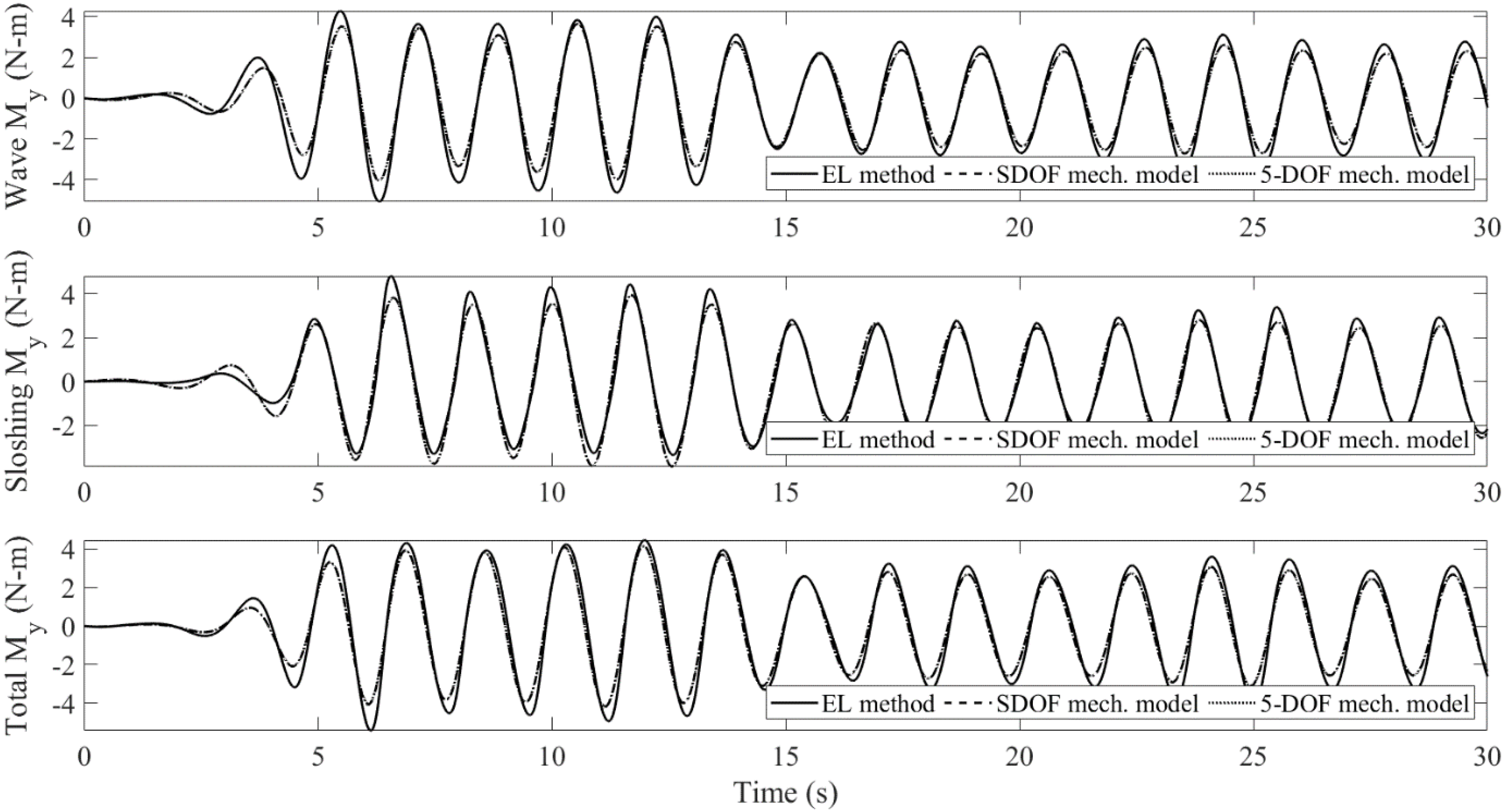
4.1. Sloshing in a Tank Filled with Porous Media: EL Method vs. Mechanical Model
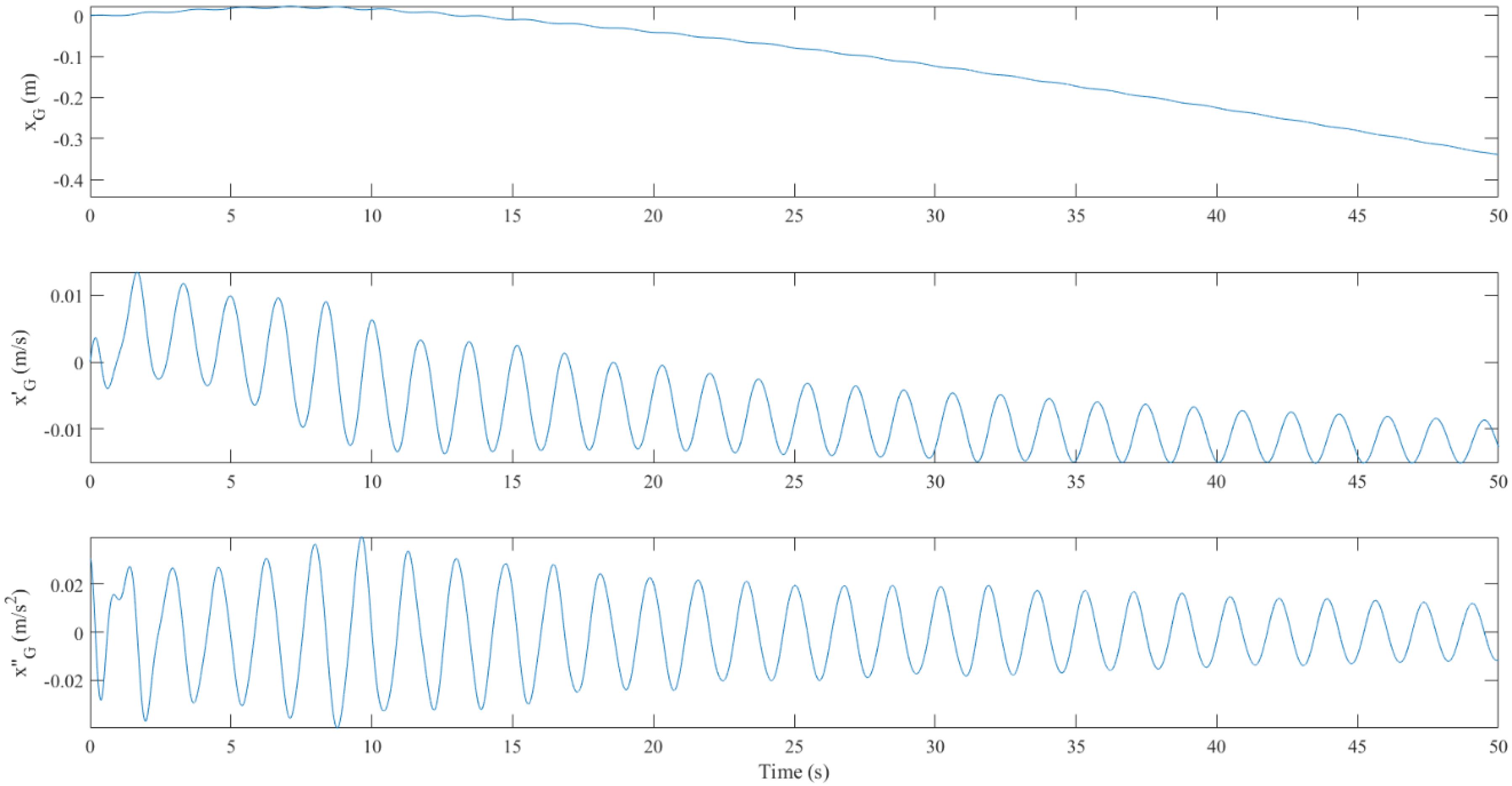
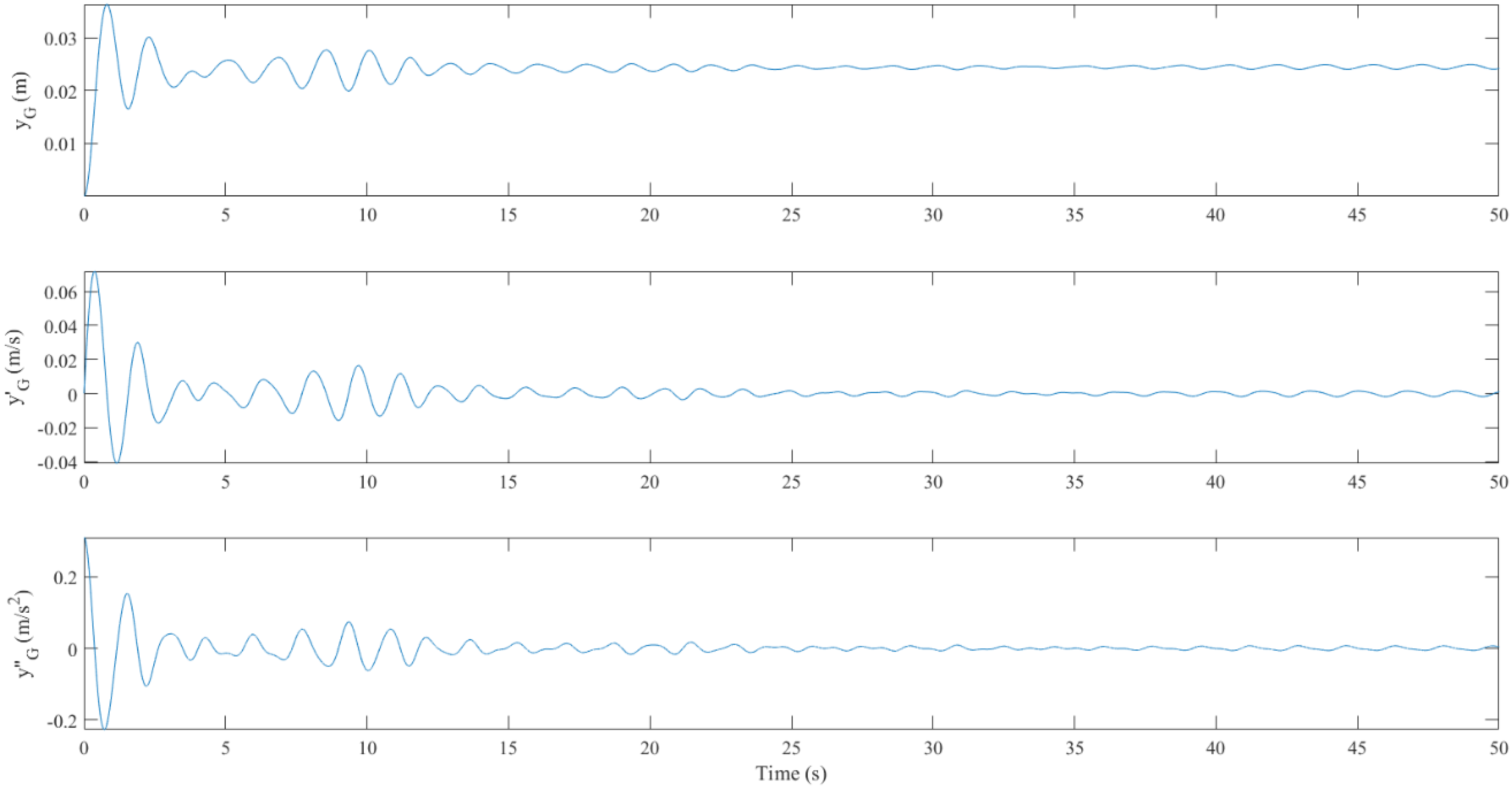
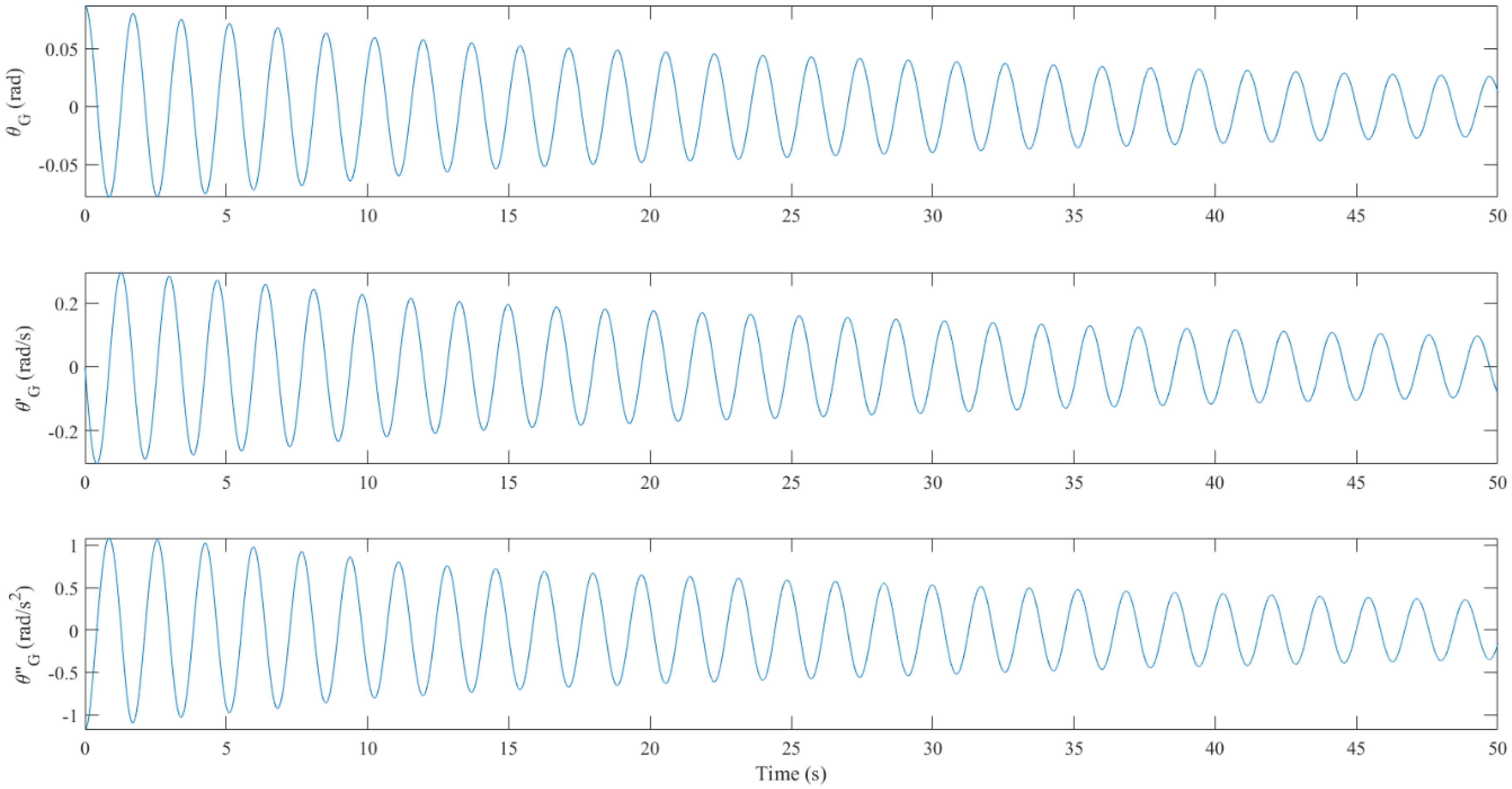
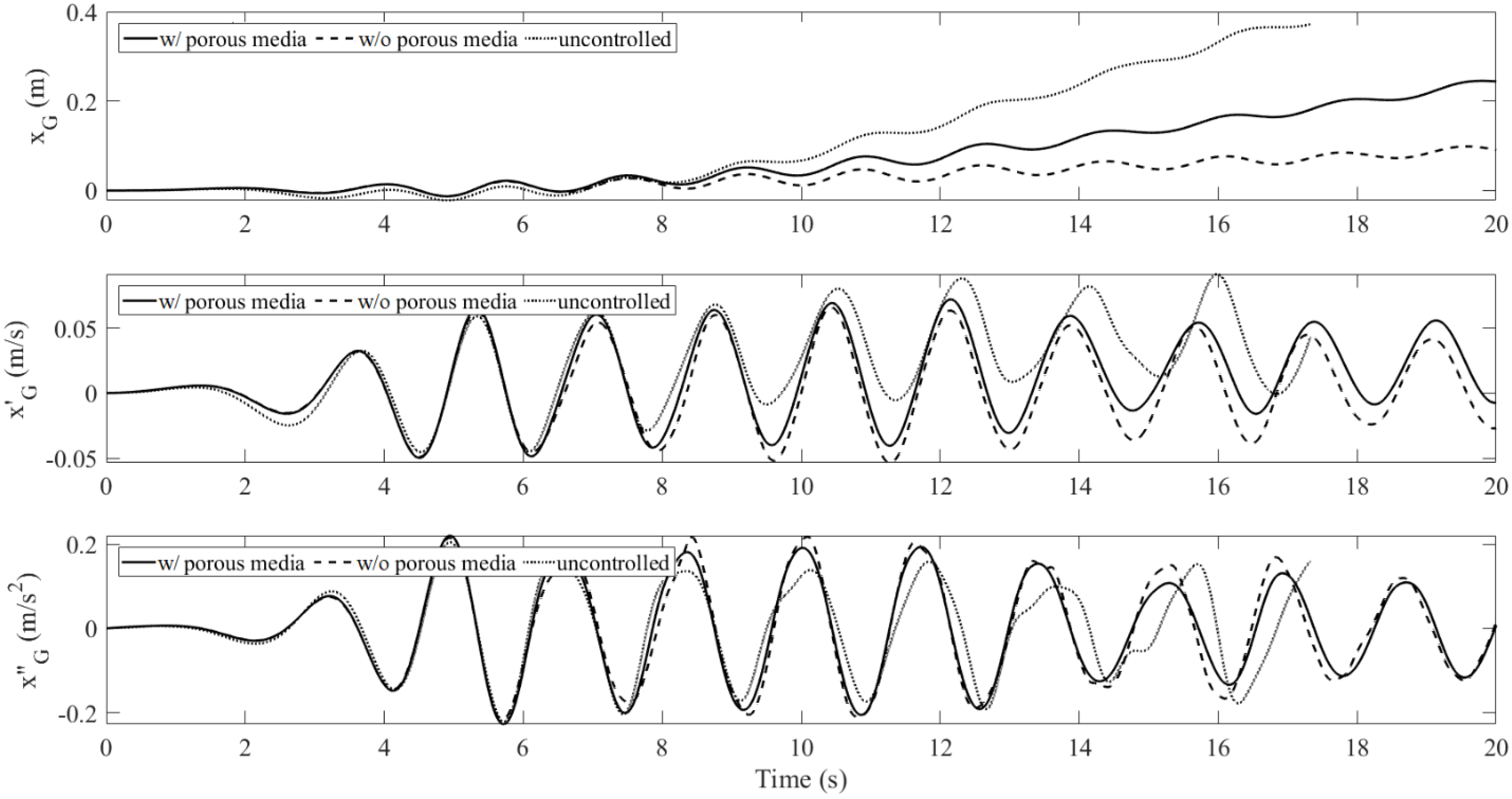
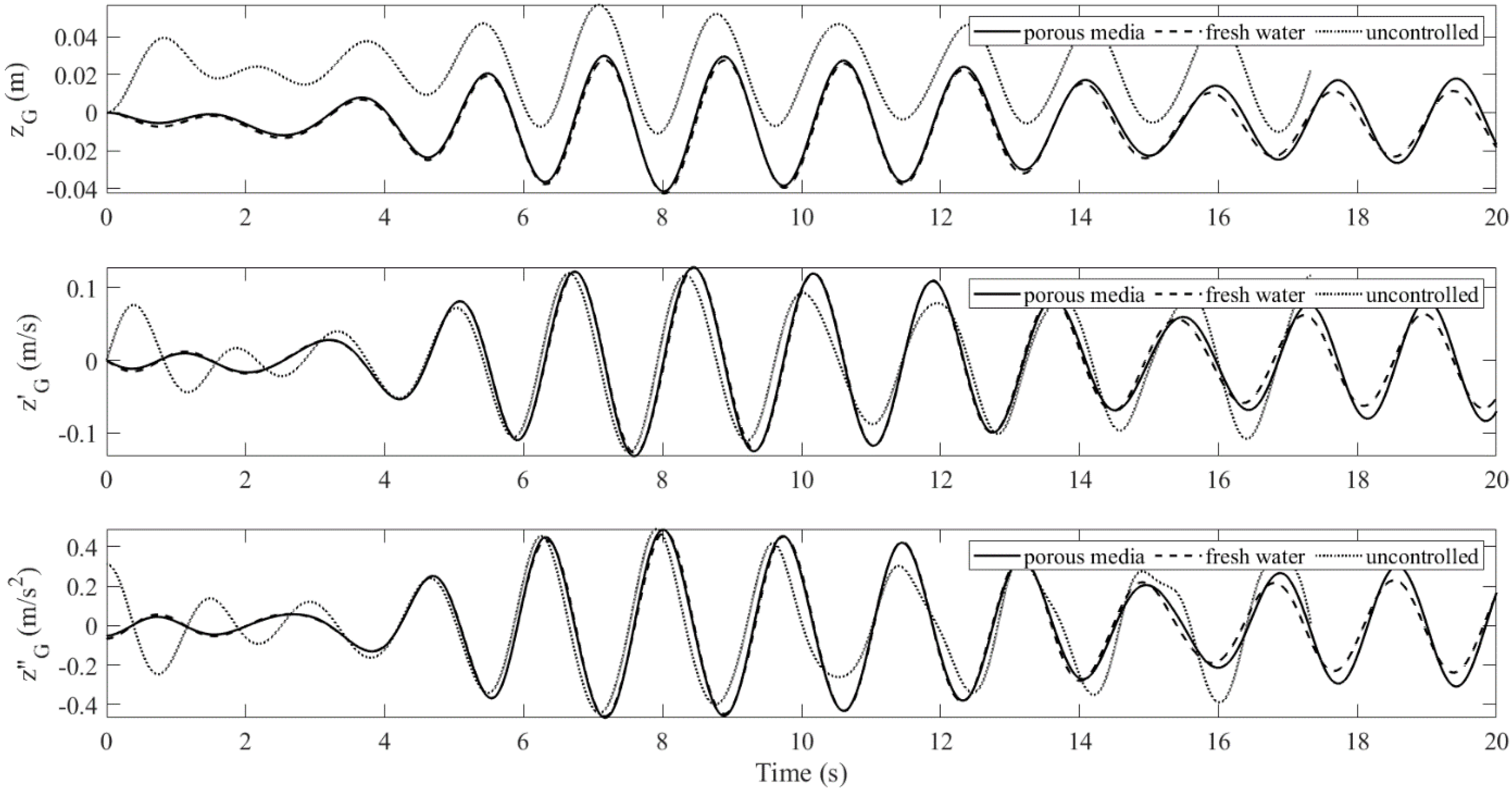
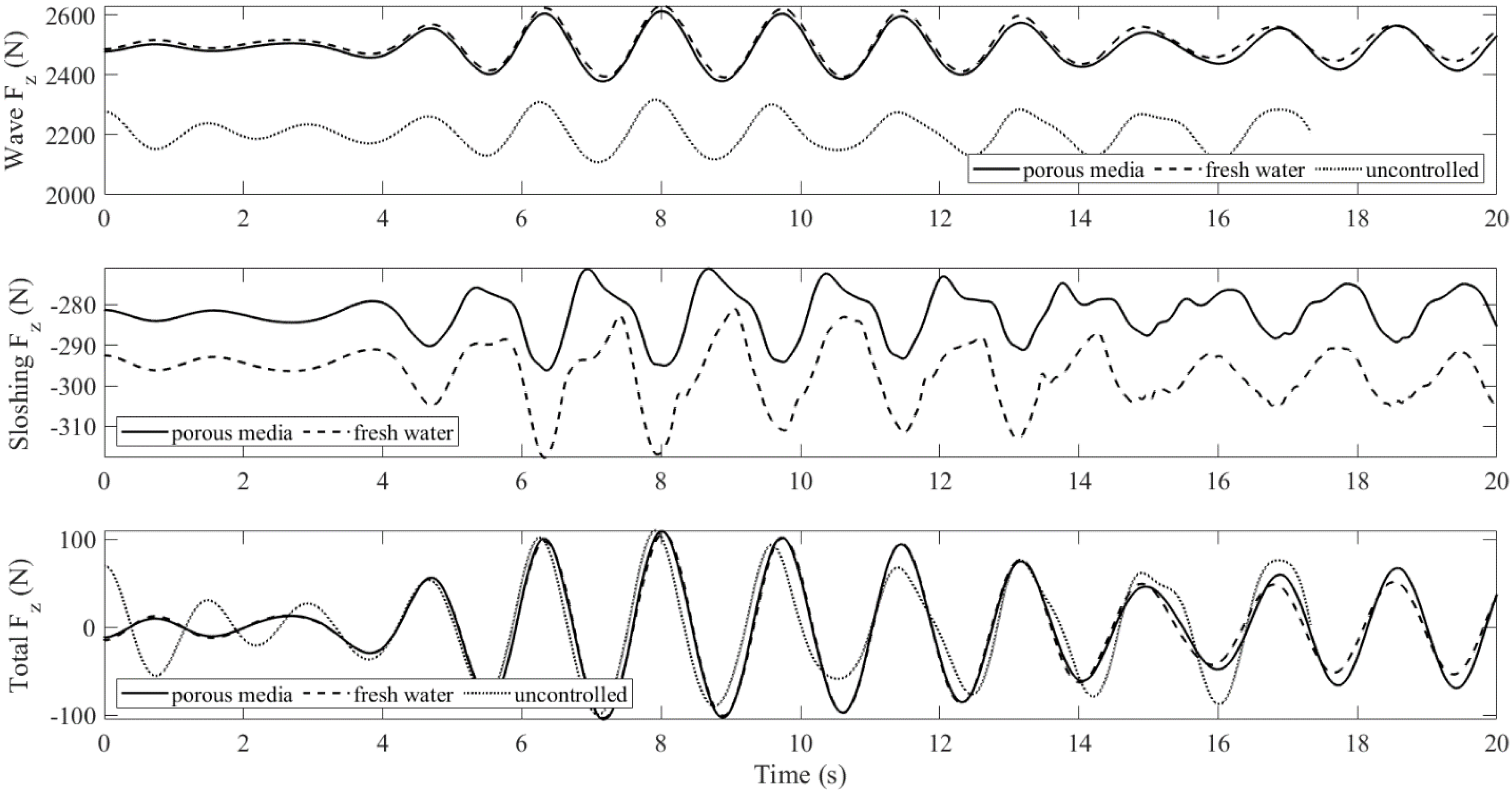
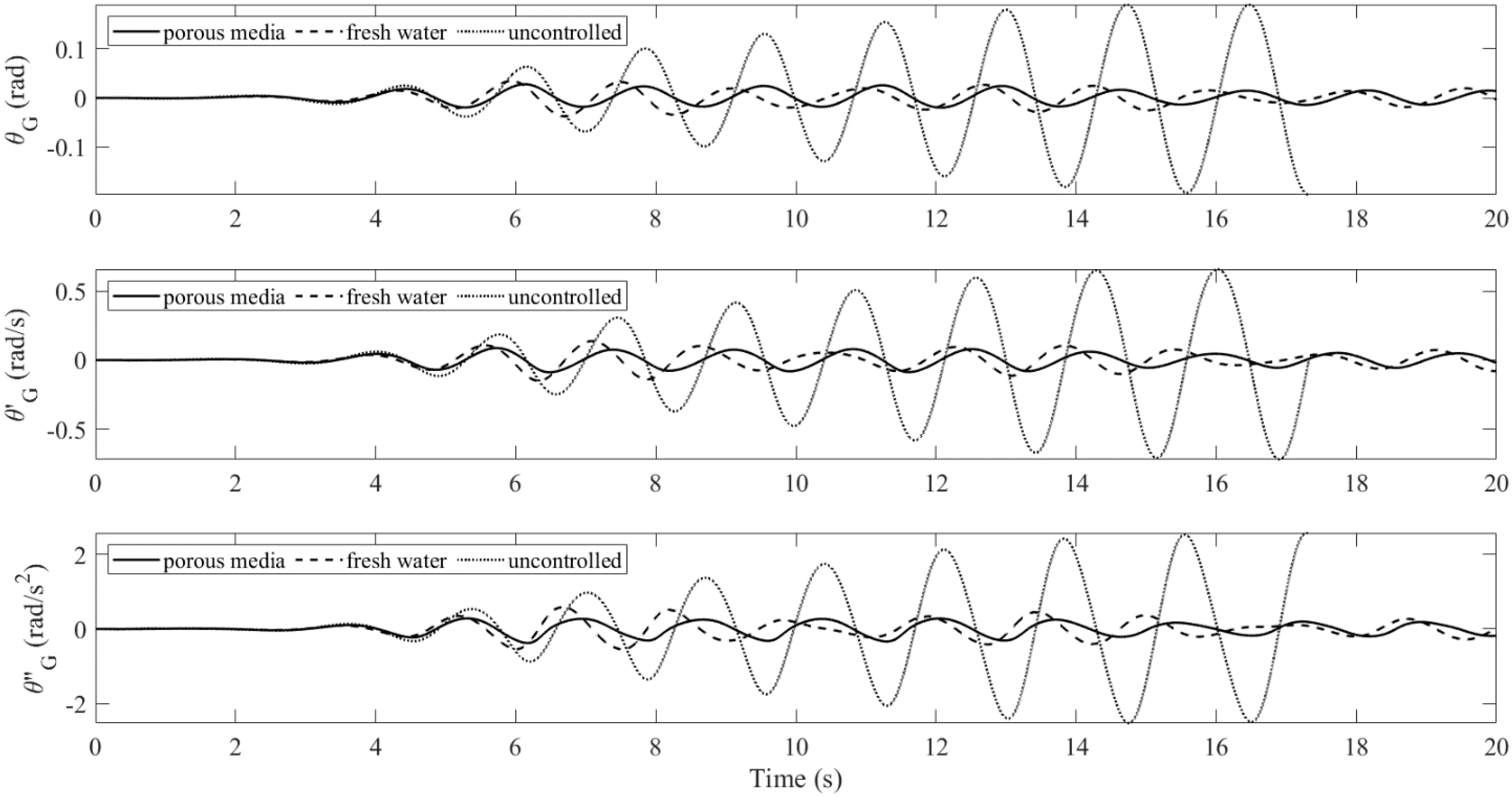
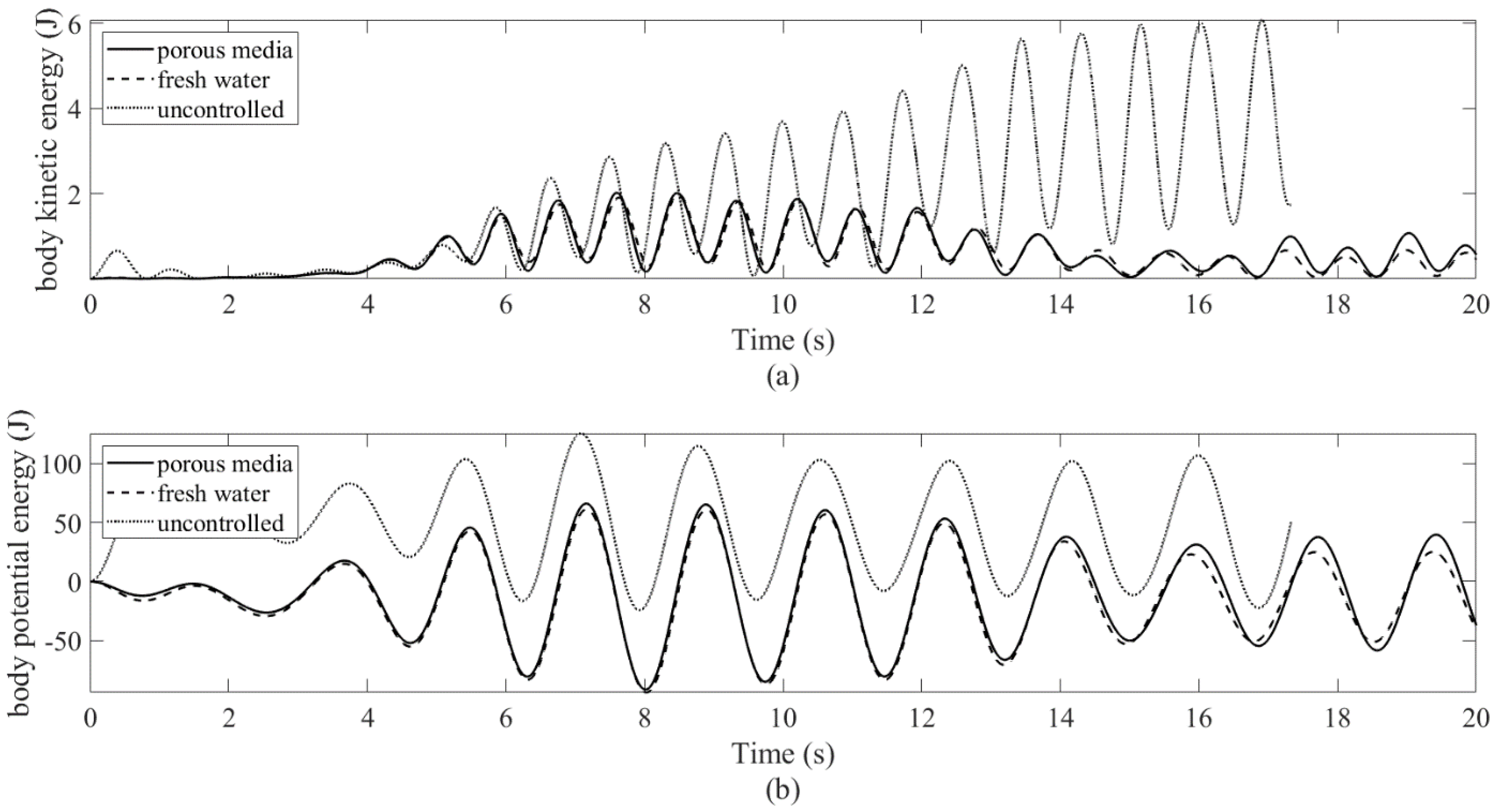
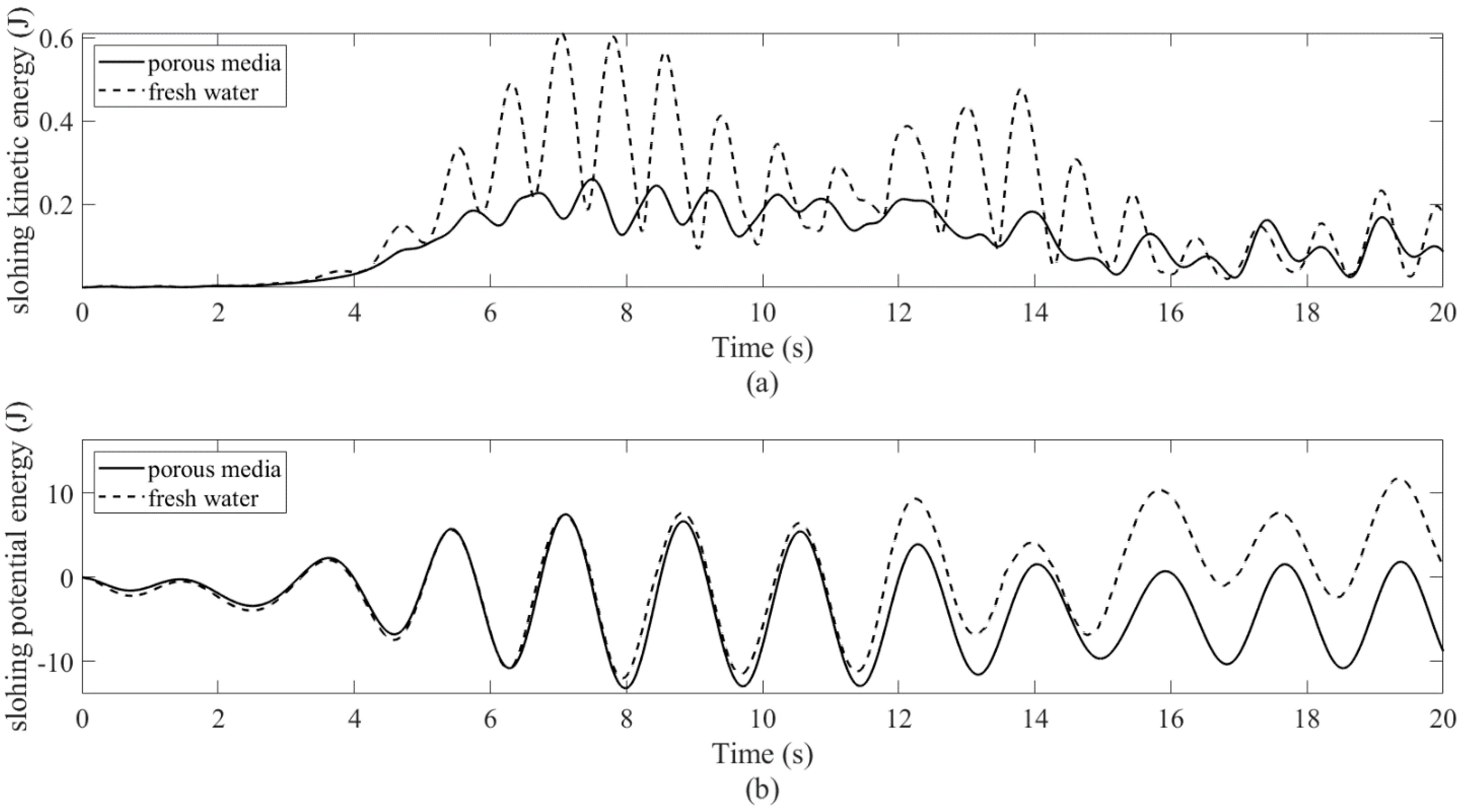
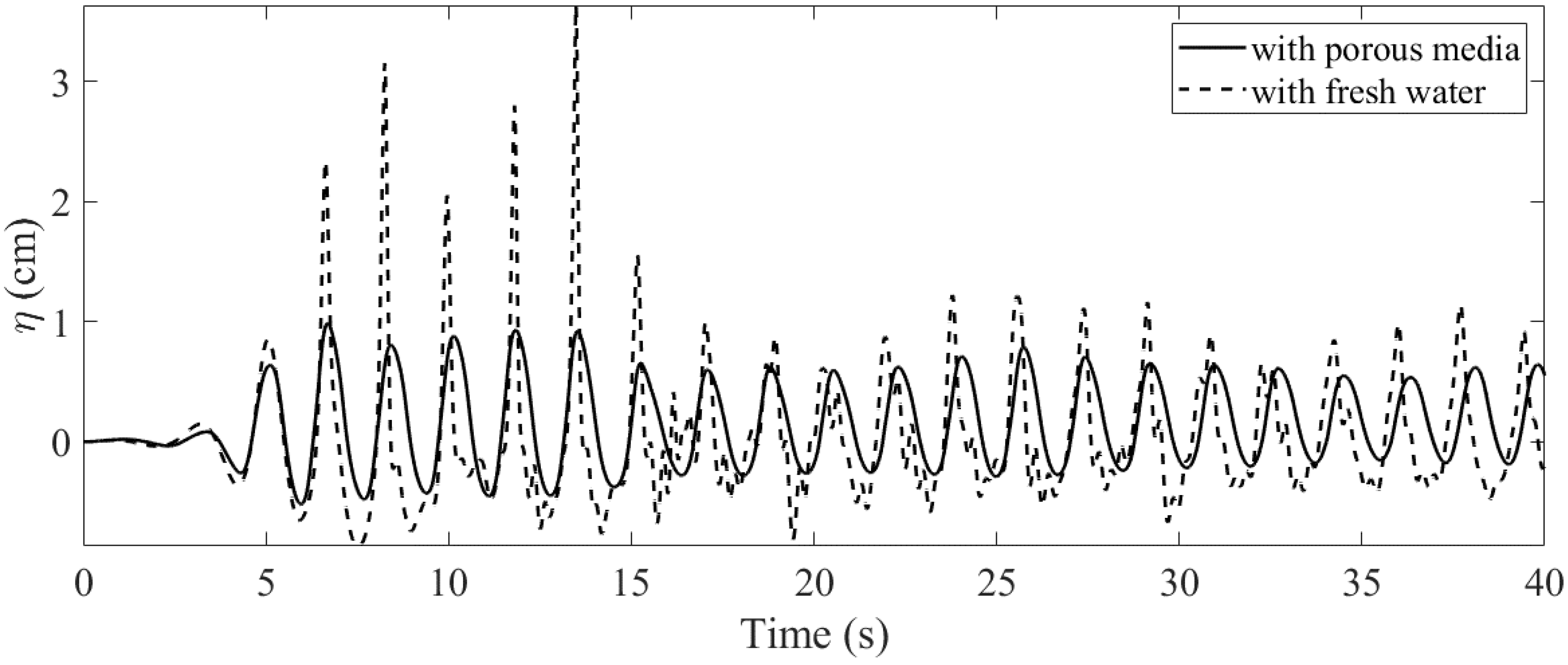
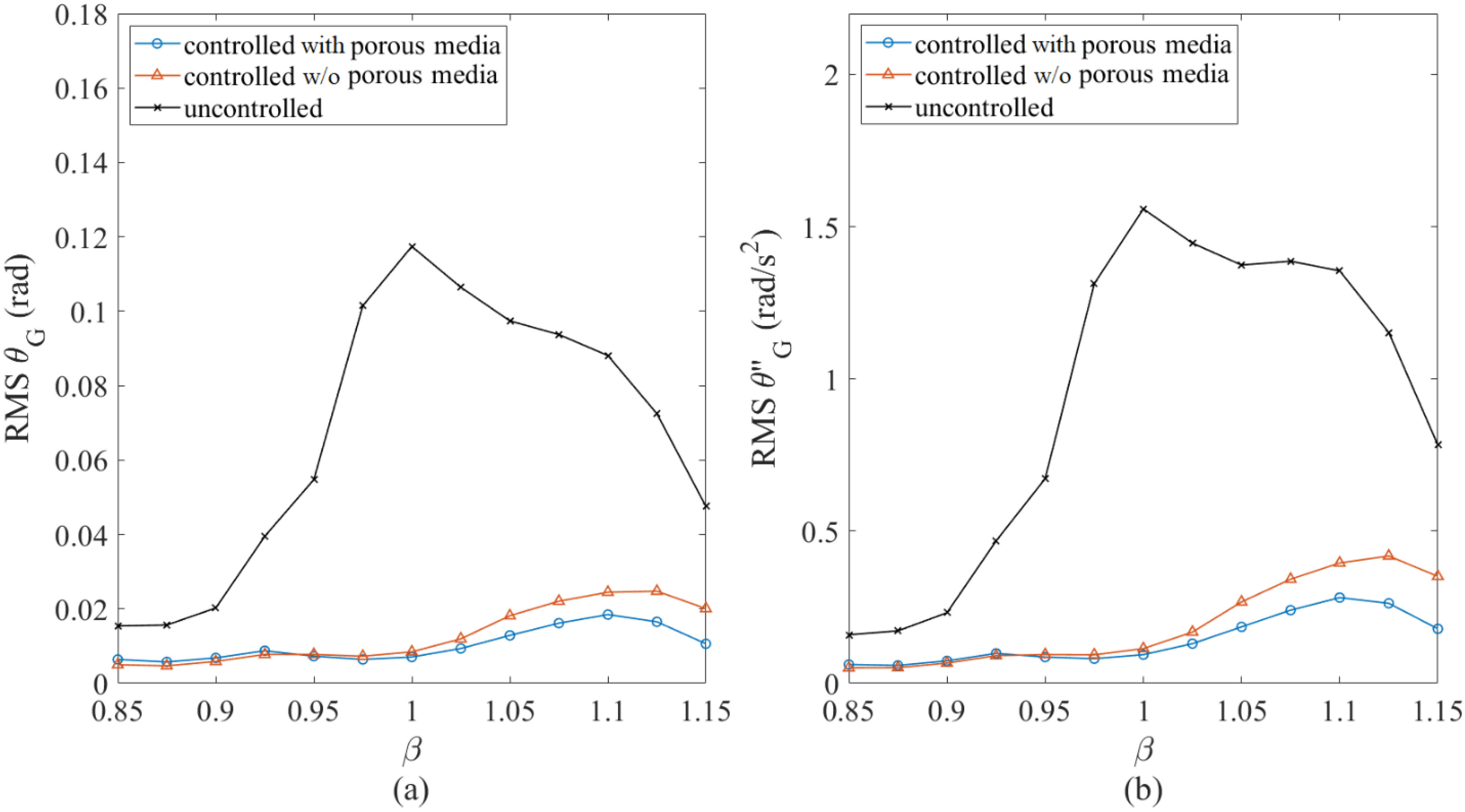
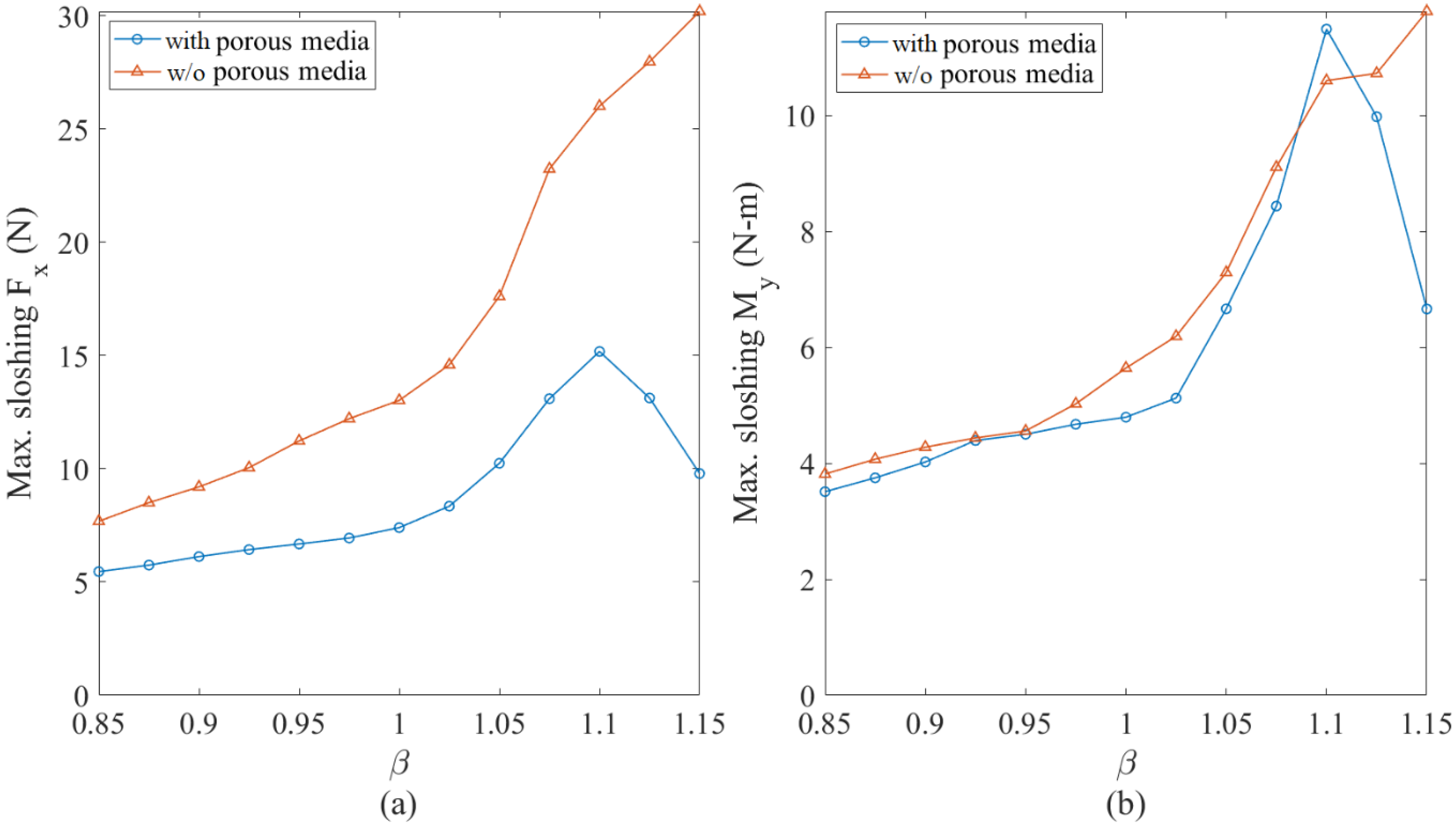
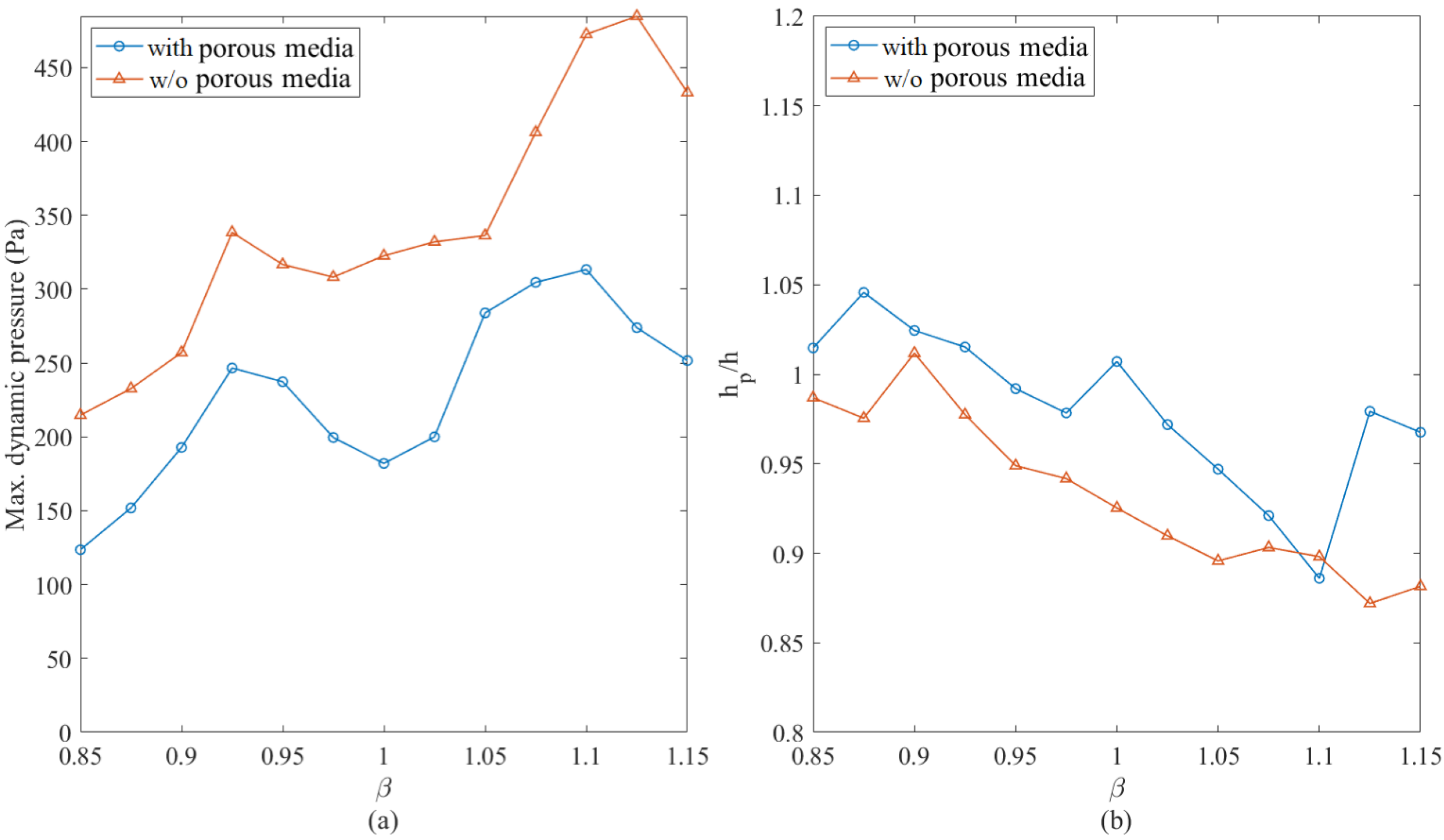
4.2. Floating Body in Resonant Waves: Controlled vs. Uncontrolled
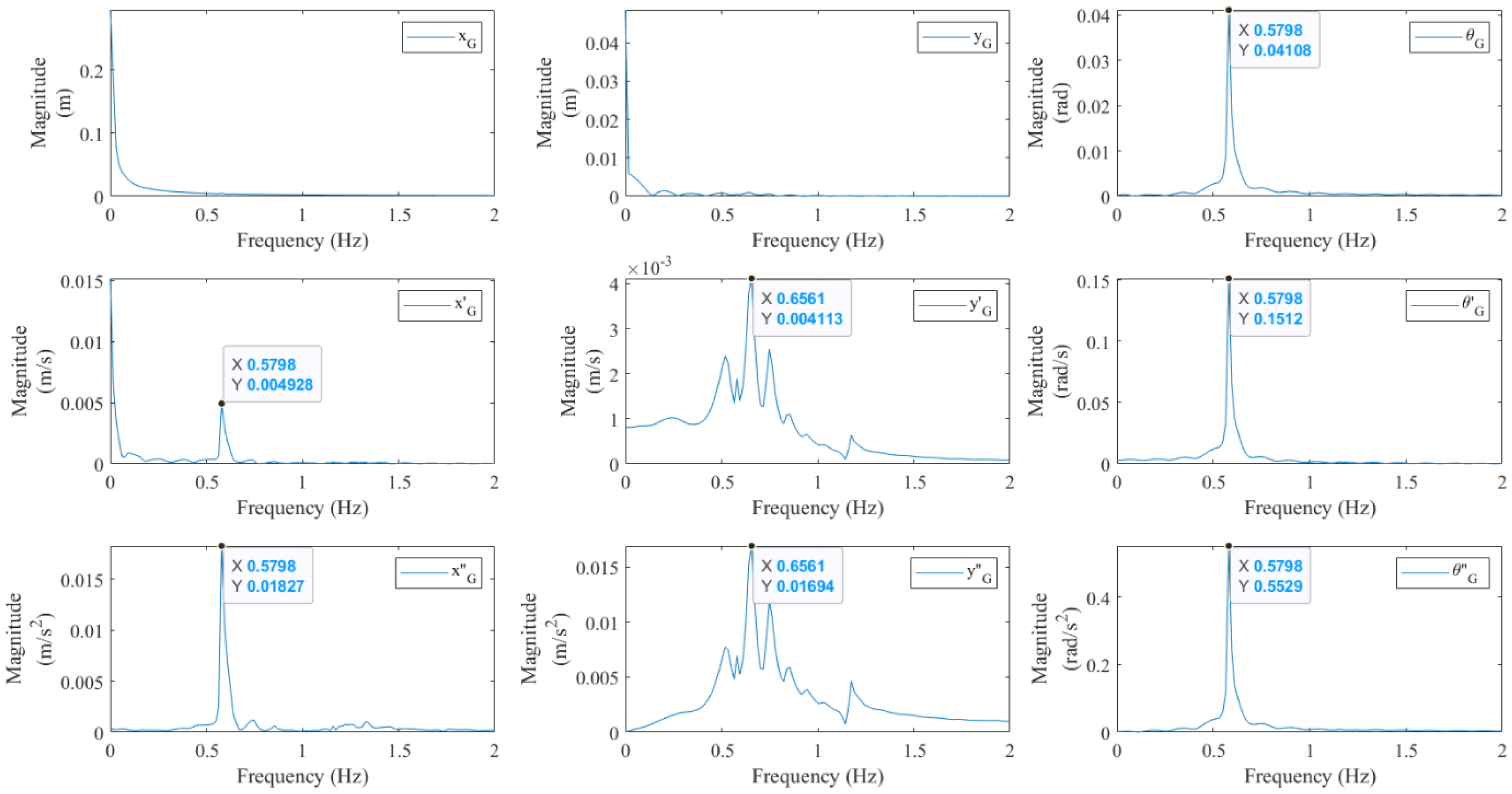
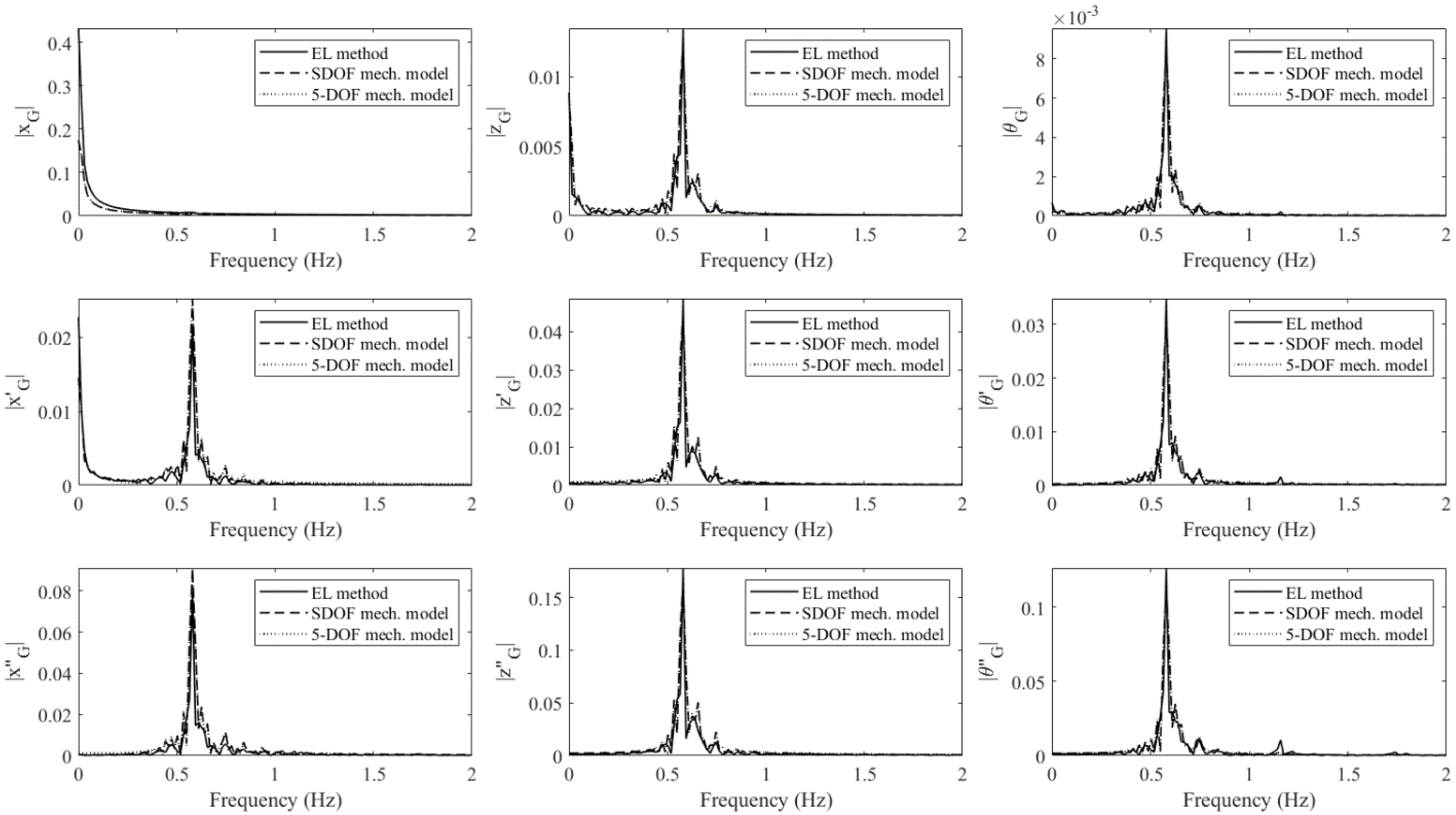
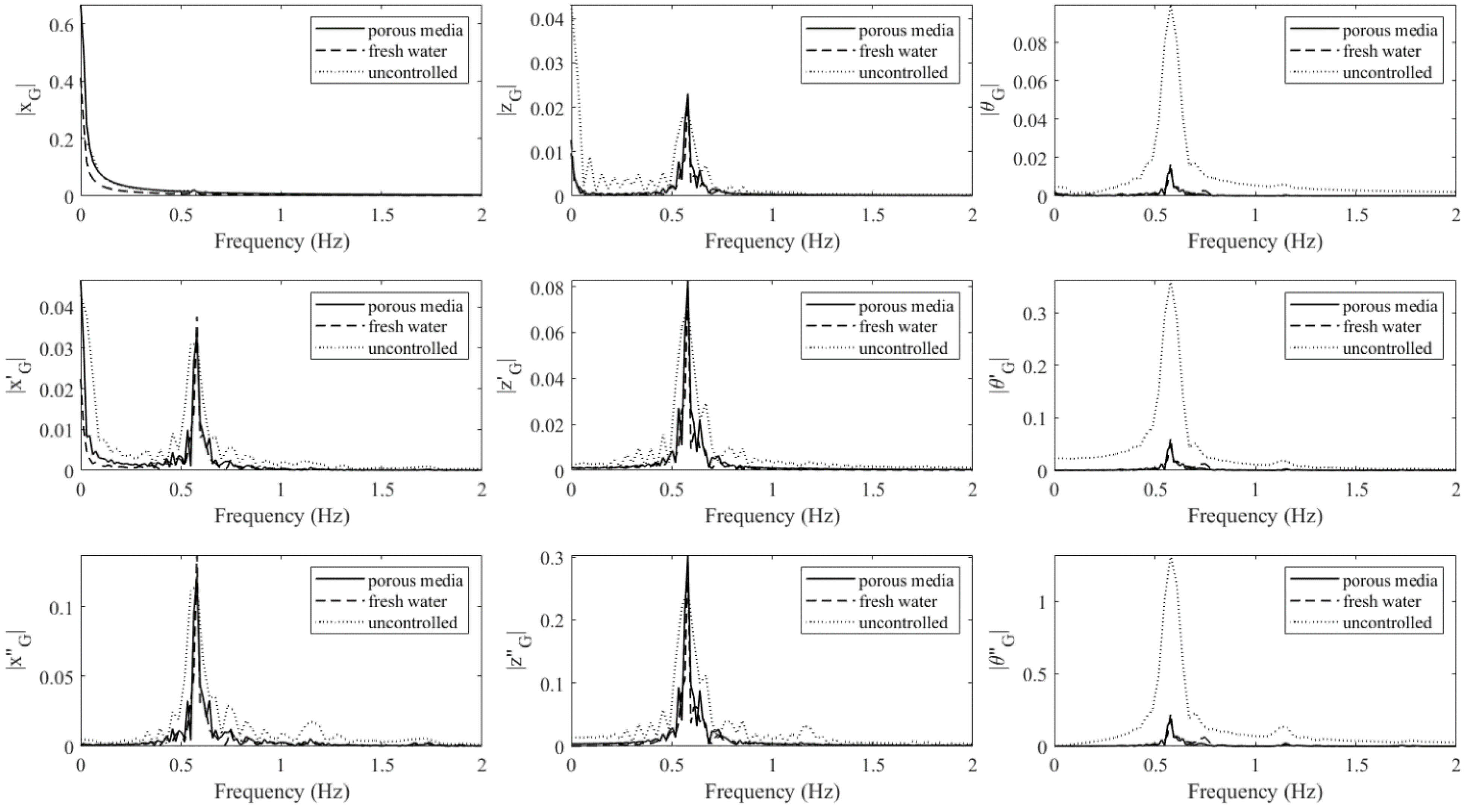
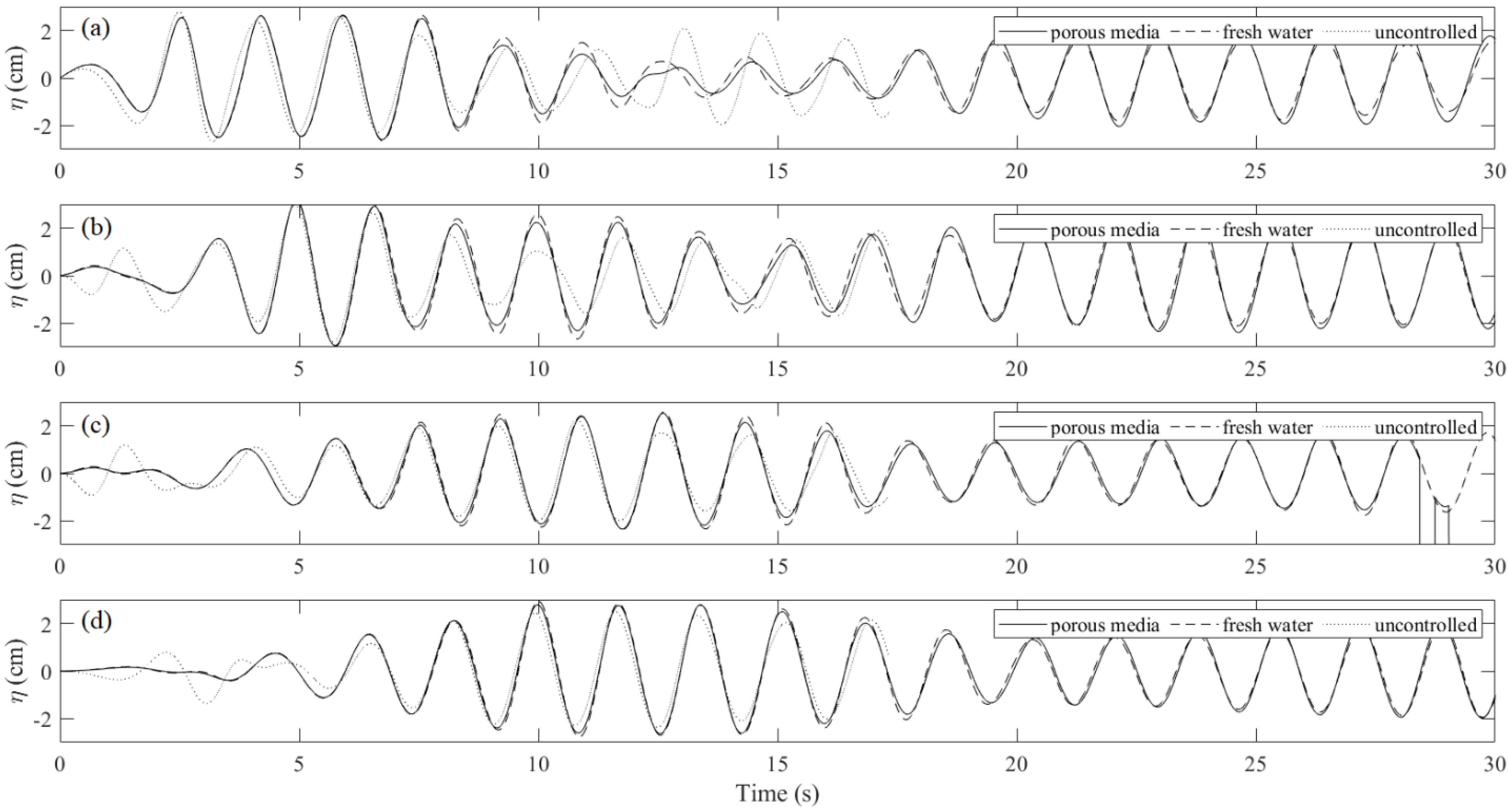
4.3. Frequency Response Analysis
5. Conclusions
- Porous media can accelerate the energy transmission in the FSI process, enhance the damping capability of the sloshing fluid, and reduce the sloshing velocity and deformation.
- The sloshing fluid will create a control force on the body. Under certain circumstances, it will cancel the wave loading. When it happens, the work done by incident waves is transferred to the fluid in the water tank (meanwhile, the wave-induced sloshing behavior appears), and then dissipated by the damping mechanism of porous media.
- The mechanical model produces linear sloshing reactions, which affects the accuracy of the amplitude of the body’s pitch motion for the large-wave case. However, it still captures the oscillatory frequencies very well. For the small-wave case, the difference is insignificant. When the tank is subject to pitch motion, the first modal sloshing response dominates.
- In the near-resonance tests, the average reduction in the RMS pitch motion by the porous-media TLD was 85%. It did not produce an effective control force for the heave motion. Moreover, the force cancellation in the horizontal motion was weak. Therefore, the application in surge mitigation is uncertain. Compared to the fresh-water TLD, the mistuning effect was alleviated.
- Porous media can effectively decrease the hydrodynamic pressure by up to 45%. The integrity of the liquid container and the stability of the liquid carrier can be improved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cariou, A.; Casella, G. Liquid sloshing in ship tanks: A comparative study of numerical simulation. Mar. Struct. 1999, 12, 183–198. [Google Scholar] [CrossRef]
- Kim, Y.; Nam, B.W.; Kim, D.W.; Kim, Y.S. Study on coupling effects of ship motion and sloshing. Ocean Eng. 2007, 34, 2176–2187. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, M.H.; Lee, D.H.; Kim, J.W.; Kim, Y.H. The effects of LNG-tank sloshing on the global motions of LNG carriers. Ocean Eng. 2007, 34, 10–20. [Google Scholar] [CrossRef]
- Lyu, W.J.; Riesner, M.; Peters, A.; Moctar, O. A hybrid method for ship response coupled with sloshing in partially filled tanks. Mar. Struct. 2019, 67, 102643. [Google Scholar] [CrossRef]
- Burger, W.; Corbet, A.G. Chapter III—Anti-Rolling Devices in General. In Ship Stabilizers: A Handbook for Merchant Navy Officers; 1966; pp. 31–37. Available online: https://www.sciencedirect.com/science/article/pii/B9780080115047500095 (accessed on 1 May 2022).
- Chen, Y.H.; Ko, C.H. Active tuned liquid column damper with propellers. Earthq. Eng. Struct. Dyn. 2003, 32, 1627–1638. [Google Scholar] [CrossRef]
- Yalla, S.K.; Kareem, A.; Kantor, J.C. Semi-active tuned liquid column dampers for vibration control of structures. Eng. Struct. 2001, 23, 1469–1479. [Google Scholar] [CrossRef]
- Marzouk, O.A.; Nayfeh, A.H. Control of ship roll using passive and active anti-roll tanks. Ocean Eng. 2009, 36, 661–671. [Google Scholar] [CrossRef]
- Gattulli, V.; Ghanem, R. Adaptive control of flow-induced oscillations including vortex effects. Int. J. Non-Linear Mech. 1999, 34, 853–868. [Google Scholar] [CrossRef]
- Kawano, K. Active control effects on dynamic response of offshore structures. In Proceedings of the Third International Offshore and Polar Engineering Conference, Singapore, 6–11 June 1993; pp. 594–598. [Google Scholar]
- Stewart, G.; Lackner, M. Offshore wind turbine load reduction employing optimal passive tuned mass damping systems. IEEE Trans. Control Syst. Technol. 2013, 21, 1090–1104. [Google Scholar] [CrossRef]
- Si, Y.; Karimi, H.R.; Gao, H. Modelling and optimization of a passive structural control design for a spar-type floating wind turbine. Eng. Struct. 2014, 69, 168–182. [Google Scholar] [CrossRef]
- Dinh, V.N.; Basu, B. Passive control of floating offshore wind turbine nacelle and spar vibrations by multiple tuned mass dampers. Struct. Control Health Monit. 2014, 22, 152–176. [Google Scholar] [CrossRef]
- Tong, X.; Zhao, X.; Karcanias, A. Passive vibration control of an offshore floating hydrostatic wind turbine model. Wind Energy 2018, 21, 697–714. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhan, G.; Zhao, Y. Application of spherical tuned liquid damper in vibration control of wind turbine due to earthquake excitations. Struct. Des. Tall Spec. Build. 2016, 25, 431–443. [Google Scholar] [CrossRef]
- Chen, Y.H.; Hwang, W.S.; Tsao, W.H. Nonlinear dynamic characteristics of rectangular and cylindrical TLD’s. J. Eng. Mech. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Zahrai, S.M.; Abbasi, S.; Samali, B.; Vrcelj, Z. Experimental investigation of utilizing TLD with baffles in a scaled down 5-story benchmark building. J. Fluids Struct. 2012, 28, 194–210. [Google Scholar] [CrossRef]
- Warnitchai, P.; Pinkaew, T. Modelling of liquid sloshing in rectangular tanks with flow-dampening devices. Eng. Struct. 1998, 20, 293–600. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Firoozkoohi, R.; Timokha, A.N. Analytical modeling of liquid sloshing in a two-dimensional rectangular tank with a slat screen. J. Eng. Math. 2011, 70, 93–109. [Google Scholar] [CrossRef] [Green Version]
- Hamelin, J.; Love, J.; Tait, M.; Wison, J. Tuned liquid dampers with a Keulegan-Carpenter number-dependent screen drag coefficient. J. Fluids Struct. 2013, 43, 271–286. [Google Scholar] [CrossRef]
- Tait, M.J. Modelling and preliminary design of a structure-TLD system. Eng. Struct. 2008, 30, 2644–2655. [Google Scholar] [CrossRef]
- Tsao, W.H.; Hwang, W.S. Tuned liquid dampers with porous media. Ocean Eng. 2018, 167, 55–64. [Google Scholar] [CrossRef]
- Tsao, W.H.; Hwang, W.S. Dynamic characteristics of liquid sloshing in cylindrical tanks filled with porous media. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 351. [Google Scholar]
- Tsao, W.H.; Chang, T.J. Sloshing phenomenon in rectangular and cylindrical tanks filled with porous media: Supplementary solution and impulsive-excitation experiment. J. Eng. Mech. 2020, 146, 04020139. [Google Scholar] [CrossRef]
- Tsao, W.H.; Huang, L.H.; Hwang, W.S. An equivalent mechanical model with nonlinear damping for sloshing rectangular tank with porous media. Ocean Eng. 2021, 242, 110145. [Google Scholar] [CrossRef]
- Tsao, W.H.; Huang, Y.L. Sloshing force in a rectangular tank with porous media. Results Eng. 2021, 11, 100250. [Google Scholar] [CrossRef]
- Sen, D. Numerical simulation of motions of two-dimensional floating bodies. J. Ship Res. 1993, 37, 307–330. [Google Scholar] [CrossRef]
- Van Daalen, E.F.G. Numerical and Theoretical Studies of Water Waves and Floating Bodies. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 1993. [Google Scholar]
- Tanizawa, K. A nonlinear simulation method of 3D body motions in waves. J. Soc. Nav. Archit. Jpn. 1995, 178, 179–191. [Google Scholar] [CrossRef]
- Jung, K.H.; Chang, K.A.; Jo, H.J. Viscous effect on the roll motion of a rectangular structure. J. Eng. Mech. 2006, 132, 190–200. [Google Scholar] [CrossRef]
- Guerber, E.; Benoit, M.; Grilli, S.T.; Buvat, C. A fully nonlinear implicit model for wave interactions with submerged structures in forced or free motion. Eng. Anal. Bound. Elem. 2012, 36, 1151–1163. [Google Scholar] [CrossRef] [Green Version]
- Dombre, E.; Benoit, M.; Violeau, D.; Peyrard, C.; Grilli, S.T. Simulation of floating structure dynamics in waves by implicit coupling of a fully non-linear potential flow model and a rigid body motion approach. J. Ocean Eng. Mar. Energy 2015, 1, 55–76. [Google Scholar] [CrossRef] [Green Version]
- Vinje, T.; Brevig, P. Nonlinear, Two-Dimensional Ship Motions; Technical Report; Norwegian Institute of Technology: Trondheim, Norway, 1981; p. R-112.81. [Google Scholar]
- Belibassakis, K.A. A boundary element method for the hydrodynamic analysis of floating bodies in variable bathymetry regions. Eng. Anal. Bound. Elem. 2008, 32, 796–810. [Google Scholar] [CrossRef]
- Wu, G.X.; Eatock-Taylor, R. Transient motion of a floating body in steep water waves. In Proceedings of the 11th Workshop on Water Waves and Floating Bodies, Hamburg, Germany, 17–20 March 1996. [Google Scholar]
- Matthies, H.G.; Niekamp, R.; Steindorf, J. Algorithms for strong coupling procedures. Comput. Methods Appl. Mech. Eng. 2006, 195, 2028–2049. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Paredes, G.M.; Bergdahl, L. Coupled mooring analysis of floating wave energy converters using CFD: Formulation and Validation. Int. J. Mar. Energy 2016, 16, 83–99. [Google Scholar] [CrossRef] [Green Version]
- Tezduyar, T.E. Finite element methods for flow problems with moving boundaries and interfaces. Comput. Methods Eng. 2001, 8, 83–130. [Google Scholar] [CrossRef]
- Rakhsha, M.; Kees, C.E.; Negrut, D. Lagrangian vs. Eulerian: An analysis of two solution methods for free-surface flows and fluid solid interaction problems. Fluids 2021, 6, 460. [Google Scholar] [CrossRef]
- Karimirad, M.; Michailides, C.; Nematbakhsh, A. Offshore Mechanics: Structural and Fluid Dynamics for Recent Applications. 2018. Available online: https://www.wiley.com/en-us/Offshore+Mechanics%3A+Structural+and+Fluid+Dynamics+for+Recent+Applications-p-9781119216629 (accessed on 1 May 2022).
- Grilli, S.T.; Skourup, J.; Svendsen, I.A. An efficient boundary element method for nonlinear water waves. Eng. Anal. Bound. Elem. 1989, 6, 97–107. [Google Scholar] [CrossRef]
- Grilli, S.T.; Horrillo, J. Numerical generation and absorption of fully nonlinear periodic waves. J. Eng. Mech. 1997, 123, 1060–1069. [Google Scholar] [CrossRef] [Green Version]
- Tsao, W.H.; Kinnas, S.A. Local simulation of sloshing jet in a rolling tank by viscous-inviscid interaction method. Results Eng. 2021, 11, 100270. [Google Scholar] [CrossRef]
- Nield, A.D.; Bejan, A. Convection in Porous Media, 4th ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Ursell, F.; Dean, R.G.; Yu, Y.S. Forced small-amplitude water waves: A comparison of theory and experiment. J. Fluid Mech. 1960, 7, 33–52. [Google Scholar] [CrossRef]
- Chen, Y.H.; Hwang, W.S.; Tsao, W.H. Nonlinear sloshing analysis by regularized boundary integral method. J. Eng. Mech. 2017, 143, 040170046. [Google Scholar] [CrossRef]
- Currie, I.G. Fundamental Mechanics of Fluids, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Delorme, L.; Colagrossi, A.; Souto-Iglesias, A.; Zamora-Rodríguez, R.; Botia-Vera, E. A set of canonical problems in sloshing, Part I: Pressure field in forced roll comparison between experimental results and SPH. Ocean Eng. 2009, 36, 168–178. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsao, W.-H.; Chen, Y.-C.; Kees, C.E.; Manuel, L. The Effect of Porous Media on Wave-Induced Sloshing in a Floating Tank. Appl. Sci. 2022, 12, 5587. https://doi.org/10.3390/app12115587
Tsao W-H, Chen Y-C, Kees CE, Manuel L. The Effect of Porous Media on Wave-Induced Sloshing in a Floating Tank. Applied Sciences. 2022; 12(11):5587. https://doi.org/10.3390/app12115587
Chicago/Turabian StyleTsao, Wen-Huai, Ying-Chuan Chen, Christopher E. Kees, and Lance Manuel. 2022. "The Effect of Porous Media on Wave-Induced Sloshing in a Floating Tank" Applied Sciences 12, no. 11: 5587. https://doi.org/10.3390/app12115587
APA StyleTsao, W.-H., Chen, Y.-C., Kees, C. E., & Manuel, L. (2022). The Effect of Porous Media on Wave-Induced Sloshing in a Floating Tank. Applied Sciences, 12(11), 5587. https://doi.org/10.3390/app12115587






