5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation
Abstract
:1. Introduction
2. Background and Index Terms
2.1. One Dimensional Gauss Map
2.2. Classification of Encrypted Images
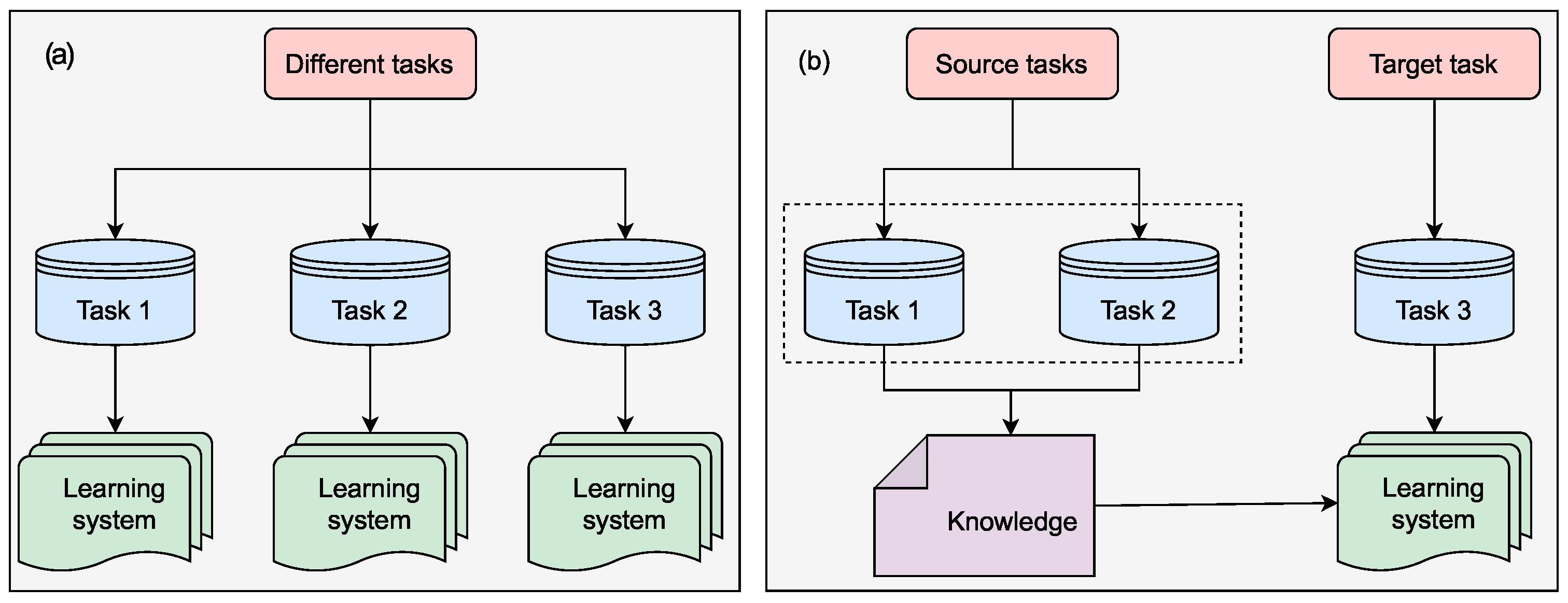
2.3. Transfer Learning vs. Machine Learning
- It allows you to train systems with less labeled data by reusing popular models that have previously been trained on massive datasets, making transfer learning a popular approach;
- It has the potential to cut down on training time and computer resources. The weights are not learned from starting with transfer learning since the pre-trained model has previously learned them based on earlier learning;
- You can use model topologies produced by the deep learning scientific community, such as AlexNet, GoogLeNet, and ResNet, which are popular designs
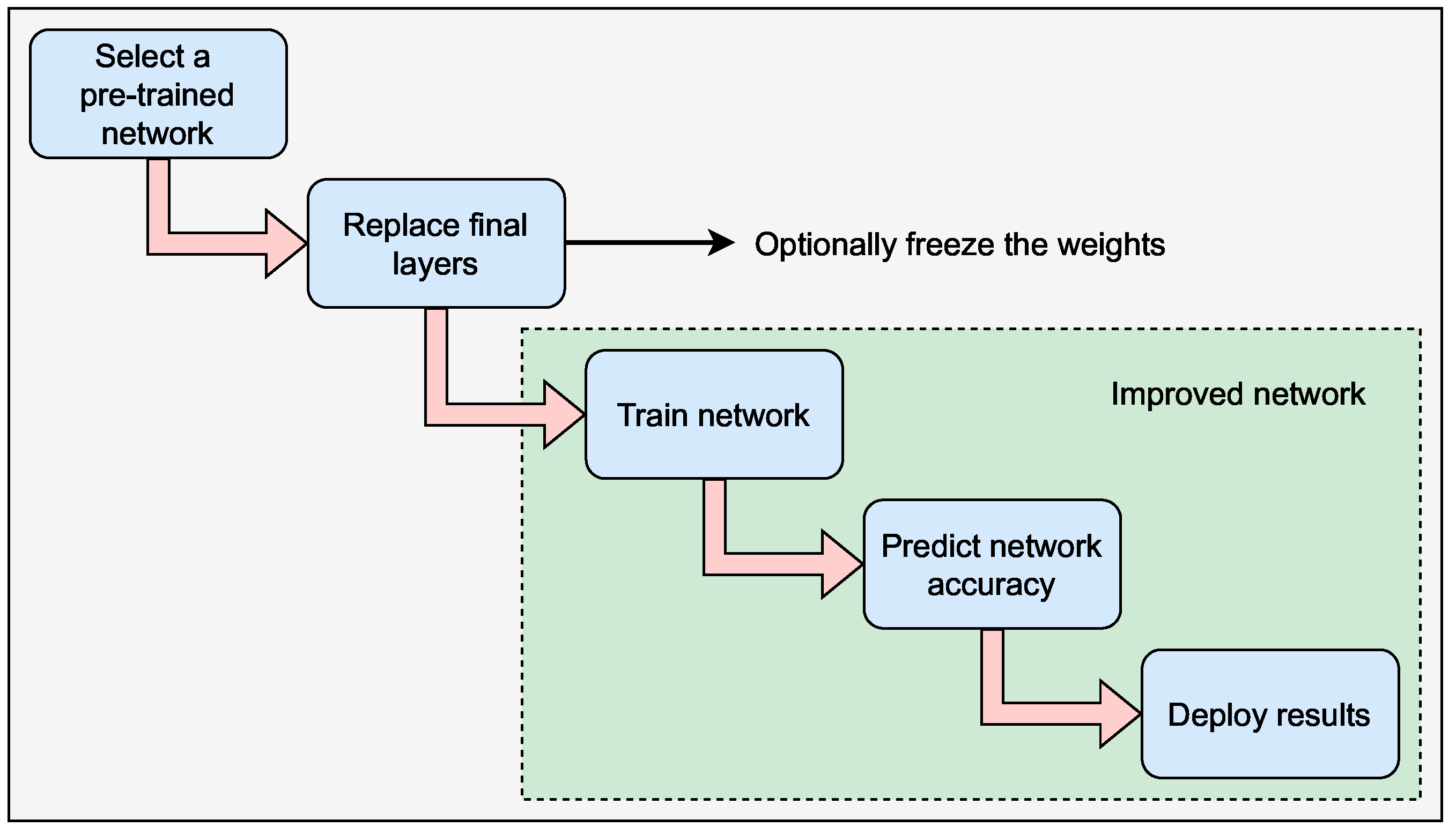
- 1.
- Selecting a pre-trained model: It is simpler to function with pre-trained models since there are many of them accessible on multiple platforms such as Googlenet, Squeezenet, and others;
- 2.
- Replacement of final layers: The final layers of the chosen pre-trained model are changed to retrain the network and to categorize a fresh batch of images and classes. The final wholly linked layer is changed to get a similar number of nodes as the number of new classes and a new classification layer that will provide an output based on the probabilities estimated by the layer. The final wholly linked layer will describe the new number of network classes that will it learn after the layers have been modified. The classification layer will select outputs from the new output categories accessible after modifying the layers;
- 3.
- Freezing the weights (Optional): By limiting the learning rates in such layers to zero, the weights of earlier layers in the network may be frozen. As a result, the characteristics of frozen layers are not modified throughout training; this significantly accelerates network training. In addition, freezing weights can help the network prevent overfitting if the new data set is tiny;
- 4.
- Retraining the model. The network will be retrained to understand and recognize the attributes associated with the new data and categories. Retraining usually needs less data than training a model from the start;
- 5.
- Predicting and assessing network accuracy. For example, one may classify fresh images and evaluate how well the network works once the model has been retrained [22].
2.4. Deep Network Designing with MATLAB
- Time Series Forecasting;
- Classification of Sequences;
- Regression from one sequence to the next;
- Classification of Text Data;
- Classification of Image Data;
- Semantic Segmentation of Multispectral Images;
- Speech Recognition;
- Image Deblocking;
- Removing noise from a Color Image Using Pretrained models, and so on.
2.5. Transfer Learning Using AlexNet
3. Proposed Method
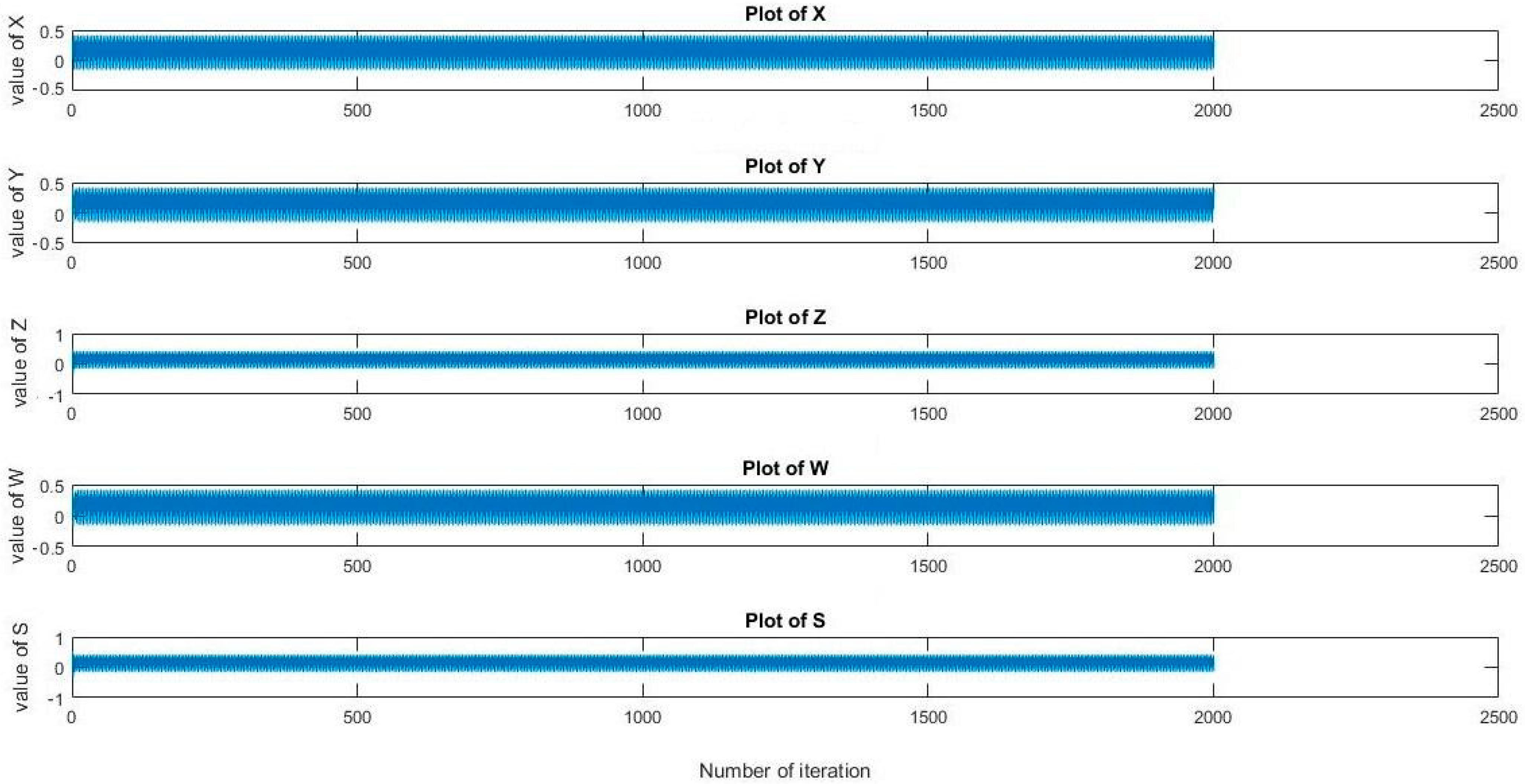
3.1. 5D Gauss Map Equation and Plot (Iteration)
3.2. Algorithm for Image Encryption
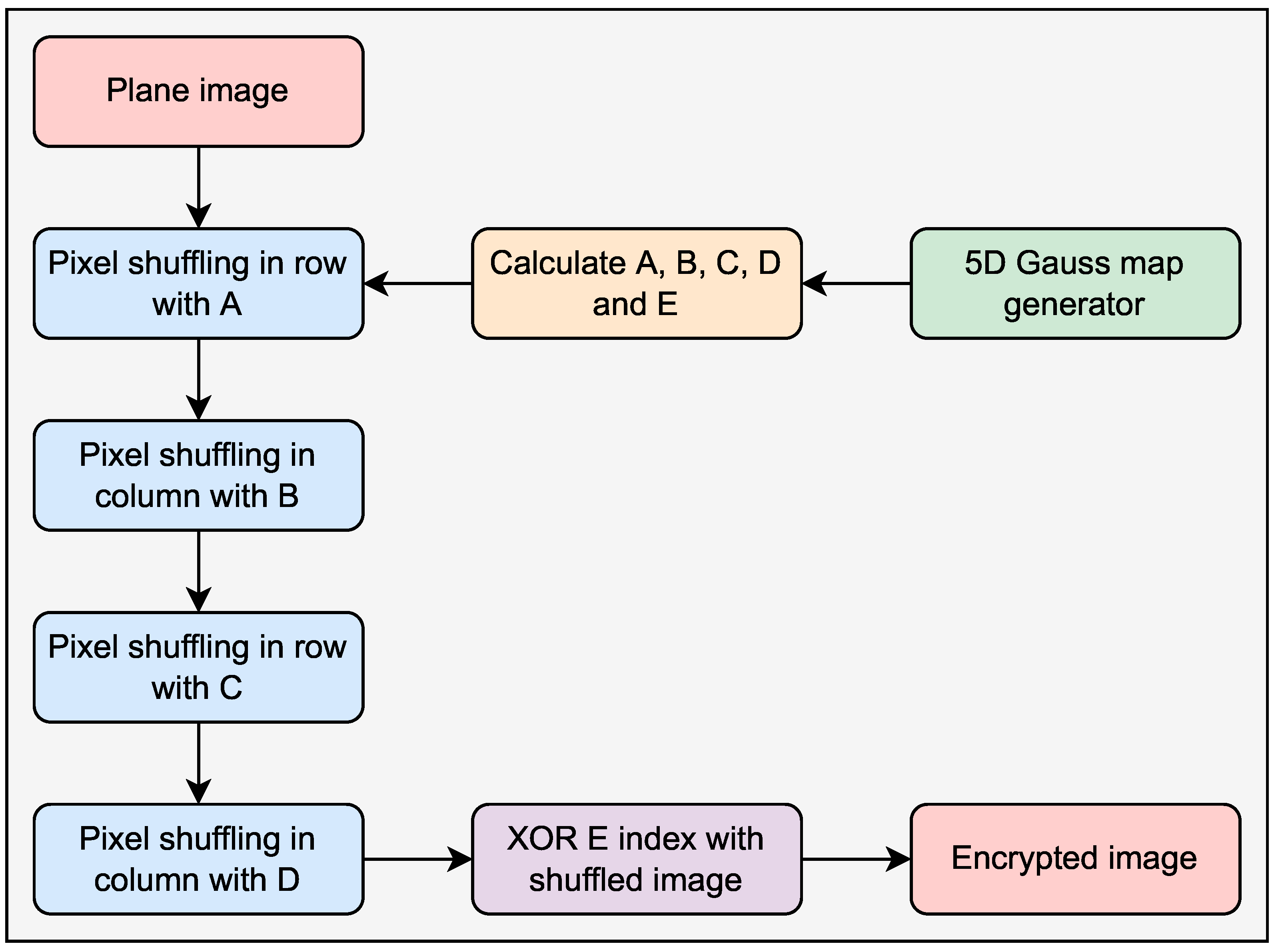
3.2.1. 5D Gauss Generator
3.2.2. Permutation
- Random numbers are selected to achieve pixel permutation, P, Q, and R;
- With the help of these numbers, five sequences or indexes A, B, C, D, and E are generated;
- A pixel is shuffled in a row with sequence A and in a column with sequence B to create confusion;
- Here two times shuffling is done with row and column, the first time with A, B sequence and the second time with C and D sequence;
- The XOR process is the final stage in this encryption procedure. When using the XOR technique, the pixel intensities are changed to a new one, which cannot be inverted unless having the chaos key.
- Step 1: Read plaintext image I (the image size is set to pixels);
- Step 3: Using random numbers and chaotic sequences, generate index sequences A, B, C, D, and E;
- Step 4: To produce a confusion matrix, bring the index sequence A from Step 1 and shuffle the pixels in rows and columns with sequence B;
- Step 5: Pixels are shuffled in the row with sequence C and in the column with sequence D once more, resulting in scrambled image ;
- Step 6: The index sequence E is then XORed with the scrambled image , resulting in the encrypted image.
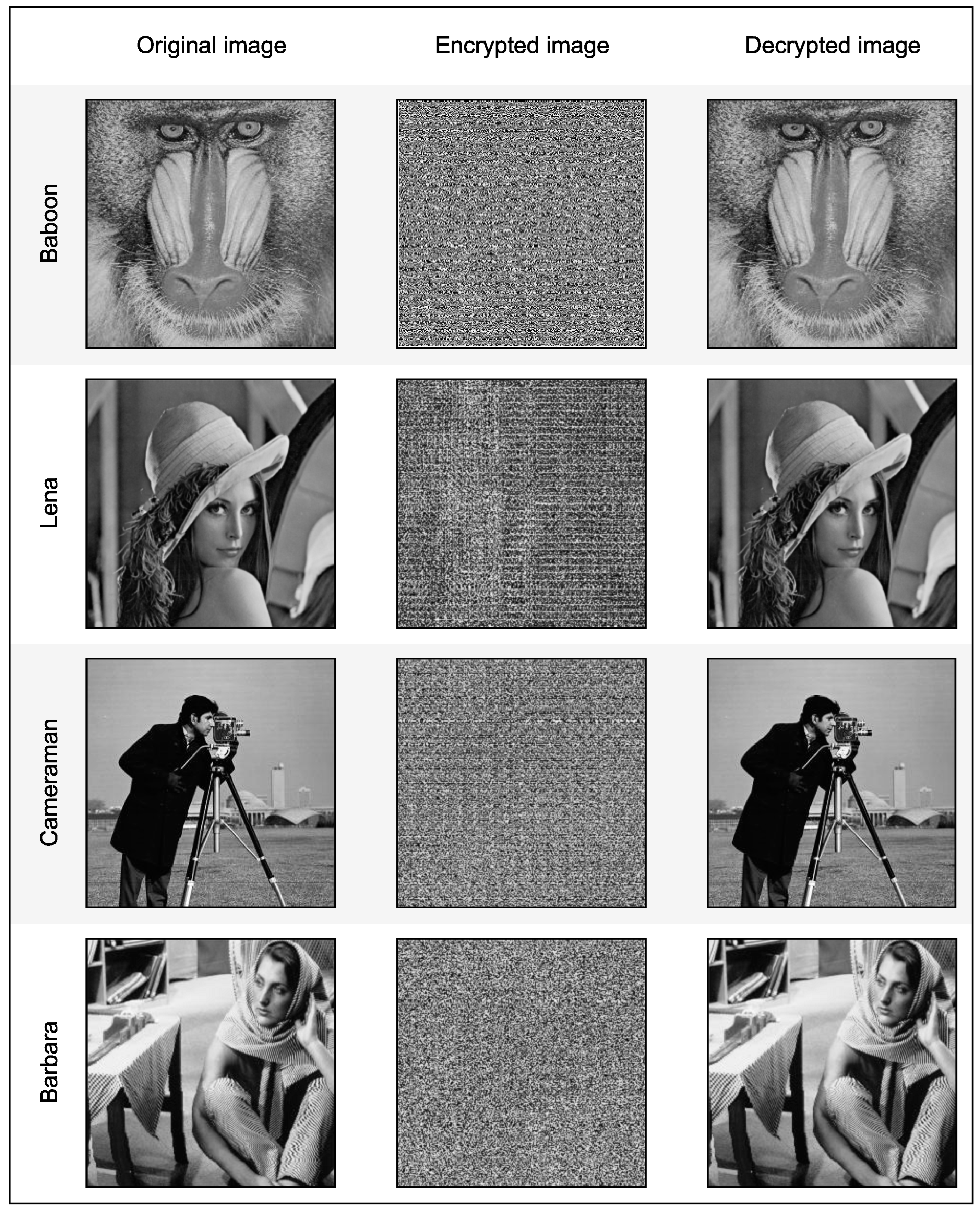
4. Results and Facts
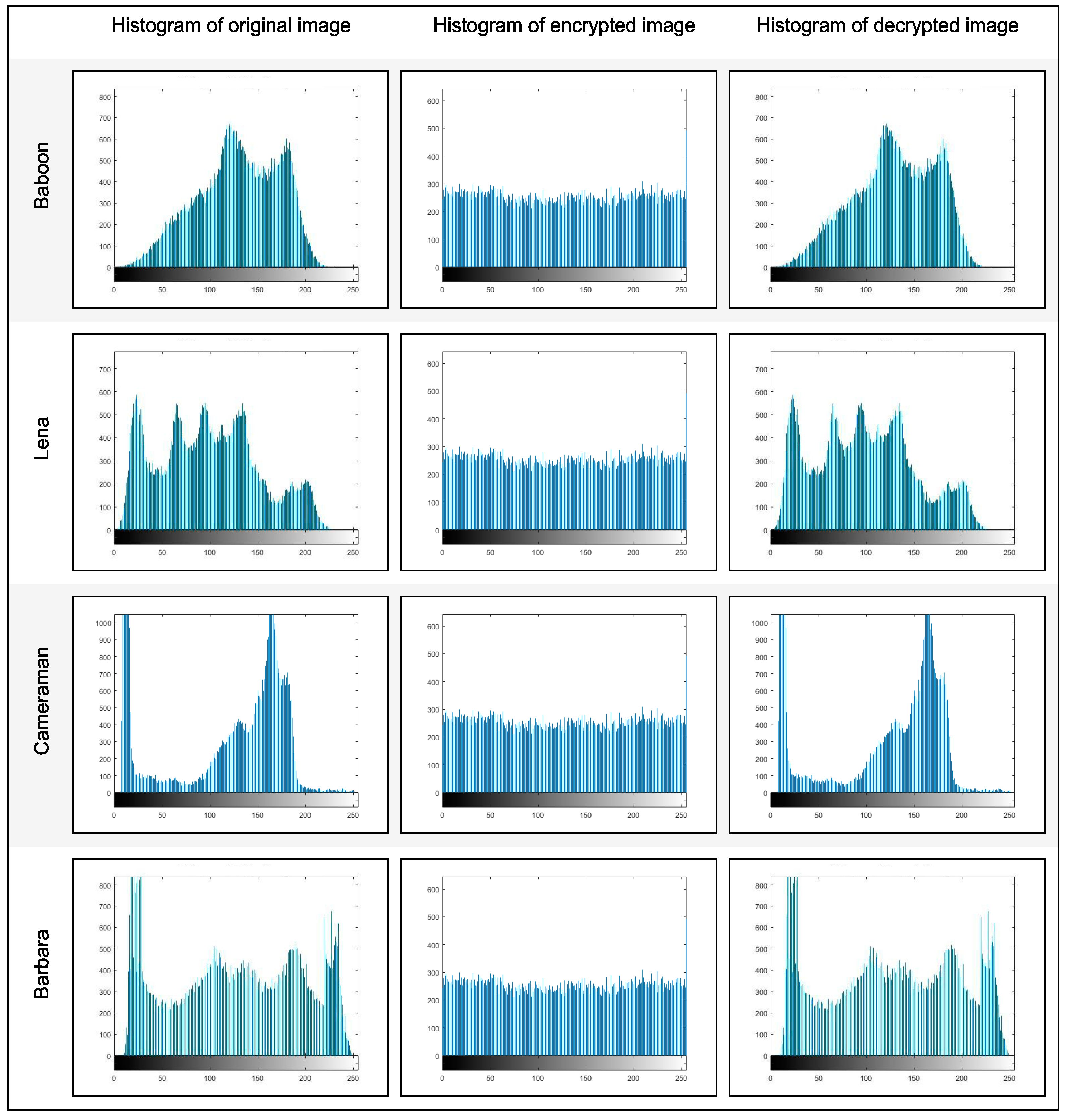
4.1. Information Entropy
4.2. Correlation Coefficient (CC)
4.3. PSNR, MSE, and SSIM
4.4. Differential Attack
4.5. Keyspace
4.6. Noise and Cropping Attack
4.7. NIST Test
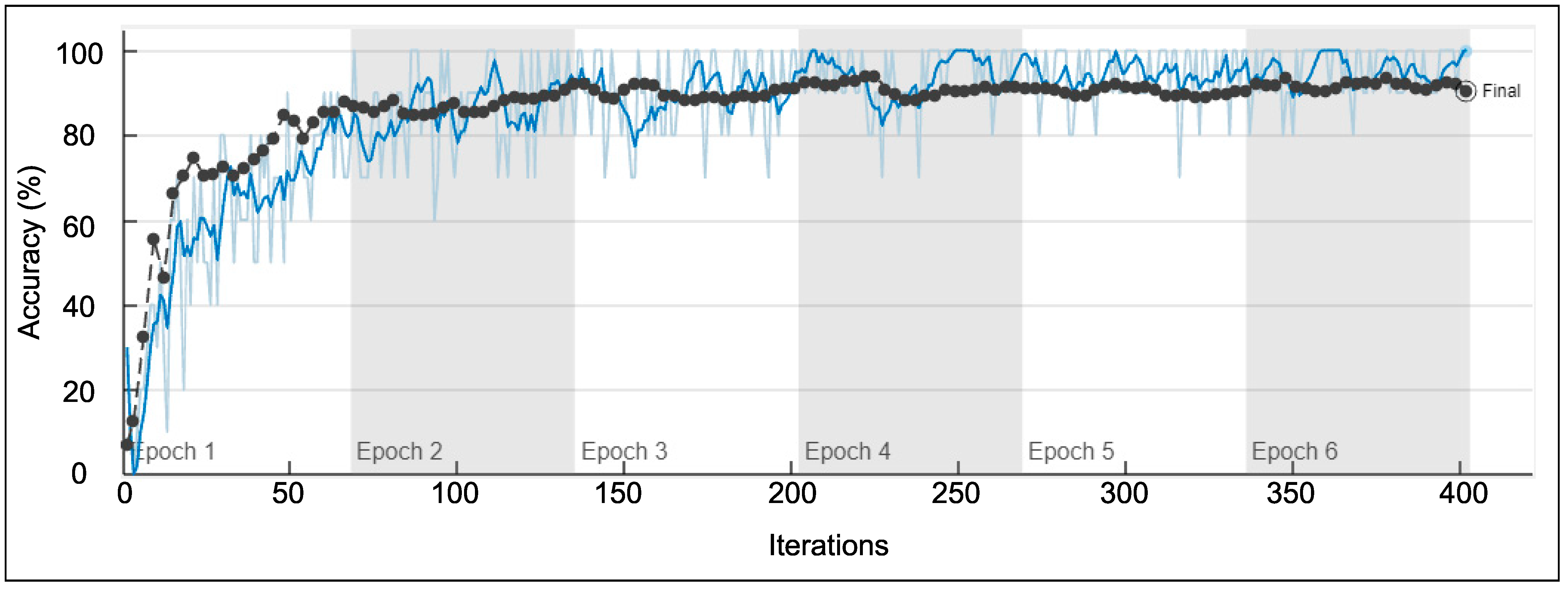
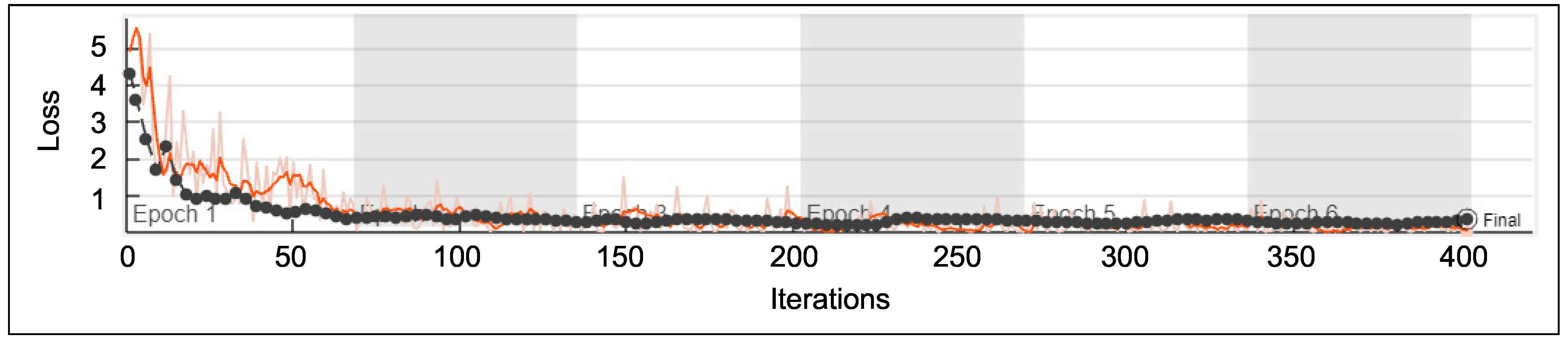
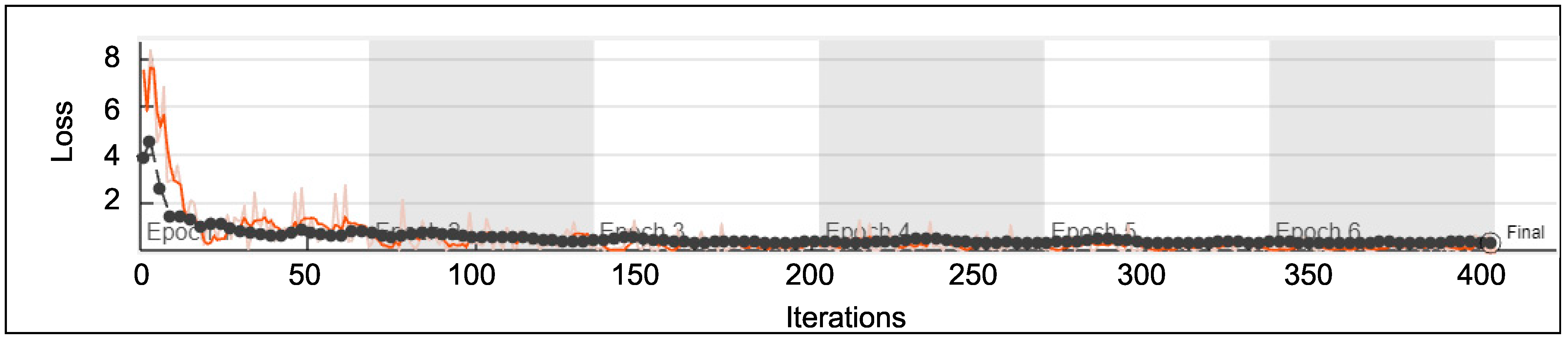
5. Validation of Classification Accuracy
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| 5D | Five Dimensional |
| 1D | One Dimensional |
| AES | Advanced Encryption Standard |
| ANN | Artificial Neural Network |
| CC | Correlation Coefficients |
| CNN | Convolutional Neural Network |
| D | Diagonal |
| DES | Data Encryption Standard |
| H | Horizontal |
| HD | High Dimensional |
| MSE | Mean Square Error |
| PSNR | Peak Signal to Noise Ratio |
| SAE | Sparse Auto Encoder |
| SSIM | Structural Similarity Index Measure |
| V | Vertical |
References
- Wong, K.W.; Kwok, B.S.H.; Yuen, C.H. An efficient diffusion approach for chaos-based image encryption. Chaos Solitons Fractals 2009, 41, 2652–2663. [Google Scholar] [CrossRef] [Green Version]
- Patro, K.A.K.; Acharya, B.; Nath, V. Secure, lossless, and noise-resistive image encryption using chaos, hyper-chaos, and DNA sequence operation. IETE Tech. Rev. 2020, 37, 223–245. [Google Scholar] [CrossRef]
- Liu, W.; Sun, K.; Zhu, C. A fast image encryption algorithm based on chaotic map. Opt. Lasers Eng. 2016, 84, 26–36. [Google Scholar] [CrossRef]
- Yu, C.; Li, H.; Wang, X. SVD-based image compression, encryption, and identity authentication algorithm on cloud. IET Image Process. 2019, 13, 2224–2232. [Google Scholar] [CrossRef]
- Bisht, A.; Dua, M.; Dua, S.; Jaroli, P. A color image encryption technique based on bit-level permutation and alternate logistic maps. J. Intell. Syst. 2020, 29, 1246–1260. [Google Scholar] [CrossRef]
- Veena, G.; Ramakrishna, M. A survey on image encryption using chaos-based techniques. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 379–384. [Google Scholar]
- Jridi, M.; Alfalou, A. Real-time and encryption efficiency improvements of simultaneous fusion, compression and encryption method based on chaotic generators. Opt. Lasers Eng. 2018, 102, 59–69. [Google Scholar] [CrossRef]
- Faragallah, O.S.; Afifi, A.; El-Shafai, W.; El-Sayed, H.S.; Naeem, E.A.; Alzain, M.A.; Al-Amri, J.F.; Soh, B.; Abd El-Samie, F.E. Investigation of chaotic image encryption in spatial and FrFT domains for cybersecurity applications. IEEE Access 2020, 8, 42491–42503. [Google Scholar] [CrossRef]
- Tang, Z.; Yang, Y.; Xu, S.; Yu, C.; Zhang, X. Image encryption with double spiral scans and chaotic maps. Secur. Commun. Netw. 2019, 2019, 8694678. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.R.; Xiao, Z.Y. Image encryption algorithm based on compressive sensing and fractional DCT via polynomial interpolation. Int. J. Autom. Comput. 2020, 17, 292–304. [Google Scholar] [CrossRef]
- Sahay, A.; Pradhan, C. Gauss iterated map based RGB image encryption approach. In Proceedings of the 2017 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; pp. 0015–0018. [Google Scholar]
- Al-Abaidy, S.A.F. Optimal Use Of ANN In The Integration Between Digital Image Processing And Encryption Technique. Turk. J. Comput. Math. Educ. (TURCOMAT) 2021, 12, 950–958. [Google Scholar] [CrossRef]
- Hajjaji, M.A.; Dridi, M.; Mtibaa, A. A medical image crypto-compression algorithm based on neural network and PWLCM. Multimed. Tools Appl. 2019, 78, 14379–14396. [Google Scholar] [CrossRef]
- Hu, F.; Wang, J.; Xu, X.; Pu, C.; Peng, T. Batch image encryption using generated deep features based on stacked autoencoder network. Math. Probl. Eng. 2017, 2017, 3675459. [Google Scholar] [CrossRef]
- Man, Z.; Li, J.; Di, X.; Sheng, Y.; Liu, Z. Double image encryption algorithm based on neural network and chaos. Chaos Solitons Fractals 2021, 152, 111318. [Google Scholar] [CrossRef]
- Rahmawati, W.; Liantoni, F. Image Compression and Encryption Using DCT and Gaussian Map. IOP Conf. Ser. Mater. Sci. Eng. 2019, 462, 012035. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Xu, J.; Mou, J.; Yang, F. Fractional-order 4D hyperchaotic memristive system and application in color image encryption. EURASIP J. Image Video Process. 2019, 2019, 22. [Google Scholar] [CrossRef]
- Al-Khasawneh, M.A.; Uddin, I.; Shah, S.A.A.; Khasawneh, A.M.; Abualigah, L.; Mahmoud, M. An improved chaotic image encryption algorithm using Hadoop-based MapReduce framework for massive remote sensed images in parallel IoT applications. Clust. Comput. 2021, 25, 999–1013. [Google Scholar] [CrossRef]
- Hashmi, M.F.; Katiyar, S.; Keskar, A.G.; Bokde, N.D.; Geem, Z.W. Efficient pneumonia detection in chest xray images using deep transfer learning. Diagnostics 2020, 10, 417. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Maniyath, S.R.; Thanikaiselvan, V. An efficient image encryption using deep neural network and chaotic map. Microprocess. Microsyst. 2020, 77, 103134. [Google Scholar] [CrossRef]
- Hosny, K.M.; Kassem, M.A.; Fouad, M.M. Classification of skin lesions into seven classes using transfer learning with AlexNet. J. Digit. Imaging 2020, 33, 1325–1334. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Lei, Y.; Jian, C. Research on digital image encryption algorithm based on double logistic chaotic map. EURASIP J. Image Video Process. 2018, 2018, 142. [Google Scholar] [CrossRef]
- Thoms, G.R.; Muresan, R.; Al-Dweik, A. Chaotic encryption algorithm with key controlled neural networks for intelligent transportation systems. IEEE Access 2019, 7, 158697–158709. [Google Scholar] [CrossRef]
- Ferdush, J.; Begum, M.; Uddin, M.S. Chaotic lightweight cryptosystem for image encryption. Adv. Multimed. 2021, 2021, 5527295. [Google Scholar] [CrossRef]
- Talhaoui, M.Z.; Wang, X.; Midoun, M.A. Fast image encryption algorithm with high security level using the Bülban chaotic map. J. Real-Time Image Process. 2021, 18, 85–98. [Google Scholar] [CrossRef]
- Mondal, B.; Behera, P.K.; Gangopadhyay, S. A secure image encryption scheme based on a novel 2D sine–cosine cross-chaotic (SC3) map. J. Real-Time Image Process. 2021, 18, 1–18. [Google Scholar] [CrossRef]
- Ahuja, B.; Doriya, R. A novel hybrid compressive encryption cryptosystem based on block quarter compression via DCT and fractional Fourier transform with chaos. Int. J. Inf. Technol. 2021, 13, 1837–1846. [Google Scholar] [CrossRef]









| Images | PSNR | SSIM | MSE | Entropy Plain Image | Entropy Encrypted Image |
|---|---|---|---|---|---|
| Lena | ∞ | 1 | 0 | 7.5694 | 7.9621 |
| Man | ∞ | 1 | 0 | 7.0097 | 7.8529 |
| Peppers | ∞ | 1 | 0 | 7.5487 | 7.9533 |
| Barbara | ∞ | 1 | 0 | 7.3410 | 7.9043 |
| Baboon | ∞ | 1 | 0 | 7.3705 | 7.9578 |
| Boat | ∞ | 1 | 0 | 7.1894 | 7.8794 |
| Images | NPCR (%) | UACI (%) |
|---|---|---|
| Lena | 99.62 | 33.42 |
| Man | 99.59 | 33.35 |
| Peppers | 99.58 | 33.34 |
| Barbara | 99.57 | 33.33 |
| Baboon | 99.61 | 33.41 |
| Boat | 99.64 | 33.43 |
| Images | Original | Encrypted | ||||
|---|---|---|---|---|---|---|
| CC (H) | CC (V) | CC (D) | CC (H) | CC (V) | CC (D) | |
| Lena | 0.9502 | 0.9712 | 0.9282 | 0.1100 | −0.0664 | −0.0752 |
| Man | 0.9416 | 0.9630 | 0.9136 | 0.0843 | −0.0591 | −0.0682 |
| Peppers | 0.9682 | 0.9725 | 0.9425 | 0.0007 | 0.0155 | −0.0042 |
| Barbara | 0.8262 | 0.8942 | 0.8501 | 0.0061 | −0.0159 | −0.0123 |
| Baboon | 0.6940 | 0.6039 | 0.6027 | 0.0391 | 0.0131 | −0.0080 |
| Boat | 0.8864 | 0.9204 | 0.8400 | 0.1569 | −0.1549 | −0.1117 |
| Images | Horizontal | Vertical | Diagonal | Entropy |
|---|---|---|---|---|
| Proposed | 0.1100 | −0.0664 | −0.0752 | 7.9621 |
| [26] | −0.0414 | −0.0342 | 0.1083 | 7.4077 |
| [27] | 0.0039 | 0.0059 | −0.0050 | 7.9994 |
| [28] | 0.0008 | 0.0004 | 0.0020 | 7.9995 |
| Images | PSNR of the Cropped Encrypted Image | PSNR of the Noisy Encrypted Image |
|---|---|---|
| Lena | 16.707916 | 32.354713 |
| Man | 17.296258 | 31.669253 |
| Peppers | 17.900450 | 32.064819 |
| Barbara | 16.708817 | 31.032769 |
| Baboon | 18.526831 | 32.952549 |
| Boat | 18.855763 | 33.389143 |
| Test | Values | Results |
|---|---|---|
| Frequency | 0.8315 | Pass |
| Block Frequency | 0.2888 | Pass |
| Cumulative Sums Forward | 0.5120 | Pass |
| Cumulative Sums Reverse | 1.0000 | Pass |
| Runs | 0.6572 | Pass |
| Longest Run | 0.1339 | Pass |
| Rank | 0.1885 | Pass |
| FFT | 0.6250 | Pass |
| Overlapping Template | 0.3525 | Pass |
| Approximate Entropy | 0.9875 | Pass |
| Linear Complexity | 0.1045 | Pass |
| Serial | 0.1514 | Pass |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salunke, S.; Ahuja, B.; Hashmi, M.F.; Marriboyina, V.; Bokde, N.D. 5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation. Appl. Sci. 2022, 12, 5321. https://doi.org/10.3390/app12115321
Salunke S, Ahuja B, Hashmi MF, Marriboyina V, Bokde ND. 5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation. Applied Sciences. 2022; 12(11):5321. https://doi.org/10.3390/app12115321
Chicago/Turabian StyleSalunke, Sharad, Bharti Ahuja, Mohammad Farukh Hashmi, Venkatadri Marriboyina, and Neeraj Dhanraj Bokde. 2022. "5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation" Applied Sciences 12, no. 11: 5321. https://doi.org/10.3390/app12115321
APA StyleSalunke, S., Ahuja, B., Hashmi, M. F., Marriboyina, V., & Bokde, N. D. (2022). 5D Gauss Map Perspective to Image Encryption with Transfer Learning Validation. Applied Sciences, 12(11), 5321. https://doi.org/10.3390/app12115321







