Image Style Transfer via Multi-Style Geometry Warping
Abstract
:1. Introduction
2. Related Work
3. Materials and Methods
3.1. Object Detection
3.2. Feature Detection and Warping
3.2.1. Determining Correspondences with NBB
3.2.2. Applying Warping with DST
3.3. Final Composition
3.4. Style Transfer
4. Results
4.1. Dataset and Test Parameters
4.2. Performance Metrics
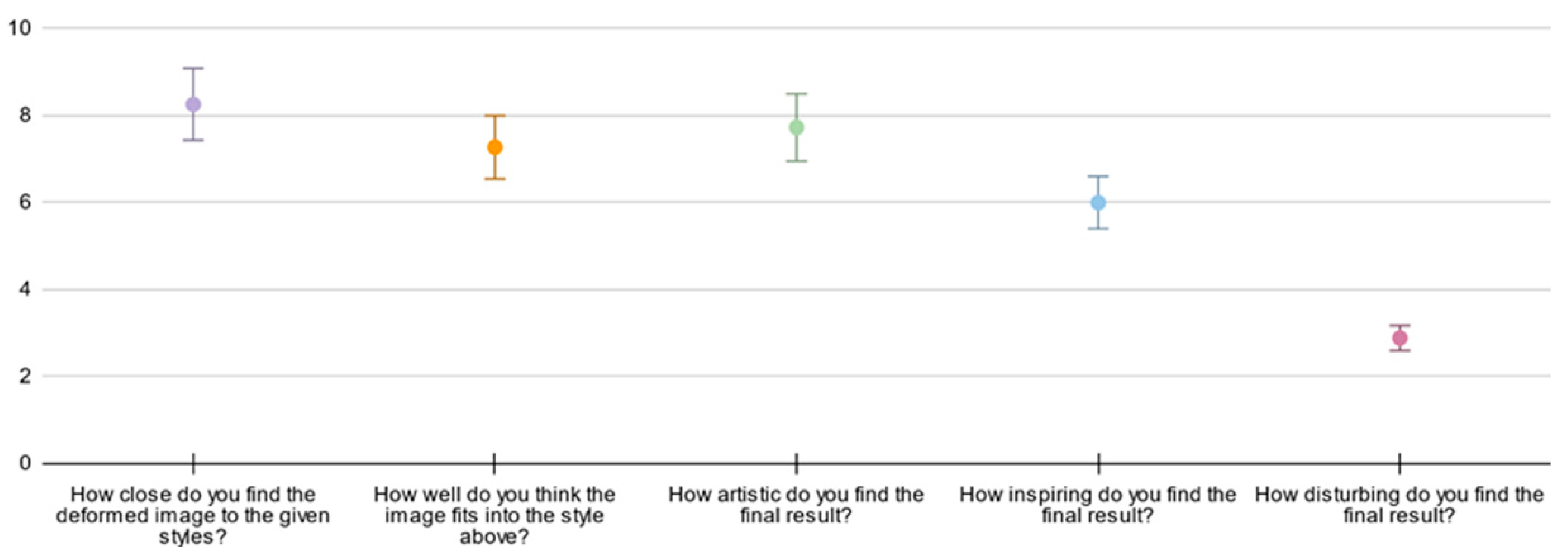
4.3. Human Evaluation
4.4. Heuristics
4.5. Generated Images
5. Discussion
5.1. Improvements to State-of-the-Art
5.2. Limitations of the Proposed Solution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Gatys, L.A.; Ecker, A.S.; Bethge, M. Image Style Transfer Using Convolutional Neural Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2414–2423. [Google Scholar] [CrossRef]
- Yaniv, J.; Newman, Y.; Shamir, A. The Face of Art: Landmark Detection and Geometric Style in Portraits. ACM Trans. Graph. 2019, 38, 1–15. [Google Scholar] [CrossRef]
- Yang, S.; Liu, J.; Lian, Z.; Guo, Z. Awesome Typography: Statistics-Based Text Effects Transfer. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2886–2895. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.S.Y.; Kolkin, N.; Salavon, J.; Shakhnarovich, G. Deformable Style Transfer. In Computer Vision—ECCV 2020. ECCV 2020. Lecture Notes in Computer Science; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; Volume 12371. [Google Scholar]
- Aberman, K.; Liao, J.; Shi, M.; Lischinski, D.; Chen, B.; Cohen-Or, D. Neural Best-Buddies: Sparse Cross-Domain Correspondence. ACM Trans. Graph. 2018, 37, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Pérez, P.; Gangnet, M.; Blake, A. Poisson Image Editing. ACM Trans. Graph. 2003, 22, 313–318. [Google Scholar] [CrossRef]
- Haeberli, P. Paint by Numbers: Abstract Image Representations. SIGGRAPH Comput. Graph. 1990, 24, 207–214. [Google Scholar] [CrossRef]
- Collomosse, J.P.; Hall, P.M. Cubist Style Rendering from Photographs. IEEE Trans. Vis. Comput. Graph. 2003, 9, 443–453. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, L.; Zhang, H.-C. Arcimboldo-like Collage Using Internet Images. ACM Trans. Graph. 2011, 30, 155. [Google Scholar] [CrossRef]
- Cole, F.; Belanger, D.; Krishnan, D.; Sarna, A.; Mosseri, I.; Freeman, W.T. Synthesizing Normalized Faces from Facial Identity Features. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3386–3395. [Google Scholar] [CrossRef] [Green Version]
- Champandard, A.J. Semantic Style Transfer and Turning Two-Bit Doodles into Fine Artworks. arXiv 2016, arXiv:1603.01768. [Google Scholar] [CrossRef]
- Li, C.; Wand, M. Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis. arXiv 2016, arXiv:1601.04589. [Google Scholar] [CrossRef]
- Kolkin, N.; Salavon, J.; Shakhnarovich, G. Style Transfer by Relaxed Optimal Transport and Self-Similarity. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 10043–10052. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Yan, X.; Liu, N.; Qiu, T.; Ni, B. Anisotropic Stroke Control for Multiple Artists Style Transfer. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 3246–3255. [Google Scholar]
- Liu, X.-C.; Li, X.-Y.; Cheng, M.-M.; Hall, P. Geometric Style Transfer. arXiv 2020, arXiv:2007.05471. [Google Scholar]
- Liu, X.-C.; Yang, Y.-L.; Hall, P. Learning to Warp for Style Transfer. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3701–3710. [Google Scholar] [CrossRef]
- Jocher, G.; Chaurasia, A.; Stoken, A.; Borovec, J.; NanoCode012; Kwon, Y.; TaoXie; Fang, J.; imyhxy; Michael, K.; et al. Ultralytics/Yolov5: V6.1—TensorRT, TensorFlow Edge TPU and OpenVINO Export and Inference. Zenodo 2022. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar] [CrossRef] [Green Version]
- Caesar, H.; Uijlings, J.; Ferrari, V. COCO-Stuff: Thing and Stuff Classes in Context. arXiv 2018, arXiv:1612.03716. [Google Scholar] [CrossRef]









| Name | Tested Values | Preferred Value | Description |
|---|---|---|---|
| 1 | 1 | Threshold to remove pairs with lower activation values for NBB | |
| 3–10 | 5 | Threshold to remove pairs that are too close to one another for NBB | |
| 10–100 | 80 | Maximum number of pair points to consider for NBB | |
| 1–10 | 8 | Content loss multiplier for DST | |
| 1–10 | 1 | Warp loss multiplier for DST | |
| 1–10 | 5 | Regularizer multiplier for DST | |
| 0.001–1 | 0.1 | DST learning rate | |
| 10–500 | 250 | Total number of epochs to run training for DST | |
| 0.8 | 0.8 | The weight applied to style content for STROTSS | |
| 1024 | 1024 | The final texture size to consider for STROTSS |
| Methods | Runtime(s) | |||
|---|---|---|---|---|
| Geometric Warping | Texture Rendering | |||
| 256 × 256 | 512 × 512 | 1024 × 1024 | ||
| Our method | 76–119 | 65 | 111 | 183 |
| Gatys et al. | N/A | 13.7 | 31.1 | 117 |
| AdaIN | N/A | 0.04 | 0.14 | 0.52 |
| DST | 84–130 | 61 | 103 | 164 |
| Learning to Warp | 0.3–1.2 | 16 | 47 | 144 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexandru, I.; Nicula, C.; Prodan, C.; Rotaru, R.-P.; Voncilă, M.-L.; Tarbă, N.; Boiangiu, C.-A. Image Style Transfer via Multi-Style Geometry Warping. Appl. Sci. 2022, 12, 6055. https://doi.org/10.3390/app12126055
Alexandru I, Nicula C, Prodan C, Rotaru R-P, Voncilă M-L, Tarbă N, Boiangiu C-A. Image Style Transfer via Multi-Style Geometry Warping. Applied Sciences. 2022; 12(12):6055. https://doi.org/10.3390/app12126055
Chicago/Turabian StyleAlexandru, Ioana, Constantin Nicula, Cristian Prodan, Răzvan-Paul Rotaru, Mihai-Lucian Voncilă, Nicolae Tarbă, and Costin-Anton Boiangiu. 2022. "Image Style Transfer via Multi-Style Geometry Warping" Applied Sciences 12, no. 12: 6055. https://doi.org/10.3390/app12126055
APA StyleAlexandru, I., Nicula, C., Prodan, C., Rotaru, R.-P., Voncilă, M.-L., Tarbă, N., & Boiangiu, C.-A. (2022). Image Style Transfer via Multi-Style Geometry Warping. Applied Sciences, 12(12), 6055. https://doi.org/10.3390/app12126055






