The New Method of Searching Cut-Sets in the System Reliability Analysis of Plane Steel Trusses
Abstract
:1. Introduction
2. Materials and Methods
- is the section factor for steel members insulated by fire protection material (according to Table 4.3 in EC 3-1-2 [29]);
- is the temperature-dependent specific heat of steel from Section 3 of EC 3 [29];
- is the temperature-independent specific heat of fire protection material;
- is the thickness of the fire protection material;
- is the time interval; it should not be taken as more than 5 s for insulated elements;
- is the steel temperature at time, t;
- is the ambient gas temperature at time, t;
- is the increase of the ambient gas temperature during the time interval, ;
- is the unit’s mas steel;
- is the unit mass of the fire protection material.
- —the design load-bearing capacity of a tension member with a uniform temperature θa;
- —the design buckling capacity at time, t, of a compression member;
- NRd—the design-bearing capacity of the cross-section, Npl,Rd, for normal temperature design, according to EN-1993-1-1 [31];
- —the reduction factor for the yield strength of steel at the temperature, θa, reached at time, t, according to Table 3.1 in EC-1993-1-2 [29],
- an elemental area of the cross-section;
- fy—yield strength;
- γM,0, γM,fi—partial safety coefficient (in the paper they are neglected, because to conduct the reliability analysis characteristic values are needed);
- χfi is the reduction factor for flexural buckling in a fire design situation and is defined as follows:where:
- Ri—the reliability of the i-th element;
- n—number of system elements.
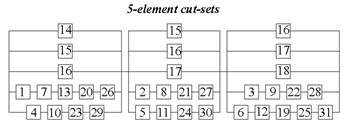
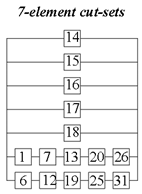
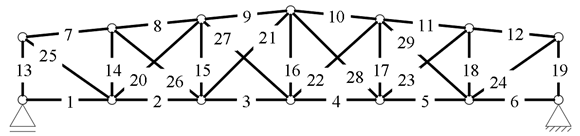
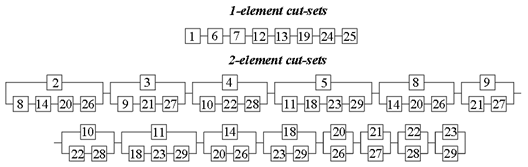
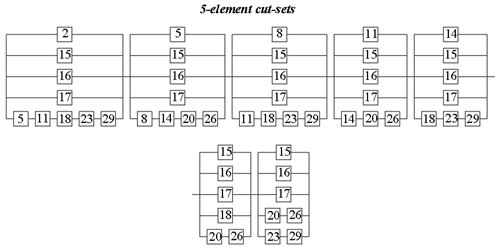
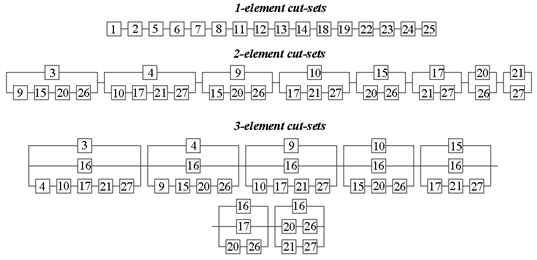
3. Results
3.1. Computational Study
- the structure was under the fully developed fire, and all elements were heated from each side,
- the temperature field was homogeneous along the bar length and along cross-section height,
- the forces applied in the nodes were the only load (in addition to fire load),
- the structures were considered to be in the elastic range,
- all random variables were assumed to have a normal distribution,
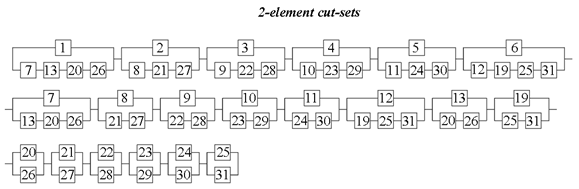
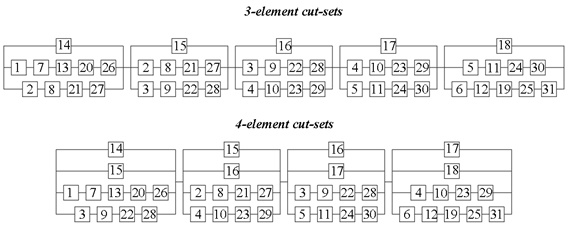
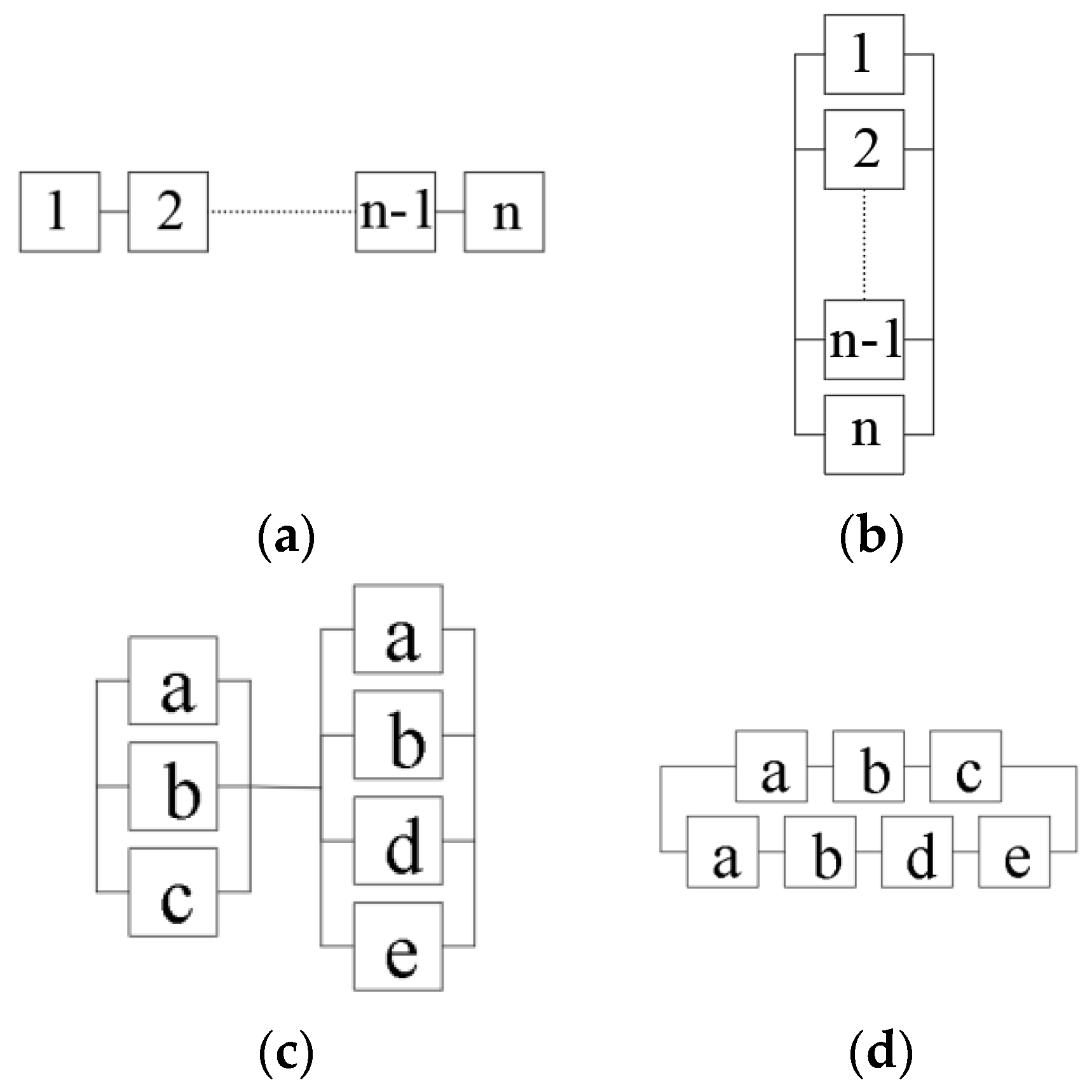
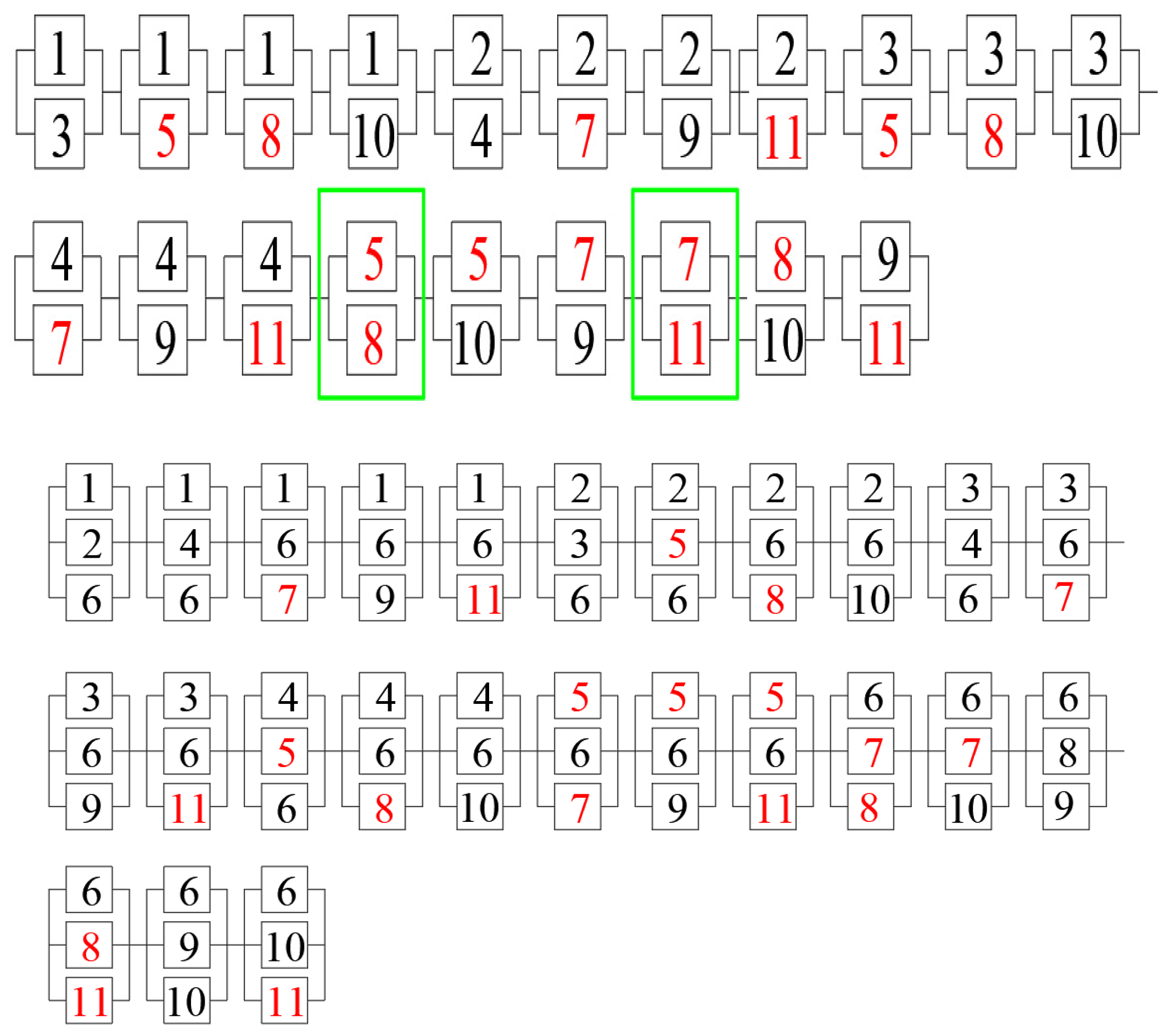
- cut-sets with common causative elements were separated,
- the reliabilities of joints are much higher than reliability of bars, so only the last one could be causative elements.
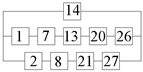
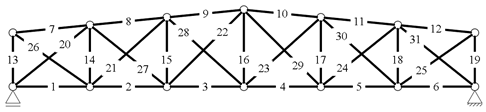
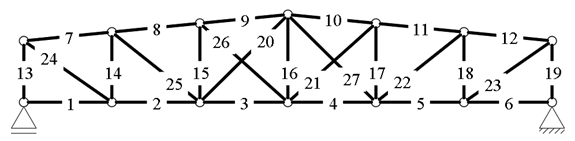
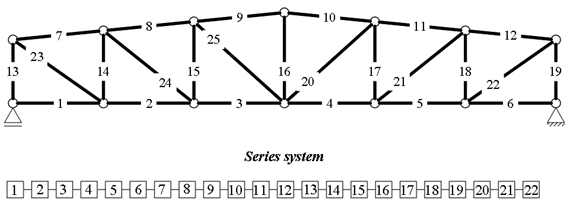
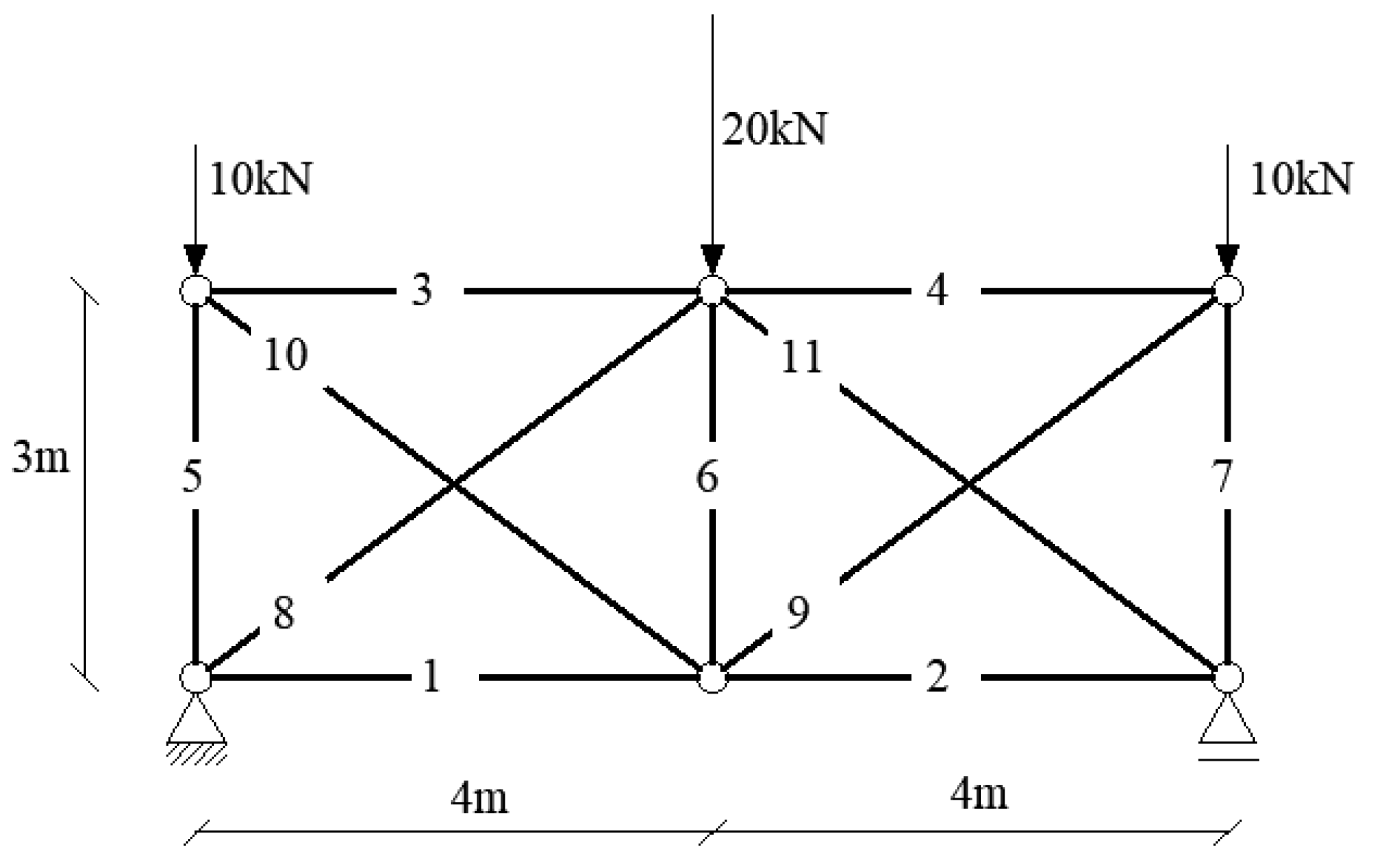
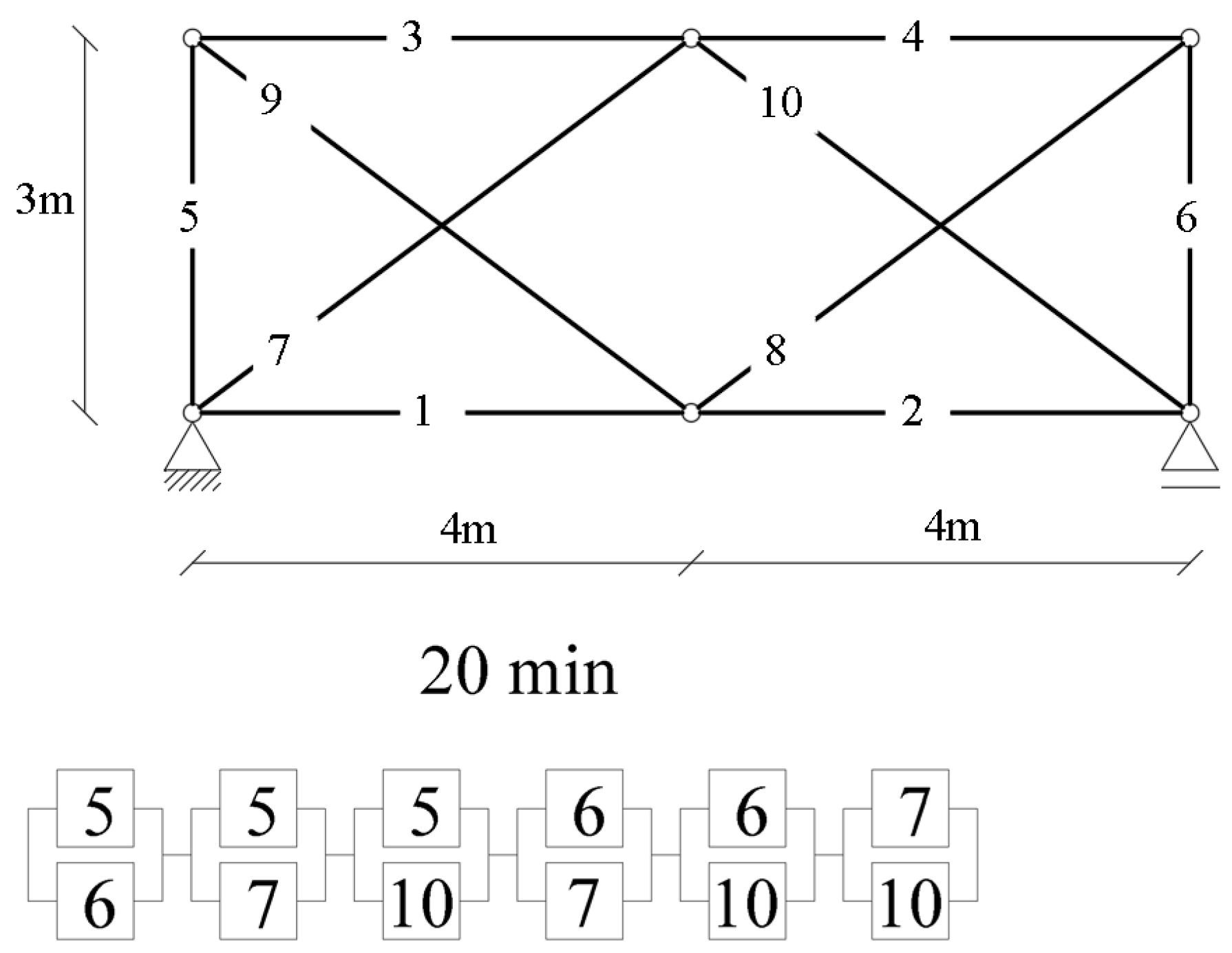
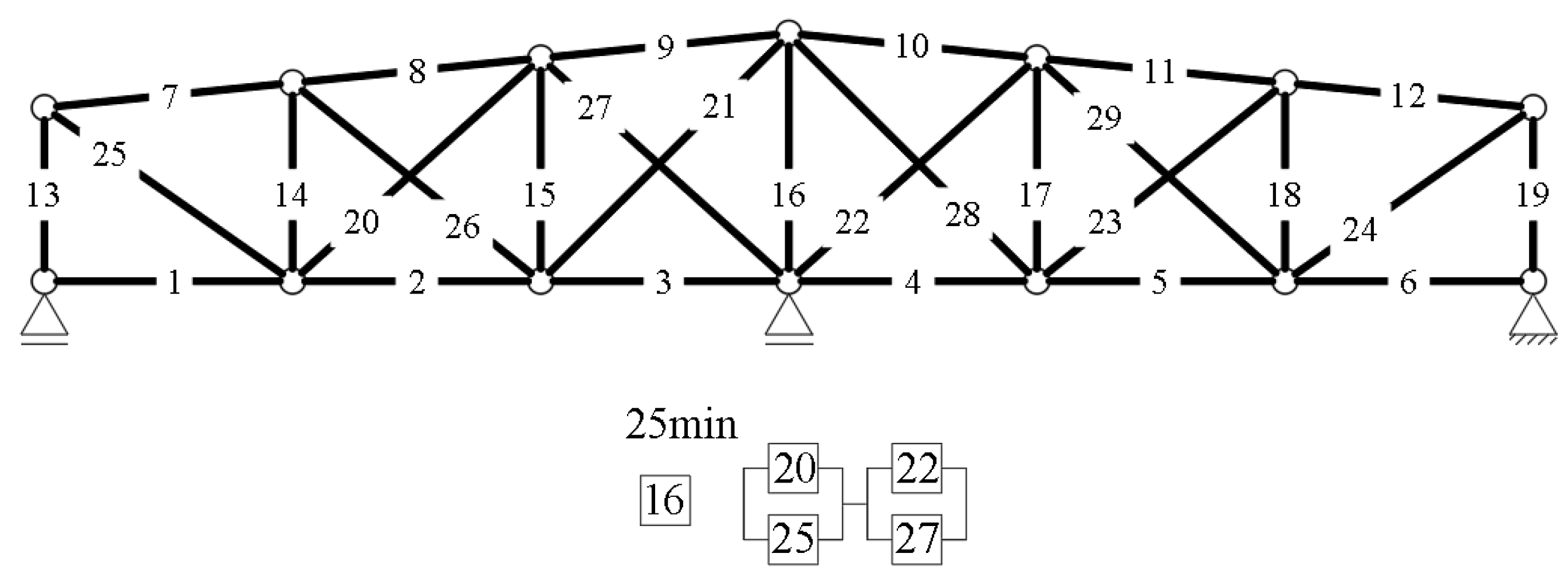
3.1.1. Example 1: Statically Indeterminate Truss with Two Degrees of Freedom
3.1.2. Example 2: Statically Indeterminate Truss with Six Degrees of Freedom
4. Discussion
5. Conclusions
- analysis of the structure under the load of true nature, taking into account different types of distribution (not only normal),
- analysis of the structure in a fire design situation in elastic-plastic range,
- analysis of the structure under fire load with different fire curves and with elements heated in different types (not only from each side and/or with inhomogeneous temperature distribution),
- development of system analysis for structures with common causative elements in two or more cut-sets (resignation from the assignment about separating the cut-sets).
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




References and Notes
- Nowak, A.; Collins, K. Reliability of Structures, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Thoft-Christensen, P.; Baker, M. Structural Reliability. Theory and Its Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Murzewski, J. Reliability of Engineering Structures; Arkady: Warszawa, Poland, 1989. (In Polish) [Google Scholar]
- Zhao, Y.-G.; Ono, T. A general procedure for first/second-order reliability method (FORM/SORM). Struct. Saf. 1999, 21, 95–112. [Google Scholar] [CrossRef]
- Ditlevsen, O. On the choice of expansion point in form or sorm. Struct. Saf. 1987, 4, 243–245. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, C.; Wang, G.G.; Han, X. First and second order approximate reliability analysis methods using evidence theory. Reliab. Eng. Syst. Saf. 2015, 137, 40–49. [Google Scholar] [CrossRef]
- Kang, B.-J.; Kim, J.-H.; Kim, Y. Engineering criticality analysis on an offshore structure using the first- and second-order reliability method. Int. J. Nav. Archit. Ocean. Eng. 2016, 8, 577–588. [Google Scholar] [CrossRef] [Green Version]
- Papaioannou, I.; Straub, D. Variance-based reliability sensitivity analysis and the FORM α-factors. Reliab. Eng. Syst. Saf. 2021, 210, 107496. [Google Scholar] [CrossRef]
- Hurd, C.C. A note on early Monte Carlo computations and scientific meeting. Ann. Hist. Comput. 1985, 7, 141–155. [Google Scholar] [CrossRef]
- Bucher, C.G. Adaptive sampling-an iterative fast Monte Carlo procedure. Struct. Saf. 1988, 5, 119–126. [Google Scholar] [CrossRef]
- Doliński, K. Importance Sampling Techniques in Reliability Calculation; IPPT—IFTR Reports; 1988; pp. 1–33. ISSN 2299-3657. Available online: https://scholar.google.pl/scholar?q=Importance+Sampling+Techniques+in+Reliability+Calculation+11.%09Doli%C5%84ski&hl=pl&as_sdt=0&as_vis=1&oi=scholart (accessed on 3 April 2022).
- Rackwitz, R.; Fujita, M. Updating first and second order reliability estimates by importance sampling. Jpn. Soc. Civ. Eng. 1988, 392, 53–59. [Google Scholar]
- Menz, M.; Dubreuil, S.; Morio, J.; Gogu, C.; Bartoli, N.; Chiron, M. Variance based sensivity analysis for Monte Carlo and importance sampling reliability assessment with Gaussian processes. Struct. Saf. 2021, 93, 102116. [Google Scholar] [CrossRef]
- Shojai, S.; Schaumann, P.; Brömer, T. Probabilistic modelling of pitting corrosion and its impact on stress concentrations in steel structures in the offshore wind energy. Mar. Struct. 2022, 84, 103232. [Google Scholar] [CrossRef]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput.-Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Waszczyszyn, Z.; Kaliszuk, J. Reliability analysis of structures by neural network supported Monte Carlo methods. Neural Netw. Soft Comput. 2002, 19, 745–759. [Google Scholar]
- Dudzik, A.; Potrzeszcz-Sut, B. Hybrid approach to the first order reliability method in the reliability analysis of a spatial structure. Appl. Sci. 2021, 11, 648. [Google Scholar] [CrossRef]
- Dang, H.V.; Trestian, R.; Bui-Tien, T.; Nguyen, H.X. Probabilistic method for time-varying reliability analysis of structure via variational Bayesian neural network. Structures 2021, 34, 3703–3715. [Google Scholar] [CrossRef]
- Qiu, Z.; Yang, D.; Elishakoff, I. Probabilistic interval reliability of structural systems. Int. J. Solids Struct. 2008, 45, 2850–2860. [Google Scholar] [CrossRef] [Green Version]
- Kubicka, K.; Radoń, U.; Szaniec, W. Comparison of the reliability methods for steel trusses subjected to fire. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 032061. [Google Scholar] [CrossRef] [Green Version]
- Mochocki, W.; Radoń, U. Analysis of basic failure scenarios of a truss tower in a probabilistic approach. Appl. Sci. 2019, 9, 2662. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhang, H.; Hou Ch Han, L.-H.; Mu, T.-M. Reliability calibration for the design of multiple-chord CFST trusses by advanced analysis. Struct. Saf. 2021, 89, 102051. [Google Scholar] [CrossRef]
- Kamiński, M.; Solecka, M. Optimization of the truss-type structures using the generalized perturbation-based Stochastic Finite Element Method. Finite Elem. Anal. Des. 2013, 63, 69–79. [Google Scholar] [CrossRef]
- Zheng, Z.; Dai, H. Structural stochastic response determination via a sample-based stochastic finite element method. Comput. Methods Appl. Mech. Eng. 2021, 381, 113824. [Google Scholar] [CrossRef]
- Kłosowska, J.; Obara, P.; Turant, J. Kinematically admissible failure mechanisms for plane trusses. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022022. [Google Scholar] [CrossRef] [Green Version]
- Safari, J. Multi-objective reliability optimization of series parallel systems with a choice of redundancy strategies. Reliab. Eng. Syst. Saf. 2012, 108, 10–20. [Google Scholar] [CrossRef]
- Kim, D.-S.; Ok, S.-Y.; Song, J.; Koh, H.-M. System reliability analysis using dominant failure modes identified by selective searching technique. Reliab. Eng. Syst. Saf. 2013, 119, 316–331. [Google Scholar] [CrossRef]
- Shao, S.; Murotsu, M. Approach to failure mode analysis of large structures. Probabilistic Eng. Mech. 1999, 14, 169–177. [Google Scholar] [CrossRef]
- Eurocode 3-1-2: General rules: Structural fire design.
- Eurocode 1: Actions on structures-Part 1-2:General actions-Actions on structures exposed to fire.
- Eurocode 3: Design of steel structures-Part 1-1:General rules and rules for buildings.
- Kubicka, K.; Pawlak, U.R.U. Influence of the thermal insulation type and thickness on the structure mechanical response under fire conditions. Appl. Sci. 2019, 9, 2606. [Google Scholar] [CrossRef] [Green Version]
- JCSS Probabilistic Model Code. Available online: https://www.jcss-lc.org/jcss-probabilistic-model-code/ (accessed on 3 April 2022).
- Kubicka, K.; Radoń, U. Assessment of randomness of buckling coefficient on the reliability index’s value under fire conditions. Arch. Civ. Eng. 2018, 64, 173–179. [Google Scholar]
- Kubicka, K.; Radoń, U.; Szaniec, W.; Pawlak, U. Comparative analysis of the reliability of steel structure with pinned and rigid nodes subjected to fire. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 022051. [Google Scholar] [CrossRef]
- Biegus, A. Probabilistic Analysis of Steel Structures; PWN: Warszawa, Poland, 1999. (In Polish) [Google Scholar]
- Kubicka, K.; Obara, P.; Radoń, U.; Szaniec, W. Assessment of steel truss fire safety in terms of the system reliability analysis. Arch. Civ. Mech. Eng. 2019, 19, 417–427. [Google Scholar] [CrossRef]
- EN 1990: Basis of structural design.
- Maślak, M. Assessment of the safety level ensured by a steel load bearing structure when subjected to a fire. In Proceedings of the ICASS 2015: Eigth International Conference on Advances in Steel Structures, Lisbon, Portugal, 21–24 July 2015. [Google Scholar]
- Wong, J.K.S. Reliability of Structural Fire Design; Fire Engineering Research Report 99/16; University of Canterbury: Canterbury, New Zealand, 1999. [Google Scholar]
- Kubicka, K.; Radoń, U. The impact of support type on the reliability of steel trusses subjected to the action of a fire. Appl. Sci. 2020, 10, 7916. [Google Scholar] [CrossRef]


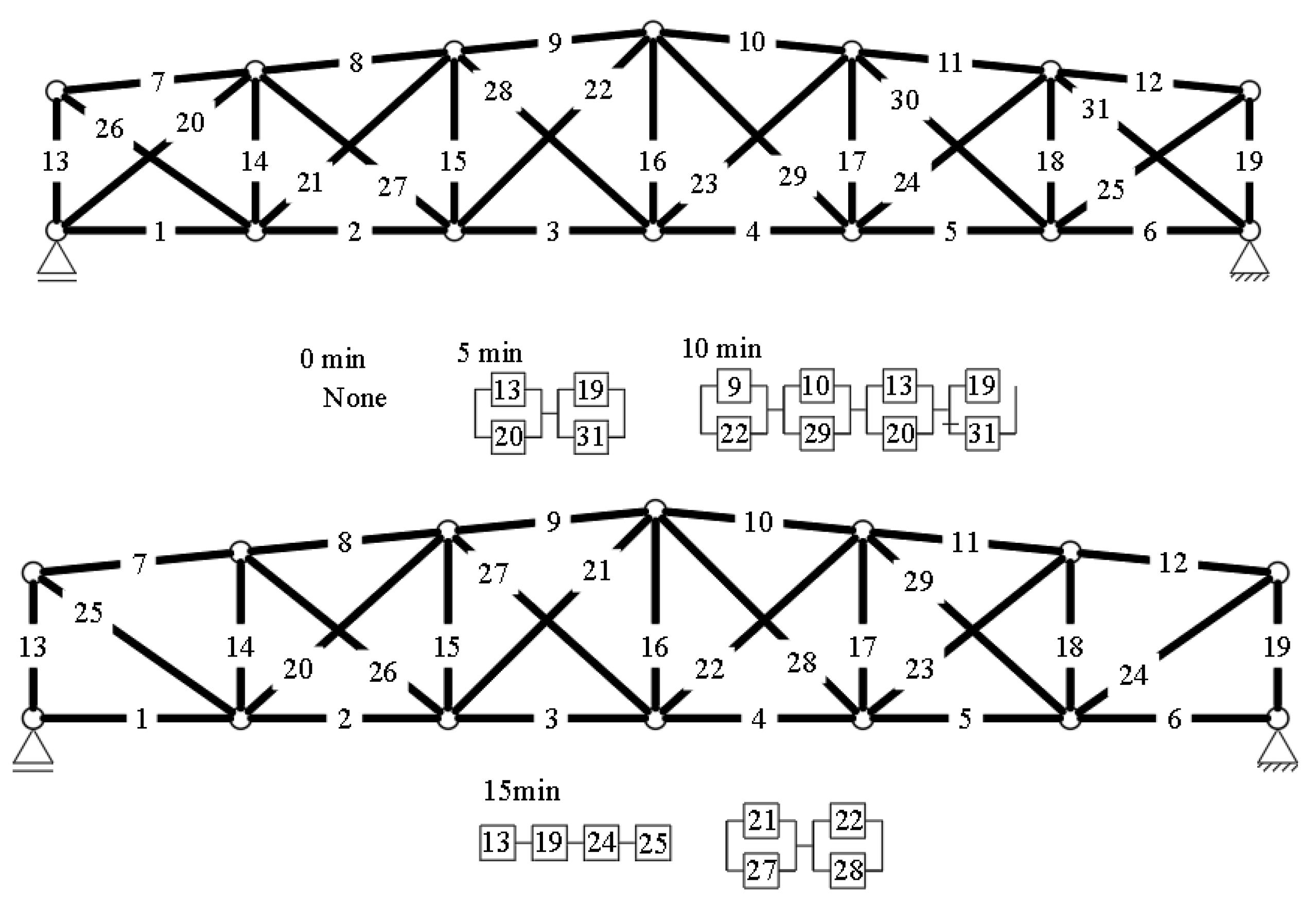
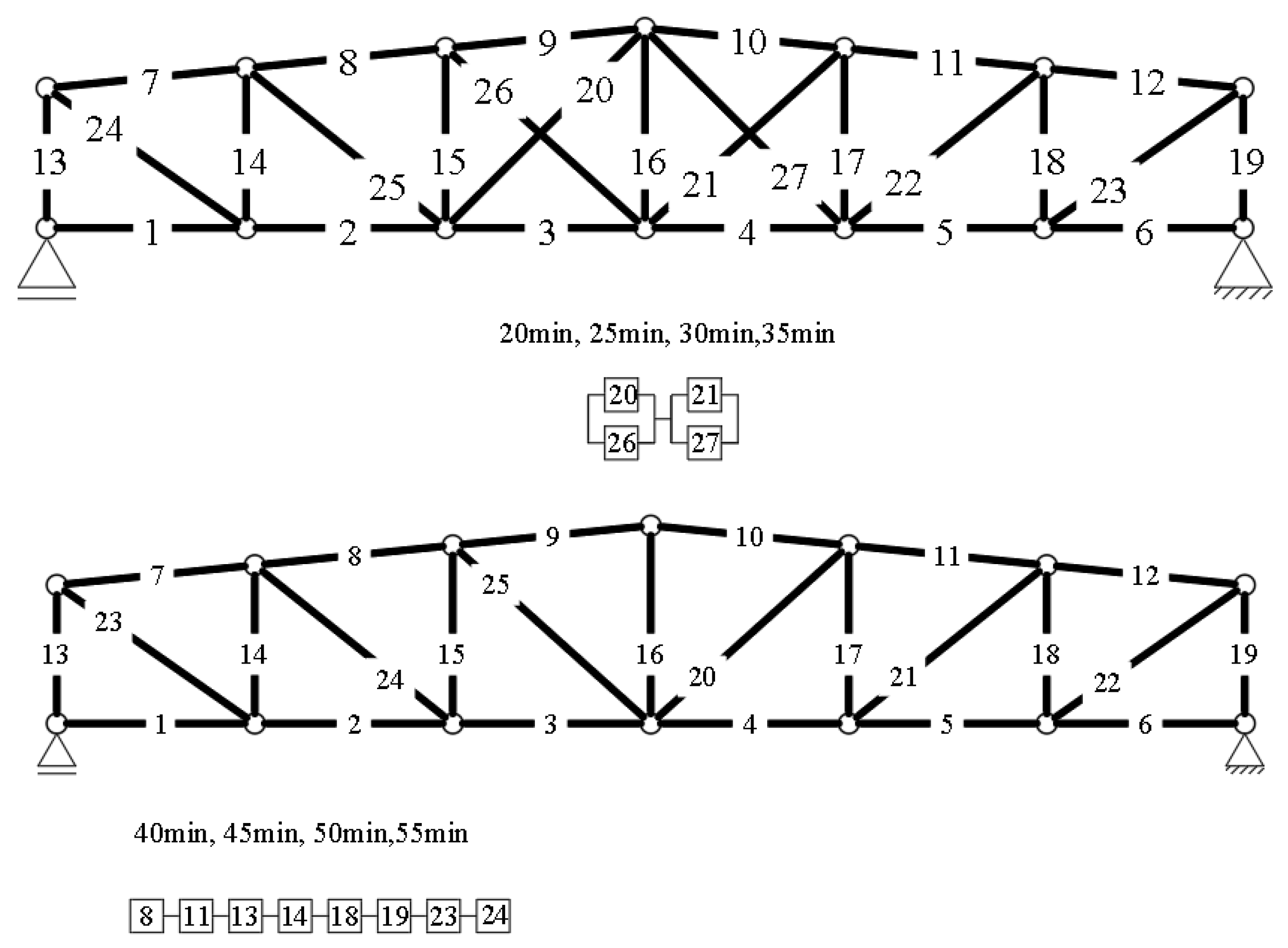
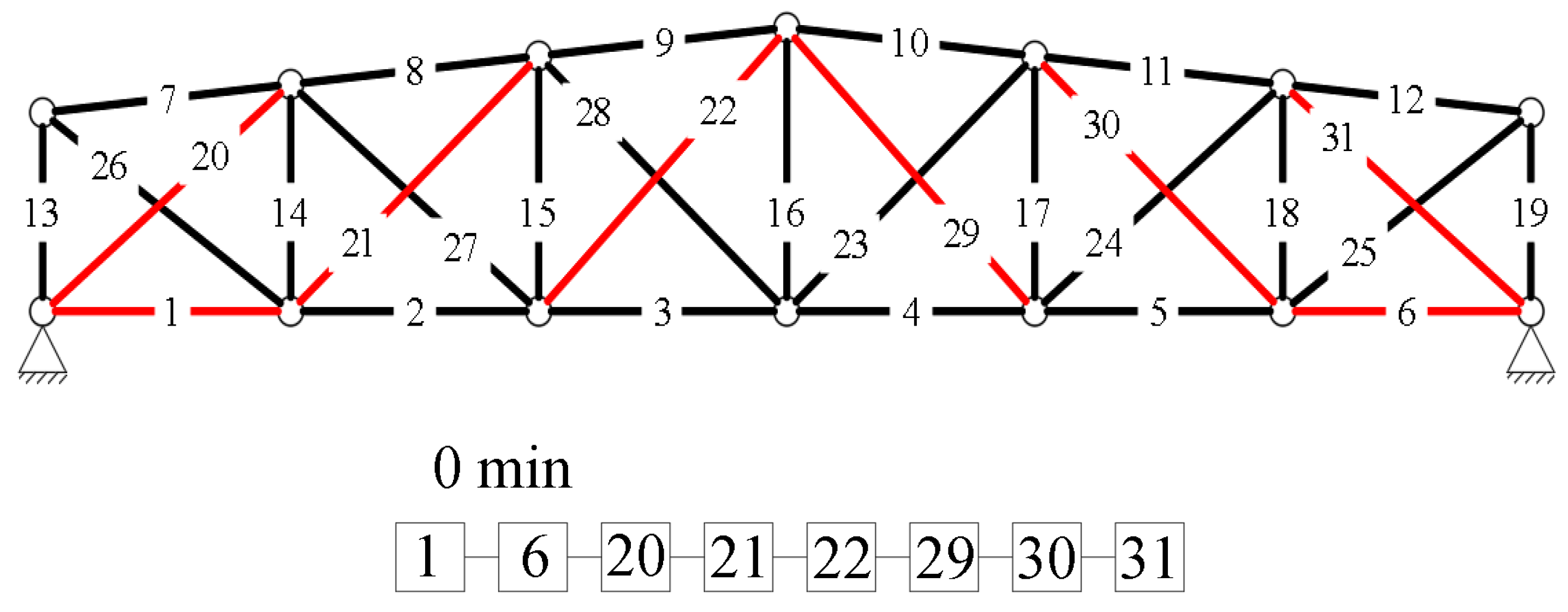
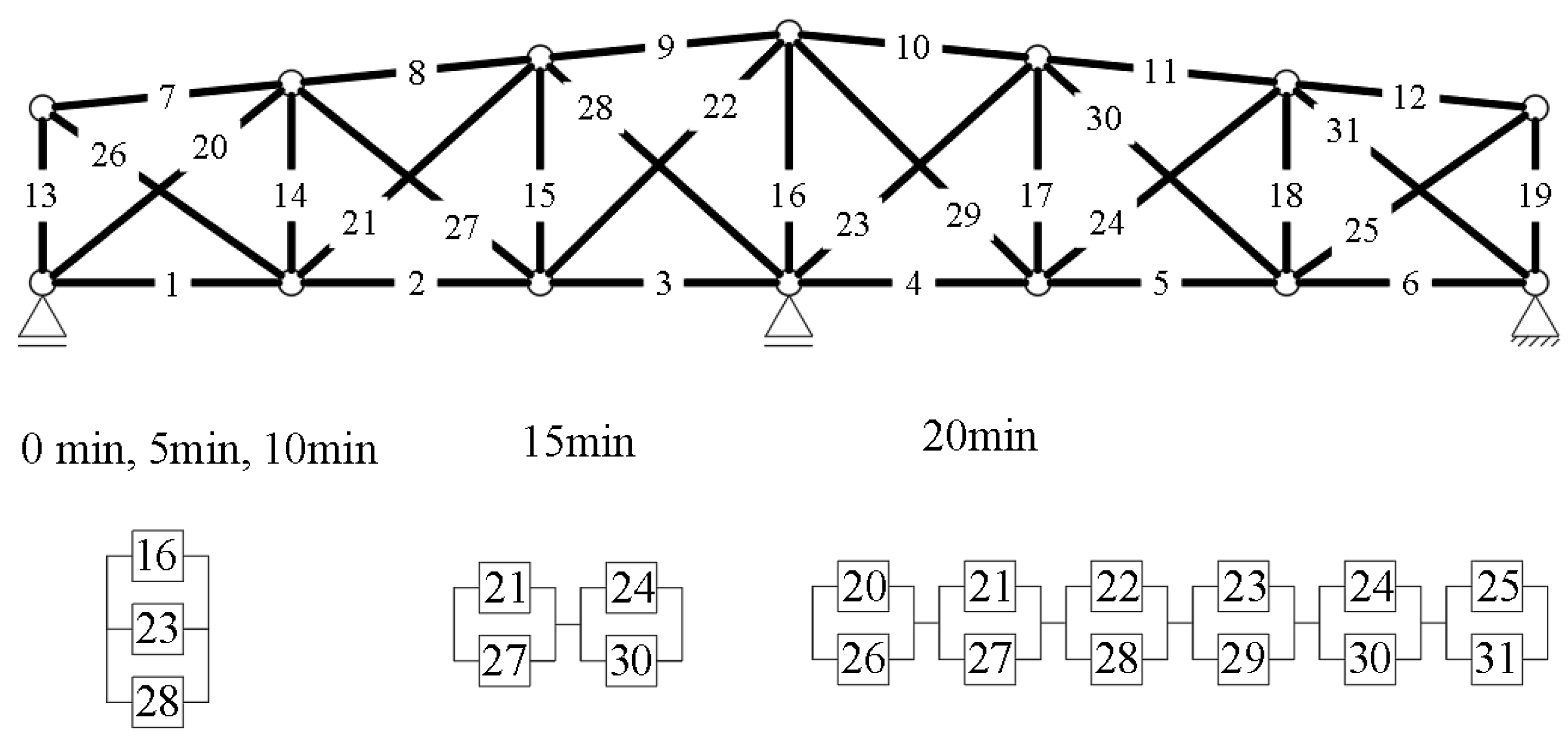

| Variable | Symbol | Coefficient of Variation ν [%] |
|---|---|---|
| Effect of action | E | 6 |
| Cross-sectional area | A | 6 |
| Yield strength | fy | 8 |
| Load bearing capacity | N | 10 |
| No. | Profiles | [kN] | σE [kN] | [kN] | σN [kN] | [kN] | σM [kN] | t [-] |
|---|---|---|---|---|---|---|---|---|
| 1 | IPE 100 | 8.93 | 0.54 | 221.45 | 22.15 | 212.52 | 22.15 | 9.59 |
| 2 | IPE 100 | 8.93 | 0.54 | 221.45 | 22.15 | 212.52 | 22.15 | 9.59 |
| 3 | IPE 160 | 4.41 | 0.26 | 75.64 | 7.56 | 71.23 | 7.57 | 9.41 |
| 4 | IPE160 | 4.41 | 0.26 | 75.64 | 7.56 | 71.23 | 7.57 | 9.41 |
| 5 | CHS 51 × 4 | 13.31 | 0.80 | 33.19 | 3.32 | 19.88 | 3.41 | 5.82 |
| 6 | CHS 51 × 4 | 6.61 | 0.40 | 33.19 | 3.32 | 26.58 | 3.34 | 7.95 |
| 7 | CHS 51 × 4 | 13.31 | 0.80 | 33.19 | 3.32 | 19.88 | 3.41 | 5.82 |
| 8 | CHS 60.3 × 4 | 11.16 | 0.67 | 21.48 | 2.15 | 10.32 | 2.25 | 4.59 |
| 9 | CHS 60.3 × 4 | 5.51 | 0.33 | 152.00 | 15.20 | 146.49 | 15.20 | 9.64 |
| 10 | CHS 60.3 × 4 | 5.51 | 0.33 | 152.00 | 15.20 | 146.49 | 15.20 | 9.64 |
| 11 | CHS 60.3 × 4 | 11.16 | 0.67 | 21.48 | 2.15 | 10.32 | 2.25 | 4.59 |
| No. | t [-] | Pf [-] | R [-] | |||||
| 1 | 9.59 | 4.24 × 10−22 | 1.0000000 | |||||
| 2 | 9.59 | 4.24 × 10−22 | 1.0000000 | |||||
| 3 | 9.41 | 2.45 × 10−21 | 1.0000000 | |||||
| 4 | 9.41 | 2.45 × 10−21 | 1.00000000 | |||||
| 5 | 5.82 | 2.88 × 10−9 | 0.9999999971195 | |||||
| 6 | 7.95 | 9.19 × 10−16 | 1.0000000000000 | |||||
| 7 | 5.82 | 2.88 × 10−9 | 0.9999999971195 | |||||
| 8 | 4.59 | 2.25 × 10−6 | 0.9999977492376 | |||||
| 9 | 9.64 | 2.84 × 10−22 | 1.0000000000000 | |||||
| 10 | 9.64 | 2.84 × 10−22 | 1.0000000000000 | |||||
| 11 | 4.59 | 2.25 × 10−6 | 0.9999977492376 | |||||
| Fire Duration [min] | 0 | 5 | 10 | 15 | 20 |
| Reliability index β [-] | 7.62 | 6.89 | 7.04 | 3.68 | 1.15 |
| Truss | Number of Cut-Sets | Time of Searching Cut-Sets [h] |
|---|---|---|
| Truss 1 | 325 | ≈11 |
| Truss 2 | 4888 | ≈19 |
| Truss 3 | 14,160 | ≈98 |
| No. of Element | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Effect of action [kN] | −222 | −201 | −195 | −195 | −201 | −222 | −2 | −33 | −44 | −44 | −33 |
| Load bearing capacity [kN] | 173 | 173 | 173 | 173 | 173 | 173 | 254 | 254 | 245 | 254 | 254 |
| No. of Element | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| Effect of action [kN] | −2 | −7 | 17 | 14 | 17 | 14 | 17 | −7 | −46 | −27 | −15 |
| Load bearing capacity [kN] | 254 | 75 | 158 | 158 | 158 | 158 | 158 | 75 | 35 | 32 | 30 |
| No. of Element | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
| Effect of action [kN] | −13 | −5 | 2 | 2 | −5 | −13 | −15 | −27 | −46 | ||
| Load bearing capacity [kN] | 32 | 35 | 158 | 158 | 35 | 32 | 30 | 32 | 35 |
| Fire Duration [min] | Reliability Index β [-] | ||
|---|---|---|---|
| Truss 1 | Truss 2 | Truss 3 | |
| 0 | - | 0.84 | - |
| 5 | 7.77 | - | - |
| 10 | 7.94 | - | - |
| 15 | 4.7 | - | - |
| 20 | 4.52 | - | 6.22 |
| 25 | 4.33 | - | 0.34 |
| 30 | 3.53 | - | 1.88 |
| 35 | 2.08 | - | 1.59 |
| 40 | 3.42 | - | 1.19 |
| 45 | 2.98 | - | 0.64 |
| 50 | 2.43 | - | 0.06 |
| 55 | 1.05 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubicka, K. The New Method of Searching Cut-Sets in the System Reliability Analysis of Plane Steel Trusses. Appl. Sci. 2022, 12, 5276. https://doi.org/10.3390/app12105276
Kubicka K. The New Method of Searching Cut-Sets in the System Reliability Analysis of Plane Steel Trusses. Applied Sciences. 2022; 12(10):5276. https://doi.org/10.3390/app12105276
Chicago/Turabian StyleKubicka, Katarzyna. 2022. "The New Method of Searching Cut-Sets in the System Reliability Analysis of Plane Steel Trusses" Applied Sciences 12, no. 10: 5276. https://doi.org/10.3390/app12105276
APA StyleKubicka, K. (2022). The New Method of Searching Cut-Sets in the System Reliability Analysis of Plane Steel Trusses. Applied Sciences, 12(10), 5276. https://doi.org/10.3390/app12105276





