Integrated Earthquake Catalog of the Eastern Sector of the Russian Arctic

Abstract

The objective of this study was to create a representative earthquake catalog for the Eastern Sector of the Arctic zone of the Russian Federation that combines all available data from Russian and international seismological agencies, with magnitude reduction to a uniform scale. The article describes the catalog compilation algorithm, as well as formalized procedures for removing duplicates and choosing the optimal magnitude scale. Due to different network configurations and record processing methods, different agencies may register/miss different events. This results in the absence of some events in different earthquake catalogs. Therefore, merging the data of various seismological agencies will provide the most complete catalog for the studied region. When merging catalogs, the problem of identifying duplicates (records related to the same seismic event) necessarily arises. An additional difficulty arises when distinguishing between aftershocks and duplicates since both are events that are close in space and time. To solve this problem, we used a modified nearest neighbor method developed earlier by the authors. The modified version, which is focused on identifying duplicates and distinguishing between duplicates and aftershocks, uses a probabilistic metric in the network error space to determine the epicenters and times of seismic events. In the present paper, a comparison and regression analysis of the different magnitude types of the integrated catalog is carried out, and based on the obtained ratios, the magnitude estimates are unified.

1. Introduction

As is known, the Eastern Sector of the Arctic zone of the Russian Federation (AZRF) is a seismically active region [1,2,3,4]. Rather strong earthquakes can occur within its limits. For example, only in the last two decades, events with magnitudes of M ≥ 6 have occurred there: the Olyutorsk earthquake, with M = 7.6, on 20 April 2006; the Ilin-Tas (Abyi) earthquake, with M = 6.6, on February 14 2013; the earthquake near the border of Kamchatka and Chukotka, with M = 6.4, on 9 January 2020; and others [5,6,7,8,9,10]. The analysis of the seismic regime of the Arctic territories of Russia and the construction of seismic hazard maps [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] are topical problems today. The solution to these problems is impossible without the creation of a representative instrumental earthquake catalog [26]. The importance of these problems for the study and development of the Arctic is emphasized by the increasing level of industrial development in the region.

Earthquake studies in the Eastern part of the AZRF started not so long ago. The authors of the New Catalog of Strong Earthquakes in the U.S.S.R. from ancient times through 1977 [27], Nikolay Shebalin and Nadezhda Kondorskaya, made the first step in these studies in the late 1970s. Intensive earthquake catalog projects concerning the AZRF were implemented in the early 2000s by V.I. Ulomov [22], V.S. Imaev, and L.P. Imaeva, B.M. Koz’min, et al. [5,6]. The seismic zonation map of the AZRF (as a part of the general seismic zoning map of Russian Federation) was created in recent years.

At the same time, there still remains a need in the AZRF representative Eastern Sector catalog which combines data from available Russian and international sources with the magnitude reduction to a uniform scale. This paper describes the results of the study on such catalog creation.

Nowadays, the seismic monitoring of the Russian Arctic is carried out by regional branches of the Geophysical Survey of the Russian Academy of Sciences (GS RAS) (http://www.gsras.ru/new/eng/catalog/, (accessed on 20 March 2022)). In the Eastern part of the Russian Arctic, this work is carried out by the Yakutsk, Magadan, and, partially, the Kamchatka Branches of the GS RAS. In addition, detailed information on earthquakes can be found in the global catalog of the International Seismological Center (ISC) (http://www.isc.ac.uk/isc-ehb/search/catalogue/, (accessed on 20 March 2022)), which combines the data from several global and national seismological networks. It has to be noted that a comparative analysis of the catalogs showed that for the Eastern Sector of the Russian Arctic, the ISC catalog does not contain many events that are presented in the regional catalogs of the GS RAS. This is explained, among other things, by the fact that the survey reports bulletins to the ISC for events starting at a certain magnitude threshold. For this reason, the information on low-magnitude seismicity is mainly contained in regional catalogs.

It should be also noted that due to the different configurations of seismic networks and methods for processing records, some agencies may skip earthquakes recorded by other networks. Thus, merging earthquake catalogs is a method for improving the completeness and representativeness of seismic events in the final catalog [28,29,30,31,32].

When merging catalogs, the problem of identifying duplicates arises. The main difficulty is discrimination [33] between aftershocks and duplicates since both of them are similar events in space and time. This problem is analogous to the discrimination between aftershocks and independent seismic events. In [34], an algorithm for merging two earthquake catalogs was developed, the main task of which was to identify the resulting duplicates and separate them from the aftershocks. The algorithm is based on the author’s modification of the nearest neighbor method [35,36] for duplicate identification. It is based on the fact that, unlike aftershocks, duplicates do not have a causal relationship. The algorithm establishes a correspondence between the events from two catalogs, after which the classification of earthquakes into unique and duplicates is performed using the Euclidean metric. The sequential application of the algorithm automates the integration of any number of earthquake catalogs. The developed algorithm efficiency was demonstrated in [34] using the example of merging the ComCat Advanced National Seismic System and the Japan Meteorological Agency catalogs for the aftershock sequence of the 2011 Tohoku earthquake.

In this paper, a unified earthquake catalog is created for the Eastern Sector of the Arctic zone of the Russian Federation. For this purpose, the following main issues are solved:

• The sequential merging of three regional catalogs of the GS RAS and the ISC catalog, which implies the identification of duplicate events in the border areas of responsibility of the different networks; and
• The unification of magnitude estimates in the integrated catalog by constructing regression relationships for the different types of magnitude/energy class due to the exact association of data from the different catalogs related to the same event.

2. Materials and Methods

The studied region represents a geographical area limited by the following coordinates: 60° N, 100° E; 77° N, 100° E; 77° N, 165° W; 57.5° N, 165° W; 57.5° N, 138° E; and 60° N, 138° E (dashed line in Figure 1). All of the following four existing earthquake catalogs for the period 1962–2020 were considered as the initial data (Table 1 and Table 2):

Figure 1. Studied region. The circles are the earthquake epicenters from the YAK (black), NER (red), and KAM (blue) catalogs.

Table 1. Data of Russian agencies.

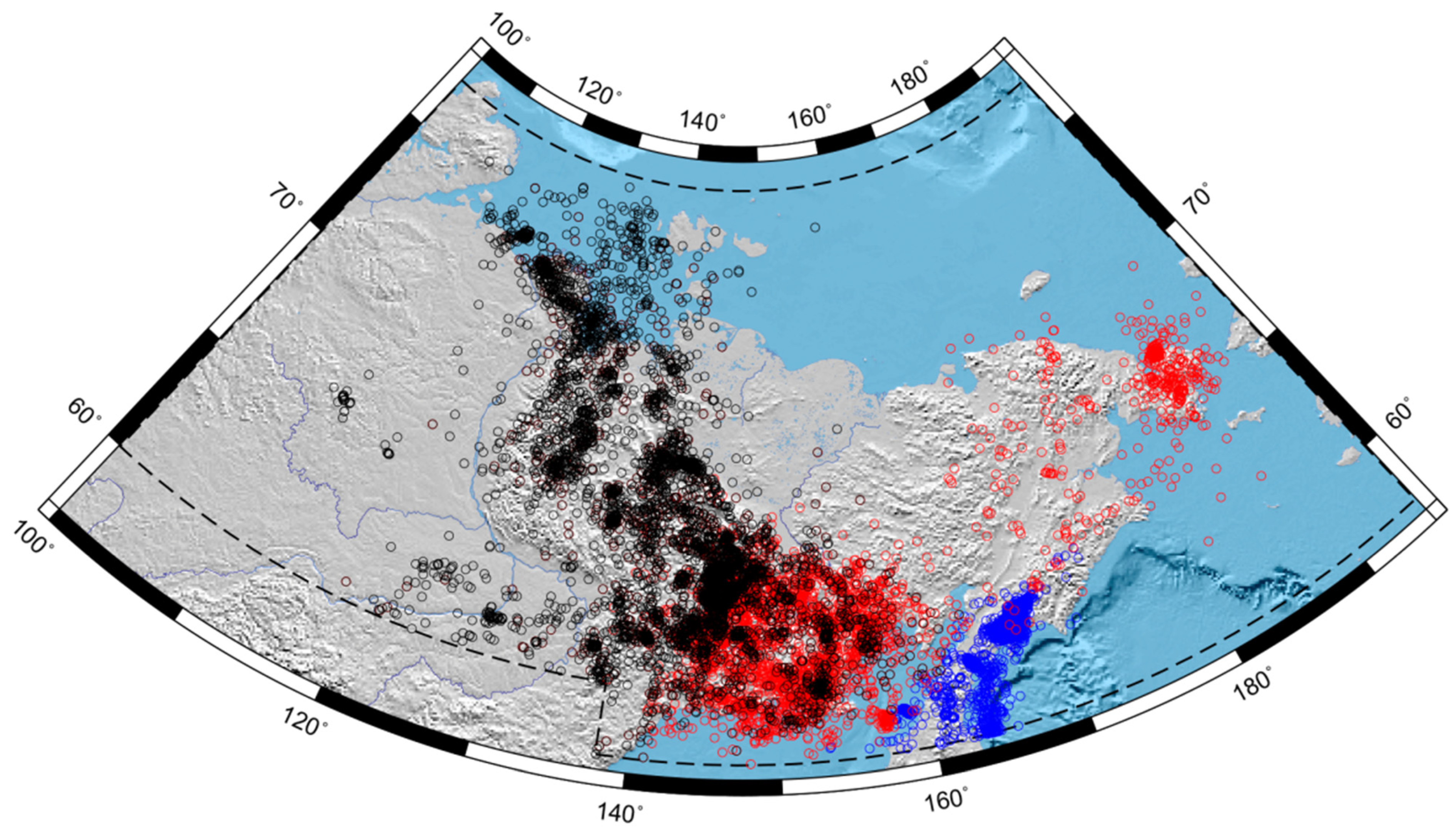
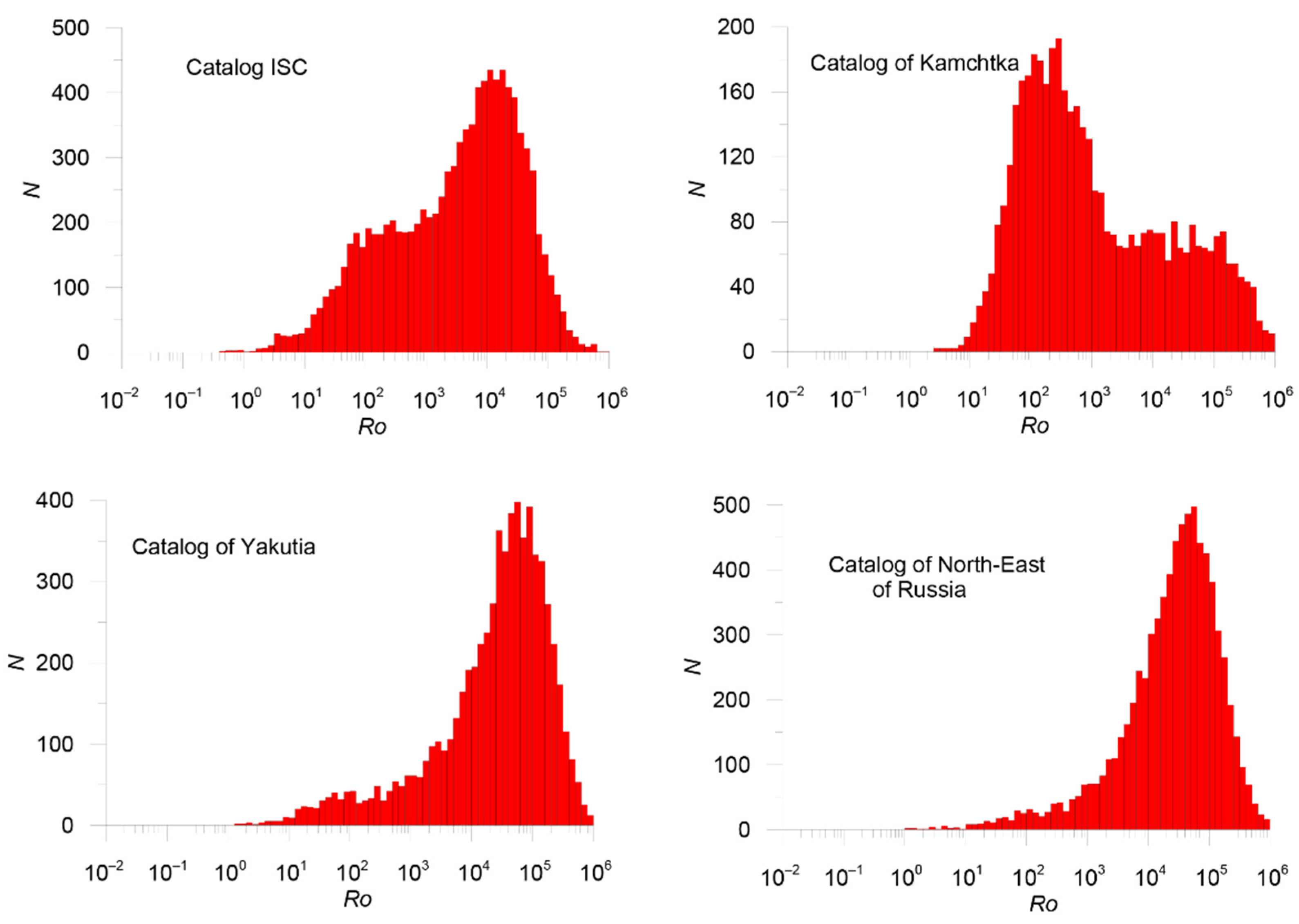
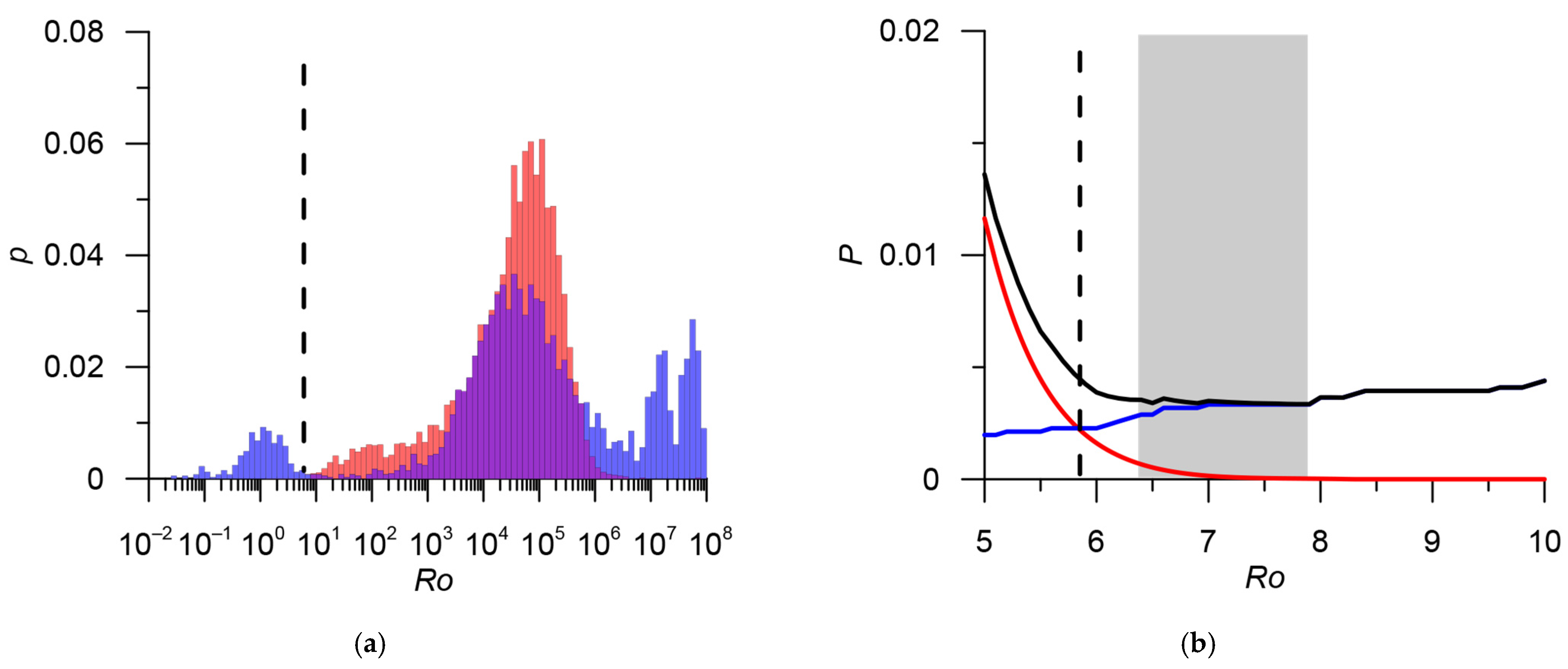
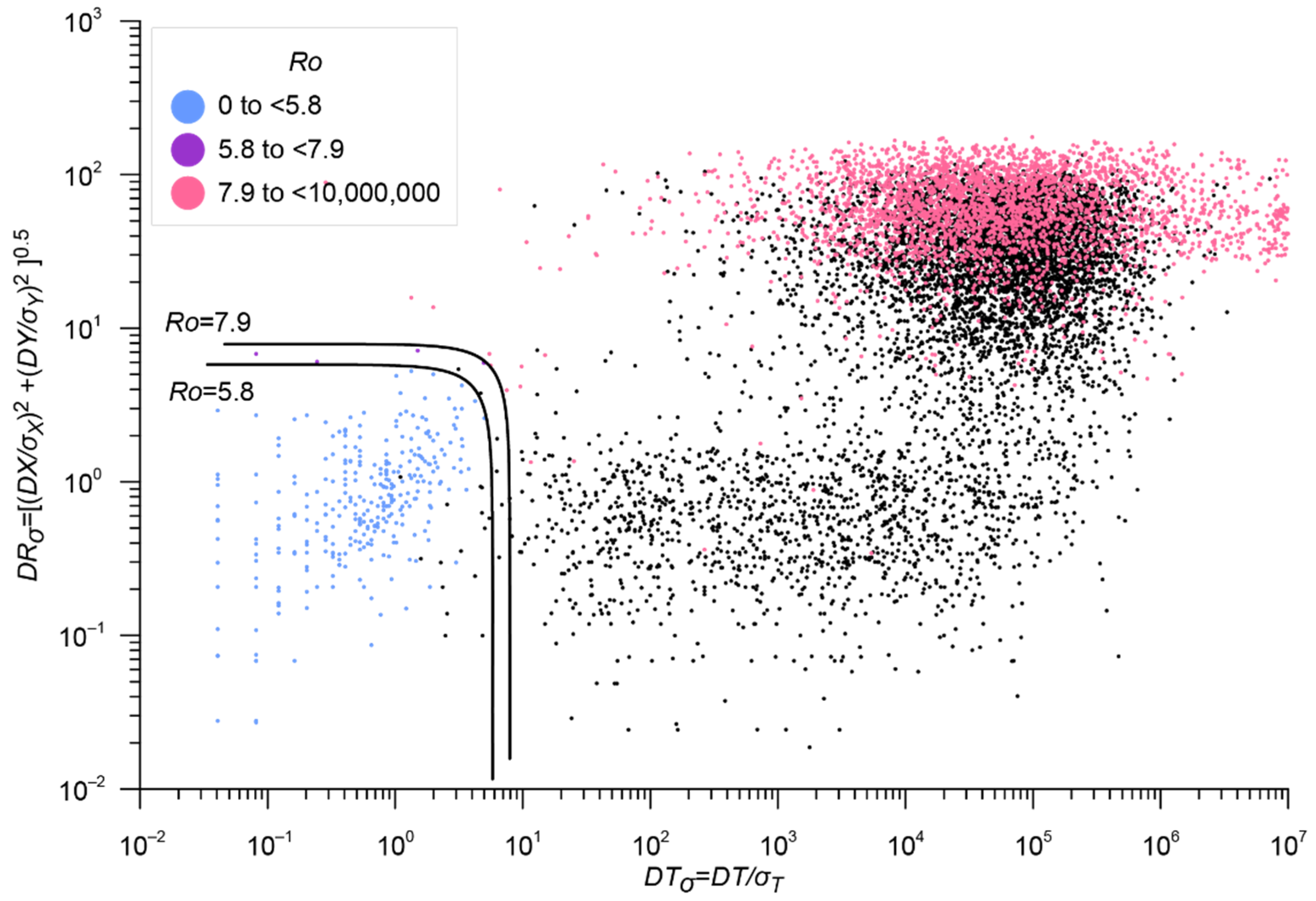
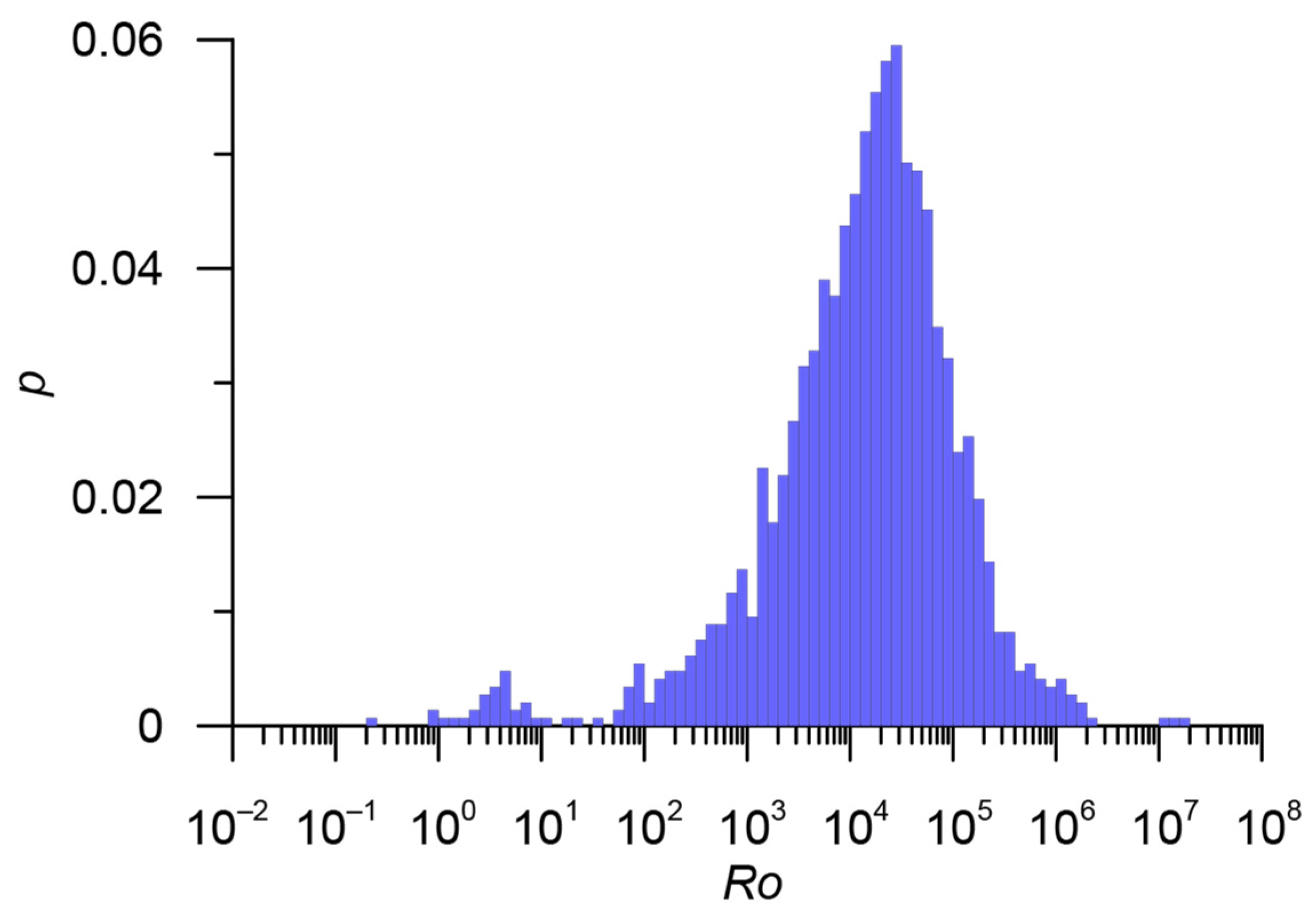
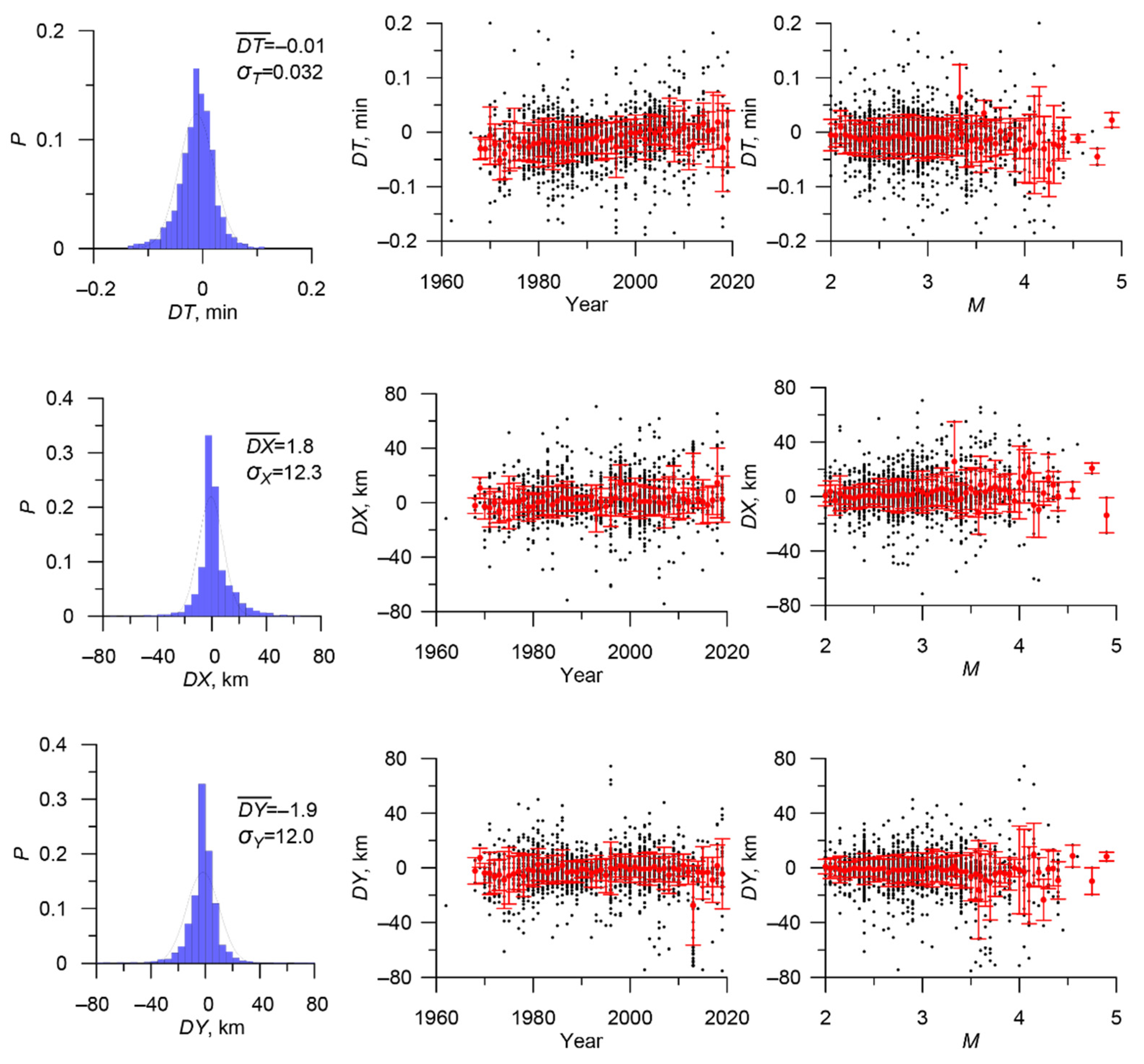
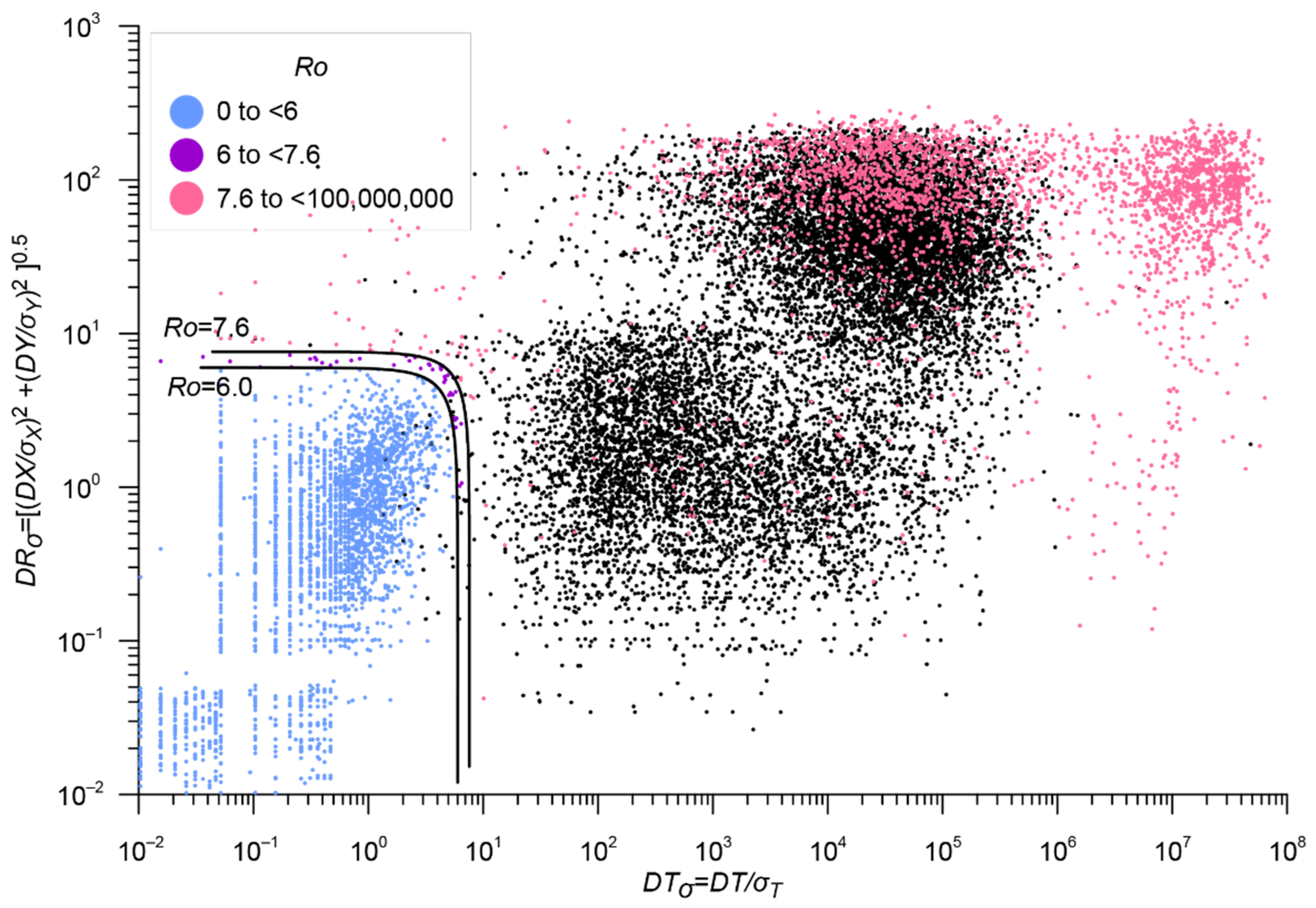
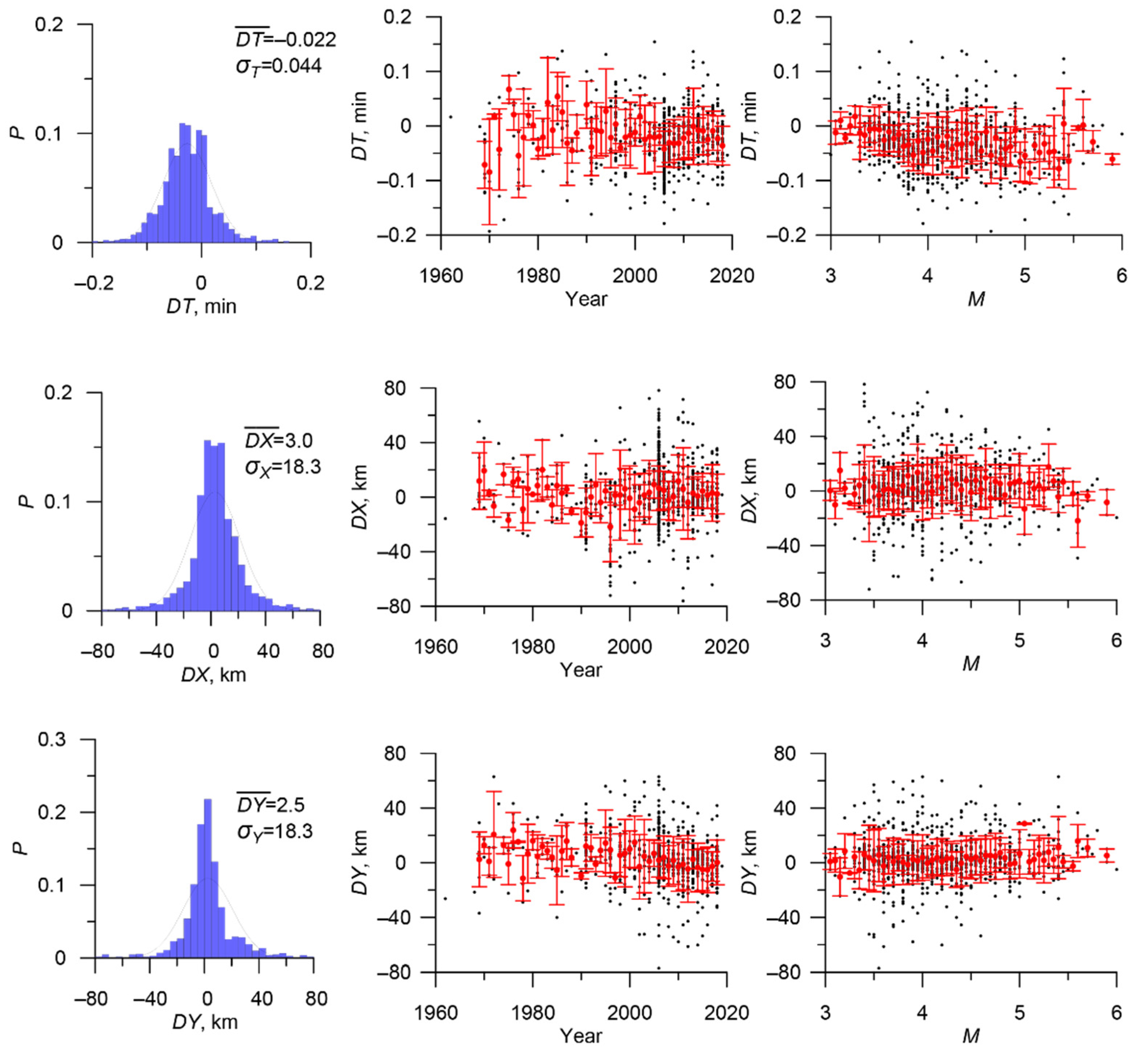
Catalog	Period	Number of Earthquakes with Energy Classes and/or Magnitudes	Number of Earthquakes with Unknown Energy Classes and Magnitudes
YAK	1962, 1968–2019	6600	46
NER	1968–2019	7668	1
KAM	1962–2019	4498	0

Table 2. ISC catalog statistics from 1962–2020.

Agency Abbreviation	Agency	Number of Earthquakes with Energy Classes and/or Magnitudes *
AEIC	Alaska Earthquake Information Center, USA	184
ANDRE	USSR	16
ANF	USArray Array Network Facility, USA	2
BJI	China Earthquake Networks Center, China	1
BYKL	Baykal Regional Seismological Centre, GS SB RAS, Russia	4
DNAG	USA	13
EIDC	Experimental (GSETT3) International Data Center, USA	22
GCMT	The Global CMT Project, USA	1
IDC	International Data Centre, CTBTO, Austria	123
ISC	International Seismological Centre, United Kingdom	1507
KRSC	Kamchatka Branch of the Geophysical Survey of the RAS, Russia	2684
MATSS	USSR	1400
MOS	Geophysical Survey of Russian Academy of Sciences, Russia	26
MSUGS	Michigan State University, Department of Geological Sciences, USA	2585
NEIC	National Earthquake Information Center, USA	192
NEIS	National Earthquake Information Service, USA	1
NERS	North Eastern Regional Seismological Centre, GS RAS, Russia	4688
NKSZ	USSR	8
SBDV	USSR	107
SYKES	Sykes Catalogue of earthquakes 1950 onwards	2
USCGS	United States Coast and Geodetic Survey, NEIC, USA	1
WASN	USA	328
YARS	Yakutiya Regional Seismological Center, GS SB RAS, Russia	2256
ZEMSU	USSR	1884
	Total:	18,035

* The ISC catalog contains 6441 events with unknown energy classes and magnitudes.

• The regional catalog of Yakutia from the annual journals Earthquakes in the USSR (1962–1991), Earthquakes in Northern Eurasia (1992–2014), and Earthquakes in Russia (2015–2019) (GS RAS) (hereinafter YAK);
• The regional catalog of the northeast of Russia from the annual journals Earthquakes in the USSR (1968–1991), Earthquakes in Northern Eurasia (1992–2014), and Earthquakes of Russia (2015–2019) (GS RAS) (hereinafter NER);
• The regional catalog of earthquakes in Kamchatka of the Kamchatka Branch of the GS RAS, 1962–2019 (hereinafter KAM); and
• The ISC 1962–2020 catalog, which is a composite catalog containing data from many world and Russian agencies.

It has to be noted that the technique developed in [34] allows the pairwise merging of earthquake catalogs. Thus, any two chosen catalogs are merged in the first step. Then, another catalog is merged with them, and so on. At the same time, we emphasize that the list of events in the integrated catalog weakly depend on the sequence of pairwise merging. It was shown in [34] that the merging procedure is symmetric. In other words, when two catalogs are merged, the same events are selected as duplicates, regardless of the catalogs’ merging sequence. The only difference will be which version of the earthquake record (from which input catalog) falls into the merged catalog.

We believe that earthquake identification based on global network data is the most reliable. A subset of these events from the ISC catalog is the core—the main catalog to which other catalogs will be added. The core only contains information about strong and moderate earthquakes in the region because weak earthquakes are not registered by global networks. Further, it is logical to add data from local networks, which provide information about weak earthquakes in the region. In the final merge step, we use the data from the ISC catalog that was not included in the core. Thus, to merge catalogs (Table 1 and Table 2), the following sequence for sources of the initial data was chosen:

• Earthquakes from the ISC global catalog (the abbreviation of the ISC and GCMT agency in Table 2) with the magnitudes M_W^GCMT and/or mb^ISC are the core (hereinafter CORE) (1393 events);
• Earthquakes from Russian catalogs with local estimates for the magnitude of weak events. In the intersection zones, preference is given to the data from the catalog of Yakutia (Table 1);
• Other earthquakes from the ISC (abbreviation of the ISC agency in Table 2, without the magnitude data M_W^GCMT or mb^ISC), as well as data from other agencies in the ISC catalog (16,642 events). This selection from the ISC catalog will be further denoted by ISC_Other.

To discriminate and remove duplicates resulting from the merging of catalogs, we apply the modified nearest neighbor method and the Euclidean metric in the space of the variance in the definitions of seismic event parameters by different networks [34]. We apply a basic three-parameter model that takes into account the differences in time and the coordinates of the epicenter, the effectiveness of which was shown in [34]. We do not analyze the difference in depth because for a significant number of events, information on the hypocentral depth is not presented in the original catalogs or a standard value of 10 km is given. The magnitude is also excluded from consideration because different catalogs use different types of magnitude.

At the input, there are two catalogs: main Catalog 1 and additional Catalog 2. We believe that neither Catalog 1 nor Catalog 2 contain duplicates within themselves, since the modern automatic processing of seismic records almost completely eliminates technical errors. The problem is to find records in Catalogs 1 and 2 that will correspond to the same seismic events (duplicates) and divide Catalog 2 into events that have duplicates in Catalog 1 and unique events.

A modification of the nearest neighbor method is based on the assumption that duplicates form pairs in which the events must belong to different source catalogs. As a result of applying the modified nearest neighbor method, a set of pairs of potential duplicates is formed. We consider the events of the additional Catalog 2, with the value of the neighborhood function as less than the threshold one, as duplicates. The rest of the Catalog 2 events are declared unique and added to Catalog 1. Further, any number of catalogs can be sequentially added.

The choice of the proximity function is based on a probabilistic model. We assume that the difference in earthquake detection by different networks is a random variable with a normal distribution and zero mean for each of the parameters:

$$f\left(DT\right)=\frac{1}{{\sigma }_T\sqrt{2\pi }}\exp \left(-\frac{D{T}^2}{2{\sigma }_T{}^2}\right),$$

$$f\left(DX\right)=\frac{1}{{\sigma }_X\sqrt{2\pi }}\exp \left(-\frac{D{X}^2}{2{\sigma }_X{}^2}\right),$$

$$f\left(DY\right)=\frac{1}{{\sigma }_Y\sqrt{2\pi }}\exp \left(-\frac{D{Y}^2}{2{\sigma }_Y{}^2}\right).$$

Here DT, DX, and DY are the differences in time, longitude, and latitude, respectively, between different determinations of a seismic event, and ${\sigma }_T$, ${\sigma }_X$, and ${\sigma }_Y$ are the corresponding standard deviations. If we assume that all errors are independent, then the duplicate probability density will be the product of the error probabilities for all parameters. This will be the multivariate normal distribution, as follows:

$$f\left(DT,DX,DY\right)=\frac{1}{{\sigma }_T{\sigma }_X{\sigma }_Y{\left(2\pi \right)}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}} ·\exp \left(-\left(\frac{D{T}^2}{2{\sigma }_T{}^2}+\frac{D{X}^2}{2{\sigma }_X{}^2}+\frac{D{Y}^2}{2{\sigma }_Y{}^2}\right)\right).$$

Thus, we naturally arrive at the Euclidean metric:

$$Ro=\sqrt{\frac{D{T}^2}{{\sigma }_T{}^2}+\frac{D{X}^2}{{\sigma }_X{}^2}+\frac{D{Y}^2}{{\sigma }_Y{}^2}}$$

(1)

The preliminary identification of duplicates is done with the standard metric parameters in (1): ${\sigma }_{0T}=0.05$ min and ${\sigma }_{0X}={\sigma }_{0Y}=15$ km. The initial values of the parameters have little effect on the identification of duplicates; however, they significantly affect the value of the duplicate probability and the estimate of the percentage of errors. At this stage, we check that each of the parameters follows a normal distribution, and we refine the values of the standard deviations ${\sigma }_T$, ${\sigma }_X$, and ${\sigma }_Y$. After that, the final identification of duplicates is performed. The choice of the optimal metric threshold for identifying duplicates and the estimation of the percentage of errors will be explained in detail below.

Before proceeding with the merging process of the four catalogs, we checked each of them for internal duplicates. For this reason, we built the distribution of metric (1) for the nearest events within each catalog (Figure 2). The analysis was performed with the metric parameters ${\sigma }_T=0.05$ min and ${\sigma }_X={\sigma }_Y=15$ km. As a result of the analysis, no events with the same time and epicenter coordinates were found in any of the four catalogs. For such events, Ro = 0, and, thereafter, we will call them absolute duplicates. Statistical analysis also did not reveal anomalous groups of nearest events. The duplicates are characterized by the value Ro < 10. The value Ro = 10 corresponds to a distance of 150 km or a time interval of 0.5 min. From our experience, we know that duplicates have smaller differences in instrumental catalogs, and the number of such nearest events within each of the catalogs is very small. These are mainly the early aftershocks of the Olyutorsk earthquake, with M = 7.6, on 20 April 2006, and the Ilin-Tas earthquake, with M = 6.6, on 14 February 2013. There is no reason to consider such events as duplicates since the early aftershocks can occur at very small distances and time intervals. Thus, the necessary condition for applying the method in [34] is met.

Figure 2. Distribution of metric (1) for events within the source catalogs (Table 1 and Table 2). The catalogs are indicated on the histograms.

3. Results

3.1. Merging Catalogs

At the initial stage, the regional data from the catalogs of the Russian agencies YAK, NER, and KAM were merged and then combined with ISC data. The earthquakes with unknown magnitudes/classes were not included in the merging. Below is a sequence of the stages of merging the catalogs.

3.1.1. Stage 1. Merging YAK and NER

YAK was considered as the main catalog and NER as the additional one. The preliminary analysis of duplicates was performed with the distribution parameters ${\sigma }_T=0.05$ min and ${\sigma }_X={\sigma }_Y=15$ km. As a result, 1834 absolute duplicates and about 370 potential duplicates (events with a small metric) were identified. The preliminary threshold was determined by the minimum distribution of the metric. Absolute duplicates were not used to determine the dispersions (Figure 3). It was verified that each of the parameters followed a normal distribution and that the mean was small compared to the standard deviation for all three parameters (DT, DX, and DY). It was also verified that the variance was almost independent of the event magnitude and time (Figure 3).

Figure 3. Distributions of DT, DX, and DY for the nearest events from the YAK and NER catalogs, and the dependence of the standard deviations ${\sigma }_T$, ${\sigma }_X$, and ${\sigma }_Y$ and the mean values $\overline{DT}, \overline{ DX}, \mathrm{and} \overline{DY}$ on the time and magnitude of the events. The red dots and bars are the population mean values and standard deviations, respectively.

The final duplicate analysis was performed with the parameters ${\sigma }_T=0.041$ min, ${\sigma }_X=17.4$ km, and ${\sigma }_Y=16.3$ km. The metric values between the nearest events of the YAK catalog were also calculated. This made it possible to estimate the probability that the duplicate was chosen incorrectly due to the high density of earthquakes. Figure 4a shows the distributions of metric (1) for the YAK/NER pairs and the same metric for the YAK/YAK earthquakes (the algorithm for calculating the metric is the same as for two different catalogs, but only the comparison of the earthquake with itself is excluded). A group of anomalously close YAK/NER events is identified well. The optimization of the threshold value of the metric is illustrated in Figure 4b. The red line is the probability of missing a duplicate in the 3D normal distribution model (error of the first kind) and the blue line is the probability of a false duplicate (error of the second kind), which is defined as the ratio of the number of YAK/YAK pairs for a given value of the metric Ro to the number of events in the YAK catalog.

Figure 4. (a) Comparison of the metric distribution for YAK/NER pairs (blue histogram) and the same metric for YAK/YAK earthquakes (red histogram). (b) Threshold optimization: the red line shows the probability of missing a duplicate in the model with metric (1), the blue line is the probability of a false duplicate (see text), the black line is the total probability of errors of the first and second kind, the dashed line Ro = 5.8 corresponds to an equal number of errors of the first and of the second kind (the number of false duplicates is equal to the number of missed duplicates), the estimate of the total number of errors is approximately 0.5%, and the gray bar shows the range of values for the metric Ro = 6.3 ÷ 7.9, minimizing the total number of errors (approximately 0.4%).

An equal number of errors of the first and second kind is achieved at Ro = 5.8. In the NER catalog, only 15 earthquakes have a distance to the nearest neighbor of Ro < 5.8. This made it possible to estimate the probability that the duplicate was chosen incorrectly due to the high density of earthquakes. The upper estimate of the probability of false duplicates P = 15/6600 = 0.0023 is approximately 0.25%. At Ro = 7.9, the number of such earthquakes increases to 26, which corresponds to a probability of 0.4% (see the blue line in Figure 4b).

The choice of the metric threshold for identifying duplicates depends on the objective of further research of the integrated catalog. If it is important to ensure that duplicates are removed, then a higher Ro threshold is preferable. If it is important to keep the integral characteristics of the catalog, then the Ro threshold that ensures the equality of errors of the first and second kind is preferable.

We chose the threshold Ro = 5.8. In this case, in addition to 1834 absolute duplicates, 319 more duplicates were identified. In total, 5515 unique events were identified in the NER catalog in the study area. These events were added to the YAK catalog, and thus a merged YAK_NER catalog containing 12,115 events was obtained. Figure 5 shows the spatio–temporal structure of the YAK/NER duplicates and the naturally grouped events in the YAK catalog. The metric values for earthquakes in the YAK catalog are significantly larger than those for the YAK/NER duplicates. The metric (1) level lines provide a close-to-optimal separation of duplicates and naturally grouped events (the lower cluster of black dots).

Figure 5. Distribution of normalized DT and DR and metric level lines (1). The colored dots are YAK/NER pairs and the black dots are the distances between YAK/YAK events in metric (1). The metric levels Ro = 5.8 and Ro = 7.9 are shown by black lines, and absolute duplicates are not shown.

3.1.2. Stage 2. Merging YAK_NER and KAM into the RUS Catalog

The catalog YAK_NER, obtained in the previous step, was taken as the main one, with KAM as an additional catalog. The preliminary analysis of the duplicates was performed with the distribution parameters determined for the NER and YAK catalogs: ${\sigma }_T=0.041$ min, ${\sigma }_X=17.4$ km, and ${\sigma }_Y=16.3$ km. Twenty-eight potential duplicates were identified (Figure 6), which is not enough to determine the variances. For this reason, the metric parameters defined for the YAK and NER catalogs were used. With Ro = 5.8, the KAM catalog contains 26 duplicates and 4472 unique events that have been added to the YAK_NER catalog. The merged RUS catalog obtained in this way contains 16,587 events.

Figure 6. Metric distributions for the YAK_NER and KAM pairs.

3.1.3. Stage 3. Merging RUS and Data from the ISC_Other Catalog

The ISC catalog contains a large amount of data from Russian agencies (Table 2). Accordingly, at this stage of the merging procedure, a large number of duplicates, including absolute ones, are expected.

When merging, the catalog RUS obtained at Stage 2 was taken as the main one and ISC_Other was taken as the additional. The resulting catalog will be designated RUS_ISC. The preliminary analysis of duplicates was performed with the standard distribution parameters ${\sigma }_T=0.05$ min, ${\sigma }_X=15$ km, and ${\sigma }_Y=15$ km (Figure 7).

Figure 7. Distributions of DT, DX, and DY for the nearest events from the RUS and ISC_Other catalogs, and the dependence of the standard deviations ${\sigma }_T$, ${\sigma }_X$, and ${\sigma }_Y$ and the mean values $\overline{DT}, \overline{DX}, and \overline{DY}$ on the time and magnitude of the events. The red dots and bars are the population mean values and standard deviations, respectively.

More than 10,000 potential duplicates have been identified, about 5000 of which have the same times and/or epicenters. Such pairs represent the same registration of events by the networks of the GS RAS, which are included in the Russian catalogs and the ISC catalog. They were excluded to determine the variances. We have verified that each of the parameters follows a normal distribution and that the mean is small compared to the standard deviation for all three parameters (DT, DX, and DY) (Figure 7). It was also verified that the variance is almost independent of the event magnitude and time. The final analysis of duplicates was performed with the parameters ${\sigma }_T=0.032$ min, ${\sigma }_X=12.3$ km, and ${\sigma }_Y=12.0$ km. We calculated the metric values between events of the RUS catalog. This made it possible to estimate the probability that the duplicate was determined incorrectly due to the high density of earthquakes.

We chose the threshold Ro = 6.0 (Figure 8). In this case, in addition to 4802 absolute duplicates, another 5706 potential duplicates are identified. Many pairs of earthquakes have the same time or the same coordinates of the epicenter, and 73 of such pairs have large metric values of Ro > 6. An analysis of these pairs indicates that the records in the RUS and ISC catalogs differ in one digit. Most likely, these are technical errors of the era of manual information entry, which were corrected when compiling the catalog Earthquakes of Northern Eurasia. These events are considered to be duplicates and they are not included in the integrated catalog, despite the large values of the metric.

Figure 8. (a) Comparison of the metric distribution for RUS/ISC_Other pairs (blue histogram) and the same metric for RUS/RUS earthquakes (red histogram). (b) Threshold optimization: the red line is the probability of missing a duplicate in the model with metric (1), the blue line is the probability of a false duplicate, the black line is the total probability of errors of the first and second kind, the dashed line Ro = 6.0 corresponds to an equal number of errors of the first and second kind (number of false duplicates is equal to the number of missed duplicates), the estimate of the total number of errors is approximately 0.3%, and the gray bar shows the range of values for the metric Ro = 6.7 ÷ 7.6, minimizing the total number of errors (approximately 0.2%).

Figure 9 shows the spatio–temporal structure of the duplicates in RUS/ISC_Other and the naturally grouped events in the RUS catalog. The metric values for the earthquakes in the RUS catalog are significantly larger than for the RUS/ISC_Other duplicates. The metric level lines Ro = 6 and Ro = 7.6 provide close-to-optimal separation of the duplicates and naturally grouped events (the lower cluster of black dots). In total, for the studied territory there are 6411 unique events in the ISC_Other catalog. These events have been added to the RUS catalog. The merged catalog RUS_ISC contains 22,998 events.

Figure 9. Distribution of normalized DT and DR, and metric level lines (1). The colored dots are the RUS/ISC_Other pairs and the black dots are the distances between the RUS/RUS events in metric (1). The metric levels Ro = 6 and Ro = 7.6 are shown by the black lines, and absolute duplicates are not shown.

3.1.4. Stage 4. Merging RUS_ISC and CORE

As the main catalog selected, CORE includes events from the ISC catalog with the magnitudes M_W^GCMT or mb^ISC. As an additional catalog, we consider RUS_ISC, obtained at the previous stage. The preliminary analysis of the duplicates was performed with the standard catalog distribution parameters ${\sigma }_T=0.05$ min, ${\sigma }_X=15$ km, and ${\sigma }_Y=15$ km. Approximately 1000 duplicates were identified and used to determine the variances. It was verified that each of the parameters follows a normal distribution and that the mean is small compared to the standard deviation for all three parameters (DT, DX, and DY). It was also verified that the variance is almost independent of the event magnitude and time (Figure 10).

Figure 10. Distributions of DT, DX, and DY for the nearest events from the CORE/RUS_ISC catalogs, and the dependence of the standard deviations ${\sigma }_T$, ${\sigma }_X$, and ${\sigma }_Y$ and the mean values $\overline{DT}, \overline{DX}, \mathrm{and} \overline{DY}$ on the time and magnitude of the events. The red dots and bars are the population mean values and standard deviations, respectively.

The final analysis of the duplicates was performed with the parameters ${\sigma }_T=0.044$ min and ${\sigma }_X={\sigma }_Y=18.3$ km. The metric values between the events of the CORE catalog were also calculated. This made it possible to estimate the probability that the duplicate was chosen incorrectly due to the high density of earthquakes.

The value Ro = 5.9 was chosen as a threshold (Figure 11). In this case, 1011 duplicates are detected. In total for the studied territory, there are 21,987 unique events in the RUS_ISC catalog. These events were added to the CORE catalog, and a combined ARCTIC catalog containing 23,370 events was obtained. Figure 12 shows the space–time structure of the CORE/RUS_ISC duplicates and the naturally grouped events in the CORE catalog. The metric level lines Ro = 5.9 and Ro = 8.4 provide close-to-optimal separation of the duplicates and naturally grouped events (the lower cluster of black dots).

Figure 11. (a) Comparison of the distribution of the metric for the CORE/RUS_ISC pairs (blue histogram) and the same metric for the CORE/CORE earthquakes (red histogram). (b) Threshold optimization: the red line is the probability of missing a duplicate in the model with metric (1), the blue line is the probability of a false duplicate, the black line is the total probability of errors of the first and second kind, the dashed line Ro = 5.9 corresponds to an equal number of errors of the first and second kind (number of false duplicates is equal to the number of missed duplicates), the estimate of the total number of errors is approximately 0.4%, and the gray bar shows the range of values of the metric Ro = 6.5 ÷ 8.4, minimizing the total number of errors (approximately 0.3%).

Figure 12. Distribution of normalized DT and DR and metric level lines (1). The colored dots are the CORE/RUS_ISC pairs and the black dots are the distances between the CORE/CORE events in metric (1). The metric levels Ro = 5.9 and Ro = 8.4 are shown by lines.

3.1.5. Stage 5. Exclusion of Explosions

At the final stage, we check the catalog for any type of explosion. The information about the 12 explosions in the ISC catalog is given in the ISC bulletins. In addition, 104 events are labeled “exp” or “exp?” in the NER and YAK catalogs from the annual journal Earthquakes in Northern Eurasia. In the annual journal Earthquakes in Russia, explosions are excluded by the authors. We merged all explosions into the EXP catalog and performed duplicate analysis.

We choose EXP as the main catalog and ARCTIC, which was obtained as a result of combining ISC and Russian data, as the additional one. The duplicate analysis was performed with the standard distribution parameters ${\sigma }_T=0.05$ min and ${\sigma }_X={\sigma }_Y=15$ km. All 116 events of the EXP catalog are absolute duplicates of the events from the ARCTIC catalog. After the explosions were removed, the final integrated catalog of the Eastern Sector of the Arctic zone of the Russian Federation, E_ARCTIC, contains 23,254 events. The assembly scheme, statistics, and parameters for excluding duplicates are presented in Table 3.

Table 3. Scheme and compilation parameters of the integrated catalog.

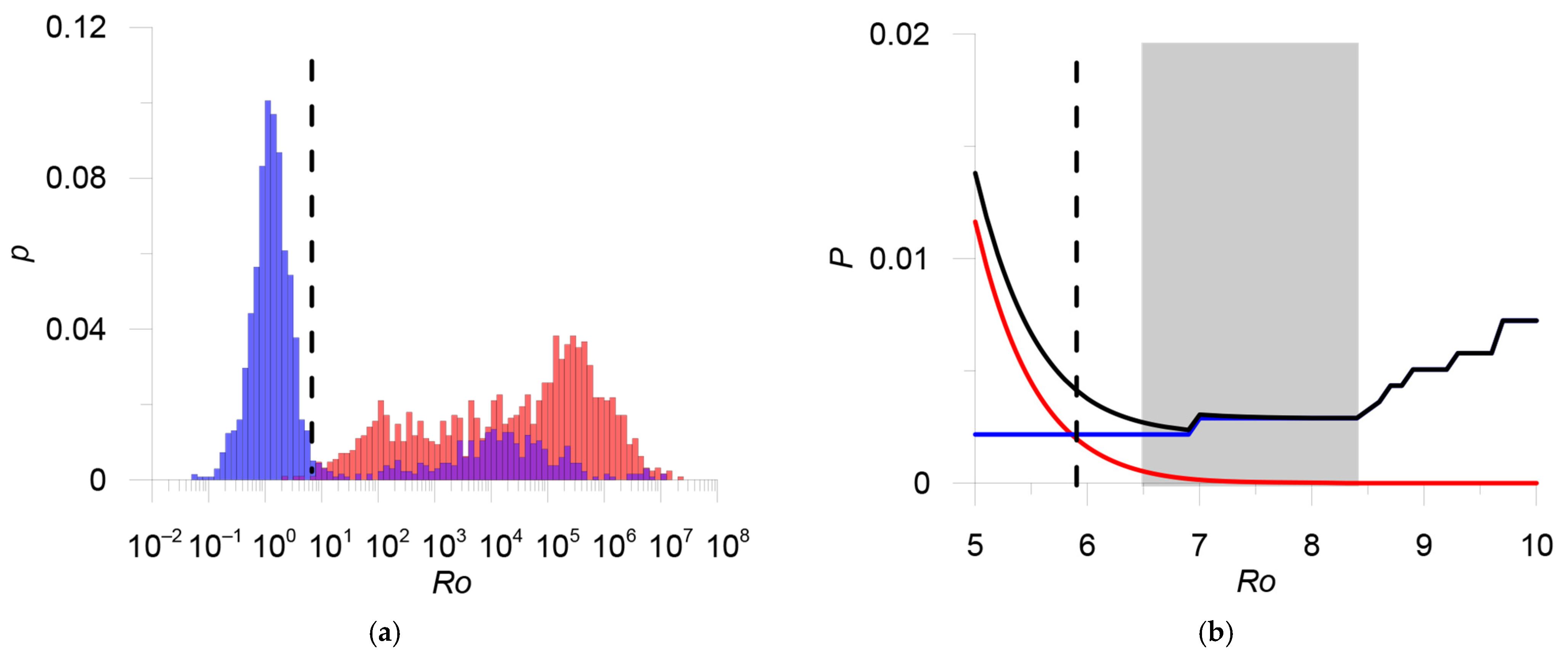
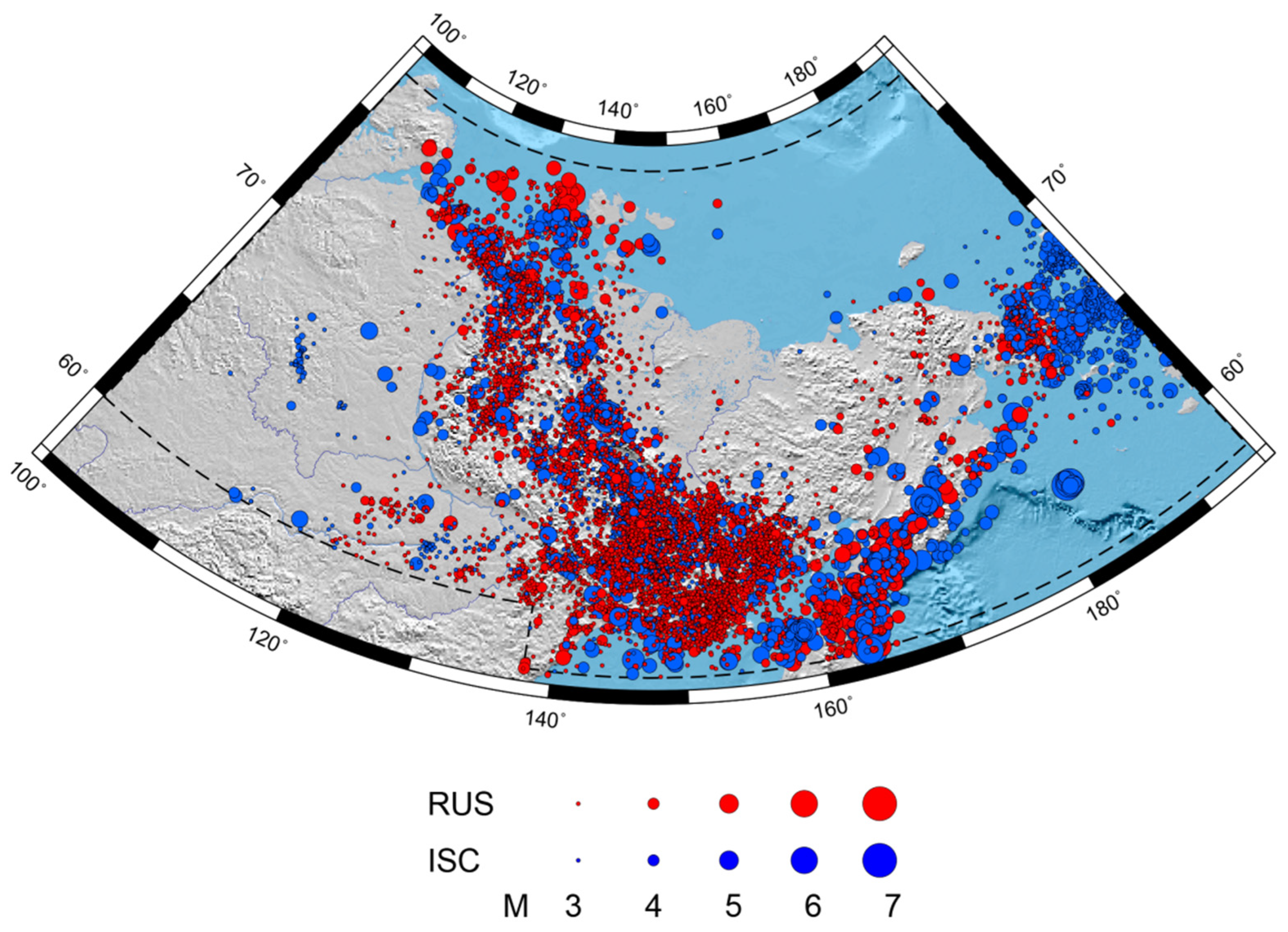
Stage	Main Catalog	Additional Catalog	$\mathbf{Metric}\mathbf{Parameters}{\mathit{\sigma }}_{\mathit{T}}$$\mathbf{min},{\mathit{\sigma }}_{\mathit{X}}$$\mathbf{km},\mathbf{and}{\mathit{\sigma }}_{\mathit{Y}}\mathbf{km}$	Threshold Value of the Metric	Estimation of the Number of Errors	Number of Duplicates	Merged Catalog
1	Catalog of Yakutia YAK 6600 events	Catalog of the Northeast of Russia NER 7668 events	0.041; 17.4; 16.3	5.8	0.5%	2153	YAK_NER 12,115 events
2	YAK_NER 12,115 events	Earthquake catalog of the Kamchatka Branch of the GS RAS KAM 4498 events	0.041; 17.4; 16.3	5.8 *	–	26 *	RUS 16,587 events
3	RUS 16,587 events	ISC, events of various agencies ISC_Other 16,642 events	0.032; 12.3; 12.0	6.0	0.3%	10,231	RUS_ISC 22,998 events
4	CORE 1383 events	RUS_ISC 22,998 events	0.044; 18.3; 18.3	5.9	0.4%	1011	ARCTIC 23,370 events
5	Exclusion of explosions EXP 116 events	ARCTIC 23,370 events	0.05; 15.0; 15.0	–	0%	116 **	E_ARCTIC 23,254 events

* A small number of duplicates does not allow estimating the number of errors and optimizing the metric threshold. ** All duplicates are absolute.

3.2. Magnitudes in the Integrated Catalog of the Eastern Sector of the Russian Arctic

The integrated catalog of the Eastern Sector of the Russian Arctic contains 23,254 events that have different types of magnitude estimates determined by different agencies (Table 4). It is necessary to unify them (bring them to the reference scale of magnitudes).

Table 4. Magnitudes in the unified catalog of the Eastern Sector of the Russian Arctic.

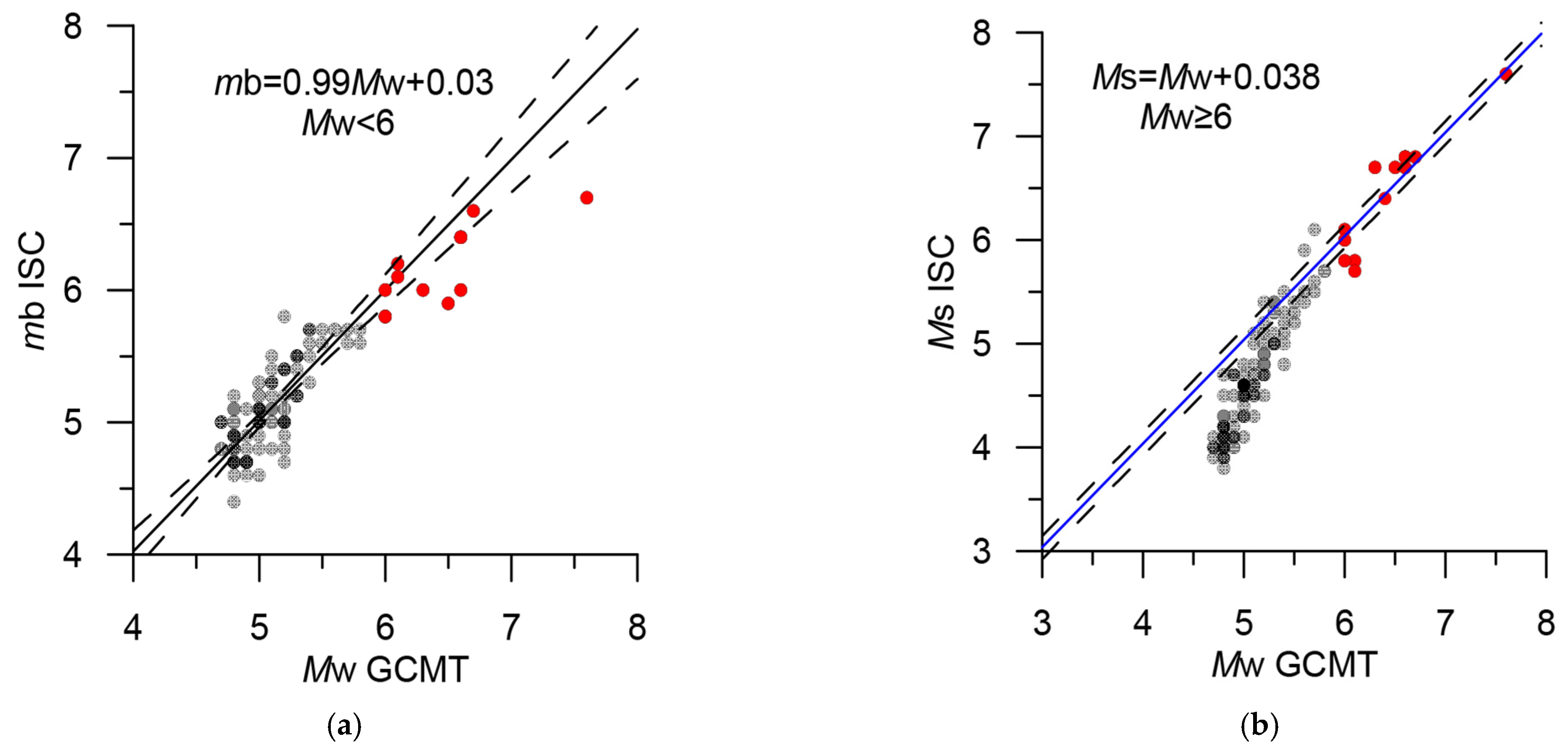
Agency	Type of Magnitude	Priority	Number of Events	Formula for Magnitude in the Integrated Catalog	Figure	Mmin–Mmax. Initial Magnitude Scale	Note
GCMT	MW	1	105	M = MWGCMT		4.7–7.6
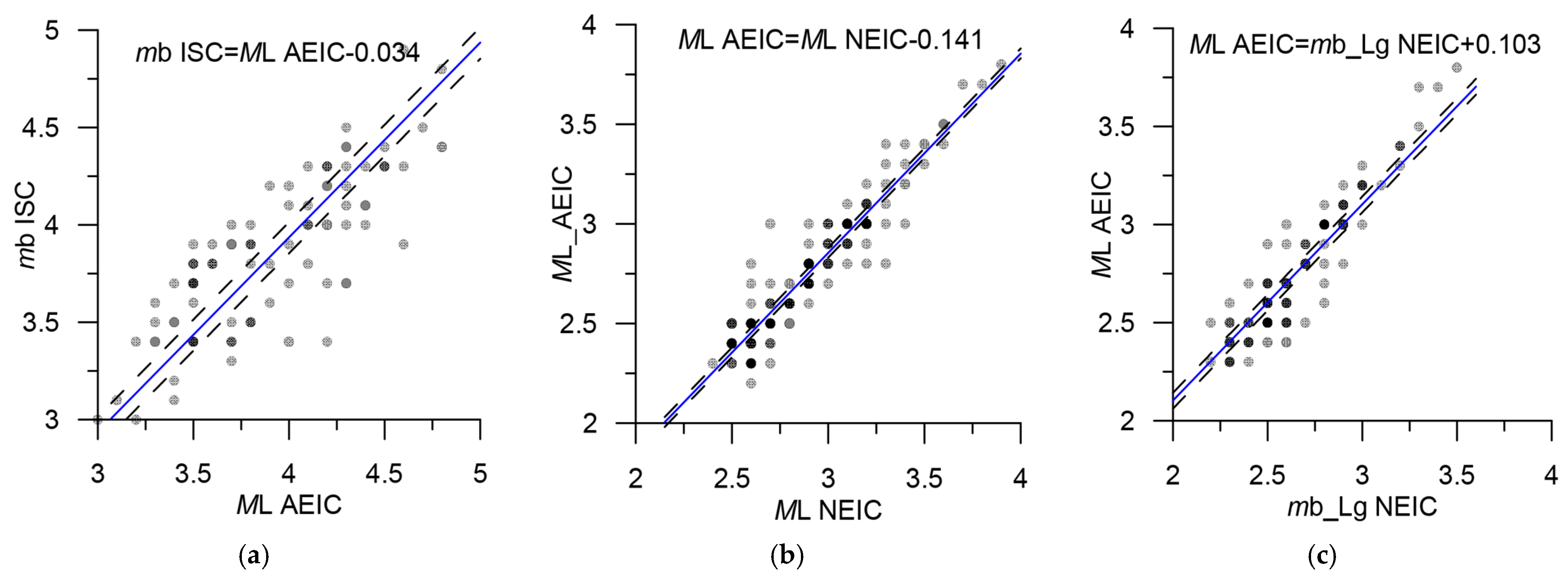
ISC	mb	2	1287	M = mbISC	Figure 13a	3.0–5.9
ISC	MS	1	4	M = MSISC	Figure 13b	5.7–7.5	Strong events before 1976
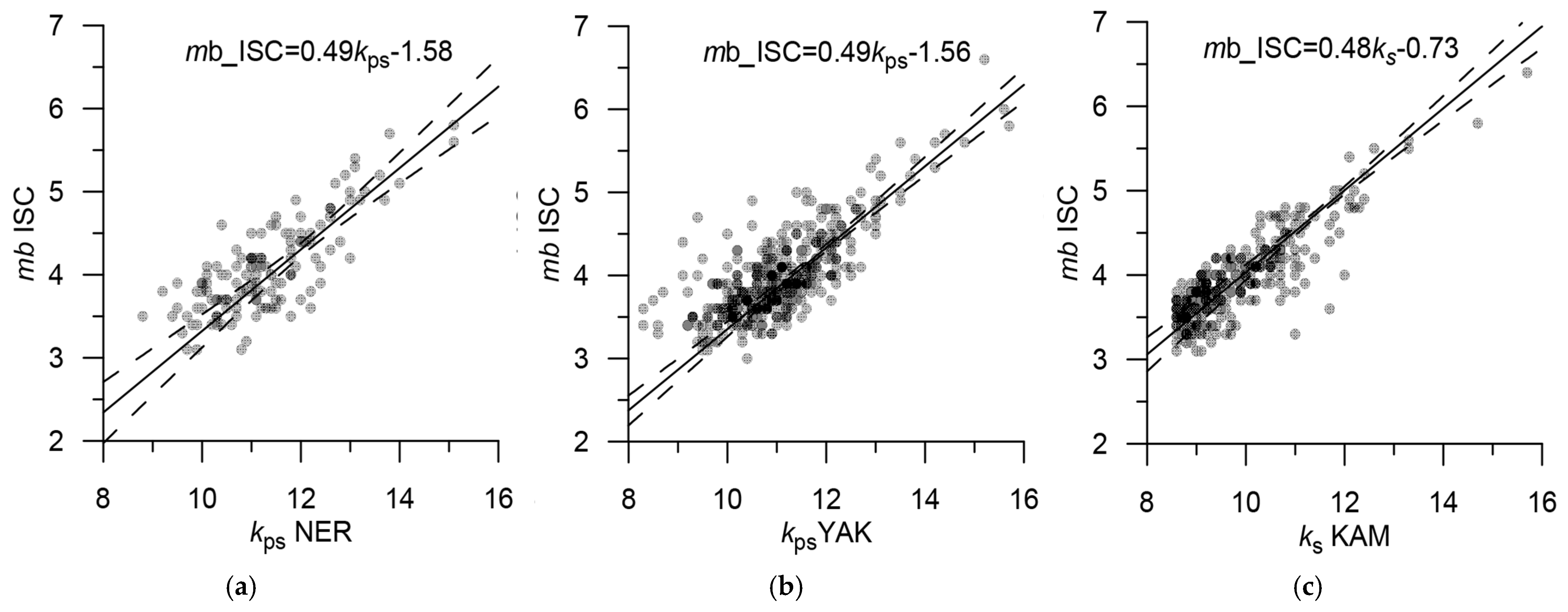
YAK, NER, agencies of Russia and the USSR from ISC	KPS	3	16,301	M = 0.5 KPS − 1.6	Figure 14a,b	0.6–14.0	Information about energy classes is given in the ISC bulletins
KAM, KRSC	KS	3	4050	M = 0.5KS − 0.75	Figure 14c	3.0–13.1
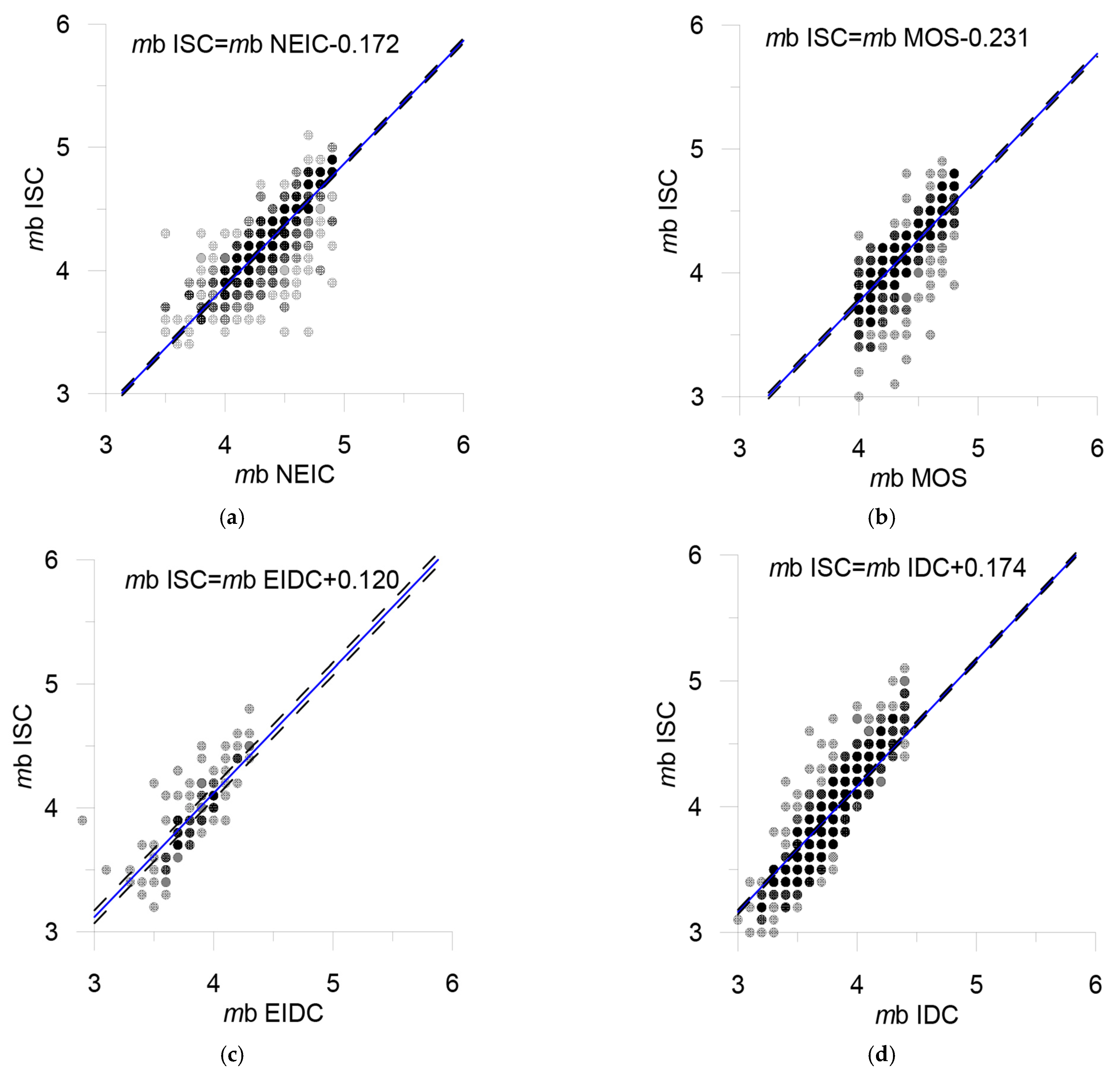
NEIC, NEIS	mb	4	27	M = mbNEIC − 0.2	Figure 15a	3.5–4.9
MOS	mb	4	16	M = mbMOS − 0.2	Figure 15b	4.0–4.8
EIDC	mb	4	24	M = mbEIDC + 0.2	Figure 15c	3.0–4.3
IDC	mb	4	107	M = mbIDC + 0.2	Figure 15d	2.9–4.4
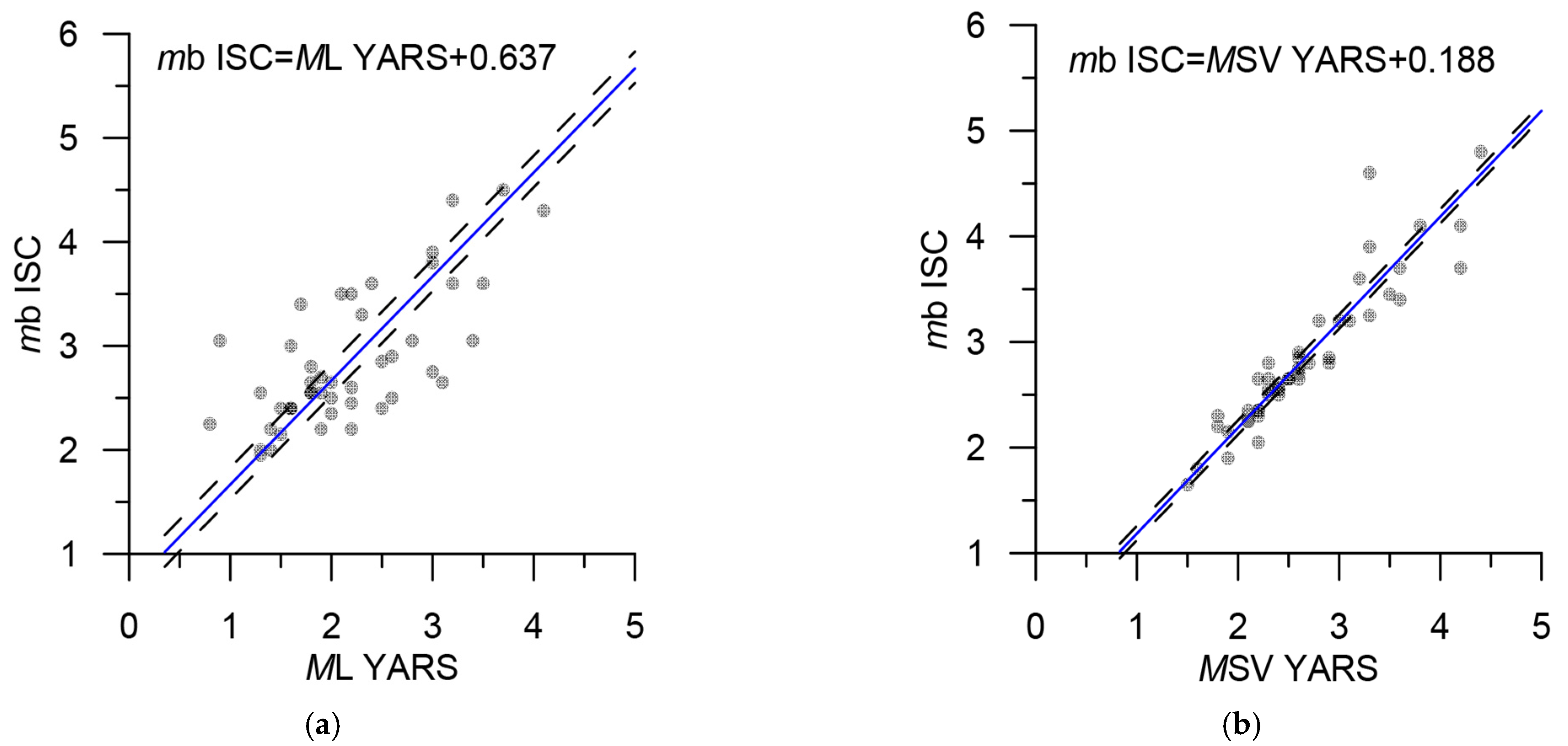
YARS	ML	4	357	M = MLYARS + 0.6	Figure 16a	0.5–3.0	Unreliable correlation
YARS	MSV	4	95	M = MSVYARS + 0.2	Figure 16b	0.0–2.1	Unreliable correlation
AEIC	ML	4	351	M = MLAEIC	Figure 17a	2.2–4.2
MSUGS	M	4	24	M = MMSUGS + 0.1	Figure 18a	0.1–4.6
USCGS	mb	4	1	M = mbUSCGS	Figure 18b	4.1	Unreliable correlation
YARS	M	4	104	M = MYARS + 0.1		3.2–3.3	Indirect correlation with energy class. The magnitude MYARS represents a conversion from the energy class KS according to the formula of Rautian MYARS = (KS − 4)/1.8. For M[3.2–3.3] up to rounding, this is a shift of 0.1.
NERS	M	4	24	M = MNERS + 0.2		2.3–2.5	Indirect correlation with energy class. The magnitude MNERS represents a conversion from the energy class KPS according to the formula of Rautian MNERS = (KPS − 4)/1.8. For M[2.3–2.5] up to rounding, this is a shift of 0.2.
NEIC	ML	4	13	M = MLNEIC − 0.1	Figure 17b	2.5–4.2	Unreliably used indirect correlation MLAEIC
NEIC	mbLg	4	2	M = mbLgNEIC + 0.1	Figure 17c	2.6–3.0	Unreliably used indirect correlation MLAEIC
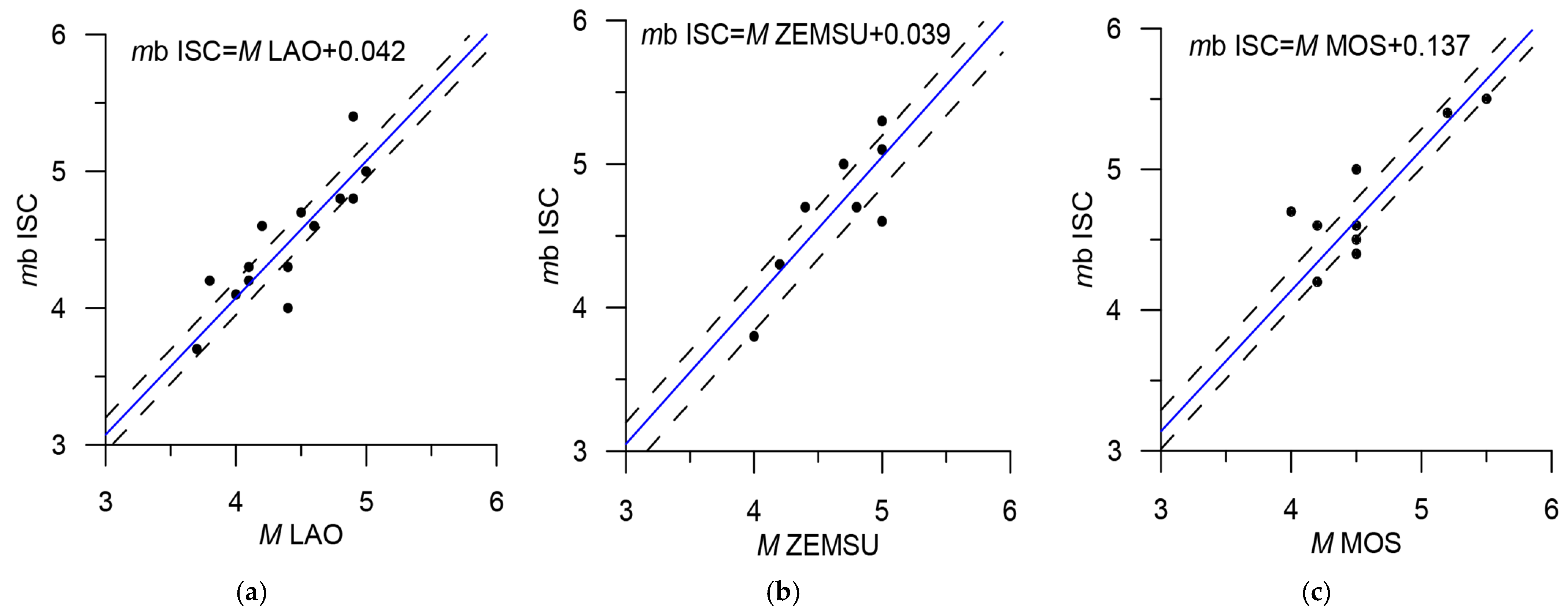
LAO	M	4	2	M = MLAO	Figure 19a	4.0	Very unreliable correlation
ZEMSU	M	4	2	M = MZEMSU	Figure 19b	3.4–4.5	Very unreliable correlation
MOS	M	4	1	M = MMOS + 0.1	Figure 19c	5.0	Very unreliable correlation
NEIC	M	4	6	M = MNEIC		2.5–4.9	Very unreliable correlation. Only three events with two magnitudes were found, MNEIC = mbISC.
ANF	ML	4	2	M = MLANF − 1		4.2–4.3	Very unreliable correlation. Found only two events with two magnitudes, MLANF>>mbISC.
DNAG	M	4	14	M = MDNAG		2.5–4.4	Correlation not established
WASN	M	4	328	M = MWASN		0.1–4.4	Correlation not established
ZEMSU	MPV	4	1	M = MPVZEMSU		4.5	Correlation not established
YARS	MU	4	2	M = MU_YARS		1.7–2.1	Correlation not established
OTT	ML	4	1	M = MLOTT		3.9	Correlation not established
PAL	M	4	1	M = MPAL		4.7	Correlation not established
BJI	mb	4	1	M = mbBJI		4.8	Correlation not established
EIDC	ML	4	1	M = MLEIDC		2.8	Correlation not established
Total			23,254

At present, the only physical magnitude scale is the seismic moment-based magnitude M_W, which is preferable when analyzing estimates of different magnitude scales [37,38]. However, when moving from large to small magnitudes (from global estimates to regional ones), discrepancies in M_W estimates are observed everywhere at M < 5.0 [39,40]. It should be noted that the Eastern Arctic region was not considered in [39].

In the present work, we use only global estimates of the M_W^GCMT magnitude. If the global estimate of moment magnitude is unknown, we prefer the magnitude mb^ISC, which is used by ISC in its practice to obtain “quasi-M_W” estimates in the range M < 5.0 [41].

A feature of the catalogs used is the presence of estimates of energy classes, and not magnitudes. Theoretically, the energy class estimate proposed by T.G. Rautian [42] was assumed to be the same physical parameter as the radiated seismic energy, or moment magnitude, which was presented later [43]. However, it was shown in [40] that, in practice, the Rautian energy classes are rather a magnitude characteristic (with its saturation) than a physical one. It should also be noted that there are two approaches for index in the energy class abbreviation. It can be “K_R”, “K_F”, or “K_S” for Rautian, Fedotov, or Solov`ev, respectively, or “K_P”, “K_S”, or “K_PS” for the wave type, which were used for calculation. In this paper, we stand for the second approach to emphasize the difference in energy class scales. Therefore, the estimates expressed in energy classes were converted to M_W using regression relations. In the studied territory, the number of earthquakes with the known magnitude M_W^GCMT is small, so regressions with the magnitude mb^ISC are built, which is well aligned with M_W^GCMT [41].

It is necessary to notice that about 7% of the events in the integrated catalog have other types of magnitudes. If an event has several magnitudes, then preference was given to those for which it is possible to construct a correlation with magnitude mb^ISC. In few cases, when there were no pairs to determine direct correlations to mb^ISC, we used indirect correlations with other magnitudes, and we consider these correlations unreliable (indicated in the “Note” column of Table 4). The 95% confidence intervals are constructed by the Grapher Golden Software built-in tool (https://www.goldensoftware.com/products/grapher, (accessed on 20 March 2022)).

Thus, we adhere to the following priority when choosing the optimal magnitude estimate:

• M_W^GCMT or M_S^ISC for strong earthquakes before 1976;
• mb^ISC;
• Magnitude by energy class; and
• Other magnitudes.

Statistics on magnitudes in the integrated catalog are given in Table 4.

Figure 13a shows the correlation between the M_W^GCMT and mb^ISC magnitudes in the studied territory (mb = 0.99M_W + 0.03). Earthquakes with an M_W of <6.0 were used to construct the best linear approximation. For stronger earthquakes, the magnitude mb saturates and becomes smaller than M_W. The magnitude M_S ≈ M_W is used for earthquakes with an M_W of ≥6.0. For weaker earthquakes, M_S < M_W (Figure 13b) is used, which generally agrees with previously obtained correlations [41].

Figure 13. Correlation ratios of GCMT and ISC magnitudes: (a) M_W^GCMT and mb^ISC for M_W < 6.0 and (b) M_W^GCMT and M_S^ISC for M_W ≥ 6.0. The dashed lines show 95% confidence intervals. The events with an M_W of ≥6.0 are highlighted in red.

There are 105 events in the integrated catalog with the magnitude M_W^GCMT. During the considered period, 15 earthquakes with an M of >6.0 occurred. Two strong earthquakes occurred in 1969 (mb = 6.4 and M_S = 7.5) and 1971 (mb = 6.0 and M_S = 7.0). For these earthquakes, the M_S estimate is preferred (Figure 13b, Table 5). For the remaining 13 strong earthquakes, the magnitude M_W^GCMT is known.

Table 5. Strong earthquakes in the Eastern Arctic.

	Date	TIME	Lat	Lon	Dep	Mag
1	22.11.1969	23:09:38	57.67	163.51	25.6	7.5	MSISC
2	18.05.1971	22:44:41	63.93	145.96	1.5	7.0	MSISC
3	08.03.1991	11:36:31	60.83	167.08	16.5	6.6	MWGCMT
4	24.10.1996	19:31:55	66.92	−173.04	22.2	6.0	MWGCMT
5	20.04.2006	23:25:02	60.88	167.05	23.9	7.6	MWGCMT
6	21.04.2006	4:32:44	60.45	165.96	14.6	6.1	MWGCMT
7	21.04.2006	11:14:16	61.30	167.75	22.8	6.0	MWGCMT
8	29.04.2006	16:58:06	60.45	167.62	10.9	6.6	MWGCMT
9	22.05.2006	11:11:59	60.73	165.81	13.9	6.6	MWGCMT
10	22.06.2008	23:56:30	67.70	141.39	18.8	6.1	MWGCMT
11	30.04.2010	23:11:43	60.46	−177.91	14.7	6.5	MWGCMT
12	30.04.2010	23:16:29	60.48	−177.60	18.3	6.3	MWGCMT
13	24.06.2012	3:15:01	57.50	163.41	16	6.0	MWGCMT
14	14.02.2013	13:13:52	67.52	142.70	8.9	6.7	MWGCMT
15	09.01.2020	8:38:08	62.36	171.06	10	6.4	MWGCMT

To determine the magnitude by energy class, the correlation with the magnitude mb^ISC was used (Figure 14). The Yakutsk and Northeastern branches of the GS RAS estimate the Rautian K_PS class [42], while the Kamchatka Branch estimates the Fedotov K_S class [44]. Earthquakes in Kamchatka were selected only in the studied territory, north of latitude 57.5°.

Figure 14. Correlation ratios of the energy classes K_PS and K_S and the magnitude mb^ISC. (a) Northeast, K_PS; (b) Yakutia, K_PS; and (c) Kamchatka, K_S. The dashed lines show 95% confidence intervals.

The magnitude ratio of mb^ISC and K_PS is the same in Yakutia and in the northeast. The ratio for K_S in Kamchatka is noticeably different since in the formula of energy classes according to Fedotov [43,44], K_S = 2lgA_peak + f(r), while in the classes according to Rautian [42,43], K_PS = 1.8lgA_peak + f(r), where A_peak is a peak amplitude of an S-wave or the sum of peak amplitudes of P- and S-waves, and f(r) is an attenuation function.

In the unified catalog, 1551 earthquakes have other types of magnitudes. We try to give estimates in M_W, which is an absolute scale in the first approximation. Therefore, a shift-type transformation M = M + constant was used, corresponding to the approach of [45], which assumed that one day, relative logarithmic magnitude estimates would be converted to absolute energy estimates by adding a constant (“Since the scale is logarithmic, any future reduction to an absolute scale can be accomplished by adding a constant to the scale numbers”). Taking into account that such ratios were obtained for limited ranges of magnitudes, and, in particular, magnitude ranges within M < 5, we consider that the assumption of the absence of nonlinear effects can be applied.

The number of earthquakes with the magnitude M_W^GCMT is small; therefore, to construct correlations, we used all earthquakes from the ISC catalog for which the magnitude mb^ISC and the studied magnitude are known. Reliable correlations with mb^ISC are determined for 617 earthquakes. For 609 events, unreliable correlations are determined. This is due either to a small number of events or to the use of an indirect correlation with other magnitudes.

No correlations are defined for 349 events, and 324 of these are reported by the WASN agency (Table 4). Correlations of different magnitudes are shown in Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19.

Figure 15. (a) NEIC; (b) MOS; (c) EIDC; and (d) IDC. Correlations of the “shift” type are determined in the interval of the magnitudes indicated in Table 4. The dashed lines show 95% confidence intervals.

Figure 16. Correlation ratios “shift” of the magnitudes YARS and mb^ISC. (a) ML^YARS. (b) MSV^YARS. The dashed lines show 95% confidence intervals.

Figure 17. Correlation ratios “shift” of (a) the ML^AEIC and mb^ISC magnitudes; indirect relationships; (b) ML^AEIC and ML^NEIC; and (c) ML^AEIC and mbLG^NEIC. The dashed lines show 95% confidence intervals.

Figure 18. Correlation ratios of the magnitudes MSUGS, USCGS, and mb^ISC. (a). M^MSUGS. (b) mb^USCGS. The dashed lines show 95% confidence intervals.

Figure 19. Poorly defined “shift” correlations with the magnitude mb^ISC. (a) M^LAO; (b) M^ZEMSU; and (c) M^MOS. The dashed lines show 95% confidence intervals.

4. Conclusions

Based on the generalization and integration of data from the various networks that serve the Eastern Sector of the Arctic zone of the Russian Federation, the most complete and representative earthquake catalog has been compiled. The catalog contains information on 23,254 seismic events for the period 1962–2020, of which 7781 events are from ISC and 15,473 events are from the Russian catalogs of GS RAS. Such a detailed and universal catalog for the whole Eastern part of the AZRF never existed before. Before 1968, the catalog contained quite a small number of events. In 2020, the catalog contained the events only from the ISC because the GS RAS catalog was not completed yet. The integrated catalog is to be updated accordingly once the former catalog is available.

The correlation of the magnitude types in the catalog was analyzed for various seismic networks. Based on the relations obtained, the unification of the magnitude estimates was carried out. For the most earthquakes, the quasi-M_W magnitude is calculated by converting the energy class using the original regression relationships (Table 4). The distribution of event magnitudes over time and magnitude–frequency graphs are shown in Figure 20. The integrated catalog completeness is quite heterogeneous. A detailed analysis of the changes in the level of registration in space and time is a big work that goes beyond the scope of the present study. We plan to conduct this work in the future.

Figure 20. (a) Distribution of the magnitude of events in time. (b,c) Magnitude–frequency graphs before 1982 (b) and after 1982 (c). Before 1982, the energy classes were integers, and so the magnitudes are in increments of 0.5.

The creation of the unified magnitude-based integrated earthquake catalog realized in this paper opens new prospects in earthquake studies in the Arctic region. Further development of the Russian Arctic seismic zonation and systems analysis of strong earthquake-prone areas are among them.

The map of earthquake epicenters of the integrated catalog is shown in Figure 21. The catalog developed in this article is made available to the public on the website of the World Data Center for Solid Earth Physics, Moscow, at http://www.wdcb.ru/arctic_antarctic/arctic_seism.html, (accessed on 20 March 2022).

Figure 21. Map of earthquake epicenters of the integrated catalog of the Eastern Sector of the Arctic zone of the Russian Federation. The red and blue circles are the epicenters from the catalogs of GS RAS and ISC, respectively.