Contribution of Etalon Observation to Earth Rotation Parameters under a New Observation Scenario
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methodology
3. Results
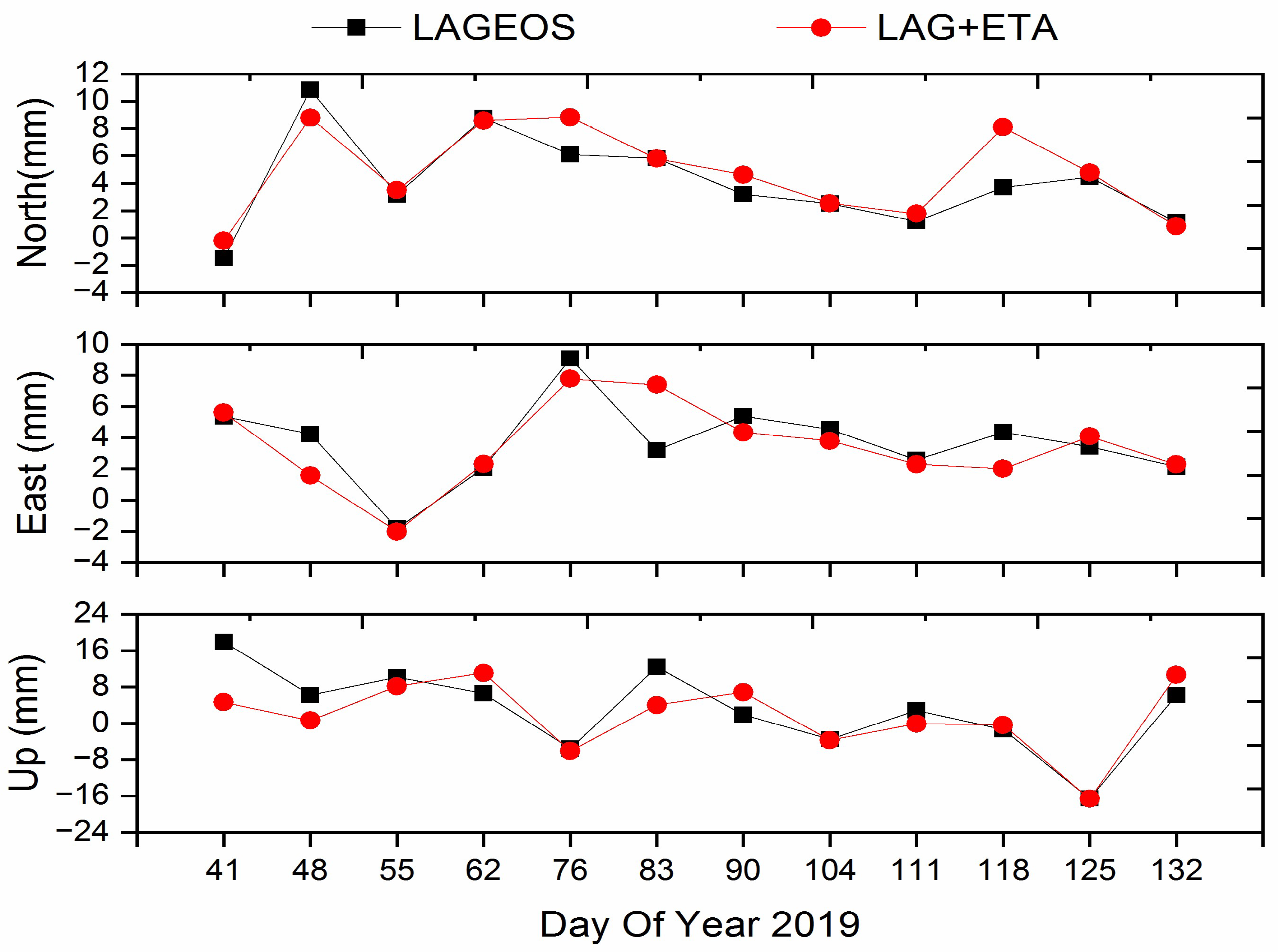
3.1. Station Coordinates
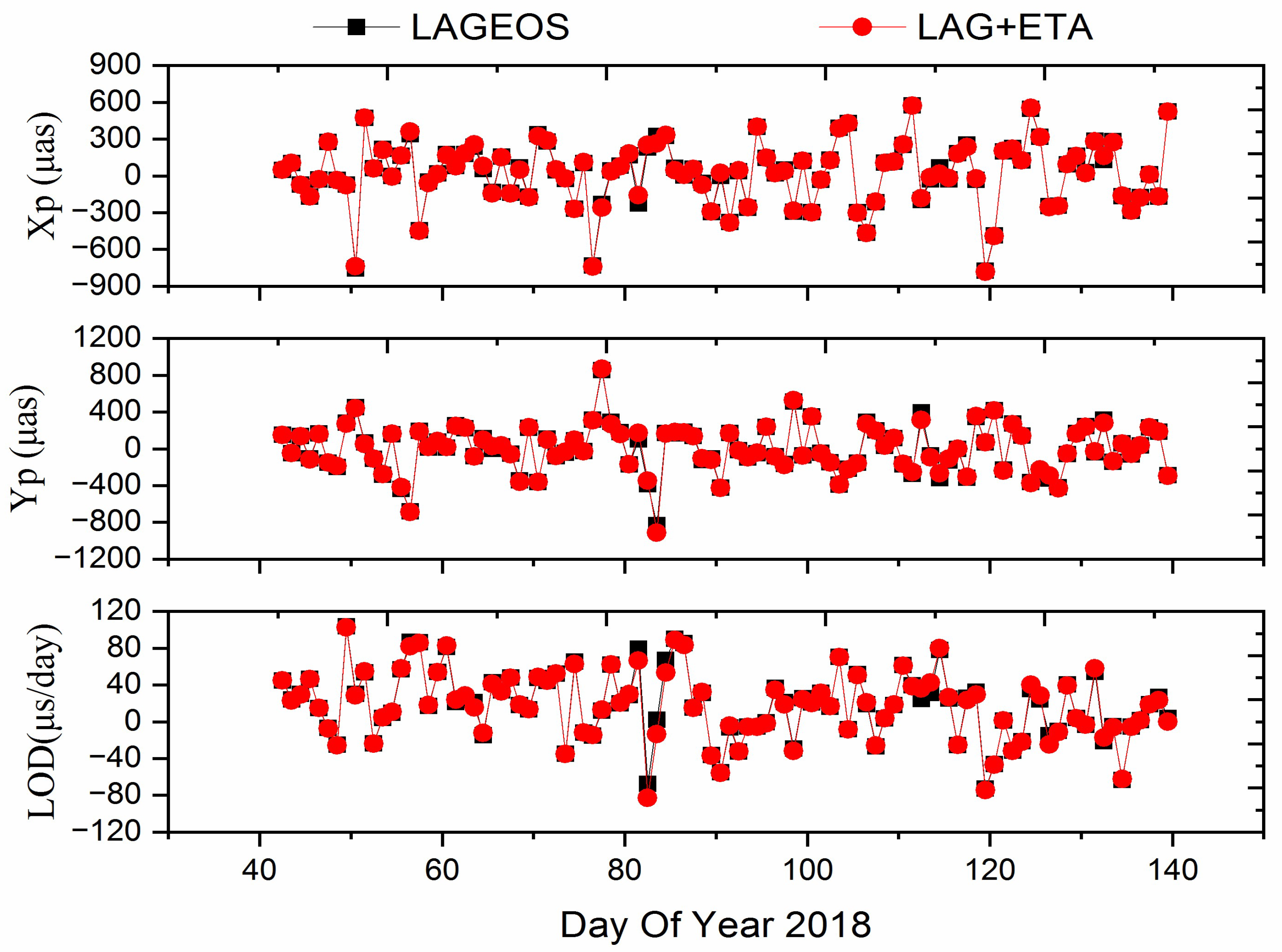
3.2. Earth Rotation Parameters
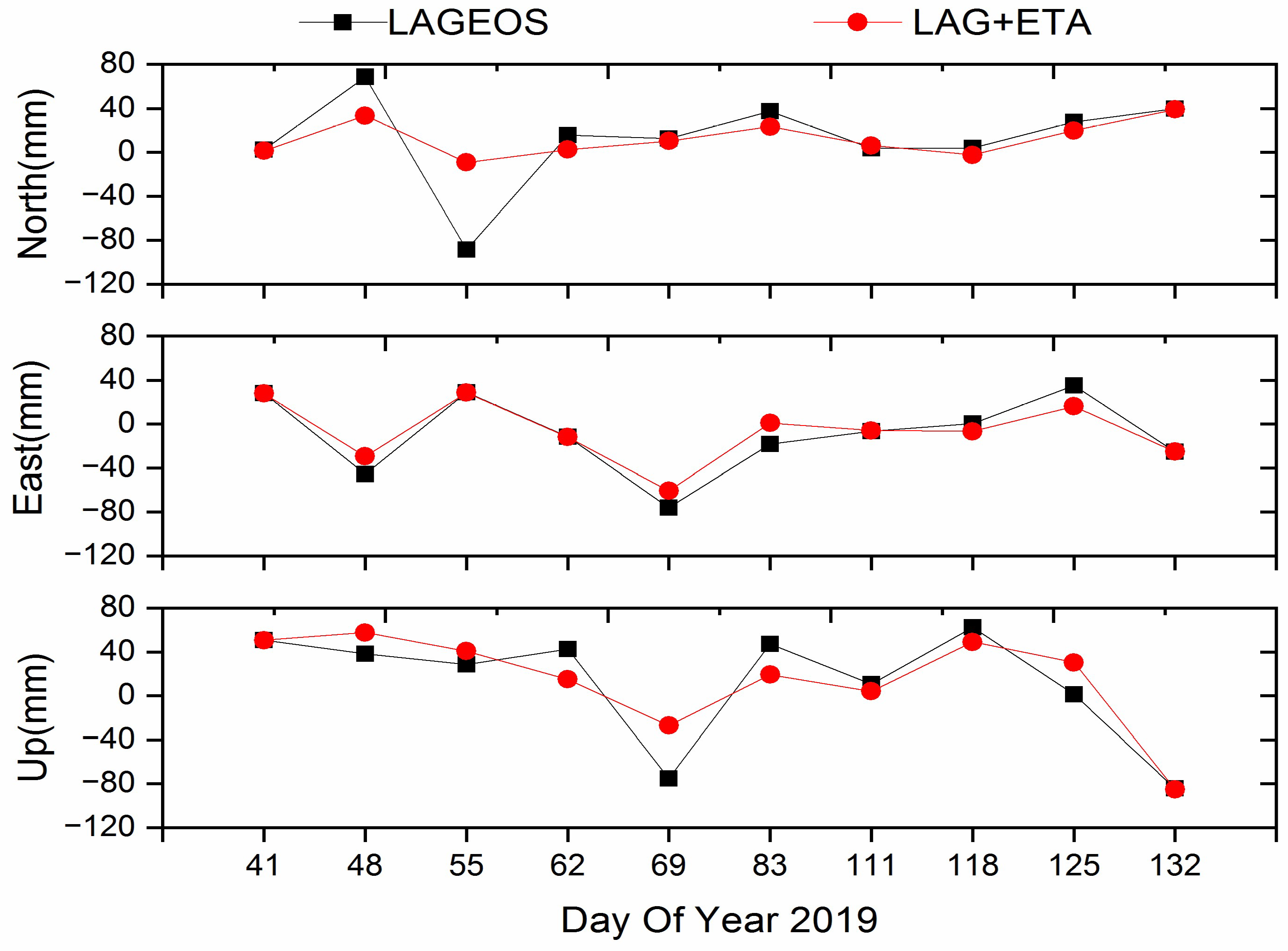
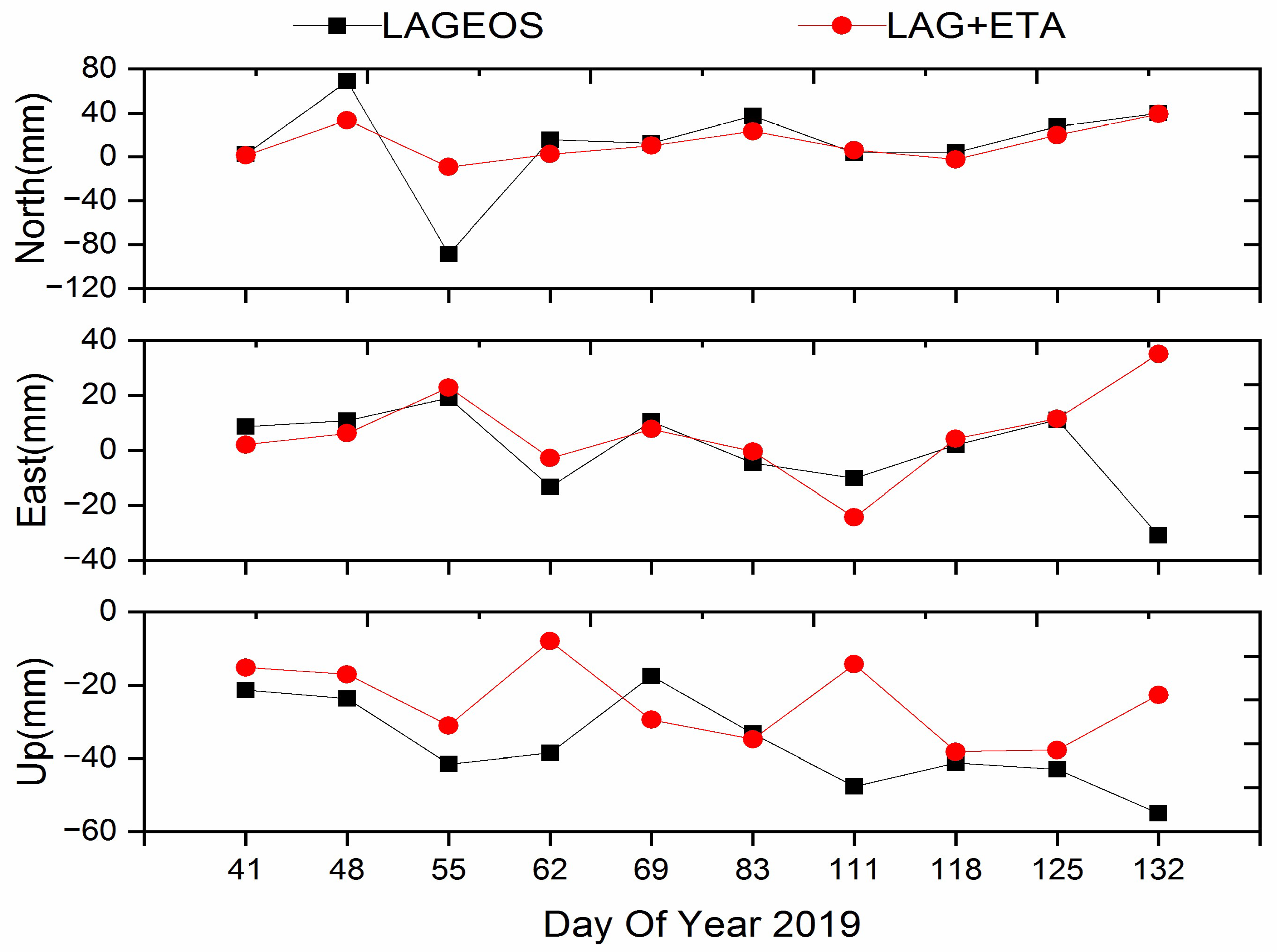
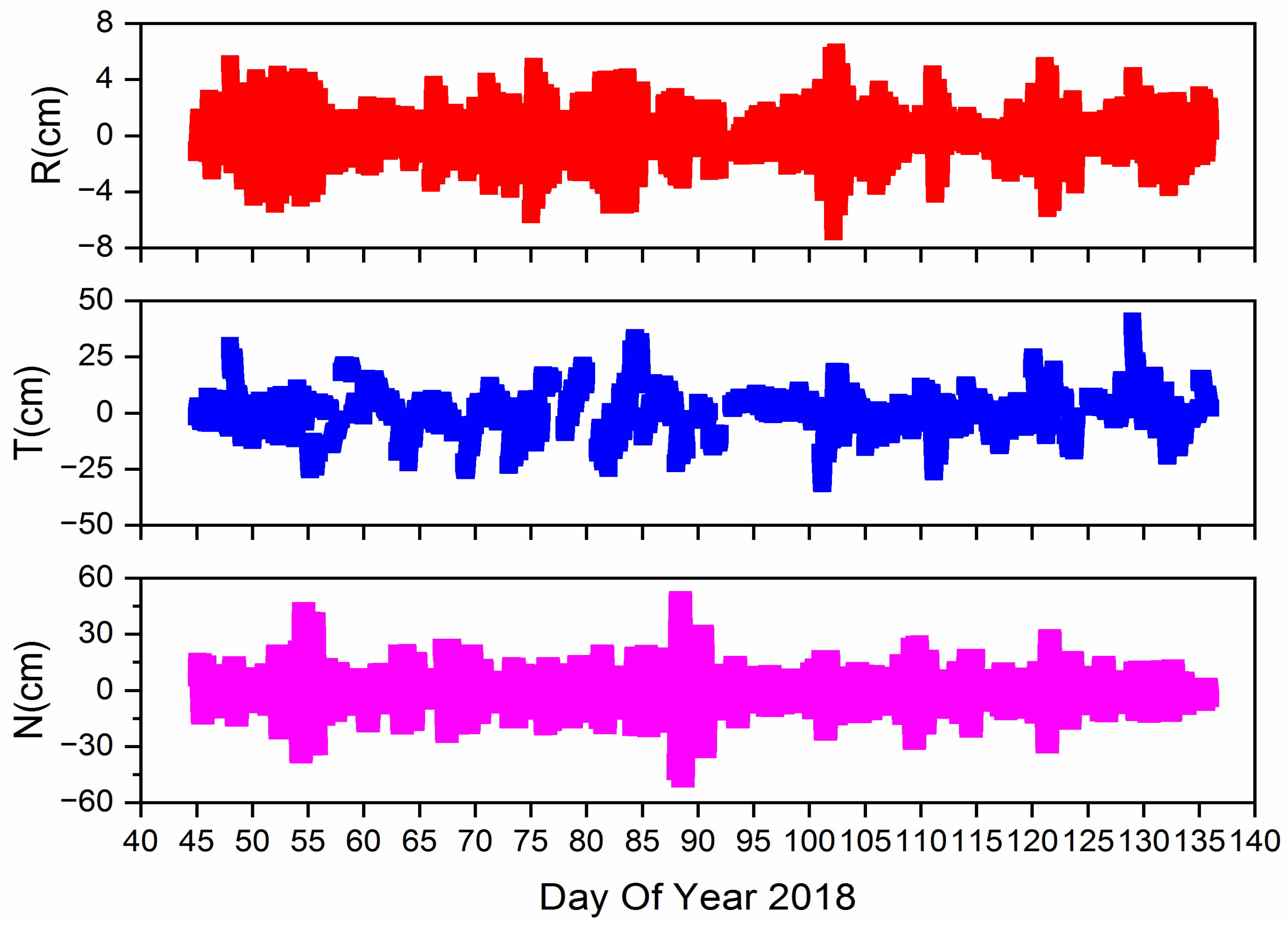
3.3. Orbit
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pavlis, E.C. High resolution Earth orientation parameters from LAGEOS SLR data analysis at GSFC. In IERS Technical Note 16; IERS: Washington, DC, USA, 1994. [Google Scholar]
- Sosnica, K.; Jaeggi, A.; Thaller, D.; Beutler, G.; Dach, R. Contribution of Starlette, Stella, and AJISAI to the SLR-derived global reference frame. J. Geod. 2014, 88, 789–804. [Google Scholar] [CrossRef] [Green Version]
- Blossfeld, M.; Gerstl, M.; Hugentobler, U.; Angermann, D.; Mueller, H. Systematic effects in LOD from SLR observations. Adv. Space Res. 2014, 54, 1049–1063. [Google Scholar] [CrossRef]
- Glaser, S.; Fritsche, M.; Sośnica, K.; Rodríguez-Solano, C.; Wang, K.; Dach, R.; Hugentobler, U.; Rothacher, M.; Dietrich, R. A consistent combination of GNSS and SLR with minimum constraints. J. Geod. 2015, 89, 1165–1180. [Google Scholar] [CrossRef]
- Bloßfeld, M.; Rudenko, S.; Kehm, A.; Panafidina, N.; Müller, H.; Angermann, D.; Hugentobler, U.; Seitz, M. Consistent estimation of geodetic parameters from SLR satellite constellation measurements. J. Geod. 2018, 92, 1003–1021. [Google Scholar] [CrossRef]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Blossfeld, M.; Müller, H.; Gerstl, M.; Tefka, V.; Bouman, J.; Gttl, F.; Horwath, M. Second-degree Stokes coefficients from multi-satellite SLR. J. Geod. 2015, 89, 857–871. [Google Scholar] [CrossRef]
- Sosnica, K.; Jaeggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time variable Earth’s gravity field from SLR satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.; Ries, J. The unexpected signal in GRACE estimates of C20. J. Geod. 2017, 97, 897–914. [Google Scholar] [CrossRef]
- Pardini, C.; Anselmo, L.; Lucchesi, D.M.; Peron, R. On the secular decay of the LARES semi-major axis. Acta Astronaut. 2017, 140, 469–477. [Google Scholar] [CrossRef]
- Strugarek, D.; Sośnica, K.; Jäggi, A. Characteristics of GOCE orbits based on Satellite Laser Ranging. Adv. Space Res. 2019, 63, 417–431. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Degnan, J.J.; Bosworth, J.M. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Appleby, G.M. Long-arc analyses of SLR observations of the Etalon geodetic satellites. J. Geod. 1998, 72, 333–342. [Google Scholar] [CrossRef]
- Altamimi, Z.; Boucher, C.; Willis, P. Terrestrial reference frame requirements within GGOS perspective. J. Geod. 2005, 40, 363–374. [Google Scholar] [CrossRef]
- Plag, H.P.; Pearlman, M. Global Geodetic Observing System: Meeting the Requirements of a Global Society on a Changing Planet in 2020; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Beutler, G.; Drewes, H.; Verdun, A. The new structure of the International Association of Geodesy (IAG) viewed from the perspective of history. J. Geod. 2004, 77, 560–584. [Google Scholar] [CrossRef]
- Luceri, V.; Pirri, M.; Rodriguez, J.; Appleby, G.; Pavlis, E.C.; Mueller, H. Systematic errors in SLR data and their impact on the ILRS products. J. Geod. 2019, 93, 2357–2366. [Google Scholar] [CrossRef]
- Zajdel, R.; Sonica, K.; Drodewski, M.; Bury, G.; Strugarek, D. Impact of network constraining on the terrestrial reference frame realization based on SLR observations to LAGEOS. J. Geod. 2019, 93, 2293–2313. [Google Scholar] [CrossRef] [Green Version]
- Drożdżewski, M.; Sośnica, K. Tropospheric and range biases in Satellite Laser Ranging. J. Geod. 2021, 95, 100. [Google Scholar] [CrossRef]
- Drożdżewski, M.; Sośnica, K.; Zus, F. Troposphere delay modeling with horizontal gradients for satellite laser ranging. J. Geod. 2019, 93, 1853–1866. [Google Scholar] [CrossRef] [Green Version]
- Gourine, B.; Hasni, K.; Belmehdi, F.B. Analysis of 04 years (2002–2005) of laser data on Starlette, Stella and LAGEOS-I/II satellites for stations coordinates and Earth Orientation Parameters (EOP). In Proceedings of the 1st International Electronic Conference on Geosciences, Virtual, 15–30 June 2018. [Google Scholar]
- Schillak, S.; Lejba, P.; Michałek, P. Analysis of the Quality of SLR Station Coordinates Determined from Laser Ranging to the LARES Satellite. Sensors 2021, 21, 737. [Google Scholar] [CrossRef]
- Sośnica, K.; Bury, G.; Zajdel, R. Contribution of Multi-GNSS Constellation to SLR-Derived Terrestrial Reference Frame. Geophys. Res. Lett. 2018, 45, 2339–2348. [Google Scholar] [CrossRef]
- Sośnica, K.; Bury, G.; Zajdel, R.; Drożdżewski, M.; Kazmierski, K. Estimating global geodetic parameters using SLR observations to Galileo, GLONASS, BeiDou, GPS, and QZSS. Earth Planets Space 2019, 71, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Strugarek, D.; Sonica, K.; Arnold, D.; Jggi, A.; Drodewski, M. Determination of Global Geodetic Parameters Using Satellite Laser Ranging Measurements to Sentinel-3 Satellites. Remote Sens. 2019, 11, 2282. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Zhang, H.; Zhang, K.; Yuan, Y.; Zhang, W.; Qin, Y. Earth Rotation Parameters Estimation Using GPS and SLR Measurements to Multiple LEO Satellites. Remote Sens. 2022, 13, 3046. [Google Scholar] [CrossRef]
- Strugarek, D.; Sośnica, K.; Arnold, D.; Jäggi, A.; Zajdel, R.; Bury, G. Determination of SLR station coordinates based on LEO, LARES, LAGEOS, and Galileo satellites. Earth Planets Space 2021, 73, 1–21. [Google Scholar] [CrossRef]
- Pavlis, E.; Kuzmicz-Cieslak, M. SLR and the next generation global geodetic networks of low satellites. In Proceedings of the 16th International Workshop on Laser Ranging, Poznan, Poland, 13–17 October 2008; Schilliak, S., Ed.; JCET/UMBC and NASA Goddard: Greenbelt, MA, USA, 2008. [Google Scholar]
- Otsubo, T.; Matsuo, K.; Aoyama, Y.; Yamamoto, K.; Hobiger, T.; Kubo-Oka, T. Effective expansion of satellite laser ranging network to improve global geodetic parameters. Earth Planets and Space 2018, 68, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Thaller, D.; Sosnica, K.; Dach, R.; Jäggi, A.; Beutler, G. LAGEOS-ETALON solutions using the Bernese Software; Mittlungen Des Bundesamtes Für Kartogr. Und Geodsie: Frankfurt, Germany, 2012; Volume 48, pp. 333–336. ISBN 978-3-89888-999-5. [Google Scholar]
- Thaller, D.; So’Snica, K.; Dach, R.; Jäggi, A.; Richter, B. Geocenter Coordinates from GNSS and Combined GNSS-SLR Solutions Using Satellite Co-Locations; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Andritsch, F.; Grahsl, A.; Dach, R.; Schildknecht, T.; Jggi, A. Simulation of tracking scenarios to LAGEOS and Etalon satellites. J. Geod. 2020, 94, 1–15. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar]
- Mendes, V.B.; Pavlis, E.C. High-accuracy zenith delay prediction at optical wavelengths. Geophys. Res. Lett. 2004, 31, 189–207. [Google Scholar] [CrossRef] [Green Version]
- Petit, G.; Luzum, B. IERS Conventions. (IERS Technical Note; No. 36) Frankfurt am Main: Verlag des Bundesamts für Kartographie und Geodäsie; IERS Technical Note: Frankfurt, Germany, 2010; p. 179. [Google Scholar]
- Otsubo, T.; Appleby, G. System dependent center of mass correction for spherical geodetic satellites. J Geophys Res. 2003, 108, B4. [Google Scholar] [CrossRef]
- Luceri, V.; Pavlis, E.C.; Pace, B.; Ku´zmicz-Cie’slak, M.; König, M.; Bianco, G.; Evans, K. The ILRS Contribution to the Development of the ITRF2014. In Proceedings of the 26th IUGG General Assembly, Prague, Czech Republic, 22 June–2 July 2015. [Google Scholar]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.F. The development and evaluation of Earth Gravitational Model (EGM2008). J. Geophys. Res. Atmos. 2012, 117, B4. [Google Scholar]
- Eanes, R. An Improved Global Ocean Tide Model from TOPEX/Poseidon Altimetry: CSR4.0. In Proceedings of the EGS 24th General Assembly, Hague, The Netherlands, 19–23 April 1999. [Google Scholar]
- Standish, E.M., Jr. The observational basis for JPL’s DE 200, the planetary ephemerides of the Astronomical Almanac. Astron. Astrophys. 1990, 233, 252–271. [Google Scholar]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2018, 93, 621–633. [Google Scholar] [CrossRef]
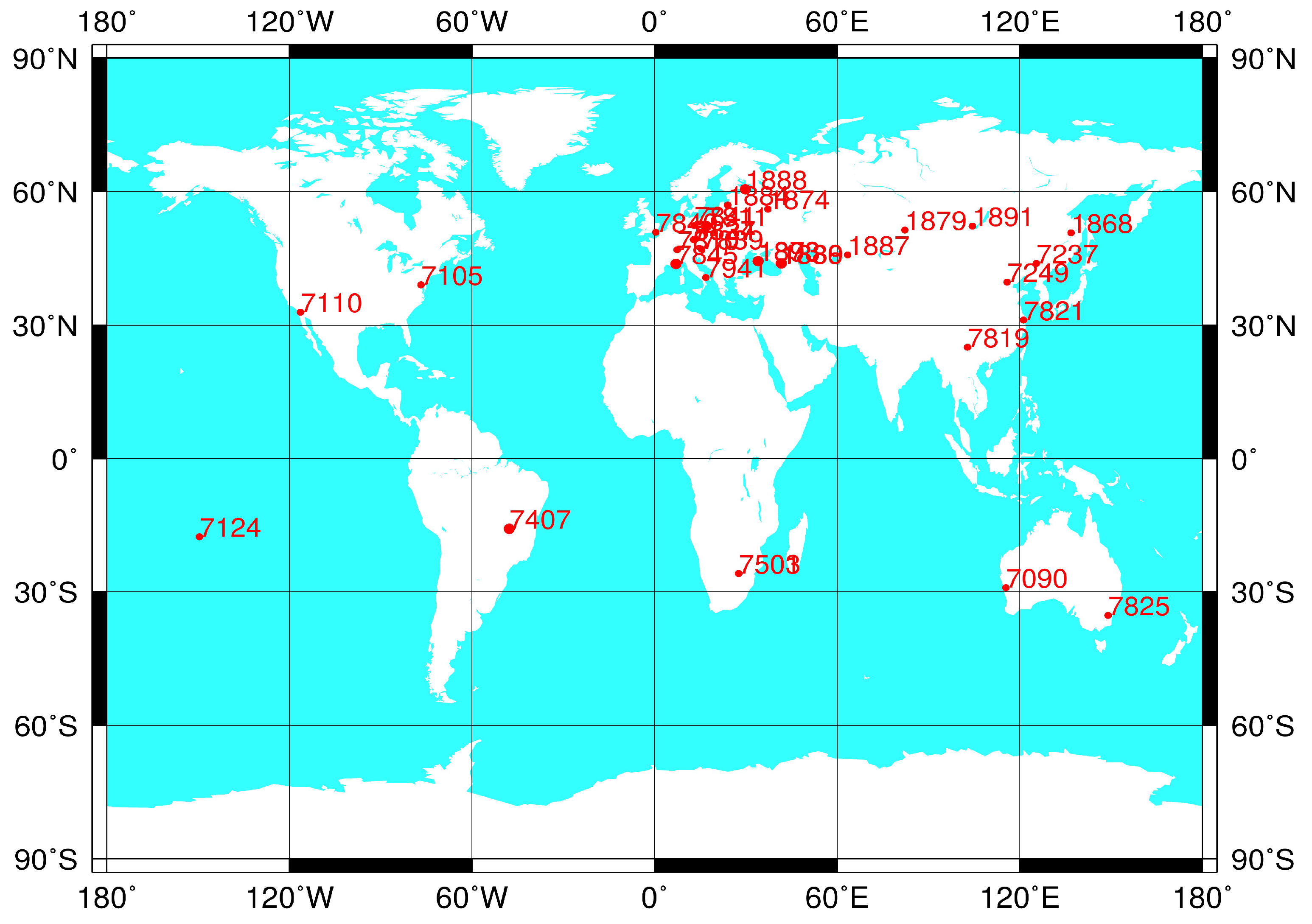

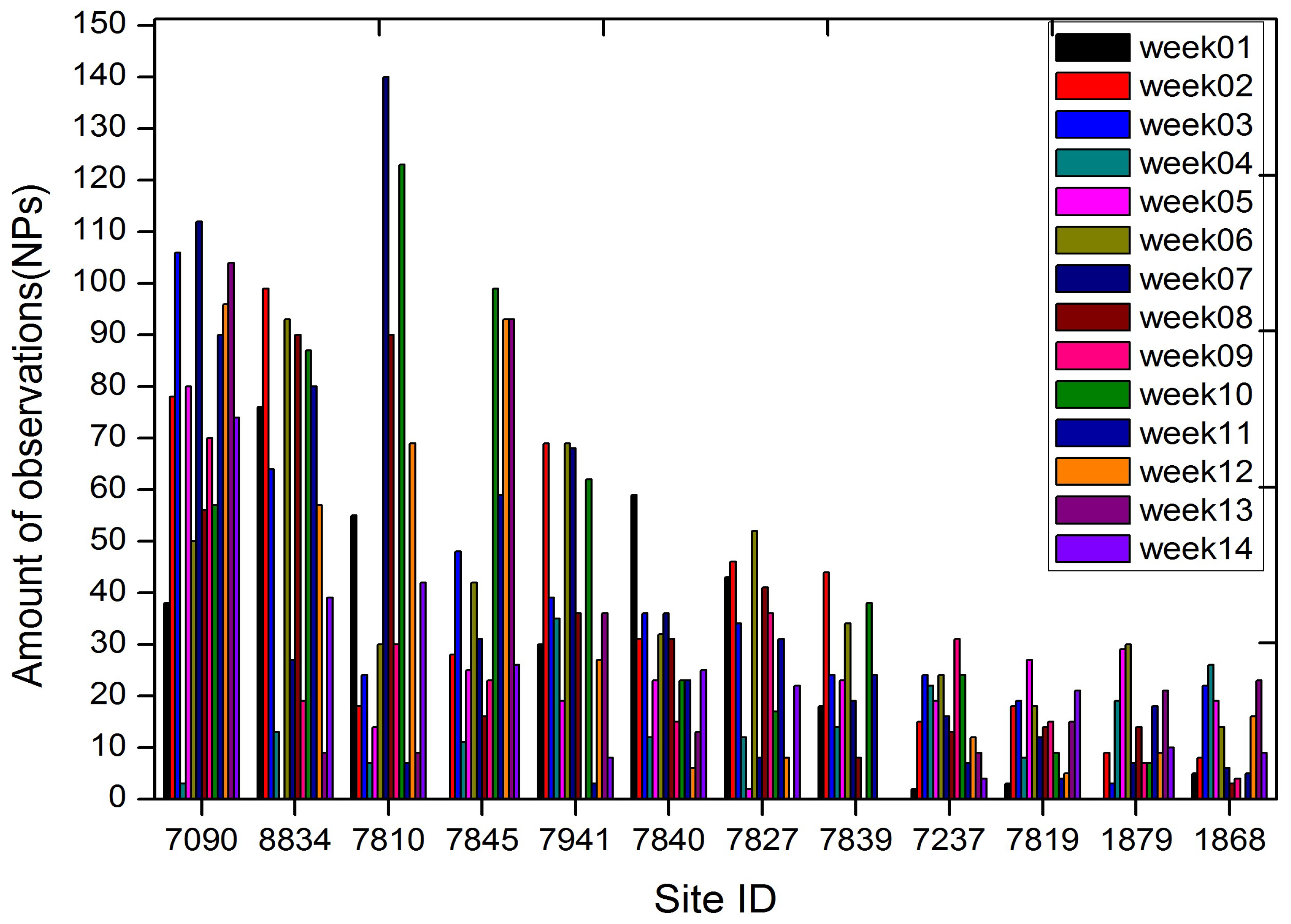
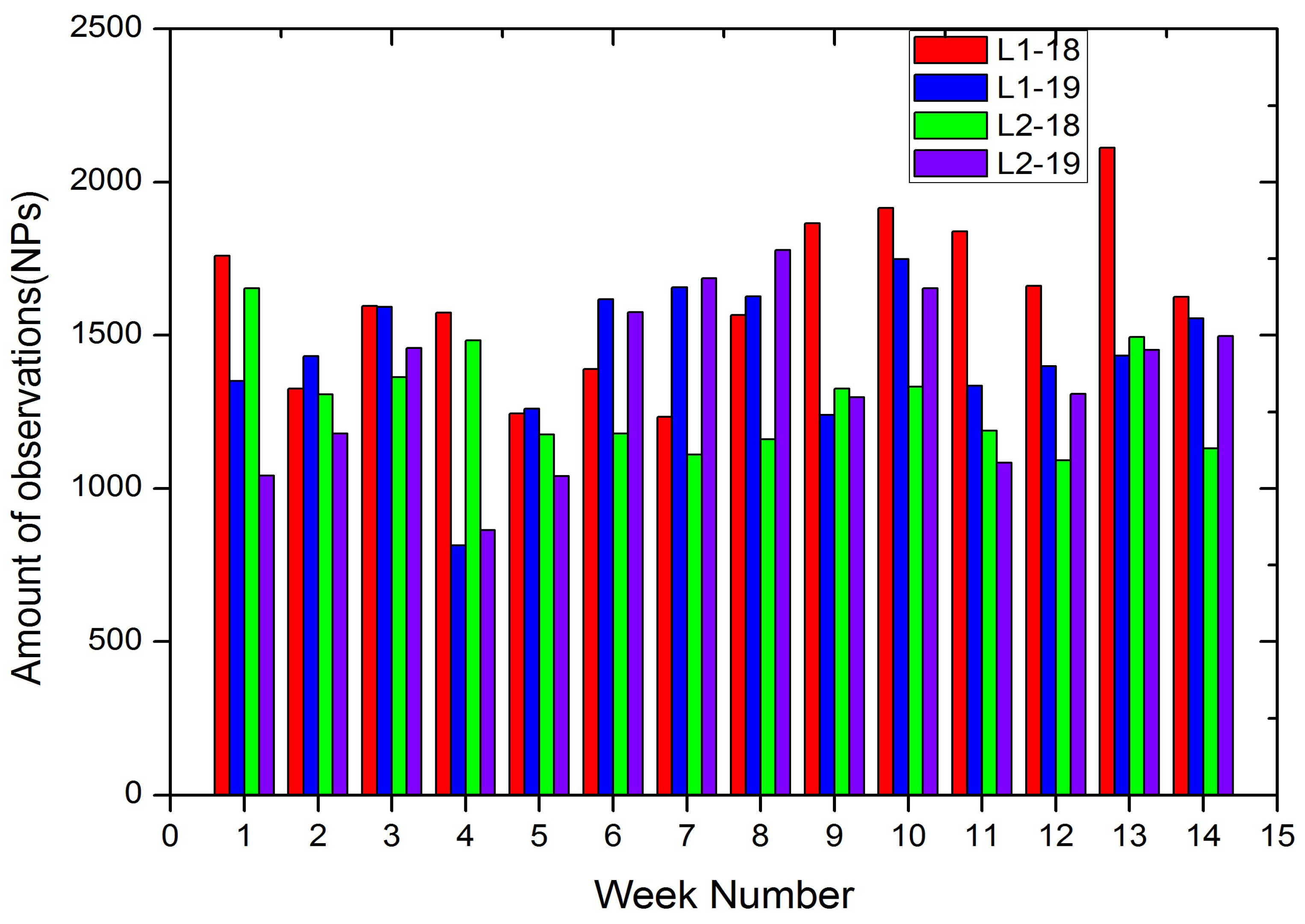
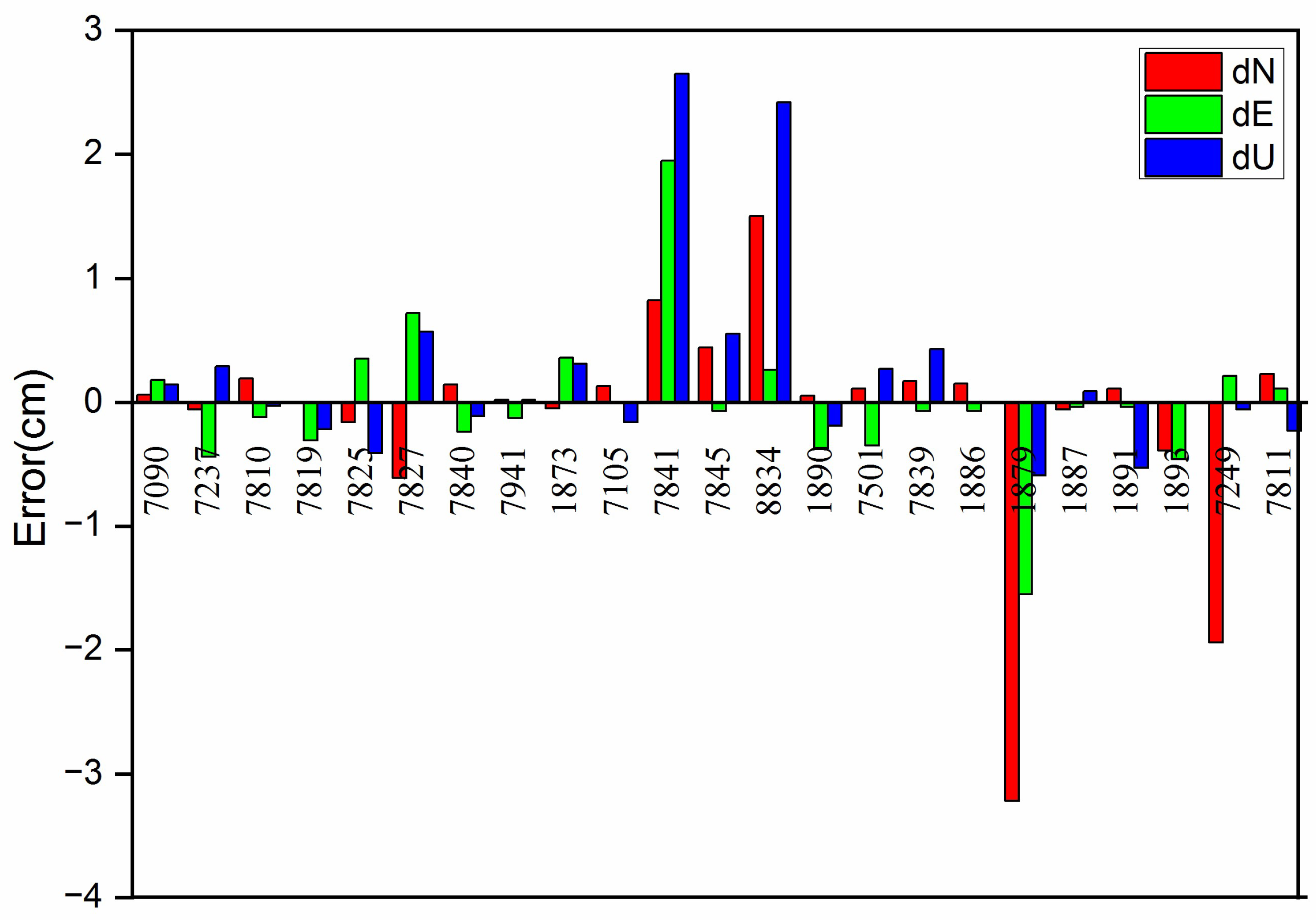


| Site ID | DOMES | Location | Country | X (m) | Y (m) | Z (m) |
|---|---|---|---|---|---|---|
| 1868 | 12341S001 | Komsomolsk-na-Amure | Russia | −2,948,545.553 | 2,774,312.979 | 4,912,302.412 |
| 1873 | 12337S003 | Simeiz | Ukraine | 3,783,902.151 | 2,551,405.114 | 4,441,257.548 |
| 1874 | 12309S003 | Mendeleevo | Russia | 2,844,591.622 | 2,161,111.992 | 5,266,356.882 |
| 1879 | 12372S001 | Altay | Russia | 543,405.811 | 3,955,302.296 | 4,957,821.036 |
| 1884 | 12302S002 | Riga | Latvia | 3,183,895.637 | 1,421,497.208 | 5,322,803.793 |
| 1886 | 12373S001 | Arkhyz | Russia | 3,466,773.366 | 3,059,757.881 | 4,381,456.800 |
| 1887 | 25603S001 | Baikonur | Kazakhstan | 2,001,873.318 | 3,987,633.388 | 4,542,477.667 |
| 1888 | 12350S002 | Svetloe | Russia | 2,730,138.911 | 1,562,328.755 | 5,529,998.665 |
| 1889 | 12351S002 | Zelenchukskya | Russia | 3,451,135.973 | 3,060,335.220 | 4,391,970.306 |
| 1891 | 12313S007 | Irkutsk | Russia | −968,340.229 | 3,794,415.115 | 5,018,178.124 |
| 1893 | 12337S006 | Katzively | Ukraine | 3,785,944.345 | 2,550,780.789 | 4,439,461.397 |
| 7090 | 50107M001 | Yarragadee | Australia | −2,389,007.534 | 5,043,329.448 | −3,078,524.223 |
| 7105 | 40451M105 | Greenbelt | America | 1,130,719.438 | −4,831,350.580 | 3,994,106.573 |
| 7110 | 40497M001 | Monument Peak | America | −2,386,278.627 | −4,802,353.816 | 3,444,881.772 |
| 7124 | 92201M007 | Tahiti | French Polynesia | −5,246,407.299 | −3,077,284.309 | −1,913,813.757 |
| 7237 | 21611S001 | Changchun | China | −2,674,387.081 | 3,757,189.194 | 4,391,508.287 |
| 7249 | 21601S004 | Beijing | China | −2,148,760.760 | 4,426,759.548 | 4,044,509.606 |
| 7394 | 23907S002 | Sejong City | Republic of Korea | −3,110,108.284 | 4,082,170.384 | 3,774,911.853 |
| 7407 | 48081S001 | Brasilia | Brazil | 4,119,502.121 | −4,553,595.202 | −1,722,855.131 |
| 7501 | 30302M003 | Hartebeesthoek | South Africa | 5,085,401.092 | 2,668,330.330 | −2,768,688.650 |
| 7503 | 30301S010 | Hartebeesthoek | South Africa | 5,085,428.440 | 2,668,340.694 | −2,768,641.399 |
| 7810 | 14001S007 | Zimmerwald | Switzerland | 4,331,283.485 | 567,549.979 | 4,633,140.413 |
| 7811 | 12205S001 | Borowiec | Poland | 3,738,332.592 | 1,148,246.687 | 5,021,816.135 |
| 7819 | 21609S004 | Kunming | China | −1,281,301.323 | 5,640,724.593 | 2,682,905.687 |
| 7821 | 21605S010 | Shanghai | China | −2,830,744.597 | 4,676,580.229 | 3,275,072.784 |
| 7825 | 50119S003 | Mt Stromlo | Australia | −4,467,064.778 | 2,683,034.887 | −3,667,007.319 |
| 7827 | 14201S045 | Wettzell | Germany | 4,075,530.996 | 931,781.927 | 4,801,620.007 |
| 7839 | 11001S002 | Graz | Austria | 4,194,426.293 | 1,162,694.265 | 4,647,246.785 |
| 7840 | 13212S001 | Herstmonceux | United Kingdom | 4,033,463.542 | 23,662.700 | 4,924,305.303 |
| 7841 | 14106S011 | Potsdam | Germany | 3,800,432.096 | 881,692.172 | 5,029,030.173 |
| 7941 | 12734S008 | Matera | Italy | 4,641,978.617 | 1,393,067.723 | 4,133,249.623 |
| 8834 | 14201S018 | Wettzell | Germany | 4,075,576.651 | 931,785.679 | 4,801,583.698 |
| Type of Model | Description |
|---|---|
| Arc length | 7 days |
| Elevation angle cutoff | 3 degrees |
| Sampling interval | LAGEOS-1/2: 120 sc Etalon-1/2: 300 sc |
| Satellite weighting | LAGEOS-1/2: 10 mm Etalon-1/2: 30 mm |
| Troposphere delay | ZTD: Mendes-Pavlis model Mapping function: Mendes-Pavlis model |
| Ionosphere delay | Not modeled |
| Range biases | Estimated for some selected stations |
| Relativistic delay | IERS Convention 2010 |
| Tide loading | Ocean tide loading: FES2004 model Earth tide loading: IERS Convention 2010 |
| Satellite center of mass | Tables of CoM values from ILRS |
| Data edit | 2.5 sigma editing, maximum overall sigma: 30 mm |
| Parameters | Description |
|---|---|
| Orbit parameters | One set per week arc 6 Keplerian orbit elements (7 days) and 5 empirical parameters, S0, SS, SC, WS, WC |
| Station coordinates | One set per week arc Core stations: Network constrains Minimum constraint: no net rotation and no net translation Noncore stations: freely estimated |
| Range biases | One set per week arc, estimated only for selected stations recommended by ILRS |
| ERPs | Xp, Yp, LOD (1-day), piecewise constant |
| Geocenter coordinates | Three parameters in x, y, z components, piecewise constant |
| Table 2008 | Description |
|---|---|
| Geopotential | EGM2008 model (degree and order 30) |
| Third-body | DE405: Sun, Moon, Jupiter, Venus, Mars; |
| Tide forces | Ocean tides: CSR 4.0A Solid Earth tides: IERS conventions 2010 Atmospheric tides: Ray and Ponte model 2003 |
| Solar radiation pressure | Direct radiation: applied CR: 1.13 for LAGEOS-1/2 CR: 1.20 for Etalon-1/2 |
| Albedo radiation | Not applied |
| Earth thermal radiation | Applied |
| Relativistic correction | IERS Conventions 2010 |
| Numerical integration | Adams collocation method; 12th order, step size: 120 s |
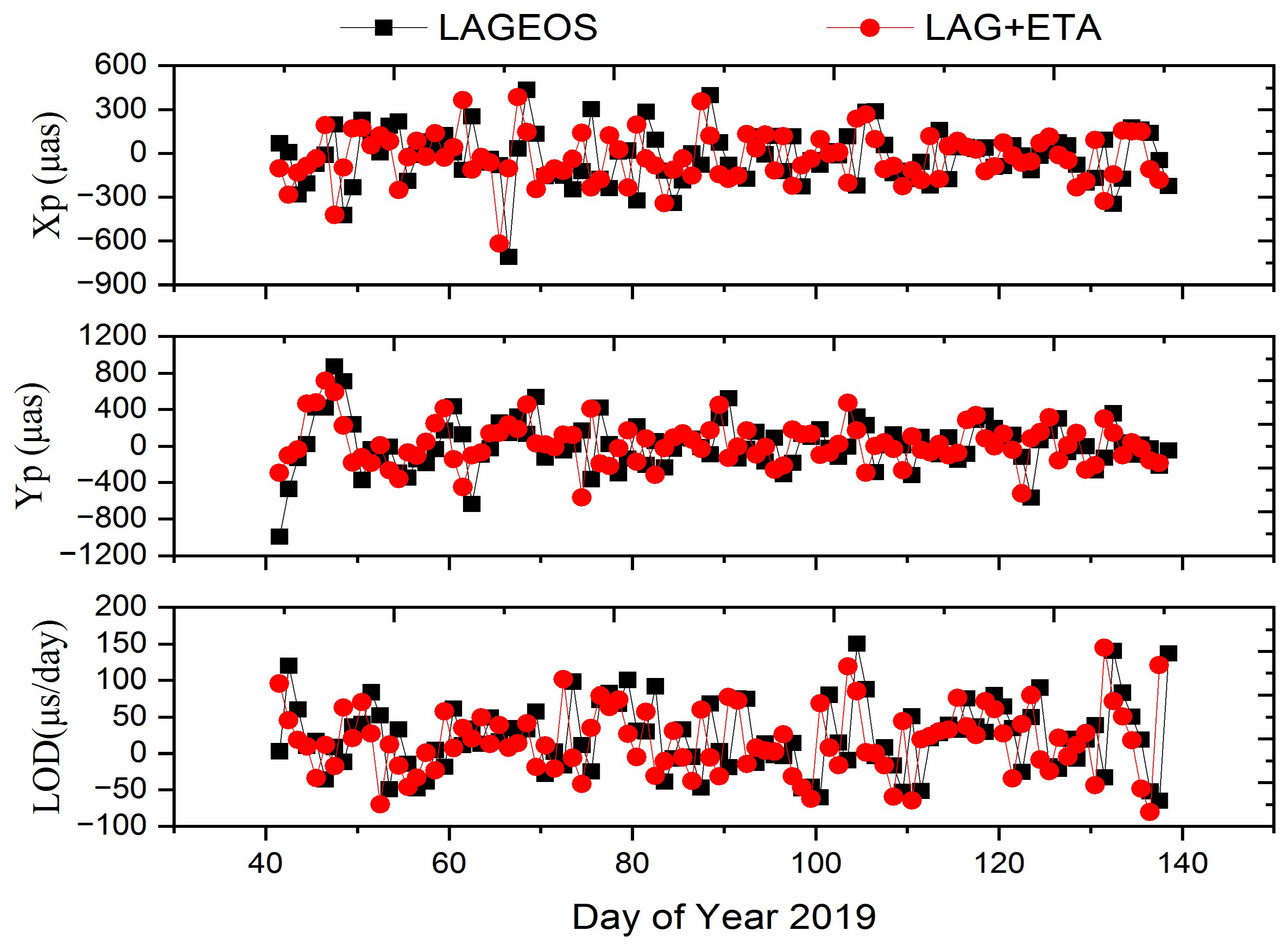
| LAGEOS-Only | LAGEOS+Etalon | |||||
|---|---|---|---|---|---|---|
| Xp (μas) | Yp (μas) | LOD (μs/day) | XP (μas) | Yp (μas) | LOD (μs/day) | |
| Maximum | 574.00 | 853.00 | 103.80 | 574.00 | 873.00 | 102.70 |
| Minimum | −774.00 | −831.00 | −72.80 | −784.00 | −913.00 | −82.80 |
| Mean | 19.87 | 0.24 | 18.25 | 19.77 | 0.23 | 17.69 |
| Standard deviation | 263.37 | 259.08 | 36.66 | 263.36 | 259.86 | 36.93 |
| Parameter | LAGEOS-Only | LAGEOS+Etalon | ||||
|---|---|---|---|---|---|---|
| Xp (μas) | Yp (μas) | LOD (μs/day) | XP (μas) | Yp (μas) | LOD (μs/day) | |
| Maximum | 433.00 | 874.00 | 150.30 | 387.00 | 715.00 | 144.80 |
| Minimum | −710.00 | −997.00 | −64.90 | −617.00 | −560.00 | −80.80 |
| Mean | −29.15 | 11.86 | 22.69 | −30.85 | 22.99 | 17.41 |
| Standard deviation | 179.97 | 270.45 | 47.58 | 167.64 | 231.90 | 45.13 |
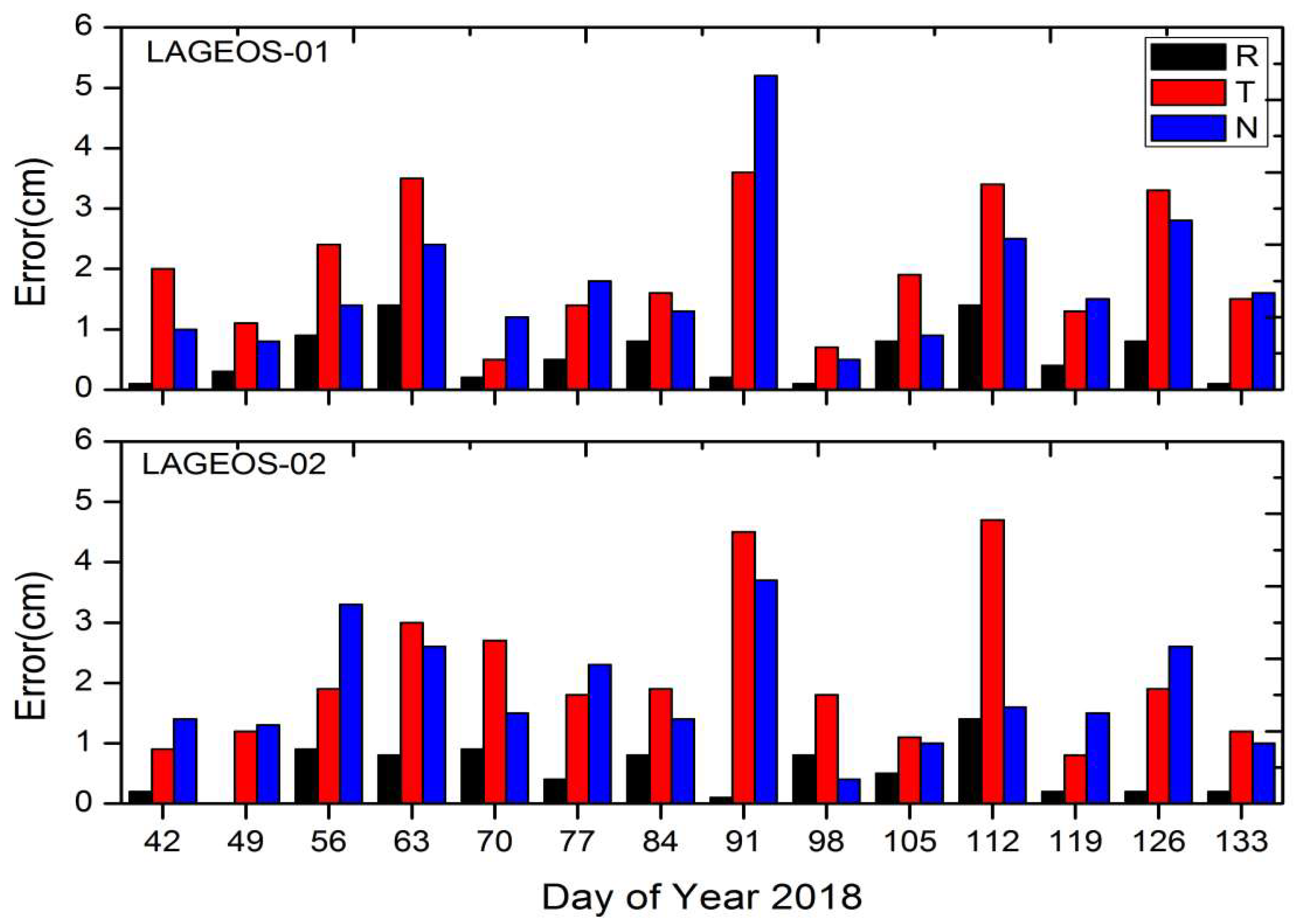
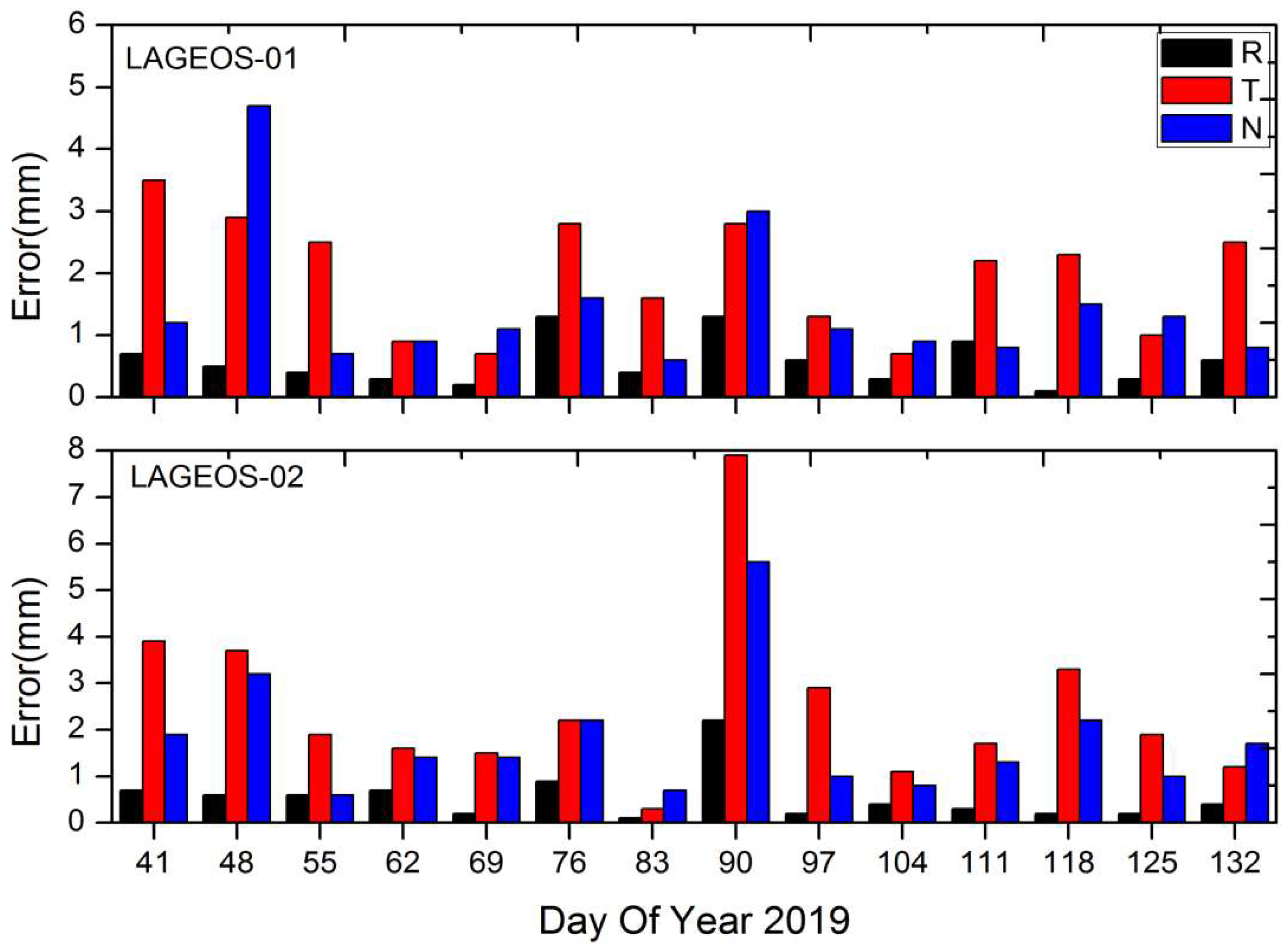
| Satellites | Parameters | 2018 | 2019 | ||||
|---|---|---|---|---|---|---|---|
| R (cm) | T (cm) | N (cm) | R (cm) | T (cm) | N (cm) | ||
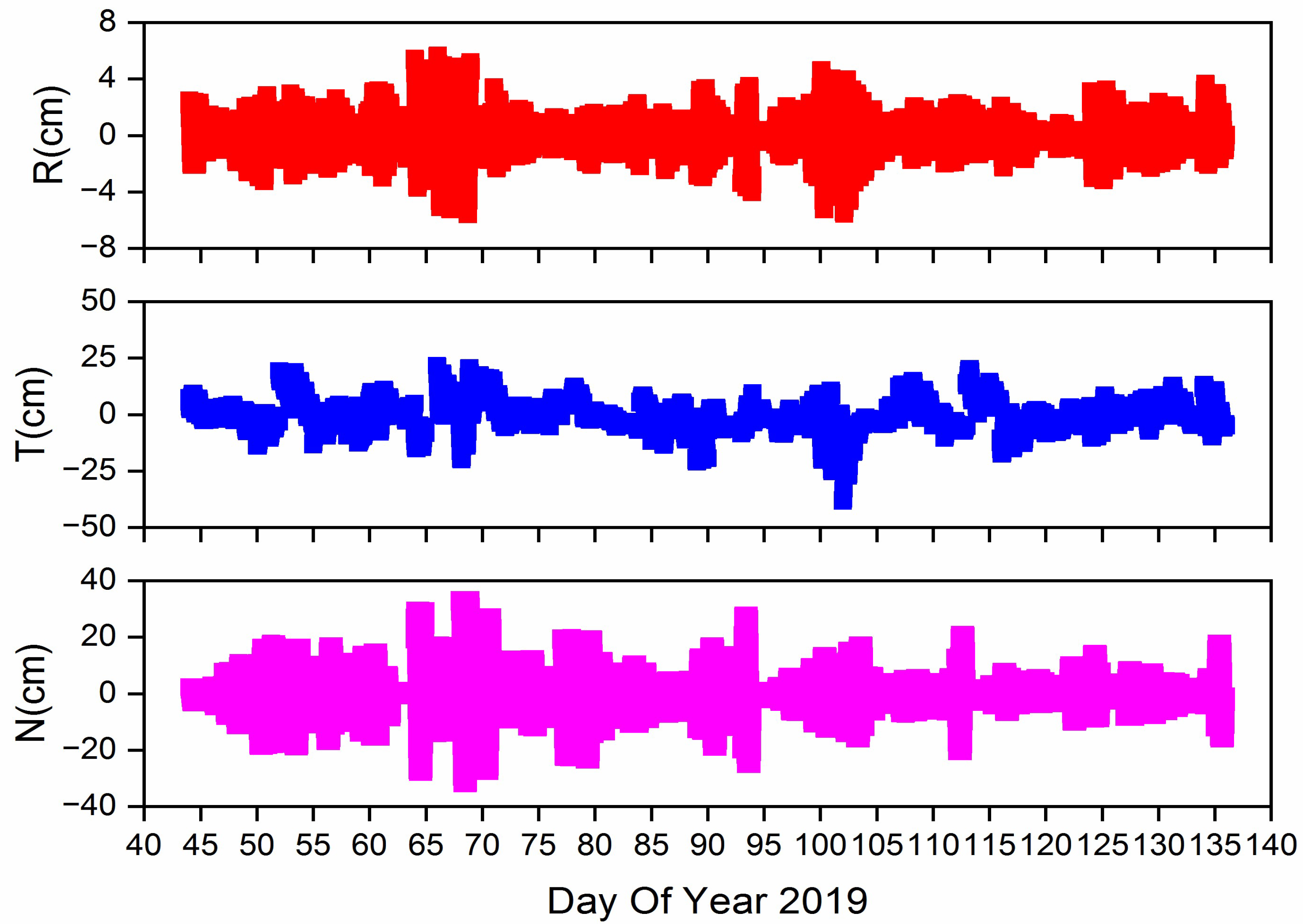
| Etalon-1 | Maximum | 6.73 | 27.82 | 37.64 | 5.71 | 21.80 | 33.39 |
| Minimum | −8.38 | −37.68 | −43.17 | −5.64 | −38.56 | −32.08 | |
| Mean | 0.03 | 2.85 | −0.05 | −0.004 | −0.41 | −0.19 | |
| RMS | 1.49 | 7.85 | 10.55 | 1.46 | 6.64 | 8.22 | |
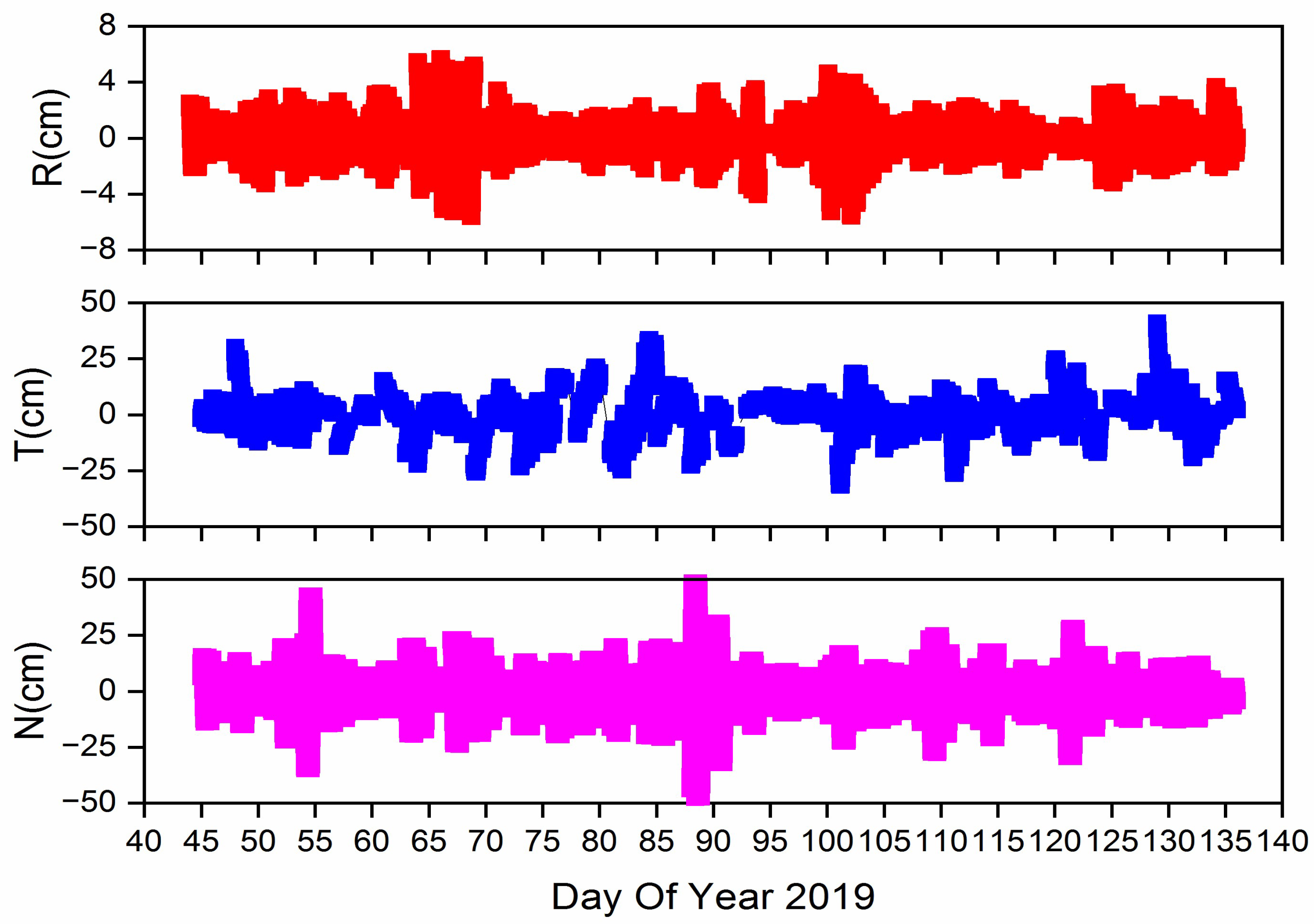
| Etalon-2 | Maximum | 5.99 | 41.15 | 48.85 | 5.46 | 20.66 | 27.26 |
| Minimum | −6.88 | −31.77 | −47.61 | −5.18 | −41.41 | −23.46 | |
| Mean | −0.03 | 0.30 | 0.57 | −0.01 | −1.25 | 0.22 | |
| RMS | 1.68 | 8.61 | 10.06 | 1.48 | 7.15 | 7.15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Kong, Y.; Lu, X.; Zou, D. Contribution of Etalon Observation to Earth Rotation Parameters under a New Observation Scenario. Appl. Sci. 2022, 12, 4936. https://doi.org/10.3390/app12104936
Zhang X, Kong Y, Lu X, Zou D. Contribution of Etalon Observation to Earth Rotation Parameters under a New Observation Scenario. Applied Sciences. 2022; 12(10):4936. https://doi.org/10.3390/app12104936
Chicago/Turabian StyleZhang, Xiaozhen, Yao Kong, Xiaochun Lu, and Decai Zou. 2022. "Contribution of Etalon Observation to Earth Rotation Parameters under a New Observation Scenario" Applied Sciences 12, no. 10: 4936. https://doi.org/10.3390/app12104936
APA StyleZhang, X., Kong, Y., Lu, X., & Zou, D. (2022). Contribution of Etalon Observation to Earth Rotation Parameters under a New Observation Scenario. Applied Sciences, 12(10), 4936. https://doi.org/10.3390/app12104936







