A Note on “Wiener Index of a Fuzzy Graph and Application to Illegal Immigration Networks”

Abstract

Connectivity parameters have an important role in the study of communication networks. Wiener index is such a parameter with several applications in networking, facility location, cryptology, chemistry, and molecular biology, etc. In this paper, we show two notes related to the Wiener index of a fuzzy graph. First, we argue that Theorem 3.10 in the paper “Wiener index of a fuzzy graph and application to illegal immigration networks, Fuzzy Sets and Syst. 384 (2020) 132–147” is not correct. We give a correct statement of Theorem 3.10. Second, by using a new operator on matrix, we propose a simple and polynomial-time algorithm to compute the Wiener index of a fuzzy graph.

1. Introduction

In many real world problems we get only partial information about the problem, and the vagueness in the description and uncertainty has led to the growth of fuzzy graph theory. A mathematical framework to describe uncertainty in real life situation was first suggested by A.L. Zadeh [1]. Rosenfeld [2] introduced the notion of fuzzy graph and several fuzzy analogs of graph theoretic concepts such as paths, cycles and connectedness. Wiener index of graphs has been studied in the field of mathematics, chemistry, and molecular biology [3,4,5].

There are many situations which are modeled by a connected fuzzy graph. Wiener index is such an accepted index used in various fields like communication networks, facility location, crytopology, medicine, etcs. Let us start with a basic definition and concepts of fuzzy graphs; most of them can be found in [6].

Let S be a set. A fuzzy graph $G=(\sigma ,\mu )$ is a pair of membership functions on fuzzy sets $\sigma :S\to [0,1]$ and $\mu :S\times S\to [0,1]$ such that $\mu (u,v)\le \sigma \left(u\right)\wedge \sigma \left(v\right)$. Here ∧ represents the minimum. Throughout the paper, we assume that S is finite and nonempty, $\mu$ is reflexive and symmetric. We denote the underlying crisp graph by $G^{*}=({\sigma }^{*},{\mu }^{*})$ where ${\sigma }^{*}=\{u\in V:\sigma \left(u\right)>0\}$ and ${\mu }^{*}=\{(u,v)\in V\times V:\mu (u,v)>0\}$. We denote an element $(x,y)$ of ${\mu }^{*}$ by $xy$ and call it an edge of G. Elements of ${\sigma }^{*}$ are called vertices of the fuzzy graph G. A fuzzy graph $H=(\tau ,\nu )$ is called a partial fuzzy subgraph of $G=(\sigma ,\mu )$ if $\tau \left(v\right)=\sigma \left(v\right)$ for all $vs.\in {\tau }^{*}$ and $\nu \left(uv\right)=\mu \left(uv\right)$ for all $uv\in {\nu }^{*}$. Note that $G-uv$ denotes the fuzzy subgraph of G in which $\mu \left(uv\right)=0$ and $G-u$ is used for the fuzzy subgraph of G in which $\sigma \left(u\right)=0$.

In a fuzzy graph $G=(\sigma ,\mu )$, a path P of length n is a sequence of distinct vertices $u_0,u_1,\dots ,u_n$ such that $\mu (u_{i-1},u_i)>0$, $i=1,2,\dots ,n$ and the degree of membership of a weakest edge is defined to be the strength of the path P. A path P is called a cycle if $u_0=u_n$.

For any two vertices x and y, let $d(x,y)$ denotes the length of the shortest path between x and y. The diameter of G, denoted by $diam\left(G\right)$, is the maximum distance $d(x,y)$ for any two vertices x, y in G. The strength of connectedness between two vertices x and y is defined as the maximum of the strengths of all paths between x and y and is denoted by $Con{n}_G(x,y)$. If the strength of a path P is equal to $Con{n}_G(x,y)$, then a path P is called a strongest $x-y$ path. A fuzzy graph $G=(\sigma ,\mu )$ is connected if for every $u,v\in {\sigma }^{*}$, $Con{n}_G(u,v)>0$. An edge $xy$ of a fuzzy graph $G=(\sigma ,\mu )$ is called $\alpha$-strong if $\mu \left(xy\right)>Con{n}_{G-xy}(x,y).$ An edge $xy$ of a fuzzy graph $G=(\sigma ,\mu )$ is called $\beta$-strong if $\mu \left(xy\right)=Con{n}_{G-xy}(x,y).$ An edge $xy$ of a fuzzy graph $G=(\sigma ,\mu )$ is called $\delta$-strong if $\mu \left(xy\right)<Con{n}_{G-xy}(x,y).$ An edge is called strong if it is either $\alpha$-strong or $\beta$-strong. A path P is called a strong path if all of its edges are strong. Let $G=(\sigma ,\mu )$ be a fuzzy graph and $x,y\in {\sigma }^{*}.$ A strong path P from x to y is called geodesic if there is no shorter strong path from x to y. The weight of a geodesic is the sum of membership values of all edges in the geodesic. Let $G=(\sigma ,\mu )$ be a fuzzy graph. The Wiener index (WI) of G is defined by $WI\left(G\right)={\sum }_{u,v\in {\sigma }^{*}}\sigma \left(u\right)\sigma \left(v\right)d_S(u,v)$, where $d_S(u,v)$ is the minimum sum of weights of geodesic from u to v. In this paper, it is assumed that $\sigma \left(u\right)=1$ for $u\in {\sigma }^{*}$ in all examples of fuzzy graphs $G=(\sigma ,\mu )$, for convenience. The outline of this paper is organized as follows. In Section 2, it is shown that Theorem 3.10 in the paper “Wiener index of a fuzzy graph and application to illegal immigration networks, Fuzzy Sets and Syst. 384 (2020) 132–147” is not correct. A corrected statement of Theorem 3.10 is given. In Section 3, we present a simple algorithm to compute the wiener index of a fuzzy graph by using a new operator on matrix.

2. Counterexamples and Revision

At first, we recall the Theorem 3.10 of [7] and give two counterexamples to it.

Theorem 1

(Theorem 3.10 of [7]). Let $G=(\sigma ,\mu )$ be a fuzzy graph. For $s,t\in {\sigma }^{*}$, let $P_{s,t}$ denote the path which has the minimum sum of membership values among all shortest strong paths between s and t. Let $uv\in {\mu }^{*}$. If $uv$ is an α or β-strong edge and $uv$ is not a part of any $P_{s,t}$ for $s,t\in {\sigma }^{*}$ with $\{s,t\}\ne \{u,v\}$, then $WI(G-uv)\ne WI\left(G\right)$.

Theorem 3.10 of [7] is not correct as shown in the following two counterexamples. In the following two graphs, $uv$ is an $\alpha$-strong edge and $\beta$-strong edge, respectively.

Example 1.

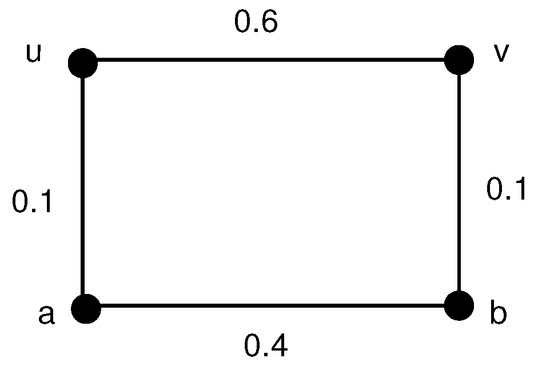
Let $G=(\sigma ,\mu )$ be the fuzzy graph shown in Figure 1 with vertex set $\{a,b,u,v\}$ and $\sigma \left(x\right)=1$ for any $x\in {\sigma }^{*}$, $\mu \left(ua\right)=0.1$, $\mu \left(ab\right)=0.4$, $\mu \left(bv\right)=0.1$, $\mu \left(uv\right)=0.6$. Then each edge of the graph G is strong. So $d_S(u,a)=0.1$, $d_S(a,b)=0.4$, $d_S(b,v)=0.1$, $d_S(u,v)=0.6$, $d_S(u,b)=0.5$ and $d_S(a,v)=0.5$. Therefore, $WI\left(G\right)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S(x,y)=2.2$. It is obvious that $uv$ is an α-strong edge and $uv$ is not a part of any $P_{s,t}$ for $s,t\in {\sigma }^{*}$ with $\{s,t\}\ne \{u,v\}$. For any two vertices $x,y\in {\sigma }^{*}$, the number $d_S^{G-uv}(x,y)$ in $G-uv$ is equal to the number $d_S(x,y)$ in G. Then $WI(G-uv)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S^{G-uv}(x,y)=2.2$ and $WI(G-uv)=WI\left(G\right)$.

Figure 1. $uv$ is an $\alpha$-strong edge and $WI\left(G\right)=WI(G-uv)$.

Example 2.

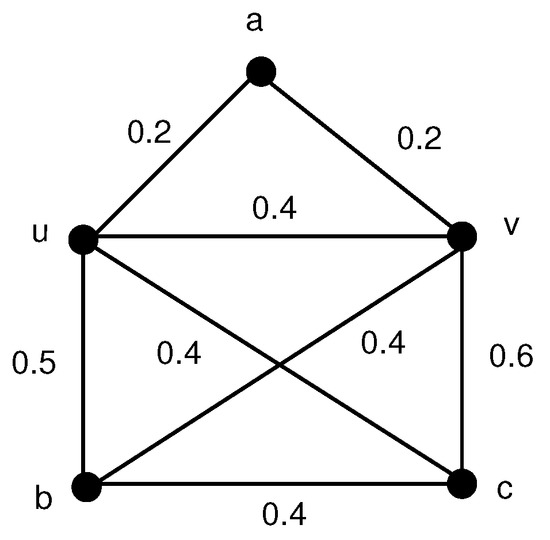
Let $G=(\sigma ,\mu )$ be the fuzzy graph shown in Figure 2 with vertex set $\{a,b,c,u,v\}$ and $\sigma \left(x\right)=1$ for any $x\in {\sigma }^{*}$, $\mu \left(au\right)=\mu \left(av\right)=0.2$, $\mu \left(uv\right)=\mu \left(uc\right)=\mu \left(bv\right)=\mu \left(bc\right)=0.4$, $\mu \left(ub\right)=0.5$, $\mu \left(cv\right)=0.6$. Then each edge of the graph G is strong. So $d_S(a,u)=d_S(a,v)=0.2$, $d_S(u,v)=d_S(u,c)=d_S(b,v)=d_S(b,c)=0.4$, $d_S(u,b)=0.5$, $d_S(c,v)=0.6$, $d_S(a,b)=0.6$ and $d_S(a,c)=0.6$. Therefore, $WI\left(G\right)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S(x,y)=4.3$. It is obvious that $uv$ is an β-strong edge and $uv$ is not a part of any $P_{s,t}$ for $s,t\in {\sigma }^{*}$ with $\{s,t\}\ne \{u,v\}$. For any two vertices $x,y\in {\sigma }^{*}$, the number $d_S^{G-uv}(x,y)$ in $G-uv$ is equal to the number $d_S(x,y)$ in G. So $WI(G-uv)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S^{G-uv}(x,y)=4.3$ and $WI(G-uv)=WI\left(G\right)$.

Figure 2. $uv$ is an $\beta$-strong edge and $WI\left(G\right)=WI(G-uv)$.

Therefore, Theorem 3. 10 of [7] can be changed as follows

Theorem 2.

Let $G=(\sigma ,\mu )$ be a fuzzy graph with each edge being strong. For $s,t\in {\sigma }^{*}$, let $P_{s,t}$ denote the path which has the minimum sum of membership values among all shortest strong paths between s and t. Suppose that $uv$ is not a part of any $P_{s,t}$ for $s,t\in {\sigma }^{*}$ with $\{s,t\}\ne \{u,v\}$. Then

(1) If $d_S^{G-uv}(u,v)>\mu \left(uv\right)$, then $WI(G-uv)>WI\left(G\right)$.

(2) If $d_S^{G-uv}(u,v)=\mu \left(uv\right)$, then $WI(G-uv)=WI\left(G\right)$.

(3) If $d_S^{G-uv}(u,v)<\mu \left(uv\right)$, then $WI(G-uv)<WI\left(G\right)$.

Proof. 

Since each edge of G is strong, it follows that each edge in $G-uv$ is also strong edge. Owing to $uv$ being a strong edge in G, $d_S^G(u,v)=\mu \left(uv\right)$. Let $\{a,b\}\ne \{u,v\}$. Since $uv$ is not part of any $P_{a,b}$, $d_S^{G-uv}(a,b)=d_S^G(a,b)$. Thus, $WI(G-uv)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S^{G-uv}(x,y)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S^G(x,y)+(d_S^{G-uv}(u,v)-d_S^G(u,v))=WI\left(G\right)+(d_S^{G-uv}(u,v)-\mu \left(uv\right))$. So, if $d_S^{G-uv}(u,v)>\mu \left(uv\right)$, then $WI(G-uv)>WI\left(G\right)$. If $d_S^{G-uv}(u,v)=\mu \left(uv\right)$, then $WI(G-uv)=WI\left(G\right)$. If $d_S^{G-uv}(u,v)<\mu \left(uv\right)$, then $WI(G-uv)<WI\left(G\right)$.    □

Note: The condition “each edge is strong” is necessary in Theorem 2. For example, let $G=(\sigma ,\mu )$ be the fuzzy graph shown in Figure 3 with vertex set $\{a,b,c,u,v\}$ and $\sigma \left(x\right)=1$ for any $x\in {\sigma }^{*}$, $\mu \left(uv\right)=0.95$, $\mu \left(au\right)=\mu \left(ab\right)=0.3$, $\mu \left(cu\right)=\mu \left(cb\right)=0.1$, $\mu \left(vb\right)=0.5$, $\mu \left(ub\right)=0.4$ . Then each edge of the graph G except edge $ub$ is strong. Edge $ub$ is a weak edge in G. So $d_S(u,v)=0.95$, $d_S(a,u)=d_S(a,b)=0.3$, $d_S(c,u)=d_S(c,b)=0.1$, $d_S(v,b)=0.5$, $d_S(a,c)=0.4$, $d_S(a,v)=0.8$, $d_S(u,b)=0.2$ and $d_S(c,v)=0.6$. Therefore, $WI\left(G\right)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S(x,y)=4.25$. It is obvious that $uv$ is a strong edge and $uv$ is not a part of any $P_{s,t}$ for $s,t\in {\sigma }^{*}$ with $\{s,t\}\ne \{u,v\}$. It is obvious that $ub$ is a strong edge in $G-uv$. Hence, $d_S^{G-uv}(u,v)=0.9$, $d_S^{G-uv}(a,u)=d_S^{G-uv}(a,b)=0.3$, $d_S^{G-uv}(c,u)=d_S^{G-uv}(c,b)=0.1$, $d_S^{G-uv}(v,b)=0.5$, $d_S^{G-uv}(u,b)=0.4$, $d_S^{G-uv}(a,c)=0.4$, $d_S^{G-uv}(a,v)=0.8$ and $d_S^{G-uv}(c,v)=0.6$. So $WI(G-uv)={\sum }_{x,y\in {\sigma }^{*}}\sigma \left(x\right)\sigma \left(y\right)d_S^{G-uv}(x,y)=4.4$. Though $d_S^{G-uv}(u,v)<\mu \left(uv\right)$, $WI(G-uv)>WI\left(G\right)$.

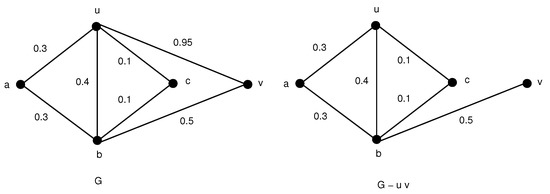
Figure 3. Fuzzy graphs G and $G-uv$.

3. A New Algorithm to Compute Wiener Index of a Fuzzy Graph

Let $G=(\sigma ,\mu )$ be a fuzzy graph with $|{\sigma }^{*}|=n$. The underlying graph of $G=(\sigma ,\mu )$ is denoted by $G^{*}=({\sigma }^{*},{\mu }^{*})$, where ${\sigma }^{*}=\left\{v\right|\sigma \left(v\right)>0\}$ and ${\mu }^{*}=\left\{uv\right|\mu \left(uv\right)>0\}$. M. Binu et al. in [7] give an Algorithm 1 to compute Wiener index of a fuzzy graph as follows.

Algorithm 1: Computing Wiener index of a fuzzy graph [7].

Step 1. Identify strong edges of G using the algorithm in [8]. Step 2. Let $G^{\prime }=({\sigma }^{\prime },{\mu }^{\prime })$ be the fuzzy subgraph of G obtained by deleting the $\delta$-edges of G. Step 3. Use Dijkstra’s algorithm to identify geodesics between u and v in $G^{{}^{\prime }*}$, for each $u,v\in {\sigma }^{*}$. Let $P^1,P^2,\cdots ,P^k$ be the geodesics connecting u and v in $G^{{}^{\prime }*}$. Step 4. Calculate $S_{p^i}$ for $i=1,2,\cdots ,k$, where $S_{p^i}$ is the sum of membership values of edges of $P^i$. Step 5. Let $d_S(u,v)=\wedge \left\{S_{P^i}\right|i=1,2,\cdots ,k\}$. Step 6. Construct an $n\times n$ matrix D corresponding to $G=(\sigma ,\mu )$ with the following properties. Each row and column corresponds to vertices in ${\sigma }^{*}$. If row i corresponds to vertex u and column j corresponds to vertex v, then $d_S(u,v)$ is the entry corresponds to row i and column j. Step 7. Calculate $WI\left(G\right)={\sum }_{u,v\in {\sigma }^{*}}\sigma \left(u\right)\sigma \left(v\right)d_S(u,v)$.

    The main drawback of the Algorithm 1 in [7] is as follows.

Dijkstra’s algorithm is only used to identify the length of the shortest path between u and v in $G^{{}^{\prime }*}$. However, it can not be used to identify the number k of the shortest path. For any big graph, the total number of the shortest path between u and v can be very high. In such case, it is difficult to perform Step 3 and Step 4.

In order to give a simple algorithm to compute Wiener index of a fuzzy graph $G=(\sigma ,\mu )$, we define an operator ⊛ on matrix as follows. Let $G^{\prime }=({\sigma }^{\prime },{\mu }^{\prime })$ be the fuzzy subgraph of G obtained by deleting the $\delta$-edges of G. Let $A^1={\left(a_{ij}^1\right)}_{n\times n}$ be the adjacent matrix of the fuzzy graph $G^{\prime }$, where $a_{ii}^1=0$ and $a_{ij}^1={\mu }^{\prime }\left(v_i{v}_j\right)$ for $i,j\in \{1,2,\cdots ,n\}$. Let $A^k={\left(a_{ij}^k\right)}_{n\times n}$ for $i=2,3,\cdots , diam\left(G^{{}^{\prime }*}\right)$, where $diam\left(G^{{}^{\prime }*}\right)$ denote the diameter of $G^{{}^{\prime }*}$. Define $A^{k+1}=A^k⊛A^1$ as follows:

$$a_{ij}^{k+1}=\left\{\begin{array}{cc}0,\hfill & \mathrm{if} i=j\hfill \\ a_{ij}^k,\hfill & \mathrm{if} i\ne j \mathrm{and} a_{\mathit{ij}}^k\ne 0\hfill \\ \underset{1\le t\le n}{min}\{a_{it}^k+a_{tj}^1|a_{it}^k\ne 0,a_{tj}^1\ne 0\},\hfill & \mathrm{if} i\ne j \mathrm{and} a_{\mathit{ij}}^k=0\hfill \end{array}\right.$$

Theorem 3.

Let $G^{\prime }=({\sigma }^{\prime },{\mu }^{\prime })$ be a fuzzy graph such that every edge is strong edge. If $a_{ij}^k=0$ and $a_{ij}^{k+1}\ne 0$, then $d(v_i,v_j)=k+1$ and $d_S(v_i,v_j)=a_{ij}^{k+1}$, where $d(v_i,v_j)$ is the distance between $v_i$ and $v_j$ in $G^{{}^{\prime }*}$.

Proof. 

We will prove it by induction on the number k. Suppose $k=1$. If $a_{ij}^1\ne 0$, then $v_i{v}_j\in {\mu }^{{}^{\prime }}$ and $a_{ij}^1={\mu }^{\prime }\left(v_i{v}_j\right)$. Since every edge in $G^{\prime }$ is strong edge, then $d(v_i,v_j)=1$ and $d_S(v_i,v_j)=a_{ij}^1$. Suppose that $a_{ij}^1=0$ and $a_{ij}^2\ne 0$. Then $v_i{v}_j\notin {\mu }^{{}^{\prime }}$. Since $a_{ij}^2={min}_{1\le t\le n}\{a_{it}^1+a_{tj}^1|a_{it}^1\ne 0,a_{tj}^1\ne 0\}$, it follows that $d(v_i,v_j)=2$ and $d_S(v_i,v_j)=a_{ij}^2$.

Assume that the theorem holds for $k<l$. Suppose that $a_{ij}^l=0$ and $a_{ij}^{l+1}\ne 0$. By definition, $a_{ij}^{l+1}={min}_{1\le t\le n}\{a_{it}^l+a_{tj}^1|a_{it}^l\ne 0,a_{tj}^1\ne 0\}$. For any $a_{it}^l\ne 0$ and $a_{tj}^1\ne 0$, if there exists $l^{\prime }<l$ such that $a_{it}^{l^{\prime }}\ne 0$, then $a_{ij}^{l^{\prime }+1}\ne 0$. Since $l^{\prime }+1\le l$, it follows that $a_{ij}^l\ne 0$, which is a contradiction. Hence for any $l^{\prime }<l$, $a_{it}^{l^{\prime }}=0$. That is $a_{it}^{l-1}=0$ and $a_{it}^l\ne 0$. By inductive hypotheses on k, it follows that $d(v_i,v_t)=l$ and $d_S(v_i,v_t)=a_{it}^l$. Since $a_{ij}^{l+1}={min}_{1\le t\le n}\{a_{it}^l+a_{tj}^1|a_{it}^l\ne 0,a_{tj}^1\ne 0\}$, there exists t such that $a_{ij}^{l+1}=a_{it}^l+a_{tj}^1$, where $a_{it}^l\ne 0$ and $a_{tj}^1\ne 0$. Since $d(v_i,v_t)=l$ and $d_S(v_i,v_t)=a_{it}^l$, it follows that $d(v_i,v_j)=l+1$ and $d_S(v_i,v_j)=a_{ij}^{l+1}$.    □

Corollary 1.

Let $G^{\prime }=({\sigma }^{\prime },{\mu }^{\prime })$ be a fuzzy graph such that every edge is strong edge. Let $diam\left(G^{{}^{\prime }*}\right)$ be the diameter of $G^{{}^{\prime }*}$. Then for any two vertices $v_i,v_j\in {\sigma }^{\prime }$, $d_S(v_i,v_j)=a_{ij}^{diam\left(G^{{}^{\prime }*}\right)}$, where $i,j\in \{1,2,\cdots ,n\}$.

Algorithm 2: A new algorithm to compute Wiener index of a fuzzy graph.

Step 1. Identify strong edges of G using the algorithm in [8]. Step 2. Let $G^{{}^{\prime }}=({\sigma }^{\prime },{\mu }^{\prime })$ be the fuzzy subgraph of G obtained by deleting the $\delta$-edges of G. Step 3. Calculate $A^1,A^2,\cdots ,A^{diam\left(G^{{}^{\prime }*}\right)}$, where $d_S(v_i,v_j)=a_{ij}^{diam\left(G^{{}^{\prime }*}\right)}$ for $1\le i<j\le n$. Step 4. Calculate $WI\left(G\right)={\sum }_{u,v\in {\sigma }^{*}}\sigma \left(u\right)\sigma \left(v\right)d_S(u,v)$.

Obviously, it is a polynomial-time algorithm. The correctness of the Algorithm 2 follows from Theorem 3 and Corollary 1. So we have the following:

Theorem 4.

Let $G=(\sigma ,\mu )$ be a fuzzy graph. Let $A^1,A^2,\cdots ,A^{diam\left(G^{{}^{\prime }*}\right)}$ be defined as in the Algorithm 2. Then $WI\left(G\right)={\sum }_{1\le i<j\le n}\sigma \left(v_i\right)\sigma \left(v_j\right)a_{ij}^{diam\left(G^{{}^{\prime }*}\right)}$.

Proof. 

By Theorem 3, let $G^{\prime }=({\sigma }^{\prime },{\mu }^{\prime })$ be a fuzzy graph such that every edge is strong edge. If $a_{ij}^k=0$ and $a_{ij}^{k+1}\ne 0$, then $d(v_i,v_j)=k+1$ and $d_S(v_i,v_j)=a_{ij}^{k+1}$. By the definition on the new operator on matrix, for any two vertices $v_i,v_j\in {\sigma }^{\prime }$, $d_S(v_i,v_j)=a_{ij}^{diam\left(G^{{}^{\prime }*}\right)}$, where $i,j\in \{1,2,\cdots ,n\}$. So, $WI\left(G\right)={\sum }_{1\le i<j\le n}\sigma \left(v_i\right)\sigma \left(v_j\right)a_{ij}^{diam\left(G^{{}^{\prime }*}\right)}$. □

Example 3.

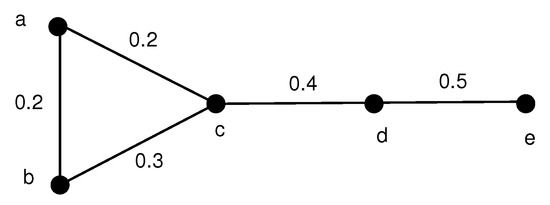
Let $G=(\sigma ,\mu )$ be the fuzzy graph shown in Figure 4 with vertex set $\{a,b,c,d,e\}$ and $\sigma \left(v\right)=1$ for any $v\in {\sigma }^{*}$, $\mu \left(ab\right)=0.2$, $\mu \left(ac\right)=0.2$, $\mu \left(bc\right)=0.3$, $\mu \left(cd\right)=0.4$, $\mu \left(de\right)=0.5$. Then each edge of the graph G is strong.

Figure 4. Fuzzy graph G with $diam\left(G^{{}^{\prime }*}\right)=3$.

By using Algorithm 2 and $diam\left(G^{{}^{\prime }*}\right)=3$, we can compute $A^1,A^2,$ and $A^3$ as follows:

$A^1$ a b c d e a 0 0.2 0.2 0 0 b 0.2 0 0.3 0 0 c 0.2 0.3 0 0.4 0 d 0 0 0.4 0 0.5 e 0 0 0 0.5 0

$A^2$ a b c d e a 0 0.2 0.2 0.6 0 b 0.2 0 0.3 0.7 0 c 0.2 0.3 0 0.4 0.9 d 0.6 0.7 0.4 0 0.5 e 0 0 0.9 0.5 0

$A^3$	a	b	c	d	e
a	0	0.2	0.2	0.6	1.1
b	0.2	0	0.3	0.7	1.2
c	0.2	0.3	0	0.4	0.9
d	0.6	0.7	0.4	0	0.5
e	1.1	1.2	0.9	0.5	0

As membership values of all vertices are one, the sum of all upper triangular entries of $A^3$ will be the $WI$ of G. Hence $WI\left(G\right)=6.1$.

4. Conclusions

In this work, we discussed two problems related to the Wiener index of a fuzzy graph. First, we argued that Theorem 3.10 in the paper “Wiener index of a fuzzy graph and application to illegal immigration networks, Fuzzy Sets and Syst. 384 (2020) 132–147” is not correct. We gave a correct statement of Theorem 3.10, where a different result is given for the same conditions. Second, by using a new operator on matrix, we proposed a simple algorithm to compute the wiener index of a fuzzy graph. The main contribution of the proposed algorithm is as follows: First, for a general fuzzy graph, computation of the Wiener index by hand is possible. At the same time, the algorithm is easily realized in the computer. Furthermore, the new algorithm is simpler and more efficient, which is a polynomial-time algorithm. The property on Wiener index can help us to understand the critical property on the communication network. That is, when some edge is deleted, the Wiener index in communication network may be changed.