Investigation of Deep Shaft-Surrounding Rock Support Technology Based on a Post-Peak Strain-Softening Model of Rock Mass
Abstract
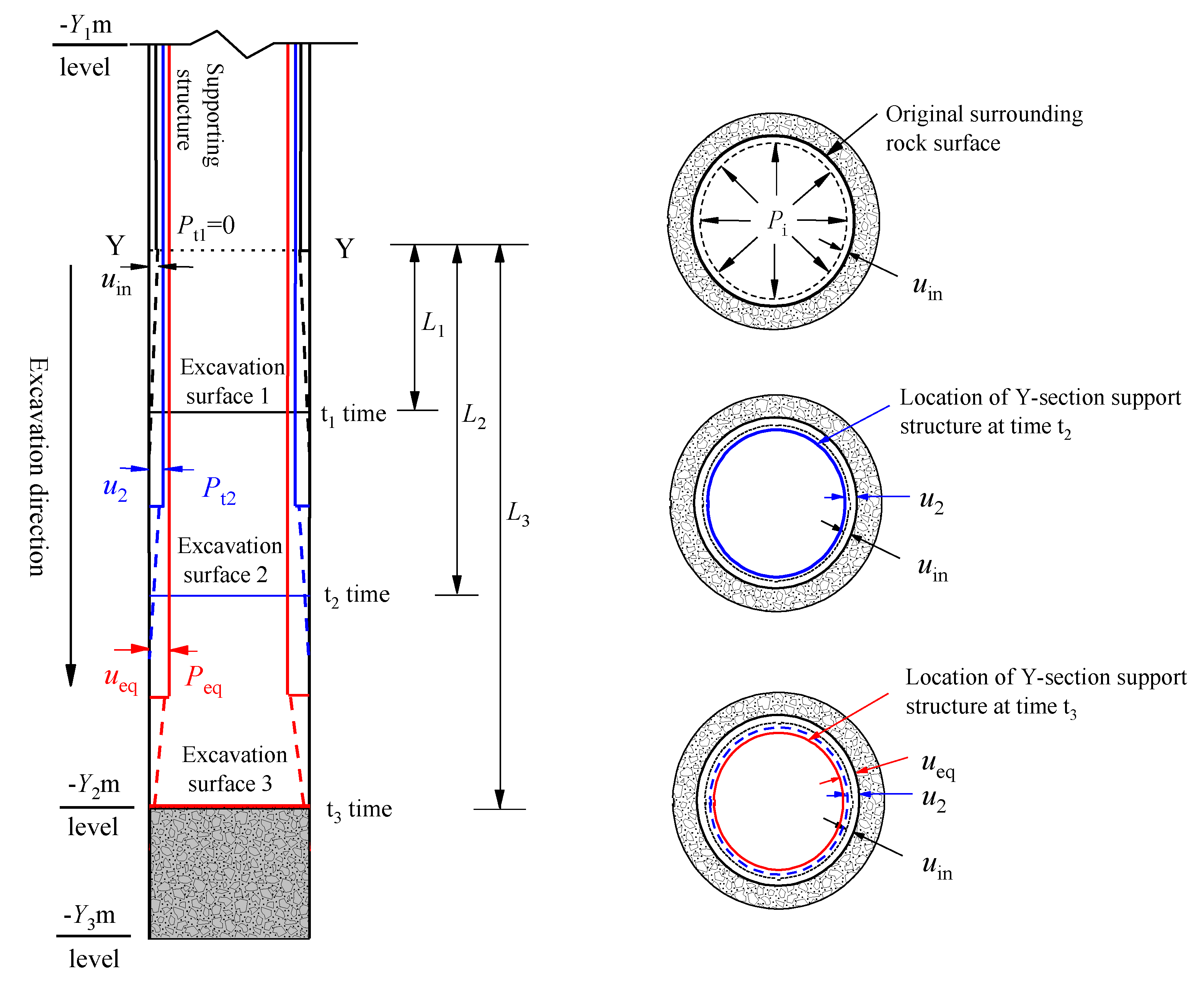
:1. Introduction
2. Theoretical Basis
2.1. Equivalent Strain-Softening Model for Jointed Rock Mass
2.1.1. Quantifying the Surrounding Rock Grading System Using the GSI (Geological Strength Index) Series
2.1.2. Strain-Softening Model of Equivalent Jointed Rock Mass
2.2. Principle of Convergence–Constraint Method
2.3. Shaft Support Characteristic Curve
3. Model Validation and Analysis
3.1. Triaxial Compression Tests of Surrounding Rock
3.2. Parameter Determination of Equivalent Strain-Softening Model
3.3. Validation and Analysis of Model Reliability
4. Design and Stability Analysis of Surrounding Rock-Supporting Structure of Shaft
4.1. Engineering Example
4.2. Rock Mass Mechanical Properties
4.3. Original Support Scheme Design
4.4. Numerical Calculation Model and Model Parameters
4.5. Analysis of Original Supporting Structure Calculation Results
4.5.1. GRC, SCC, and LDP Curves
4.5.2. Damage Status and Cause Analysis of the Original Supporting Structure
4.6. Support Plan Design Optimization
4.7. Optimization Scheme Numerical Calculation Results Analysis
4.8. Monitoring of Support Effect
5. Discussion
5.1. Comparative Analysis of Numerical Calculation Results of Original Plan and Monitoring Data of Surrounding Rock Deformation
5.2. Deviation Analysis
5.3. Comparative Analysis of Calculation Results of Optimized Support Plan and Surrounding Rock Deformation Monitoring Data
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, G.; He, F. Deformation failure mechanism of high stress deep soft roadway and its control. J. Min. Saf. Eng. 2015, 32, 571–577. [Google Scholar] [CrossRef]
- Li, H.; Wang, X. Deformation and Failure Law and Control Technology of Surrounding Rock in Deep Shaft. Met. Mine 2020, 49, 11. [Google Scholar] [CrossRef]
- Fang, X.; Zhao, J.; Hong, M. Failure Mechanism and Control Measure of Roadway Deformation with Fractured Surrounding Rock in Deep Mine. J. Min. Saf. Eng. 2012, 29, 1–7. [Google Scholar] [CrossRef]
- Wang, J.; Luo, N.; Bai, Z. On the relation between interlayer glide caused by coal extraction and the shaft rupture occurring in coal mines in huanghuai area. Chin. J. Rock Mech. Eng. 2003, 22, 1072–1077. [Google Scholar] [CrossRef]
- Zhang, W.Q.; Lu, Y.H.; Gong, H.Y.; Meng, X.J.; Guan, Y.Z. Causes analysis of shaft wall damage in Yan-Teng Mining District and its prevention and contyolling method. Rock Soil Mech. 2004, 12. [Google Scholar] [CrossRef]
- Liu, J.L.; Chen, L.W.; Wang, J.L. Characteristic analysis of temperature stresses of shaft wall. Rock Soil Mech. 2011, 32, 2386–2390. [Google Scholar]
- Yang, H.; Jiang, X.Y. Mechanical Model and Analysis of Shaft Wall Fracture Mechanism. J. Shandong Inst. Build. Mater. 2003, 17, 383–385. [Google Scholar] [CrossRef]
- Sun, X.; Li, G.; Zhao, C.; Liu, Y.; Miao, C. Investigation of Deep Mine Shaft Stability in Alternating Hard and Soft Rock Strata Using Three-Dimensional Numerical Modeling. Processes 2018, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Cao, S.; Luo, F.; Cheng, C.; Li, G.D.; Guo, P. Surrounding rock control of shaft in water enriched fault fracture zone. Chin. J. Rock Mech. Eng. 2014, 33, 1536–1545. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, Q.; Xi, H.; Gong, G. Improved compound support system for coal mine tunnels in densely faulted zones: A case study of China’s Huainan coal field. Eng. Geol. 2018, 240, 10–20. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Wang, Q.; Liu, S. Vertical Shaft Excavation Shaping and Surrounding Rock Control Technology Under the Coupling Action of High Ground Stress and Fracture Formation. J. Perform. Constr. Facil. 2020, 34, 04020116. [Google Scholar] [CrossRef]
- Gao, Y.F.; Wang, B.; Wang, J.; Li, B.; Xing, F.; Wang, Z.G.; Jin, T.L. Test on structural property and application of concrete-filled steel tube support of deep mine and soft rock roadway. Chin. J. Rock Mech. Eng. 2010, 29 (Suppl. S1), 2604–2609. [Google Scholar]
- Yao, Z.S.; Yu, G.H.; Cheng, H.; Rong, C.X. Research on vertical bearing capacity of shaft lining structure of high strength concrete and double steel cylinders in super-thick alluvium. Rock Soil Mech. 2010, 6. [Google Scholar] [CrossRef]
- Yu, W.; Wang, W.; Wu, G.; Yu, X.; Peng, W. Three Zones and Support Technique for Large Section Incline Shaft Crossing Goaf. Geotech. Geol. Eng. 2017, 35, 1921–1931. [Google Scholar] [CrossRef]
- Peng, W.Q.; Wang, W.J.; Yuan, C. Supporting Technology Research in Deep Well Based on Modified Terzaghi Formula. Adv. Civ. Eng. 2018, 2018 Pt 10, 9483538. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.; Liu, Z.; An, B.; Liu, F.; Wang, Y. Numerical Calculation and Stability of the Yield and Enhanced Support Technology for Shaft. Geotech. Geol. Eng. 2019, 37, 3127–3140. [Google Scholar] [CrossRef]
- Chen, S.; Wu, A.; Wang, Y.; Chen, X.; Yan, R.; Ma, H. Study on repair control technology of soft surrounding rock roadway and its application. Eng. Fail. Anal. 2018, 92, 443–455. [Google Scholar] [CrossRef]
- Peng, R.; Meng, X.; Zhao, G.; Li, Y.; Zhu, J. Experimental research on the structural instability mechanism and the effect of multi-echelon support of deep roadways in a kilometre-deep well. PLoS ONE 2018, 13, e0192470. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.; Kaiser, P.K.; Uno, H.; Tasaka, Y.; Minami, M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2004, 41, 3–19. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Minami, M. Determination of residual strength parameters of jointed rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2007, 44, 247–265. [Google Scholar] [CrossRef]
- Cai, M.; Kaiser, P. Visualization of rock mass classification systems. Geotech. Geol. Eng. 2006, 24, 1089–1102. [Google Scholar] [CrossRef]
- Alejano, L.R.; Rodríguez-Dono, A.; Veiga, M. Plastic radii and longitudinal deformation profiles of tunnels excavated in strain-softening rock masses. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2012, 30, 169–182. [Google Scholar] [CrossRef]
- Yang, W.; Li, G.; Ranjith, P.G.; Fang, L. An experimental study of mechanical behavior of brittle rock-like specimens with multi-non-persistent joints under uniaxial compression and damage analysis. Int. J. Damage Mech. 2019, 28, 1490–1522. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Empirical strength criterion for rock masses. J. Geotech. Eng. Div. 1980, 106, 1013–1035. [Google Scholar] [CrossRef]
- Hoek, E.; Brown E, T. The Hoek–Brown failure criterion and GSI—2018 edition. J. Rock Mech. Geotech. Eng. 2018, 11, 445–463. [Google Scholar] [CrossRef]
- Alejano, L.R.; Rodriguez-Dono, A.; Alonso, E.; Manín, G.F. Ground reaction curves for tunnels excavated in different quality rock masses showing several types of post-failure behaviour. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2009, 24, 689–705. [Google Scholar] [CrossRef]
- Lee, Y.L. Explicit analysis for the ground-support interaction of a circular tunnel excavation in anisotropic stress fields. J. Chin. Inst. Eng. 2019, 43, 13–26. [Google Scholar] [CrossRef]
- De La Fuente, M.; Taherzadeh, R.; Sulem, J.; Nguyen, X.S.; Subrin, D. Applicability of the Convergence-Confinement Method to Full-Face Excavation of Circular Tunnels with Stiff Support System. Rock Mech. Rock Eng. 2019, 52, 2361–2376. [Google Scholar] [CrossRef]
- Oreste, P.; Hedayat, A.; Spagnoli, G. Effect of Gravity of the Plastic Zones on the Behavior of Supports in Very Deep Tunnels Excavated in Rock Masses. Int. J. Geomech. 2019, 19, 04019107. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. Underground Excavations in Rock; Institution of Mining and Metallurgy: London, UK, 1980; ISBN 9780429178122. [Google Scholar]
- Basarir, H.; Genis, M.; Ozarslan, A. The analysis of radial displacements occurring near the face of a circular opening in weak rock mass. Int. J. Rock Mech. Min. Sci. 2010, 47, 771–783. [Google Scholar] [CrossRef]
- González-Nicieza, C.; Álvarez-Vigil, A.E.; Menéndez-Díaz, A.; González-Palacio, C. Influence of the depth and shape of a tunnel in the application of the convergence–confinement method. Tunn. Undergr. Space Technol. 2008, 23, 25–37. [Google Scholar] [CrossRef]
- Oreste, P.P.; Pella, D. Modelling progressive hardening of shotcrete in convergence-confinement approach to tunnel design. Tunn. Undergr. Space Technol. 1997, 12, 425–431. [Google Scholar] [CrossRef]
- Oreste, P.P.; Peila, D. Radial passive rockbolting in tunnelling design with a new convergence-confinement model. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1996, 33, 443–454. [Google Scholar] [CrossRef]
- Regulation for Testing the Physical and Mechanical Properties of Rock—Part 20: Test for Determining the Strength of Rock in Triaxial Compression. Available online: https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=SCHF&dbname=SCHF&filename=SCHF201907216&uniplatform=NZKPT&v=mUzF6YZFkG_IqrMzThtGHwg3CMhC-KJzwqoiF7SVoCehKjgOKZlgeqHHKToQcy6a (accessed on 24 October 2021).
- Hoek, E.; Diederichs, M.S. Empirical estimation of rock mass modulus. Int. J. Rock Mech. Min. Sci. 2006, 43, 203–215. [Google Scholar] [CrossRef]
- Peng, J.; Rong, G.; Wang, X. An empirical model for determination of mi in Hoek−Brown failure criterion for intact rocks. J. Cent. South Univ. (Sci. Technol.) 2013, 44, 4617–4623. [Google Scholar]
- Yuan, L.; Xue, J.; Liu, Q. Surrounding rock stability control theory and support technique in deep rock roadway for coal mine. J. China Coal Soc. 2011, 36, 535–543. [Google Scholar]
- Zhang, C.; Feng, X.; Zhou, H. Study of some problems about application of stress release method to tunnel excavation simulation. Rock Soil Mech. 2008, 29, 31–37. [Google Scholar] [CrossRef]
- Zhu, Y.; Chen, L.; Zhang, H.; Zhou, Z.; Chen, S. Physical and Mechanical Characteristics of Soft Rock Tunnel and the Effect of Excavation on Supporting Structure. Appl. Sci. 2019, 9, 1517. [Google Scholar] [CrossRef] [Green Version]













| Confining Pressureσ3/MPa | σ3 = 0 | σ3 = 1 | σ3 = 3 | σ3 = 7 |
|---|---|---|---|---|
| Peak stress/MPa | 4.156 | 5.534 | 8.399 | 14.305 |
| Peak strain/10−2 | 0.875 | 1.289 | 2.068 | 3.882 |
| Residual stress/MPa | 0.709 | 1.787 | 3.812 | 8.051 |
| residual strain/10−2 | 1.668 | 4.148 | 6.134 | 10.115 |
| Confining Pressure σ3/MPa | 0 | 1 | 3 | 7 |
|---|---|---|---|---|
| mi | 10.00 | 9.67 | 9.08 | 8.02 |
| mb | 2.40 | 2.31 | 2.17 | 1.92 |
| GSIP | GSIr | SP (10−3) | Sr (10−3) | D | σc (MPa) | E (GPa) | φ (°) | v | C (MPa) | η* (10−3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 60 | 33 | 11.74 | 0.58 | 0 | 4.156 | 4.4 | 26 | 0.25 | 2.2 | 19 |
| The Depth of Measuring Point/m | σH/MPa | σh/MPa | σv/MPa | αH/(°) |
|---|---|---|---|---|
| 21 | 35.23 | 28.22 | 25.61 | 85 |
| 24 | 35.30 | 28.26 | 25.82 | 83 |
| Peak Parameter | Residual Parameters | |
|---|---|---|
| σc/MPa | 4.2 | 4.2 |
| GSI | 60 | 33 |
| c/MPa | 2.2 | 1.4 |
| φ/° | 26 | 18 |
| E/GPa | 4.4 | 4.4 |
| Ψ | 0 | 0 |
| v | 0.25 | 0.25 |
| Pv | 26 | 26 |
| PH | 36 | 36 |
| Ph | 29 | 29 |
| Well Circle | Resin Anchor Rod (End Anchor) | Concrete | |||
|---|---|---|---|---|---|
| Shed Distance d1 (m) | Diameter Φ (mm) | Length L (m) | Row Spacing d2 × d3 (m) | Thickness t (mm) | |
| Original plan one | 1.5 | 22.0 | 2.5 | 1.0 × 1.2 | 600 (C30) |
| Original plan two | 1.2 | 22.0 | 2.5 | 1.0 × 1.2 | 700 (C30) |
| Pmax (MPa) | K/ (MPa·m−1) | umax/ (mm) | E/ (GPa) | |||
|---|---|---|---|---|---|---|
| Well ring (No.28 A-shaped I-beam) | 0.29 | 230 | 31 | 210 | ||
| Anchor rod | 0.31 | 12 | 150 | 180 | ||
| High-strength anchor | 0.46 | 25 | 220 | 220 | ||
| Concrete | C30 | t = 600 mm | 2.48 | 1023 | 28 | 30 |
| t = 700 mm | 2.88 | 1214 | 29 | 30 | ||
| C35 | t = 700 mm | 3.36 | 1275 | 26 | 31.5 | |
| Initial Support | Secondary Support | |||||
|---|---|---|---|---|---|---|
| Resin Anchor Rod (End Anchor) | Well Circle | Concrete | ||||
| Diameter Φ (mm) | Row Spacing d2 × d3 (m) | Length L (m) | Shed Distance d1 (m) | Thickness t (mm) | ||
| Original plan one | 22.0 | 1.0 × 1.2 | 2.5 | 1.5 | 600 (C30) | |
| Original plan two | 22.0 | 1.0 × 1.2 | 2.5 | 1.2 | 700 (C30) | |
| High-strength anchor cable (steel strand) | Well circle | Concrete | ||||
| Diameter Φ (mm) | Row spacing d2 × d3 (m) | Length L1 (m) | Length of anchoring section L2 (m) | Shed distance d1 (m) | Thickness t (mm) | |
| Optimization plan one | 22.0 | 1.0 × 1.2 | 8.0 | 3 | 1.5 | 600 (C30) |
| Optimization plan two | 22.0 | 1.0 × 1.0 | 8.0 | 3 | 1.2 | 700 (C35) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, Y.; Yao, B.; Chen, D.; Sun, C.; Jia, B. Investigation of Deep Shaft-Surrounding Rock Support Technology Based on a Post-Peak Strain-Softening Model of Rock Mass. Appl. Sci. 2022, 12, 253. https://doi.org/10.3390/app12010253
Zhang J, Wang Y, Yao B, Chen D, Sun C, Jia B. Investigation of Deep Shaft-Surrounding Rock Support Technology Based on a Post-Peak Strain-Softening Model of Rock Mass. Applied Sciences. 2022; 12(1):253. https://doi.org/10.3390/app12010253
Chicago/Turabian StyleZhang, Jianjun, Yang Wang, Baicong Yao, Dongxu Chen, Chuang Sun, and Baoxin Jia. 2022. "Investigation of Deep Shaft-Surrounding Rock Support Technology Based on a Post-Peak Strain-Softening Model of Rock Mass" Applied Sciences 12, no. 1: 253. https://doi.org/10.3390/app12010253
APA StyleZhang, J., Wang, Y., Yao, B., Chen, D., Sun, C., & Jia, B. (2022). Investigation of Deep Shaft-Surrounding Rock Support Technology Based on a Post-Peak Strain-Softening Model of Rock Mass. Applied Sciences, 12(1), 253. https://doi.org/10.3390/app12010253





