Protective Measurement—A New Quantum Measurement Paradigm: Detailed Description of the First Realization
Abstract
1. Introduction
Theoretical Framework
2. Experimental Implementation
Experimental Setup
3. Results
- An acquisition with only the crystals in the optical path and or , which allows us to calibrate the system;
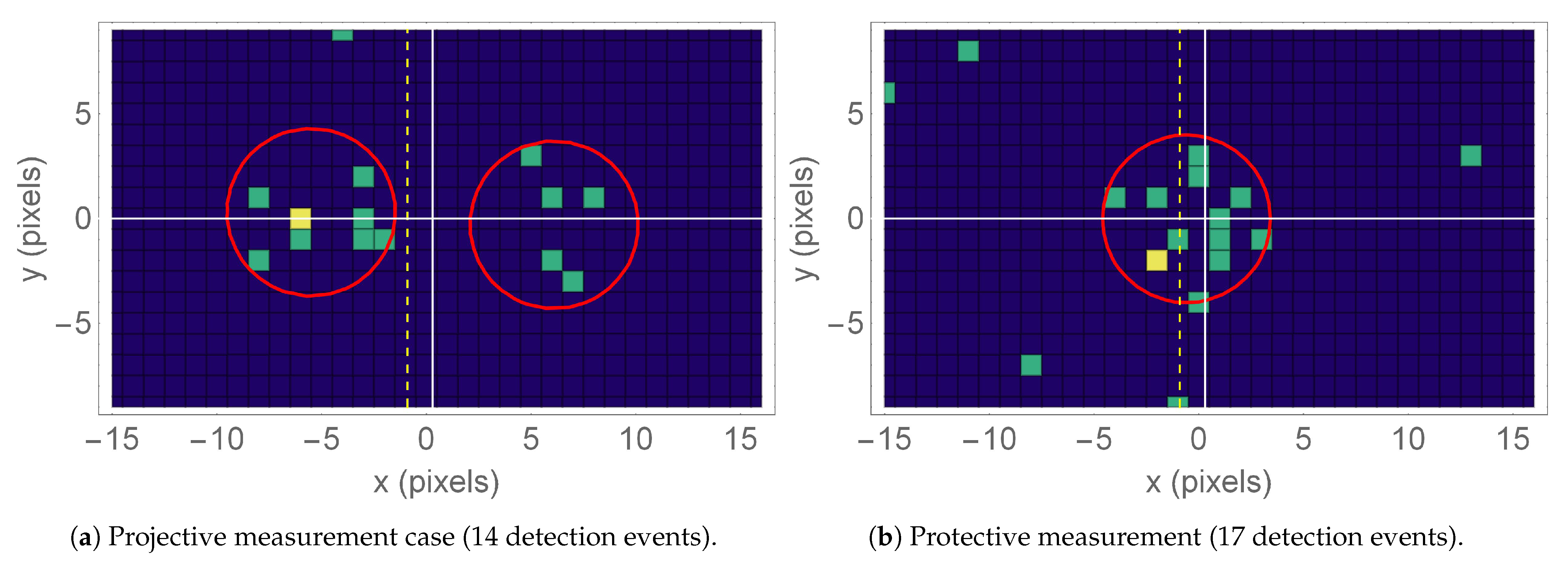
- An acquisition without protection (only crystals in the optical path), corresponding to the traditional PJ scenario;
- An acquisition with both weak interaction and active Zeno-like protection (both birefringent crystals and polarizers in the optical path), realizing the PM;
- Two acquisitions, one with only the polarizing plates and one with a free optical path, allowing us to complete the system calibration by evaluating and properly subtracting unwanted position biases introduced by crystals and polarizing plates.
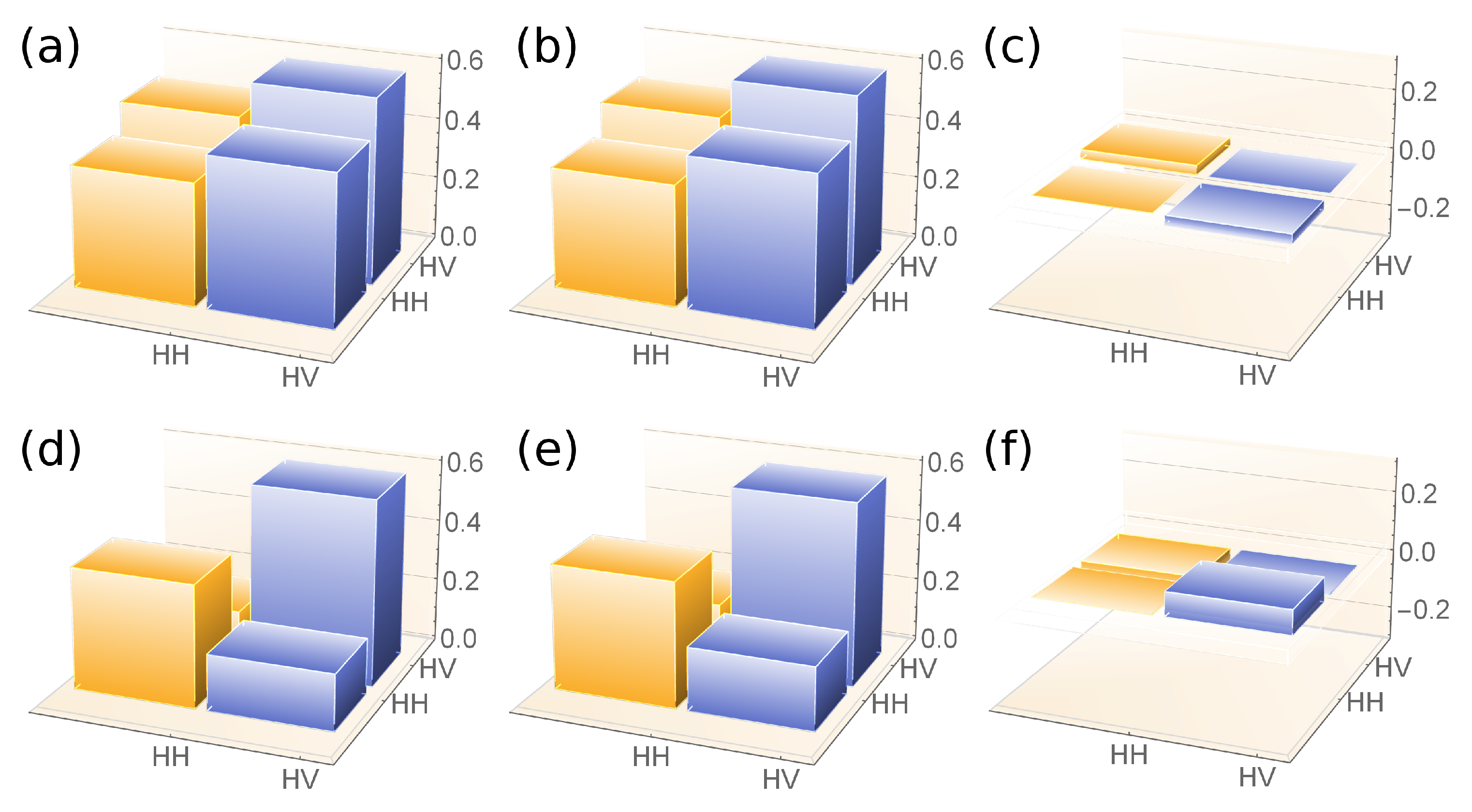
3.1. Output State Verification
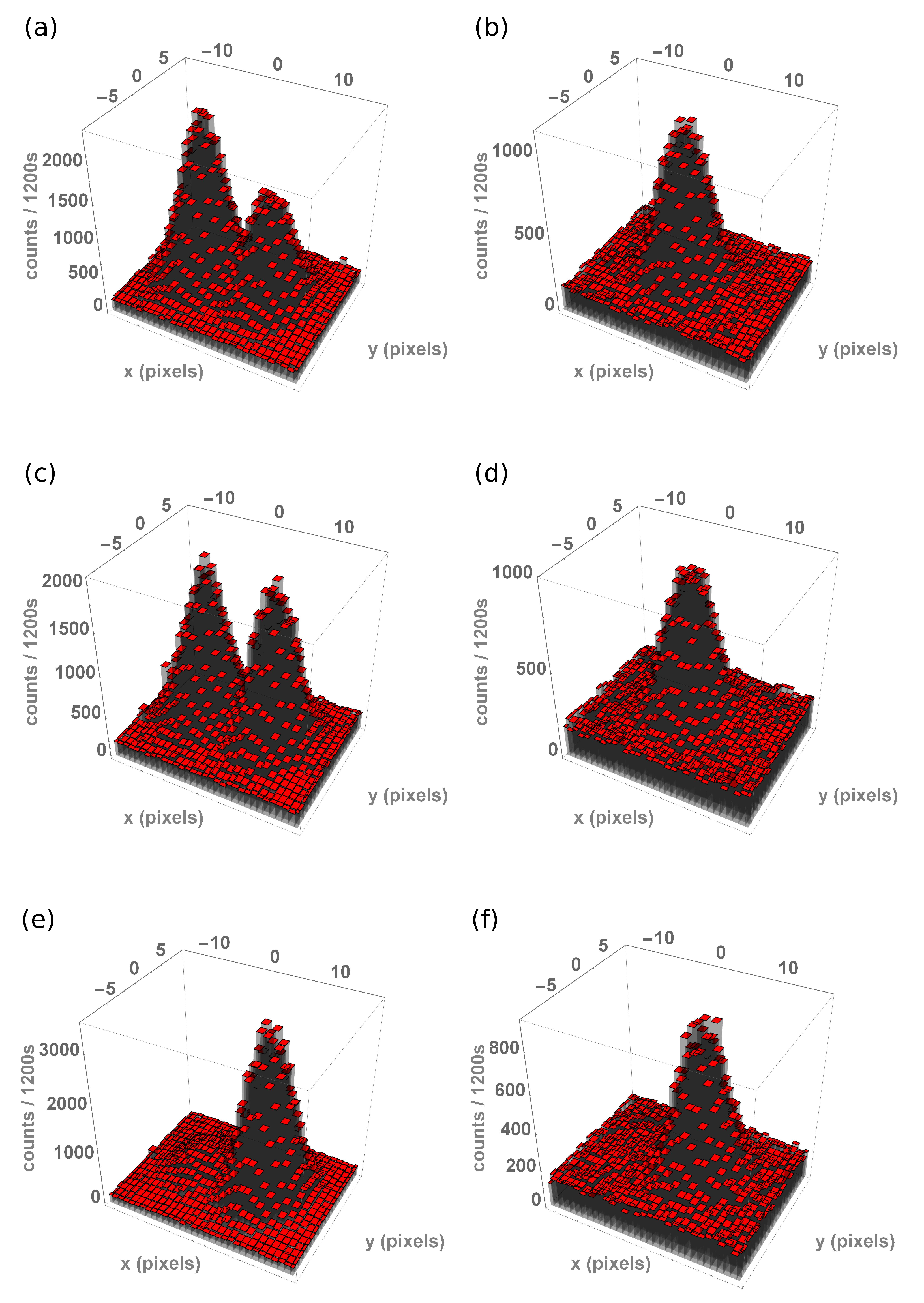
3.2. Expectation Values
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Expectation Value Analysis
Appendix A.1. Projective Measurements
Appendix A.2. Protective Measurements
References
- Aharonov, Y.; Albert, D.Z.; Vaidman, L. How the result of a measurement of a component of the spin of a spin-1/2 particle can turn out to be 100. Phys. Rev. Lett. 1988, 60, 1351–1354. [Google Scholar] [CrossRef]
- Tamir, B.; Cohen, E. Introduction to weak measurements and weak values. Quanta 2013, 2, 7–17. [Google Scholar] [CrossRef]
- Aharonov, Y.; Vaidman, L. Measurement of the Schrödinger wave of a single particle. Phys. Lett. A 1993, 178, 38–42. [Google Scholar] [CrossRef]
- Aharonov, Y.; Anandan, J.; Vaidman, L. The Meaning of Protective Measurements. Found. Phys. 1996, 26, 117–126. [Google Scholar] [CrossRef]
- Vaidman, L. Protective measurements. In Compendium of Quantum Physics; Greenberger, D., Hentschel, K., Weinert, F., Eds.; Springer: Berlin, Germany, 2009; pp. 505–508. [Google Scholar]
- Vaidman, L. Protective measurements. In Protective Measurement and Quantum Reality; Gao, S., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 15–27. [Google Scholar]
- Georgiev, D.; Cohen, E. Analysis of single-particle nonlocality through the prism of weak measurements. Int. J. Quantum Inf. 2020, 18, 1941024. [Google Scholar] [CrossRef]
- Ritchie, N.; Story, J.; Hulet, R. Realization of a measurement of a “weak value”. Phys. Rev. Lett. 1991, 66, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Hosten, O.; Kwiat, P. Observation of the Spin Hall Effect of Light via Weak Measurements. Science 2008, 319, 787–790. [Google Scholar] [CrossRef]
- Dixon, P.; Starling, D.; Jordan, A.; Howell, J. Ultrasensitive Beam Deflection Measurement via Interferometric Weak Value Amplification. Phys. Rev. Lett. 2009, 102, 173601. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Kedem, Y.; Sun, K.; Vaidman, L.; Li, C.; Guo, G. Phase Estimation with Weak Measurement Using a White Light Source. Phys. Rev. Lett. 2013, 111, 033604. [Google Scholar] [CrossRef]
- Piacentini, F.; Avella, A.; Levi, M.P.; Lussana, R.; Villa, F.; Tosi, A.; Zappa, F.; Gramegna, M.; Brida, G.; Degiovanni, I.P.; et al. Experiment Investigating the Connection between Weak Values and Contextuality. Phys. Rev. Lett. 2016, 116, 180401. [Google Scholar] [CrossRef]
- Cimini, V.; Gianani, I.; Piacentini, F.; Degiovanni, I.P.; Barbieri, M. Anomalous values, Fisher information, and contextuality, in generalized quantum measurements. Quantum Sci. Technol. 2020, 5, 025007. [Google Scholar] [CrossRef]
- Lundeen, J.; Sutherland, B.; Patel, A.; Stewart, C.; Bamber, C. Direct measurement of the quantum wavefunction. Nature 2011, 474, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Goggin, M.; Almeida, M.P.; Barbieri, M.; Lanyon, B.P.; O’Brien, J.L.; White, A.G.; Pryde, G.J. Violation of the Leggett-Garg inequality with weak measurements of photons. Proc. Natl. Acad. Sci. USA 2011, 108, 1256–1261. [Google Scholar] [CrossRef] [PubMed]
- Magaña-Loaiza, O.; Mirhosseini, M.; Rodenburg, B.; Boyd, R. Amplification of Angular Rotations Using Weak Measurements. Phys. Rev. Lett. 2014, 112, 200401. [Google Scholar] [CrossRef]
- Resch, K.J.; Steinberg, A.M. Extracting Joint Weak Values with Local, Single-Particle Measurements. Phys. Rev. Lett. 2004, 92, 130402. [Google Scholar] [CrossRef]
- Hallaji, M.; Feizpour, A.; Dmochowski, G.; Sinclair, J.; Steinberg, A.M. Weak-value amplification of the nonlinear effect of a single photon. Nat. Phys. 2017, 13, 540. [Google Scholar] [CrossRef]
- Avella, A.; Piacentini, F.; Borsarelli, M.; Barbieri, M.; Gramegna, M.; Lussana, R.; Villa, F.; Tosi, A.; Degiovanni, I.P.; Genovese, M. Anomalous weak values and the violation of a multiple-measurement Leggett-Garg inequality. Phys. Rev. A 2017, 96, 052123. [Google Scholar] [CrossRef]
- Ferrie, C.; Combes, J. How the Result of a Single Coin Toss Can Turn Out to be 100 Heads. Phys. Rev. Lett. 2014, 113, 120404. [Google Scholar] [CrossRef]
- Sinclair, J.; Spierings, D.; Brodutch, A.; Steinberg, A. Interpreting weak value amplification with a toy realist model. Phys. Lett. A 2019, 383, 2839–2845. [Google Scholar] [CrossRef]
- Mundarain, D.; Orszag, M. Quantumness of the anomalous weak measurement value. Phys. Rev. A 2016, 93, 032106. [Google Scholar] [CrossRef]
- Mitchinson, G.; Jozsa, R.; Popescu, S. Sequential weak measurement. Phys. Rev. A 2007, 76, 062105. [Google Scholar] [CrossRef]
- Piacentini, F.; Avella, A.; Levi, M.P.; Gramegna, M.; Brida, G.; Degiovanni, I.P.; Cohen, E.; Lussana, R.; Villa, F.; Tosi, A.; et al. Measuring Incompatible Observables by Exploiting Sequential Weak Values. Phys. Rev. Lett. 2016, 117, 170402. [Google Scholar] [CrossRef] [PubMed]
- Thekkadath, G.S.; Giner, L.; Chalich, Y.; Horton, M.J.; Banker, J.; Lundeen, J.S. Direct Measurement of the Density Matrix of a Quantum System. Phys. Rev. Lett. 2016, 117, 120401. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, Y.-S.; Lee, S.-Y.; Han, S.-W.; Moon, S.; Kim, Y.-H.; Cho, Y.-W. Direct quantum process tomography via measuring sequential weak values of incompatible observables. Nat. Commun. 2018, 9, 192. [Google Scholar] [CrossRef]
- Foletto, G.; Calderaro, L.; Tavakoli, A.; Schiavon, M.; Picciariello, F.; Cabello, A.; Villoresi, P.; Vallone, G. Experimental Certification of Sustained Entanglement and Nonlocality after Sequential Measurements. Phys. Rev. Appl. 2020, 13, 044008. [Google Scholar] [CrossRef]
- Foletto, G.; Calderaro, L.; Vallone, G.; Villoresi, P. Experimental demonstration of sequential quantum random access codes. Phys. Rev. Res. 2020, 2, 033205. [Google Scholar]
- Foletto, G.; Padovan, M.; Avesani, M.; Tebyanian, H.; Villoresi, P.; Vallone, G. Experimental Test of Sequential Weak Measurements for Certified Quantum Randomness Extraction. arXiv 2021, arXiv:2101.12074. [Google Scholar]
- Salazar-Serrano, L.J.; Guzmán, D.A.; Valencia, A.; Torres, J.P. Demonstration of a highly-sensitive tunable beam displacer with no use of beam deflection based on the concept of weak value amplification. Opt. Expr. 2015, 23, 10097. [Google Scholar] [CrossRef]
- Calderón-Losada, O.; Moctezuma Quistian, T.T.; Cruz-Ramirez, H.; Murgueitio Ramirez, S.; U’Ren, A.B.; Botero, A.; Valencia, A. A weak values approach for testing simultaneous Einstein–Podolsky–Rosen elements of reality for non-commuting observables. Commun. Phys. 2020, 3, 117. [Google Scholar] [CrossRef]
- Piacentini, F.; Avella, A.; Gramegna, M.; Lussana, R.; Villa, F.; Tosi, A.; Brida, G.; Degiovanni, I.P.; Genovese, M. Investigating the Effects of the Interaction Intensity in a Weak Measurement. Sci. Rep. 2018, 8, 6959. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, J.; Cohen, E.; Wu, C.W.; Chen, P.X.; Davidson, N. Weak-to-strong transition of quantum measurement in a trapped-ion system. Nat. Phys. 2020, 16, 1206–1210. [Google Scholar] [CrossRef]
- Pan, W.W.; Xu, X.Y.; Kedem, Y.; Wang, Q.Q.; Chen, Z.; Jan, M.; Sun, K.; Xu, J.S.; Han, Y.J.; Li, C.F.; et al. Direct Measurement of a Nonlocal Entangled Quantum State. Phys. Rev. Lett. 2019, 123, 150402. [Google Scholar] [CrossRef]
- Cho, Y.W.; Kim, Y.; Choi, Y.H.; Kim, Y.S.; Han, S.W.; Lee, S.Y.; Moon, S.; Kim, Y.H. Emergence of the geometric phase from quantum measurement back-action. Nat. Phys. 2019, 15, 665–670. [Google Scholar] [CrossRef]
- Shikano, Y.; Hosoya, A. Weak values with decoherence. J. Phys. A Math. Theor. 2009, 43, 025304. [Google Scholar] [CrossRef]
- Shikano, Y.; Hosoya, A. Strange weak values. J. Phys. A Math. Theor. 2010, 43, 385307. [Google Scholar]
- Susa, Y.; Shikano, Y.; Hosoya, A. Optimal probe wave function of weak-value amplification. Phys. Rev. A 2012, 85, 052110. [Google Scholar] [CrossRef]
- Kobayashi, H.; Puentes, G.; Shikano, Y. Extracting joint weak values from two-dimensional spatial displacements. Phys. Rev. A 2012, 86, 053805. [Google Scholar] [CrossRef]
- Vaidman, L. Weak value controversy. Philos. Trans. R. Soc. A 2017, 375, 2106. [Google Scholar] [CrossRef] [PubMed]
- Aharonov, Y.; Anandan, J.; Vaidman, L. Meaning of the wave function. Phys. Rev. A 1993, 47, 4616–4626. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C. Comment on “Meaning of the wave function”. Phys. Rev. A 1994, 50, 2788–2792. [Google Scholar] [CrossRef]
- Unruh, W.G. Reality and measurement of the wave function. Phys. Rev. A 1994, 50, 882–887. [Google Scholar] [CrossRef]
- Dickson, M. An empirical reply to empiricism: Protective measurement opens the door for quantum realism. Philos. Sci. 1995, 62, 122–140. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Yuen, H.P. Impossibility of measuring the wave function of a single quantum system. Phys. Rev. Lett. 1996, 76, 2832–2835. [Google Scholar] [CrossRef]
- Dass, N.H.; Qureshi, T. Critique of protective measurements. Phys. Rev. A 1999, 59, 2590–2601. [Google Scholar] [CrossRef]
- Uffink, J. How to protect the interpretation of the wave function against protective measurements. Phys. Rev. A 1999, 60, 3474–3481. [Google Scholar] [CrossRef]
- Gao, S. On Uffink’s criticism of protective measurements. Stud. Hist. Philos. Sci. 2013, 44, 513–518. [Google Scholar] [CrossRef]
- Genovese, M. Interpretations of quantum mechanics and measurement problem. Adv. Sci. Lett. 2010, 3, 249–258. [Google Scholar] [CrossRef]
- Pusey, M.F.; Barrett, J.; Rudolph, T. On the reality of the quantum state. Nat. Phys. 2012, 8, 475–478. [Google Scholar] [CrossRef]
- Hardy, L. Are quantum states real? Int. J. Mod. Phys. B 2013, 27, 1345012. [Google Scholar] [CrossRef]
- Ringbauer, M.; Duffus, B.; Branciard, C.; Cavalcanti, E.G.; White, A.G.; Fedrizzi, A. Measurements on the reality of the wavefunction. Nat. Phys. 2015, 11, 249–254. [Google Scholar] [CrossRef]
- Gao, S. Protective Measurement and Quantum Reality; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Gao, S. Protective Measurements and the Reality of the Wave Function. arXiv 2020, arXiv:2001.09262. [Google Scholar] [CrossRef]
- Khrennikov, A. Emergence of Quantum Mechanics from Theory of Random Fields. J. Russ. Laser Res. 2017, 38, 9–26. [Google Scholar] [CrossRef]
- Pan, A.K. Two definitions of maximally ψ-epistemic ontological model and preparation non-contextuality. arXiv 2020, arXiv:2012.13881. [Google Scholar]
- Piacentini, F.; Avella, A.; Rebufello, E.; Lussana, R.; Villa, F.; Tosi, A.; Gramegna, M.; Brida, G.; Cohen, E.; Vaidman, L.; et al. Determining the quantum expectation value by measuring a single photon. Nat. Phys. 2017, 13, 1191–1194. [Google Scholar] [CrossRef]
- Zhang, D.-J.; Gong, J. Dissipative adiabatic measurements: Beating the quantum Cramér-Rao bound. Phys. Rev. Res. 2020, 2, 023418. [Google Scholar] [CrossRef]
- von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Misra, B.; Sudarshan, E.C.G. The zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef]
- Itano, W.M.; Heinzen, D.J.; Bollinger, J.J.; Wineland, D.J. Quantum zeno effect. Phys. Rev. A 1990, 41, 2295. [Google Scholar] [CrossRef] [PubMed]
- Kwiat, P.; Weinfurter, H.; Herzog, T.; Zeilinger, A.; Kasevich, M.A. Interaction-Free Measurement. Phys. Rev. Lett. 1995, 74, 4763. [Google Scholar] [CrossRef] [PubMed]
- Kofman, A.G.; Kurizki, G. Quantum Zeno effect on atomic excitation decay in resonators. Phys. Rev. A 1996, 54, R3750. [Google Scholar] [CrossRef] [PubMed]
- Kofman, A.G.; Kurizki, G. Acceleration of quantum decay processes by frequent observations. Nature 2000, 405, 546. [Google Scholar] [CrossRef] [PubMed]
- Kofman, A.G.; Kurizki, G. Universal Dynamical Control of Quantum Mechanical Decay: Modulation of the Coupling to the Continuum. Phys. Rev. Lett. 2001, 87, 270405. [Google Scholar] [CrossRef]
- Fischer, M.C.; Gutiérrez-Medina, B.; Raizen, M.G. Observation of the quantum Zeno and anti-Zeno effects in an unstable system. Phys. Rev. Lett. 2001, 87, 040402. [Google Scholar] [CrossRef] [PubMed]
- Facchi, P.; Pascazio, S. Quantum zeno subspaces. Phys. Rev. Lett. 2002, 89, 080401. [Google Scholar] [CrossRef] [PubMed]
- Facchi, P.; Pascazio, S. Quantum Zeno dynamics: Mathematical and physical aspects. J. Phys. A 2008, 41, 493001. [Google Scholar] [CrossRef]
- Smerzi, A. Zeno dynamics, indistinguishability of state, and entanglement. Phys. Rev. Lett. 2012, 109, 150410. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, F.; Herrera, I.; Cherukattil, S.; Lovecchio, C.; Cataliotti, F.S.; Caruso, F.; Smerzi, A. Experimental realization of quantum zeno dynamics. Nat. Commun. 2014, 5, 3194. [Google Scholar] [CrossRef]
- Signoles, A.; Facon, A.; Grosso, D.; Dotsenko, I.; Haroche, S.; Raimond, J.-M.; Brune, M.; Gleyzes, S. Confined quantum Zeno dynamics of a watched atomic arrow. Nat. Phys. 2014, 10, 715. [Google Scholar] [CrossRef]
- Gherardini, S.; Gupta, S.; Cataliotti, F.S.; Smerzi, A.; Caruso, F.; Ruffo, S. Stochastic quantum Zeno by large deviation theory. New J. Phys. 2016, 18, 013048. [Google Scholar] [CrossRef]
- Müller, M.M.; Gherardini, G.; Caruso, F. Noise-robust quantum sensing via optimal multi-probe spectroscopy. Sci. Rep. 2016, 6, 38650. [Google Scholar] [CrossRef]
- Gherardini, S.; Lovecchio, C.; Müller, M.M.; Lombardi, P.; Caruso, F.; Cataliotti, F.S. Ergodicity in randomly perturbed quantum systems. Quantum Sci. Technol. 2017, 2, 015007. [Google Scholar] [CrossRef]
- Müller, M.M.; Gherardini, S.; Caruso, F. Quantum Zeno dynamics through stochastic protocols. Ann. Phys. 2017, 529, 1600206. [Google Scholar] [CrossRef]
- Harel, G.; Kofman, A.G.; Kozhekin, A.; Kurizki, G. Control of non-Markovian decay and decoherence by measurements and interference. Opt. Express 1998, 2, 355. [Google Scholar] [CrossRef][Green Version]
- Gordon, G.; Erez, N.; Kurizki, G. Universal dynamical decoherence control of noisy single-and multi-qubit systems. J. Phys. B 2007, 40, S75. [Google Scholar] [CrossRef]
- Kurizki, G.; Shahmoon, E.; Zwick, A. Thermal baths as quantum resources: Morefriends than foes? Phys. Scr. 2015, 90, 128002. [Google Scholar] [CrossRef]
- Elliott, T.J.; Vedral, V. Quantum quasi-Zeno dynamics: Transitions mediated by frequent projective measurements near the Zeno regime. Phys. Rev. A 2016, 94, 012118. [Google Scholar] [CrossRef]
- Virzí, S.; Avella, A.; Piacentini, F.; Gramegna, M.; Opatrný, T.; Kurizki, G.; Gherardini, S.; Caruso, F.; Degiovanni, I.P.; Genovese, M. Quantum Zeno and Anti-Zeno probes of noise correlations in photon polarisation. arXiv 2021, arXiv:2103.03698. [Google Scholar]
- Gerlach, W.; Stern, O. Der experimentelle nachweis der richtungsquantelung im magnetfeld. Z. Phys. 1922, 9, 349–352. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Single-photon sources and detectors. Rev. Scient. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef] [PubMed]
- Sinha, U.; Sahoo, S.N.; Singh, A.; Joarder, K.; Chatterjee, R.; Chakraborti, S. Single-Photon Sources. Opt. Photonics News 2019, 30, 32–39. [Google Scholar] [CrossRef]
- Grangier, P.; Roger, G.; Aspect, A. Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences. EPL 1986, 1, 173–179. [Google Scholar] [CrossRef]
- Chunnilall, C.J.; Degiovanni, I.P.; Kück, S.; Mü, I.; Sinclair, A.G. Metrology of single-photon sources and detectors: A review. Opt. Eng. 2014, 53, 081910. [Google Scholar] [CrossRef]
- Villa, F.; Lussana, R.; Bronzi, D.; Tisa, S.; Tosi, A.; Zappa, F.; Dalla Mora, A.; Contini, D.; Durini, D.; Weyers, S.; et al. Cmos imager with 1024 spads and tdcs for single-photon timing and 3-d time-of-flight. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 364–373. [Google Scholar] [CrossRef]
- Altepeter, J.; Jeffrey, E.; Kwiat, P. Photonic state tomography. In Advances in Atomic, Molecular, and Optical Physics; Berman, P., Lin, C., Eds.; Academic Press: Cambridge, MA, USA, 2005; Volume 52, pp. 105–159. [Google Scholar]
- Bogdanov, Y.I.; Brida, G.; Genovese, M.; Kulik, S.P.; Moreva, E.V.; Shurupov, A.P. Statistical Estimation of the Efficiency of Quantum State Tomography Protocols. Phys. Rev. Lett. 2010, 105, 010404. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.; Chuang, I. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bengstonn, I.; Zyczkowski, K. Geometry of Quantum States; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photon. 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Genovese, M. Experimental Quantum Enhanced Optical Interferometry. arXiv 2021, arXiv:2101.02891. [Google Scholar]
- Polino, E.; Valeri, M.; Spagnolo, N.; Sciarrino, F. Photonic Quantum Metrology. AVS Quantum Sci. 2020, 2, 024703. [Google Scholar] [CrossRef]
- Paris, M.G.A. Quantum estimation for quantum technology. Int. J. Quantum Inf. 7 2009, 1, 125–137. [Google Scholar] [CrossRef]
- Seveso, L.; Rossi, M.A.C.; Paris, M.G.A. Quantum metrology beyond the quantum Cramér-Rao theorem. Phys. Rev. A 2017, 95, 012111. [Google Scholar] [CrossRef]
- Seveso, L.; Paris, M.G.A. Quantum enhanced metrology of hamiltonian parameters beyond the Cramér-Rao bound. Int. J. Quantum Inf. 2020, 18, 2030001. [Google Scholar] [CrossRef]


| State | |||||
|---|---|---|---|---|---|
| 0.999 | 0.998 | 0.720 | 0.998 | 0.540 | |
| 0.996 | 0.999 | 0.751 | 0.992 | 0.520 | |
| 0.992 | 0.999 | 0.894 | 0.992 | 0.789 |
| State | |||
|---|---|---|---|
| 0 | |||
| −0.208 | |||
| 0.707 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rebufello, E.; Piacentini, F.; Avella, A.; Lussana, R.; Villa, F.; Tosi, A.; Gramegna, M.; Brida, G.; Cohen, E.; Vaidman, L.; et al. Protective Measurement—A New Quantum Measurement Paradigm: Detailed Description of the First Realization. Appl. Sci. 2021, 11, 4260. https://doi.org/10.3390/app11094260
Rebufello E, Piacentini F, Avella A, Lussana R, Villa F, Tosi A, Gramegna M, Brida G, Cohen E, Vaidman L, et al. Protective Measurement—A New Quantum Measurement Paradigm: Detailed Description of the First Realization. Applied Sciences. 2021; 11(9):4260. https://doi.org/10.3390/app11094260
Chicago/Turabian StyleRebufello, Enrico, Fabrizio Piacentini, Alessio Avella, Rudi Lussana, Federica Villa, Alberto Tosi, Marco Gramegna, Giorgio Brida, Eliahu Cohen, Lev Vaidman, and et al. 2021. "Protective Measurement—A New Quantum Measurement Paradigm: Detailed Description of the First Realization" Applied Sciences 11, no. 9: 4260. https://doi.org/10.3390/app11094260
APA StyleRebufello, E., Piacentini, F., Avella, A., Lussana, R., Villa, F., Tosi, A., Gramegna, M., Brida, G., Cohen, E., Vaidman, L., Degiovanni, I. P., & Genovese, M. (2021). Protective Measurement—A New Quantum Measurement Paradigm: Detailed Description of the First Realization. Applied Sciences, 11(9), 4260. https://doi.org/10.3390/app11094260











