Knowledge of Quantum Hidden Variables Enables Backwards-In-Time Signaling

Abstract

Bell’s theorem implies that any completion of quantum mechanics which uses hidden variables (that is, preexisting values of all observables) must be nonlocal in the Einstein sense. This customarily indicates that knowledge of the hidden variables would permit superluminal communication. Such superluminal signaling, akin to the existence of a preferred reference frame, is to be expected. However, here we provide a protocol that allows an observer with knowledge of the hidden variables to communicate with her own causal past, without superluminal signaling. That is, such knowledge would contradict causality, irrespectively of the validity of relativity theory. Among the ways we propose for bypassing the paradox there is the possibility of hidden variables that change their values even when the state does not, and that means that signaling backwards in time is prohibited in Bohmian mechanics.

1. Introduction

In this paper, we provide a protocol that allows any party with knowledge of quantum hidden variables [1,2,3] to communicate to her own past, leading to a breakdown of causality in the strong sense. By “causality”, here we simply mean that “a cause temporally precedes all its effects” (in the absence of closed timelike curves [4]). We will specify better the distinction between “cause” and “effect” in Section 5. By “hidden variables”, here we mean “whatever information that is necessary to describe values of observables as preexisting before the measurement”, which is their usual definition. Namely, the hidden variables encode the properties that are assigned to the outcome once the measurement is performed.

Our protocol is based on quantum contextuality, and the context is chosen after the values of the hidden variables are discovered. Since the context determines the value of the hidden variables and different contexts will lead to different values, this value must have been “sent back in time”. This applies to contextual hidden variables. We will not consider non-contextual hidden variables, since it is known that non-contextual hidden variables cannot be used to describe quantum mechanics [5,6].

In other words, the future choice of context affects the past values of the hidden variables, and this can be used to send information back to one’s own causal past as we shall show below.

Bell’s theorem [7,8,9] implies that such hidden variables are nonlocal: a measurement on one system may change the hidden variables of a distant second system that may be causally disconnected from the first. If the hidden variables exist, this type of nonlocality (which we will call “Einstein nonlocality”) is incompatible with the conjunction of special relativity and causality. Indeed, a person with knowledge of the hidden variables will be able to communicate superluminally [10], which means that for another observer the temporal order of cause and effect can be flipped. An example can illustrate this: suppose that Alice uses a superluminal projectile (or signal) to shoot a distant target. The other observer, Bob, in uniform motion with respect to Alice, can see these two spacelike-separated events with opposite time ordering: he can see the target is hit before Alice pulls the trigger. Interestingly, we note that superluminal signals are not, by themselves, incompatible with relativity if one relaxes causality [11]. If Alice is a mafia hit-man, she will be acquitted from killing her target thanks to Bob’s testimony that the target died before she even pulled the trigger. In other words, the three hypotheses (i) “special relativity”, (ii) “weak causality” (a cause temporally precedes an effect) and (iii) “superluminal signaling” lead to a contradiction: either one has to drop causality (namely, Alice walks free), or one has to drop superluminal signaling (these projectiles do not exist), or one has to drop special relativity. In other words, Bell’s theorem implies that the knowledge of hidden variables violates the causal relations of another observer, under the assumption that special relativity holds.

In this paper we prove a stronger statement that one can communicate with one’s own past without any assumption about relativity. Namely, we show that knowledge of contextual hidden variables enables Backwards-In-Time Signaling (BITS). This is a stronger statement as is evident from the observation that Newtonian mechanics is a theory that does allow superluminal communication but does not allow any communication with one’s own past. In addition, a version of quantum mechanics where the collapse of the wave function happens instantaneously in some preferred reference frame will not allow one to communicate to one’s own past [If one assumes relativity, superluminal communication by itself may allow one to communicate to one’s own past, under the hypothesis that an observer can communicate to spacelike separated points that are in the “future” with respect to the observer’s simultaneity hyperplane. Indeed, if Alice communicates superluminally a signal to Bob, Bob then accelerates to a large fraction of c so that his hyperplane of simultaneity intersects Alice’s timeline at a time before she sent the signal and then he resends Alice’s signal along such hyperplane (superluminally in Bob’s new reference frame), then Alice receives her signal back before she sent it].

Retrocausality, as well as weaker variants of the BITS property of ontic quantum mechanical models have been pointed out in the literature under additional hypotheses, e.g., when considering fundamentally time-symmetric versions of quantum mechanics (i.e., even in the presence of collapse) [12,13,14,15,16,17,18,19]. However, when addressing Bell tests, such retrocausal models only assume the existence of hidden variables that will be measured in the future. Hence these arguments assume communication to the past from the onset. Here, instead, we use plain textbook quantum mechanics together with the hypothesis that one could somehow know quantum hidden variables (as defined above) to prove they must be BITS. Nevertheless, the aforementioned retrocausal frameworks showcase the existence of BITS models which are consistent with standard approaches to quantum mechanics since they strictly prohibit knowledge of the hidden variables.

An important interpretation of quantum mechanics that uses hidden variables is Bohmian Mechanics [20,21,22]. In Bohmian Mechanics spin hidden variables do not exist, and the only hidden variables are the positions of particles [23], however we show below in which sense our argument also applies to this case.

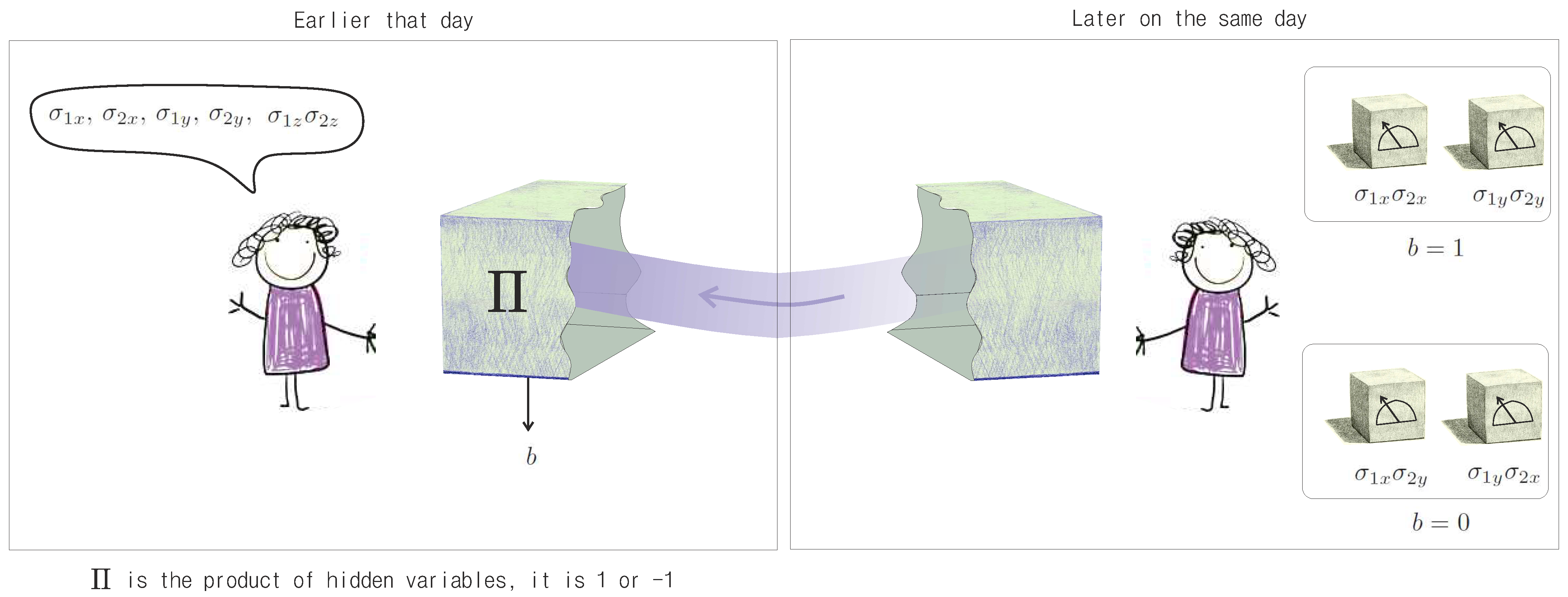
2. The Protocol

Consider the Peres–Mermin square [6,24] composed of the operators

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}{\sigma }_{1x}& {\sigma }_{2x}& {\sigma }_{1x}{\sigma }_{2x}\\ {\sigma }_{2y}& {\sigma }_{1y}& {\sigma }_{1y}{\sigma }_{2y}\\ {\sigma }_{1x}{\sigma }_{2y}& {\sigma }_{1y}{\sigma }_{2x}& {\sigma }_{1z}{\sigma }_{2z}\end{array}\right]\end{array}$$

(1)

where ${\sigma }_{1j}$ are the operators that refer to the spin components of a first spin-1/2 particle and ${\sigma }_{2j}$ of a second spin-1/2 particle, both located in Alice’s lab. In Peres’ words: “The three operators in each row and each column commute, and their product is $+1$, except those of the last column, whose product is $-1$. There is obviously no way of assigning numerical values $\pm 1$ to these nine operators with this multiplicative property” [6]. This implies that we cannot assign definite values to the spin components of the two particles that are independent of what is (was, will be) measured on the other particle: a very simple consequence of quantum contextuality of hidden variables. Since non-contextual hidden variables are impossible [5,6,24], one must conclude that the values of the hidden variables of the spins must be fixed by the context, which is our assumption here. The idea of our protocol is to delay the choice of the context to a time successive to when the values of the hidden variables have been used to determine some “signal”. This can be achieved through the protocol composed by the following steps (see Figure 1):

• Alice finds out the (contextual) hidden values of ${\sigma }_{1x}$, ${\sigma }_{2x}$, ${\sigma }_{1y},$ ${\sigma }_{2y}$, ${\sigma }_{1z}{\sigma }_{2z}$. Of course, quantum mechanics prevents us from knowing these values because they refer to non-commuting (complementary) properties. However, the explicit assumption here is that Alice can know the hidden variables. As proven by Peres, the hidden variables are contextual, but the context will be established by Alice in the future. Clearly, we suppose that the values of the hidden variables reflect the values that are (or were or will be) uncovered by the experiments that are (or were or will be) performed. As specified above, this is the minimal requirement for “hidden variables”. We emphasize the distinction between attaining knowledge of hidden variables and performing a quantum measurement. If one knew the hidden variable, one could predict the measurement outcome. Here we assume that one could somehow know the hidden variables without performing a quantum measurement. All interpretations of quantum mechanics prevent the knowledge of hidden variables (hence the name), but here we explore what would happen if it were possible to know them: if one assumes they exist, it is natural to ask what would happen if they could be known.
• Consider the products in (1): take the product of the hidden values of ${\sigma }_{1x}$, ${\sigma }_{2x}$, ${\sigma }_{1y},$ ${\sigma }_{2y}$ and ${\sigma }_{1z}{\sigma }_{2z}$. If this product is equal to $+1$, then set a bit $b=0$, if the product is equal to $-1$, then set $b=1$. The first choice is consistent with looking at the last line of the Peres–Mermin square, the second choice with looking at the last column.
• Then in the (distant) future, Alice can retroactively decide the value of b by deciding what to measure. If she measures ${\sigma }_{1x}{\sigma }_{2x}$ and ${\sigma }_{1y}{\sigma }_{2y}$ (which commute), then she sets $b=1$. Since the hidden variables, by assumption, reflect the preexisting values of the observables, this means that by setting $b=1$ she sends back to her past self $b=1$. Instead, if she measures ${\sigma }_{1x}{\sigma }_{2y}$ and ${\sigma }_{1y}{\sigma }_{2x}$ (which also commute), then she sends back to herself $b=0$. Note that quantum complementarity forces Alice to choose one of these two possibilities: she cannot perform the measurements connected to both choices since they do not commute.

The accessible information of the ancient Alice is one bit, which has been transferred to her from the recent Alice. Indeed, the bit that the recent Alice wants to transfer to the past is stored in some other degree of freedom f (see below for a detailed discussion), and the mutual information between this bit and the bit uncovered by the previous Alice is equal to

$$I(b:f)=H\left(b\right)+H\left(f\right)-H(b,f),$$

where $H\left(b\right)=H\left(f\right)=1$ (the bits can have both values with equal probability) and $H(b,f)=1$ (the bits are correlated, as explained in the protocol above).

The measurements in point 3 of the protocol can be performed in the following way. The joint measurement of ${\sigma }_{1x}{\sigma }_{2x}$ and ${\sigma }_{1y}{\sigma }_{2y}$ can be performed through a measurement that has Bell states as eigenstates. Indeed, consider $|a\rangle ,|b\rangle$ eigenstates of ${\sigma }_x$ and $|\pm \rangle =\left(\right|a\rangle \pm |b\rangle )/\sqrt{2}$ eigenstates of ${\sigma }_y$, then

$$\begin{array}{c}\hfill |aa\rangle +|bb\rangle =|++\rangle +|--\rangle :{\sigma }_{1x}{\sigma }_{2x}=+1,{\sigma }_{1y}{\sigma }_{2y}=+1\\ \hfill |aa\rangle -|bb\rangle =|+-\rangle +|-+\rangle :{\sigma }_{1x}{\sigma }_{2x}=+1,{\sigma }_{1y}{\sigma }_{2y}=-1\\ \hfill |ab\rangle +|ba\rangle =|++\rangle -|--\rangle :{\sigma }_{1x}{\sigma }_{2x}=-1,{\sigma }_{1y}{\sigma }_{2y}=+1\\ \hfill |ab\rangle -|ba\rangle =|+-\rangle -|-+\rangle :{\sigma }_{1x}{\sigma }_{2x}=-1,{\sigma }_{1y}{\sigma }_{2y}=-1\end{array}$$

(2)

Analogously, the joint measurement of ${\sigma }_{1x}{\sigma }_{2y}$ and ${\sigma }_{1y}{\sigma }_{2x}$ can be performed by the measurement that has the following two-spin maximally entangled states as eigenstates:

$$\begin{array}{c}\hfill |a+\rangle +|b-\rangle =|+a\rangle +|-b\rangle :{\sigma }_{1x}{\sigma }_{2y}=+1,{\sigma }_{1y}{\sigma }_{2x}=+1\\ \hfill |a+\rangle -|b-\rangle =|+b\rangle +|-a\rangle :{\sigma }_{1x}{\sigma }_{2y}=+1,{\sigma }_{1y}{\sigma }_{2x}=-1\\ \hfill |a-\rangle +|b+\rangle =|+a\rangle -|-b\rangle :{\sigma }_{1x}{\sigma }_{2y}=-1,{\sigma }_{1y}{\sigma }_{2x}=+1\\ \hfill |a-\rangle -|b+\rangle =|+b\rangle -|-a\rangle :{\sigma }_{1x}{\sigma }_{2y}=-1,{\sigma }_{1y}{\sigma }_{2x}=-1\end{array}$$

(3)

Both of these observables are incompatible (do not commute) with the measurement of the single spins, represented by the observables ${\sigma }_{1x}\otimes {\mathbb{1}}_2$, ${\mathbb{1}}_1\otimes {\sigma }_{2x}$, etc. Thus, textbook quantum mechanics does not lead to paradoxes, namely either the local values are defined or the joint values are determined by the measurements defined in Equations (2) and (3). The Peres–Mermin argument shows that an apparent paradox arises if one can determine both the local values (through the spin hidden variables) and the joint values. Our protocol hinges on this.

3. Ways to Bypass the Argument?

Here we consider two ways in which our argument can be apparently bypassed: either by introducing additional hidden variables, or by introducing a time dependence of the hidden variables.

The first possible objection is that one could argue that the hidden variable for the joint measurements are unrelated to the hidden variables of the local measurements. Namely that the hidden variable of the product ${\sigma }_{1x}{\sigma }_{2x}$ is different from the product of the hidden variables ${\sigma }_{1x}·{\sigma }_{2x}$, but fundamentally, not only statistically (at the level of expectation values) [25] and not necessarily within a pre- and post-selected ensemble [26,27]. From the abstract point of view, this may be an acceptable objection, but it leads to an implausible ontology. Indeed, the observables connected to the product ${\sigma }_{1x}\otimes {\sigma }_{2x}$ and the single values ${\sigma }_{1x}\otimes {\mathbb{1}}_2$ and ${\mathbb{1}}_1\otimes {\sigma }_{2x}$ all commute, namely they can be determined at the same time. Clearly when this is done, the results must agree in any sensible ontology. Indeed, consider a scenario where two people may possess either a yellow or a red apple, and suppose they both have a yellow apple (namely the “value” of their apple is $+1$). Yet, if one assumes that the value of the product is different from the product of the values, they may conclude that their apples have different color (namely the product of their “values” is $-1$), a nonsensical conclusion. The fact that the measurements in Equations (2) and (3) are incompatible with the local measurements is irrelevant to this argument, since it refers to the ontological “true” values, not to the way these are measured (namely the context, which is determined only in the future).

A second possible objection is that one may postulate that the measurement itself is changing the hidden variables, namely that the measurements of Equations (2) and (3) are not constrained by the hidden values of the spins. This indeed removes the possibility of using Alice’s choice of context to communicate back in time. However, it also changes the meaning of hidden variables. If the measurements can change the hidden values, then the hidden values do not pre-determine the measurement outcomes, namely the hidden variables do not encode the “true” value of the property uncovered by the measurement. Then they would be completely useless, and one could just as well claim that there is no true value and the measurement outcome is “created” at the time of the measurement, as in the Copenhagen interpretation of quantum mechanics. In other words, if one claims that the choice of the context may change the values of the hidden variables at the time of the choice, one cannot describe situations (such as the ones of our protocol) where the context is deliberately left undetermined until the values of the hidden variables have been used. This changes the meaning of hidden variables.

In conclusion, to bypass our argument either one needs to introduce a nonsensical ontology where two identical apples are different, or one must change the meaning of hidden variables.

4. Bohmian Mechanics

In the de Broglie–Bohm interpretation of quantum mechanics [28], spins do not have hidden variables: the only hidden variables are the particles’ positions, but our argument employs spin hidden variables. Nonetheless, we can easily translate the spin degrees of freedom into trajectories. Consider a “full loop Stern–Gerlach apparatus” (FULO) where we do not determine whether the particle goes up or down, but where we just subject the particle to a magnetic field gradient and then we use the opposite magnetic field gradient to re-merge the two arms of the wave function (e.g., see [29]). Such an apparatus does not measure anything: it is described by an identity transformation in quantum mechanics, as it is a unitary transformation followed by its inverse unitary. Nonetheless, the spin information is transferred into the trajectory information inside the FULO. To determine the $x,y,z$ spin hidden variables, Alice can perform one FULO along the x axis followed by one FULO along the y axis and one FULO along the z axis and track (but not measure!) the internal trajectories.

These trajectories encode the spin “hidden variables” because the trajectories in the FULOs are consistent when repeated: if an x-directed FULO is followed by a y-directed one and then by a second x-directed one, the trajectories along the two x-directed ones coincide. Namely, any time dependence of the trajectories is irrelevant in the encoding of the spin hidden values into FULOs trajectories. Moreover, the FULOs trajectory encodes the outcome of future spin measurements (as requested by the hidden variable definition we use in this paper), since the measurement trivially consists of measuring in which of the two arms the particle is present, and since the trajectories in successive FULOs match. Then, we can conclude that the trajectory in the w-directed FULO encodes the w hidden value of the spin for $w=x,y,z$. Namely, the “non-existent” hidden variables for spin are translated into hidden variables for position.

Then our argument seemingly applies: by knowing (not measuring!) the trajectories of the particles through the three successive FULOs, Alice seemingly would be able to signal back in time. Indeed, we have shown how Alice can map the spin quantum degree of freedom into position degrees of freedom of a particle which are the hidden variables of Bohmian mechanics.

However, in reality, our argument is not applicable to Bohmian mechanics because of the time evolution of the hidden variables. Since only position is a hidden variable in Bohmian mechanics, one must also postulate that positions at different times may be connected to different (incompatible) hidden variables. In our protocol we must postulate that the successive FULOs refer to the spin hidden variables at the same time. While this is a reasonable postulate, it is false. It is reasonable because the FULOs are just identity transformations for quantum mechanics and they do not change the quantum state at all, so one would expect that they cannot change the hidden variables that encode the “true” value of the spin (as confirmed by the fact that the trajectories match in successive FULOs oriented along the same directions). However, it is false because if one looks at the trajectory across two FULOs that are rotated by 180 degrees, one finds a trajectory inconsistent with the hidden variable (see Figure 2). Namely, if one looks at the trajectory along a FULO oriented along the x direction and then at the trajectory along a flipped FULO oriented along $-x$, one must conclude that the hidden variable for ${\sigma }_x$ is flipped by the second FULO.

In other words, Bohmian mechanics cannot be used for signaling back in time by our protocol because Bohmian mechanics is an explicit realization of the second way to bypass the argument that we discussed in the previous section. The time dependence of the hidden variables is nontrivial: even unitary evolutions may change the hidden variables of spins. Therefore associating hidden variables with spins (and other observables except for positions) is superfluous in Bohmian mechanics [30].

5. Causal Relations between Past and Future Events

In this section, we elaborate more carefully on how one can distinguish a “cause” event from an “effect” event.

Indeed, a nontrivial subtlety is implicit in all protocols claiming to send information back in time: such protocols establish a correlation between two variables, in the past and in the future, and one must prove that it is the future value that is “causing” the past one and not vice versa (since obviously, correlation does not imply causation). In other words, we have to establish without doubt that the above protocol is sending the value of b to the past, rather than trivially asserting that the past value of b determines the future one. This can be established, but it comes at the price of further assumptions. Different, alternative, assumptions are possible and are enumerated here:

• Undetermined choice. In the above narrative we supposed that in the future Alice will be “free” to choose whatever value of b she wants, namely that her choice is not determined by the value of b that was found in the past. This is tricky, since whatever her (free) choice, it will indeed be equal to the value of b that was found in the past: that value is what she will choose to send (her choice is already known before she makes it). This is the very meaning of communication to the past. It implies that, even though she is free to choose whatever b she wants, she cannot choose to send the value opposite to the one that was found in the past: whatever value is found in the past is the one she will (freely) choose in the future. While it is not strange that the value of her choice is known after she chose it, because of BITS, the value of her choice is known even before she chose it. Causality here is somewhat confusing because the temporal order of events is reversed with respect to usual expectations. Therefore, asking what Alice will feel if she decides to send back to the past the value opposite of b is meaningless, since she cannot decide to send back the opposite of what she actually decided to send. Sometimes what we called “undetermined choice” is termed “free will”, but the adherents to compatibilism have long argued that free will is not inconsistent with determinism (e.g., [31]), whereas here we simply require Alice’s choice to be not pre-determined. As a result that the “free will” and “undetermined choice” are quite slippery concepts, especially for those interpretations that consider quantum mechanics a deterministic theory, one would possibly want to avoid physical consequences being attached to this hypothesis, so we will list other three that can replace it. Namely, the following three hypotheses are compatible with a “no free will” condition according to which Alice is not “free” to choose the value of the bit, which is determined by some other process.
• Evolutionary principle. This principle states that “knowledge comes into existence only through evolutionary processes” [32]. This means that complex meaningful information (such as a Renaissance painting or a physics textbook) does not appear instantaneously from a random fluctuation, but it is the result of a lengthy evolutionary process or computation. For example, a Neolithic caveman could not have had the knowledge or the technique to paint Leonardo’s Mona Lisa painting, and Newton could not have had the knowledge to write a quantum mechanics textbook. This implies that by tying the transmitted bit to the result of a long evolutionary process, one is guaranteed that the value of the bit cannot have been already known in the past. For example, we could tie the value of b to some information that no one knows today, such as “will Apple stock shares increase in value in ten years?”. This guarantees that indeed the bit was transmitted, and not known beforehand. Communication with the past together with the evolutionary principle lead to a chronology paradox [32]: suppose that Alice sends to Leonardo a picture of his painting and he painted it by copying her picture, then the painting would be generated spontaneously since Alice obtained it from Leonardo and Leonardo from Alice.
• Relativistic causality (strictly enforcing non-superluminal communication of at least one event). A completely independent way of ensuring that b is sent to the past is to assume relativity and causality (as defined above) and tie the value of b to the unknown value of some degree of freedom that is spacelike separated from the observer at step 2 of the above protocol, but is accessible at step 3 of the protocol when one must “choose” the value of b. For example: “has the star Betelgeuse turned into a supernova?” (Betelgeuse, in Orion, is a supernova candidate [33]). The supernova event is spacelike separated from step 2 and hence inaccessible if relativity plus causality is assumed, but it will become accessible at step 3, when it enters in step 3’s past lightcone. A caveat is in order here. As discussed above, relativity + causality is incompatible with superluminal communication, but the knowledge of hidden variables immediately implies superluminal communication. Therefore, one can assume relativity + causality for the event that causes the value of b (e.g., the supernova explosion) only if one is sure that the event in question is not communicated superluminally through some quantum hidden variables.
• Ontic randomness for some hidden variable. This entails that, at least in some cases, the outcomes of quantum measurements are intrinsically random. This is what the Copenhagen interpretation of quantum mechanics suggests, but an interpretation that uses hidden variables could say that randomness only arises because of lack of knowledge of the hidden variables. Indeed, hidden variables are based on the idea that a definite, pre-determined value existed prior to the measurement. Therefore, to be really intrinsically random, the hidden variables themselves must possess (at least in some cases) an ontic intrinsic randomness. Under this hypothesis, Alice may perform a ${\sigma }_z$ measurement of a qubit in an eigenstate of ${\sigma }_x$ using an ancillary qubit whose hidden value is not predetermined. She then sends back the outcome as the value of b, which could not have been determined in the far past under this hypothesis.

Any of the above four hypotheses can be employed to conclude that in the above protocol the communication proceeds from the future to the past and not vice versa.

6. Conclusions

All interpretations of quantum mechanics that rely on hidden variables, such as the de Broglie–Bohm theory [28], have some kind of censorship mechanism which prevents the revelation of the values of the hidden variables in practice, e.g., see [34]. Hence, one may claim that our protocol is of no practical relevance. Even without such censorship, previous investigations on whether Bohmian mechanics implies change of the past hidden variables in the context of quantum erasure concluded that “there is no change of the past whatsoever” [35]. Nevertheless, the protocol presented in our paper reaches the opposite conclusion for a wide class of hidden variables by making use of quantum contextuality. While we agree with previous findings that there is no change of the past in Bohmian mechanics, our results show that it is misleading to think of Bohmian mechanics as a “hidden variables” theory because defining hidden variables for all observables except positions is in Bohmian mechanics superfluous. From an instrumental point of view, Bohmian mechanics is best viewed as a theory of positions of macroscopic objects explained in terms of microscopic positions of their constituents, without any sharp borderline between “non-hidden” macroscopic positions and the “hidden” microscopic ones [34].

In previous works [36,37,38] we have seen that quantum uncertainty is vital for reconciling quantum nonlocality in space and time with relativistic causality. Indeed, full access to the hidden variables in our protocol renders quantum uncertainty ineffective and thus it cannot circumvent the BITS.

One can then take the implications of our argument as further evidence that the censorship mechanism that prevents the knowledge of the hidden variables must be strongly enforced if one wants to preserve chronology. In other words, knowing the hidden variables not only allows for superluminal communication, but it even allows for communication to the past. As explained above, this is a stronger statement than simply requiring that Einstein locality (i.e., no superluminal communication) is satisfied. Of course, if hidden variables are unknowable as a matter of principle, they can then be considered unphysical for all intents and might be relegated to the realm of metaphysics as “unperformed experiments have no results” [39,40]. That is the core implication of this paper.

In essence, our conclusion is that in contextual (fully deterministic) hidden variables models for quantum theory, where agents have underdetermined choice and can know the values of the hidden variables, communication to one’s own causal past would be possible, negating the non-relativistic notion of causality. The same conclusion holds also under slightly broader hypotheses that do not require undetermined choices on the part of an agent, as discussed in Section 5.