Impact of Minutiae Errors in Latent Fingerprint Identification: Assessment and Prediction
Abstract
1. Introduction
- What is the impact of human errors in the performance of Automatic Fingerprint Identification Systems?
- Are there minutiae having a higher impact on the identification performance when missed?
- If so, is there any feature of a minutia that can help determine its importance?
- To the best of our knowledge, this is the first study related to the matching algorithms’ performance when minutiae are missed from latent fingerprints.
- We quantify and discuss the impact of missing minutiae in the latent fingerprint on two latent fingerprint matching algorithms’ performance by removing manually marked minutiae from latent fingerprints and calculating their matching score and rank, and comparing them to the original ground-truth latent fingerprints.
2. Previous Works
2.1. Research on the Performance of Experts in Latent Fingerprint Analysis
2.2. Impact of Fingerprint Variations in Automatic Fingerprint Recognition
3. Forensic Fingerprint Analysis: Role of Human Errors
- Reveal: in this stage, an expert should use specific powders, based on the surface and shape of the object, to reveal the latent fingerprint. The errors one may incur at this stage are:
- Using a revealing powder that does not correspond to the surface or shape of the object where the latent fingerprint is, which could wrongly reveal the ridges of the latent fingerprints.
- Using more revealing powder than necessary, creating a filling among the fingerprint ridges, and consequently, making it hard to be of use on the next stages.
- Capture: in this stage, an expert must be careful at capturing the latent fingerprint under the best possible conditions. Errors that are typically observed at this stage are:
- While lifting the latent fingerprint, deformations might be created in the ridges creating false bifurcations or false ends on the ridges. As a result, errors are induced that may severely affect the feature extraction stage.
- Output an out of focus or low-resolution photo of the latent fingerprint.
- Lack of use of a rule next to the latent fingerprint that may enable one to estimate the real scale of the fingerprint.
- Feature extraction: during this stage, the examiners will extract all features necessary for the identification stage. The more common flaws one may experience at this stage are:
- False features can be added from errors originated at the capture stage.
- Actual features could be missed by examiners.
- The position or angle of some features could be shifted due to human perception.
- Identification: any flaw committed at previous stages will affect identification performance. However, the main errors that may show up at this stage are:
- The ranking provides the corresponding impression, but the experts obviate this matching.
- The ranking does not provide the corresponding impression due to human errors issued at the previous stages.
- The expert issues a true positive identification when really it is a false positive.
4. Materials and Methods
- Minutia Cylinder-Code (MCC) [41]: Matching algorithm based on a three-dimensional representation constructed using basic minutiae features such as angles and distances to other minutiae.
- Deformable Minutiae Clustering using Cylinder-Codes (DMCCC) [19]: A matching algorithm independent of minutiae descriptors based on the use of clustering to improve robustness to non-linear transformations. In this case, we use Minutia Cylinder-Code as the minutiae descriptor.
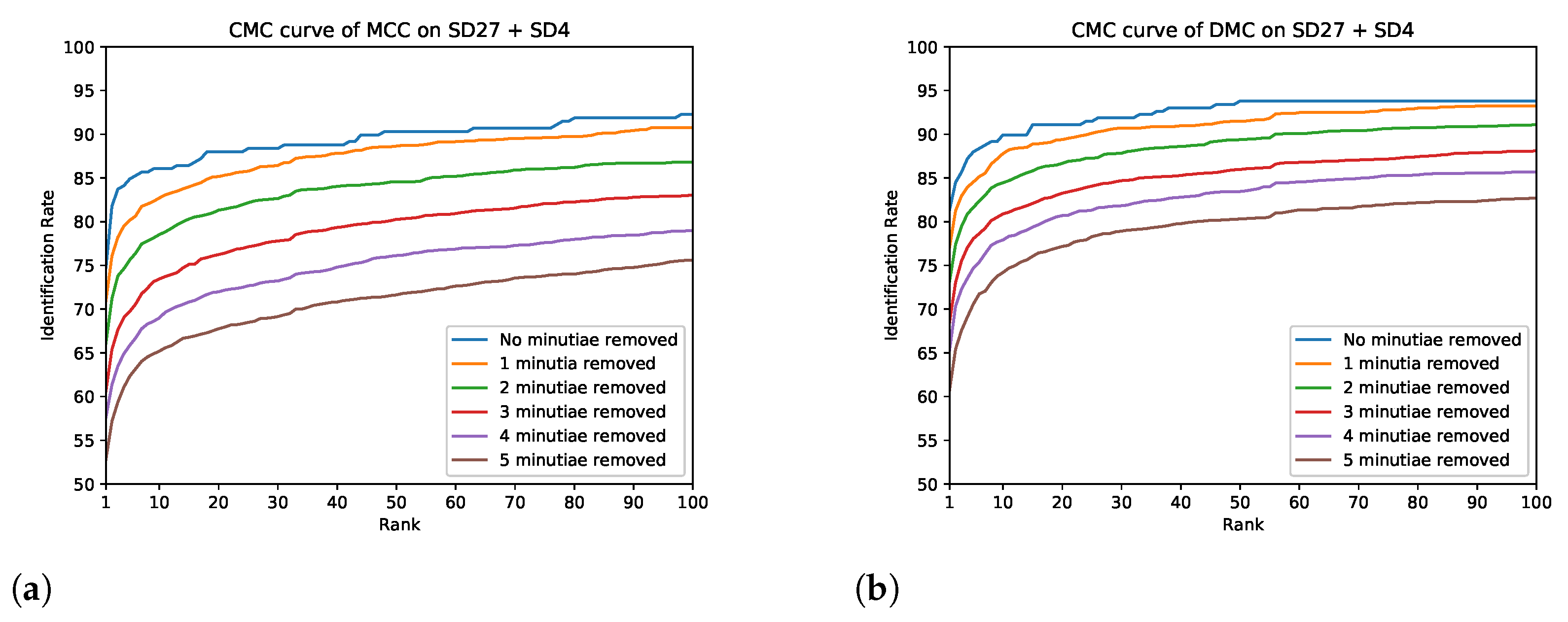
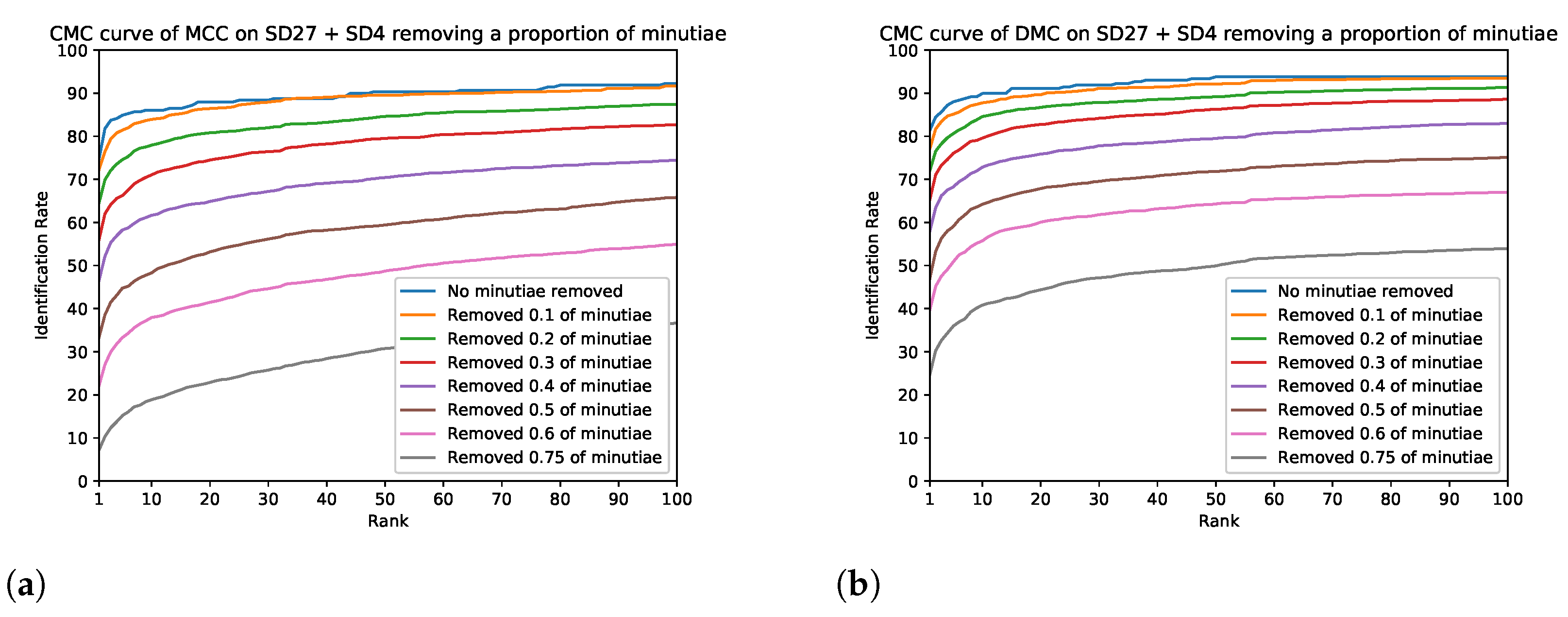
- The first set of experiments consists of randomly removing minutiae from latent fingerprints in the database and comparing the resulting CMC curves in a closed set comparison. We ran 35 experiments; the first 20 experiments consisted of removing a fixed number of minutiae from each latent fingerprint, from 1 to 20. The next 15 experiments consisted of removing a percent of minutiae from each latent fingerprint, from to . Each experiment was run 10 times with different randomly-selected removed minutiae, and the results of the 10 experiments are then averaged.
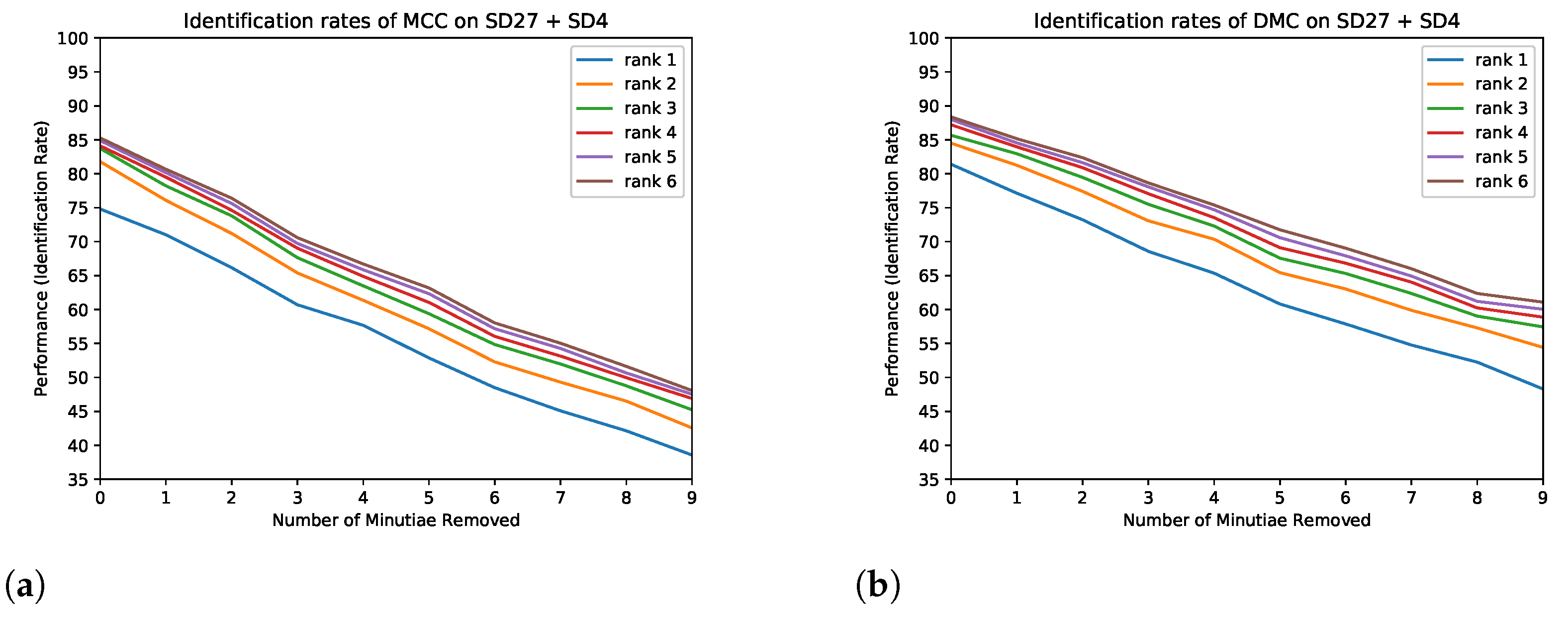
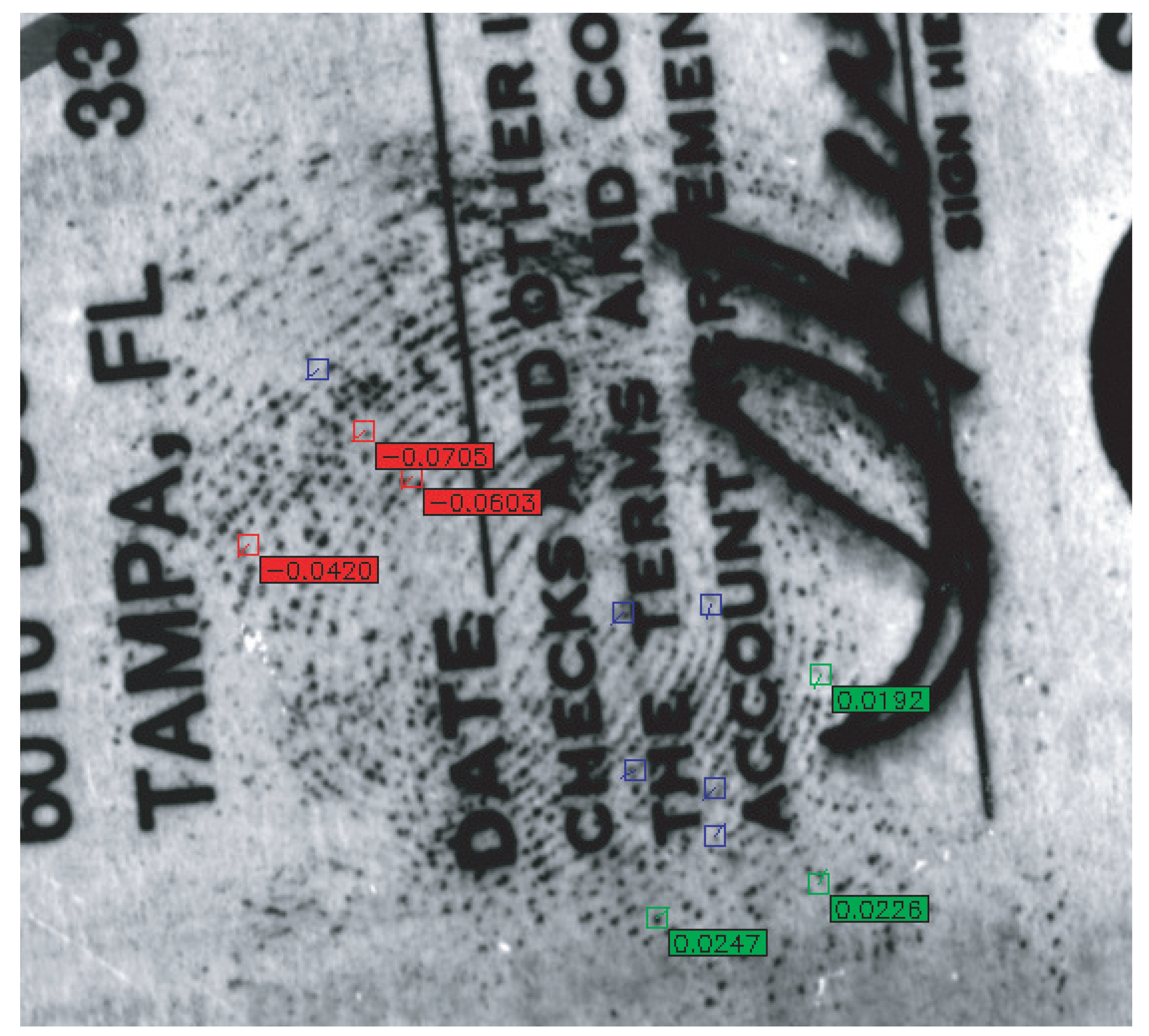
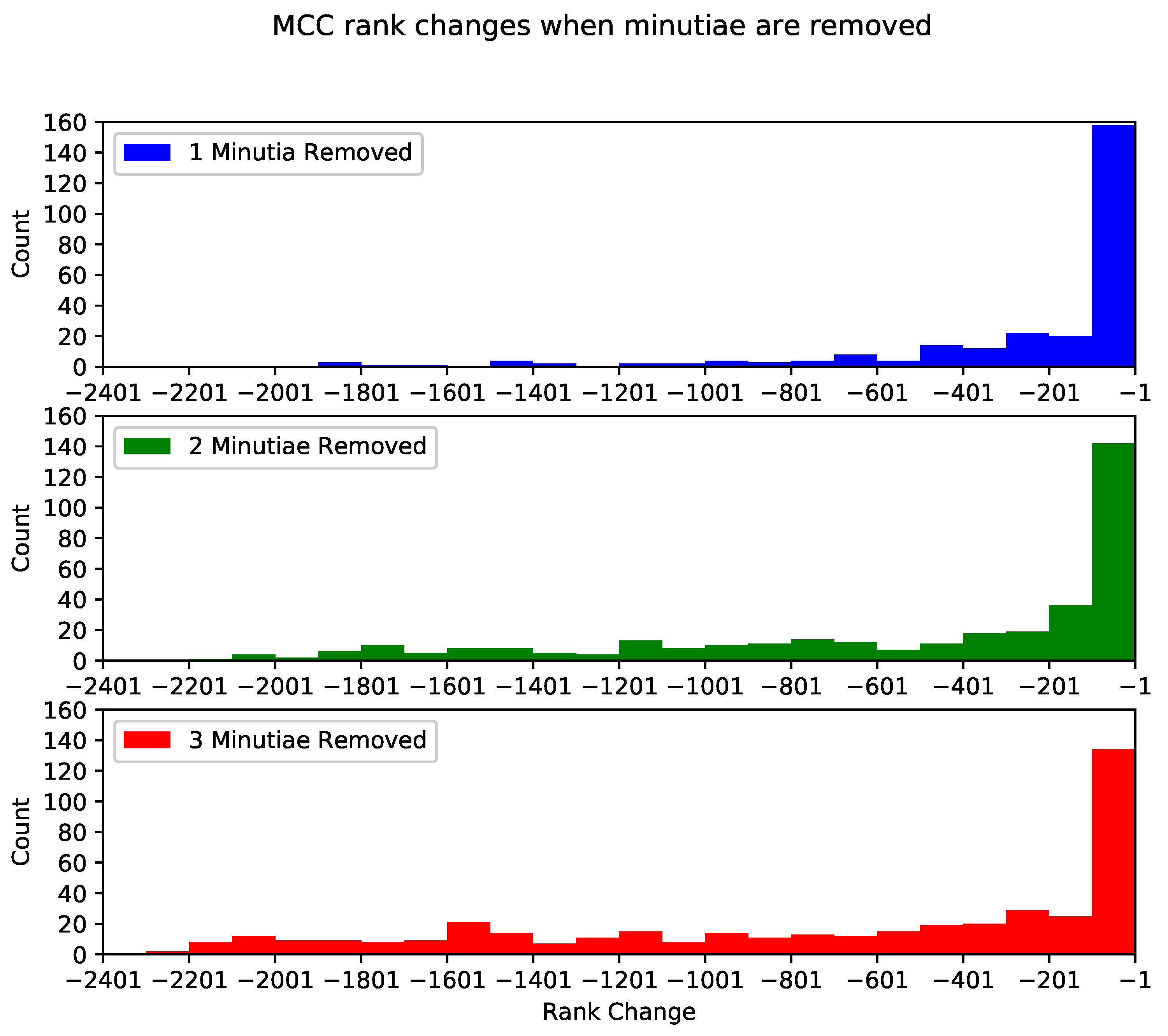
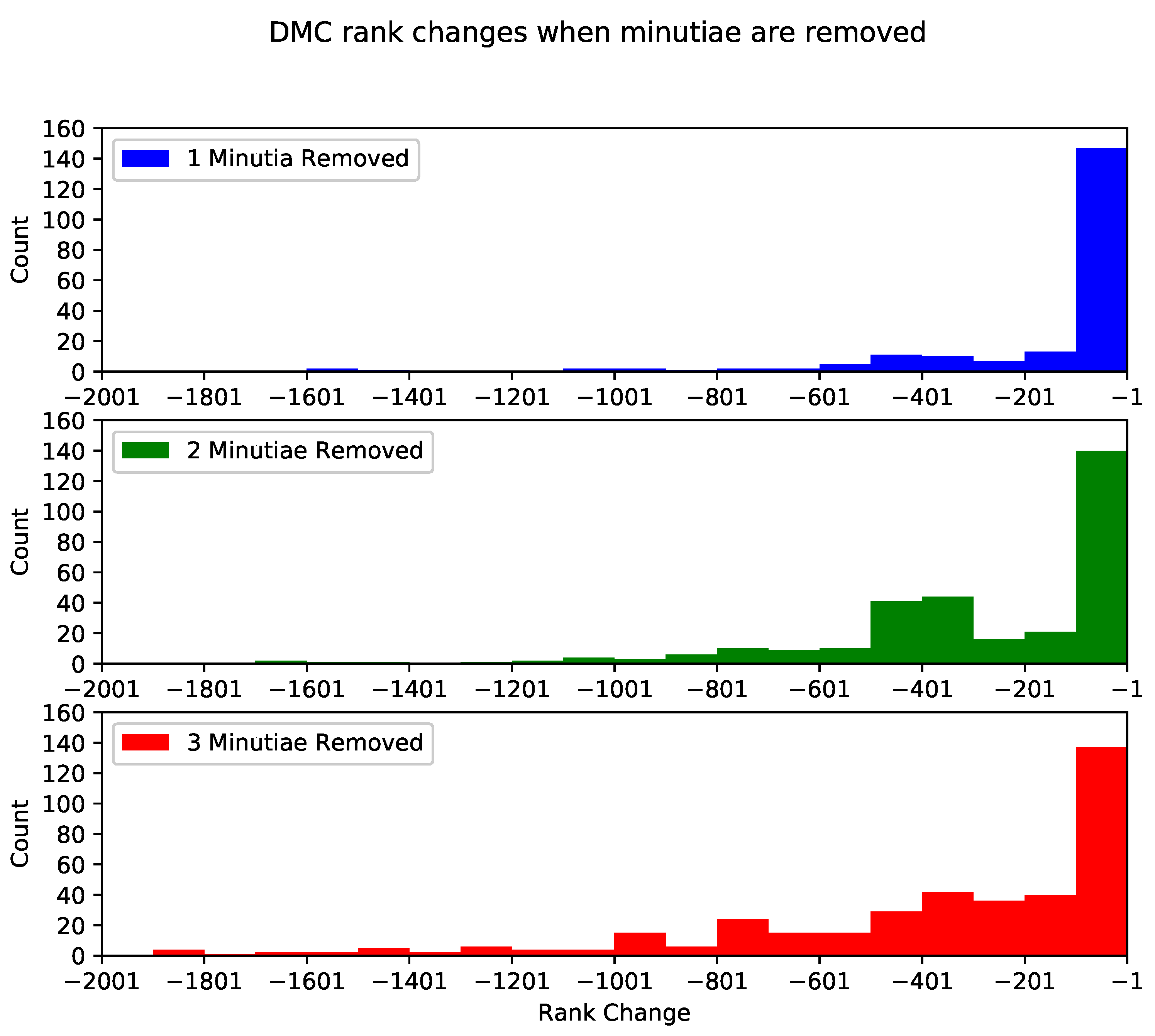
- The second set of experiments aims to measure the matching algorithms’ negative impact when minutiae are removed. We remove every possible combination of one, two, and three minutiae from every fingerprint (more than 1,100,000 combinations for all fingerprints in the NIST SD27) for this set of experiments. Every new fingerprint (with the removed minutiae) was tested with the two selected matching algorithms to obtain their matching score and compared with the matching score obtained from the original fingerprints (without removed minutiae).
- The third set of experiments consists of determining the set of minutiae that less decreased the score and those that decreased the most the score. Using our second experiment results, we selected six combinations of minutiae for each fingerprint and each matching algorithm to see how the change in score is reflected in the CMC curve and the rank-100 identification. The three combinations which lowered the score the most are considered the “lower” class. The three combinations which lowered the score the least are considered the “higher” class.
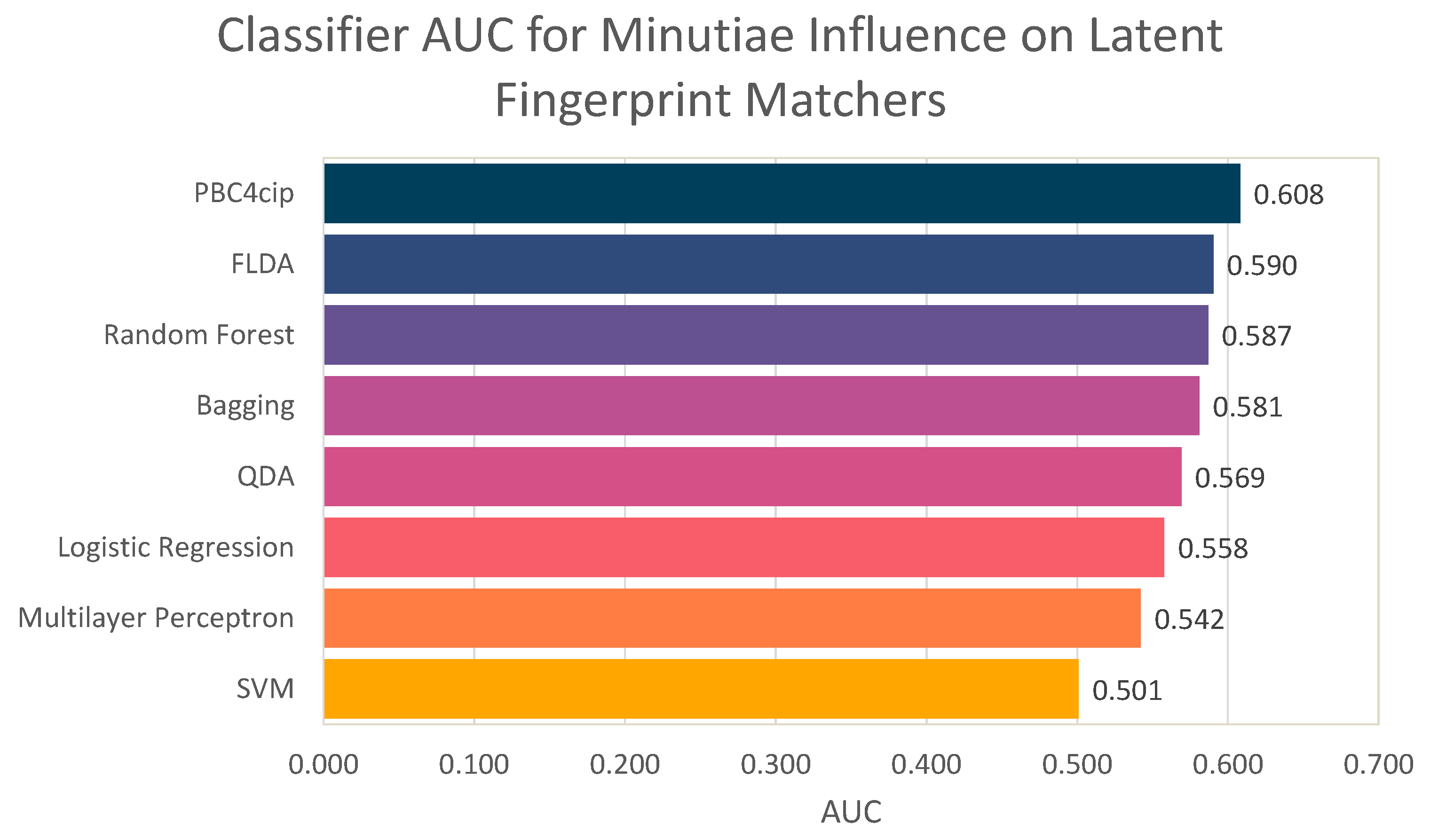
- Finally, we perform one last experiment aimed to determine if it is possible to predict if removing a minutia will have a positive or negative effect on the matching score.
5. Evaluating the Impact of Minutiae Errors
6. Predicting the Impact of Minutiae Errors
- d[1–6]: Each of these features has the distance from the minutia to the closest minutia (d[1]), to the second closest minutia (d[2]), and so on.
- r[15, 30, 45, 60, 75, 90]: Each of these features counts how many minutiae there are in a radius (of 15 pixels, 30 pixels, and so on) around the specified minutia.
- class: Either a positive or negative impact on the matching score.
7. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Loyola-González, O. Black-Box vs. White-Box: Understanding Their Advantages and Weaknesses From a Practical Point of View. IEEE Access 2019, 7, 154096–154113. [Google Scholar] [CrossRef]
- Gupta, R.; Khari, M.; Gupta, D.; Crespo, R.G. Fingerprint image enhancement and reconstruction using the orientation and phase reconstruction. Inf. Sci. 2020, 530, 201–218. [Google Scholar] [CrossRef]
- Alonso-Fernandez, F.; Bigun, J.; Fierrez, J.; Fronthaler, H.; Kollreider, K.; Ortega-Garcia, J. Fingerprint Recognition. In Guide to Biometric Reference Systems and Performance Evaluation; Petrovska-Delacretaz, D., Chollet, G., Dorizzi, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Jain, A.K.; Flynn, P.; Ross, A.A. Handbook of Biometrics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Alonso-Fernandez, F.; Fierrez, J. Fingerprint Databases and Evaluation. In Encyclopedia of Biometrics; Li, S.Z., Jain, A.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 599–606. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Mora, M.; Barrientos, R.J.; Hernández-García, R.; Naranjo-Torres, J. Fingerprint Classification through Standard and Weighted Extreme Learning Machines. Appl. Sci. 2020, 10, 4125. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, H.; Cao, Z.; Guo, F.; Pang, L. A Customized Semantic Segmentation Network for the Fingerprint Singular Point Detection. Appl. Sci. 2020, 10, 3868. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Li, Z.; Zhao, L. Robust and Accurate Wi-Fi Fingerprint Location Recognition Method Based on Deep Neural Network. Appl. Sci. 2020, 10, 321. [Google Scholar] [CrossRef]
- Pititheeraphab, Y.; Thongpance, N.; Aoyama, H.; Pintavirooj, C. Vein Pattern Verification and Identification Based on Local Geometric Invariants Constructed from Minutia Points and Augmented with Barcoded Local Feature. Appl. Sci. 2020, 10, 3192. [Google Scholar] [CrossRef]
- Maltoni, D.; Maio, D.; Jain, A.K.; Prabhakar, S. Handbook of Fingerprint Recognition, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Ramírez-Sáyago, E.; Loyola-González, O.; Medina-Pérez, M.A. Towards Inpainting and Denoising Latent Fingerprints: A Study on the Impact in Latent Fingerprint Identification. In Pattern Recognition; Figueroa Mora, K.M., Anzurez Marín, J., Cerda, J., Carrasco-Ochoa, J.A., Martínez-Trinidad, J.F., Olvera-López, J.A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 76–86. [Google Scholar]
- Gonzalez-Rodriguez, J.; Fierrez-Aguilar, J.; Ramos-Castro, D.; Ortega-Garcia, J. Bayesian analysis of fingerprint, face and signature evidences with automatic biometric systems. Forensic Sci. Int. 2005, 155, 126–140. [Google Scholar] [CrossRef] [PubMed]
- Krish, R.P.; Fierrez, J.; Ramos, D.; Alonso-Fernandez, F.; Bigun, J. Improving Automated Latent Fingerprint Identification using Extended Minutia Types. Inf. Fusion 2019, 50, 9–19. [Google Scholar] [CrossRef]
- Nedjah, N.; Wyant, R.S.; Mourelle, L.M.; Gupta, B.B. Efficient fingerprint matching on smart cards for high security and privacy in smart systems. Inf. Sci. 2019, 479, 622–639. [Google Scholar] [CrossRef]
- Lan, S.; Guo, Z.; You, J. Pre-registration of translated/distorted fingerprints based on correlation and the orientation field. Inf. Sci. 2020, 520, 292–304. [Google Scholar] [CrossRef]
- Champod, C.; Lennard, C.; Margot, P.; Stoilovic, M. Fingerprints and Other Ridge Skin Impressions, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Tistarelli, M.; Champod, C. Handbook of Biometrics for Forensic Science; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Alonso-Fernandez, F.; Fierrez, J.; Ortega-Garcia, J.; Gonzalez-Rodriguez, J.; Fronthaler, H.; Kollreider, K.; Bigun, J. A comparative study of fingerprint image-quality estimation methods. IEEE Trans. Inf. Forensics Secur. 2007, 2, 734–743. [Google Scholar] [CrossRef]
- Medina-Pérez, M.A.; Moreno, A.M.; Ballester, M.Á.F.; García-Borroto, M.; Loyola-González, O.; Altamirano-Robles, L. Latent fingerprint identification using deformable minutiae clustering. Neurocomputing 2016, 175, 851–865. [Google Scholar] [CrossRef]
- Ramos, D.; Krish, R.P.; Fierrez, J.; Meuwly, D. From Biometric Scores to Forensic Likelihood Ratios. In Handbook of Biometrics for Forensic Science; Tistarelli, M., Champod, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 305–327. [Google Scholar] [CrossRef]
- Valdes-Ramirez, D.; Medina-Pérez, M.A.; Monroy, R.; Loyola-González, O.; Rodríguez, J.; Morales, A.; Herrera, F. A Review of Fingerprint Feature Representations and Their Applications for Latent Fingerprint Identification: Trends and Evaluation. IEEE Access 2019, 7, 48484–48499. [Google Scholar] [CrossRef]
- Rodríguez-Ruiz, J.; Medina-Pérez, M.A.; Monroy, R.; Loyola-González, O. A survey on minutiae-based palmprint feature representations, and a full analysis of palmprint feature representation role in latent identification performance. Expert Syst. Appl. 2019, 131, 30–44. [Google Scholar] [CrossRef]
- Garris, M.D. NIST Special Database 27: Fingerprint Minutiae from Latent and Matching Tenprint Images; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2000. [Google Scholar]
- Budowle, B.; Buscaglia, J.; Perlman, R.S. Review of the scientific basis for friction ridge comparisons as a means of identification: Committee findings and recommendations. Forensic Sci. Commun. 2006, 8. Available online: https://go.gale.com/ps/anonymous?id=GALE|A144388747 (accessed on 24 April 2021).
- Morales, A.; Morocho, D.; Fierrez, J.; Vera-Rodriguez, R. Signature Authentication based on Human Intervention: Performance and Complementarity with Automatic Systems. IET Biom. 2017, 6, 307–315. [Google Scholar] [CrossRef]
- Ulery, B.T.; Hicklin, R.A.; Buscaglia, J.; Roberts, M.A. Accuracy and reliability of forensic latent fingerprint decisions. Proc. Natl. Acad. Sci. USA 2011, 108, 7733–7738. [Google Scholar] [CrossRef]
- Ulery, B.T.; Hicklin, R.A.; Roberts, M.A.; Buscaglia, J. Changes in latent fingerprint examiners’ markup between analysis and comparison. Forensic Sci. Int. 2015, 247, 54–61. [Google Scholar] [CrossRef]
- Ulery, B.T.; Hicklin, R.A.; Roberts, M.A.; Buscaglia, J. Interexaminer variation of minutia markup on latent fingerprints. Forensic. Sci. Int. 2016, 264, 89–99. [Google Scholar] [CrossRef]
- Kukucka, J.; Dror, I.E.; Yu, M.; Hall, L.; Morgan, R.M. The impact of evidence lineups on fingerprint expert decisions. Appl. Cogn. Psychol. 2020, 35, 1143–1153. [Google Scholar] [CrossRef]
- Valdes-Ramirez, D.; Medina-Pérez, M.A.; Monroy, R. An ensemble of fingerprint matching algorithms based on cylinder codes and mtriplets for latent fingerprint identification. Pattern Anal. Appl. 2020, 1–12. [Google Scholar] [CrossRef]
- Alonso-Fernandez, F.; Fierrez-Aguilar, J.; Ortega-Garcia, J. An enhanced Gabor filter-based segmentation algorithm for fingerprint recognition systems. In Proceedings of the IEEE International Symposium on Image and Signal Processing and Analysis, ISPA, Special Session on Signal and Image Processing for Biometrics, Zagreb, Croatia, 15–17 September 2005; pp. 239–244. [Google Scholar]
- Alonso-Fernandez, F.; Fierrez, J.; Ortega-Garcia, J. Quality Measures in Biometric Systems. IEEE Secur. Priv. 2012, 10, 52–62. [Google Scholar] [CrossRef]
- Fierrez-Aguilar, J.; Nanni, L.; Ortega-Garcia, J.; Cappelli, R.; Maltoni, D. Combining multiple matchers for fingerprint verification: A case study in FVC2004. In Proceedings of the 13th IAPR International Conference on Image Analysis and Processing, Cagliari, Italy, 6–8 September 2005; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3617, pp. 1035–1042. [Google Scholar]
- Fierrez, J.; Morales, A.; Vera-Rodriguez, R.; Camacho, D. Multiple Classifiers in Biometrics. Part 1: Fundamentals and Review. Inf. Fusion 2018, 44, 57–64. [Google Scholar] [CrossRef]
- Simon-Zorita, D.; Ortega-Garcia, J.; Fierrez-Aguilar, J.; Gonzalez-Rodriguez, J. Image quality and position variability assessment in minutiae-based fingerprint verification. IEE Proc. Vision Image Signal Process. 2003, 150, 402–408. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the International Conference on Knowledge Discovery and Data Mining (KDD-96), AAAI, Portland, OR, USA, 2–6 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Grosz, S.A.; Engelsma, J.J., Jr.; Paulter, N.G.; Jain, A.K. White-box evaluation of fingerprint matchers: Robustness to minutiae perturbations. arXiv 2019, arXiv:1909.00799. [Google Scholar]
- Cappelli, R.; Maio, D.; Maltoni, D. SFinGe: An approach to synthetic fingerprint generation. In Proceedings of the International Workshop on Biometric Technologies (BT2004), Calgary, AB, Canada, 22–23 June 2004; pp. 147–154. [Google Scholar]
- Krish, R.; Fierrez, J.; Ramos, D.; Ortega-Garcia, J.; Bigun, J. Pre-Registration of Latent Fingerprints based on Orientation Field. IET Biom. 2015, 4, 42–52. [Google Scholar] [CrossRef]
- Watson, C.I.; Wilson, C.L. NIST Special Database 4; Technical report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1992. [Google Scholar]
- Cappelli, R.; Ferrara, M.; Maltoni, D. Minutia Cylinder-Code: A New Representation and Matching Technique for Fingerprint Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2128–2141. [Google Scholar] [CrossRef] [PubMed]
- Grother, P.; Micheals, R.J.; Phillips, P.J. Face Recognition Vendor Test 2002 Performance Metrics. In Audio- and Video-Based Biometric Person Authentication; Kittler, J., Nixon, M.S., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 937–945. [Google Scholar]
- INTERPOL. Guidelines concerning transmission of Fingerprint Crime Scene Marks; INTERPOL: Lyon, France, 2012. [Google Scholar]
- Alonso-Fernandez, F.; Fierrez, J.; Ramos, D.; Gonzalez-Rodriguez, J. Quality-Based Conditional Processing in Multi-Biometrics: Application to Sensor Interoperability. IEEE Trans. Syst. Man Cybern. Part A 2010, 40, 1168–1179. [Google Scholar] [CrossRef]
- Fierrez-Aguilar, J.; Chen, Y.; Ortega-Garcia, J.; Jain, A.K. Incorporating image quality in multi-algorithm fingerprint verification. In Proceedings of the IAPR International Conference on Biometrics, ICB, LNCS, New Delhi, India, 29 March 2006; Volume 3832, pp. 213–220. [Google Scholar]
- Fronthaler, H.; Kollreider, K.; Bigun, J.; Fierrez, J.; Alonso-Fernandez, F.; Ortega-Garcia, J.; Gonzalez-Rodriguez, J. Fingerprint Image Quality Estimation and its Application to Multi-Algorithm Verification. IEEE Trans. Inf. Forensics Secur. 2008, 3, 331–338. [Google Scholar] [CrossRef]
- Fierrez, J.; Morales, A.; Vera-Rodriguez, R.; Camacho, D. Multiple Classifiers in Biometrics. Part 2: Trends and Challenges. Inf. Fusion 2018, 44, 103–112. [Google Scholar] [CrossRef]
- Moreno-Torres, J.G.; Sáez, J.A.; Herrera, F. Study on the impact of partition-induced dataset shift on k-fold cross-validation. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 1304–1312. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. Introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Loyola-González, O.; Medina-Pérez, M.A.; Martínez-Trinidad, J.F.; Carrasco-Ochoa, J.A.; Monroy, R.; García-Borroto, M. PBC4cip: A new contrast pattern-based classifier for class imbalance problems. Knowl. Based Syst. 2017, 115, 100–109. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- le Cessie, S.; van Houwelingen, J. Ridge Estimators in Logistic Regression. Appl. Stat. 1992, 41, 191–201. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
Short Biography of Authors
 | Octavio Loyola-González received his Ph.D. degree in Computer Science from the National Institute for Astrophysics, Optics, and Electronics, Mexico, in 2017. He has won several awards from different institutions due to his research work on applied projects; consequently, he is a Member of the National System of Researchers in Mexico (Rank1). He worked as a distinguished professor and researcher at Tecnologico de Monterrey, Campus Puebla, for undergraduate and graduate programs of Computer Sciences. Currently, he is responsible for running Machine Learning and Artificial Intelligence practice inside Altair Management Consultants Corp., where he is involved in the development and implementation using analytics and data mining in the Altair Compass department. He has outstanding experience in the fields of big data and pattern recognition, cloud computing, IoT, and analytical tools to apply them in sectors where he has worked for as Banking and Insurance, Retail, Oil and Gas, Agriculture, Cybersecurity, Biotechnology, and Dactyloscopy. From these applied projects, Dr. Loyola-González has published several books and papers in well-known journals, and he has several ongoing patents as a manager and researcher in Altair Compass. |
 | Emilio Francisco Ferreira Mehnert obtained his Bachelor’s of Engineering degree in Software Engineering from Tecnológico de Monterrey, Campus Santa Fe in 2017. He received his Master of Science degree in Computer Science from Tecnológico de Monterrey, Campus Estado de México in 2020. His interests include machine learning, deep learning, and software development. |
 | Aythami Morales Moreno received his M.Sc. (Electronical Engineering) and Ph.D. (Artificial Intelligence) degrees from Universidad de Las Palmas de Gran Canaria in 2006 and 2011, respectively. Since 2017, he is an Associate Professor with the Universidad Autonoma de Madrid. He has conducted research stays at Michigan State University, Hong Kong Polytechnic University, University of Bologna, and the Schepens Eye Research Institute. He has authored over 100 scientific articles in topics related to machine learning, trustworthy AI, and biometric signal processing. |
 | Julian Fierrez (Member, IEEE) received his M.Sc. and the Ph.D. degrees in Telecommunications Engineering from Universidad Politecnica de Madrid, Spain, in 2001 and 2006, respectively. Since 2004, he is at Universidad Autonoma de Madrid, where he is an Associate Professor since 2010. His research is on signal and image processing, AI fundamentals and applications, HCI, forensics, and biometrics for security and human behavior analysis. He is actively involved in large EU projects in these topics (e.g., BIOSECURE, TABULA RASA and BEAT in the past; now IDEA-FAST, PRIMA, and TRESPASS-ETN). Since 2016, he is an Associate Editor for Elsevier’s Information Fusion and IEEE Trans. on Information Forensics and Security, and since 2018 also for IEEE Trans. on Image Processing. He has been a General Chair of IAPR CIARP 2018 and IAPR IbPRIA 2019. Since 2020, he is member of the ELLIS Society. Prof. Fierrez has received best papers awards at AVBPA, ICB, IJCB, ICPR, ICPRS, and Pattern Recognition Letters. He is also a recipient of several world-class research distinctions, including: EBF European Biometric Industry Award 2006; EURASIP Best Ph.D. Award 2012; Miguel Catalan Award to the Best Researcher under 40 in the Community of Madrid in the general area of Science and Technology; and IAPR Young Biometrics Investigator Award 2017, given to a single researcher worldwide every two years under the age of 40 whose research has had a major impact in biometrics. |
 | Miguel Angel Medina-Pérez received a Ph.D. in Computer Science from the National Institute of Astrophysics, Optics, and Electronics, Mexico, in 2014. He is currently a Research Professor with the Tecnologico de Monterrey, Campus Estado de Mexico, where he is also a member of the GIEE-ML (Machine Learning) Research Group. He has rank 1 in the Mexican Research System. His research interests include pattern recognition, data visualization, explainable artificial intelligence, fingerprint recognition, and palmprint recognition. He has published tens of papers in referenced journals, such as “Information Fusion,” “IEEE Transactions on Affective Computing,” “Pattern Recognition,” “IEEE Transactions on Information Forensics and Security,” “Knowledge-Based Systems,” “Information Sciences,” and “Expert Systems with Applications.” He has extensive experience developing software to solve pattern recognition problems. A successful example is a fingerprint and palmprint recognition framework which has more than 1.3 million visits and 135 thousand downloads. |
 | Raúl Monroy obtained a Ph.D. degree in Artificial Intelligence from Edinburgh University, in 1998, under the supervision of Prof. Alan Bundy. He has been in Computing at Tecnologico de Monterrey, Campus Estado de México, since 1985. In 2010, he was promoted to (full) Professor in Computer Science. Since 1998, he is a member of the CONACYT-SNI National Research System, rank three. Together with his students and members of his group, Machine Learning Models (GIEE – MAC), Prof. Monroy studies the discovery and application of novel model machine learning models, which he often applies to cybersecurity problems. At Tecnologico de Monterrey, he is also the Head of the graduate program in computing, at region CDMX. |


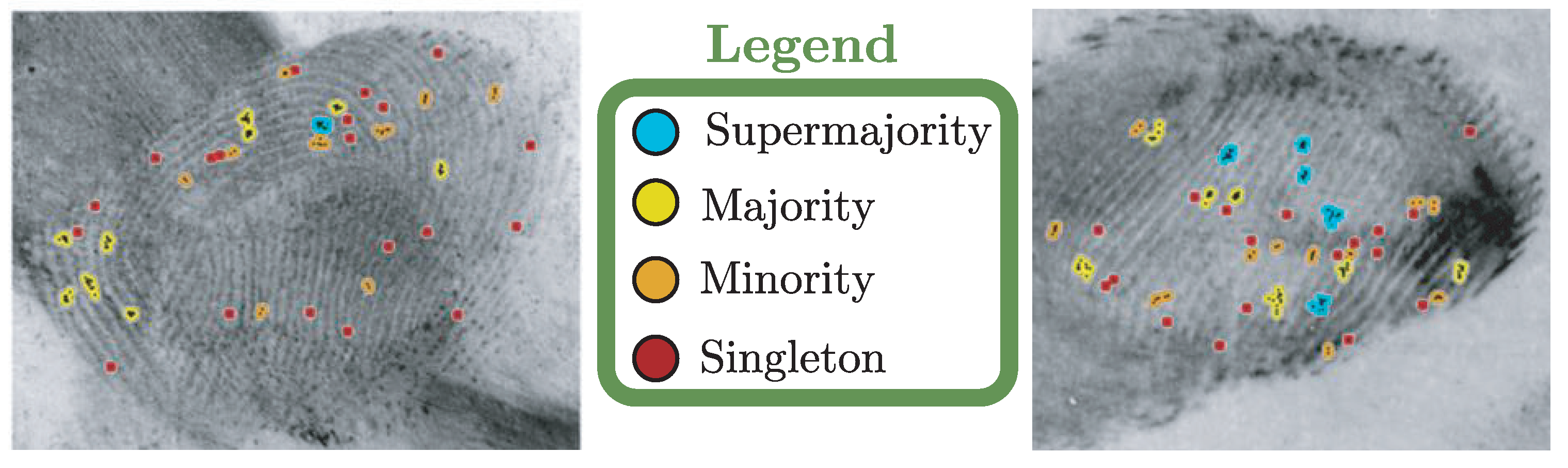

| Num. Minutiae Removed | #MCC | #DMCCC |
|---|---|---|
| 1 | −5.53% | −3.37% |
| 2 | −3.86% | −0.69% |
| 3 | −3.86% | −0.57% |
| Num. Minutiae Removed | #MCC | #DMCCC |
|---|---|---|
| 1 | −35.63% | −27.67% |
| 2 | −48.76% | −42.84% |
| 3 | −60.80% | −55.65% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loyola-González, O.; Ferreira Mehnert, E.F.; Morales, A.; Fierrez, J.; Medina-Pérez, M.A.; Monroy, R. Impact of Minutiae Errors in Latent Fingerprint Identification: Assessment and Prediction. Appl. Sci. 2021, 11, 4187. https://doi.org/10.3390/app11094187
Loyola-González O, Ferreira Mehnert EF, Morales A, Fierrez J, Medina-Pérez MA, Monroy R. Impact of Minutiae Errors in Latent Fingerprint Identification: Assessment and Prediction. Applied Sciences. 2021; 11(9):4187. https://doi.org/10.3390/app11094187
Chicago/Turabian StyleLoyola-González, Octavio, Emilio Francisco Ferreira Mehnert, Aythami Morales, Julian Fierrez, Miguel Angel Medina-Pérez, and Raúl Monroy. 2021. "Impact of Minutiae Errors in Latent Fingerprint Identification: Assessment and Prediction" Applied Sciences 11, no. 9: 4187. https://doi.org/10.3390/app11094187
APA StyleLoyola-González, O., Ferreira Mehnert, E. F., Morales, A., Fierrez, J., Medina-Pérez, M. A., & Monroy, R. (2021). Impact of Minutiae Errors in Latent Fingerprint Identification: Assessment and Prediction. Applied Sciences, 11(9), 4187. https://doi.org/10.3390/app11094187









