X-ray Phase-Contrast Computed Tomography for Soft Tissue Imaging at the Imaging and Medical Beamline (IMBL) of the Australian Synchrotron
Abstract
1. Introduction
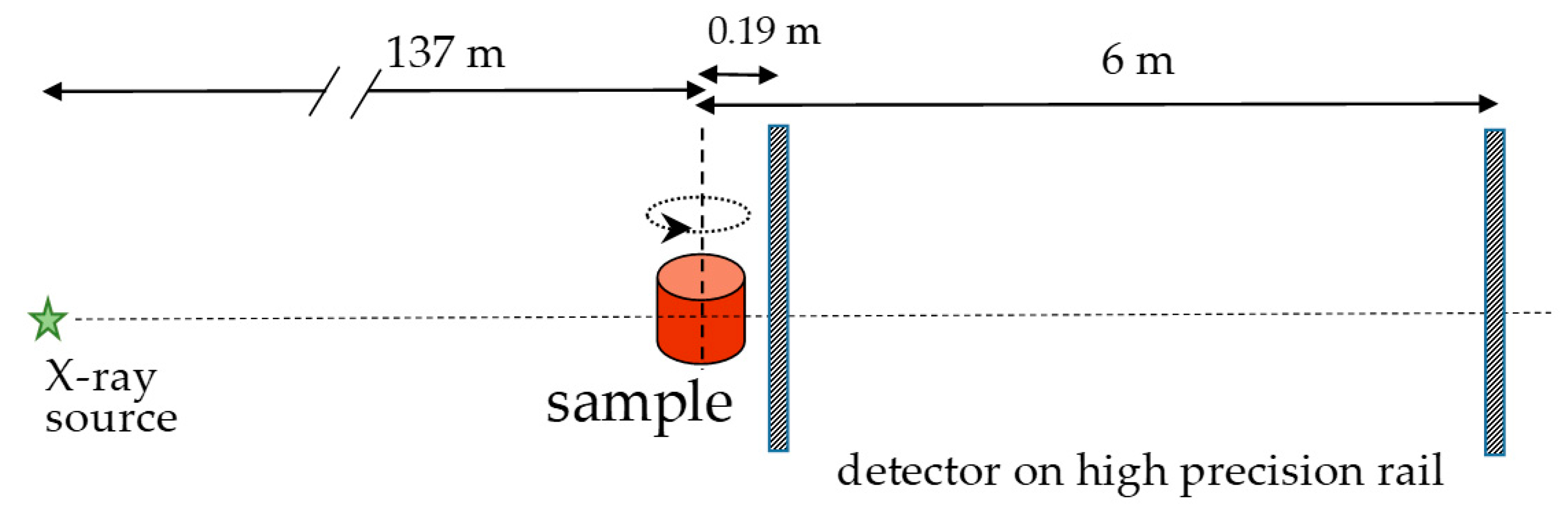
2. Materials and Methods
3. Results
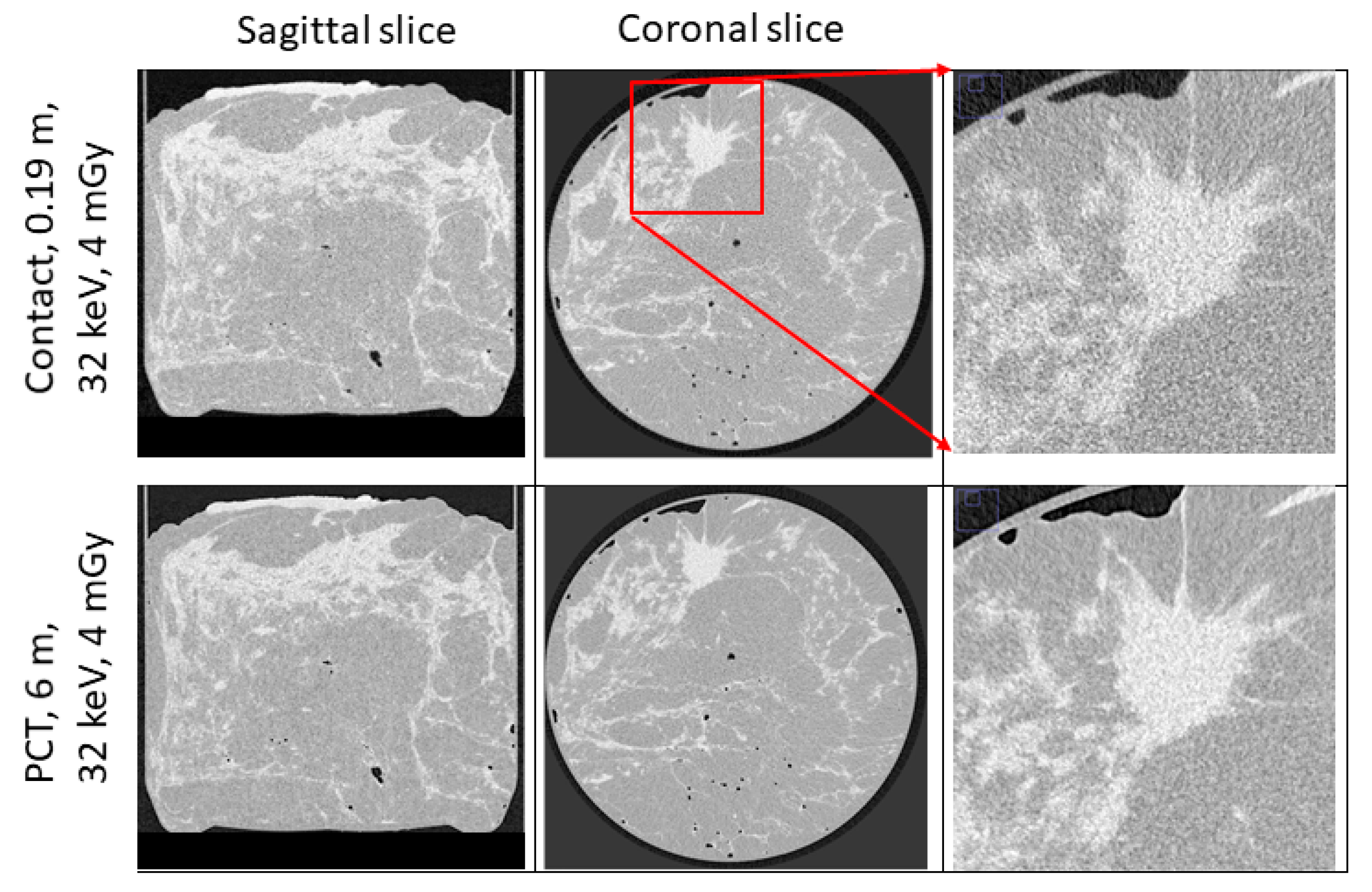
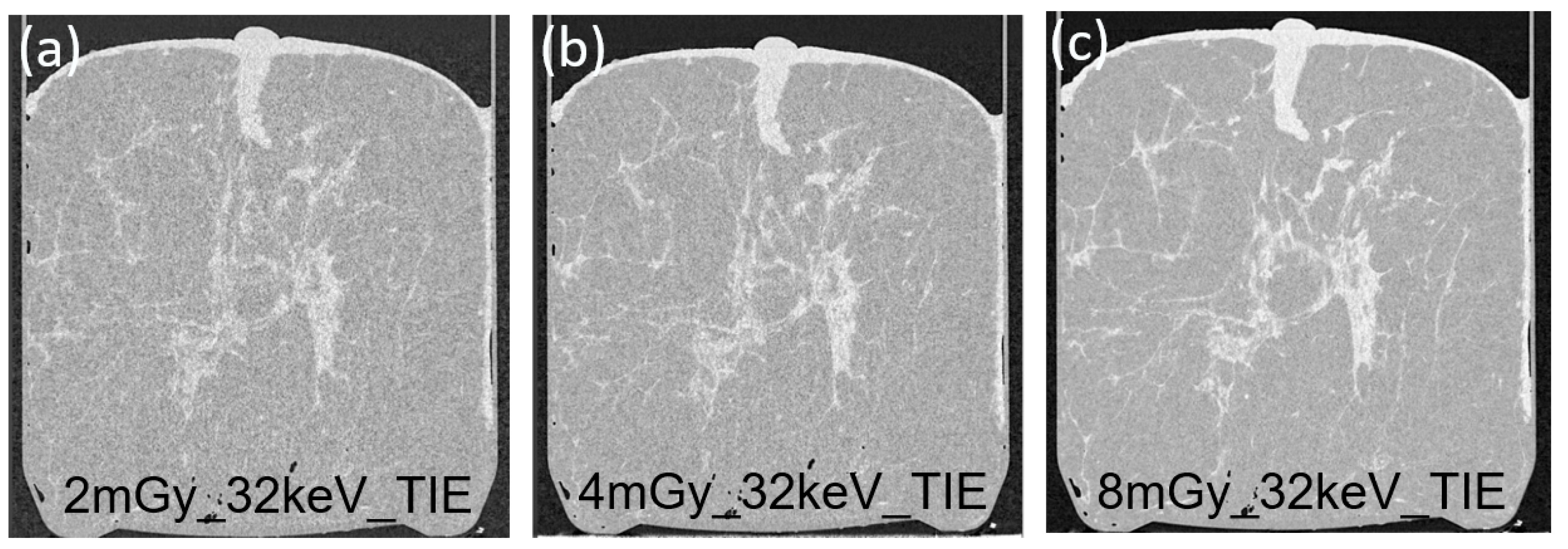
3.1. X-ray Phase-Contrast CT Results
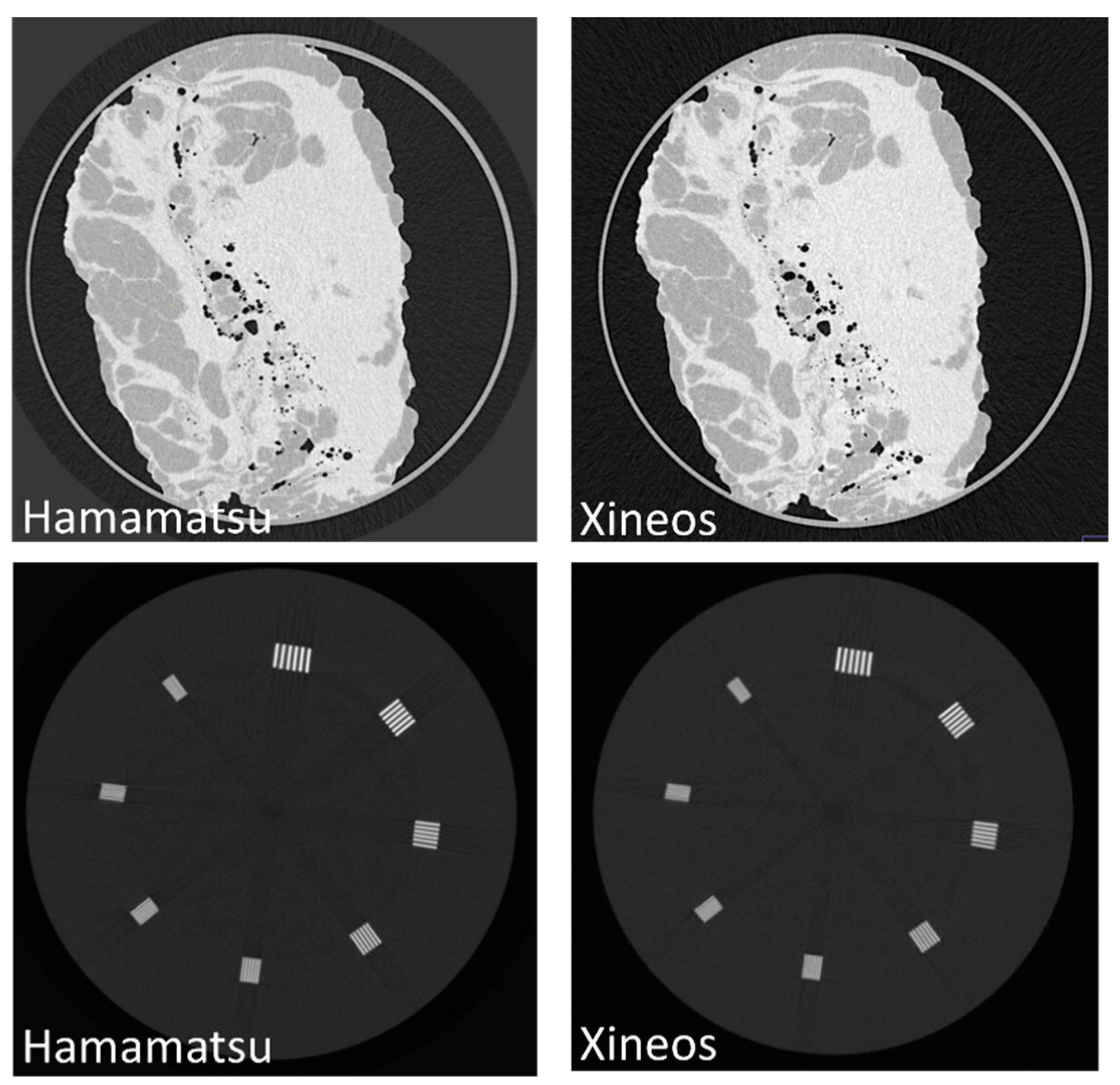
3.2. Detector Comparison
Image Quality Assessment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boldeman, J.W.; Einfeld, D. The physics design of the Australian synchrotron storage ring. Nucl. Instrum. Methods Phys. Res. A 2004, 521, 306–317. [Google Scholar] [CrossRef]
- Mayo, S.C.; McCann, T.; Day, L.; Favaro, J.; Tuhumury, H.; Thompson, D.; Maksimenko, A. Rising dough and baking bread at the Australian synchrotron. AIP Conf. Proc. 2016, 1696, 020006. [Google Scholar] [CrossRef]
- Thornton, J.; Arhatari, B.D.; Sesso, M.; Wood, C.; Zonneveldt, M.; Kim, S.Y.; Kimpton, J.A.; Hall, C. Failure Evaluation of a SiC/SiC Ceramic Matrix Composite During In-Situ Loading Using Micro X-ray Computed Tomography. Microsc. Microanal. 2019, 25, 583–591. [Google Scholar] [CrossRef]
- van Aarle, W.; Palenstijn, W.J.; Cant, J.; Janssens, E.; Bleichrodt, F.; Dabravolski, A.; De Beenhouwer, J.; Joost Batenburg, K.; Sijbers, J. Fast and flexible X-ray tomography using the ASTRA toolbox. Opt. Express 2016, 24, 25129–25147. [Google Scholar] [CrossRef] [PubMed]
- Nesterets, Y.I.; Gureyev, T.E.; Mayo, S.C.; Stevenson, A.W.; Thompson, D.; Brown, J.M.; Kitchen, M.J.; Pavlov, K.M.; Lockie, D.; Brun, F.; et al. A feasibility study of X-ray phase-contrast mammographic tomography at the Imaging and Medical beamline of the Australian Synchrotron. J. Synchrotron Radiat. 2015, 22, 1509–1523. [Google Scholar] [CrossRef]
- Stevenson, A.W.; Mayo, S.C.; Hausermann, D.; Maksimenko, A.; Garrett, R.F.; Hall, C.J.; Wilkins, S.W.; Lewis, R.A.; Myers, D.E. First experiments on the Australian Synchrotron Imaging and Medical beamline, including investigations of the effective source size in respect of X-ray imaging. J. Synchrotron Radiat. 2010, 17, 75–80. [Google Scholar] [CrossRef]
- Morgan, K.S.; Paganin, D.M.; Siu, K.K.W. Quantitative single-exposure x-ray phase contrast imaging using a single attenuation grid. Opt. Express 2011, 19, 19781–19789. [Google Scholar] [CrossRef] [PubMed]
- Pavlov, K.M.; Li, H.; Paganin, D.M.; Berujon, S.; Rougé-Labriet, H.; Brun, E. Single-Shot X-Ray Speckle-Based Imaging of a Single-Material Object. Phys. Rev. Appl. 2020, 13, 054023. [Google Scholar] [CrossRef]
- Ruben, G.; Pinar, I.; Brown, J.M.C.; Schaff, F.; Pollock, J.A.; Crossley, K.; Maksimenko, A.; Hall, C.; Hausermann, D.; Uesugi, K.; et al. Full field X-ray Scatter Tomography. arXiv 2020, arXiv:2012.09371. [Google Scholar]
- Gureyev, T.E.; Paganin, D.M.; Arhatari, B.; Taba, S.T.; Lewis, S.; Brennan, P.C.; Quiney, H.M. Dark-field signal extraction in propagation-based phase-contrast imaging. Phys. Med. Biol. 2020, 65, 215029. [Google Scholar] [CrossRef]
- Donnelley, M.; Morgan, K.S.; Gradl, R.; Klein, M.; Hausermann, D.; Hall, C.; Maksimenko, A.; Parsons, D.W. Live-pig-airway surface imaging and whole-pig CT at the Australian Synchrotron Imaging and Medical Beamline. J. Synchrotron Radiat. 2019, 26, 175–183. [Google Scholar] [CrossRef]
- Morgan, K.S.; Parsons, D.; Cmielewski, P.; McCarron, A.; Gradl, R.; Farrow, N.; Siu, K.; Takeuchi, A.; Suzuki, Y.; Uesugi, K.; et al. Methods for dynamic synchrotron X-ray respiratory imaging in live animals. J. Synchrotron Radiat. 2020, 27, 164–175. [Google Scholar] [CrossRef]
- Livingstone, J.; Adam, J.F.; Crosbie, J.C.; Hall, C.J.; Lye, J.E.; McKinlay, J.; Pelliccia, D.; Pouzoulet, F.; Prezado, Y.; Stevenson, A.W.; et al. Preclinical radiotherapy at the Australian Synchrotron’s Imaging and Medical Beamline: Instrumentation, dosimetry and a small-animal feasibility study. J. Synchrotron Radiat. 2017, 24, 854–865. [Google Scholar] [CrossRef]
- Butler, D.J.; Stevenson, A.W.; Wright, T.E.; Harty, P.D.; Lehmann, J.; Livingstone, J.; Crosbie, J.C. High spatial resolution dosimetric response maps for radiotherapy ionization chambers measured using kilovoltage synchrotron radiation. Phys. Med. Biol. 2015, 60, 8625–8641. [Google Scholar] [CrossRef]
- Yang, Y.; Crosbie, J.C.; Paiva, P.; Ibahim, M.; Stevenson, A.; Rogers, P.A.W. In Vitro Study of Genes and Molecular Pathways Differentially Regulated by Synchrotron Microbeam Radiotherapy. Radiat. Res. 2014, 182, 626–639. [Google Scholar] [CrossRef]
- Stevenson, A.W.; Hall, C.J.; Mayo, S.C.; Hausermann, D.; Maksimenko, A.; Gureyev, T.E.; Nesterets, Y.I.; Wilkins, S.W.; Lewis, R.A. Analysis and interpretation of the first monochromatic X-ray tomography data collected at the Australian Synchrotron Imaging and Medical beamline. J. Synchrotron Radiat. 2012, 19, 728–750. [Google Scholar] [CrossRef]
- Trinajstic, K.; Boisvert, C.; Long, J.; Maksimenko, A.; Johanson, Z. Pelvic and reproductive structures in placoderms (stem gnathostomes). Biol. Rev. 2015, 90, 467–501. [Google Scholar] [CrossRef]
- Khosravani, M.R.; Reinicke, T. On the Use of X-ray Computed Tomography in Assessment of 3D-Printed Components. J. Nondestruct. Eval. 2020, 39, 75. [Google Scholar] [CrossRef]
- Mehta, V.; Ahmad, N. Cone beamed computed tomography in pediatric dentistry: Concepts revisited. J. Oral Biol. Craniofacial Res. 2020, 10, 210–211. [Google Scholar] [CrossRef]
- Stevenson, A.W.; Crosbie, J.C.; Hall, C.J.; Hausermann, D.; Livingstone, J.; Lye, J.E. Quantitative characterization of the X-ray beam at the Australian Synchrotron Imaging and Medical Beamline (IMBL). J. Synchrotron Radiat. 2017, 24, 110–141. [Google Scholar] [CrossRef]
- Wypych, G. 1-Photophysics. In Handbook of Material Weathering, 6th ed.; Wypych, G., Ed.; ChemTec Publishing: Scarborough, ON, Canada, 2018; pp. 1–26. [Google Scholar] [CrossRef]
- Yokhana, V.S.K.; Arhatari, B.D.; Gureyev, T.E.; Abbey, B. Soft-tissue differentiation and bone densitometry via energy-discriminating X-ray microCT. Opt. Express 2017, 25, 29328–29341. [Google Scholar] [CrossRef]
- Ingal, V.N.; Beliaevskaya, E.A.; Brianskaya, A.P.; Merkurieva, R.D. Phase mammography—A new technique for breast investigation. Phys. Med. Biol. 1998, 43, 2555–2567. [Google Scholar] [CrossRef] [PubMed]
- Snigirev, A.; Snigreva, I.; Kohn, V.; Kuznetsov, S.; Schelokov, I. On the possibilities of X-ray phase contrast microimaging by coherent high-energy synchrotron radiation. Rev. Sci. Instrum. 1995, 66, 5486–5492. [Google Scholar] [CrossRef]
- Teague, M.R. Deterministic phase retrieval: A Green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Wilkins, S.W.; Gureyev, T.E.; Gao, D.; Pogany, A.; Stevenson, A.W. Phase-contrast imaging using polychromatic hard X-rays. Nature 1996, 384, 335–338. [Google Scholar] [CrossRef]
- Nugent, K.A.; Gureyev, T.E.; Cookson, D.F.; Paganin, D.; Barnea, Z. Quantitative phase imaging using hard X rays. Phys. Rev. Lett. 1996, 77, 2961–2964. [Google Scholar] [CrossRef] [PubMed]
- Arhatari, B.D.; De Carlo, F.; Peele, A.G. Direct quantitative tomographic reconstruction for weakly absorbing homogeneous phase objects. Rev. Sci. Instrum. 2007, 78, 053701. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Paganin, D.M.; Myers, G.R.; Nesterets, Y.I.; Wilkins, S.W. Phase and amplitude computer tomography. Appl. Phys. Lett. 2006, 89, 0341021–0341023. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Roberts, A.; Nugent, K.A. Partially Coherent Fields, The Transport-Of-Intensity Equation, And Phase Uniqueness. J. Opt. Soc. Am. A 1995, 12, 1942–1946. [Google Scholar] [CrossRef]
- Paganin, D.; Mayo, S.; Gureyev, T.E.; Miller, P.R.; Wilkins, S.W. Simultaneous phase and amplitude extraction from a single defocused image of a homogeneous object. J. Microsc. 2002, 206, 33–40. [Google Scholar] [CrossRef]
- Baran, P.; Pacile, S.; Nesterets, Y.I.; Mayo, S.C.; Dullin, C.; Dreossi, D.; Arfelli, F.; Thompson, D.; Lockie, D.; McCormack, M.; et al. Optimization of propagation-based x-ray phase-contrast tomography for breast cancer imaging. Phys. Med. Biol. 2017, 62, 2315–2332. [Google Scholar] [CrossRef]
- Beltran, M.A.; Paganin, D.M.; Siu, K.K.W.; Fouras, A.; Hooper, S.B.; Reser, D.H.; Kitchen, M.J. Interface-specific x-ray phase retrieval tomography of complex biological organs. Phys. Med. Biol. 2011, 56, 7353–7369. [Google Scholar] [CrossRef] [PubMed]
- Nesterets, Y.I.; Gureyev, T.E. Noise propagation in x-ray phase-contrast imaging and computed tomography. J. Phys. D Appl. Phys. 2014, 47, 105402. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586–2589. [Google Scholar] [CrossRef]
- Ferlay, J.; Soerjomataram, I.; Dikshit, R.; Eser, S.; Mathers, C.; Rebelo, M.; Parkin, D.M.; Forman, D.; Bray, F. Cancer incidence and mortality worldwide: Sources, methods and major patterns in GLOBOCAN 2012. Int. J. Cancer 2015, 136, E359–E386. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Nesterets, Y.I.; Baran, P.M.; Taba, S.T.; Mayo, S.C.; Thompson, D.; Arhatari, B.; Mihocic, A.; Abbey, B.; Lockie, D.; et al. Propagation-based x-ray phase-contrast tomography of mastectomy samples using synchrotron radiation. Med. Phys. 2019, 46, 5478–5487. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T.E.; Mayo, S.C.; Myers, D.E.; Nesterets, Y.; Paganin, D.M.; Pogany, A.; Stevenson, A.W.; Wilkins, S.W. Refracting Röntgen’s rays: Propagation-based X-ray phase contrast for biomedical imaging. J. Appl. Phys. 2009, 105, 102005. [Google Scholar] [CrossRef]
- Kitchen, M.J.; Buckley, G.A.; Gureyev, T.E.; Wallace, M.J.; Andres-Thio, N.; Uesugi, K.; Yagi, N.; Hooper, S.B. CT dose reduction factors in the thousands using X-ray phase contrast. Sci. Rep. 2017, 7, 15953. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T.E.; Nesterets, Y.I.; Kozlov, A.; Paganin, D.M.; Quiney, H.M. On the “unreasonable” effectiveness of transport of intensity imaging and optical deconvolution. J. Opt. Soc. Am. A 2017, 34, 2251–2260. [Google Scholar] [CrossRef] [PubMed]
- Mayo, S.C.; Miller, P.R.; Wilkins, S.W.; Davis, T.J.; Gao, D.; Gureyev, T.E.; Paganin, D.; Parry, D.J.; Pogany, A.; Stevenson, A.W. Quantitative X-ray projection microscopy: Phase-contrast and multi-spectral imaging. J. Microsc. 2002, 207, 79–96. [Google Scholar] [CrossRef] [PubMed]
- Specification for Hamamatsu C10900D Detector. Available online: https://dtsheet.com/doc/569688/hamamatsu-c10900d (accessed on 21 April 2021).
- Specification for Xineos 3030HR Detector. Available online: https://www.teledynedalsa.com/en/products/imaging/medical-x-ray-detectors/xineos-large-area/xineos-3030hr/ (accessed on 21 April 2021).
- Gureyev, T.; Nesterets, Y.; Ternovski, D.; Thompson, D.; Wilkins, S.; Stevenson, A.; Sakellariou, A.; Taylor, J. Toolbox for Advanced X-ray Image Processing. In Proceedings of the Advances in Computational Methods for X-ray Optics II, San Diego, CA, USA, 21–24 August 2011. [Google Scholar]
- Marone, F.; Stampanoni, M. Regridding reconstruction algorithm for real-time tomographic imaging. J. Synchrotron Radiat. 2012, 19, 1029–1037. [Google Scholar] [CrossRef] [PubMed]
- Marcou, J.; Bosworth, R.; Clarken, R.; Martin, P.; Moll, A. ASCI: A Compute platform for researchers at the Australian Synchrotron. In Proceedings of the 16th International Conference on Accelerator and Large Experimental Physics Control Systems (ICALEPCS 2017), Barcelona, Spain, 8–13 October 2017. [Google Scholar]
- Tavakoli Taba, S.; Arhatari, B.D.; Nesterets, Y.I.; Gadomkar, Z.; Mayo, S.C.; Thompson, D.; Fox, J.; Kumar, B.; Prodanovic, Z.; Hausermann, D.; et al. Propagation-Based Phase-Contrast CT of the Breast Demonstrates Higher Quality Than Conventional Absorption-Based CT Even at Lower Radiation Dose. Acad. Radiol. 2021, 28, e20–e26. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T.; Mohammadi, S.; Nesterets, Y.; Dullin, C.; Tromba, G. Accuracy and precision of reconstruction of complex refractive index in near-field single-distance propagation-based phase-contrast tomography. J. Appl. Phys. 2013, 114, 1–10. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]


| Hamamatsu | Xineos | |
|---|---|---|
 |  | |
| Number of pixels | 1216 × 1232 | 2097 × 2111 |
| Pixel size | 100 µm | 99 μm |
| Exposure time | 59 ms | 25 ms |
| Frame rate | 17 fps | 40 fps |
| Max counts | 4000 (12-bit) | 16,000 (14-bit) |
| Acquisition mode | Fine mode | Mag1 (70%) |
| Adipose | Glandular | |||
|---|---|---|---|---|
| Hamamatsu | Xineos | Hamamatsu | Xineos | |
| xres (µm) | 152 ± 9 | 169 ± 7 | 147 ± 4 | 164 ± 2 |
| yres (µm) | 172 ± 11 | 183 ± 7 | 175 ± 6 | 186 ± 5 |
| SNR | 6.0 ± 0.6 | 7.6 ± 0.5 | 7.4 ± 0.9 | 9.3 ± 0.3 |
| SNR/res (µm−1) | 0.037 ± 0.004 | 0.043 ± 0.002 | 0.046 ± 0.006 | 0.053 ± 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arhatari, B.D.; Stevenson, A.W.; Abbey, B.; Nesterets, Y.I.; Maksimenko, A.; Hall, C.J.; Thompson, D.; Mayo, S.C.; Fiala, T.; Quiney, H.M.; et al. X-ray Phase-Contrast Computed Tomography for Soft Tissue Imaging at the Imaging and Medical Beamline (IMBL) of the Australian Synchrotron. Appl. Sci. 2021, 11, 4120. https://doi.org/10.3390/app11094120
Arhatari BD, Stevenson AW, Abbey B, Nesterets YI, Maksimenko A, Hall CJ, Thompson D, Mayo SC, Fiala T, Quiney HM, et al. X-ray Phase-Contrast Computed Tomography for Soft Tissue Imaging at the Imaging and Medical Beamline (IMBL) of the Australian Synchrotron. Applied Sciences. 2021; 11(9):4120. https://doi.org/10.3390/app11094120
Chicago/Turabian StyleArhatari, Benedicta D., Andrew W. Stevenson, Brian Abbey, Yakov I. Nesterets, Anton Maksimenko, Christopher J. Hall, Darren Thompson, Sheridan C. Mayo, Tom Fiala, Harry M. Quiney, and et al. 2021. "X-ray Phase-Contrast Computed Tomography for Soft Tissue Imaging at the Imaging and Medical Beamline (IMBL) of the Australian Synchrotron" Applied Sciences 11, no. 9: 4120. https://doi.org/10.3390/app11094120
APA StyleArhatari, B. D., Stevenson, A. W., Abbey, B., Nesterets, Y. I., Maksimenko, A., Hall, C. J., Thompson, D., Mayo, S. C., Fiala, T., Quiney, H. M., Taba, S. T., Lewis, S. J., Brennan, P. C., Dimmock, M., Häusermann, D., & Gureyev, T. E. (2021). X-ray Phase-Contrast Computed Tomography for Soft Tissue Imaging at the Imaging and Medical Beamline (IMBL) of the Australian Synchrotron. Applied Sciences, 11(9), 4120. https://doi.org/10.3390/app11094120






