Study of the Dependence of Solar Radiation Regarding Design Variables in Photovoltaic Solar Installations with Optimal Dual-Axis Tracking
Abstract
1. Introduction
2. Methodology
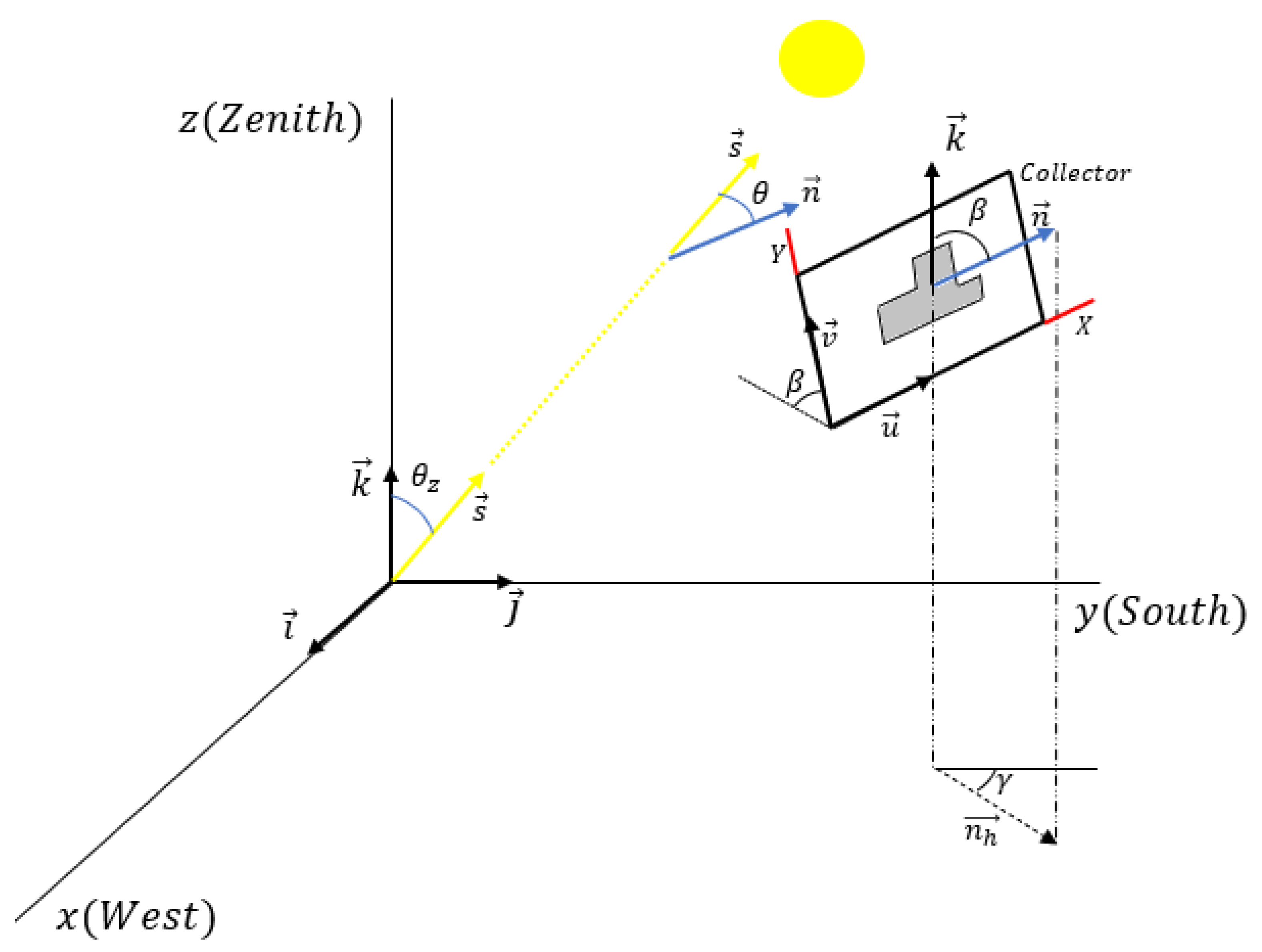
2.1. Vector Treatment of the Solar Position and the Estimation of the Solar Irradiance in the Celestial Sphere
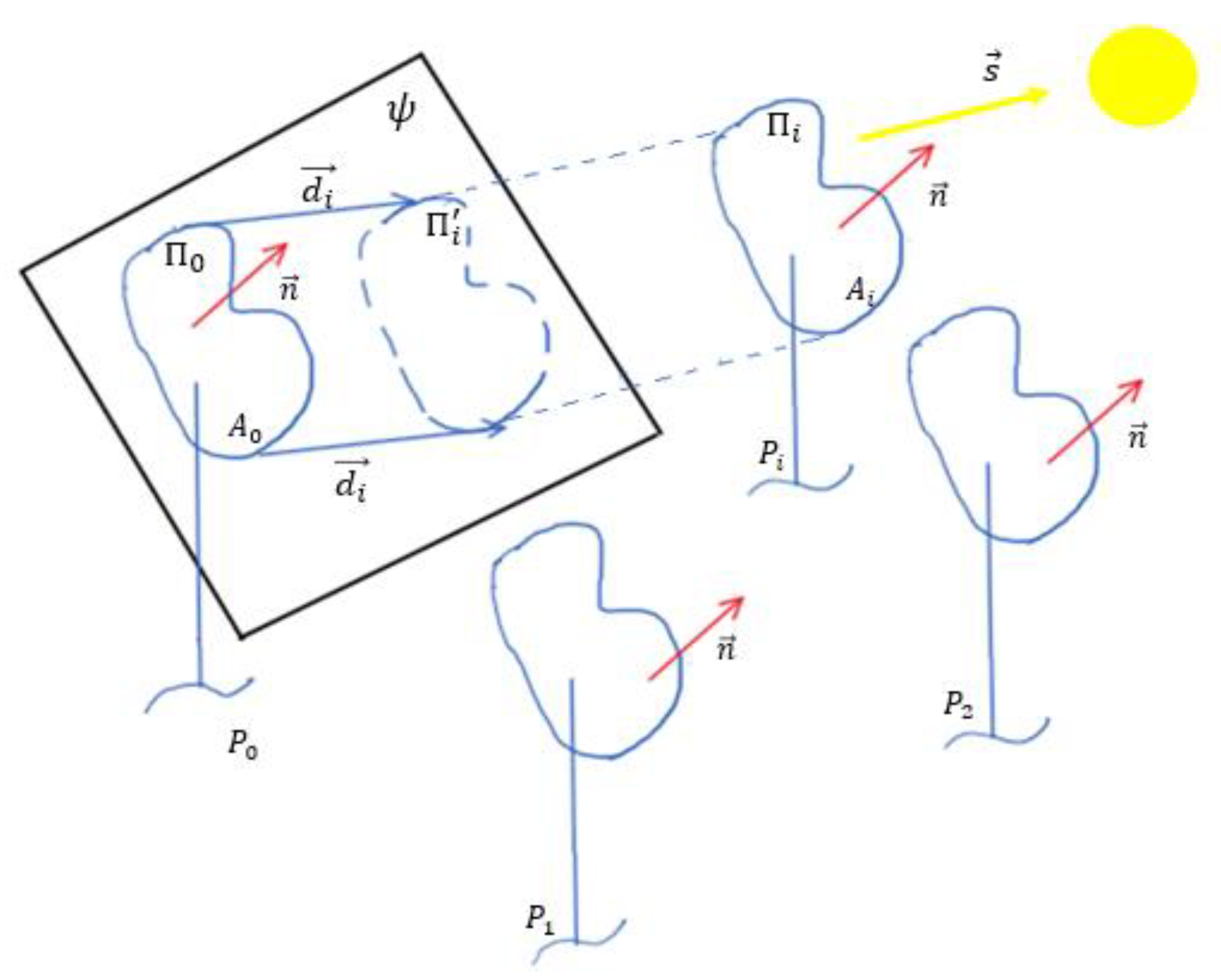
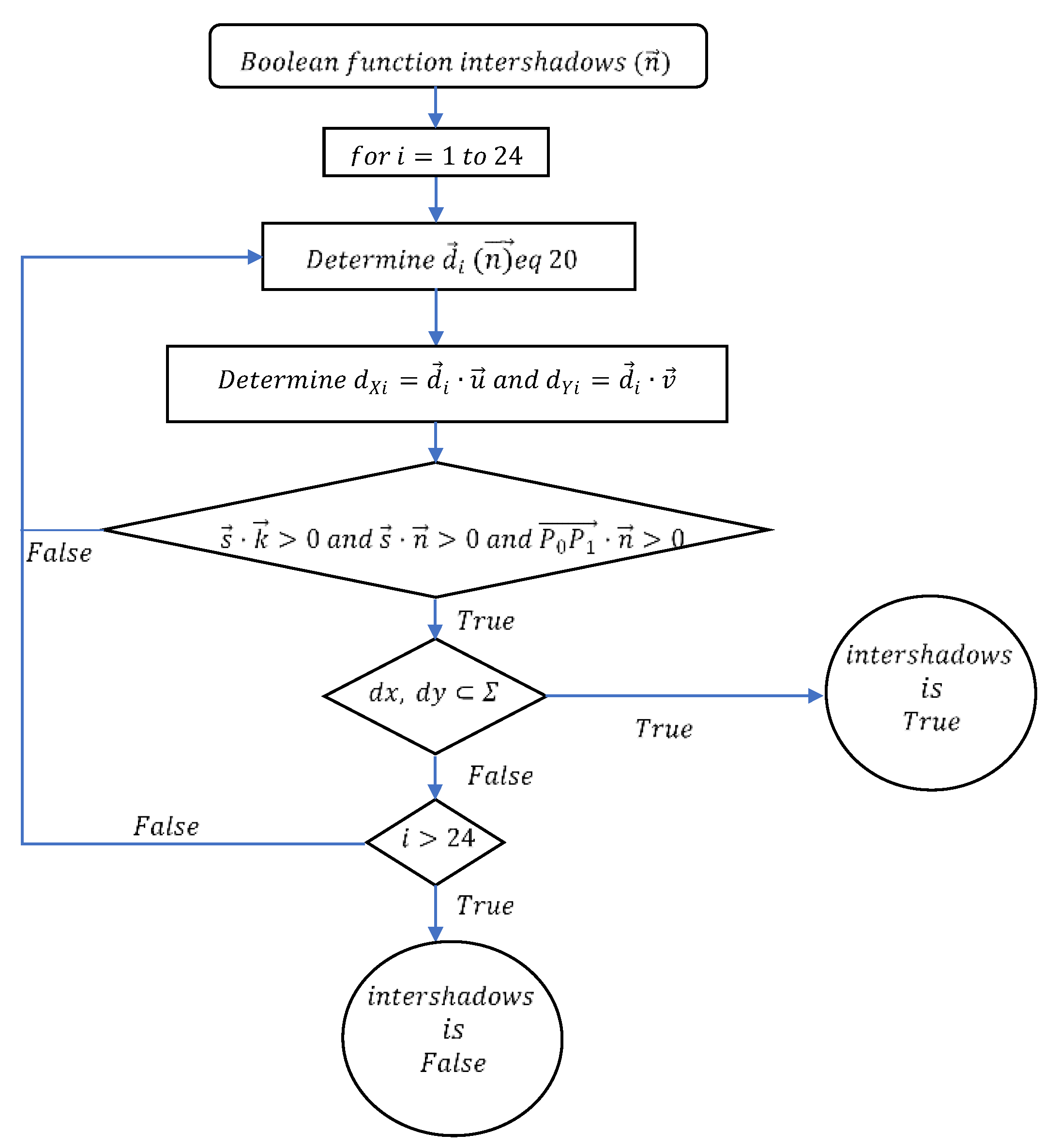
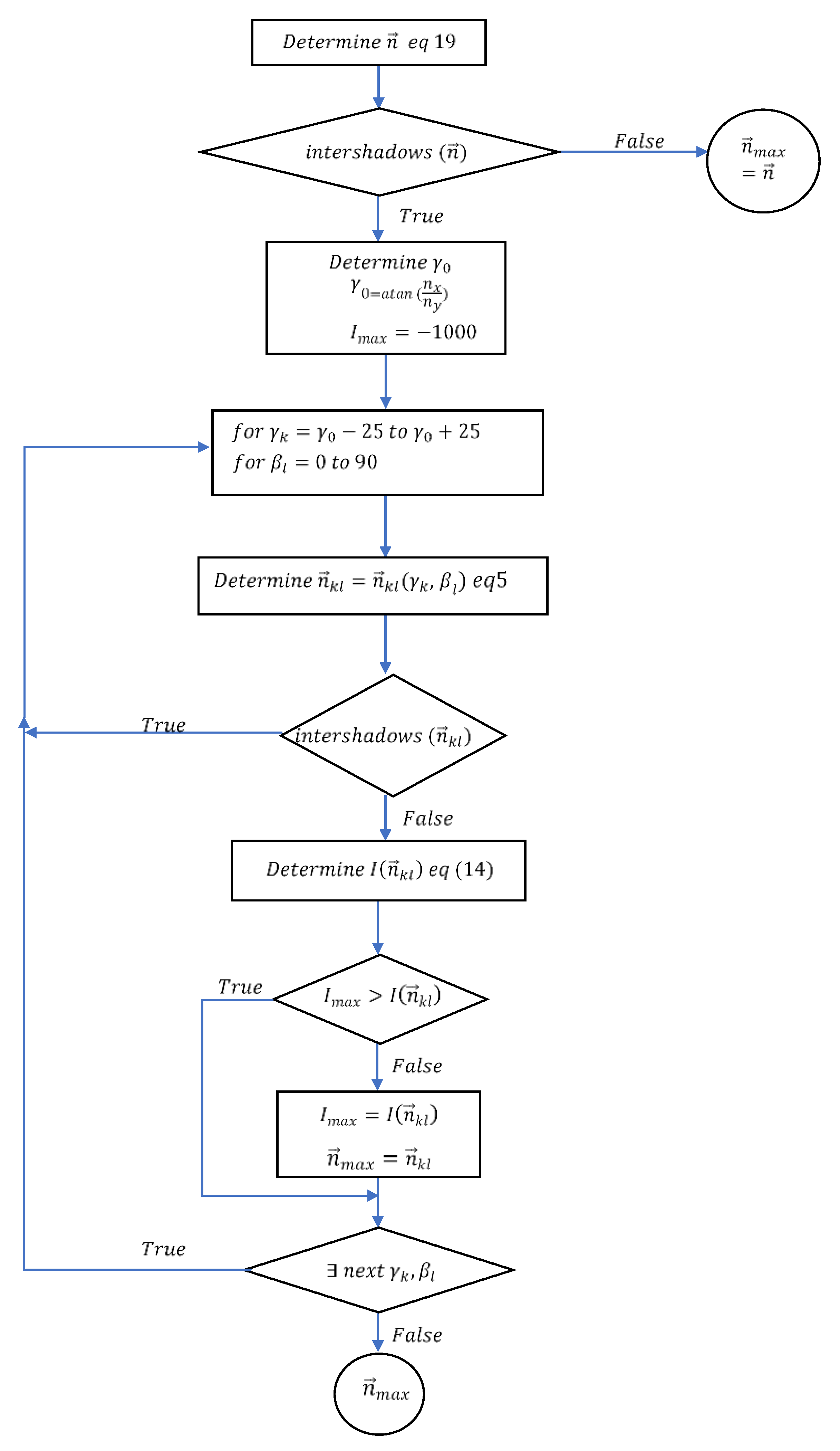
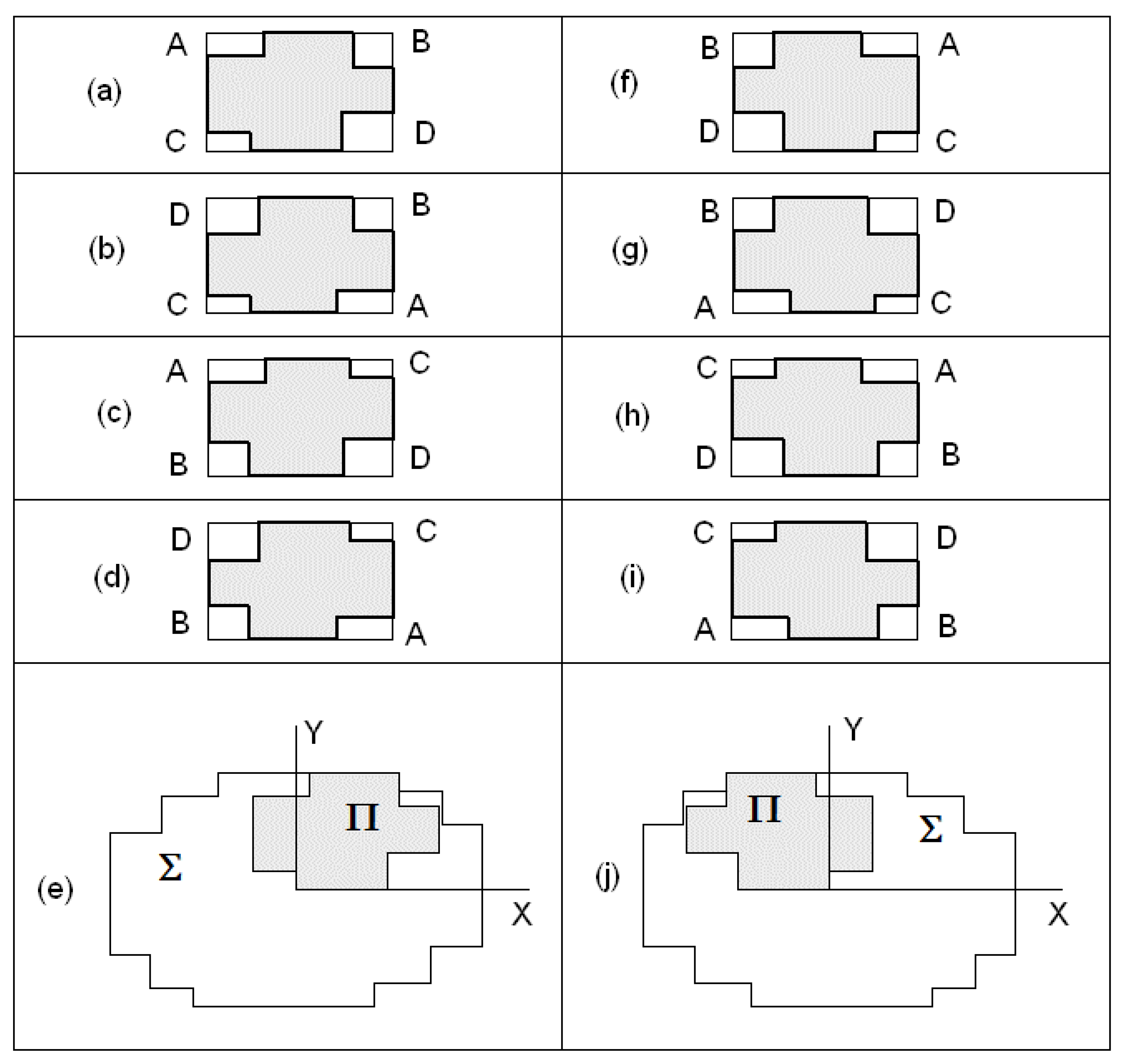
2.2. Method to Avoid Inter-Shading of Collectors
2.3. Calculation Scheme of Intercepted Solar Radiation
2.4. Cases Analyzed
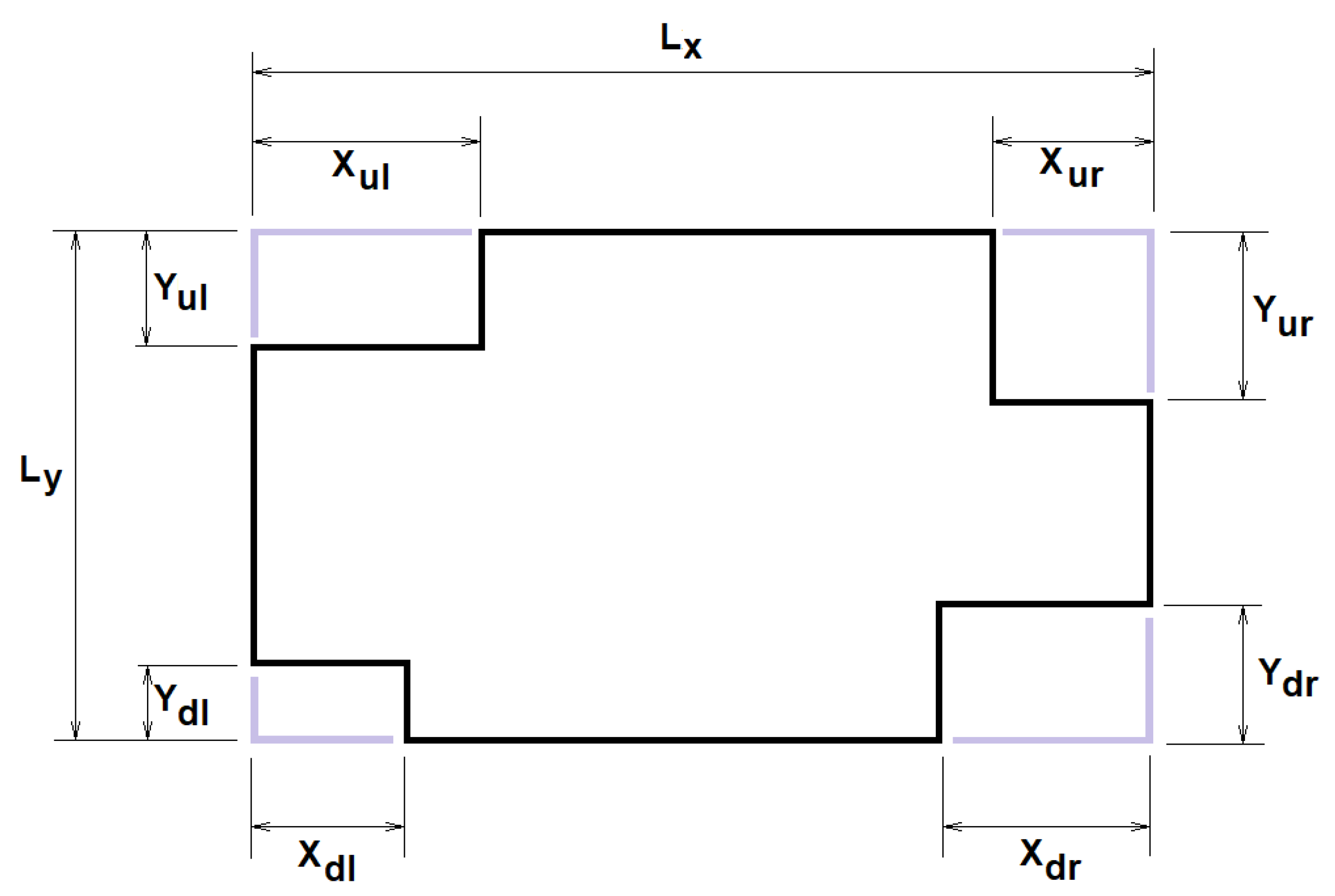
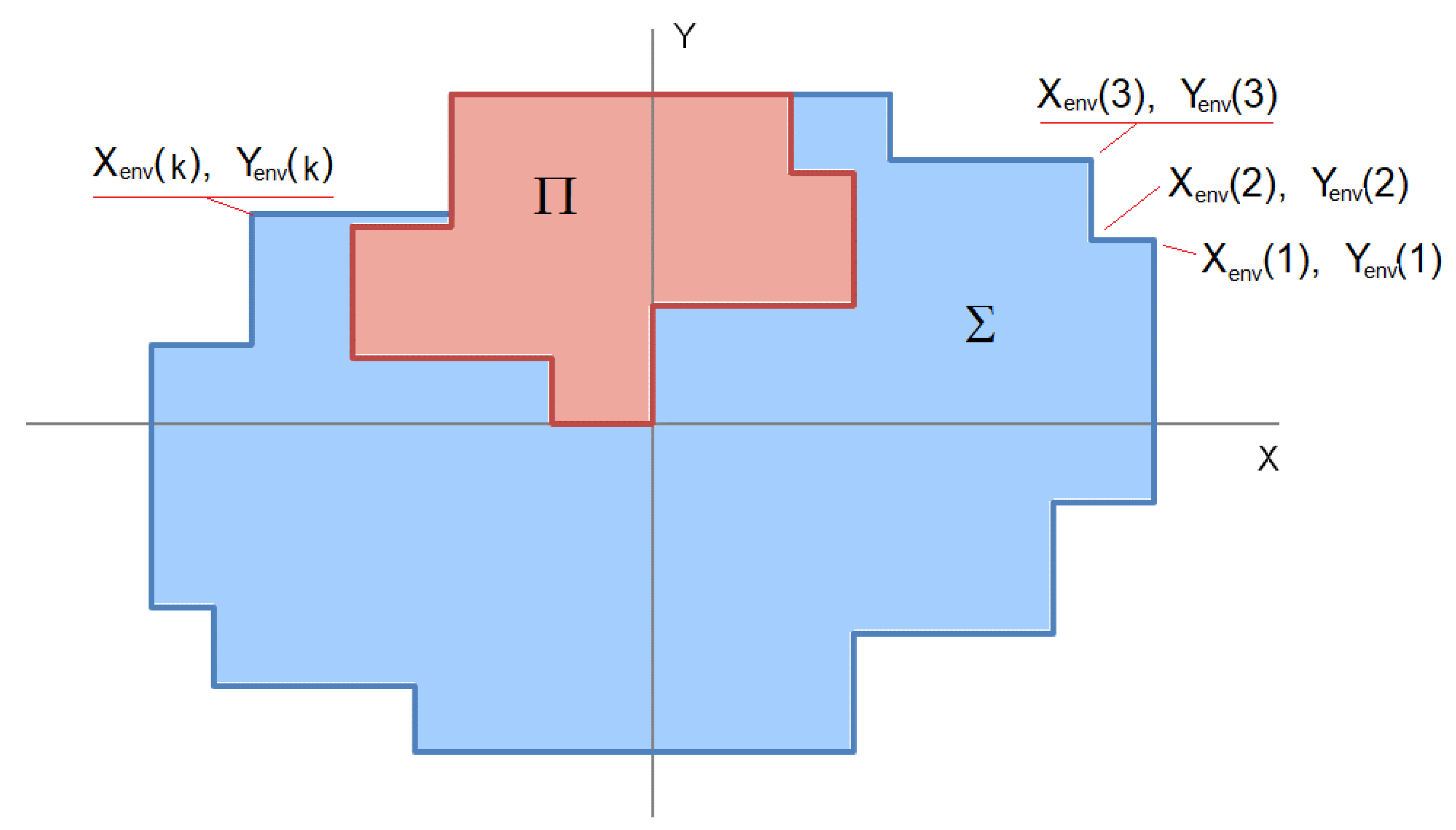
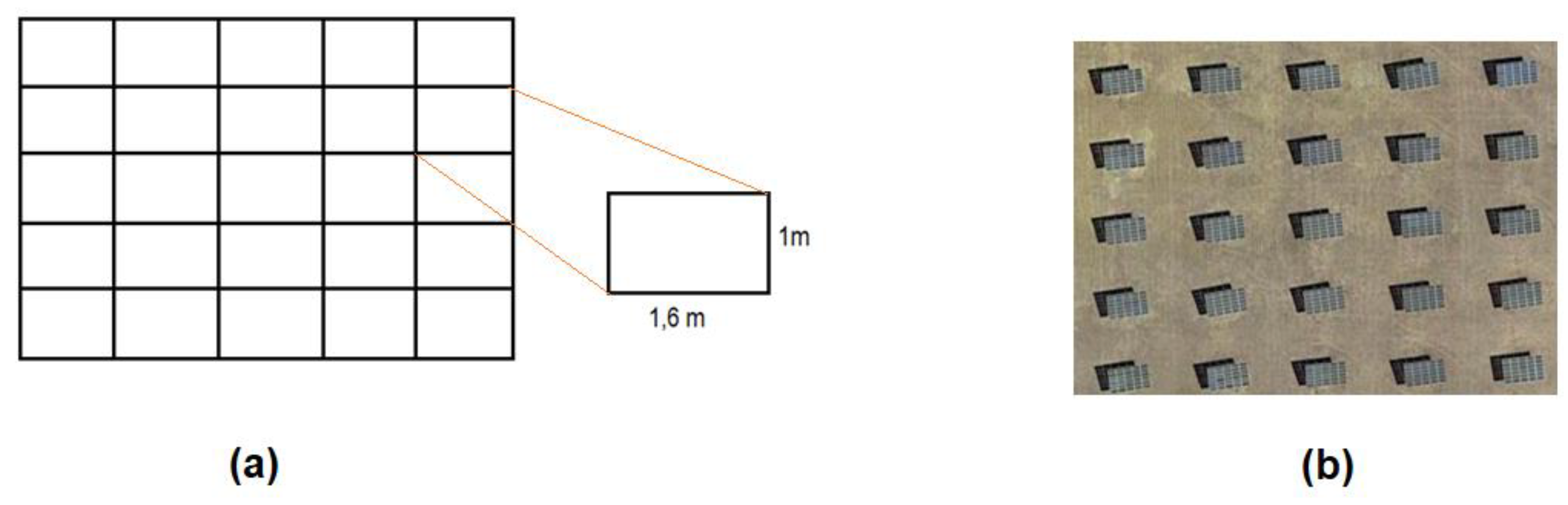
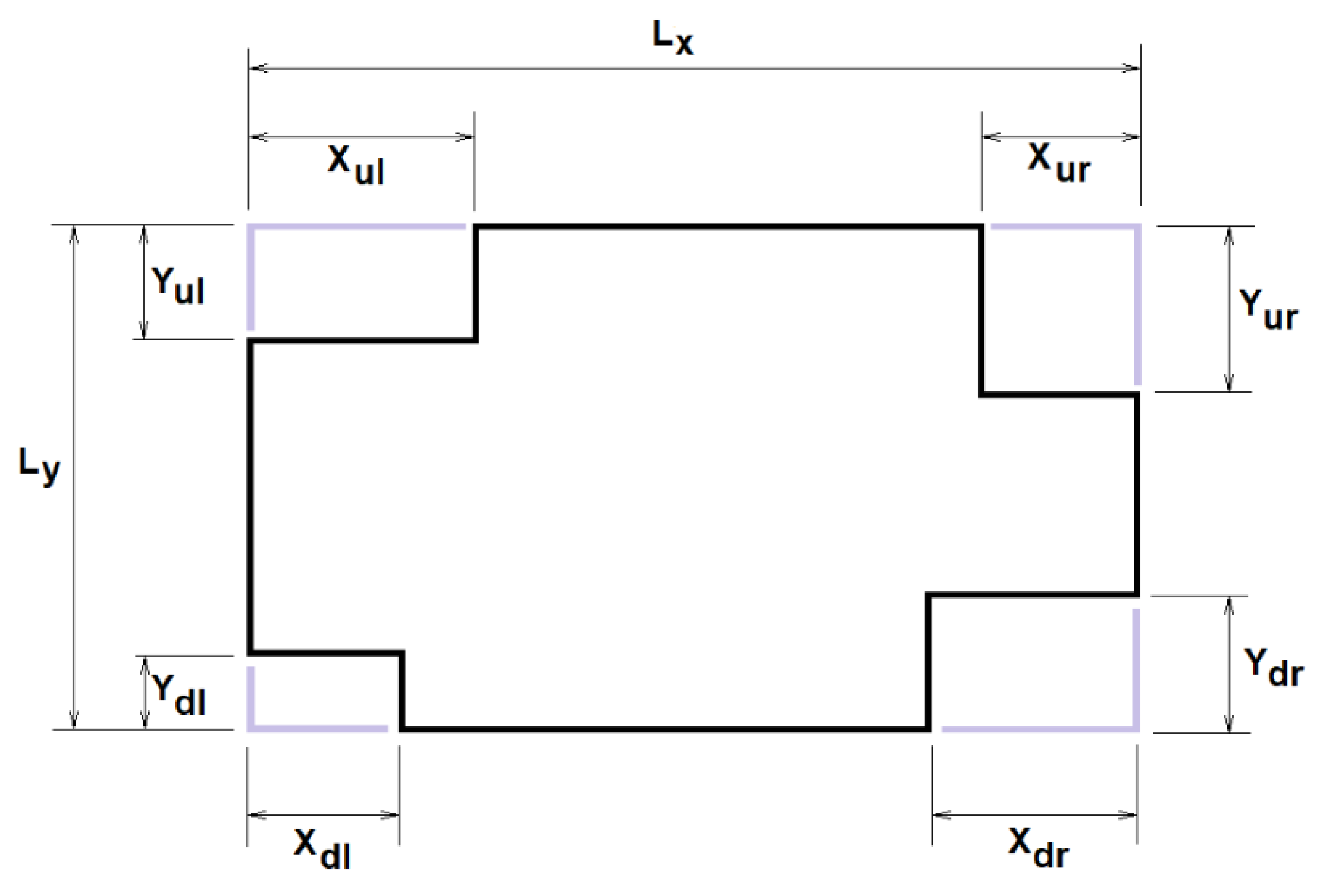
- Modification of the collector shape. The possibility of introducing cuts at the vertices has been considered to study the collectors with the shape indicated in Figure 8. Letting , , and be the coordinates of the vertices corresponding to the cuts made in the upper left, upper right, lower left, and lower right corners, the possible values considered (in metres) for each of these pairs were (0,0), (1,1.6), (1,3.2), (2,1.6), and (2,3.2). The crossing of all the possibilities generated = 54 = 625 different forms of collector.
- Modification of the inter-distances. Letting be the distance in the NS direction between rows of collectors and the distance in the EW direction between columns of collectors, the possibilities = 10 m, 12.5 m, 15 m, 17.5 m, and 20 m and = 10 m, 15 m, 20 m, and 25 m were studied. The crossing of these possibilities gave rise to = 20 designs of different distances.
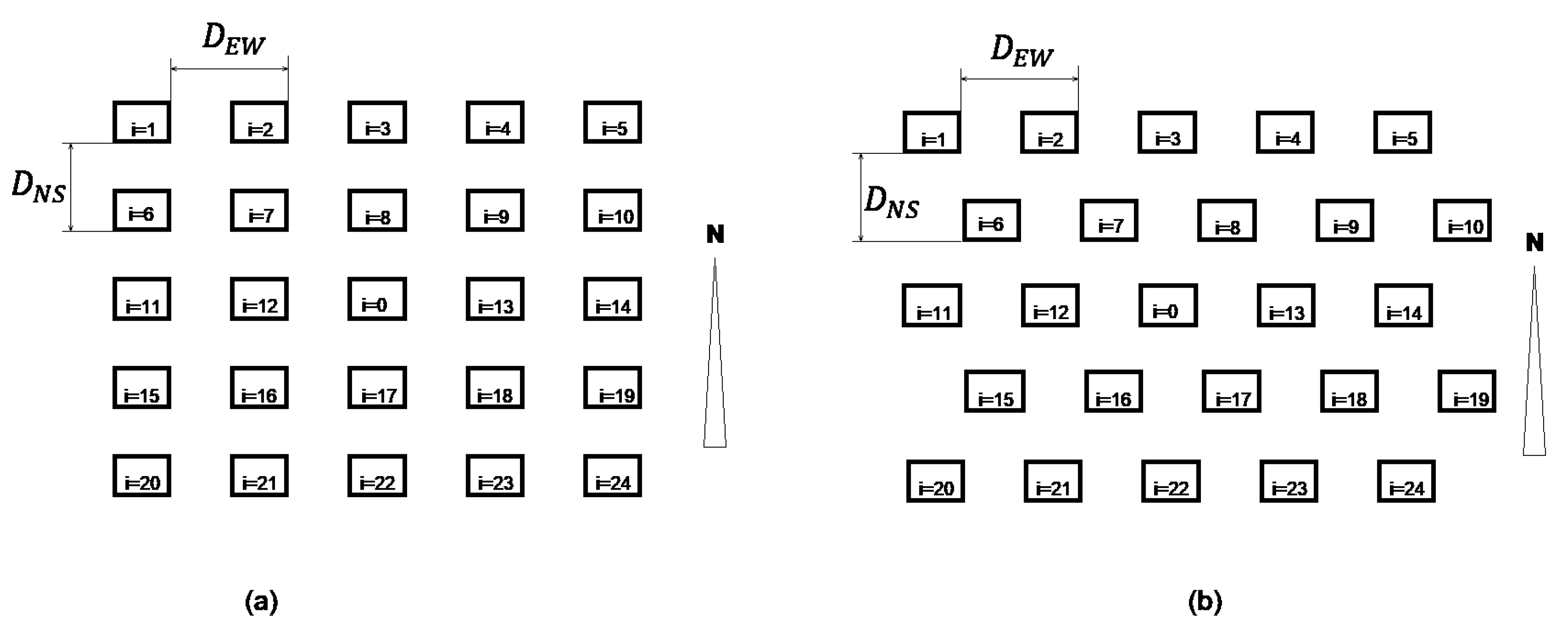
- Modification of the spatial distribution of the solar trackers. For each pair of distances , = 2, possible spatial distributions of the solar trackers in the plant were studied, both the regular grid arrangement oriented to the south (Figure 9a) and staggered (Figure 9b). In both configurations, it was considered that the reference collector in the study (i = 0) was surrounded by 24 collectors.
3. Results
- Collector surface .
- Distance between trackers in east–west direction,
- Distance between trackers in north–south direction,
- Discriminatory variable of the type of configuration T (T = 1 for staggered configurations and T = 0 for regular grids).
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| reference collector surface | |
| generic collector surface | |
| distance between trackers in east–west direction | |
| geometric displacement vector from polygon to | |
| Julian day | |
| distance between trackers in north–south direction | |
| X component of | |
| Y component of | |
| weighting factors for the decomposition of the inclined diffuse radiation | |
| ground cover ratio | |
| incident radiation on the collectors on each representative day of a month according to Klein | |
| annual global radiation | |
| annual solar irradiance on the solar collectors estimated according to Equation (28) | |
| annual solar irradiance on the solar collectors estimated according to Equation (29) | |
| unit vectors associated to a local Cartesian system | |
| global solar irradiance on the tilted collector | |
| direct solar irradiance on horizontal plane | |
| diffuse solar irradiance | |
| horizontal longitude of the collector before cuts | |
| vertical longitude of the collector before cuts | |
| normal vector to the surface | |
| different design of the inter-distances between collectors | |
| different forms of collector shape | |
| number of days in the month | |
| possible spatial distributions of the solar trackers in the plant | |
| different combinations of geometric designs result of crossing | |
| position of the reference collector | |
| position of a generic collector | |
| solar vector | |
| collector surface | |
| components of solar vector | |
| discriminatory variable of the type of configuration | |
| x-coordinate of the vertex corresponding to the cut made in the lower left corner | |
| x-coordinate of the vertex corresponding to the cut made in the lower right corner | |
| array with the x-coordinates of the collector shape | |
| x-coordinate of the vertex corresponding to the cut made in the upper left corner | |
| x-coordinate of the vertex corresponding to the cut made in the upper right corner | |
| y-coordinate of the vertex corresponding to the cut made in the lower left corner | |
| y-coordinate of the vertex corresponding to the cut made in the lower right corner | |
| array with the y-coordinates of the collector shape | |
| y-coordinate of the vertex corresponding to the cut made in the upper left corner | |
| y-coordinate of the vertex corresponding to the cut made in the upper right corner | |
| horizontal vector to the maximum slop direction of the collector plane | |
| parallel vector to the maximum slop direction of the collector plane | |
| Greek Letters | |
| inclination angle of the terrain | |
| γ | azimuth angle of the collector rotation axis |
| solar declination | |
| estimation error of the proposed model | |
| relative error of the proposed model | |
| angle of incidence of sunbeams on the inclined plane | |
| solar zenith angle | |
| albedo | |
| latitude | |
| Earth’s rotation speed | |
| daily angle | |
| reference polygon collector | |
| generic polygon collector | |
| projection of generic polygon collector over | |
| plane that contains the reference collector | |
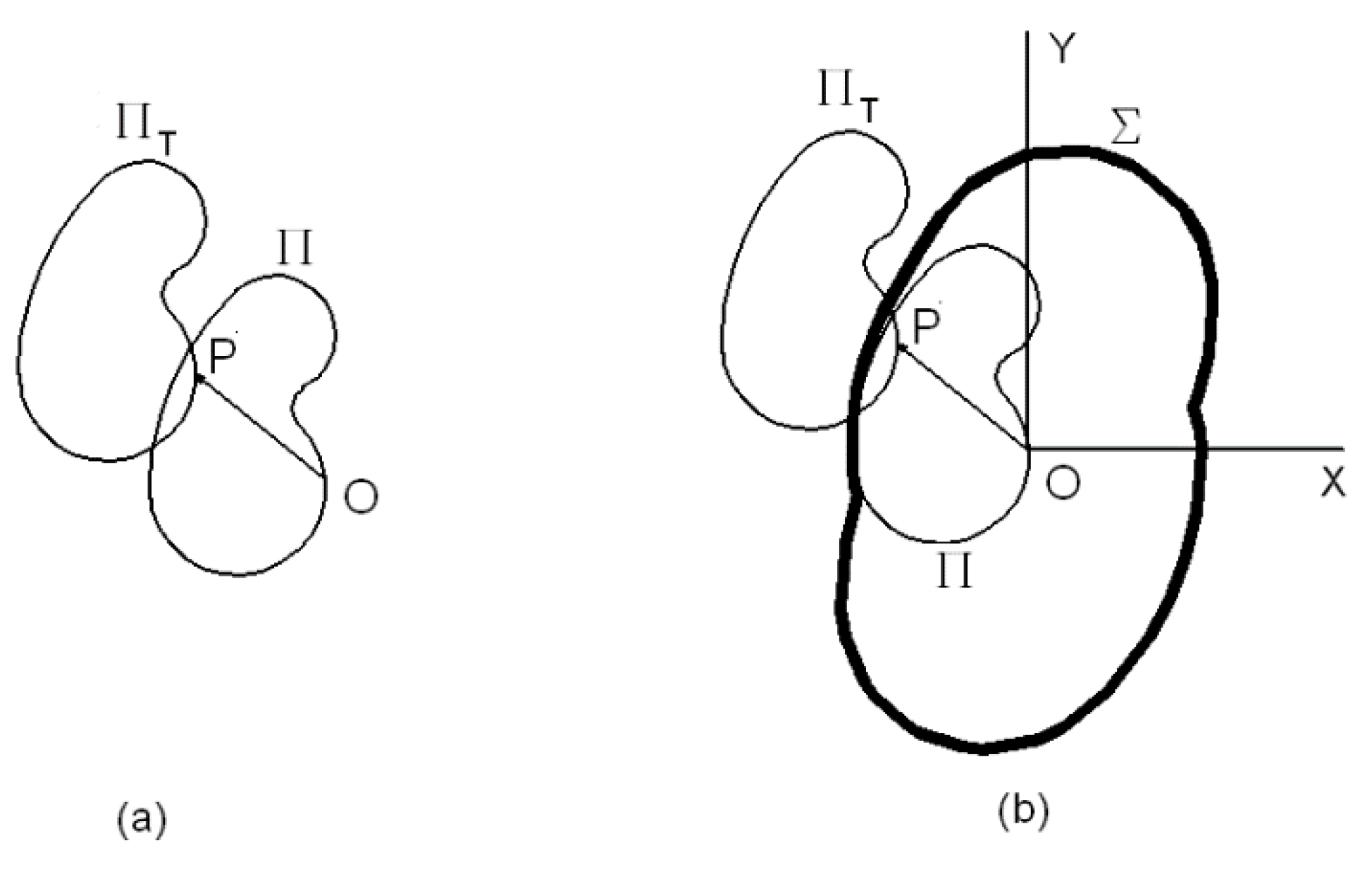
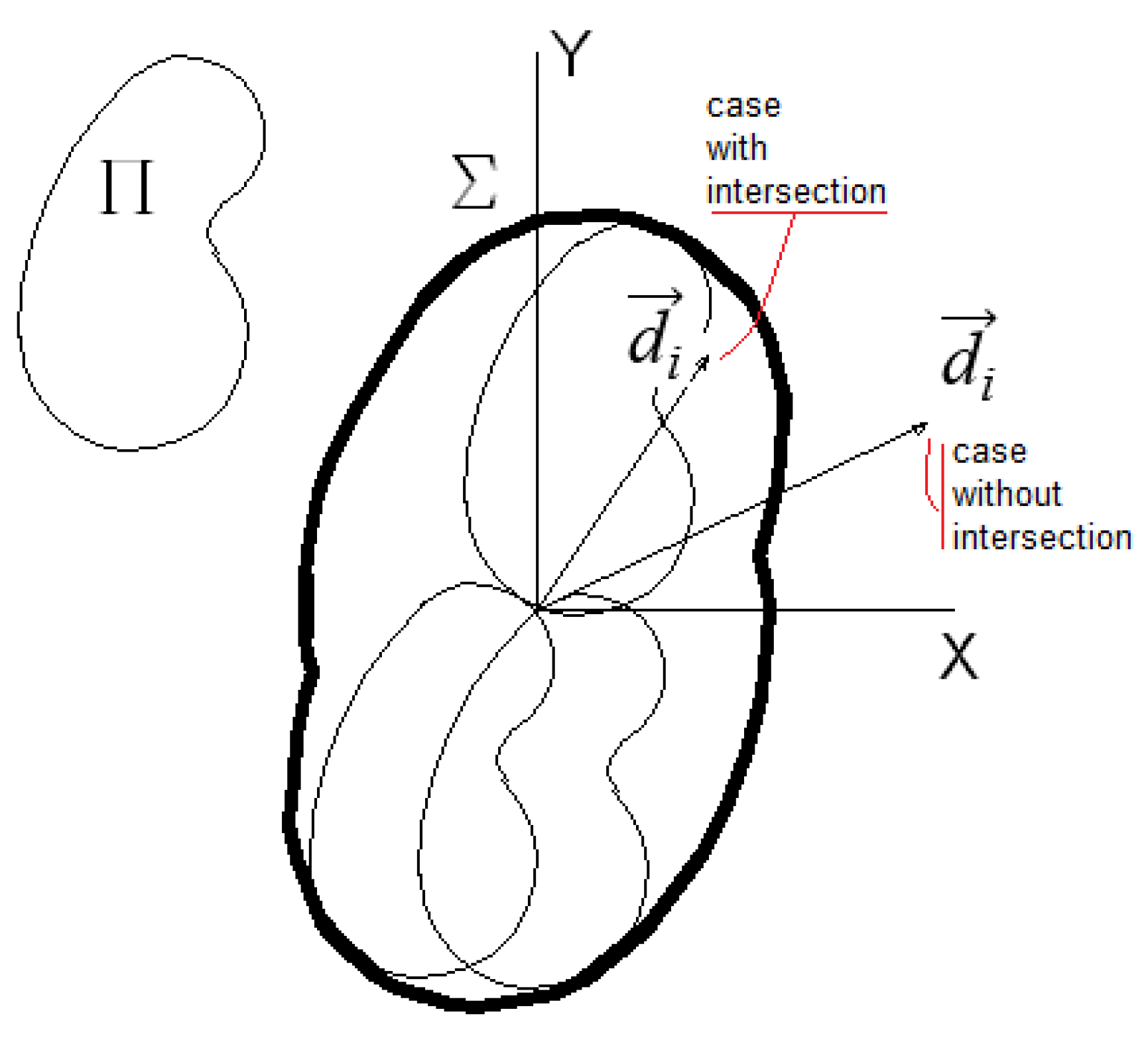
Appendix A. Demonstration of the Dicotomic Criterion for Determining the Intershading between Solar Collectors
- Step 1: If is included in , and intersect.
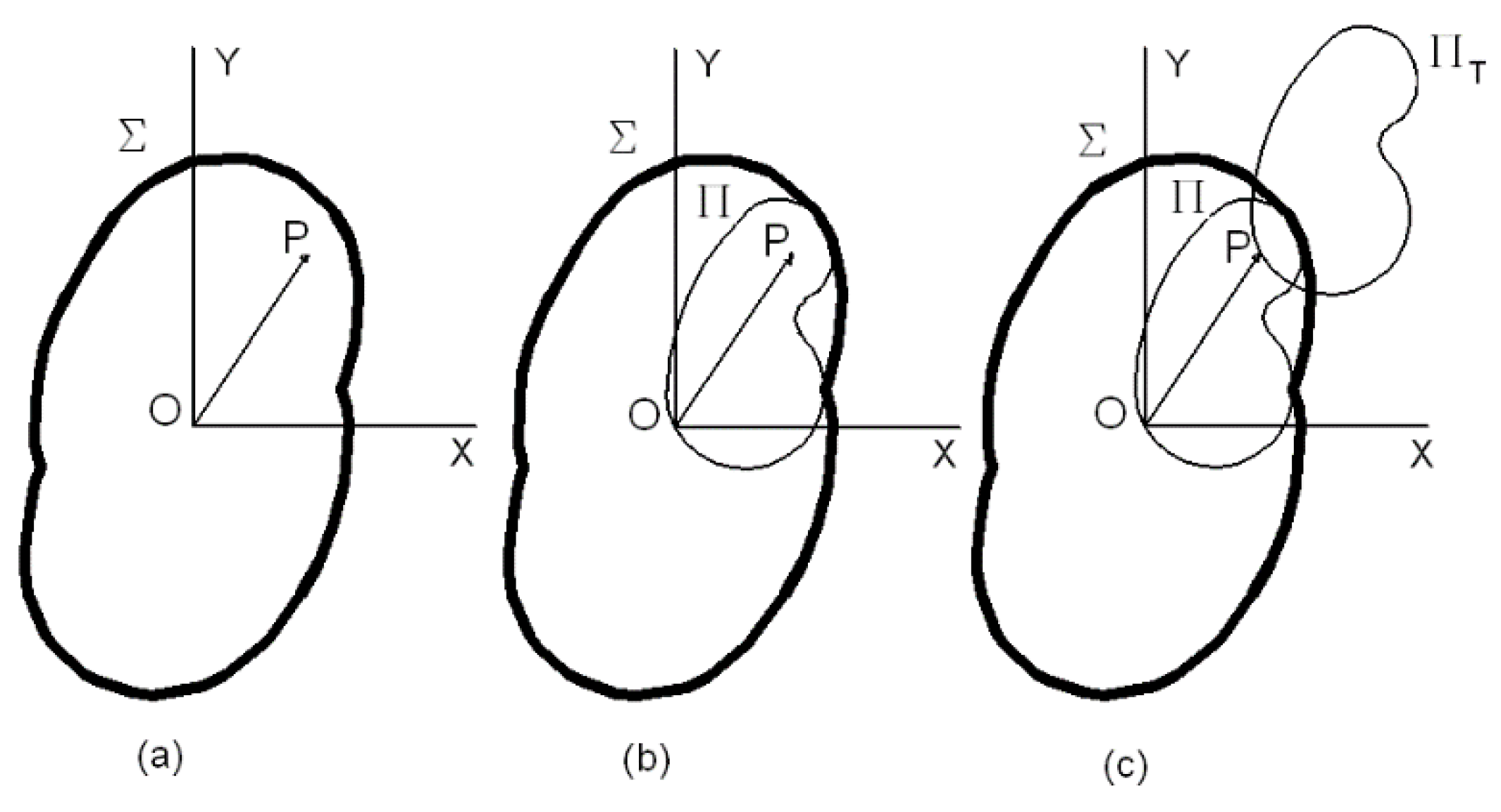
- Step 2: If and intersect, is included in .
Appendix B. Obtaining the Generic Form σ for Collectors with Cuts
References
- López, I.; Arriaga, A.; Pardo, M. La dimensión social del concepto de desarrollo sostenible: ¿La eterna Olvidada? Rev. Span. Sociol. 2018, 27. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Renewables 2020; IEA: Paris, France, 2020. [Google Scholar]
- Andre, T.; Guerra, F. Renewables Global Status Report; REN21: Paris, France, 2020; ISBN 978-3-948393-00-7. [Google Scholar]
- Kannan, N.; Vakeesan, D. Solar energy for future world: A review. Renew. Sustain. Energy Rev. 2016, 62, 1092–1105. [Google Scholar] [CrossRef]
- Eldin, S.A.S.A.S.; Abd-Elhady, M.S.S.; Kandil, H.A.A. Feasibility of solar tracking systems for PV panels in hot and cold regions. Renew. Energy 2016, 85, 228–233. [Google Scholar] [CrossRef]
- Salas, V.; Olias, E. Overview of the photovoltaic technology status and perspective in Spain. Renew. Sustain. Energy Rev. 2009, 13, 1049–1057. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, S.; Gehlot, A.; Pachauri, R. An imperative role of sun trackers in photovoltaic technology: A review. Renew. Sustain. Energy Rev. 2018, 82, 3263–3278. [Google Scholar] [CrossRef]
- AL-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Frydrychowicz-Jastrzębska, G.; Bugała, A. Modeling the Distribution of Solar Radiation on a Two-Axis Tracking Plane for Photovoltaic Conversion. Energies 2015, 8, 1025–1041. [Google Scholar] [CrossRef]
- Hafez, A.Z.; Yousef, A.M.; Harag, N.M. Solar tracking systems: Technologies and trackers drive types—A review. Renew. Sustain. Energy Rev. 2018, 91, 754–782. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Chou, P.-C.; Chiang, C.-M.; Lin, C.-F. Sun Tracking Systems: A Review. Sensors 2009, 9, 3875–3890. [Google Scholar] [CrossRef]
- Antonanzas, J.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas, F. Optimal solar tracking strategy to increase irradiance in the plane of array under cloudy conditions: A study across Europe. Sol. Energy 2018, 163, 122–130. [Google Scholar] [CrossRef]
- Bahrami, A.; Okoye, C.O. The performance and ranking pattern of PV systems incorporated with solar trackers in the northern hemisphere. Renew. Sustain. Energy Rev. 2018, 97, 138–151. [Google Scholar] [CrossRef]
- Quesada, G.; Guillon, L.; Rousse, D.R.; Mehrtash, M.; Dutil, Y.; Paradis, P.-L. Tracking strategy for photovoltaic solar systems in high latitudes. Energy Convers. Manag. 2015, 103, 147–156. [Google Scholar] [CrossRef]
- Hammad, B.; Al-Sardeah, A.; Al-Abed, M.; Nijmeh, S.; Al-Ghandoor, A. Performance and economic comparison of fixed and tracking photovoltaic systems in Jordan. Renew. Sustain. Energy Rev. 2017, 80, 827–839. [Google Scholar] [CrossRef]
- Talavera, D.L.; Muñoz-Cerón, E.; Ferrer-Rodríguez, J.P.; Pérez-Higueras, P.J. Assessment of cost-competitiveness and profitability of fixed and tracking photovoltaic systems: The case of five specific sites. Renew. Energy 2019, 134, 902–913. [Google Scholar] [CrossRef]
- Hua, Z.; Ma, C.; Lian, J.; Pang, X.; Yang, W. Optimal capacity allocation of multiple solar trackers and storage capacity for utility-scale photovoltaic plants considering output characteristics and complementary demand. Appl. Energy 2019, 238, 721–733. [Google Scholar] [CrossRef]
- Ali Jallal, M.; Chabaa, S.; Zeroual, A. A novel deep neural network based on randomly occurring distributed delayed PSO algorithm for monitoring the energy produced by four dual-axis solar trackers. Renew. Energy 2020, 149, 1182–1196. [Google Scholar] [CrossRef]
- Eke, R.; Senturk, A. Performance comparison of a double-axis sun tracking versus fixed PV system. Sol. Energy 2012, 86, 2665–2672. [Google Scholar] [CrossRef]
- Şenpinar, A.; Cebeci, M. Evaluation of power output for fixed and two-axis tracking PVarrays. Appl. Energy 2012, 92, 677–685. [Google Scholar] [CrossRef]
- Bahrami, A.; Okoye, C.O.; Atikol, U. The effect of latitude on the performance of different solar trackers in Europe and Africa. Appl. Energy 2016, 177, 896–906. [Google Scholar] [CrossRef]
- Koussa, M.; Cheknane, A.; Hadji, S.; Haddadi, M.; Noureddine, S. Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions. Appl. Energy 2011, 88, 1756–1771. [Google Scholar] [CrossRef]
- Seme, S.; Štumberger, G.; Voršič, J. Maximum efficiency trajectories of a two-axis sun tracking system determined considering tracking system consumption. IEEE Trans. Power Electron. 2011, 26, 1280–1290. [Google Scholar] [CrossRef]
- Gómez-Uceda, F.J.; Ramirez-Faz, J.; Varo-Martinez, M.; Fernández-Ahumada, L.M. New Omnidirectional Sensor Based on Open-Source Software and Hardware for Tracking and Backtracking of Dual-Axis Solar Trackers in Photovoltaic Plants. Sensors 2021, 21, 726. [Google Scholar] [CrossRef]
- Fernández-Ahumada, L.M.; Ramírez-Faz, J.; López-Luque, R.; Varo-Martínez, M.; Moreno-García, I.M.; Casares de la Torre, F. Influence of the design variables of photovoltaic plants with two-axis solar tracking on the optimization of the tracking and backtracking trajectory. Sol. Energy 2020, 208, 89–100. [Google Scholar] [CrossRef]
- Lorenzo, E.; Pérez, M.; Ezpeleta, A.; Acedo, J. Design of tracking photovoltaic systems with a single vertical axis. Prog. Photovolt. Res. Appl. 2002, 10, 533–543. [Google Scholar] [CrossRef]
- Karatepe, E.; Boztepe, M.; Çolak, M. Development of a suitable model for characterizing photovoltaic arrays with shaded solar cells. Sol. Energy 2007, 81, 977–992. [Google Scholar] [CrossRef]
- Kaushika, N.D.; Gautam, N.K. Energy yield simulations of interconnected solar PV arrays. IEEE Trans. Energy Convers. 2003, 18, 127–134. [Google Scholar] [CrossRef]
- Woyte, A.; Nijs, J.; Belmans, R. Partial shadowing of photovoltaic arrays with different system configurations: Literature review and field test results. Sol. Energy 2003, 74, 217–233. [Google Scholar] [CrossRef]
- Trzmiel, G.; Głuchy, D.; Kurz, D. The impact of shading on the exploitation of photovoltaic installations. Renew. Energy 2020, 153, 480–498. [Google Scholar] [CrossRef]
- Díaz-Dorado, E.; Suárez-García, A.; Carrillo, C.J.; Cidrás, J. Optimal distribution for photovoltaic solar trackers to minimize power losses caused by shadows. Renew. Energy 2011, 36, 1826–1835. [Google Scholar] [CrossRef]
- Martínez-Moreno, F.; Muñoz, J.; Lorenzo, E. Experimental model to estimate shading losses on PV arrays. Sol. Energy Mater. Sol. Cells 2010, 94, 2298–2303. [Google Scholar] [CrossRef]
- Perpiñán, O. Cost of energy and mutual shadows in a two-axis tracking PV system. Renew. Energy 2012, 43, 331–342. [Google Scholar] [CrossRef]
- Narvarte, L.; Lorenzo, E. Tracking and ground cover ratio. Prog. Photovolt. Res. Appl. 2008, 16, 703–714. [Google Scholar] [CrossRef]
- Panico, D.; Garvison, P.; Wenger, H.; Shugar, D. Backtracking: A novel strategy for tracking PV systems. In Proceedings of the Conference Record of the Twenty-Second IEEE Photovoltaic Specialists Conference 1991, Las Vegas, NV, USA, 7–11 October 1991; pp. 668–673. [Google Scholar]
- DEGERiberica. Referencias. Available online: https://degeriberica.com/referencias/ (accessed on 20 January 2021).
- Fernández-Ahumada, L.M.; Casares, F.J.; Ramírez-Faz, J.; López-Luque, R. Mathematical study of the movement of solar tracking systems based on rational models. Sol. Energy 2017, 150, 20–29. [Google Scholar] [CrossRef]
- Fernández-Ahumada, L.M.; Ramírez-Faz, J.; López-Luque, R.; Varo-Martínez, M.; Moreno-García, I.M.; Casares de la Torre, F. A novel backtracking approach for two-axis solar PV tracking plants. Renew. Energy 2020, 145, 1214–1221. [Google Scholar] [CrossRef]
- Braun, J.E.; Mitchell, J.C. Solar geometry for fixed and tracking surfaces. Sol. Energy 1983, 31, 439–444. [Google Scholar] [CrossRef]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Riley, D.; Hansen, C. Sun-Relative Pointing for Dual-Axis Solar Trackers Employing Azimuth and Elevation Rotations. J. Sol. Energy Eng. 2015, 137, 031008. [Google Scholar] [CrossRef]
- Kelly, N.A.; Gibson, T.L. Improved photovoltaic energy output for cloudy conditions with a solar tracking system. Sol. Energy 2009, 83, 2092–2102. [Google Scholar] [CrossRef]
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Sol. Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Avnaim, F.; Boissonnat, J.-D. Polygon placement under translation and rotation. RAIRO Theor. Inform. Appl. 1989, 23, 5–28. [Google Scholar] [CrossRef]
- Chazelle, B. The polygon containment problem. Adv. Comput. Res. 1983, 1, 1–33. [Google Scholar]
- Lozano-Pérez, T. Spatial Planning: A Configuration Space Approach. IEEE Trans. Comput. 1983. [Google Scholar] [CrossRef]
- Klein, S.A. Calculation of monthly average insolation on tilted surfaces. Sol. Energy 1977, 19, 325–329. [Google Scholar] [CrossRef]
- Posadillo, R.; López Luque, R. A sizing method for stand-alone PV installations with variable demand. Renew. Energy 2008, 33, 1049–1055. [Google Scholar] [CrossRef]

| Month | H (J/m2) | Representative Day |
|---|---|---|
| January | 7,401,000 | 17 |
| February | 11,097,000 | 47 |
| March | 14,158,000 | 75 |
| April | 17,307,000 | 105 |
| May | 19,017,000 | 135 |
| June | 24,263,000 | 162 |
| July | 25,719,000 | 198 |
| August | 23,411,000 | 228 |
| September | 17,983,000 | 258 |
| October | 11,895,000 | 288 |
| November | 8,228,000 | 318 |
| December | 6,237,000 | 344 |
| Number of Cases | 25,000 |
|---|---|
| Average | 2172.0 |
| Minimum | 2040.2 |
| Maximum | 2233.8 |
| Median | 2189.6 |
| Parameter | Units | Value |
|---|---|---|
| kWh/m2 year | 2656.366 | |
| kWh/m4 year | −0.960 | |
| kWh/m3 year | 6.921 | |
| kWh/m year | −25.783 | |
| kWh/m3year | −756.012 | |
| kWh/m4 year | 0.512 | |
| kWh/m2 year | −167.750 | |
| kWh/m2 year | 19.071 | |
| kWh/m2 year | −364.603 | |
| kWh/m2 year | −1.365 | |
| kWh/m2 year | −1.661 |
| ε (kWh/m2 year) | εrel (Dimensionless) | |
|---|---|---|
| Number of cases | 25,000 | 25,000 |
| Average | 3.302 | 1.53 × 10−3 |
| Minimum | 4.67×10−4 | 2.099 × 10−7 |
| Maximum | 35.913 | 1.66 × 10−2 |
| Median | 2.561 | 1.15 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Uceda, F.J.; Moreno-Garcia, I.M.; Perez-Castañeda, Á.; Fernández-Ahumada, L.M. Study of the Dependence of Solar Radiation Regarding Design Variables in Photovoltaic Solar Installations with Optimal Dual-Axis Tracking. Appl. Sci. 2021, 11, 3917. https://doi.org/10.3390/app11093917
Gómez-Uceda FJ, Moreno-Garcia IM, Perez-Castañeda Á, Fernández-Ahumada LM. Study of the Dependence of Solar Radiation Regarding Design Variables in Photovoltaic Solar Installations with Optimal Dual-Axis Tracking. Applied Sciences. 2021; 11(9):3917. https://doi.org/10.3390/app11093917
Chicago/Turabian StyleGómez-Uceda, Francisco Javier, Isabel Maria Moreno-Garcia, Álvaro Perez-Castañeda, and Luis Manuel Fernández-Ahumada. 2021. "Study of the Dependence of Solar Radiation Regarding Design Variables in Photovoltaic Solar Installations with Optimal Dual-Axis Tracking" Applied Sciences 11, no. 9: 3917. https://doi.org/10.3390/app11093917
APA StyleGómez-Uceda, F. J., Moreno-Garcia, I. M., Perez-Castañeda, Á., & Fernández-Ahumada, L. M. (2021). Study of the Dependence of Solar Radiation Regarding Design Variables in Photovoltaic Solar Installations with Optimal Dual-Axis Tracking. Applied Sciences, 11(9), 3917. https://doi.org/10.3390/app11093917







