Finite Element Analysis of Mandibular Anterior Teeth with Healthy, but Reduced Periodontium
Abstract
1. Introduction
2. Materials and Methods
- The steps involved in producing the 57 plans with the CBCT scan images were as follows:
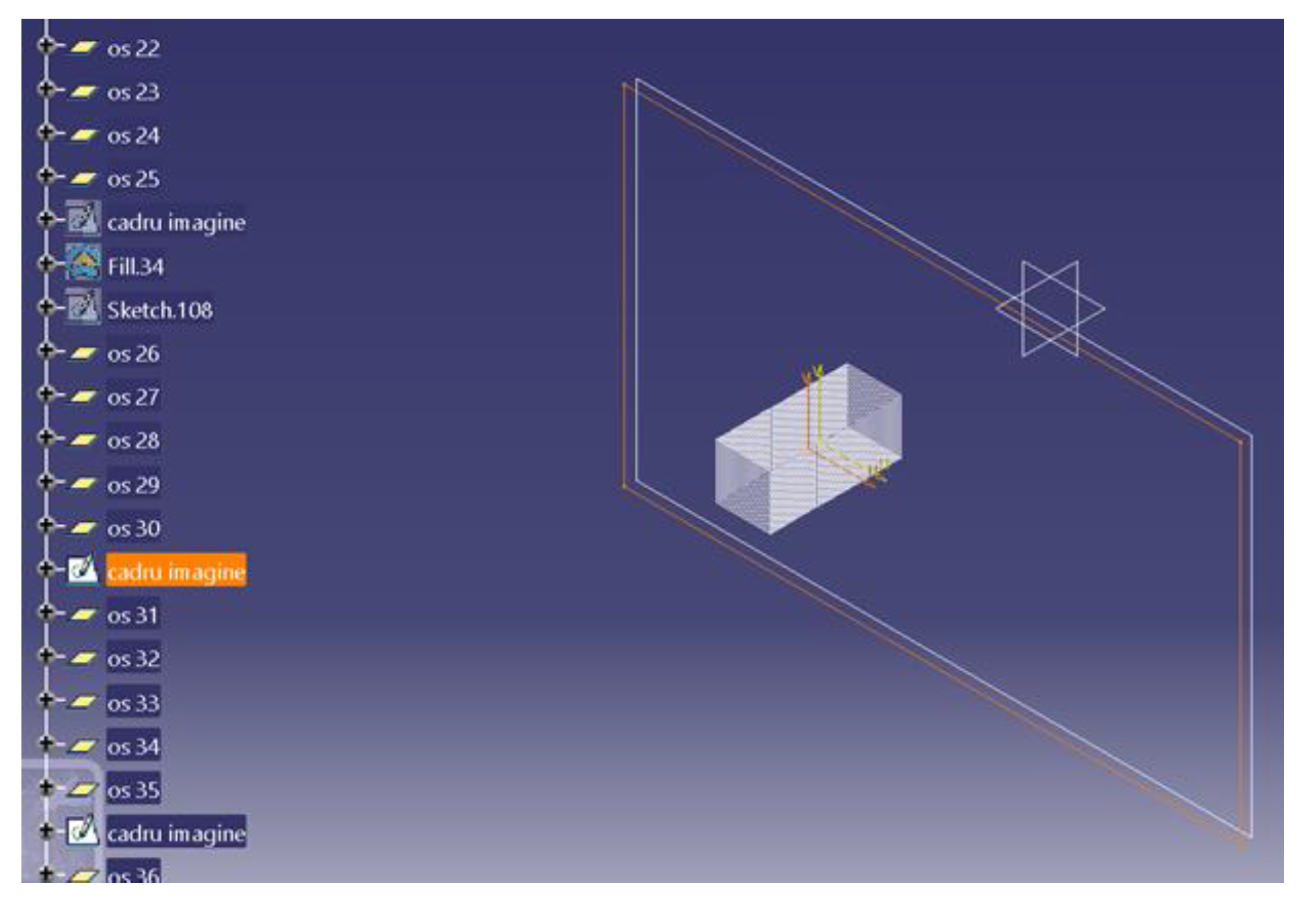
- The construction of the CBCT image placement plans. In the Catia V5R20 program, 57 planes parallel to each other were built with the help of the plane tool, at a distance of 7 mm from each other. Then, on each plane, a frame with the size 1920 × 1080, equal to the resolution of the image saved in the Planmeca Romexis® Viewer program, was inserted (Figure 1).
- The plans were constructed with CBCT images, in the GSD (Geometrical Shape Design) module of the CatiaV5 R 20 program. On each frame, introduced in the previous step, the corresponding image saved from the CBCT was introduced; after this step, the frame was transformed into a surface in the GSD module of the Catia V5R20 program. Subsequently, a material was assigned to each surface.
- The saved image from the CBCT was applied and was set to the selected plane. This was made with the help of the “texture” section of the “properties” menu of the flat surface on which the CT image was applied.
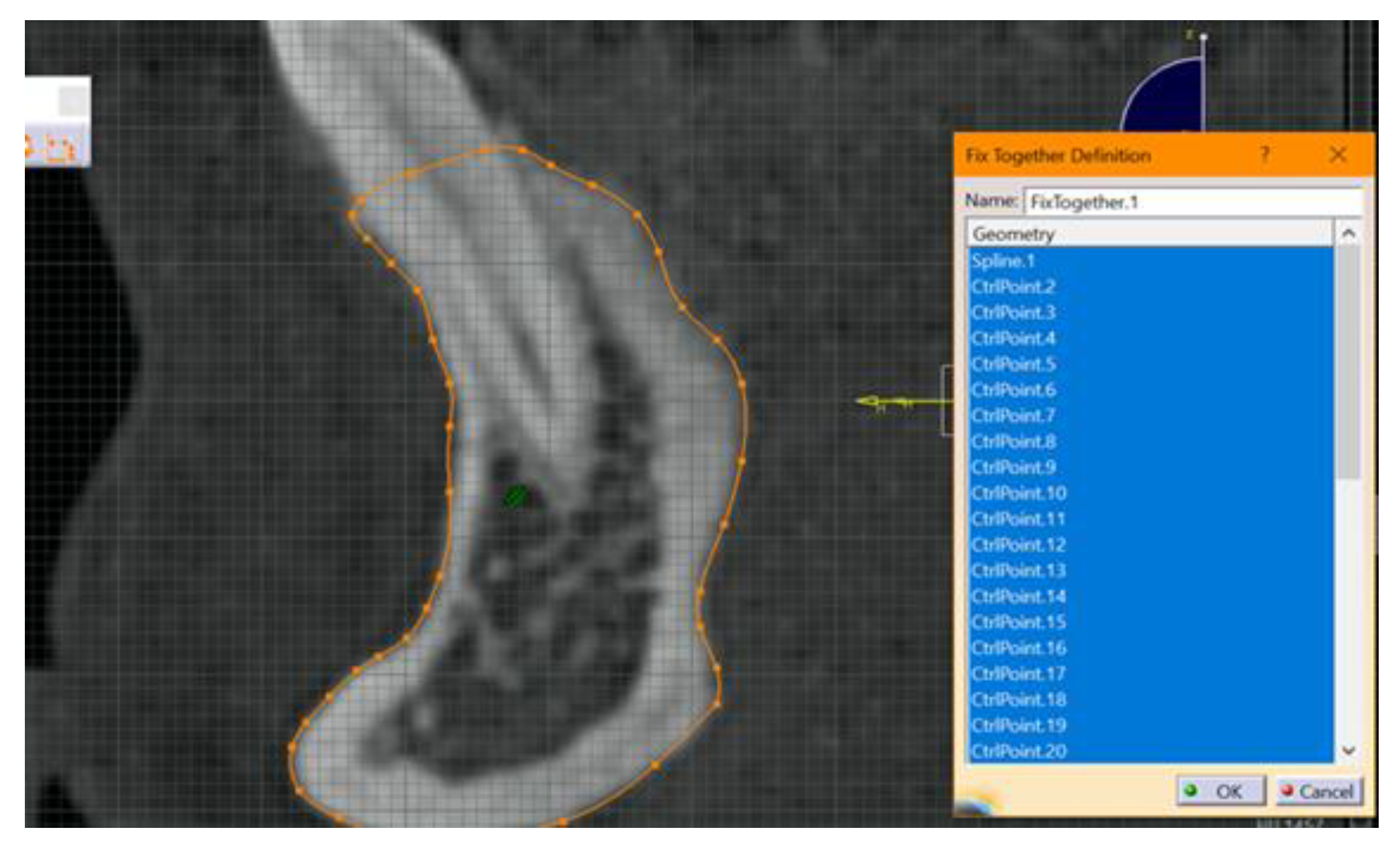
- The required outline was copied. At this stage, the outer contour of the mandibular bone structure was copied for each section. Copying was done manually using the spline function from the Part design module, from Sketch tools, in Catia V5R20. It is known that the result and quality of this step, the step of making the contour of the section through the bone, depends on the operator’s experience.
- The next step included fixing and “constraining” the obtained contour. This step is mandatory for each 2D entity in the sections obtained. The constraint aims to fix the points introduced to create curves. If this step is not performed, there is a high risk of error. This step was performed by using the fixed together tool from the Constraints menu. A dimensional constraint was also applied, with the aim of fixing the position of all points in relation to the origin of the work plane (Figure 2).
- Rearranging the operations in the operations list of the Catia V5 R20 program. This step is necessary in order to easily establish a correlation between sections to the subsequent steps of obtaining the 3D model. It was done by moving the corresponding branches one by one, for each of the 57 sections.
- Hiding the construction elements used in Catia V5 R20. This is necessary in order to make the contour for the stage of obtaining the 3D model. All the introduced elements (construction plans, frames and images from the sections) were hidden in order to be able to work continuously with the obtained sections. This was done for each plane separately.
- Obtaining the 3D model of the mandible section. The construction of the mandible was performed based on the sections from Figure 3.
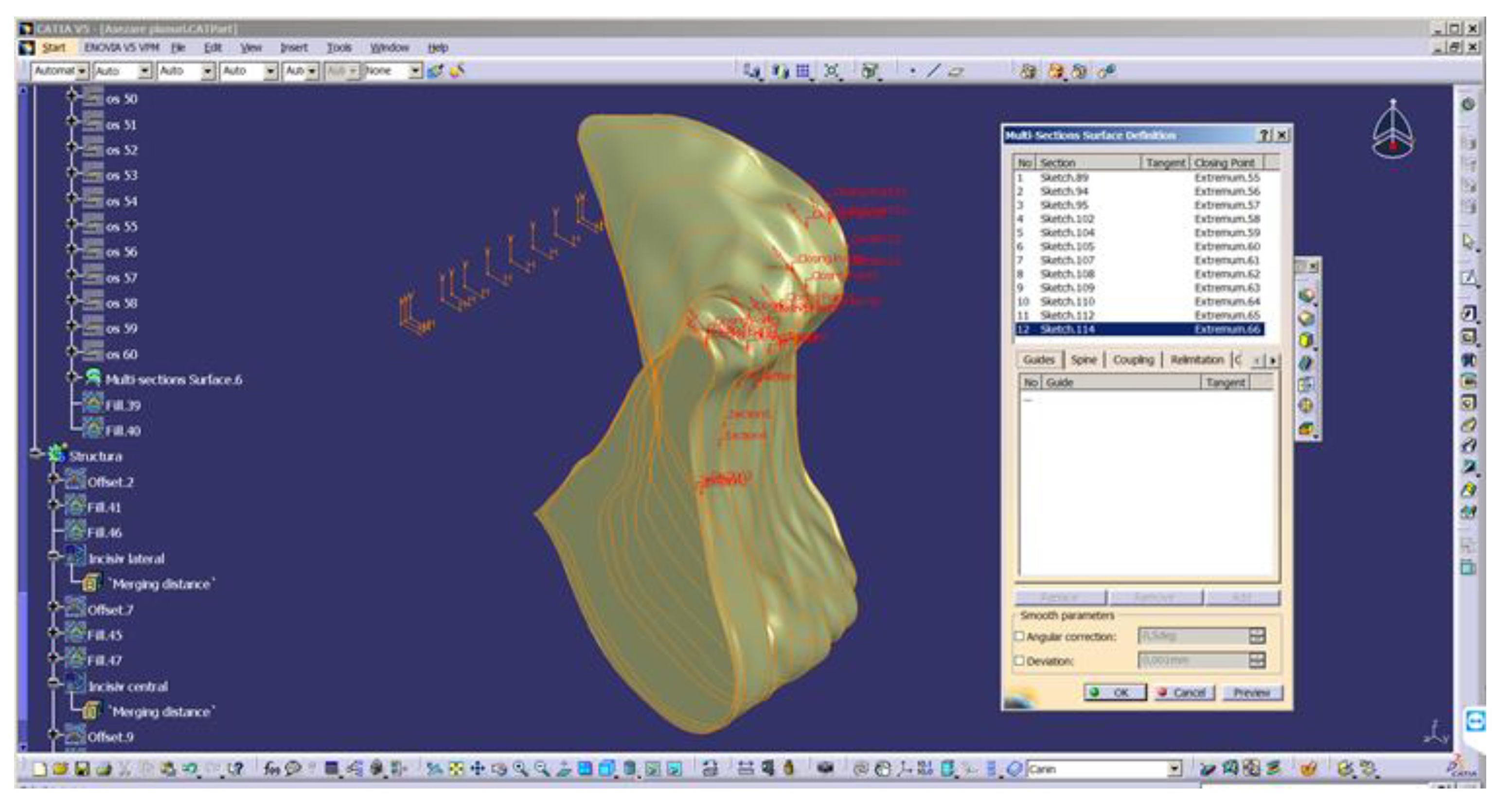
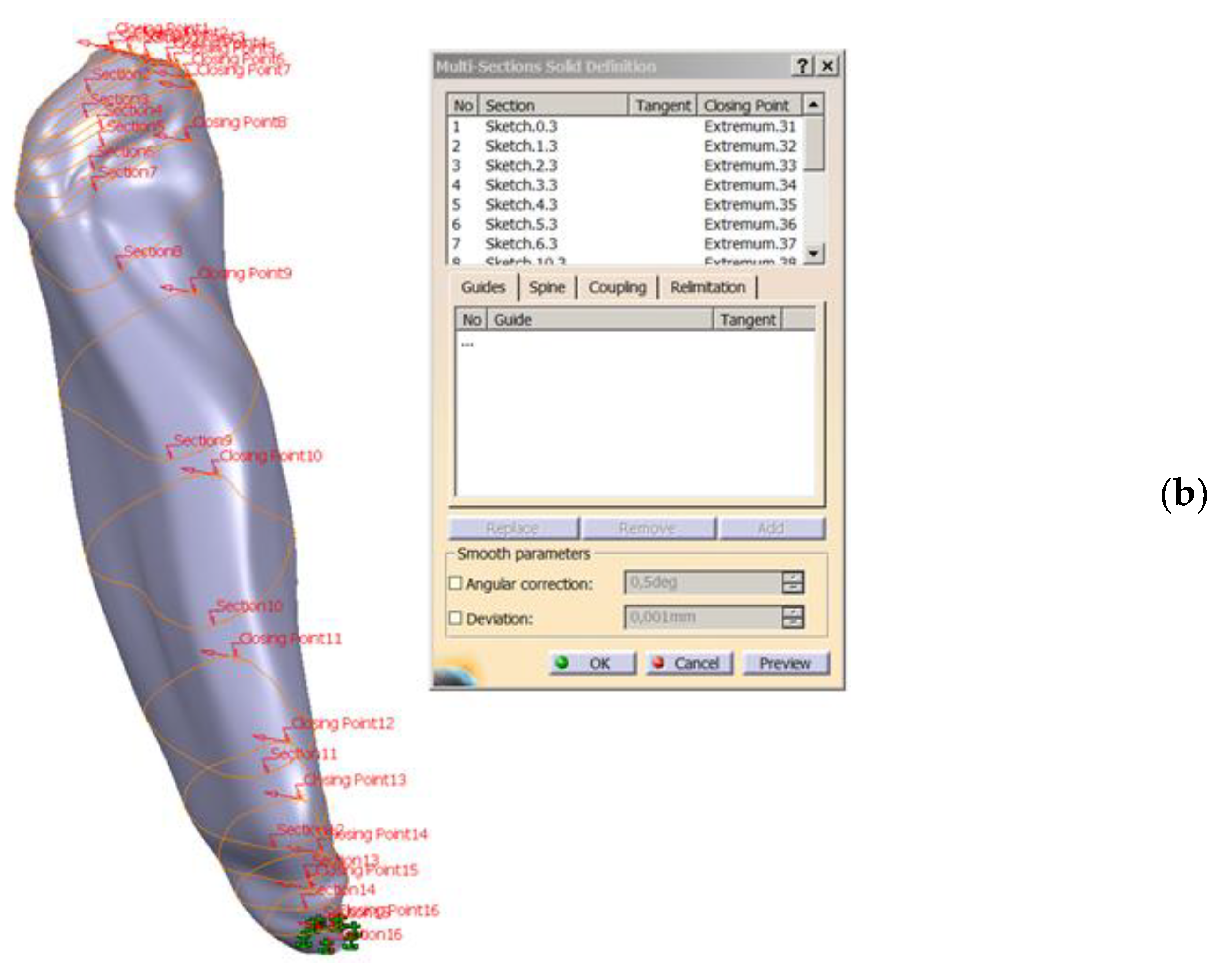
- Converting 2D sections. The “Multi-sections surface” 3D construction tool was used to convert the previously built 2D sections, as seen in Figure 4. The orientation of the curves was taken into account so that they all had the same tangent direction at the starting point. These were the starting points for the construction of 2D sections, for each section. For this reason, the construction of these sections is particularly important. The order of selection was also taken into account, as shown in the window in Figure 4.
- The final structure of the mandible. After the construction of the 3D model of the mandibular section, the 2D structure of the sections was hidden.
- Obtaining the 3D model of the teeth according to the CBCT scan model.

- C.
- Stages of periodontal ligament 3D modeling
- In the first stage, the 3D model with the dimensions obtained after copying the contours from the CBCT was scaled down to the real dimensions. In these contours, each pixel in the CBCT image represents one millimeter in the Catia V5R20 program. The resolution of the introduced images was 1920 × 1080, so that each section was much more enlarged compared to reality. In order to convert the model to a realistic size, the real length was measured on the CBCT and then it was determined in the virtual model of the Catia V5R20 length. This resulted in a ratio of scaling factor F1 = 0.05309038. This scaling factor was applied to the 3D model in order to ensure that the structure composed of the teeth, bone and PDL ligament reflected the real size. This factor was applied in turn to each component element (bone, teeth, periodontal ligament), and then the assembly was performed again in the Assembly Design module. The overall positioning was not altered because the relative positions to the coordinate system were also taken into account when resizing. After scaling, the appearance does not change, only the dimensions.
- In the second stage, the external dimensions of the ligament were built based on the geometry of the tooth. This scaling allowed the use of the actual dimensions of the ligament and the next step was the modeling of the PDL. For the construction of the ligament, an artifice frequently used in 3D modeling was used. Starting from the shape of the tooth, scaling was applied to obtain a duplicate of the tooth (its shape) at a distance of 0.4 mm from the exterior. For this, the maximum diameter of the tooth was measured in different places. Subsequently, the average value was calculated and the thickness of the ligament was added twice, because it appears on both sides of the tooth. This represented the outer diameter of the ligament. Following this, the ratio between the tooth’s diameter and the ligament’s diameter was made. The value obtained, F2 = 1.023, was used as a scaling factor to obtain the duplicate of the tooth, necessary for the construction of the ligament. In the Catia V5 R20 program, the “scales” function was used. Two parameters are needed for this function: the scale factor, 1.023, and the invariant point of scaling, meaning the scaling center. In our case, the central point of the tooth was chosen. It was built using a line that connected the tip with the apex of the tooth. On this line, the middle of the segment was highlighted and it was selected as an invariant point (reference) for scaling.
- In the last stage, the tooth geometry was displaced from the obtained ligament, and later, the geometry of the ligament was displaced from the mandibular bone.
- The ligaments for the 3 teeth were similar for the two incisors. The thickness of the ligament resulting from this procedure was not constant, but, on average, it was around 0.4 mm. We believe that this approach and construction of the tooth–ligament–bone assembly is the one that best approximates the biological nature of tissues. The obtained periodontal ligaments of the three teeth are illustrated in Figure 7.
- After obtaining the geometric model of the assembly, we performed the finite element analysis to virtually test the response to various requests. The geometric model was discretized, and, with the help of the equations that describe the reunited phenomena in the form of a basic analytical model, the FEA was performed. The module used was Catia V5 R20—Generative Structural Analysis. The basic analytical model consists of a set of equations that describe the phenomenon studied and the behavior of the material under the action of external stresses. To these, boundary conditions were added. The boundary conditions describe the body’s interaction with the environment. When the field sizes are variable over time, the analytical model must also include their initial conditions, meaning their condition at the beginning of the analysis. This analytical model is the basis for the development of the finite element analytical model, and its predictive variables are the basis of the numerical model’s simulation performance. The analytical model must therefore capture this phenomenon of deformation under the action of external forces. It will contain, in this case, the definition relations of the normal unitary effort and the specific deformations. In order to be able to individualize the behavior of a certain material under the action of external loadings, a constitutive or material law must also be included in the analytical model. For us, this is Hooke’s law, which shows that, in the case of an axially stressed solid material, as long as the external forces do not exceed a certain limit (flow limit), the unit forces are directly proportional to the specific deformations. Material properties were assigned to each component of the assembly in order to perform a finite element analysis.
- 6.
- The operating rules for each element were established in the next step. Thus, a fixing constraint (clamp) was established for the fixed body, the mandibular bone. A clamp was used on the mesial side and one on the distal side. The tooth was considered mobile and the Generative Structural Analysis (GSA) module was used to apply a Fastened Connection constraint. For the PDL, a Fastened Connection constraint in the GSA module was also applied. The next step proceeded with the construction of the model for finite element analysis. This was done by applying boundary conditions and establishing fixed surfaces. For this, the Analysis and Simulation/Generative Structural Analysis workbench was opened. Through this module, the 3D model was further discretized and the conditions of demand and degrees of freedom were imposed. For the surfaces that were in contact, boundary conditions were imposed through the General Analysis Connection tool. This is a very powerful tool that can be used to connect any part of an assembly on an overall model, with or without a handling point. This tool allows any type of geometry to be connected, and it is a general way of connecting two components. The Fastened Connection rigid assembly connection tool was used to assign specific characteristics for simulation. Its purpose was to model a fixed connection between two bodies with a common boundary and the association of a geometric assembly constraint, or a General Analysis Connection type connection. Finally, there were 6 connections between the contact surfaces of the following components: central incisor and central incisor ligament; central incisor ligament and bone; lateral incisor and lateral incisor ligament; lateral incisor ligament and bone; canine and canine ligament; canine ligament and bone.
- Size—choosing or changing the size of finite elements;
- Absolute Sag—the absolute value of the deviation from the boundary—meaning the maximum allowed deviation value for approximating the geometry of the model;
- Element Type—the type of the finished element.
3. Results
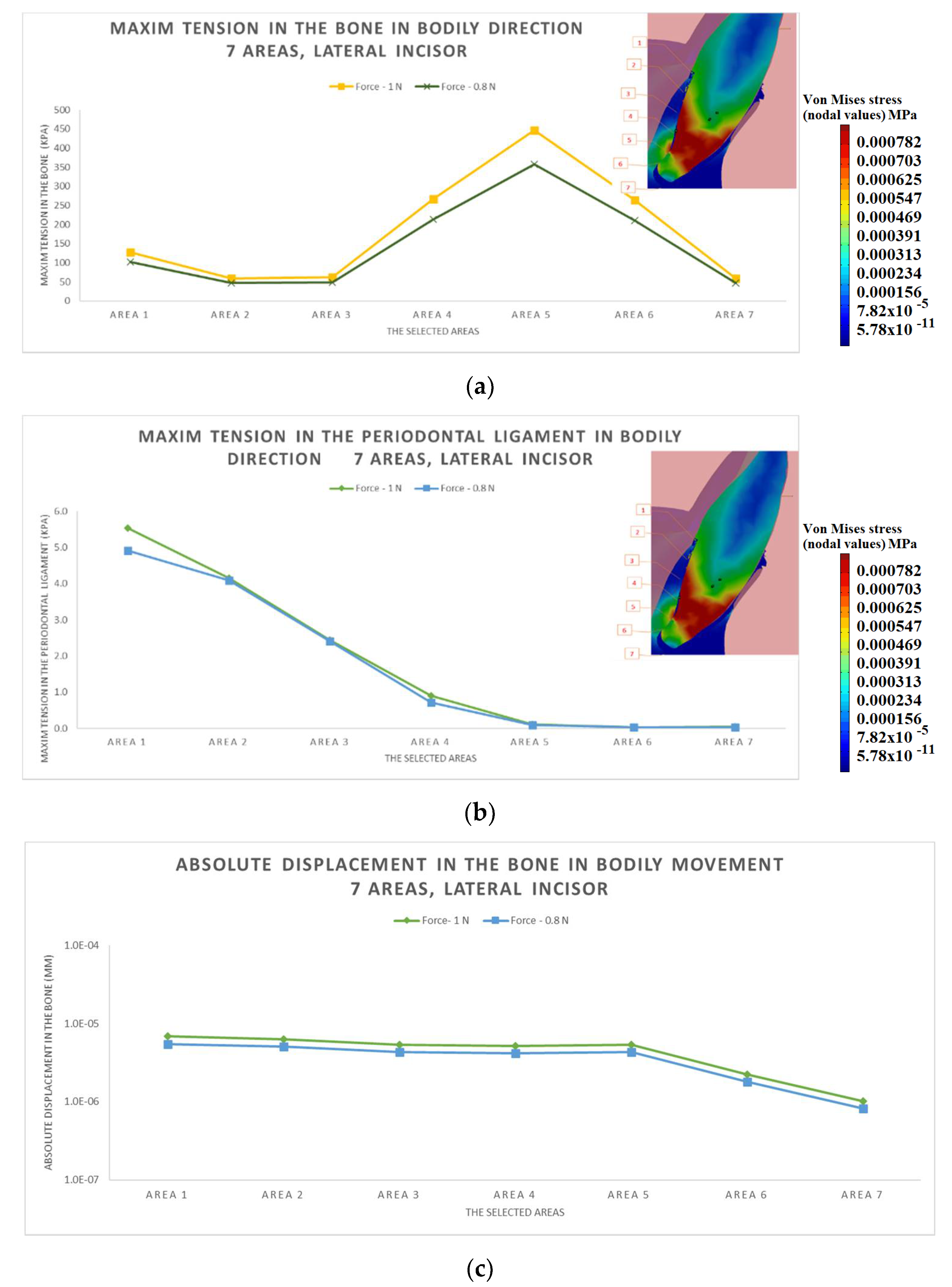
3.1. The Results after Applying the Forces on the Lateral Incisor
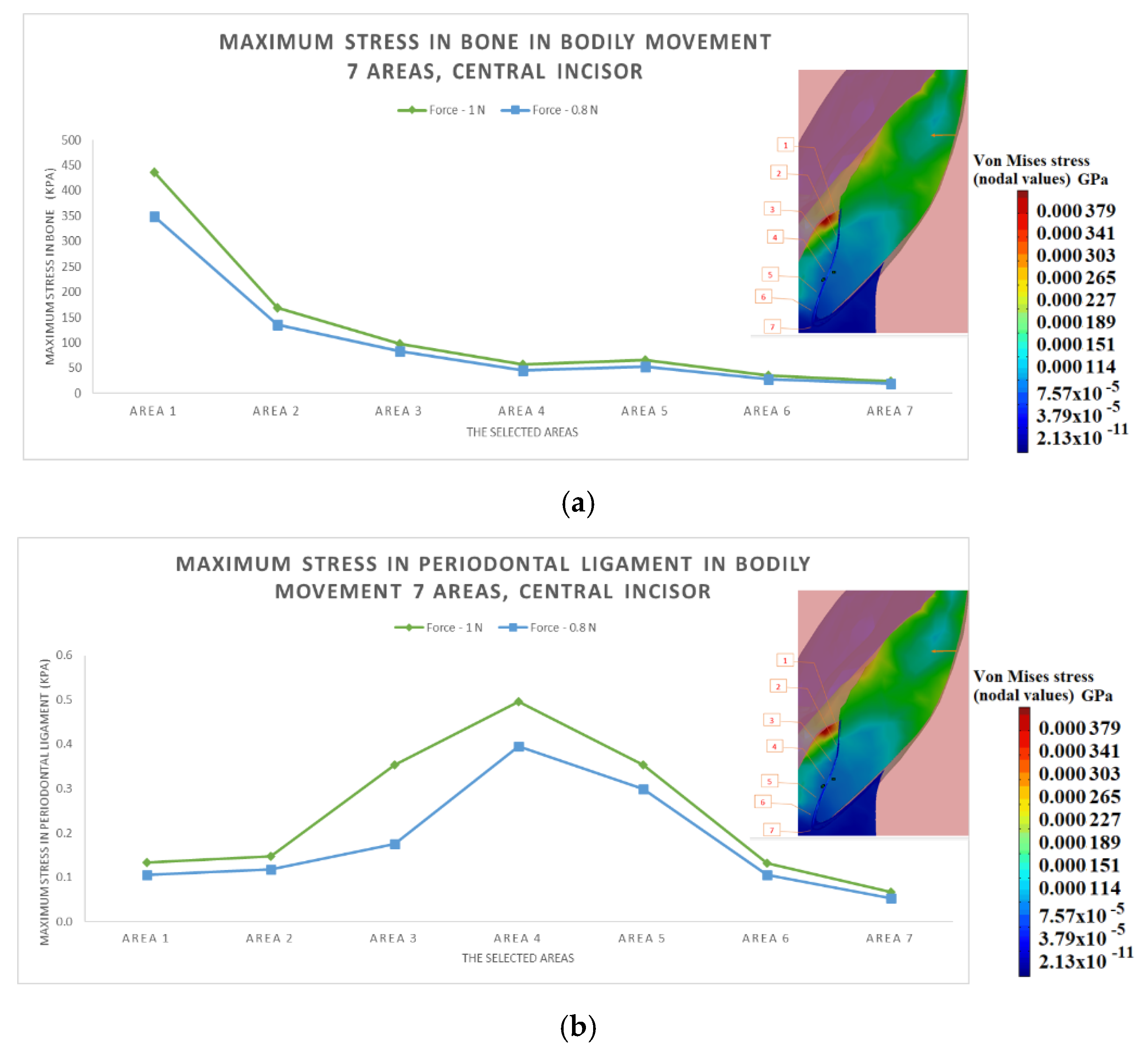
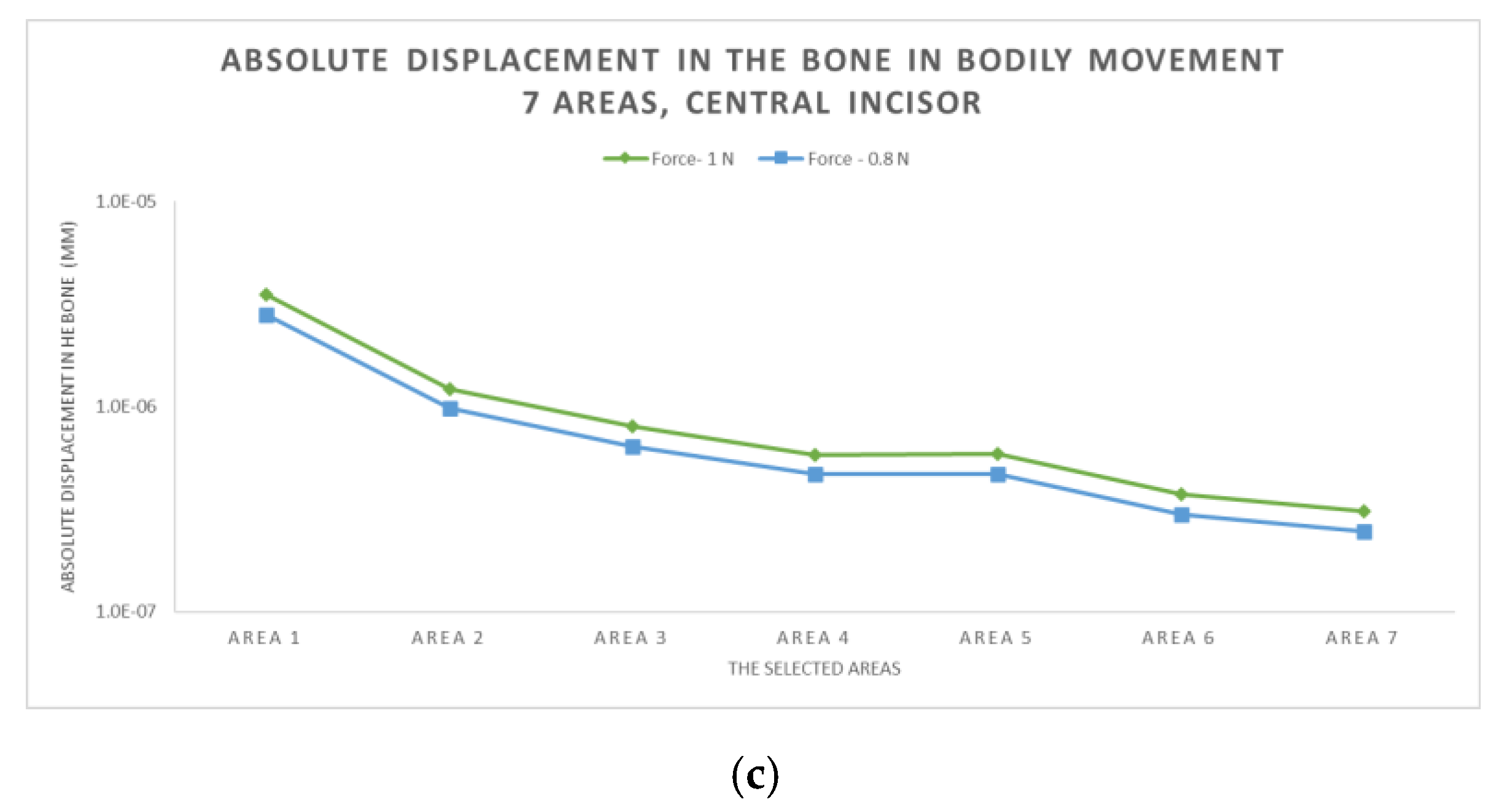
3.2. The Results after Applying the Forces on the Central Incisor
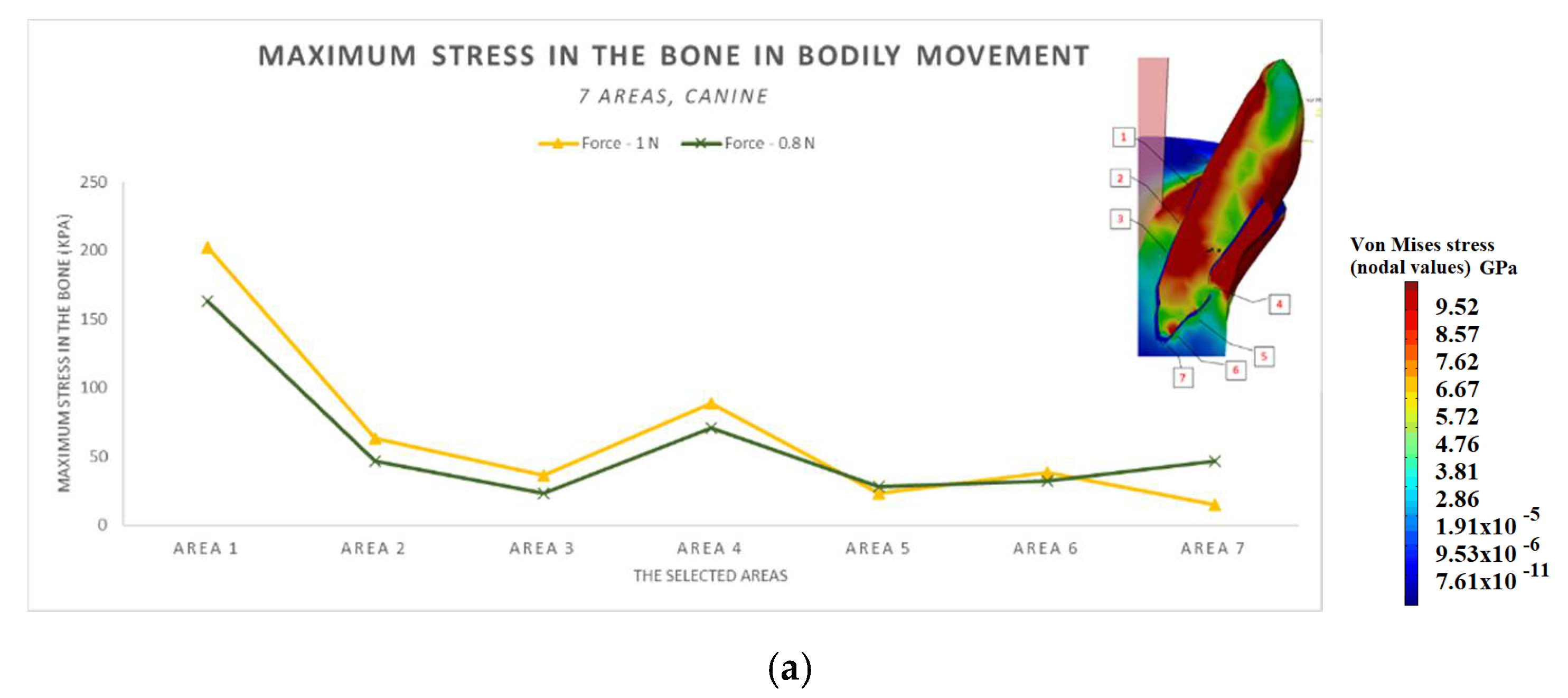
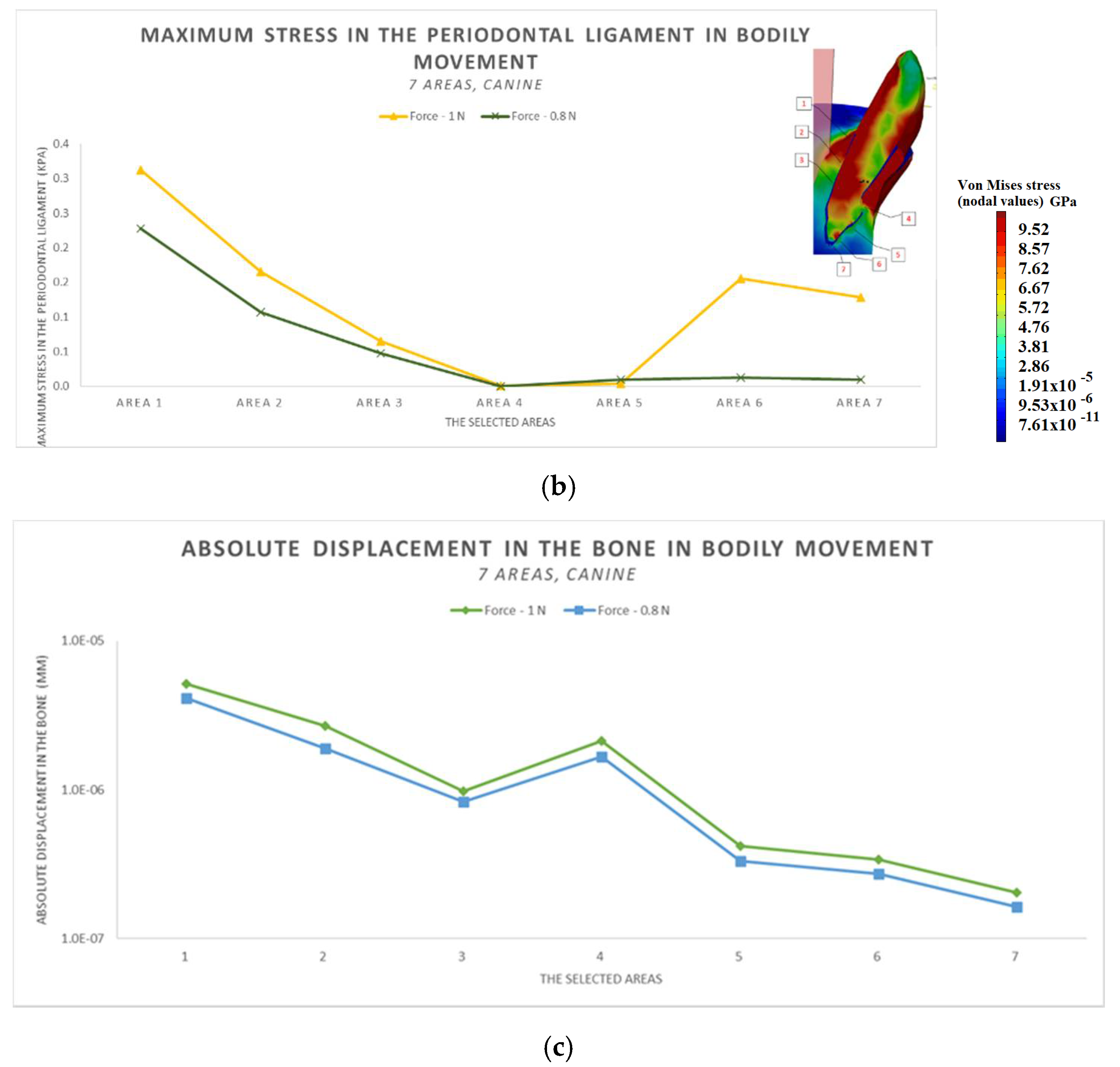
3.3. The Results after Applying the Forces on the Canine
4. Discussion
5. Conclusions
- The difference in increase is much higher at the lateral incisor (approx. 300 KPa), compared to the canine (approximately 100 KPa).
- The difference in increase is explained by the specific mode of action of the force in the two cases. For the lateral incisor, the lever is of degree 2, with the force arm between zone 5 and zone 1; for the canine, the lever is of degree 1, and the arm of force between zone 1 and zone 4.
- Due to the lever configuration, a compression force of the ligament appears in area 6–7 and this causes the PDL’s increase.
- In area 4, the risk of bone resorption due to increased stress is observed, as a result of atypical root anatomy. The minimal ligament thickness in area 4 causes increased displacement of the bone. This occurs as a result of the PDL’s function, which optimizes the transfer of the forces and regulates orthodontic tooth movement.
- The displacement is a bodily movement with tipping.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bramanti, E.; Cervino, G.; Lauritano, F.; Fiorillo, L.; D’Amico, C.; Sambataro, S.; Denaro, D.; Famà, F.; Ierardo, G.; Polimeni, A.; et al. FEM and Von Mises Analysis on Prosthetic Crowns Structural Elements: Evaluation of Different Applied Materials. Sci. World J. 2017, 3. [Google Scholar] [CrossRef]
- Lauritano, F.; Runci, M.; Cervino, G.; Fiorillo, L.; Bramanti, E.; Cicciù, M. Three-dimensional evaluation of different prosthesis retention systems using finite element analysis and the Von Mises stress test. Minerva Stomatol. 2016, 65, 353–367. [Google Scholar]
- Goel, V.K.; Khera, S.C.; Ralson, J.L.; Chang, K.H. Stresses at the dentino-enamel junction of human teeth: A finite element investigation. J. Prosthet. Dent. 1991, 66, 451–459. [Google Scholar] [CrossRef]
- Butnaru-Moldoveanu, S.A.; Munteanu, F.; Forna, N.C. Virtual Bone Augmentation in Atrophic Mandible to Assess Optimal Implant-Prosthetic Rehabilitation—A Finite Element Study. Appl. Sci. 2020, 10, 401. [Google Scholar] [CrossRef]
- Carpegna, G.; Alovisi, M.; Paolino, D.S.; Marchetti, A.; Gibello, U.; Scotti, N.; Pasqualini, D.; Scattina, A.; Chiandussi, G.; Berutti, E. Evaluation of Pressure Distribution against Root Canal Walls of NiTi Rotary Instruments by Finite Element Analysis. Appl. Sci. 2020, 10, 2981. [Google Scholar] [CrossRef]
- Huang, H.-L.; Tsai, M.-T.; Yang, S.-G.; Su, K.-C.; Shen, Y.-W.; Hsu, J.-T. Mandible Integrity and Material Properties of the Periodontal Ligament during Orthodontic Tooth Movement: A Finite-Element Study. Appl. Sci. 2020, 10, 2980. [Google Scholar] [CrossRef]
- Luchian, I.; Moscalu, M.; Martu, I.; Curca, R.; Vata, I.; Stirbu, C.; Tatarciuc, M.; Martu, S. A FEM Study regarding the Predictability of Molar Uprighting Associated with Periodontal Disease. Int. J. Med. Dent. 2018, 22, 183–188. [Google Scholar]
- Krishnan, V.; Davidovitch, Z. Cellular, molecular, and tissue-level reactions to orthodontic force. Am. J. Orthod. Dentofac. Orthop. 2006, 129, 469.e1–469.e32. [Google Scholar] [CrossRef] [PubMed]
- Theerasopon, P.; Kosuwan, W.; Charoemratrote, C. Stress assessment of mandibular incisor intrusion during initial leveling in continuous arch system with different archwire shapes of superelastic nickel-titanium: A three-dimensional finite element study. Int. J. Health Allied Sci. 2019, 8, 92–97. [Google Scholar]
- Nishihira, M.; Yamamoto, K.; Sato, Y.; Ishikawa, H.; Natali, A.N. Mechanics of periodontal ligament. Dental Biomech. 2003, 20–34. [Google Scholar] [CrossRef]
- Dorow, C.; Krstin, N.; Sander, F.G. Experiments to determine the material properties of the periodontal ligament. J. Orofac. Orthop. 2002, 63, 94–104. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.; Lapatki, B.G. Effect of variable periodontal ligament thickness and its non-linear material properties on the location of a tooth’s centre of resistance. J. Biomech. 2019, 94, 211–218. [Google Scholar] [CrossRef]
- Xia, Z.; Jiang, F.; Chen, J. Estimation of periodontal ligament’s equivalent mechanical parameters for finite element modeling. Am. J. Orthod. Dentofac. Orthop. 2013, 143, 486–491. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.R.; Kambalyal, P.; Jain, M.; Khandelwal, P. Revolution in Orthodontics: Finite element analysis. J. Int. Soc. Prev. Community Dent. 2016, 6, 110–114. [Google Scholar] [CrossRef]
- Li, Y.; Jacox, L.A.; Little, S.H.; Ko, C.C. Orthodontic tooth movement: The biology and clinical implications. Kaohsiung J. Med. Sci. 2018, 34, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Sameshima, G.T.; Sinclair, P.M. Predicting and preventing root resorption: Part I. Diagnostic factors. Am. J. Orthod. Dentofac. 2001, 119, 505–510. [Google Scholar] [CrossRef]
- Jung, Y.H.; Cho, B.H. External root resorption after orthodontic treatment: A study of contributing factors. Imaging Sci. Dent. 2011, 41, 17–21. [Google Scholar] [CrossRef]
- Nakamura, N.; Ito, A.; Kimura, T.; Kishida, A. Extracellular Matrix Induces Periodontal Ligament Reconstruction In Vivo. Int. J. Mol. Sci. 2019, 20, 3277. [Google Scholar] [CrossRef]
- Jing, Y.; Han, X.; Cheng, B.; Bai, D. Three-dimensional FEM analysis of stress distribution in dynamic maxillary canine movement. Sci. Bull. 2013, 58, 2454–2459. [Google Scholar] [CrossRef]
- Calniceanu, H.; Stratul, S.; Rusu, D.; Jianu, A.; Boariu, M.; Nica, L.; Ogodescu, A.; Sima, L.; Bolintineanu, S.; Anghel, A.; et al. Changes in clinical and microbiological parameters of the periodontium during initial stages of orthodontic movement in patients with treated severe periodontitis: A longitudinal site-level analysis. Exp. Ther. Med. 2020, 6, 199. [Google Scholar] [CrossRef]
- Machoy, M.; Szyszka-Sommerfeld, L.; Koprowski, R.; Wawrzyk, A.; Woźniak, K.; Wilczyński, S. Assessment of Periodontium Temperature Changes under Orthodontic Force by Using Objective and Automatic Classifier. Appl. Sci. 2021, 11, 2634. [Google Scholar] [CrossRef]
- Sioustis, I.-A.; Martu, M.-A.; Aminov, L.; Pavel, M.; Cianga, P.; Kappenberg-Nitescu, D.C.; Luchian, I.; Solomon, S.M.; Martu, S. Salivary Metalloproteinase-8 and Metalloproteinase-9 Evaluation in Patients Undergoing Fixed Orthodontic Treatment before and after Periodontal Therapy. Int. J. Environ. Res. Public Health 2021, 18, 1583. [Google Scholar] [CrossRef]
- Rasperini, G.; Acunzo, R.; Cannalire, P.; Farronato, G. Influence of Periodontal Biotype on Root Surface Exposure During Orthodontic Treatment: A Preliminary Study. Int. J. Periodontics Restor. Dent. 2015, 35, 655–675. [Google Scholar] [CrossRef]
- Gorbunkova, A.; Pagni, G.; Brizhak, A.; Farronato, G.; Rasperini, G. Impact of Orthodontic Treatment on Periodontal Tissues: A Narrative Review of Multidisciplinary Literature. Int. J. Dent. 2016, 4723589. [Google Scholar] [CrossRef] [PubMed]
- Abuabara, A. Biomechanical aspects of external root resorption in orthodontic therapy. Med. Oral Patol. Oral Cirugía Bucal 2007, 12, 610–613. [Google Scholar]
- Albandar, J.M. Global risk factors and risk indicators for periodontal diseases. Periodontology 2000 2002, 29, 177–206. [Google Scholar] [CrossRef]
- Wehrbein, H.; Bauer, W.; Diedrich, P. Mandibular incisors, alveolar bone and symphysis after orthodontic treatment: A retrospective study. Am. J. Orthod. Dentofac. Orthop. 1996, 110, 239–246. [Google Scholar] [CrossRef]
- Swasty, D.; Lee, J.S.; Huang, J.C.; Maki, K.; Gansky, S.A.; Hatcher, D.; Miller, A.J. Anthropometric analysis of the human mandibular cortical bone as assessed by cone-beam computed tomography. J. Oral Maxillofac. Surg. 2009, 67, 491–500. [Google Scholar] [CrossRef]
- Vasconcelos, G.; Kjellsen, K.; Preus, H.; Vandevska-Radunovic, V.; Hansen, B.F. Prevalence and severity of vestibular recession in mandibular incisors after orthodontic treatment: A case-control retrospective study. Angle Orthod. 2012, 82, 42–47. [Google Scholar] [CrossRef]

| Material | Young’s Modulus | Poisson’s Ratio |
|---|---|---|
| PDL | 7.1 × 10-4 GPa [13] | 0.4 |
| Bone | 140 GPa [14] | 0.3 |
| Tooth | 20.3 GPa [14] | 0.3 |
| Element | Size (mm) | Absolute Sag (mm) | El. Type |
|---|---|---|---|
| Bone | 0.8 | 0.5 | Linear tetrahedral |
| PDL central incisor | 0.3 | 0.1 | Linear tetrahedral |
| Central incisor | 1.272 | 0.203 | Linear tetrahedral |
| PDL lateral incisor | 0.3 | 0.1 | Linear tetrahedral |
| Lateral incisor | 1.313 | 0.21 | Linear tetrahedral |
| PDL canine | 0.3 | 0.1 | Linear tetrahedral |
| Canine | 1.484 | 0.237 | Linear tetrahedral |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sioustis, I.-A.; Axinte, M.; Prelipceanu, M.; Martu, A.; Kappenberg-Nitescu, D.-C.; Teslaru, S.; Luchian, I.; Solomon, S.M.; Cimpoesu, N.; Martu, S. Finite Element Analysis of Mandibular Anterior Teeth with Healthy, but Reduced Periodontium. Appl. Sci. 2021, 11, 3824. https://doi.org/10.3390/app11093824
Sioustis I-A, Axinte M, Prelipceanu M, Martu A, Kappenberg-Nitescu D-C, Teslaru S, Luchian I, Solomon SM, Cimpoesu N, Martu S. Finite Element Analysis of Mandibular Anterior Teeth with Healthy, but Reduced Periodontium. Applied Sciences. 2021; 11(9):3824. https://doi.org/10.3390/app11093824
Chicago/Turabian StyleSioustis, Ioana-Andreea, Mihai Axinte, Marius Prelipceanu, Alexandra Martu, Diana-Cristala Kappenberg-Nitescu, Silvia Teslaru, Ionut Luchian, Sorina Mihaela Solomon, Nicanor Cimpoesu, and Silvia Martu. 2021. "Finite Element Analysis of Mandibular Anterior Teeth with Healthy, but Reduced Periodontium" Applied Sciences 11, no. 9: 3824. https://doi.org/10.3390/app11093824
APA StyleSioustis, I.-A., Axinte, M., Prelipceanu, M., Martu, A., Kappenberg-Nitescu, D.-C., Teslaru, S., Luchian, I., Solomon, S. M., Cimpoesu, N., & Martu, S. (2021). Finite Element Analysis of Mandibular Anterior Teeth with Healthy, but Reduced Periodontium. Applied Sciences, 11(9), 3824. https://doi.org/10.3390/app11093824











