Intelligent Scheduling with Reinforcement Learning
Abstract
1. Introduction
2. Literature Review
2.1. Scheduling Problems
- Flow shop—All tasks are the same, making all operations have a uniform order of passage through the machines. The tasks are always executed in a specific order, requiring only the decision of the start of each operation’s production.
- Job Shop—Each task has its own specific operations, thus allowing the existence of different tasks. The operations of each task have a predefined order that must be respected. The order of the operations can be different from task to task.
- Open Shop—There are no ordering constraints, i.e., each operation of a task can be executed on any machine at any time.
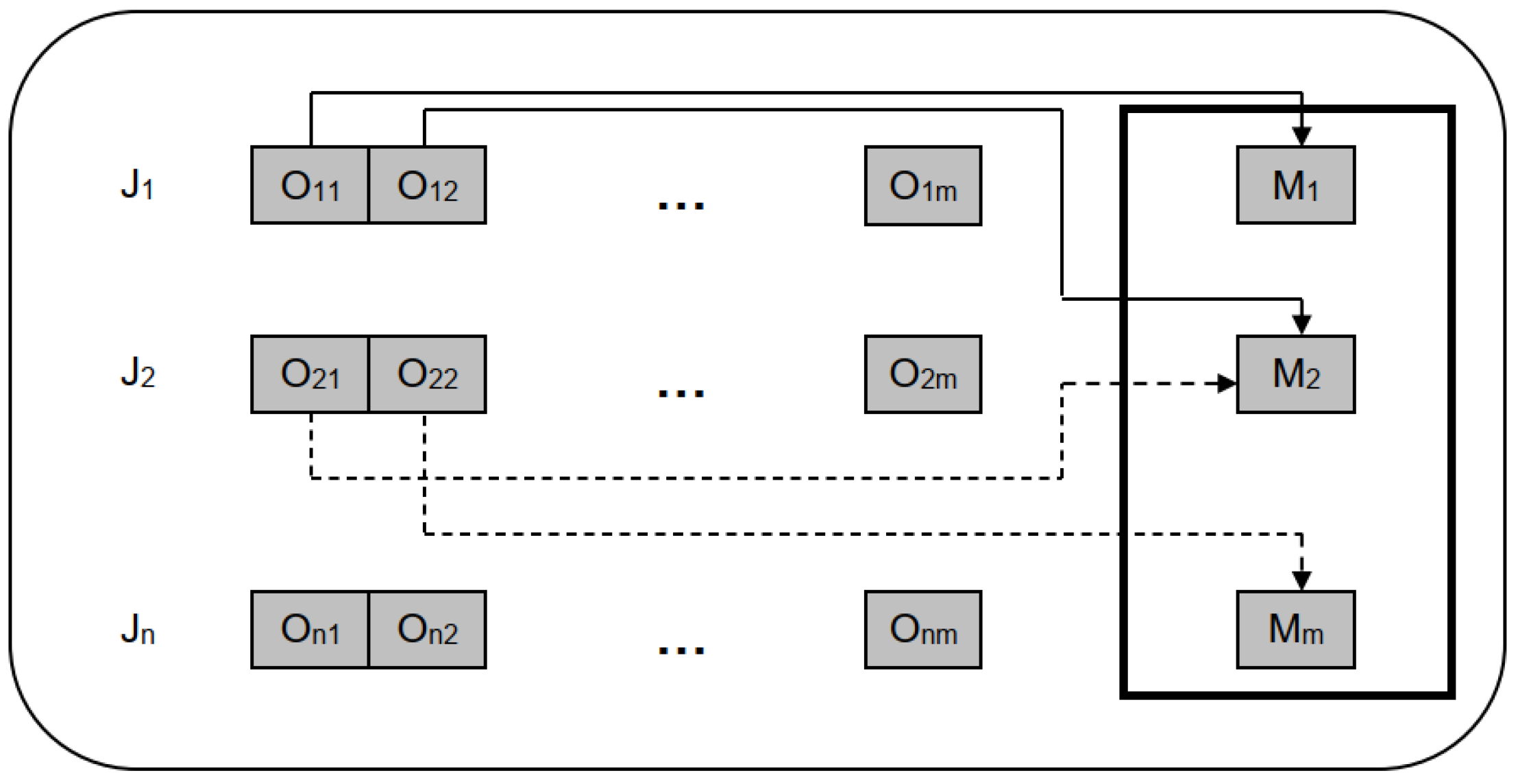
2.2. Job Shop Problem
- Date of completion
- greatest delay;
- sum of delays and advances (tasks completed ahead of schedule);
- total number of tardy jobs.
- Travel time
- (task) travel time;
- average travel time;
- maximum travel time;
- System usage
- machine usage;
- system usage, i.e., average utilization of each machine.
2.3. Machine Learning
2.4. Reinforcement Learning
3. Problem Formulation
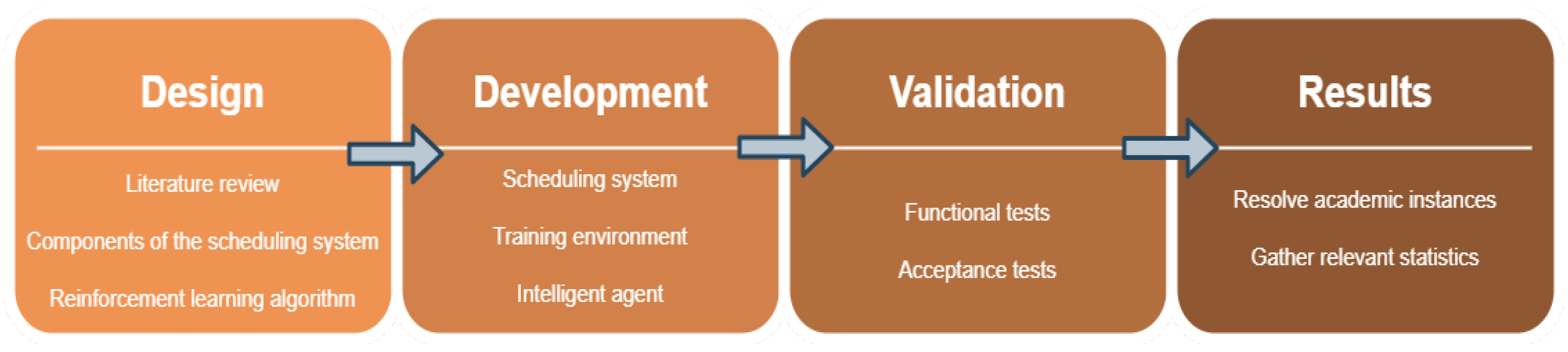
4. Scheduling System with Reinforcement Learning
4.1. Methodology
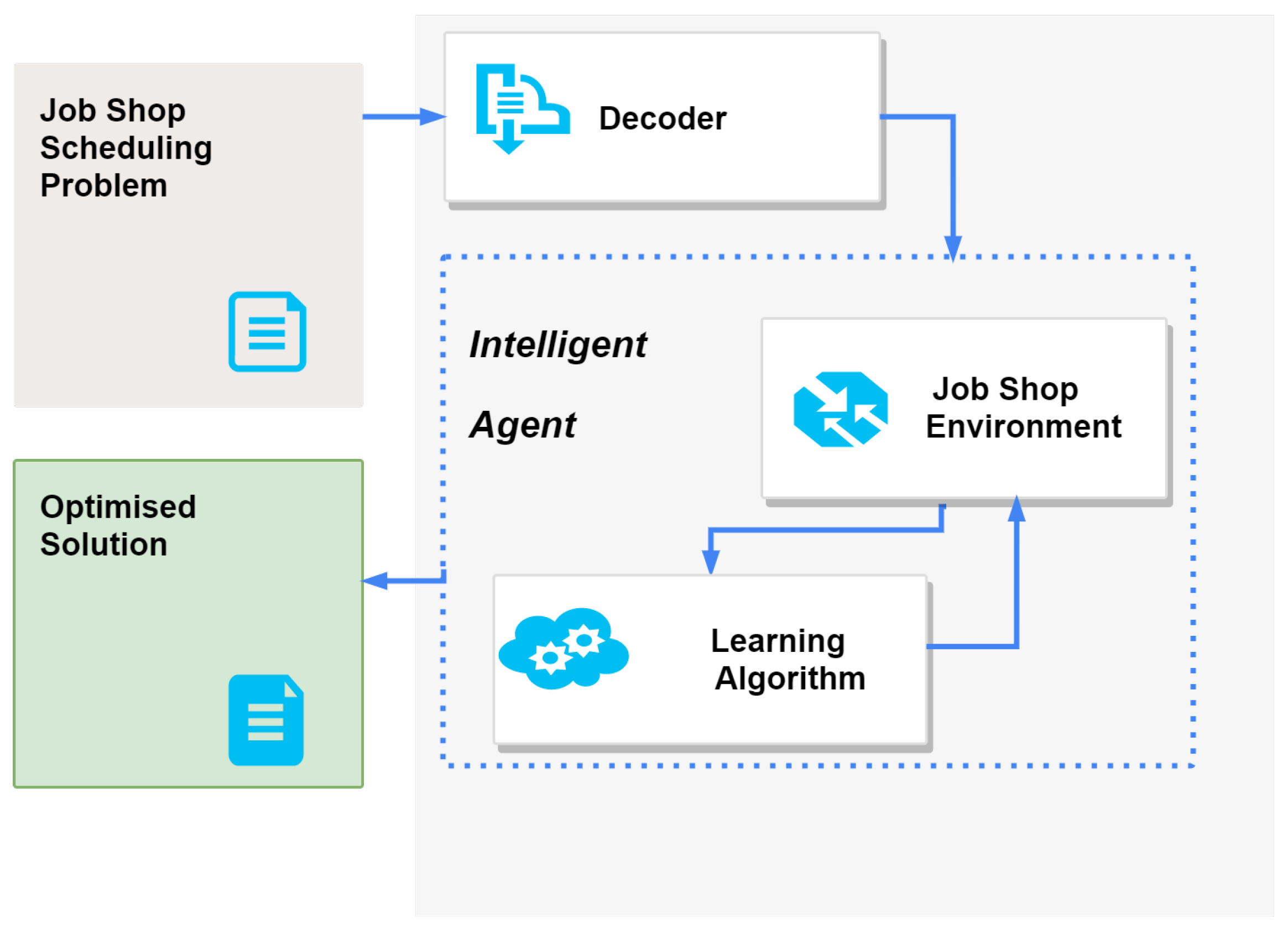
4.2. Proposed Architecture
5. Computational Study
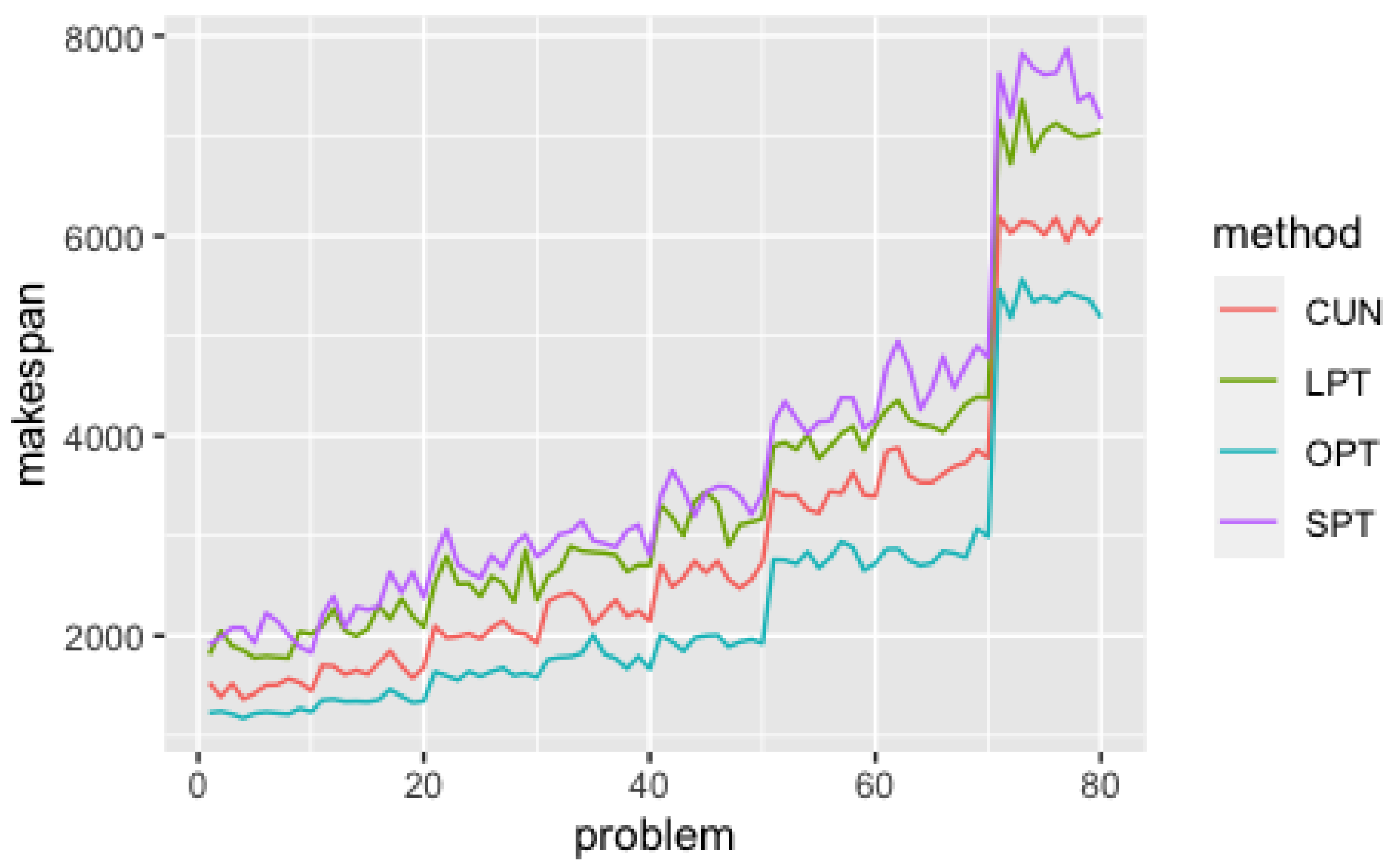
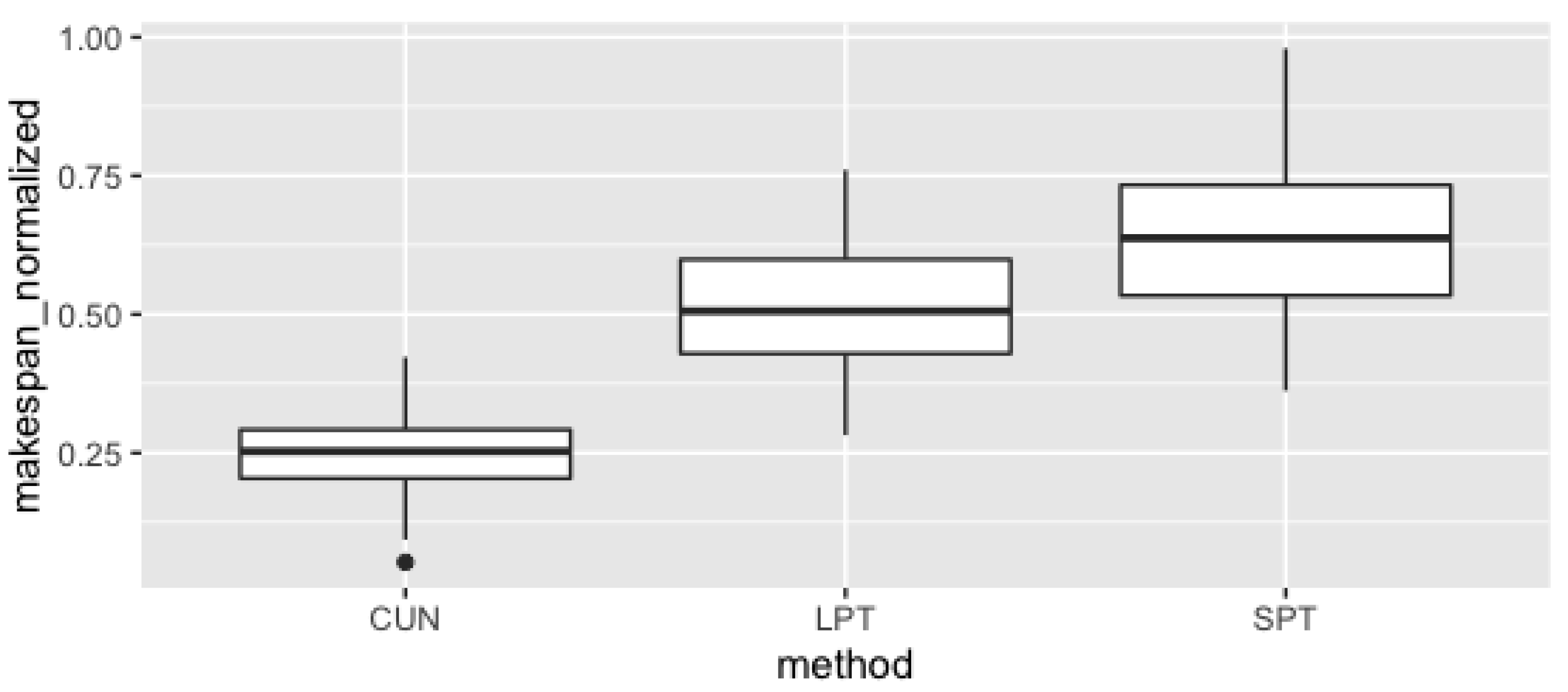
5.1. Efficiency Analysis
5.2. Quality of Solutions Analysis
5.3. Discussion of Results
6. Conclusions
- Modeling the Job Shop category scheduling problem into a reinforcement learning problem by adapting the Markov process, covering how rewards are calculated, the possible set of states and the achievement of an agent’s goals or the set of available actions.
- Design and implementation of training environment for reinforcement learning algorithms to create intelligent agents capable of solving the category Job Shop scheduling problem.
- Implementation of the complete scheduling system, composed of the artificial intelligence module, which includes the intelligent agent and the training environment used during learning, and the scheduling module, which establishes all the rules of the problem, supports the decoding of academic instances and ensures the correct definition of all the components of the problem: machines, tasks and operations.
- Execution of a computational study for the analysis and validation of the results obtained by the intelligent agent developed in this work, which analyzes the performance, in efficiency and effectiveness, using measurements of the runtimes of the approaches studied and the quality of the solutions obtained, respectively.
Author Contributions
Funding
Conflicts of Interest
References
- Brynjolfsson, E.; Hitt, L.M. Beyond computation: Information technology, organizational transformation and business performance. J. Econ. Perspect. 2000, 14, 23–48. [Google Scholar] [CrossRef]
- Cunha, B.; Madureira, A.M.; Fonseca, B.; Coelho, D. Deep Reinforcement Learning as a Job Shop Scheduling Solver: A Literature Review. In Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2020; pp. 350–359. [Google Scholar]
- Pinedo, M.L. Scheduling: Theory, Algorithms, and Systems, 5th ed.; Springer: Berlin Heidelberg, Germany, 2016; pp. 1–670. [Google Scholar] [CrossRef]
- Zhang, J.; Ding, G.; Zou, Y.; Qin, S.; Fu, J. Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 2019, 30, 1809–1830. [Google Scholar] [CrossRef]
- Madureira, A.; Pereira, I.; Falcão, D. Dynamic Adaptation for Scheduling Under Rush Manufacturing Orders With Case-Based Reasoning. In Proceedings of the International Conference on Algebraic and Symbolic Computation (SYMCOMP), Lisbon, Portugal, 9–10 September 2013. [Google Scholar]
- Villa, A.; Taurino, T. Event-driven production scheduling in SME. Prod. Plan. Control 2018, 29, 271–279. [Google Scholar] [CrossRef]
- Duplakova, D.; Teliskova, M.; Duplak, J.; Torok, J.; Hatala, M.; Steranka, J.; Radchenko, S. Determination of optimal production process using scheduling and simulation software. Int. J. Simul. Model. 2018, 17, 609–622. [Google Scholar] [CrossRef]
- Balog, M.; Dupláková, D.; Szilágyi, E.; Mindaš, M.; Knapcikova, L. Optimization of time structures in manufacturing management by using scheduling software Lekin. TEM J. 2016, 5, 319. [Google Scholar]
- Sun, X.; Wang, Y.; Kang, H.; Shen, Y.; Chen, Q.; Wang, D. Modified Multi-Crossover Operator NSGA-III for Solving Low Carbon Flexible Job Shop Scheduling Problem. Processes 2021, 9, 62. [Google Scholar] [CrossRef]
- Dupláková, D.; Telišková, M.; Török, J.; Paulišin, D.; Birčák, J. Application of simulation software in the production process of milled parts. SAR J. 2018, 1, 42–46. [Google Scholar]
- Madureira, A. Aplicação de Meta-Heurísticas ao Problema de Escalonamento em Ambiente Dinâmico de Produção Discreta. Ph.D. Thesis, Tese de Doutoramento, Universidade do Minho, Braga, Portugal, 2003. [Google Scholar]
- Gonzalez, T. Unit execution time shop problems. Math. Oper. Res. 1982, 7, 57–66. [Google Scholar] [CrossRef]
- Rand, G.K.; French, S. Sequencing and Scheduling: An Introduction to the Mathematics of the Job-Shop. J. Oper. Res. Soc. 1982, 13, 94–96. [Google Scholar] [CrossRef]
- Brucker, P. Job-shop scheduling problemJob-shop Scheduling Problem. In Encyclopedia of Optimization; Floudas, C.A., Pardalos, P.M., Eds.; Springer: Boston, MA, USA, 2009; pp. 1782–1788. [Google Scholar] [CrossRef]
- Beirão, N. Sistema de Apoio à Decisão para Sequenciamento de Operações em Ambientes Job Shop. Master’s Thesis, Faculdade de Engenharia da Universidade do Porto, Porto, Portugal, 1997. [Google Scholar]
- Cook, S.A. The complexity of theorem-proving procedures. In Proceedings of the third Annual ACM Symposium on Theory of Computing, Shaker Heights, OH, USA, 3–5 May 1971; pp. 151–158. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Yamada, T.; Yamada, T.; Nakano, R. Genetic Algorithms for Job-Shop Scheduling Problems. In Proceedings of the Modern Heuristi for Decision Support, London, UK, 18–19 March 1997; pp. 474–479. [Google Scholar]
- Madureira, A.; Cunha, B.; Pereira, J.P.; Pereira, I.; Gomes, S. An Architecture for User Modeling on Intelligent and Adaptive Scheduling Systems. In Proceedings of the Sixth World Congress on Nature and Biologically Inspired Computing (NaBIC), Porto, Portugal, 30 July–1 August 2014. [Google Scholar]
- Wang, H.; Sarker, B.R.; Li, J.; Li, J. Adaptive scheduling for assembly job shop with uncertain assembly times based on dual Q-learning. Int. J. Prod. Res. 2020, 1–17. [Google Scholar] [CrossRef]
- Ojstersek, R.; Tang, M.; Buchmeister, B. Due date optimization in multi-objective scheduling of flexible job shop production. Adv. Prod. Eng. Manag. 2020, 15. [Google Scholar] [CrossRef]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Mitchell, T.M. Machine Learning; McGraw-Hill, Inc.: New York, NY, USA, 1997; Volume 4, pp. 417–433. [Google Scholar] [CrossRef]
- Cascio, D.; Taormina, V.; Raso, G. Deep CNN for IIF Images Classification in Autoimmune Diagnostics. Appl. Sci. 2019, 9, 1618. [Google Scholar] [CrossRef]
- Cascio, D.; Taormina, V.; Raso, G. Deep Convolutional Neural Network for HEp-2 Fluorescence Intensity Classification. Appl. Sci. 2019, 9, 408. [Google Scholar] [CrossRef]
- Joshi, A.V. Machine Learning and Artificial Intelligence; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Burkov, A. The Hundred-Page Machine Learning Book; CHaleyBooks: Muncie, IN, USA, 2019; p. 141. [Google Scholar]
- Everitt, B. Cluster analysis. Qual. Quant. 1980, 14, 75–100. [Google Scholar] [CrossRef]
- Zimek, A.; Schubert, E. Outlier Detection. In Encyclopedia of Database Systems; Springe: New York, NY, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Scudder, H. Probability of error of some adaptive pattern-recognition machines. IEEE Trans. Inf. Theory 1965, 11, 363–371. [Google Scholar] [CrossRef]
- McClosky, D.; Charniak, E.; Johnson, M. Effective self-training for parsing. In Proceedings of the HLT-NAACL 2006—Human Language Technology Conference of the North American Chapter of the Association of Computational Linguistics, New York, NY, USA, 4–9 June 2006. [Google Scholar] [CrossRef]
- Yarowsky, D. Unsupervised word sense disambiguation rivaling supervised methods. In Proceedings of the 33rd Annual Meeting of the Association for Computational Linguistics, Cambridge, MA, USA, 26–30 June 1995; pp. 189–196. [Google Scholar] [CrossRef]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the Annual ACM Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Thorndike, E.L. The Law of Effect. Am. J. Psychol. 1927, 39, 212–222. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Akkaya, I.; Andrychowicz, M.; Chociej, M.; Litwin, M.; McGrew, B.; Petron, A.; Paino, A.; Plappert, M.; Powell, G.; Ribas, R.; et al. Solving Rubik’s Cube with a Robot Hand. arXiv 2019, arXiv:1910.07113. [Google Scholar]
- Nagabandi, A.; Konoglie, K.; Levine, S.; Kumar, V. Deep Dynamics Models for Learning Dexterous Manipulation. arXiv 2019, arXiv:1909.11652. [Google Scholar]
- Wu, J.; Wei, Z.; Liu, K.; Quan, Z.; Li, Y. Battery-Involved Energy Management for Hybrid Electric Bus Based on Expert-Assistance Deep Deterministic Policy Gradient Algorithm. IEEE Trans. Veh. Technol. 2020, 69, 12786–12796. [Google Scholar] [CrossRef]
- Wu, J.; Wei, Z.; Li, W.; Wang, Y.; Li, Y.; Sauer, D.U. Battery Thermal- and Health-Constrained Energy Management for Hybrid Electric Bus Based on Soft Actor-Critic DRL Algorithm. IEEE Trans. Ind. Inform. 2021, 17, 3751–3761. [Google Scholar] [CrossRef]
- Kaplan, R.; Sauer, C.; Sosa, A. Beating Atari with Natural Language Guided Reinforcement Learning. arXiv 2017, arXiv:1704.05539. [Google Scholar]
- Salimans, T.; Chen, R. Learning Montezuma’s Revenge from a Single Demonstration. arXiv 2018, arXiv:1812.03381. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning (ICML-15), Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
- Sutton, R.S. Reinforcement Learning: Past, Present and Future. In Simulated Evolution and Learning; McKay, B., Yao, X., Newton, C.S., Kim, J.H., Furuhashi, T., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 195–197. [Google Scholar]
- Zhang, T.; Xie, S.; Rose, O. Real-time job shop scheduling based on simulation and Markov decision processes. In Proceedings of the Winter Simulation Conference, Las Vegas, NV, USA, 3–6 December 2017; pp. 3899–3907. [Google Scholar] [CrossRef]
- van Hoorn, J.J. The Current state of bounds on benchmark instances of the job-shop scheduling problem. J. Sched. 2018, 21, 127–128. [Google Scholar] [CrossRef]
- Cunha, B.; Madureira, A.; Fonseca, B. Reinforcement Learning Environment for Job Shop Scheduling Problems. Int. J. Comput. Inf. Syst. Ind. Mana. Appl. 2020, 12, 231–238. [Google Scholar]
- Sommerville, I. Software Engineering, 9th ed.; Addison Wesley: Boston, MA, USA, 2011; ISBN 0137035152. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Taillard, E. Benchmarks for basic scheduling problems. Eur. J. Oper. Res. 1993, 64, 278–285. [Google Scholar] [CrossRef]
- Gamma, E.; Helm, R.; Johnson, R.; Vlissides, J. Design Patterns: Elements of Reusable Software; Addison-Wesley Professional Computing Series; Pearson Education: London, UK, 1996. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python, Scikit-learn, and TensorFlow 2; Packt Publishing Ltd.: Birmingham, UK, 2019. [Google Scholar]
- Jouppi, N. Google supercharges machine learning tasks with TPU custom chip. Google Blog May 2016, 18, 1. [Google Scholar]
- Zhang, C.Y.; Li, P.; Rao, Y.; Guan, Z. A Very Fast TS/SA Algorithm for the Job Shop Scheduling Problem. Comput. Oper. Res. 2008, 35, 282–294. [Google Scholar] [CrossRef]
- Peng, B.; Lü, Z.; Cheng, T.C.E. A tabu search/path relinking algorithm to solve the job shop scheduling problem. Comput. Oper. Res. 2015, 53, 154–164. [Google Scholar] [CrossRef]
- paul Watson, J.; Howe, A.E.; Whitley, L.D. Deconstructing Nowicki and Smutnicki’s i-TSAB Tabu Search Algorithm for the Job-Shop Scheduling Problem. Comput. Oper. Res. 2005, 33, 2623–2644. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Shylo, O.V. An Algorithm for the Job Shop Scheduling Problem based on Global Equilibrium Search Techniques. Comput. Manag. Sci. 2006, 3, 331–348. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]
- Nemenyi, P. Distribution-Free Multiple Comparisons. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1963. [Google Scholar]
- Vilím, P.; Laborie, P.; Shaw, P. Failure-Directed Search for Constraint-Based Scheduling. In International Conference on AI and OR Techniques in Constriant Programming for Combinatorial Optimization Problems; Springer: Barcelona, Spain, 2015; pp. 437–453. [Google Scholar]
- Siala, M.; Artigues, C.; Hebrard, E. Two Clause Learning Approaches for Disjunctive Scheduling. In Principles and Practice of Constraint Programming; Pesant, G., Ed.; Springer: Cham, Switzerland, 2015; pp. 393–402. [Google Scholar]


| Zhang | Peng | CUN | SPT | |
|---|---|---|---|---|
| Peng | - | - | - | |
| CUN | - | - | ||
| SPT | - | |||
| LPT | < |
| CUN | LPT | |
|---|---|---|
| LPT | - | |
| SPT | < |
Short Biography of Authors
 | Bruno Cunha is a professor at the Institute of Engineering–Polytechnic of Porto (ISEP/P.PORTO) and a researcher of the Interdisciplinary Studies Research Center (ISRC). He received his degree in informatics engineering in 2013 and master’s degree of computer science in knowledge-based and decision support technologies in 2015 from the Institute of Engineering–Polytechnic of Porto (ISEP/P.PORTO), and the PhD degree in informatics, in 2021, from the University of Trás-os-Montes and Alto Douro (UTAD). His research interests involve machine learning, optimization algorithms and computational intelligence. |
 | Ana Madureira was born in Mozambique, in 1969. She got his BSc degree in Computer Engineering in 1993 from ISEP, Master degree in Electrical and Computers Engineering–Industrial Informatics, in 1996, from FEUP, and the PhD degree in Production and Systems, in 2003, from University of Minho, Portugal. She became IEEE Senior Member in 2010. She had been Chair of IEEE Portugal Section (2015–2017), Vice-chair of IEEE Portugal Section (2011–2014) and Chair/Vice-Chair of IEEE-CIS Portuguese chapter. She was Chair of University Department of IEEE R8 Educational Activities Sub-Committee (2017–2018). She is IEEE R8 Secretary (2019–2021). She is External Member Evaluation Committee of the Agency for Assessment and Accreditation of Higher Education—A3ES for the scientific area of Informatics of Polytechnic Higher Education (since 2012). Currently she is Coordinator Professor at the Institute of Engineering–Polytechnic of Porto (ISEP/P.PORTO) and Director of the Interdisciplinary Studies Research Center (ISRC). In the last few years, she was author of more than 100 scientific papers in scientific conference proceedings, journals and books. |
 | Benjamim Fonseca is an Associate Professor with Habilitation at the University of Trás-os-Montes and Alto Douro (UTAD) and researcher at INESC TEC, in Portugal. His main research and development interests are collaborative systems, mobile accessibility and immersive systems. He authored or co-authored over a hundred publications in these fields, in several international journals, books and conference proceedings, and participates in the review and organization of various scientific publications and events. He is also co-founder and CEO of 4ALL Software, UTAD’s spin-off that works in the development of innovative software, implementing complex digital platforms and interactive solutions. |
 | João Matos is an Associate Professor at ISEP and researcher at LEMA in Porto, Portugal. He got his BSc degree in Applied Mathematics in 2005 from University of Porto, and the PhD degree in Applied Mathematics in 2015 from University of Porto. His main research interests are approximation theory, orthogonal polynomials, spectral methods and image processing. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cunha, B.; Madureira, A.; Fonseca, B.; Matos, J. Intelligent Scheduling with Reinforcement Learning. Appl. Sci. 2021, 11, 3710. https://doi.org/10.3390/app11083710
Cunha B, Madureira A, Fonseca B, Matos J. Intelligent Scheduling with Reinforcement Learning. Applied Sciences. 2021; 11(8):3710. https://doi.org/10.3390/app11083710
Chicago/Turabian StyleCunha, Bruno, Ana Madureira, Benjamim Fonseca, and João Matos. 2021. "Intelligent Scheduling with Reinforcement Learning" Applied Sciences 11, no. 8: 3710. https://doi.org/10.3390/app11083710
APA StyleCunha, B., Madureira, A., Fonseca, B., & Matos, J. (2021). Intelligent Scheduling with Reinforcement Learning. Applied Sciences, 11(8), 3710. https://doi.org/10.3390/app11083710









