A Review on Tailoring Stiffness in Compliant Systems, via Removing Material: Cellular Materials and Topology Optimization
Abstract
1. Introduction
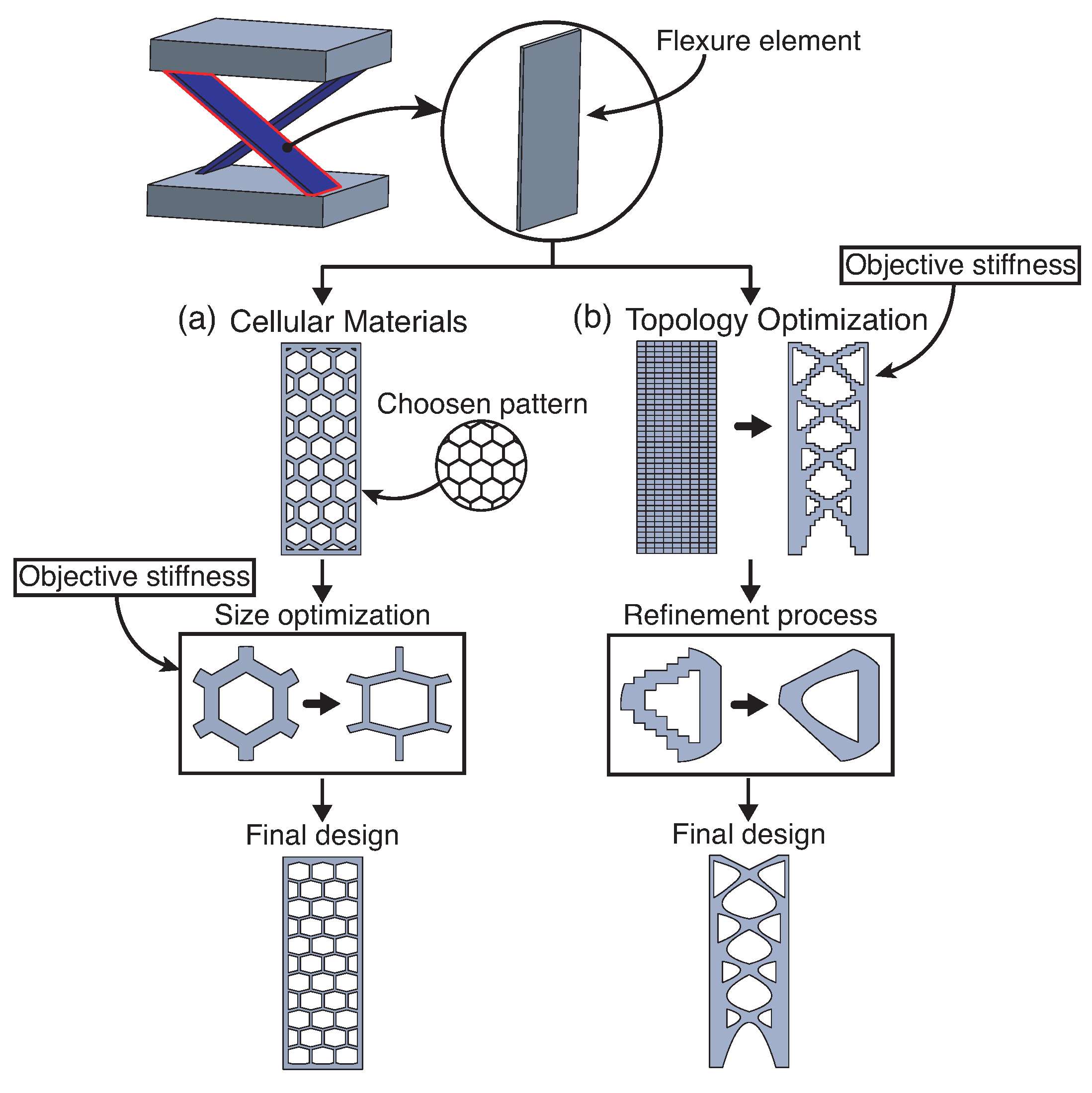
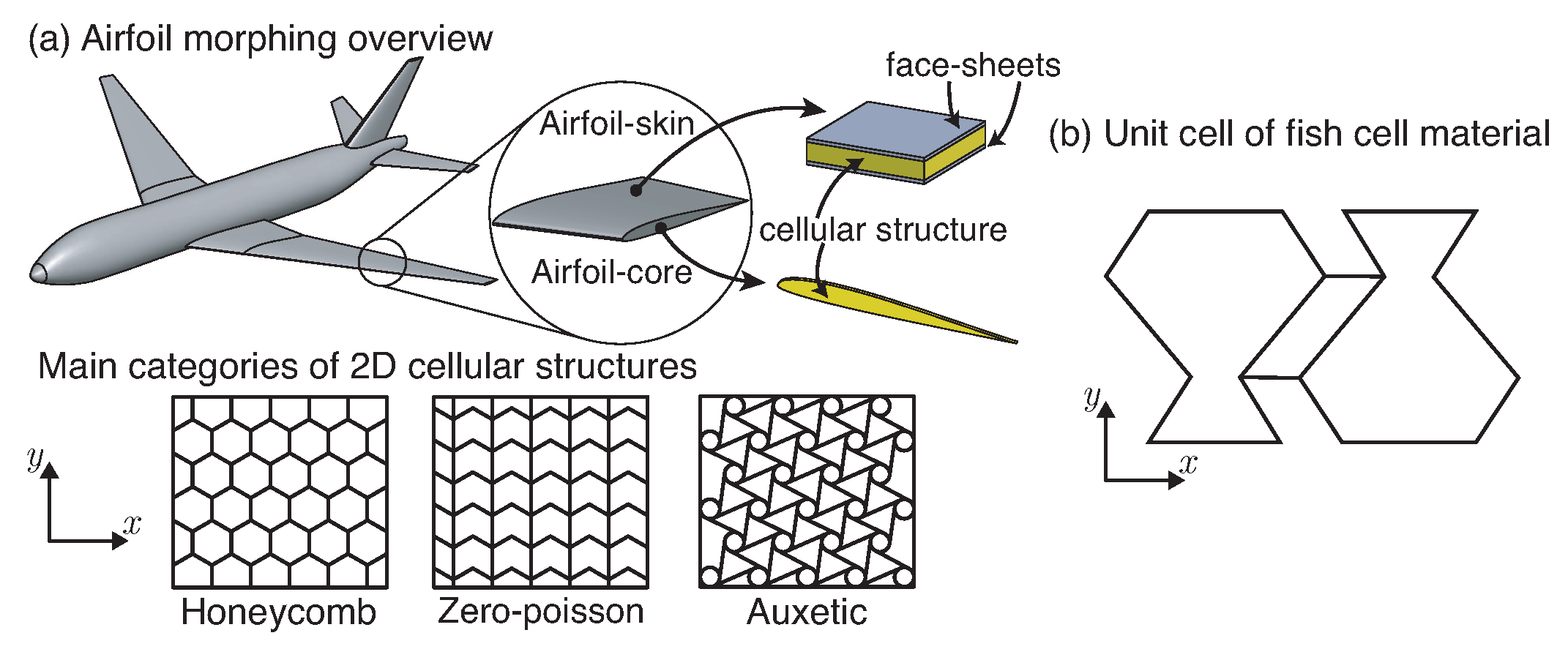
2. Tailoring Stiffness via Cellular Materials
Cellular Materials in Compliant Systems as Flexure Elements
3. Tailoring Stiffness via Topology Optimization
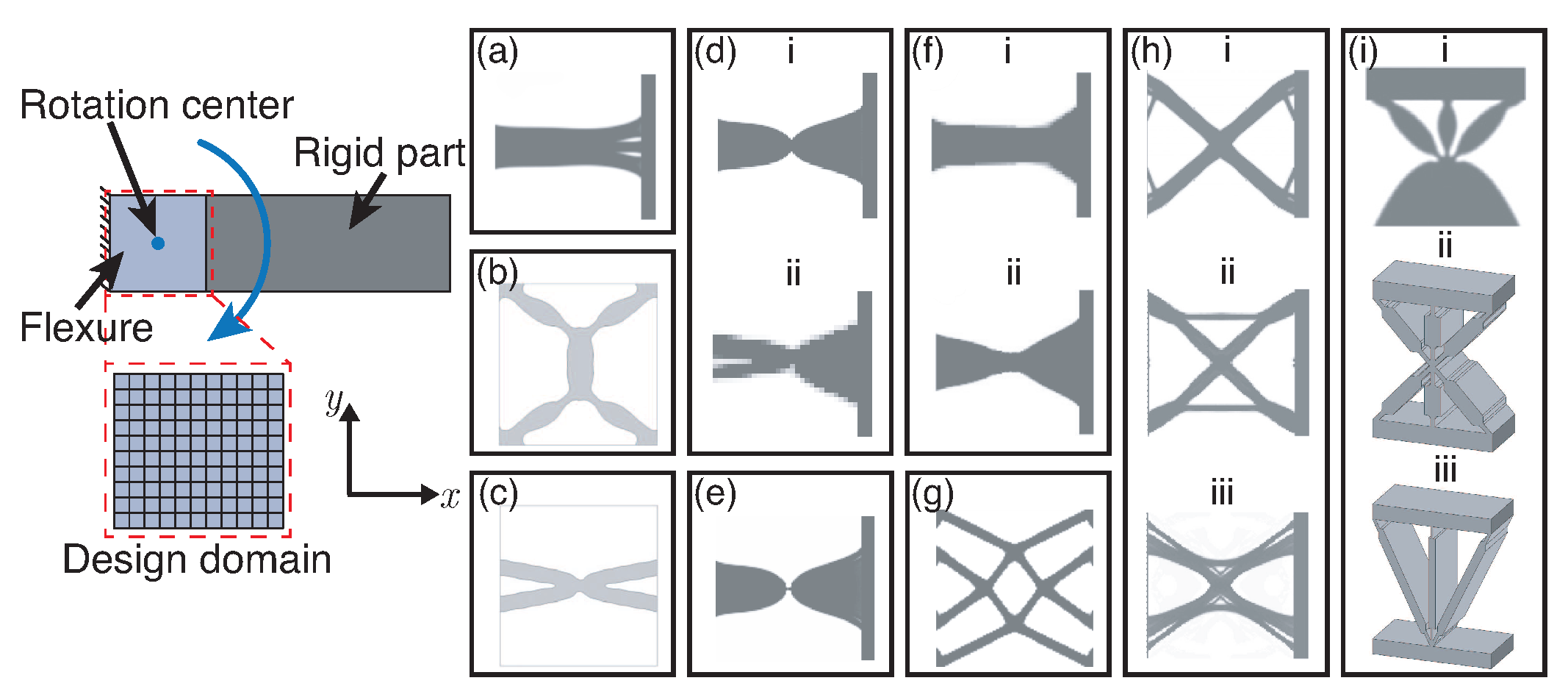
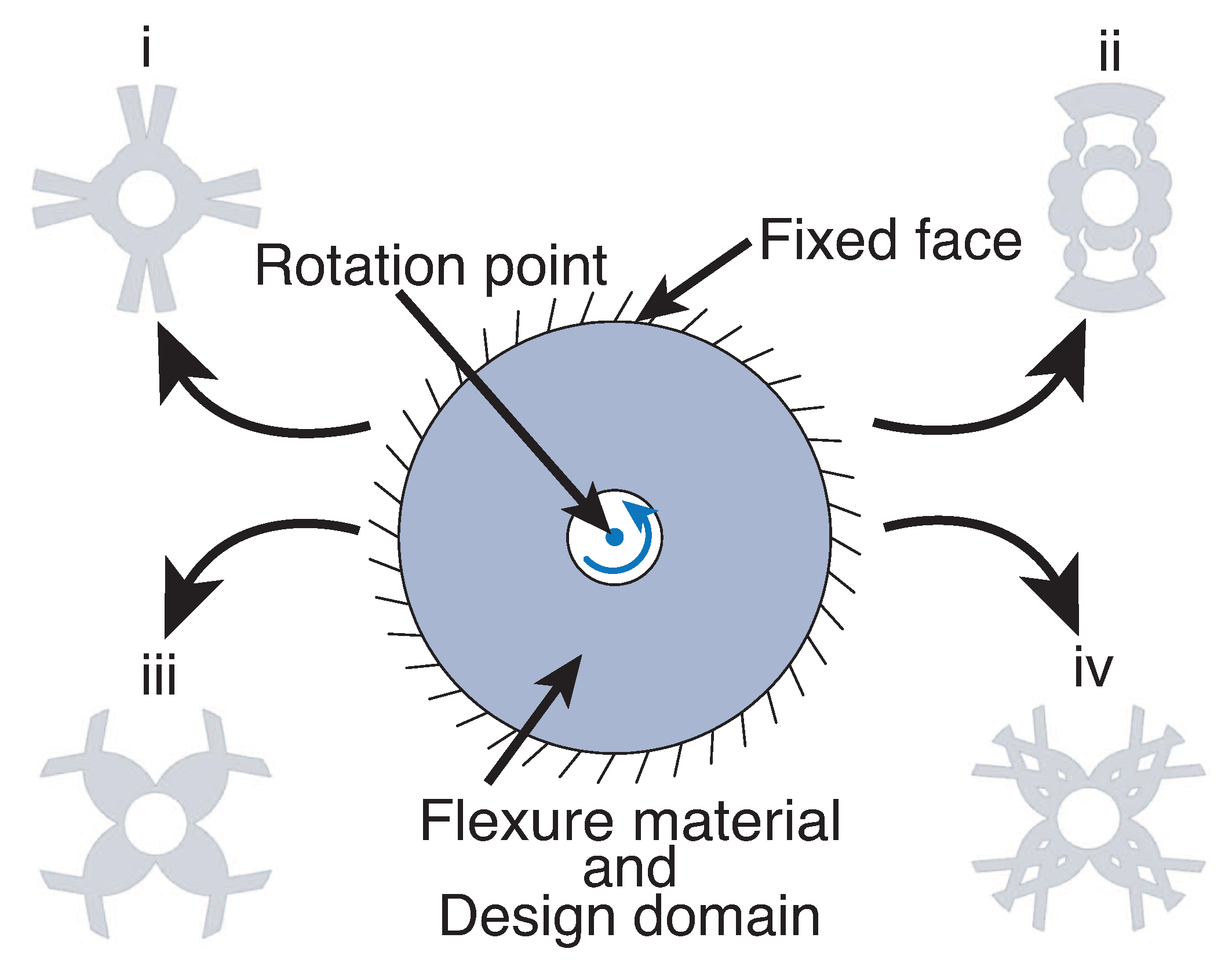
Topology Optimization in Compliant Systems as Flexure Elements
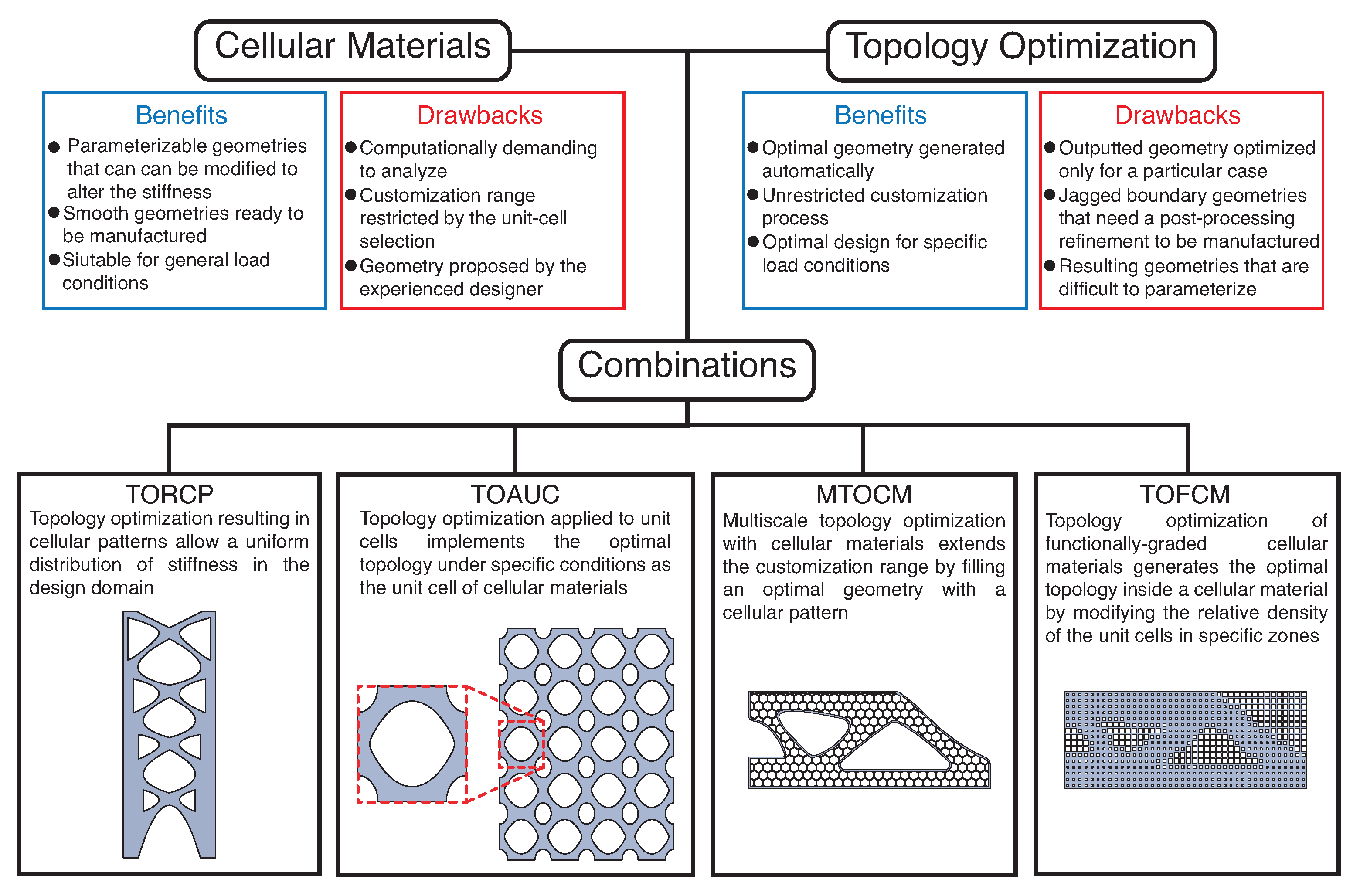
4. Remarks on Tailoring Stiffness via Cellular Materials and Topology Optimization
5. Conclusions
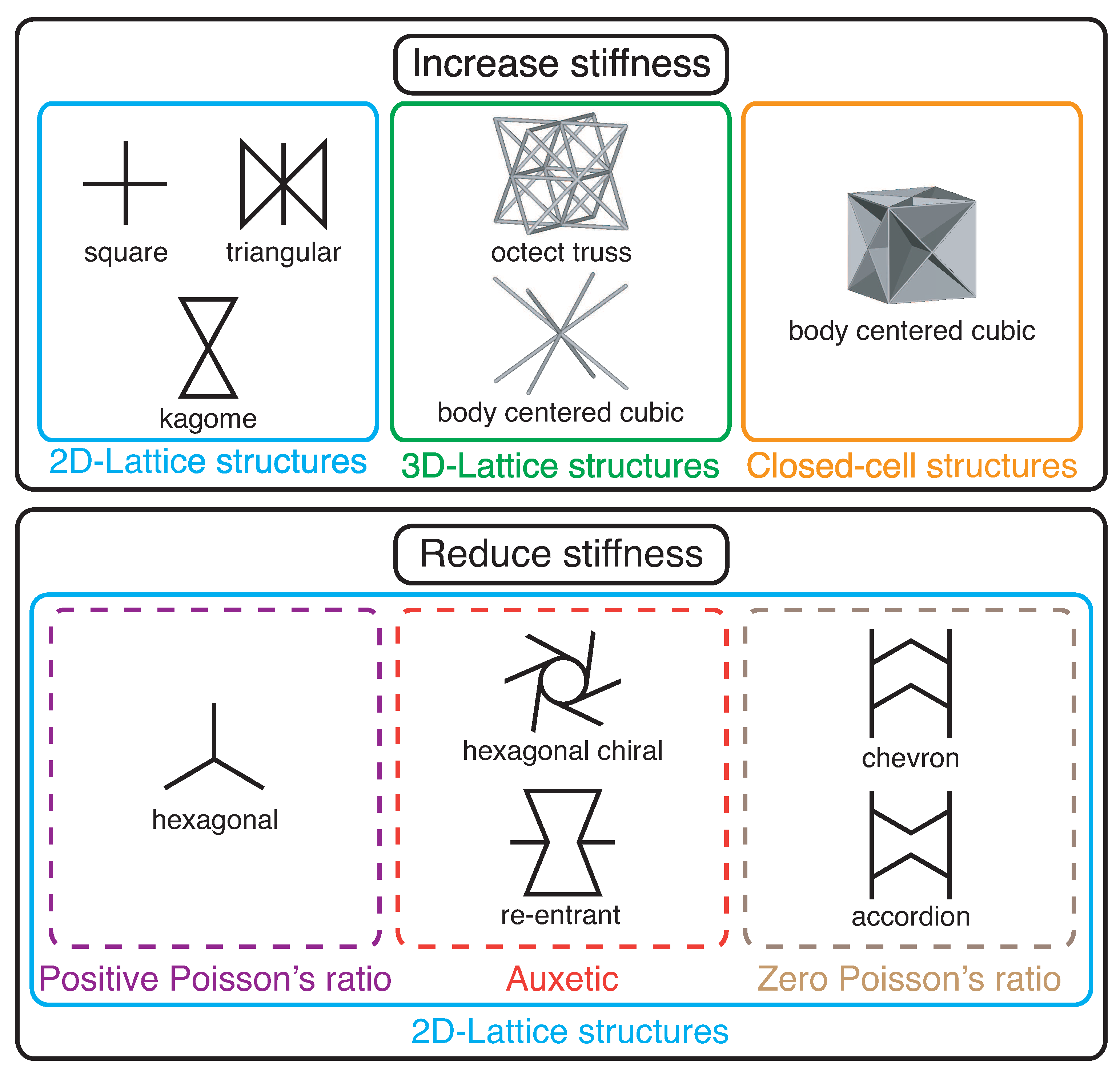
- Due to their advantages in tailoring the mechanical properties, exploring the use of closed-cell structures, 3D arrays, auxetic, and zero-Poisson architectures in tailoring the stiffness of flexure elements could lead to benefits compliant systems.
- As flexures base their functioning on the elastic response of their elements, other material properties, i.e., Poisson’s ratio, could complicate their use to build up other kinematic pairs, e.g., cylindrical. However, a correct selection of cellular pattern could be designed so that it restricts the Poisson’s ratio to 0. This opens up a new range of possibilities in compliant systems applications.
- Combining both Cellular Materials and Topology Optimization approaches (TOAUC, MTOCM, and TOFCM) to expand the possibilities in tailoring stiffness of flexure elements. This combination leads to obtain the best out of each. An example of the use of these two could be by implementing Topology Optimization at the conceptual design stage for the proposal of a flexure element. Then, employ a Cellular Material to adjust the stiffness by modifying the parameters that define the structure.
- Analytical parameterization of the Cellular Material employed can result in an accurate and precise tracking of the stiffness. This allows a controlled tailoring of stiffness in compliant systems.
- Another aspect to keep in mind is that lattice honeycombs might have in-plane anisotropy. Therefore, when used in flexures, the proper selection of orientation becomes crucial. Failure in considering this could lead to deformations in non-desired directions, i.e., parasitic motions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MEMS | Microelectromechanical Systems |
| 3D | Three-dimensional |
| DOF | Degrees of Freedom |
| 2D | Two-dimensional |
| SIMP | Solid Isotropic Material with Penalization |
| TORCP | Topology Optimization Resulting in Cellular Patterns |
| TOAUC | Topology Optimization Applied to Unit Cells |
| MTOCM | Multiscale Topology Optimization with Cellular Materials |
| TOFCM | Topology Optimization of Functionally-graded Cellular Materials |
| SARFJ | Single Axis Rotational Flexure Joints |
| FEA | Finite Element Analysis |
| QVFH | Quasi V-shaped Flexure Hinge |
| MCFH | Multi-Cavity Flexure Hinge |
| QLPFH | Quasi-Leaf Porous Flexure Hinge |
| SATFJ | Single-Axis Translational Flexure Joints |
References
- Howell, L.L. Compliant Mechanisms; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Pinskier, J.; Shirinzadeh, B. Topology optimization of leaf flexures for stiffness ratio maximization in compliant mechanisms. In Proceedings of the 2018 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, New Zealand, 9–12 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 407–412. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, D.; Shirinzadeh, B. Dynamic modelling of a flexure-based mechanism for ultra-precision grinding operation. Precis. Eng. 2011, 35, 554–565. [Google Scholar] [CrossRef]
- Cecchi, R.; Verotti, M.; Capata, R.; Dochshanov, A.; Broggiato, G.B.; Crescenzi, R.; Balucani, M.; Natali, S.; Razzano, G.; Lucchese, F.; et al. Development of micro-grippers for tissue and cell manipulation with direct morphological comparison. Micromachines 2015, 6, 1710–1728. [Google Scholar] [CrossRef]
- Zubir, M.N.M.; Shirinzadeh, B.; Tian, Y. Development of a novel flexure-based microgripper for high precision micro-object manipulation. Sensors Actuators A Phys. 2009, 150, 257–266. [Google Scholar] [CrossRef]
- Fleming, A.J.; Yong, Y.K. An ultrathin monolithic XY nanopositioning stage constructed from a single sheet of piezoelectric material. IEEE/ASME Trans. Mechatron. 2017, 22, 2611–2618. [Google Scholar] [CrossRef]
- Kota, S.; Joo, J.; Li, Z.; Rodgers, S.M.; Sniegowski, J. Design of compliant mechanisms: Applications to MEMS. Analog. Integr. Circuits Signal Process. 2001, 29, 7–15. [Google Scholar] [CrossRef]
- Sun, X.; Yang, B. A new methodology for developing flexure-hinged displacement amplifiers with micro-vibration suppression for a giant magnetostrictive micro drive system. Sens. Actuators A Phys. 2017, 263, 30–43. [Google Scholar] [CrossRef]
- Chen, B.K.; Zhang, Y.; Sun, Y. Active release of microobjects using a MEMS microgripper to overcome adhesion forces. J. Microelectromech. Syst. 2009, 18, 652–659. [Google Scholar] [CrossRef]
- Ling, M.; Howell, L.L.; Cao, J.; Chen, G. Kinetostatic and dynamic modeling of flexure-based compliant mechanisms: A survey. Appl. Mech. Rev. 2020, 72, 030802. [Google Scholar] [CrossRef]
- Lee, C.; Stepanick, C.K.; Lee, S.K.; Tarbutton, J.A. Cross-coupling effect of large range XY nanopositioning stage fabricated by stereolithography process. Precis. Eng. 2016, 46, 81–87. [Google Scholar] [CrossRef]
- Yuanqiang, L.; Wangyu, L. Analysis of the displacement of distributed compliant parallel-guiding mechanism considering parasitic rotation and deflection on the guiding plate. Mech. Mach. Theory 2014, 80, 151–165. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, W.; Wu, L. Analysis of the displacement of lumped compliant parallel-guiding mechanism considering parasitic rotation and deflection on the guiding plate and rigid beams. Mech. Mach. Theory 2015, 91, 50–68. [Google Scholar] [CrossRef]
- Cornelissen, R.; Müller, A.; Aarts, R. A Compliant and Redundantly Actuated 2-DOF 3RRR PKM: Best of Both Worlds? In Proceedings of the IFToMM World Congress on Mechanism and Machine Science, Duisburg, Germany, 26 August 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 163–171. [Google Scholar] [CrossRef]
- Yun, Y.; Li, Y. Design and analysis of a novel 6-DOF redundant actuated parallel robot with compliant hinges for high precision positioning. Nonlinear Dyn. 2010, 61, 829–845. [Google Scholar] [CrossRef]
- Merriam, E.G.; Lund, J.M.; Howell, L.L. Compound joints: Behavior and benefits of flexure arrays. Precis. Eng. 2016, 45, 79–89. [Google Scholar] [CrossRef]
- Li, S.; Yu, J. Design principle of high-precision flexure mechanisms based on parasitic-motion compensation. Chin. J. Mech. Eng. 2014, 27, 663–672. [Google Scholar] [CrossRef]
- Yong, Y.K.; Liu, K.; Moheimani, S.R. Reducing cross-coupling in a compliant XY nanopositioner for fast and accurate raster scanning. IEEE Trans. Control. Syst. Technol. 2009, 18, 1172–1179. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Yan, P. Large dynamic range tracking of an XY compliant nanomanipulator with cross-axis coupling reduction. Mech. Syst. Signal Process. 2019, 117, 757–770. [Google Scholar] [CrossRef]
- Bhagat, U.; Shirinzadeh, B.; Tian, Y.; Zhang, D. Experimental analysis of laser interferometry-based robust motion tracking control of a flexure-based mechanism. IEEE Trans. Autom. Sci. Eng. 2012, 10, 267–275. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Yan, P. A Spatial Design of a Large Stroke Compliant XY Nanomanipulator with Cross-Coupling Error Reduction. In Proceedings of the 2019 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Helsinki, Finland, 1–5 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
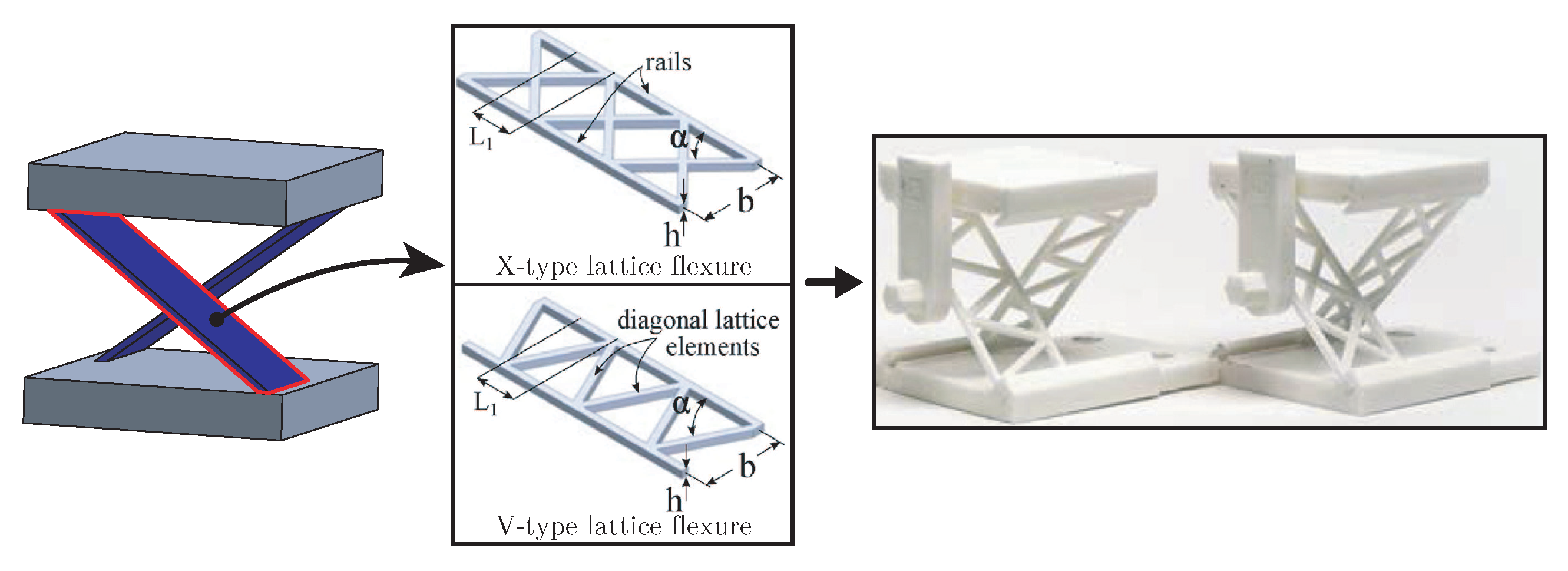
- Merriam, E.G.; Howell, L.L. Lattice flexures: Geometries for stiffness reduction of blade flexures. Precis. Eng. 2016, 45, 160–167. [Google Scholar] [CrossRef]
- Ham, R.V.; Sugar, T.; Vanderborght, B.; Hollander, K.; Lefeber, D. Compliant actuator designs. IEEE Robot. Autom. Mag. 2009, 3, 81–94. [Google Scholar] [CrossRef]
- Vanderborght, B.; Albu-Schäffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable impedance actuators: A review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Pluimers, P.J.; Tolou, N.; Jensen, B.D.; Howell, L.L.; Herder, J.L. A compliant on/off connection mechanism for preloading statically balanced compliant mechanisms. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; American Society of Mechanical Engineers (ASME): New York, NY, USA, 2012; Volume 4, pp. 373–377. [Google Scholar] [CrossRef]
- Stapel, A.; Herder, J.L. Feasibility study of a fully compliant statically balanced laparoscopic grasper. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Salt Lake City, UT, USA, 28 September–2 October 2004; Volume 2, pp. 635–643. [Google Scholar] [CrossRef]
- Merriam, E.G.; Howell, L.L. Non-dimensional approach for static balancing of rotational flexures. Mech. Mach. Theory 2015, 84, 90–98. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, S. Fully-compliant statically-balanced mechanisms without prestressing assembly: Concepts and case studies. Mech. Sci. 2011, 2, 169–174. [Google Scholar] [CrossRef]
- Dunning, A.; Tolou, N.; Herder, J. A compact low-stiffness six degrees of freedom compliant precision stage. Precis. Eng. 2013, 37, 380–388. [Google Scholar] [CrossRef]
- Morsch, F.M.; Herder, J.L. Design of a generic zero stiffness compliant joint. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 15–18 August 2010; Volume 2, pp. 427–435. [Google Scholar] [CrossRef]
- Schiavi, R.; Grioli, G.; Sen, S.; Bicchi, A. VSA-II: A novel prototype of variable stiffness actuator for safe and performing robots interacting with humans. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 2171–2176. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Yuan, Z.; Liu, J. Design and analysis of spring parallel variable stiffness actuator based on antagonistic principle. Mech. Mach. Theory 2019, 140, 44–58. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Vanderborght, B.; Caldwell, D.G. A novel actuator with adjustable stiffness (AwAS). In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 4201–4206. [Google Scholar] [CrossRef]
- Jafari, A.; Tsagarakis, N.G.; Caldwell, D.G. AwAS-II: A new actuator with adjustable stiffness based on the novel principle of adaptable pivot point and variable lever ratio. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4638–4643. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Z.; Sun, D.; He, S.; Xiao, X. Design, modeling and control of a novel compact, energy-efficient, and rotational serial variable stiffness actuator (SVSA-II). Mech. Mach. Theory 2018, 130, 123–136. [Google Scholar] [CrossRef]
- Choi, J.; Hong, S.; Lee, W.; Kang, S.; Kim, M. A robot joint with variable stiffness using leaf springs. IEEE Trans. Robot. 2011, 27, 229–238. [Google Scholar] [CrossRef]
- Wang, W.; Fu, X.; Li, Y.; Yun, C. Design of variable stiffness actuator based on modified Gear–Rack mechanism. J. Mech. Robot. 2016, 8, 061008. [Google Scholar] [CrossRef]
- Hawks, J.C.; Colton, M.B.; Howell, L.L. A variable-stiffness straight-line compliant mechanism. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 5A, p. V05AT08A011. [Google Scholar] [CrossRef]
- Xie, Z.; Qiu, L.; Yang, D. Design and analysis of a variable stiffness inside-deployed lamina emergent joint. Mech. Mach. Theory 2018, 120, 166–177. [Google Scholar] [CrossRef]
- Galloway, K.C.; Clark, J.E.; Koditschek, D.E. Variable stiffness legs for robust, efficient, and stable dynamic running. J. Mech. Robot. 2013, 5, 011009. [Google Scholar] [CrossRef]
- Wissa, A.; Tummala, Y.; Hubbard, J., Jr.; Frecker, M.I. Passively morphing ornithopter wings constructed using a novel compliant spine: Design and testing. Smart Mater. Struct. 2012, 21, 094028. [Google Scholar] [CrossRef]
- Tummala, Y.; Frecker, M.I.; Wissa, A.; Hubbard, J.E., Jr. Design and optimization of a bend-and-sweep compliant mechanism. Smart Mater. Struct. 2013, 22, 094019. [Google Scholar] [CrossRef]
- Tummala, Y.; Wissa, A.; Frecker, M.; Hubbard, J.E. Design and optimization of a contact-aided compliant mechanism for passive bending. J. Mech. Robot. 2014, 6, 031013. [Google Scholar] [CrossRef]
- Mehta, V.; Frecker, M.; Lesieutre, G.A. Stress relief in contact-aided compliant cellular mechanisms. J. Mech. Des. 2009, 131, 091009. [Google Scholar] [CrossRef]
- Mankame, N.D.; Ananthasuresh, G. A novel compliant mechanism for converting reciprocating translation into enclosing curved paths. J. Mech. Des. 2004, 126, 667–672. [Google Scholar] [CrossRef]
- Cannon, J.R.; Howell, L.L. A compliant contact-aided revolute joint. Mech. Mach. Theory 2005, 40, 1273–1293. [Google Scholar] [CrossRef]
- Guérinot, A.E.; Magleby, S.P.; Howell, L.L.; Todd, R.H. Compliant joint design principles for high compressive load situations. J. Mech. Des. 2005, 127, 774–781. [Google Scholar] [CrossRef]
- Gupta, G.; Tan, J.; Seepersad, C.C. ME Design and Freeform Fabrication of Compliant Cellular Materials with Graded Stiffness. In Proceedings of the 2006 International Solid Freeform Fabrication Symposium, Austin, TX, USA, 14–16 August 2006. [Google Scholar]
- Jovanova, J.; Nastevska, A.; Frecker, M. Tailoring energy absorption with functional grading of a contact-aided compliant mechanism. Smart Mater. Struct. 2019, 28, 084003. [Google Scholar] [CrossRef]
- Xie, Z.; Qiu, L.; Yang, D. Using the Parts Used to Be Removed to Improve Compliant Joint’s Performance. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29 August 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 5A, p. V05AT07A006. [Google Scholar] [CrossRef]
- Xie, Z.; Qiu, L.; Yang, D. Analysis of a novel variable stiffness filleted leaf hinge. Mech. Mach. Theory 2020, 144, 103673. [Google Scholar] [CrossRef]
- Pinskier, J.; Shirinzadeh, B. Topology optimization of leaf flexures to maximize in-plane to out-of-plane compliance ratio. Precis. Eng. 2019, 55, 397–407. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Zhang, H.; Liang, J.; Zang, H.; Li, H.; Wang, R. Design of compliant mechanisms using continuum topology optimization: A review. Mech. Mach. Theory 2020, 143, 103622. [Google Scholar] [CrossRef]
- Gallego, J.A.; Herder, J. Synthesis methods in compliant mechanisms: An overview. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, San Diego, CA, USA, 30 August–2 September 2009; Volume 7, pp. 193–214. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zhou, S.; Xie, Y. Topology optimization of compliant mechanisms with desired structural stiffness. Eng. Struct. 2014, 79, 13–21. [Google Scholar] [CrossRef]
- Pinskier, J.; Shirinzadeh, B.; Ghafarian, M.; Das, T.K.; Al-Jodah, A.; Nowell, R. Topology optimization of gy optimization of stiffness constrained flexure-hinges for precision and range maximization. Mech. Mach. Theory 2020, 150, 103874. [Google Scholar] [CrossRef]
- Pingen, G.; Meyer, D. Topology optimization for thermal transport. In Proceedings of the Fluids Engineering Division Summer Meeting, Vail, CO, USA, 2–6 August 2009; Volume 1, pp. 2237–2243. [Google Scholar]
- Nomura, K.; Yamasaki, S.; Yaji, K.; Bo, H.; Takahashi, A.; Kojima, T.; Fujita, K. Topology optimization of conductors in electrical circuit. Struct. Multidiscip. Optim. 2019, 59, 2205–2225. [Google Scholar] [CrossRef]
- Christensen, J.; de Abajo, F.J.G. Anisotropic metamaterials for full control of acoustic waves. Phys. Rev. Lett. 2012, 108, 124301. [Google Scholar] [CrossRef]
- Bhate, D.; Penick, C.A.; Ferry, L.A.; Lee, C. Classification and selection of cellular materials in mechanical design: Engineering and biomimetic approaches. Designs 2019, 3, 19. [Google Scholar] [CrossRef]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The Design Process of Additively Manufactured Mesoscale Lattice Structures: A Review. J. Comput. Inf. Sci. Eng. 2018, 18, 040801. [Google Scholar] [CrossRef]
- Savio, G.; Rosso, S.; Meneghello, R.; Concheri, G. Geometric Modeling of Cellular Materials for Additive Manufacturing in Biomedical Field: A Review. Appl. Bionics Biomech. 2018, 2018, 14. [Google Scholar] [CrossRef]
- Bhate, D. Lattice Design Optimization: Crowdsourcing Ideas in the Classroom. In Proceedings of the 2018 Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 13–15 August 2018; pp. 12–14. [Google Scholar]
- Schaedler, T.A.; Carter, W.B. Architected cellular materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Nguyen, J.; Park, S.I.; Rosen, D.W. Cellular structure design for lightweight components. In Innovative Developments in Virtual and Physical Prototyping; Taylor & Francis: Abingdon, UK, 2012; pp. 203–210. [Google Scholar]
- Kantareddy, S.; Roh, B.; Simpson, T.; Joshi, S.; Dickman, C.; Lehtihet, E. Saving weight with metallic lattice structures: Design challenges with a real-world example. In Proceedings of the Solid Freeform Fabrication Symposium (SFF), Austin, TX, USA, 8–10 August 2016; pp. 8–10. [Google Scholar]
- Cheng, L.; Zhang, P.; Biyikli, E.; Bai, J.; Robbins, J.; To, A. Efficient design optimization of variable-density cellular structures for additive manufacturing: Theory and experimental validation. Rapid Prototyp. J. 2017, 23, 660–677. [Google Scholar] [CrossRef]
- Chen, W.; Zheng, X.; Liu, S. Finite-element-mesh based method for modeling and optimization of lattice structures for additive manufacturing. Materials 2018, 11, 2073. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Bhate, D. Four questions in cellular material design. Materials 2019, 12, 1060. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, M.; du Plessis, A.; Ritchie, R.; Dallago, M.; Razavi, S.; Berto, F. Architected cellular materials: A review on their mechanical properties towards fatigue-tolerant design and fabrication. Mater. Sci. Eng. R Rep. 2021, 144, 100606. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Espinoza-Camacho, J.I.; Álvarez-Trejo, A.; Uribe, E.; Treviño-Quintanilla, C.D.; Crespo-Sánchez, S.E.; Gómez-Espinosa, A.; Roman-Flores, A.; Olvera-Silva, O. Elastic response of lattice arc structures fabricated using curved-layered fused deposition modeling. Mech. Adv. Mater. Struct. 2019, 1–11. [Google Scholar] [CrossRef]
- Rosso, S.; Uriati, F.; Grigolato, L.; Meneghello, R.; Concheri, G.; Savio, G. An Optimization Workflow in Design for Additive Manufacturing. Appl. Sci. 2021, 11, 2572. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Askari, M.; Hutchins, D.A.; Thomas, P.J.; Astolfi, L.; Watson, R.L.; Abdi, M.; Ricci, M.; Laureti, S.; Nie, L.; Freear, S.; et al. Additive manufacturing of metamaterials: A review. Addit. Manuf. 2020, 36, 101562. [Google Scholar] [CrossRef]
- Chen, L.M.; Chen, M.J.; Pei, Y.M.; Zhang, Y.H.; Fang, D.N. Optimal design of sandwich beams with lightweight cores in three-point bending. Int. J. Appl. Mech. 2012, 4, 1250033. [Google Scholar] [CrossRef]
- Potes, F.; Silva, J.; Gamboa, P. Development and characterization of a natural lightweight composite solution for aircraft structural applications. Compos. Struct. 2016, 136, 430–440. [Google Scholar] [CrossRef]
- Cuan-Urquizo, E.; Shalchy, F.; Bhaskar, A. Compressive stiffness of staggered woodpile lattices: Mechanics, measurement, and scaling laws. Int. J. Mech. Sci. 2020, 187, 105932. [Google Scholar] [CrossRef]
- Chu, J.; Engelbrecht, S.; Graf, G.; Rosen, D.W. A comparison of synthesis methods for cellular structures with application to additive manufacturing. Rapid Prototyp. J. 2010, 16, 275–283. [Google Scholar] [CrossRef]
- Dragoni, E. Optimal mechanical design of tetrahedral truss cores for sandwich constructions. J. Sandw. Struct. Mater. 2013, 15, 464–484. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective laser melting (SLM) of AlSi12Mg lattice structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.; Parry, L.; Wildman, R.; Tuck, C.; Ashcroft, I. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Weisgraber, T.H.; Metz, T.; Spadaccini, C.M.; Duoss, E.B.; Small, W.; Lenhardt, J.M.; Maxwell, R.S.; Wilson, T.S. A mechanical reduced order model for elastomeric 3D printed architectures. J. Mater. Res. 2018, 33, 309–316. [Google Scholar] [CrossRef]
- Wang, Y.; Groen, J.P.; Sigmund, O. Simple optimal lattice structures for arbitrary loadings. Extrem. Mech. Lett. 2019, 29, 100447. [Google Scholar] [CrossRef]
- Álvarez Trejo, A.; Cuan-Urquizo, E.; Roman-Flores, A.; Trapaga-Martinez, L.; Alvarado-Orozco, J. Bézier-based metamaterials: Synthesis, mechanics and additive manufacturing. Mater. Des. 2021, 199, 109412. [Google Scholar] [CrossRef]
- Trifale, N.T.; Nauman, E.A.; Yazawa, K. Systematic generation, analysis, and characterization of 3D micro-architected metamaterials. ACS Appl. Mater. Interfaces 2016, 8, 35534–35544. [Google Scholar] [CrossRef]
- Niknam, H.; Akbarzadeh, A.; Rodrigue, D.; Therriault, D. Architected multi-directional functionally graded cellular plates. Mater. Des. 2018, 148, 188–202. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Mohr, D. Elastically-isotropic elementary cubic lattices composed of tailored hollow beams. Extrem. Mech. Lett. 2018, 22, 13–18. [Google Scholar] [CrossRef]
- Kim, K.; Heo, H.; Ju, J. A mechanism-based architected material: A hierarchical approach to design Poisson’s ratio and stiffness. Mech. Mater. 2018, 125, 14–25. [Google Scholar] [CrossRef]
- Chen, W.; Watts, S.; Jackson, J.A.; Smith, W.L.; Tortorelli, D.A.; Spadaccini, C.M. Stiff isotropic lattices beyond the Maxwell criterion. Sci. Adv. 2019, 5, eaaw1937. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. Bi-stiffness property of motion structures transformed into square cells. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130063. [Google Scholar] [CrossRef]
- Mihai, L.A.; Alayyash, K.; Wyatt, H. The optimal density of cellular solids in axial tension. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 701–713. [Google Scholar] [CrossRef]
- Lubombo, C.; Huneault, M.A. Effect of infill patterns on the mechanical performance of lightweight 3D-printed cellular PLA parts. Mater. Today Commun. 2018, 17, 214–228. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Rosen, D.W. A hybrid geometric modeling method for large scale conformal cellular structures. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Long Beach, CA, USA, 24–28 September 2005; Volume 3, pp. 421–427. [Google Scholar] [CrossRef]
- Wang, R.; Shang, J.; Li, X.; Wang, Z.; Luo, Z. Novel topological design of 3D Kagome structure for additive manufacturing. Rapid Prototyp. J. 2018, 24, 261–269. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Li, X.; Diamantopoulou, M.; Roth, C.; Mohr, D. High strain rate response of additively-manufactured plate-lattices: Experiments and modeling. J. Dyn. Behav. Mater. 2019, 5, 361–375. [Google Scholar] [CrossRef]
- Qiao, P.; Fan, W.; Davalos, J.F.; Zou, G. Optimization of transverse shear moduli for composite honeycomb cores. Compos. Struct. 2008, 85, 265–274. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P.; Davalos, J.F. Design Optimization of Honeycomb Core Configurations for Effective Transverse Shear Stiffness. In Proceedings of the Earth & Space 2008: Engineering, Science, Construction, and Operations in Challenging Environments, Long Beach, CA, USA, 3–5 March 2008; pp. 1–8. [Google Scholar]
- Nazir, A.; Arshad, A.B.; Jeng, J.Y. Buckling and Post-Buckling Behavior of Uniform and Variable-Density Lattice Columns Fabricated Using Additive Manufacturing. Materials 2019, 12, 3539. [Google Scholar] [CrossRef]
- Lipperman, F.; Fuchs, M.B.; Ryvkin, M. Stress localization and strength optimization of frame material with periodic microstructure. Comput. Methods Appl. Mech. Eng. 2008, 197, 4016–4026. [Google Scholar] [CrossRef]
- Injeti, S.S.; Daraio, C.; Bhattacharya, K. Metamaterials with engineered failure load and stiffness. Proc. Natl. Acad. Sci. USA 2019, 116, 23960–23965. [Google Scholar] [CrossRef] [PubMed]
- Parthasarathy, J.; Starly, B.; Raman, S. A design for the additive manufacture of functionally graded porous structures with tailored mechanical properties for biomedical applications. J. Manuf. Process. 2011, 13, 160–170. [Google Scholar] [CrossRef]
- Kim, K.; Ju, J.; Kim, D.M. Cellular materials with extremely high negative and positive Poisson’s ratios: A mechanism based material design. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Diego, CA, USA, 15–21 November 2013; American Society of Mechanical Engineers: New York, NY, USA, 2013; Volume 9, p. V009T10A045. [Google Scholar] [CrossRef]
- Kim, K.; Ju, J.; Kim, D.M. Porous materials with high negative Poisson’s ratios—A mechanism based material design. Smart Mater. Struct. 2013, 22, 084007. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Auxetic cellular materials-a review. Stroj. Vestn. J. Mech. Eng. 2016, 62, 485–493. [Google Scholar] [CrossRef]
- Duoss, E.B.; Weisgraber, T.H.; Hearon, K.; Zhu, C.; Small IV, W.; Metz, T.R.; Vericella, J.J.; Barth, H.D.; Kuntz, J.D.; Maxwell, R.S.; et al. Three-dimensional printing of elastomeric, cellular architectures with negative stiffness. Adv. Funct. Mater. 2014, 24, 4905–4913. [Google Scholar] [CrossRef]
- Neff, C.; Hopkinson, N.; Crane, N.B. Selective laser sintering of diamond lattice structures: Experimental results and FEA model comparison. Solid Free Fabr. 2015, 25, 1104. [Google Scholar]
- Runkel, F.; Molinari, G.; Arrieta, A.F.; Ermanni, P. Tailorable stiffness chiral metastructure. Phys. Status Solidi RRL Rapid Res. Lett. 2017, 11, 1700233. [Google Scholar] [CrossRef]
- Ion, A.; Frohnhofen, J.; Wall, L.; Kovacs, R.; Alistar, M.; Lindsay, J.; Lopes, P.; Chen, H.T.; Baudisch, P. Metamaterial mechanisms. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 16–19 October 2016; pp. 529–539. [Google Scholar]
- Ou, J.; Ma, Z.; Peters, J.; Dai, S.; Vlavianos, N.; Ishii, H. KinetiX—Designing auxetic-inspired deformable material structures. Comput. Graph. 2018, 75, 72–81. [Google Scholar] [CrossRef]
- Soltani, Z.; Santer, M. The determination and enhancement of compliant modes for high-amplitude actuation in lattices. Int. J. Solids Struct. 2020, 206, 124–136. [Google Scholar] [CrossRef]
- Dunn, M.; Wheel, M. Size effect anomalies in the behaviour of loaded 3D mechanical metamaterials. Philos. Mag. 2020, 100, 139–156. [Google Scholar] [CrossRef]
- Gong, X.; Huang, J.; Scarpa, F.; Liu, Y.; Leng, J. Zero Poisson’s ratio cellular structure for two-dimensional morphing applications. Compos. Struct. 2015, 134, 384–392. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Bai, Y. In-plane mechanics of a novel cellular structure for multiple morphing applications. Compos. Struct. 2019, 207, 598–611. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Yang, Z.; Zhang, J.; Xiong, C. Mechanics of a novel cellular structure for morphing applications. Aerosp. Sci. Technol. 2019, 95, 105479. [Google Scholar] [CrossRef]
- Bornengo, D.; Scarpa, F.; Remillat, C. Evaluation of hexagonal chiral structure for morphing airfoil concept. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2005, 219, 185–192. [Google Scholar] [CrossRef]
- Dong, W.J.; Sun, Q. A Novel Basic Conceptual Design and Analysis of a Morphing Wing Using Re-Entrant Hexagonal Cellular Structure. Adv. Mater. Res. 2011, 308, 548–552. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, L.; Qiu, T. Design and application of cross-shaped cellular honeycombs for a variable camber wing. J. Aircr. 2012, 49, 1451–1459. [Google Scholar] [CrossRef]
- Heo, H.; Ju, J.; Kim, D.M. Compliant cellular structures: Application to a passive morphing airfoil. Compos. Struct. 2013, 106, 560–569. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Flexible skins for morphing aircraft using cellular honeycomb cores. J. Intell. Mater. Syst. Struct. 2010, 21, 1719–1735. [Google Scholar] [CrossRef]
- Olympio, K.; Gandhi, F. Zero-v cellular honeycomb flexible skins for one-dimensional wing morphing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; p. 1735. [Google Scholar] [CrossRef]
- Chen, J.; Shen, X.; Li, J. Zero Poisson’s ratio flexible skin for potential two-dimensional wing morphing. Aerosp. Sci. Technol. 2015, 45, 228–241. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Analysis and design of lattice materials for large cord and curvature variations in skin panels of morphing wings. Smart Mater. Struct. 2015, 24, 037006. [Google Scholar] [CrossRef]
- Chang, L.; Shen, X. Design of cellular based structures in sandwiched morphing skin via topology optimization. Struct. Multidiscip. Optim. 2018, 58, 2085–2098. [Google Scholar] [CrossRef]
- Naghavi Zadeh, M.; Dayyani, I.; Yasaee, M. Fish Cells, a new zero Poisson’s ratio metamaterial—Part I: Design and experiment. J. Intell. Mater. Syst. Struct. 2020, 31, 1617–1637. [Google Scholar] [CrossRef]
- Zadeh, M.N.; Dayyani, I.; Yasaee, M. Fish Cells, a new zero Poisson’s ratio metamaterial—Part II: Elastic properties. J. Intell. Mater. Syst. Struct. 2020, 31, 2196–2210. [Google Scholar] [CrossRef]
- Jenett, B.; Calisch, S.; Cellucci, D.; Cramer, N.; Gershenfeld, N.; Swei, S.; Cheung, K.C. Digital morphing wing: Active wing shaping concept using composite lattice-based cellular structures. Soft Robot. 2017, 4, 33–48. [Google Scholar] [CrossRef] [PubMed]
- Cramer, N.B.; Cellucci, D.W.; Formoso, O.B.; Gregg, C.E.; Jenett, B.E.; Kim, J.H.; Lendraitis, M.; Swei, S.S.; Trinh, G.T.; Trinh, K.V.; et al. Elastic shape morphing of ultralight structures by programmable assembly. Smart Mater. Struct. 2019, 28, 055006. [Google Scholar] [CrossRef] [PubMed]
- Habib, F.; Iovenitti, P.; Masood, S.; Nikzad, M. Fabrication of polymeric lattice structures for optimum energy absorption using Multi Jet Fusion technology. Mater. Des. 2018, 155, 86–98. [Google Scholar] [CrossRef]
- Yuan, S.; Chua, C.K.; Zhou, K. 3D-Printed Mechanical Metamaterials with High Energy Absorption. Adv. Mater. Technol. 2019, 4, 1800419. [Google Scholar] [CrossRef]
- Sarvestani, H.Y.; Akbarzadeh, A.; Mirbolghasemi, A.; Hermenean, K. 3D printed meta-sandwich structures: Failure mechanism, energy absorption and multi-hit capability. Mater. Des. 2018, 160, 179–193. [Google Scholar] [CrossRef]
- Gao, Q.; Zhao, X.; Wang, C.; Wang, L.; Ma, Z. Multi-objective crashworthiness optimization for an auxetic cylindrical structure under axial impact loading. Mater. Des. 2018, 143, 120–130. [Google Scholar] [CrossRef]
- Lai, C.Q.; Daraio, C. Highly porous microlattices as ultrathin and efficient impact absorbers. Int. J. Impact Eng. 2018, 120, 138–149. [Google Scholar] [CrossRef]
- Saxena, K.K.; Calius, E.P.; Das, R. Tailoring cellular auxetics for wearable applications with multimaterial 3D printing. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016; American Society of Mechanical Engineers: New York, NY, USA, 2016; Volume 9, p. V009T12A063. [Google Scholar] [CrossRef]
- Izard, A.G.; Alfonso, R.F.; McKnight, G.; Valdevit, L. Optimal design of a cellular material encompassing negative stiffness elements for unique combinations of stiffness and elastic hysteresis. Mater. Des. 2017, 135, 37–50. [Google Scholar] [CrossRef]
- Wang, B.; Tan, X.; Zhu, S.; Chen, S.; Yao, K.; Xu, P.; Wang, L.; Wu, H.; Sun, Y. Cushion performance of cylindrical negative stiffness structures: Analysis and optimization. Compos. Struct. 2019, 227, 111276. [Google Scholar] [CrossRef]
- Hyland, J.E.; Frecker, M.I.; Lesieutre, G.A. Optimization of honeycomb contact-Aided compliant cellular mechanism for strain energy absorption. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; Volume 4, pp. 311–320. [Google Scholar] [CrossRef]
- Khurana, J.; Hanks, B.; Frecker, M. Design for additive manufacturing of cellular compliant mechanism using thermal history feedback. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29 August 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; Volume 2A, p. V02AT03A035. [Google Scholar] [CrossRef]
- Han, B.; Zhang, Z.J.; Zhang, Q.C.; Zhang, Q.; Lu, T.J.; Lu, B.H. Recent advances in hybrid lattice-cored sandwiches for enhanced multifunctional performance. Extrem. Mech. Lett. 2017, 10, 58–69. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.; Zhang, H. A review on functionally graded structures and materials for energy absorption. Eng. Struct. 2018, 171, 309–325. [Google Scholar] [CrossRef]
- San Ha, N.; Lu, G. A review of recent research on bio-inspired structures and materials for energy absorption applications. Compos. Part B Eng. 2020, 181, 107496. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; You, Z. Large deformation and energy absorption of additively manufactured auxetic materials and structures: A review. Compos. Part B Eng. 2020, 108340. [Google Scholar] [CrossRef]
- van Dijk, N.P.; Maute, K.; Langelaar, M.; Van Keulen, F. Level-set methods for structural topology optimization: A review. Struct. Multidiscip. Optim. 2013, 48, 437–472. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Bendsøe, M.P. Optimal shape design as a material distribution problem. Struct. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Cadman, J.E.; Zhou, S.; Chen, Y.; Li, Q. On design of multi-functional microstructural materials. J. Mater. Sci. 2013, 48, 51–66. [Google Scholar] [CrossRef]
- Deaton, J.D.; Grandhi, R.V. A survey of structural and multidisciplinary continuum topology optimization: Post 2000. Struct. Multidiscip. Optim. 2014, 49, 1–38. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Huang, X.; Xie, M. Evolutionary Topology Optimization of Continuum Structures: Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Subedi, S.C.; Verma, C.S.; Suresh, K. A Review of Methods for the Geometric Post-Processing of Topology Optimized Models. J. Comput. Inf. Sci. Eng. 2020, 20, 060801. [Google Scholar] [CrossRef]
- Sigmund, O. Design of Material Structures Using Topology Optimization. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 1994. [Google Scholar]
- Eschenauer, H.A.; Olhoff, N. Topology optimization of continuum structures: A review. Appl. Mech. Rev. 2001, 54, 331–390. [Google Scholar] [CrossRef]
- Sigmund, O. A new class of extremal composites. J. Mech. Phys. Solids 2000, 48, 397–428. [Google Scholar] [CrossRef]
- Gibiansky, L.V.; Sigmund, O. Multiphase composites with extremal bulk modulus. J. Mech. Phys. Solids 2000, 48, 461–498. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef]
- Neves, M.; Rodrigues, H.; Guedes, J.M. Optimal design of periodic linear elastic microstructures. Comput. Struct. 2000, 76, 421–429. [Google Scholar] [CrossRef]
- Sigmund, O. Materials with prescribed constitutive parameters: An inverse homogenization problem. Int. J. Solids Struct. 1994, 31, 2313–2329. [Google Scholar] [CrossRef]
- Sigmund, O. Tailoring materials with prescribed elastic properties. Mech. Mater. 1995, 20, 351–368. [Google Scholar] [CrossRef]
- Osanov, M.; Guest, J.K. Topology optimization for architected materials design. Annu. Rev. Mater. Res. 2016, 46, 211–233. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Zhou, W.; Fan, R.; Yu, B.; Lu, Y.; Li, L. Topology optimization-guided lattice composites and their mechanical characterizations. Compos. Part B Eng. 2019, 160, 402–411. [Google Scholar] [CrossRef]
- Hu, Z.; Gadipudi, V.K.; Salem, D.R. Topology optimization of lightweight lattice structural composites inspired by cuttlefish bone. Appl. Compos. Mater. 2019, 26, 15–27. [Google Scholar] [CrossRef]
- Zhang, L.; Song, B.; Fu, J.; Wei, S.; Yang, L.; Yan, C.; Li, H.; Gao, L.; Shi, Y. Topology-optimized lattice structures with simultaneously high stiffness and light weight fabricated by selective laser melting: Design, manufacturing and characterization. J. Manuf. Process. 2020, 56, 1166–1177. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.; Luo, Z.; Tian, Q. Topological design optimization of lattice structures to maximize shear stiffness. Adv. Eng. Softw. 2017, 112, 211–221. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, Y.; Xiao, R.; Bai, Y.; Song, C.; Wang, D. Evaluation of topology-optimized lattice structures manufactured via selective laser melting. Mater. Des. 2018, 143, 27–37. [Google Scholar] [CrossRef]
- Yang, C.; Xu, P.; Xie, S.; Yao, S. Mechanical performances of four lattice materials guided by topology optimisation. Scr. Mater. 2020, 178, 339–345. [Google Scholar] [CrossRef]
- Challis, V.; Roberts, A.; Wilkins, A. Design of three dimensional isotropic microstructures for maximized stiffness and conductivity. Int. J. Solids Struct. 2008, 45, 4130–4146. [Google Scholar] [CrossRef]
- Barba, D.; Reed, R.C.; Alabort, E. Design of Metallic Lattices for Bone Implants by Additive Manufacturing. In Proceedings of the TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings, San Diego, CA, USA, 23–27 February 2020; pp. 745–759. [Google Scholar] [CrossRef]
- Colabella, L.; Cisilino, A.P.; Fachinotti, V.; Kowalczyk, P. Multiscale design of elastic solids with biomimetic cancellous bone cellular microstructures. Struct. Multidiscip. Optim. 2019, 60, 639–661. [Google Scholar] [CrossRef]
- Colabella, L.; Cisilino, A.; Fachinotti, V.; Capiel, C.; Kowalczyk, P. Multiscale design of artificial bones with biomimetic elastic microstructures. J. Mech. Behav. Biomed. Mater. 2020, 108, 103748. [Google Scholar] [CrossRef]
- Sutradhar, A.; Paulino, G.H.; Miller, M.J.; Nguyen, T.H. Topological optimization for designing patient-specific large craniofacial segmental bone replacements. Proc. Natl. Acad. Sci. USA 2010, 107, 13222–13227. [Google Scholar] [CrossRef] [PubMed]
- Panesar, A.; Abdi, M.; Hickman, D.; Ashcroft, I. Strategies for functionally graded lattice structures derived using topology optimisation for additive manufacturing. Addit. Manuf. 2018, 19, 81–94. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Daynes, S.; Zhang, H.; Feih, S.; Wang, M.Y. Design of graded lattice structure with optimized mesostructures for additive manufacturing. Mater. Des. 2018, 142, 114–123. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Kang, Z. Topology optimization for concurrent design of layer-wise graded lattice materials and structures. Int. J. Eng. Sci. 2019, 138, 26–49. [Google Scholar] [CrossRef]
- Xia, L.; Breitkopf, P. Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Comput. Methods Appl. Mech. Eng. 2014, 278, 524–542. [Google Scholar] [CrossRef]
- Qiu, W.; Jin, P.; Jin, S.; Wang, C.; Xia, L.; Zhu, J.; Shi, T. An Evolutionary Design Approach to Shell-infill Structures. Addit. Manuf. 2020, 34, 101382. [Google Scholar] [CrossRef]
- Jin, X.; Li, G.X.; Zhang, M. Design and optimization of nonuniform cellular structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 1280–1293. [Google Scholar] [CrossRef]
- Liu, P.; Kang, Z.; Luo, Y. Two-scale concurrent topology optimization of lattice structures with connectable microstructures. Addit. Manuf. 2020, 36, 101427. [Google Scholar] [CrossRef]
- Seyedkanani, A.; Niknam, H.; Akbarzadeh, A. Bending Behavior of Optimally Graded 3D Printed Cellular Beams. Addit. Manuf. 2020, 35, 101327. [Google Scholar] [CrossRef]
- Jia, J.; Da, D.; Loh, C.L.; Zhao, H.; Yin, S.; Xu, J. Multiscale topology optimization for non-uniform microstructures with hybrid cellular automata. Struct. Multidiscip. Optim. 2020, 62, 757–770. [Google Scholar] [CrossRef]
- Kang, D.; Park, S.; Son, Y.; Yeon, S.; Kim, S.H.; Kim, I. Multi-lattice inner structures for high-strength and light-weight in metal selective laser melting process. Mater. Des. 2019, 175, 107786. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Anisotropic design and optimization of conformal gradient lattice structures. Comput. Aided Des. 2020, 119, 102787. [Google Scholar] [CrossRef]
- Radman, A.; Huang, X.; Xie, Y. Topology optimization of functionally graded cellular materials. J. Mater. Sci. 2013, 48, 1503–1510. [Google Scholar] [CrossRef]
- Bharanidaran, R.; Ramesh, T. Numerical simulation and experimental investigation of a topologically optimized compliant microgripper. Sens. Actuators A Phys. 2014, 205, 156–163. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Pinskier, J.; Tian, Y.; Zhang, D. Topology optimisation of bridge input structures with maximal amplification for design of flexure mechanisms. Mech. Mach. Theory 2018, 122, 113–131. [Google Scholar] [CrossRef]
- Ramesh, T.; Bharanidaran, R.; Gopal, V. Design and development of XY Micro-Positioning Stage Using Modified Topology Optimization Technique. Appl. Mech. Mater. 2014, 592, 2220–2224. [Google Scholar] [CrossRef]
- Wang, J.X.; Guo, W.Z. The Topology Optimization of Controllable Path-Generating Compliant Mechanisms. J. Shanghai Jiaotong Univ. 2006, 6. [Google Scholar]
- Bharanidaran, R.; Ramesh, T. A modified post-processing technique to design a compliant based microgripper with a plunger using topological optimization. Int. J. Adv. Manuf. Technol. 2017, 93, 103–112. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Optimal cellular core topologies for one-dimensional morphing aircraft structures. J. Mech. Des. 2012, 134, 081005. [Google Scholar] [CrossRef]
- Chang, L.; Shen, X.; Dai, Y.; Wang, T.; Zhang, L. Investigation on the mechanical properties of topologically optimized cellular structures for sandwiched morphing skins. Compos. Struct. 2020, 250, 112555. [Google Scholar] [CrossRef]
- Gomes, P.; Palacios, R. Aerodynamic-driven topology optimization of compliant airfoils. Struct. Multidiscip. Optim. 2020, 62, 2117–2130. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, C.; Yang, C.; Cavalieri, V.; De Gaspari, A.; Ricci, S. Combining Density-based Approach and Optimization Refinement in the Design of Morphing Airfoil Structures. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1546. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Zhang, L.; Hao, Y.; Sercombe, T. Early plastic deformation behaviour and energy absorption in porous β-type biomedical titanium produced by selective laser melting. Scr. Mater. 2018, 153, 99–103. [Google Scholar] [CrossRef]
- Deng, H.; Cheng, L.; Liang, X.; Hayduke, D.; To, A.C. Topology optimization for energy dissipation design of lattice structures through snap-through behavior. Comput. Methods Appl. Mech. Eng. 2020, 358, 112641. [Google Scholar] [CrossRef]
- Najmon, J.; DeHart, J.; Wood, Z.; Tovar, A. Development of a Helmet Liner Through Bio-Inspired Structures and Topology Optimized Compliant Mechanism Arrays. SAE Int. J. Trans. Safety 2018, 6, 217–235. [Google Scholar] [CrossRef]
- Borovinšek, M.; Novak, N.; Vesenjak, M.; Ren, Z.; Ulbin, M. Designing 2D auxetic structures using multi-objective topology optimization. Mater. Sci. Eng. A 2020, 795, 139914. [Google Scholar] [CrossRef]
- de Lima, C.R.; Paulino, G.H. Auxetic structure design using compliant mechanisms: A topology optimization approach with polygonal finite elements. Adv. Eng. Softw. 2019, 129, 69–80. [Google Scholar] [CrossRef]
- Kaminakis, N.T.; Drosopoulos, G.A.; Stavroulakis, G.E. Design and verification of auxetic microstructures using topology optimization and homogenization. Arch. Appl. Mech. 2015, 85, 1289–1306. [Google Scholar] [CrossRef]
- Andreassen, E.; Lazarov, B.S.; Sigmund, O. Design of manufacturable 3D extremal elastic microstructure. Mech. Mater. 2014, 69, 1–10. [Google Scholar] [CrossRef]
- Deng, H.; Hinnebusch, S.; To, A.C. Topology optimization design of stretchable metamaterials with Bézier skeleton explicit density (BSED) representation algorithm. Comput. Methods Appl. Mech. Eng. 2020, 366, 113093. [Google Scholar] [CrossRef]
- Lum, G.Z.; Teo, T.J.; Yeo, S.H.; Yang, G.; Sitti, M. Structural optimization for flexure-based parallel mechanisms–Towards achieving optimal dynamic and stiffness properties. Precis. Eng. 2015, 42, 195–207. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X. A new topology optimization method for planar compliant parallel mechanisms. Mech. Mach. Theory 2016, 95, 42–58. [Google Scholar] [CrossRef]
- Jin, M.; Zhang, X.; Yang, Z.; Zhu, B. Jacobian-based topology optimization method using an improved stiffness evaluation. J. Mech. Des. 2018, 140, 011402. [Google Scholar] [CrossRef]
- Zhan, W.; He, X.; Yang, J.; Lai, J.; Zhu, D. Optimal design method for 3-DOF planar compliant mechanisms based on mapping matrix constraints. Structures 2020, 26, 1–5. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, D.; Liu, N.; Zhao, W. Multi-objective topology optimization of a compliant parallel planar mechanism under combined load cases and constraints. Micromachines 2017, 8, 279. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Zhang, C.; Feng, Y. Topological Structure Synthesis of Three-Rotational-DOF Compliant Mechanisms. In Proceedings of the 2018 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Hangzhou, China, 13–17 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 304–307. [Google Scholar] [CrossRef]
- Zhu, D.; Feng, Y.; Zhan, W. Topology optimization of three-translational degree-of-freedom spatial compliant mechanism. Adv. Mech. Eng. 2019, 11, 1–12. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Fatikow, S. Design of single-axis flexure hinges using continuum topology optimization method. Sci. China Technol. Sci. 2014, 57, 560–567. [Google Scholar] [CrossRef]
- Zhu, B.; Liu, M.; Chen, Q.; Li, H.; Zhang, X.; Fu, Y. Topology optimization of the flexure hinges for precision engineering. In Proceedings of the 2017 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Montreal, QC, Canada, 17–21 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, X.; Liu, M.; Chen, Q.; Li, H. Topological and shape optimization of flexure hinges for designing compliant mechanisms using the level set method. Chin. J. Mech. Eng. 2019, 32, 13. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Topology optimization of large-displacement flexure hinges. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Boston, MA, USA, 2–5 August 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 5A, p. V05AT08A005. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design and analysis of a high-accuracy flexure hinge. Rev. Sci. Instrum. 2016, 87, 055106. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design of flexure hinges based on stress-constrained topology optimization. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4635–4645. [Google Scholar] [CrossRef]
- Liu, M.; Zhan, J.; Zhu, B.; Zhang, X. Topology Optimization of Flexure Hinges with Distributed Stress for Flexure-Based Mechanisms. In Proceedings of the 2018 International Conference on Manipulation, Automation and Robotics at Small Scales (MARSS), Nagoya, Japan, 4–8 July 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, M.; Zhan, J.; Zhang, X. Topology optimization of distributed flexure hinges with desired performance. Eng. Optim. 2020, 52, 405–425. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design and analysis of a multi-notched flexure hinge for compliant mechanisms. Precis. Eng. 2017, 48, 292–304. [Google Scholar] [CrossRef]
- Lobontiu, N.; Cullin, M. In-plane elastic response of two-segment circular-axis symmetric notch flexure hinges: The right circular design. Precis. Eng. 2013, 37, 542–555. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.; Garcia, E.; Goldfarb, M. Corner-filleted flexure hinges. J. Mech. Des. 2001, 123, 346–352. [Google Scholar] [CrossRef]
- Smith, S.T.; Badami, V.G.; Dale, J.S.; Xu, Y. Elliptical flexure hinges. Rev. Sci. Instrum. 1997, 68, 1474–1483. [Google Scholar] [CrossRef]
- Lobontiu, N.; Paine, J.S.; O’Malley, E.; Samuelson, M. Parabolic and hyperbolic flexure hinges: Flexibility, motion precision and stress characterization based on compliance closed-form equations. Precis. Eng. 2002, 26, 183–192. [Google Scholar] [CrossRef]
- Qiu, L.; Yue, X.; Xie, Z. Design and analysis of Multicavity Flexure Hinge (MCFH) based on three-dimensional continuum topology optimization. Mech. Mach. Theory 2019, 139, 21–33. [Google Scholar] [CrossRef]
- Qiu, L.; Yue, X.; Zheng, L.; Li, Y. Design and analysis of porous flexure hinge based on dual-objective topology optimization of three-dimensional continuum. J. Braz. Soc. Mech. Sci. Eng. 2020, 42. [Google Scholar] [CrossRef]
- Li, L.; Geng, Z.; Zhong, B. Design and Optimization of Compliant Revolute Joint Based on Finite Element Method. In Intelligent Computing, Networked Control, and Their Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 115–124. [Google Scholar] [CrossRef]
- Li, L.; Geng, Z.; Zhu, X. Experimental and numerical investigation of a large stroke compliant revolute joint. Microsyst. Technol. 2019, 25, 925–935. [Google Scholar] [CrossRef]
- Li, L.; Zhu, X. Design of compliant revolute joints based on mechanism stiffness matrix through topology optimization using a parameterization level set method. Struct. Multidiscip. Optim. 2019, 60, 1475–1489. [Google Scholar] [CrossRef]




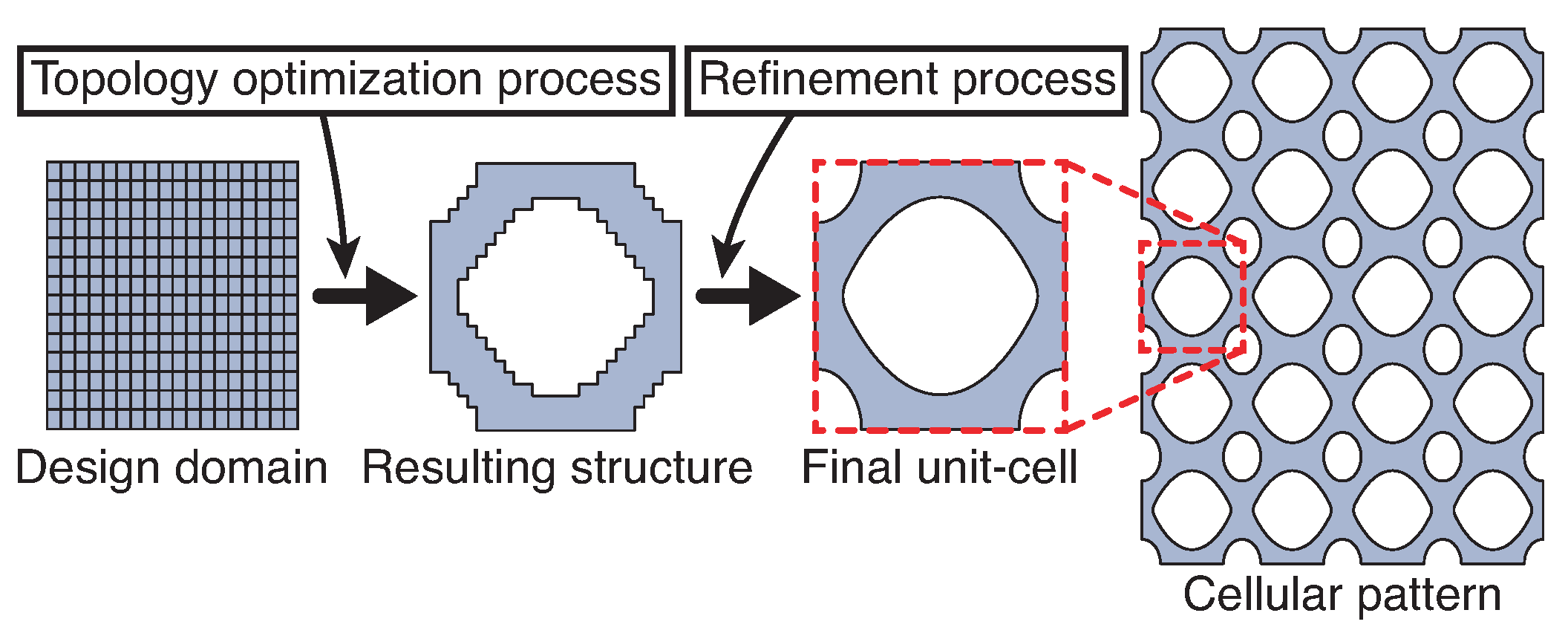
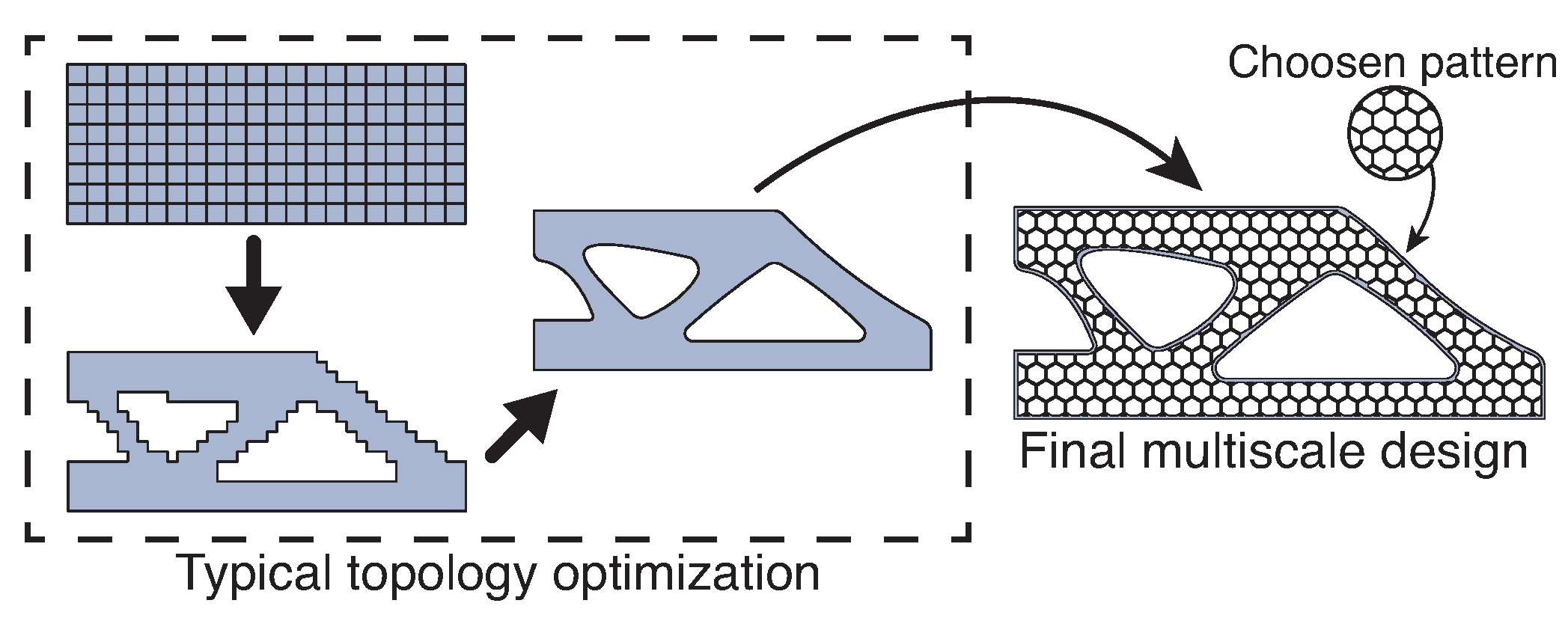
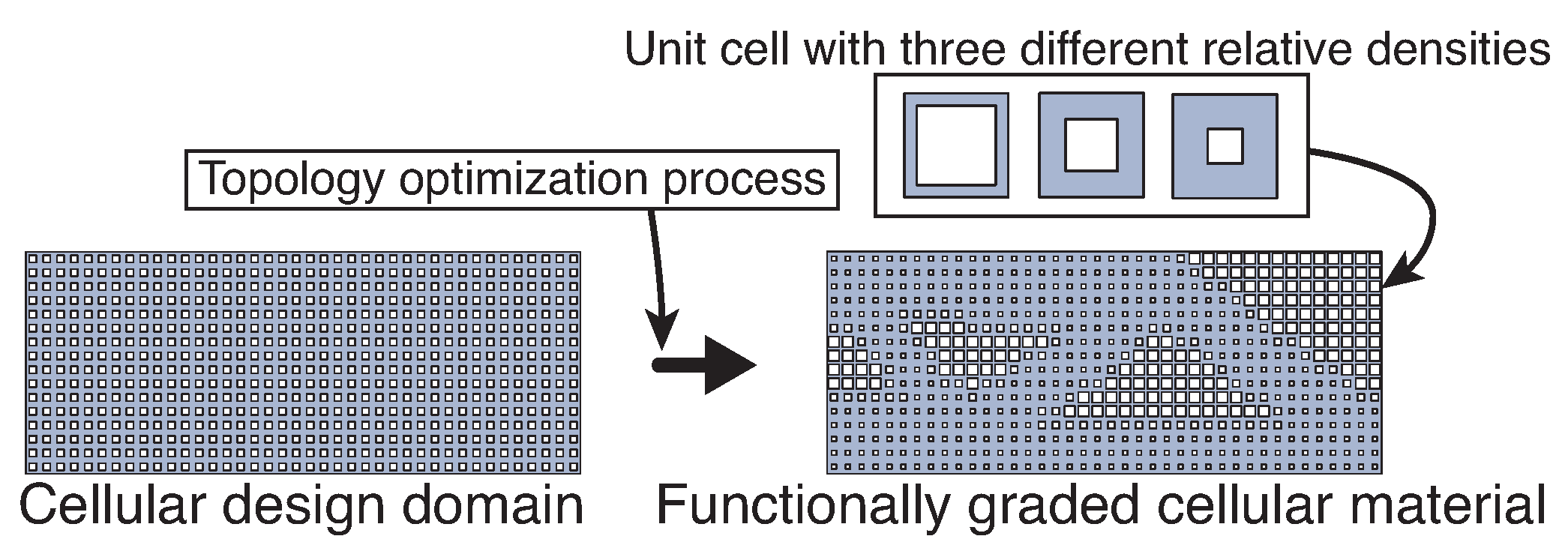
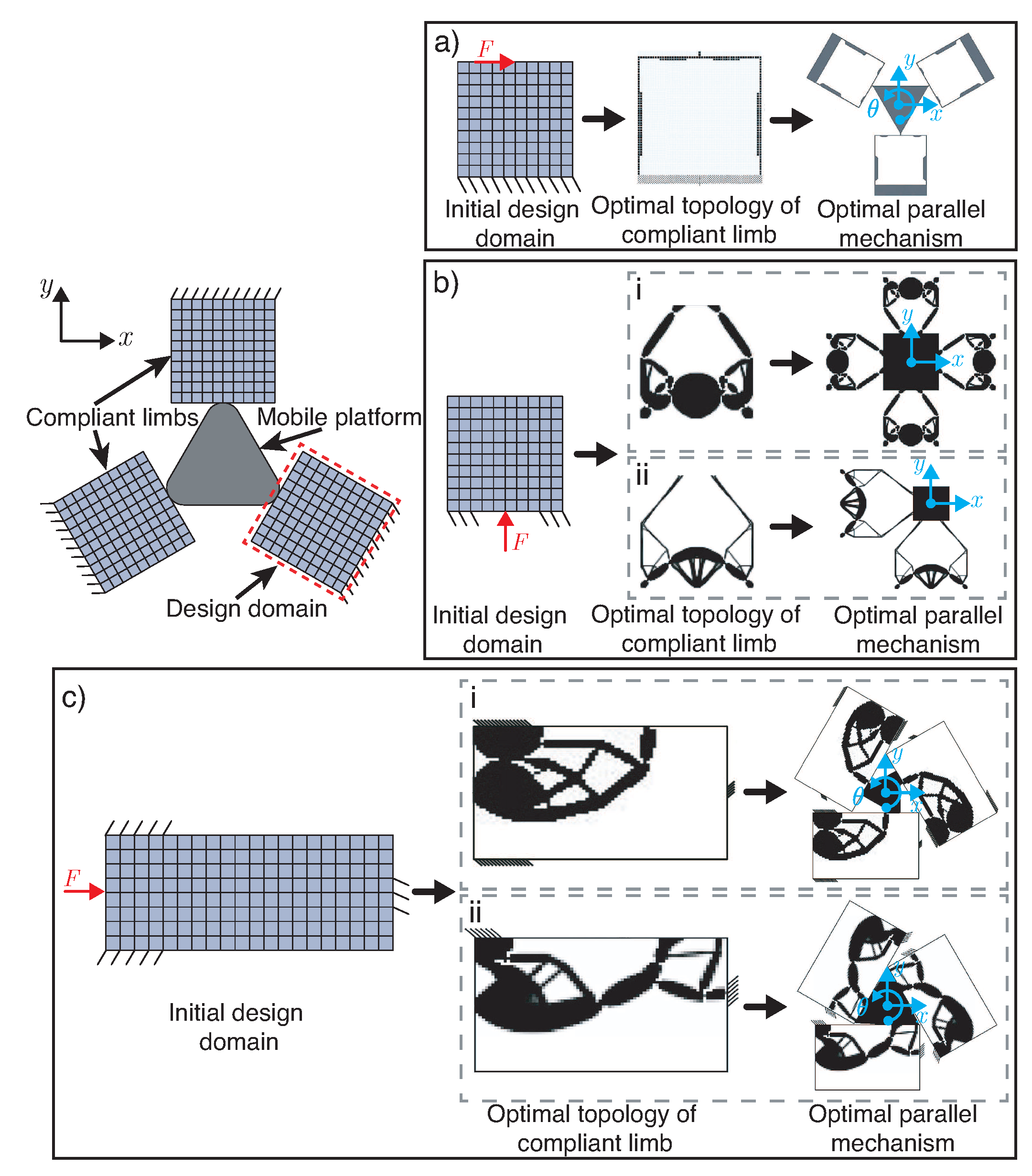



| Author | Cellular | Young’s Modulus Ratios | Weight Reduction | |
|---|---|---|---|---|
| Structure | ||||
| Bornengo et al. [116] | A—Hex. Chiral | 1.18–0.60 | 1.18–0.60 | 90−95 |
| Dong et al. [117] | A—Re-entrant | 2.51 | 1.35 | − |
| Zhang et al. [118] | P—Cross-shaped | 0.25 | 0.13 | − |
| Heo et al. [119] | A—Hex. Chiral | 11.58 | 11.58 | 90 |
| P—Hexagonal | 69.32 | 69.32 | 94 | |
| A—Re-entrant | 427.19 | 427.19 | 81 | |
| Author | Cellular | Young’s Modulus Ratios | |
|---|---|---|---|
| Structure | |||
| Olympio et al. [121] | Z—hybrid | 0.096–0.0047 | − |
| Z—Accordion | 0.0047–0.10 | − | |
| Olympio et al. [120] | P—Hexagonal | 0.39–2.88 × | 0.022–1.07 × |
| Chen et al. [122] | Z—Chevron | 0.033–2.92 × | 5.2 × –6.74 × |
| Vigliotti et al. [123] | Z—Chevron | 3.29 × | 2.05 × |
| Chang et al. [124] | P—Hexagonal | 0.015 | 0.0025 |
| Z—Accordion | 0.023 | 0.0026 | |
| Zadeh et al. [125,126] | Z—Fish cell | 1.84 × –5.75 × | 1.30 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arredondo-Soto, M.; Cuan-Urquizo, E.; Gómez-Espinosa, A. A Review on Tailoring Stiffness in Compliant Systems, via Removing Material: Cellular Materials and Topology Optimization. Appl. Sci. 2021, 11, 3538. https://doi.org/10.3390/app11083538
Arredondo-Soto M, Cuan-Urquizo E, Gómez-Espinosa A. A Review on Tailoring Stiffness in Compliant Systems, via Removing Material: Cellular Materials and Topology Optimization. Applied Sciences. 2021; 11(8):3538. https://doi.org/10.3390/app11083538
Chicago/Turabian StyleArredondo-Soto, Mauricio, Enrique Cuan-Urquizo, and Alfonso Gómez-Espinosa. 2021. "A Review on Tailoring Stiffness in Compliant Systems, via Removing Material: Cellular Materials and Topology Optimization" Applied Sciences 11, no. 8: 3538. https://doi.org/10.3390/app11083538
APA StyleArredondo-Soto, M., Cuan-Urquizo, E., & Gómez-Espinosa, A. (2021). A Review on Tailoring Stiffness in Compliant Systems, via Removing Material: Cellular Materials and Topology Optimization. Applied Sciences, 11(8), 3538. https://doi.org/10.3390/app11083538








