True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA
Abstract
1. Introduction: Random Number Generation for Security
2. All-Digital True Random Number Generators
2.1. Information Content and Entropy
2.2. Digital TRNGs
2.2.1. Transition Effect Ring Oscillator
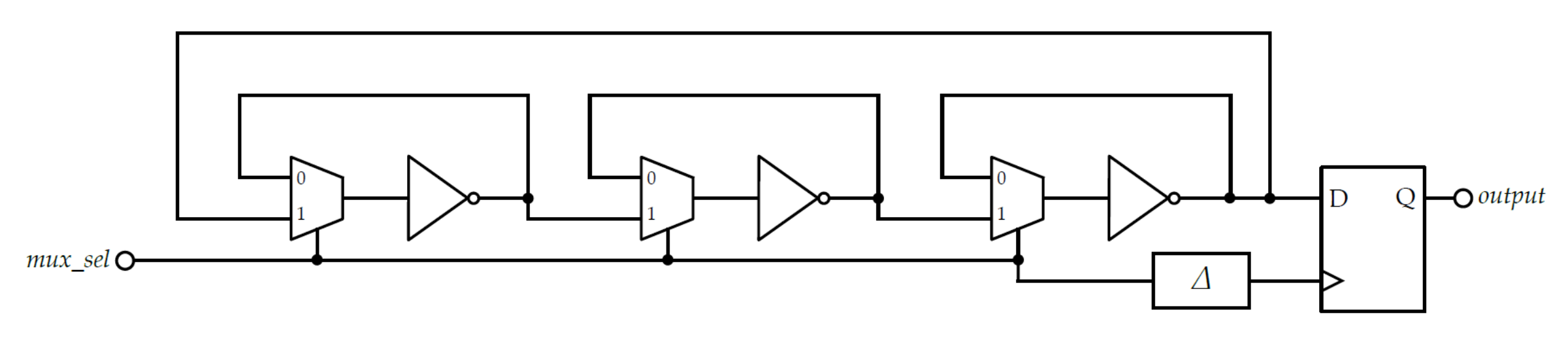
2.2.2. Metastable Ring Oscillator
- Initialization: the oscillator is brought into metastable state with . The metastable voltage is perturbed by low amplitude noise.
- Transition: signal transitions to logical 1 and the ring is recomposed. The low amplitude noise is amplified by inverters. The ring starts in a random state.
- Sampling: once the oscillator stabilizes to full-logic levels, sampling can take place using a D flip-flop. To accurately control the sampling instant, the author proposes to generate clk from the signal using a delay line.
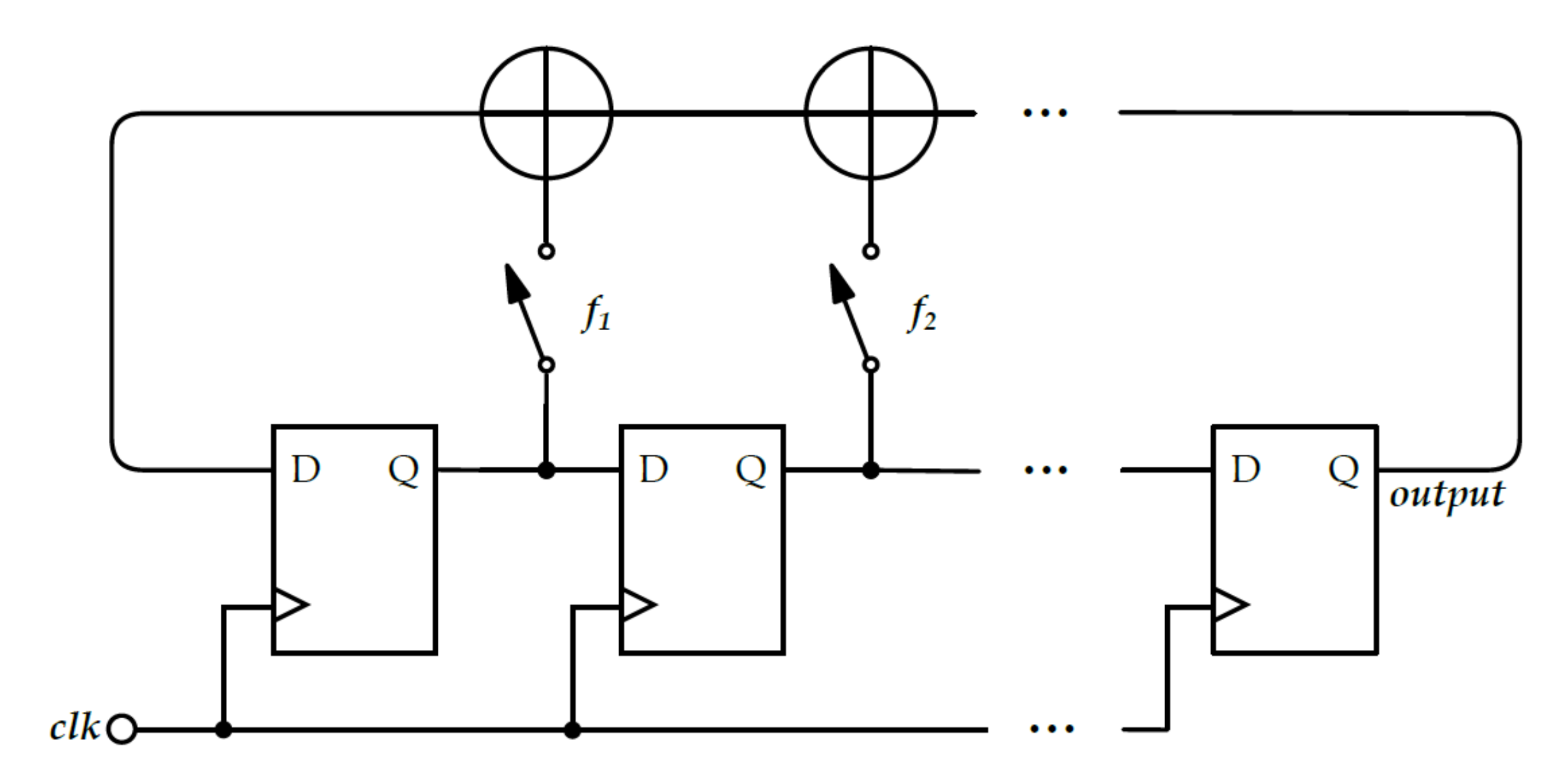
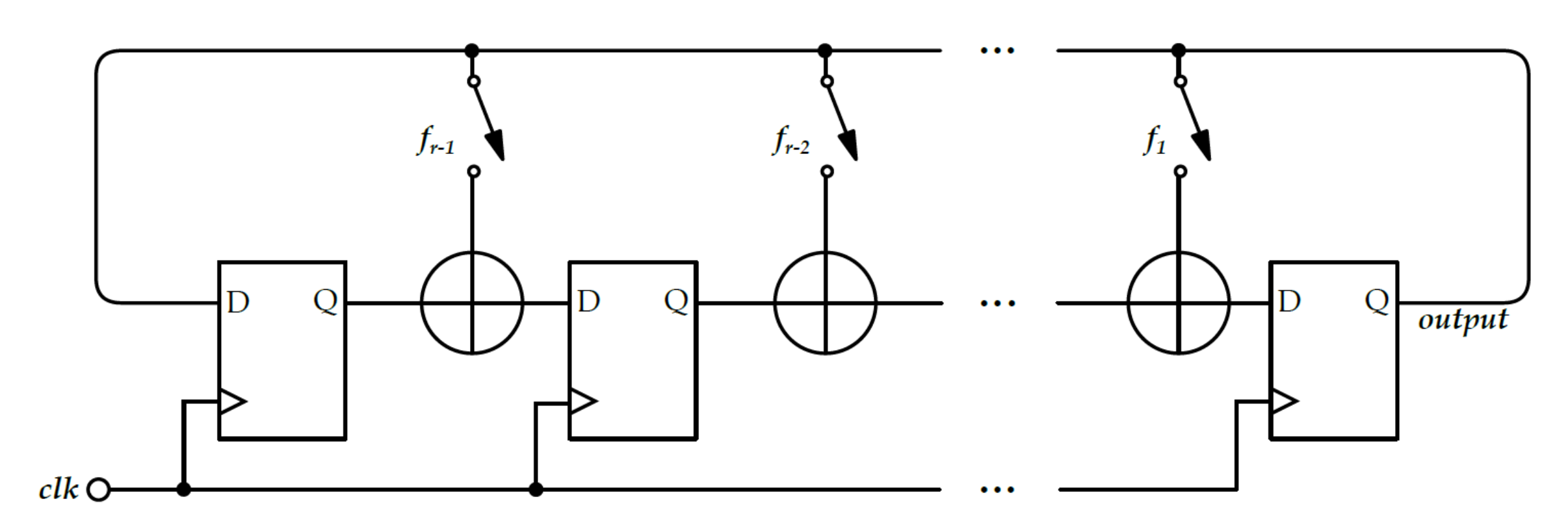
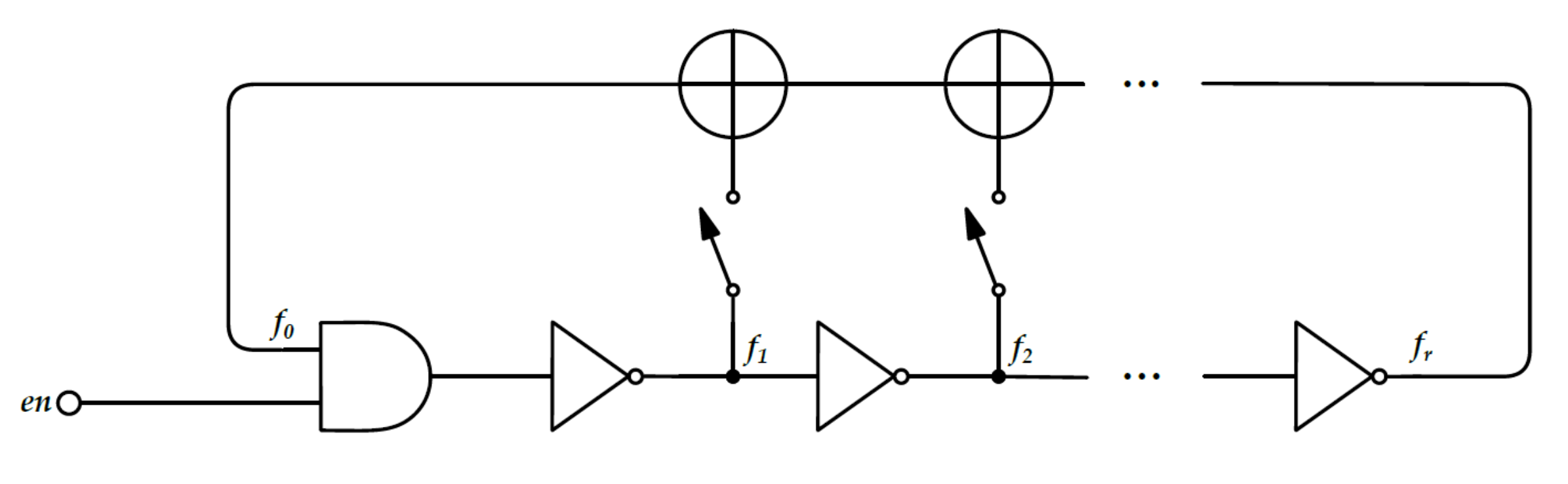
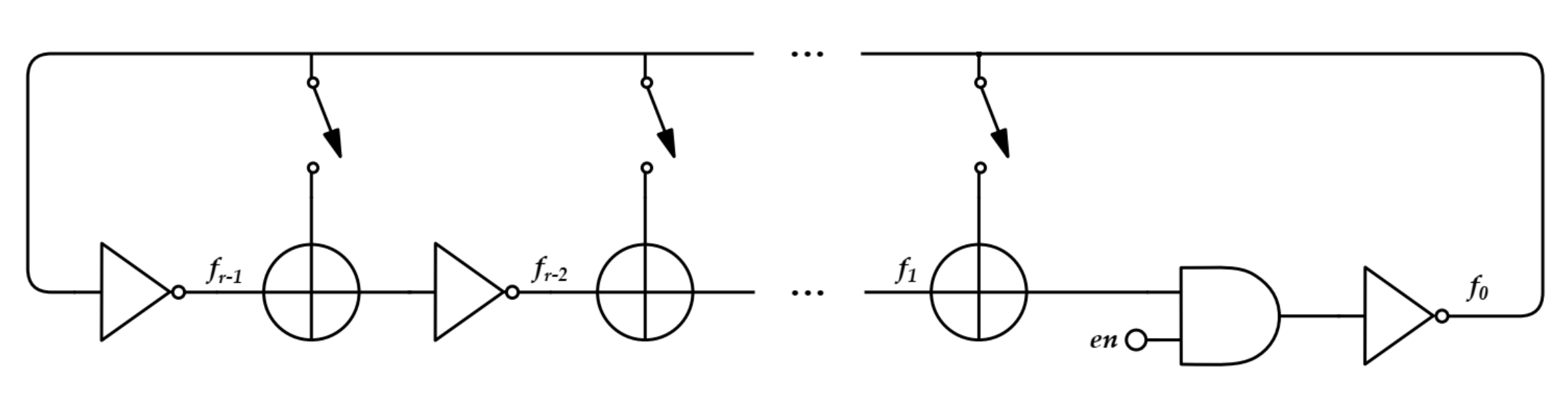
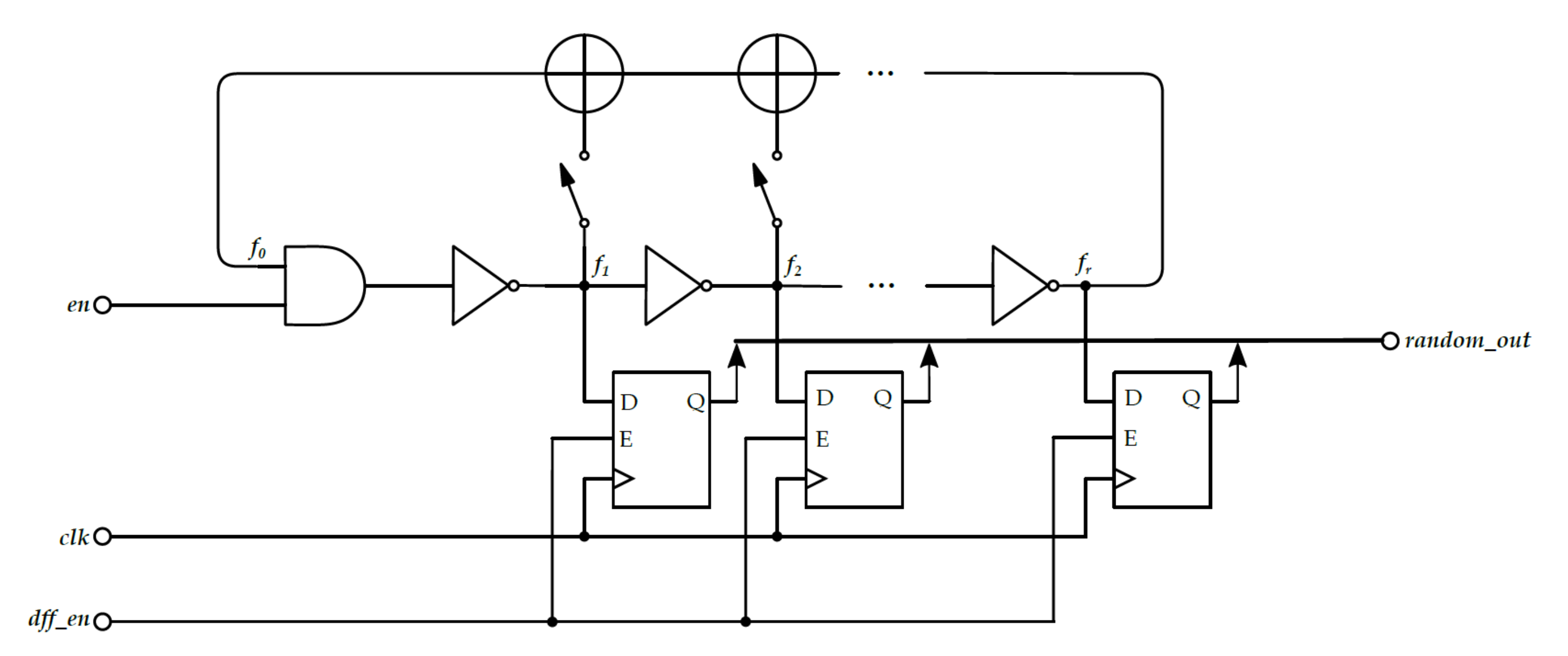
2.2.3. Fibonacci and Galois Ring Oscillators
2.2.4. FiGaRO True Random Number Generator
3. True Random Number Generators Design and Evaluation on FPGA Technology
3.1. Methods for FPGA Technology-Based TRNGs Analysis
3.2. Candidate Solutions
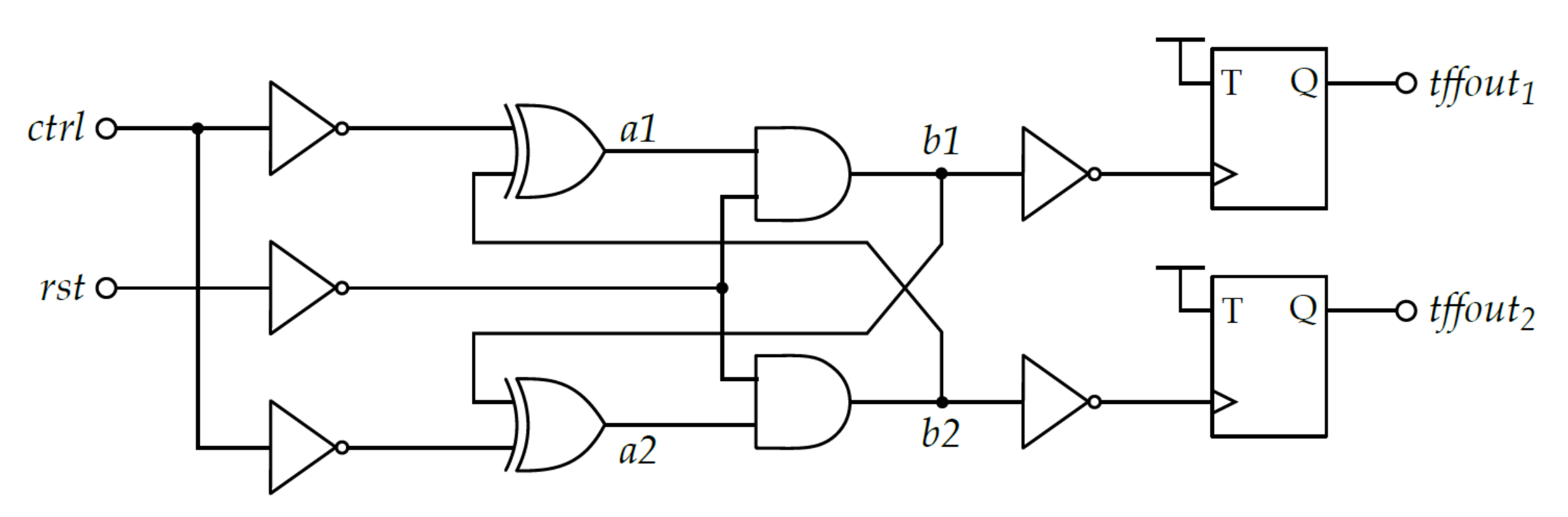
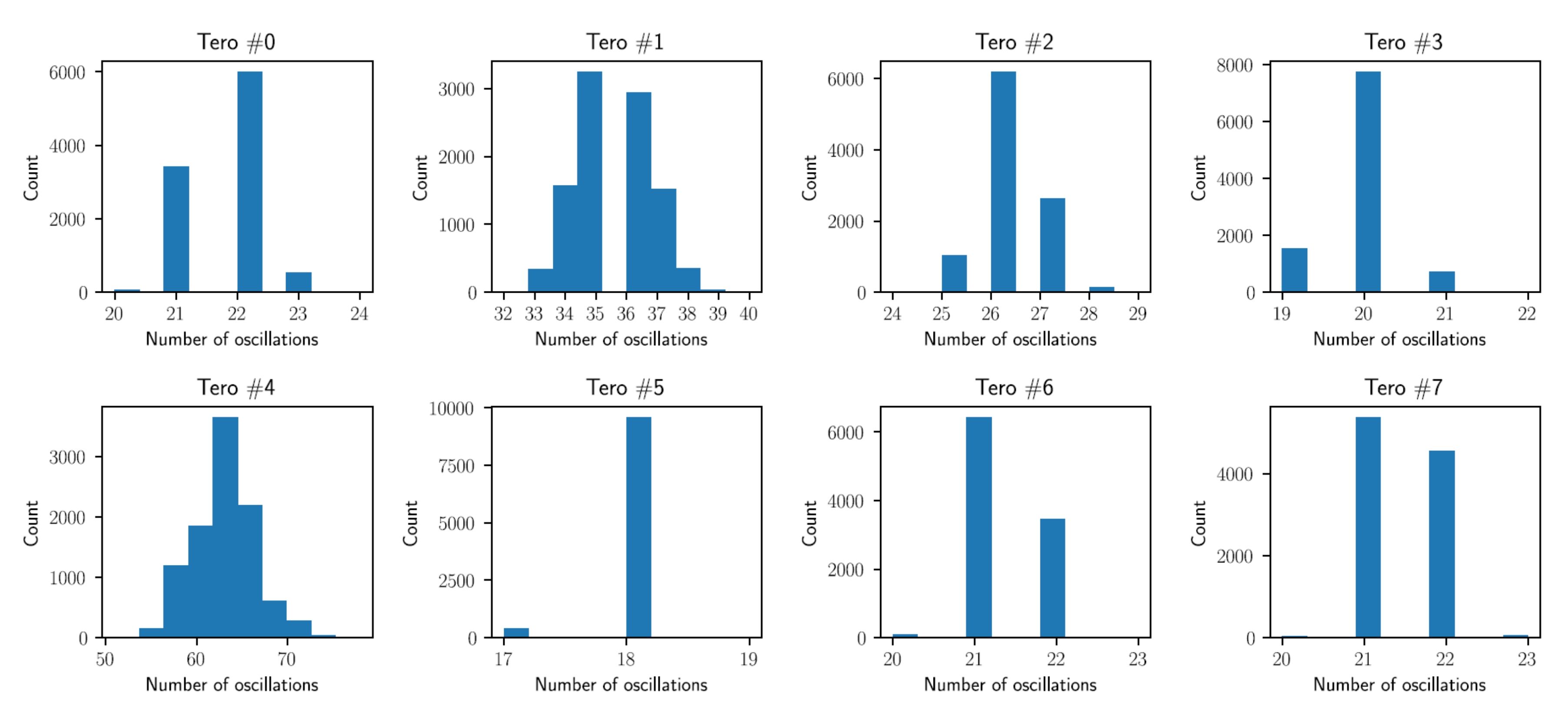
3.2.1. Transition Effect Ring Oscillator (TERO)
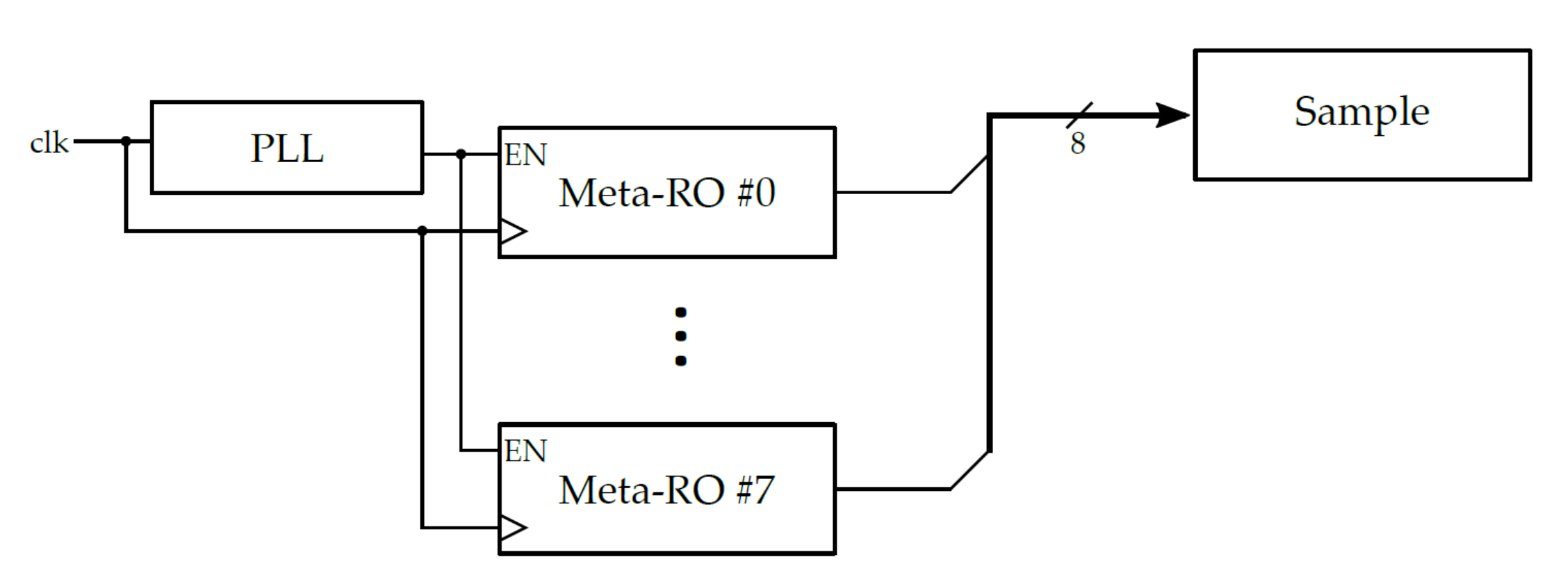
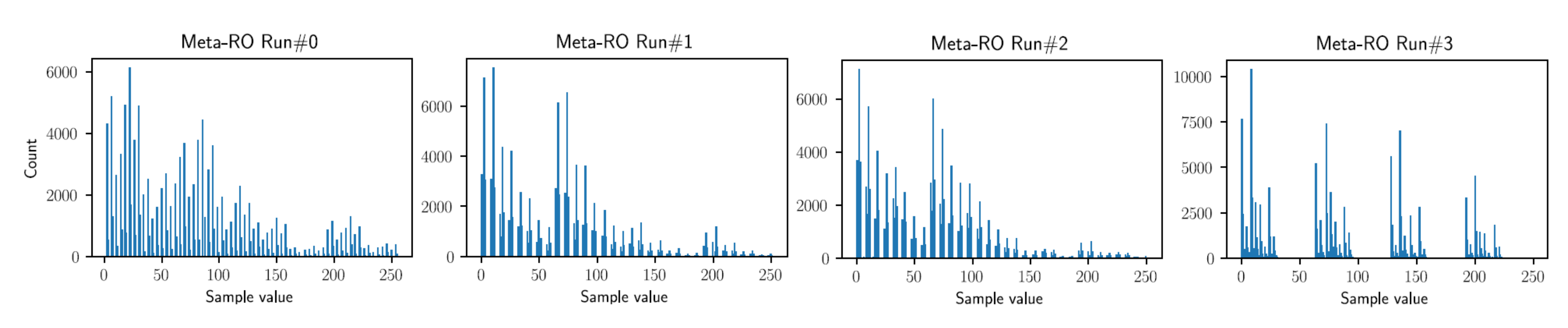
3.2.2. Meta-Ring Oscillator (Meta-RO)
3.2.3. FiRO and GaRO
3.2.4. FiGaRO
3.3. FiGaRO RNG Design
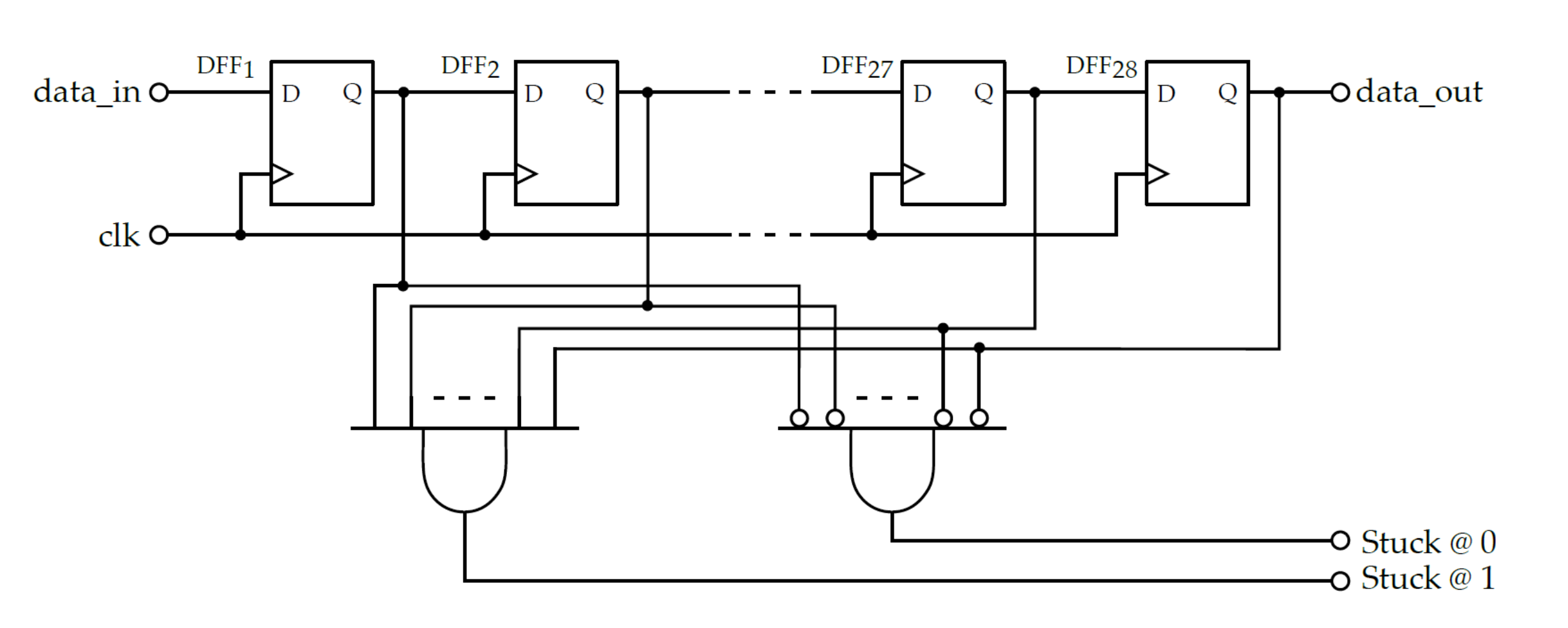
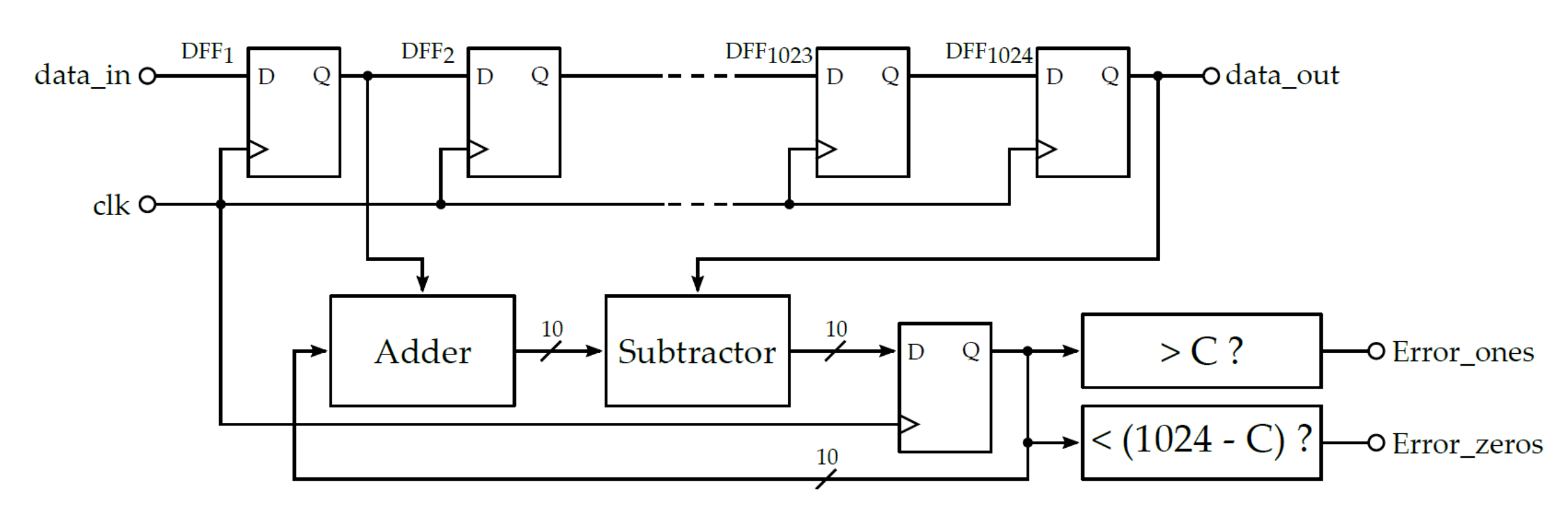
3.3.1. Health Tests
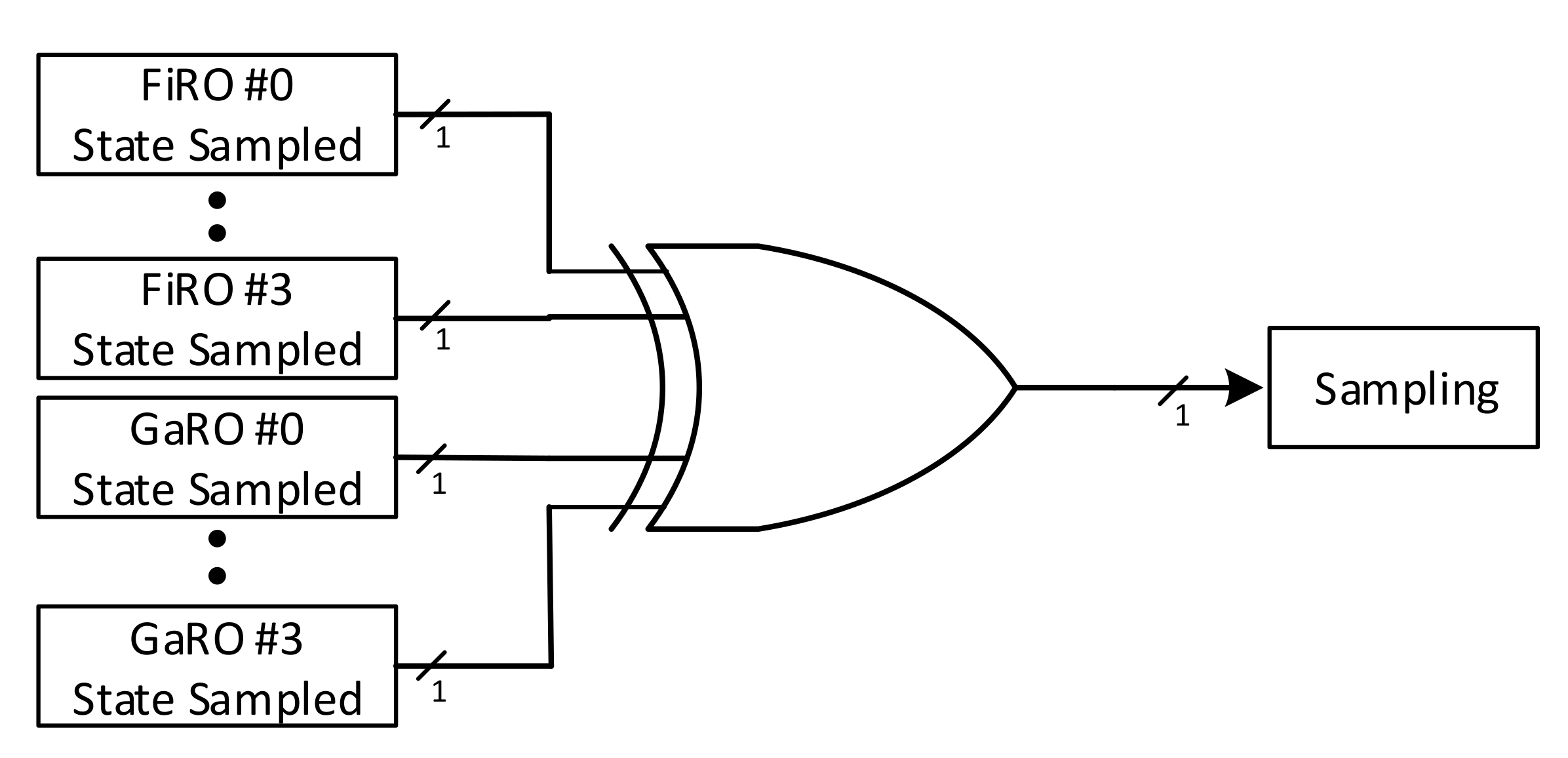
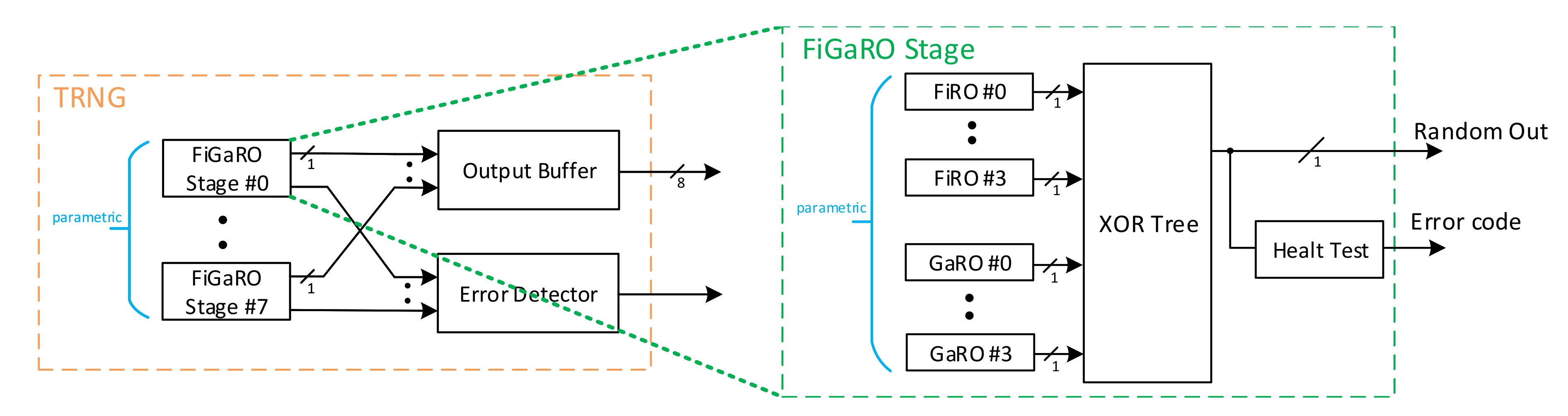
3.3.2. Overall RNG Architecture
4. Implementation Results
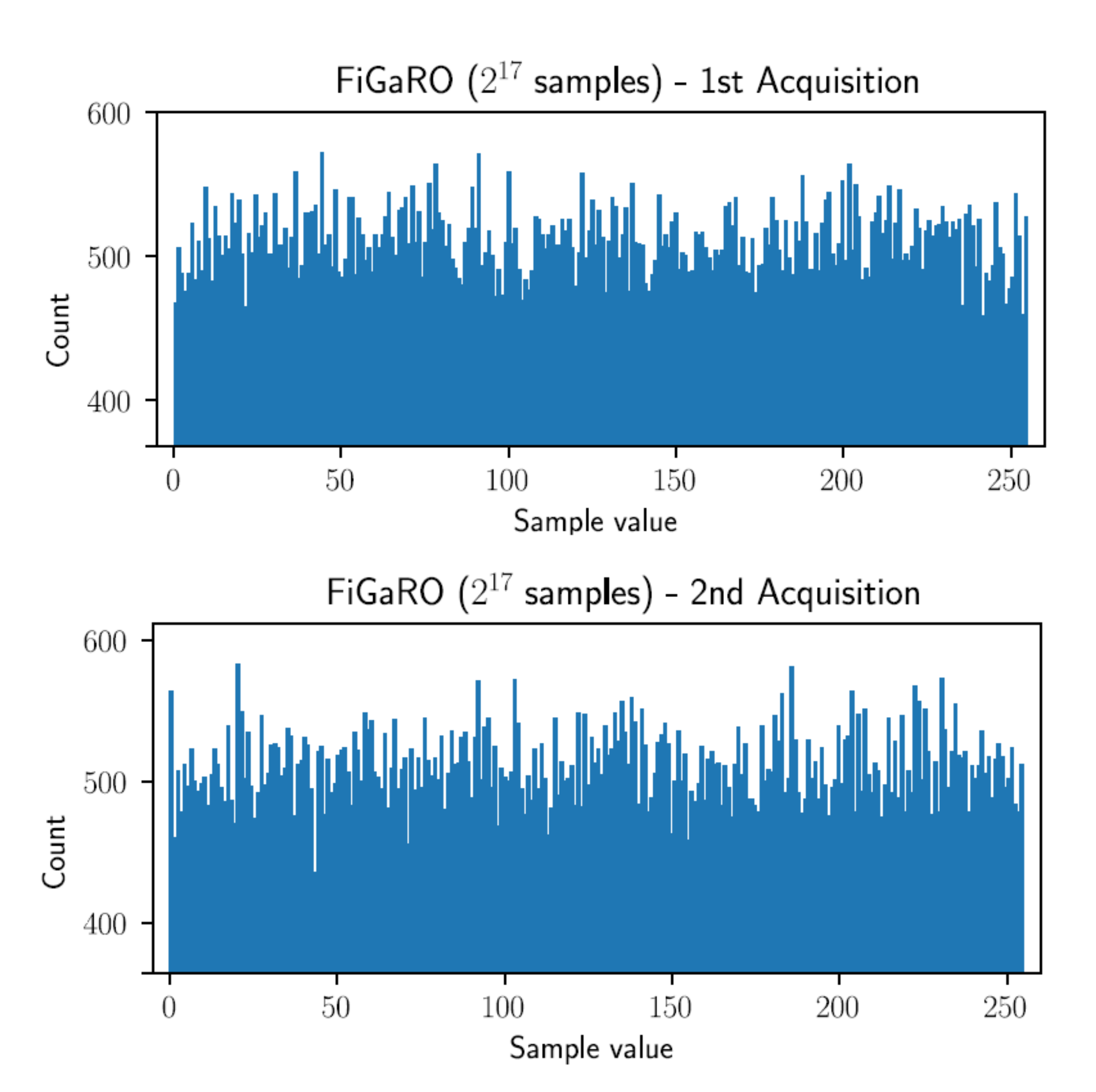
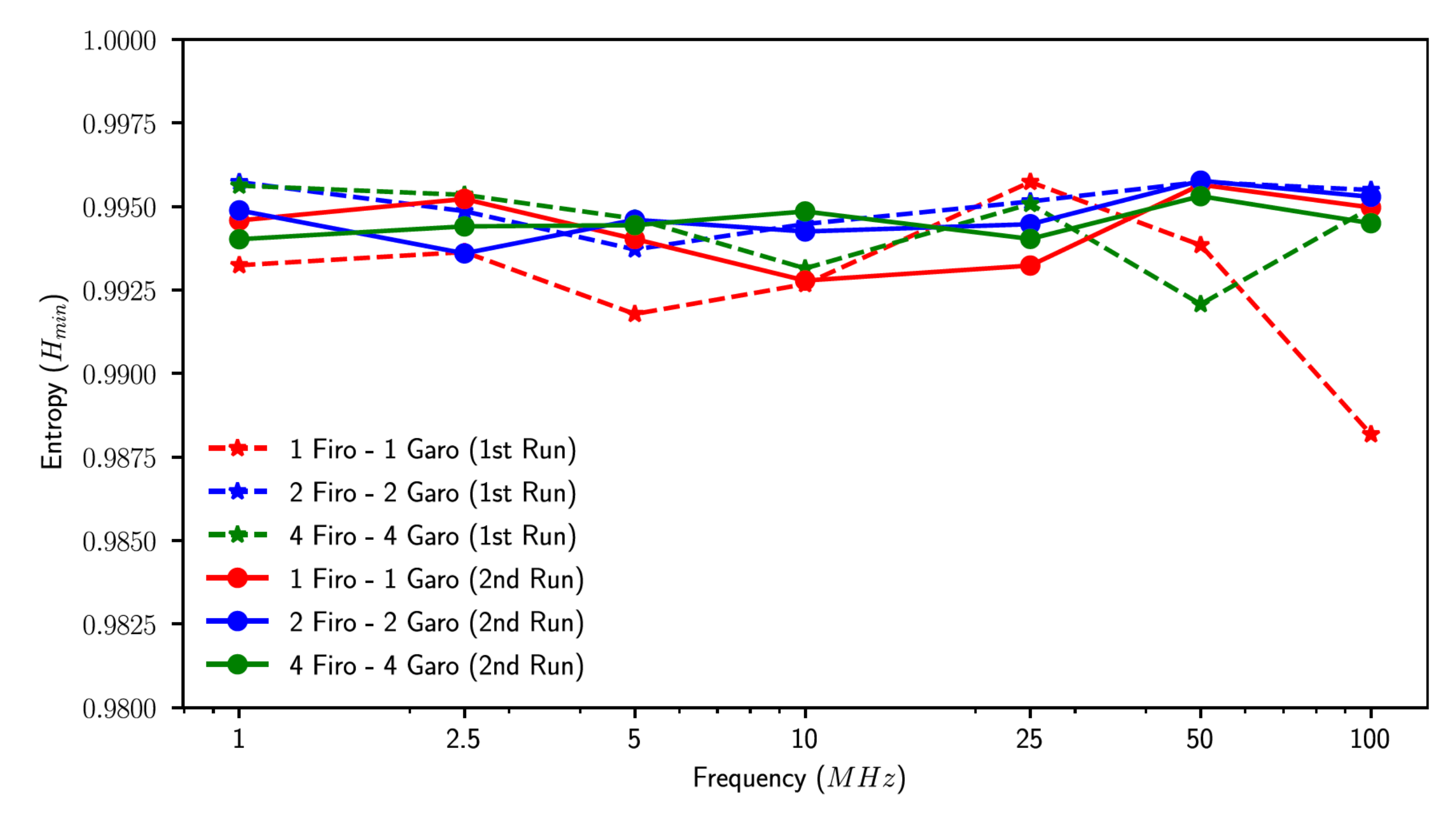
4.1. FiGaRO RNG Entropy Measurement
- The first one regards how the output quality depended on the number of elements XORed together inside each FiGaRO stage. Ideally, the more elements were used, the more the output quality was high but this depended on an assumption of device independence, which had to be verified.
- The second one regards how the output quality depended on the sampling frequency. Until this point sampling took place at 1 MHz but deriving a plot of entropy as a function of frequency may have allowed us to make a trade-off between entropy source throughput and output quality.
- 1 FiRO and 1 GaRO XORed together
- 2 FiRO and 2 GaRO XORed together
- 4 FiRO and 4 GaRO XORed together
4.2. Synthesis and Implementation Results
- 1FiRO-1GaRO Configuration was the one with smaller area footprint but also the worst entropy;
- 2FiRO-2GaRO and 4FiRO 4GaRO were comparable in terms of entropy;
- System robustness to possible stuck in the oscillation grew linearly with the number of FiRO and GaRO composing a FiGaRO stage;
- Resources usage grew linearly with the number of FiRO and GaRO composing a FiGaRO stage;
- The throughput of the system grew linearly with the number of FiGaRO stages in parallel;
- Resources usage grew linearly with the number of FiGaRO stages in parallel;
4.3. NIST Statistical Test Suite
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rostami, M.; Koushanfar, F.; Karri, R. A Primer on Hardware Security: Models, Methods, and Metrics. Proc. IEEE 2014, 102, 1283–1295. [Google Scholar] [CrossRef]
- El Mrabet, Z.; Kaabouch, N.; El Ghazi, H.; El Ghazi, H. Cyber-security in smart grid: Survey and challenges. Comput. Electr. Eng. 2018, 67, 469–482. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Badra, M.; Guillet, T.; Serhrouchni, A. Random values, nonce and challenges: Semantic meaning versus opaque and strings of data. In Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall, Anchorage, AK, USA, 20–23 September 2009; pp. 1–5. [Google Scholar]
- Jan Pelzl, C.P. Understanding Cryptography; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hong, S.L.; Liu, C. Sensor-based random number generator seeding. IEEE Access 2015, 3, 562–568. [Google Scholar] [CrossRef]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Bertolucci, M.; Belli, J.; Fanucci, L.; Saponara, S. Cryptographically secure pseudo-random number generator IP-core based on SHA2 algorithm. Sensors 2020, 20, 1869. [Google Scholar] [CrossRef] [PubMed]
- Simion, E. Entropy and Randomness: From Analogic to Quantum World. IEEE Access 2020, 8, 74553–74561. [Google Scholar] [CrossRef]
- Gong, L.; Zhang, J.; Liu, H.; Sang, L.; Wang, Y. True random number generators using electrical noise. IEEE Access 2019, 7, 125796–125805. [Google Scholar] [CrossRef]
- Tehranipoor, F.; Wortman, P.; Karimian, N.; Yan, W.; Chandy, J.A. DVFT: A Lightweight Solution for Power-Supply Noise-Based TRNG Using Dynamic Voltage Feedback Tuning System. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 1084–1097. [Google Scholar] [CrossRef]
- Rahman, M.T.; Xiao, K.; Forte, D.; Zhang, X.; Shi, J.; Tehranipoor, M. TI-TRNG: Technology independent true random number generator. In Proceedings of the 2014 51st ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 1–5 June 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Tokunaga, C.; Blaauw, D.; Mudge, T. True Random Number Generator with a Metastability-Based Quality Control. IEEE J. Solid-State Circuits 2008, 43, 78–85. [Google Scholar] [CrossRef]
- Wieczorek, P.Z.; Gołofit, K. Dual-Metastability Time-Competitive True Random Number Generator. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 134–145. [Google Scholar] [CrossRef]
- Sivaraman, R.; Rajagopalan, S.; Sridevi, A.; Rayappan, J.B.B.; Annamalai, M.P.V.; Rengarajan, A. Metastability-Induced TRNG Architecture on FPGA. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 47–57. [Google Scholar] [CrossRef]
- Amaki, T.; Hashimoto, M.; Onoye, T. An oscillator-based true random number generator with jitter amplifier. In Proceedings of the 2011 IEEE International Symposium of Circuits and Systems (ISCAS), Rio de Janeiro, Brazil, 15–18 May 2011; pp. 725–728. [Google Scholar] [CrossRef]
- Valtchanov, B.; Aubert, A.; Bernard, F.; Fischer, V. Modeling and observing the jitter in ring oscillators implemented in FPGAs. In Proceedings of the 2008 11th IEEE Workshop on Design and Diagnostics of Electronic Circuits and Systems, Bratislava, Slovakia, 16–18 April 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Zacharias, A.; Gisha, C.G.; Jose, B.A. Chaotic Ring Oscillator Based True Random Number Generator Implementations in FPGA. In Proceedings of the 2020 24th International Symposium on VLSI Design and Test (VDAT), Bhubaneswar, India, 23–25 July 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Varchola, M.; Drutarovsky, M. New high entropy element for FPGA based true random number generators. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2010; pp. 351–365. [Google Scholar]
- Vasyltsov, I.; Hambardzumyan, E.; Kim, Y.S.; Karpinskyy, B. Fast digital TRNG based on metastable ring oscillator. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 164–180. [Google Scholar]
- Schramm, M.; Dojen, R.; Heigl, M. Experimental assessment of FIRO-and GARO-based noise sources for digital TRNG designs on FPGAs. In Proceedings of the 2017 IEEE International Conference on Applied Electronics (AE), Pilsen, Czech Republic, 5–6 September 2017; pp. 1–6. [Google Scholar]
- Demir, K.; Ergün, S. A Comparative Study on Fibonacci-Galois Ring Oscillators for Random Number Generation. In Proceedings of the 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, IL, USA, 9–12 August 2020; pp. 631–634. [Google Scholar]
- Acar, B.; Ergün, S. A Robust Digital Random Number Generator Based on Transient Effect of Ring Oscillator. In Proceedings of the 2020 IEEE 11th Latin American Symposium on Circuits Systems (LASCAS), San José, Costa Rica, 25–28 February 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Reyneri, L.M.; Del Corso, D.; Sacco, B. Oscillatory metastability in homogeneous and inhomogeneous flip-flops. IEEE J. Solid State Circuits 1990, 25, 254–264. [Google Scholar] [CrossRef]
- Golic, J.D. New methods for digital generation and postprocessing of random data. IEEE Trans. Comput. 2006, 55, 1217–1229. [Google Scholar] [CrossRef]
- Haddad, P.; Fischer, V.; Bernard, F.; Nicolai, J. A physical approach for stochastic modeling of TERO-based TRNG. In International Workshop on Cryptographic Hardware and Embedded Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 357–372. [Google Scholar]
- Li, T.; Wu, L.; Zhang, X.; Wu, X.; Zhou, J.; Wang, X. A novel transition effect ring oscillator based true random number generator for a security SoC. In Proceedings of the 2017 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Hsinchu, Taiwan, 18–20 October 2017; pp. 1–2. [Google Scholar]
- Fujieda, N. On the Feasibility of TERO-Based True Random Number Generator on Xilinx FPGAs. In Proceedings of the 2020 30th International Conference on Field-Programmable Logic and Applications (FPL), Gothenburg, Sweden, 31 August–4 September 2020; pp. 103–108. [Google Scholar]
- Stanchieri, G.D.P.; De Marcellis, A.; Palange, E.; Faccio, M. A true random number generator architecture based on a reduced number of FPGA primitives. AEU Int. J. Electron. Commun. 2019, 105, 15–23. [Google Scholar] [CrossRef]
- Turan, M.S.; Barker, E.; Kelsey, J.; McKay, K.A.; Baish, M.L.; Boyle, M. Recommendation for the Entropy Sources Used for Random Bit Generation; NIST DRAFT Special Publication 800-90B; NIST: Gaithersburg, MD, USA, 2018. [Google Scholar]
- Turan, M.S.; Barker, E.; Kelsey, J.; McKay, K.A.; Baish, M.L.; Boyle, M. SP800-90B Entropy Assessment; NIST: Gaithersburg, MD, USA, 2018. [Google Scholar] [CrossRef]
- Yang, B.; Mentens, N. ES-TRNG: A high-throughput, low-area true random number generator based on edge sampling. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 267–292. [Google Scholar] [CrossRef]
- Sunar, B.; Martin, W.J.; Stinson, D.R. A provably secure true random number generator with built-in tolerance to active attacks. IEEE Trans. Comput. 2006, 56, 109–119. [Google Scholar] [CrossRef]
- Anandakumar, N.N.; Sanadhya, S.K.; Hashmi, M.S. FPGA-based true random number generation using programmable delays in oscillator-rings. IEEE Trans. Circuits Syst. II Express Briefs 2019, 67, 570–574. [Google Scholar] [CrossRef]
- Martin, H.; Peris-Lopez, P.; Tapiador, J.E.; San Millan, E. A new TRNG based on coherent sampling with self-timed rings. IEEE Trans. Ind. Inform. 2015, 12, 91–100. [Google Scholar] [CrossRef]
- Wang, X.; Liang, H.; Wang, Y.; Yao, L.; Guo, Y.; Yi, M.; Huang, Z.; Qi, H.; Lu, Y. High-Throughput Portable True Random Number Generator Based on Jitter-Latch Structure. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 741–750. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Y.; Zhao, Z.; Hui, C.; Song, Z. A New Method of True Random Number Generation based on Galois Ring Oscillator with Event Sampling Architecture in FPGA. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–29 May 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Bassham, L.; Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Leigh, S.; Levenson, M.; Vangel, M.; Heckert, N.; Banks, D. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. NIST Special Publication 800-22 (revised on 15 May 2002); 2010. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=906762 (accessed on 7 April 2021).

| Ref. | Architecture | Physical Phenomena | Preliminary |
|---|---|---|---|
| Generating Entropy | Observation | ||
| [18] | Transition Effect Ring Oscillator (TERO) | Latches oscillatory metastability | Small bandwidth, large dependence on placing |
| [19] | Metastable Ring Oscillators (Meta-RO) | Analogue metastability of inverter gates | PLL required, dependence on placing |
| [20] | Fibonacci Ring Oscillator (FiRO) | Jitter and Metastability | Good independence from placing |
| [20] | Galois Ring Oscillator (GaRO) | Jitter and Metastability | Good independence from placing |
| [21] | Fibonacci-Galois Ring Oscillator (FiGaRO) | Jitter and Metastability | Independence from placing, higher entropy and robustness respect to single Fibonacci and Galois Oscillator |
| FiRO Instance | GaRO Instance | |||||||
|---|---|---|---|---|---|---|---|---|
| #0 | #1 | #2 | #3 | #0 | #1 | #2 | #3 | |
| Count of zeros | 64,463 | 62,237 | 62,336 | 62,624 | 6274 | 65,784 | 64,161 | 58,209 |
| Count of ones | 66,609 | 68,835 | 68,736 | 68,448 | 68,308 | 65,288 | 66,911 | 72,863 |
| Difference | −2146 | −6598 | −6400 | −5824 | −5544 | 496 | −2750 | −14,654 |
| FiGaRO Instance | ||||||||
|---|---|---|---|---|---|---|---|---|
| #0 | #1 | #2 | #3 | #4 | #5 | #6 | #7 | |
| Count of zeros | 65,543 | 65,716 | 65,256 | 65,512 | 65,566 | 65,777 | 65,335 | 65,678 |
| Count of ones | 65,529 | 65,356 | 65,816 | 65,560 | 65,506 | 65,295 | 65,737 | 65,394 |
| Difference | 14 | 360 | −560 | −48 | 60 | 482 | −402 | 284 |
| FiGaRO | Configuration | Comb. | Logic |
|---|---|---|---|
| Stages | ALUTs | Regs | |
| 8 | 1FiRO 1GaRO | 291 | 186 |
| 8 | 2FiRO 2GaRO | 571 | 354 |
| 8 | 4FiRO 4GaRO | 1140 | 698 |
| 4 | 1FiRO 1GaRO | 148 | 106 |
| 4 | 2FiRO 2GaRO | 288 | 190 |
| 4 | 4FiRO 4GaRO | 572 | 358 |
| 2 | 1FiRO 1GaRO | 76 | 62 |
| 2 | 2FiRO 2GaRO | 146 | 104 |
| 2 | 4FiRO 4GaRO | 288 | 188 |
| 1 | 1FiRO 1GaRO | 40 | 40 |
| 1 | 2FiRO 2GaRO | 75 | 61 |
| 1 | 4FiRO 4GaRO | 146 | 103 |
| TRNG Type | Platform | LUTs | Registers | Bit Rate (Mbps) | Entropy | |
|---|---|---|---|---|---|---|
| This work (4 Stages, 2FiRO-2GaRO) | FiGaRO | Intel Stratix IV | 288 | 190 | 400 | 0.995 |
| [31] | ES | Xilinx Spartan 6 | 10 | 5 | 1.15 | 0.997 (Shannon Entropy) |
| [32] | RO | Xilinx Virtex 2 | – | – | 2.5 | 0.97 |
| [33] | RO—PDLs | Xilinx Spartan-3A | 528 | 177 | 6 | 0.9993 |
| [34] | STRs | Xilinx Virtex 6 | 32 | 48 | 4 | – |
| [27] | TERO | Xilinx Artix 7 | 40 | 29 | 1.91 | 0.9993 (Shannon Entropy) |
| [35] | STRs | Xilinx Virtex 6 | 56 | 19 | 100 | – |
| [36] | GaRO | Xilinx Artix 7 | 50 | 79 | 280 | 0.998 (Shannon Entropy) |
| 1FiRO-1GaRO | 2FiRO-2GaRO | 4FiRO-4GaRO | ||||
|---|---|---|---|---|---|---|
| Test Name | p-Value | Proportion | p-Value | Proportion | p-Value | Proportion |
| Frequency | 0.578763 | 0.987 | 0.959132 | 0.993 | 0.676097 | 0.984 |
| BlockFrequency | 0.701879 | 0.987 | 0.880335 | 0.990 | 0.540457 | 0.987 |
| CumulativeSums * | 0.392456 | 0.990 | 0.637119 | 0.987 | 0.001732 | 0.987 |
| Runs | 0.656634 | 0.996 | 0.141256 | 0.984 | 0.103676 | 0.996 |
| LongestRun | 0.656634 | 0.993 | 0.360699 | 0.990 | 0.005789 | 0.993 |
| Rank | 0.585209 | 0.987 | 0.839722 | 0.996 | 0.202944 | 0.981 |
| FFT | 0.794626 | 0.978 | 0.171276 | 0.990 | 0.930752 | 0.993 |
| NonOverlappingTemplate * | 0.515367 | 0.978 | 0.752361 | 0.978 | 0.019520 | 0.975 |
| OverlappingTemplate | 0.280017 | 0.990 | 0.124566 | 0.990 | 0.727346 | 0.981 |
| Universal | 0.371101 | 0.981 | 0.437274 | 0.984 | 0.875539 | 0.978 |
| ApproximateEntropy | 0.800471 | 0.993 | 0.103676 | 0.996 | 0.817667 | 0.990 |
| RandomExcursions * | 0.590375 | 0.980 | 0.063657 | 0.974 | 0.522989 | 0.984 |
| RandomExcursionsVariant * | 0.652733 | 0.976 | 0.153309 | 0.969 | 0.511916 | 0.973 |
| Serial * | 0.817667 | 0.978 | 0.017156 | 0.993 | 0.408942 | 0.984 |
| LinearComplexity | 0.553147 | 0.993 | 0.758528 | 0.993 | 0.656634 | 0.981 |
| 1FiRO-1GaRO | 2FiRO-2GaRO | 4FiRO-4GaRO | ||||
|---|---|---|---|---|---|---|
| Test Name | p-Value | Proportion | p-Value | Proportion | p-Value | Proportion |
| Frequency | 0.794626 | 0.996 | 0.739918 | 0.996 | 0.034455 | 0.993 |
| BlockFrequency | 0.103676 | 1 | 0.320988 | 0.993 | 0.199580 | 0.987 |
| CumulativeSums * | 0.880335 | 0.996 | 0.701879 | 0.990 | 0.355569 | 0.993 |
| Runs | 0.971267 | 0.981 | 0.695458 | 0.987 | 0.109597 | 0.990 |
| LongestRun | 0.365877 | 0.981 | 0.990440 | 0.987 | 0.708280 | 0.987 |
| Rank | 0.490727 | 0.990 | 0.011333 | 0.993 | 0.081137 | 0.993 |
| FFT | 0.880335 | 0.981 | 0.235285 | 0.990 | 0.235285 | 0.987 |
| NonOverlappingTemplate * | 0.969045 | 0.978 | 0.177264 | 0.978 | 0.392456 | 0.978 |
| OverlappingTemplate | 0.746157 | 0.990 | 0.250878 | 0.981 | 0.460664 | 0.987 |
| Universal | 0.288780 | 0.978 | 0.048716 | 0.975 | 0.414525 | 0.993 |
| ApproximateEntropy | 0.521600 | 0.993 | 0.371101 | 0.993 | 0.213309 | 0.990 |
| RandomExcursions * | 0.120558 | 0.985 | 0.825505 | 0.980 | 0.247472 | 0.985 |
| RandomExcursionsVariant * | 0.673507 | 0.980 | 0.334538 | 0.990 | 0.144153 | 0.985 |
| Serial * | 0.546791 | 0.990 | 0.297739 | 0.990 | 0.202944 | 0.981 |
| LinearComplexity | 0.502986 | 0.984 | 0.148968 | 0.987 | 0.159799 | 0.990 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Belli, J.; Fanucci, L.; Saponara, S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Appl. Sci. 2021, 11, 3330. https://doi.org/10.3390/app11083330
Nannipieri P, Di Matteo S, Baldanzi L, Crocetti L, Belli J, Fanucci L, Saponara S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Applied Sciences. 2021; 11(8):3330. https://doi.org/10.3390/app11083330
Chicago/Turabian StyleNannipieri, Pietro, Stefano Di Matteo, Luca Baldanzi, Luca Crocetti, Jacopo Belli, Luca Fanucci, and Sergio Saponara. 2021. "True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA" Applied Sciences 11, no. 8: 3330. https://doi.org/10.3390/app11083330
APA StyleNannipieri, P., Di Matteo, S., Baldanzi, L., Crocetti, L., Belli, J., Fanucci, L., & Saponara, S. (2021). True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Applied Sciences, 11(8), 3330. https://doi.org/10.3390/app11083330









