Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment
Abstract
1. Introduction
2. Trajectory Generation
2.1. Global Trajectory Generation
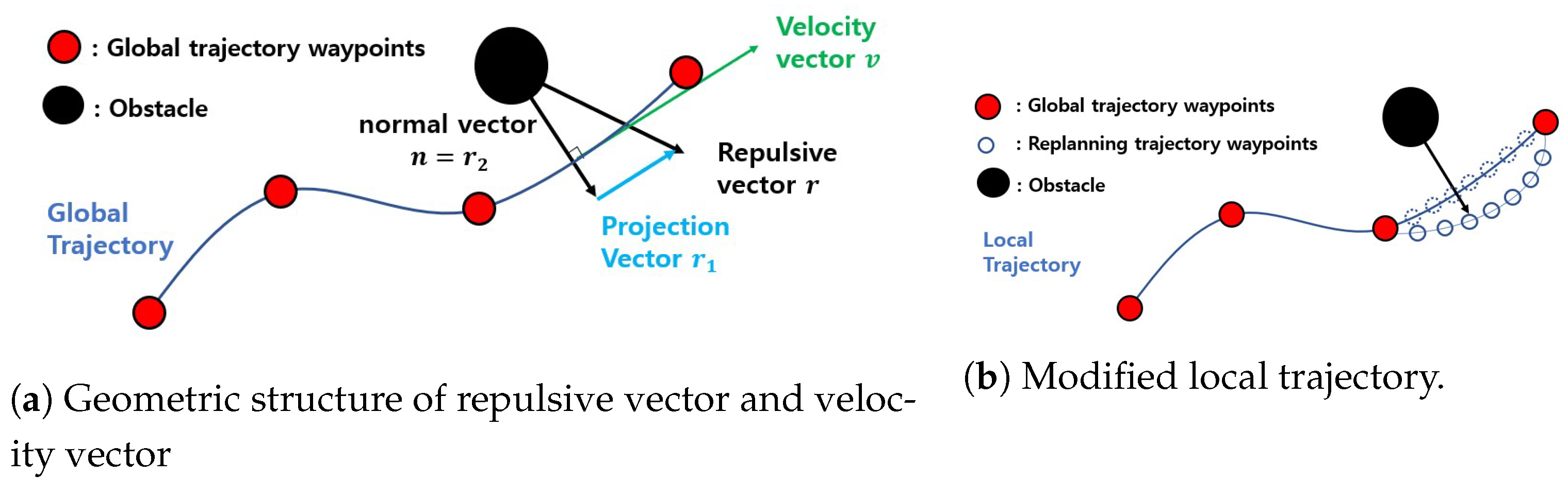
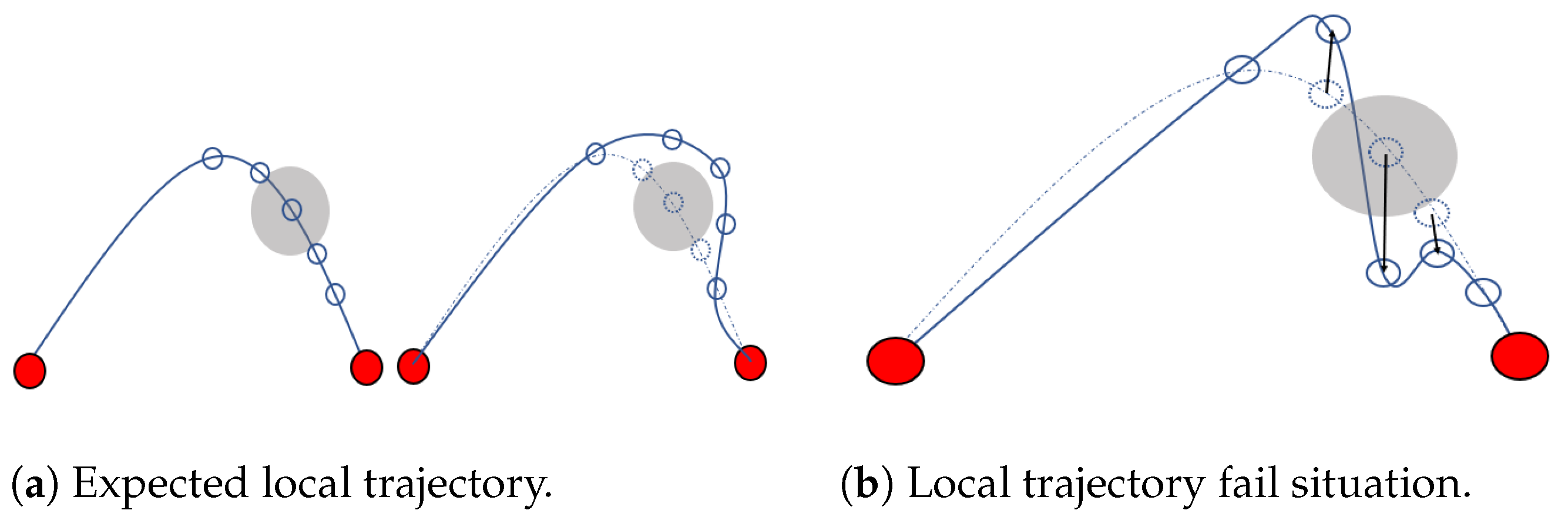
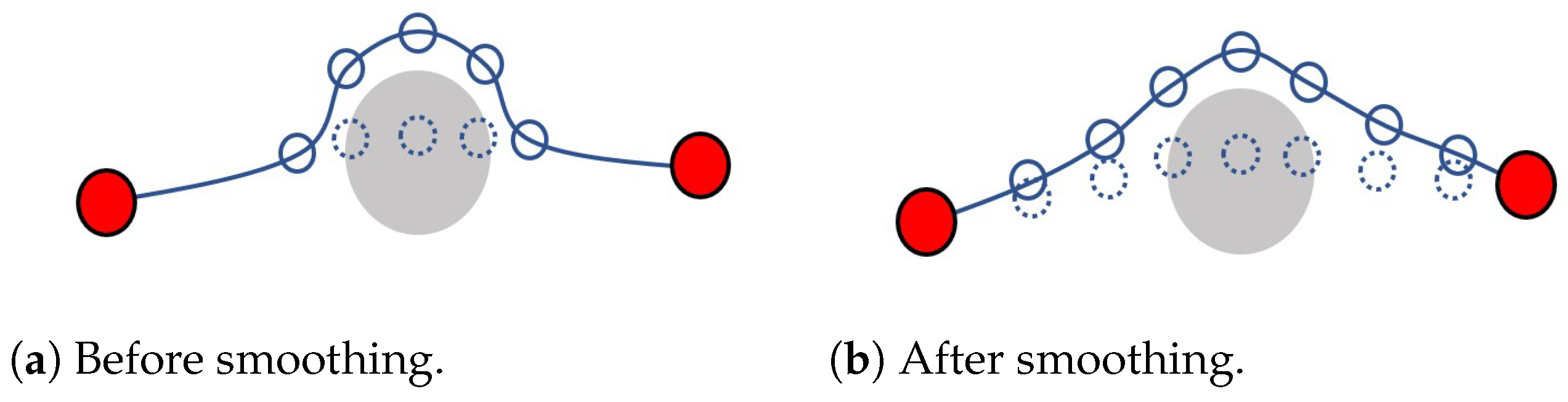
2.2. Closed-Form Local Trajectory Replanning
| Algorithm 1 Replanning waypoints. |
|
3. Results
3.1. Simulation
3.2. Experimental Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yasin, J.N.; Mohamed, S.A.; Haghbayan, M.H.; Heikkonen, J.; Tenhunen, H.; Plosila, J. Unmanned aerial vehicles (uavs): Collision avoidance systems and approaches. IEEE Access 2020, 8, 105139–105155. [Google Scholar] [CrossRef]
- Mellinger, D.; Kumar, V. Minimum snap trajectory generation and control for quadrotors. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2520–2525. [Google Scholar]
- Richter, C.; Bry, A.; Roy, N. Polynomial trajectory planning for aggressive quadrotor flight in dense indoor environments. In Robotics Research; Springer: Berlin/Heidelberg, Germany, 2016; pp. 649–666. [Google Scholar]
- Copot, C.; Hernandez, A.; Mac, T.T.; De Keyse, R. Collision-free path planning in indoor environment using a quadrotor. In Proceedings of the 2016 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 351–356. [Google Scholar]
- Penin, B.; Giordano, P.R.; Chaumette, F. Vision-based reactive planning for aggressive target tracking while avoiding collisions and occlusions. IEEE Robot. Autom. Lett. 2018, 3, 3725–3732. [Google Scholar] [CrossRef]
- Oleynikova, H.; Taylor, Z.; Fehr, M.; Siegwart, R.; Nieto, J. Voxblox: Incremental 3d euclidean signed distance fields for on-board mav planning. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1366–1373. [Google Scholar]
- Taketomi, T.; Uchiyama, H.; Ikeda, S. Visual SLAM algorithms: A survey from 2010 to 2016. IPSJ Trans. Comput. Vis. Appl. 2017, 9, 1–11. [Google Scholar] [CrossRef]
- Burri, M.; Oleynikova, H.; Achtelik, M.W.; Siegwart, R. Real-time visual-inertial mapping, re-localization and planning onboard mavs in unknown environments. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–3 October 2015; pp. 1872–1878. [Google Scholar]
- Peng, X.Z.; Lin, H.Y.; Dai, J.M. Path planning and obstacle avoidance for vision guided quadrotor UAV navigation. In Proceedings of the 2016 12th IEEE International Conference on Control and Automation (ICCA), Kathmandu, Nepal, 1–3 June 2016; pp. 984–989. [Google Scholar]
- Sanchez-Lopez, J.L.; Wang, M.; Olivares-Mendez, M.A.; Molina, M.; Voos, H. A real-time 3d path planning solution for collision-free navigation of multirotor aerial robots in dynamic environments. J. Intell. Robot. Syst. 2019, 93, 33–53. [Google Scholar] [CrossRef]
- Oleynikova, H.; Burri, M.; Taylor, Z.; Nieto, J.; Siegwart, R.; Galceran, E. Continuous-time trajectory optimization for online UAV replanning. In Proceedings of the 2016 IEEE/RSJ international conference on intelligent robots and systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5332–5339. [Google Scholar]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control. Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Gilmore, P.; Kelley, C.T. An implicit filtering algorithm for optimization of functions with many local minima. SIAM J. Optim. 1995, 5, 269–285. [Google Scholar] [CrossRef]
- Yang, H.; Qi, J.; Miao, Y.; Sun, H.; Li, J. A new robot navigation algorithm based on a double-layer ant algorithm and trajectory optimization. IEEE Trans. Ind. Electron. 2018, 66, 8557–8566. [Google Scholar] [CrossRef]
- Zhang, X.; Xian, B.; Zhao, B.; Zhang, Y. Autonomous flight control of a nano quadrotor helicopter in a GPS-denied environment using on-board vision. IEEE Trans. Ind. Electron. 2015, 62, 6392–6403. [Google Scholar] [CrossRef]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Robot Operating System (ROS): The Complete Reference (Volume 1); Springer International Publishing: Cham, Switzerland, 2016; pp. 595–625. [Google Scholar]
- Meier, L.; Tanskanen, P.; Fraundorfer, F.; Pollefeys, M. Pixhawk: A system for autonomous flight using onboard computer vision. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 2992–2997. [Google Scholar]
- Hornung, A.; Wurm, K.M.; Bennewitz, M.; Stachniss, C.; Burgard, W. OctoMap: An efficient probabilistic 3D mapping framework based on octrees. Auton. Robot. 2013, 34, 189–206. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric tracking control of a quadrotor UAV on SE (3). In Proceedings of the 49th IEEE conference on decision and control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425. [Google Scholar]
- Usenko, V.; Von Stumberg, L.; Pangercic, A.; Cremers, D. Real-time trajectory replanning for MAVs using uniform B-splines and a 3D circular buffer. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 215–222. [Google Scholar]



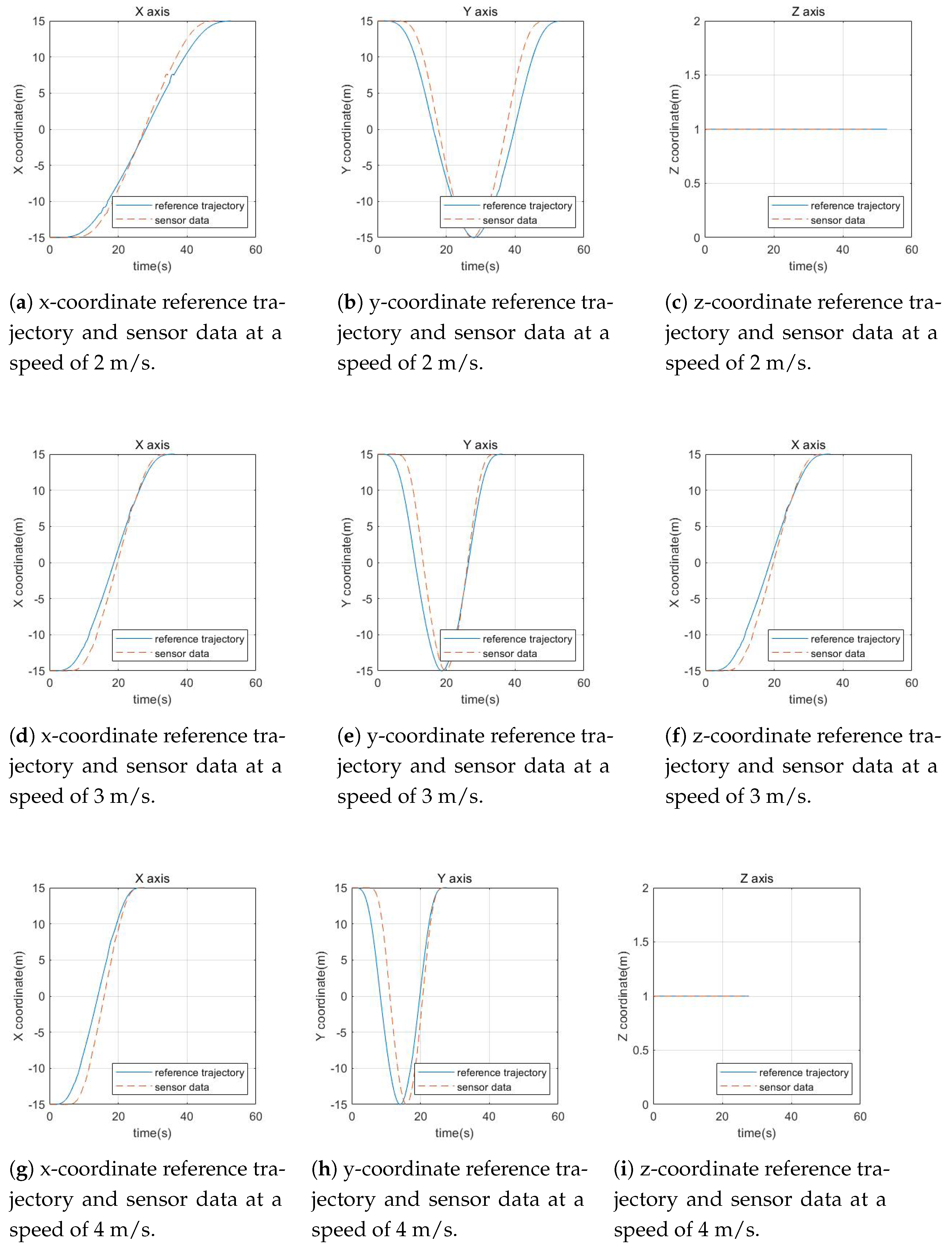


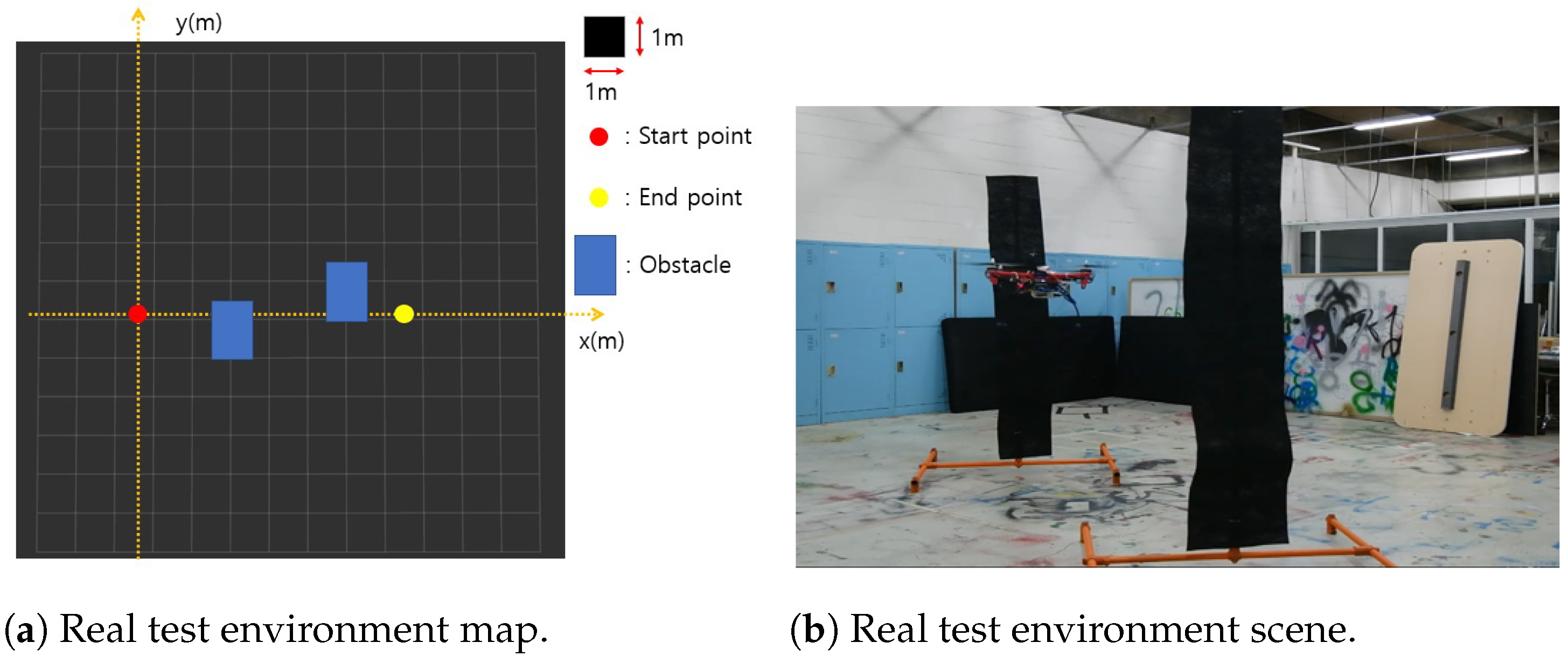
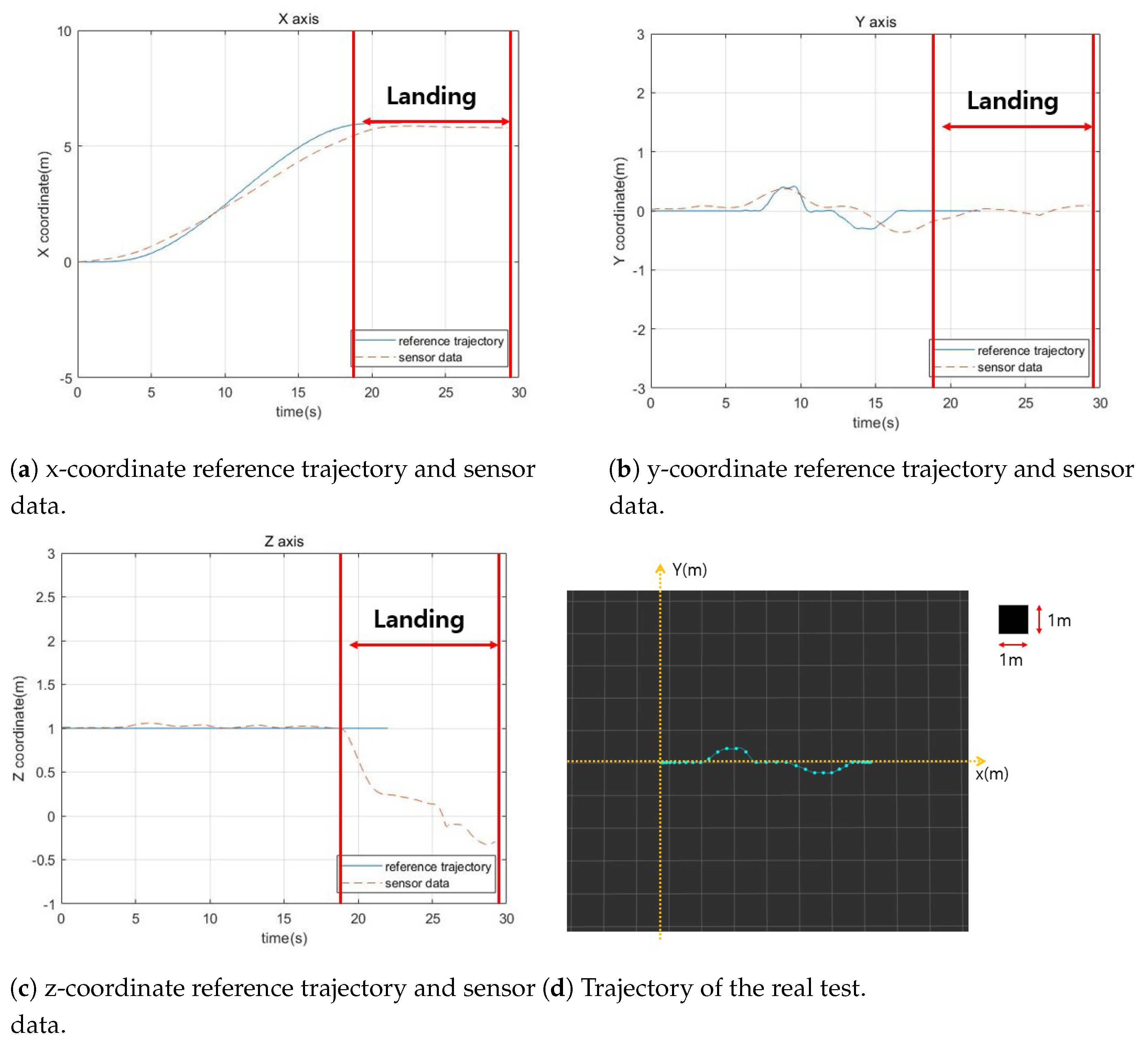
| Speed (m/s) | Number of Points | Mean Computation Time |
|---|---|---|
| 2 | 5 | 11 × s |
| 3 | 10 | 17 × s |
| 4 | 20 | 35 × s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.; Kim, W.; Moon, H. Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment. Appl. Sci. 2021, 11, 3238. https://doi.org/10.3390/app11073238
Park Y, Kim W, Moon H. Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment. Applied Sciences. 2021; 11(7):3238. https://doi.org/10.3390/app11073238
Chicago/Turabian StylePark, Yonghee, Woosung Kim, and Hyungpil Moon. 2021. "Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment" Applied Sciences 11, no. 7: 3238. https://doi.org/10.3390/app11073238
APA StylePark, Y., Kim, W., & Moon, H. (2021). Time-Continuous Real-Time Trajectory Generation for Safe Autonomous Flight of a Quadrotor in Unknown Environment. Applied Sciences, 11(7), 3238. https://doi.org/10.3390/app11073238






