Hierarchical Task Assignment and Path Finding with Limited Communication for Robot Swarms
Abstract
1. Introduction
2. Related Work
3. Hierarchical Task Assignment and Path Finding
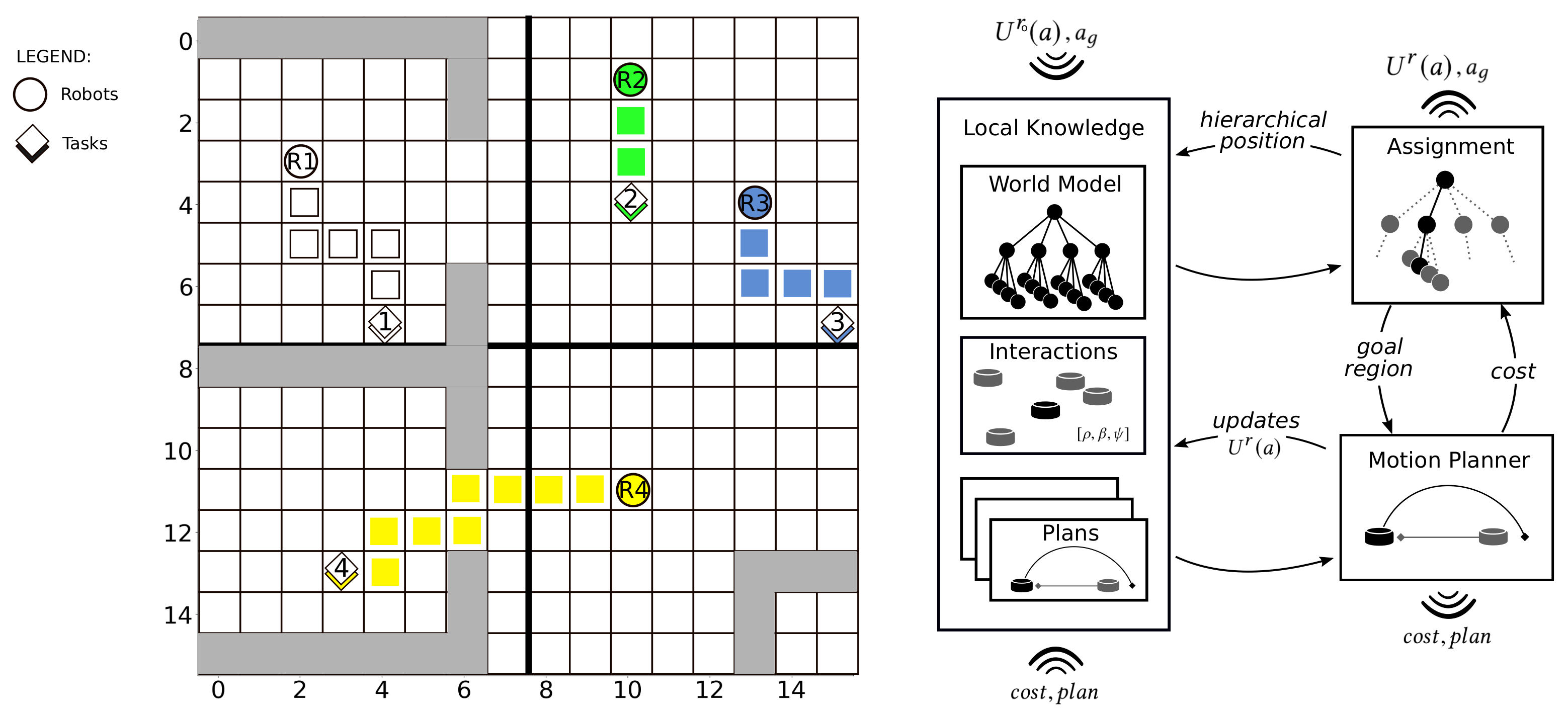
3.1. Problem Description
3.2. HTAPF: Principles and Methods
| Algorithm 1 HTAPF | |
| 1: procedure Step(, D, , ) | |
| 2: for in range do | |
| 3: | ▹ Reset transition probabilities |
| 4: | ▹ Random choice of a known robot |
| 5: | ▹ Selection of next transition type |
| 6: if then | |
| 7: | ▹ Equations (6)–(8) |
| 8: else | |
| 9: | ▹ Equations (4) and (5) |
| 10: | ▹ New hierarchical area |
| 11: | ▹ Update all ancestors |
| 12: | ▹ Collision Free Path |
| 13: | |
| 14: | ▹ in Equation (3) |
| 15: | |
3.2.1. World Model
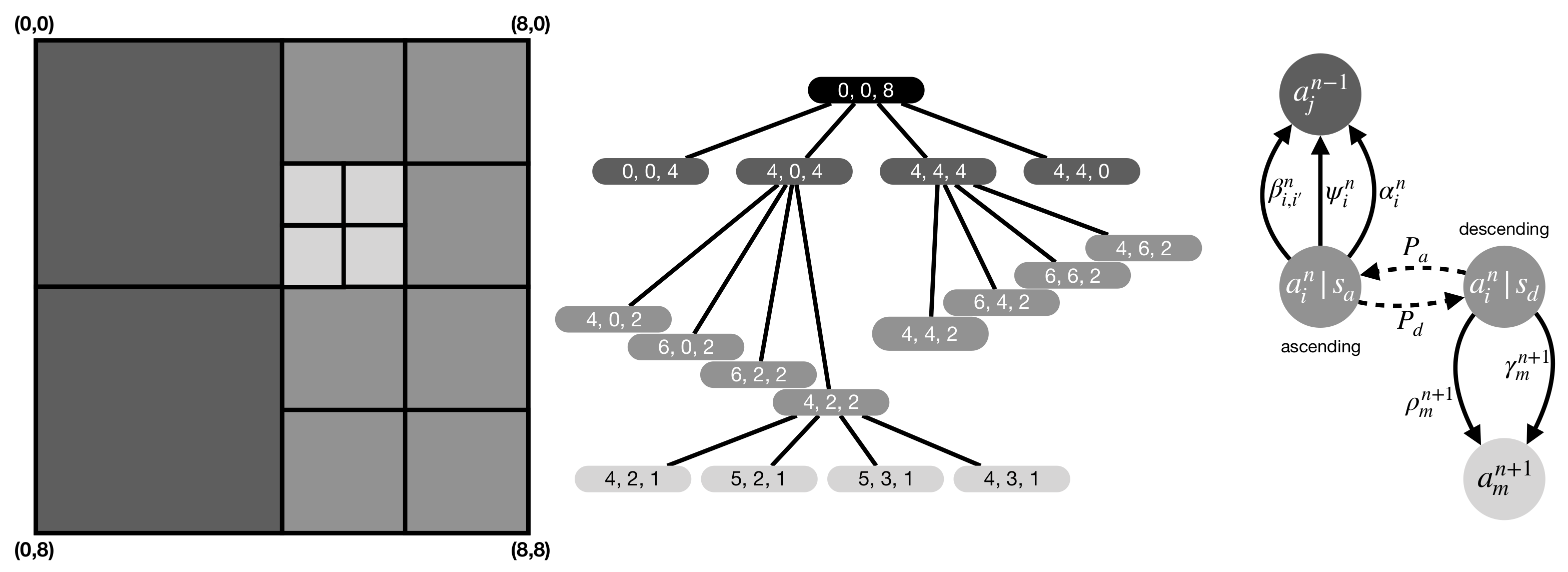
3.2.2. Decentralized Area Assignment
Descending Transitions
Ascending Transitions
Overall Algorithm and Control Parameters
3.2.3. Decentralized Task Assignment and Motion Planning
4. Experimental Evaluation
4.1. Service Robotics Simulation
4.2. Greedy and Auction-Based Strategies
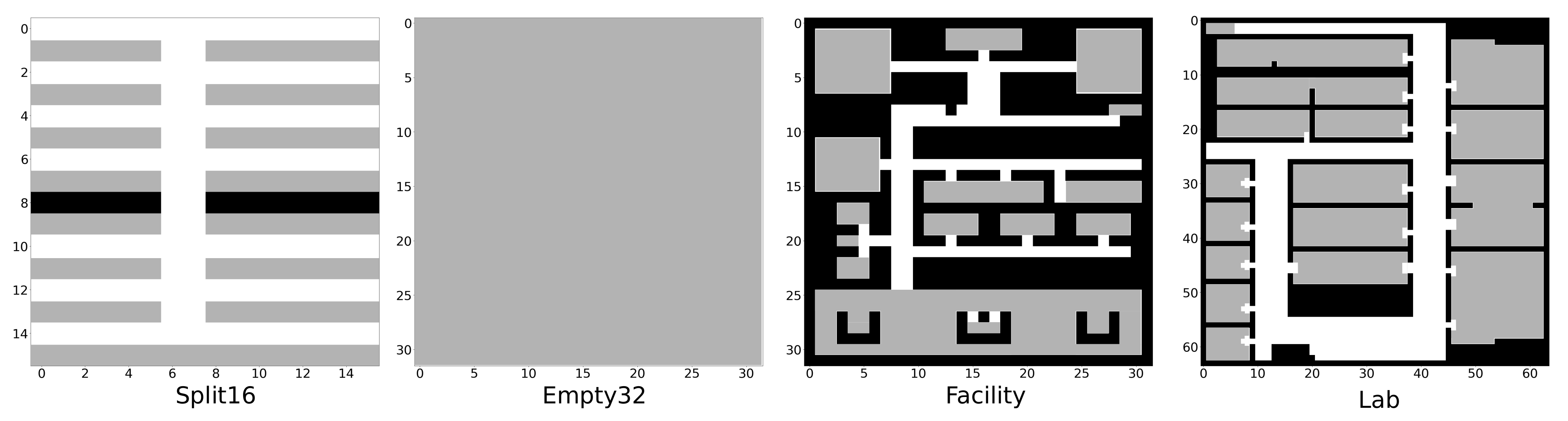
4.3. Experimental Setup
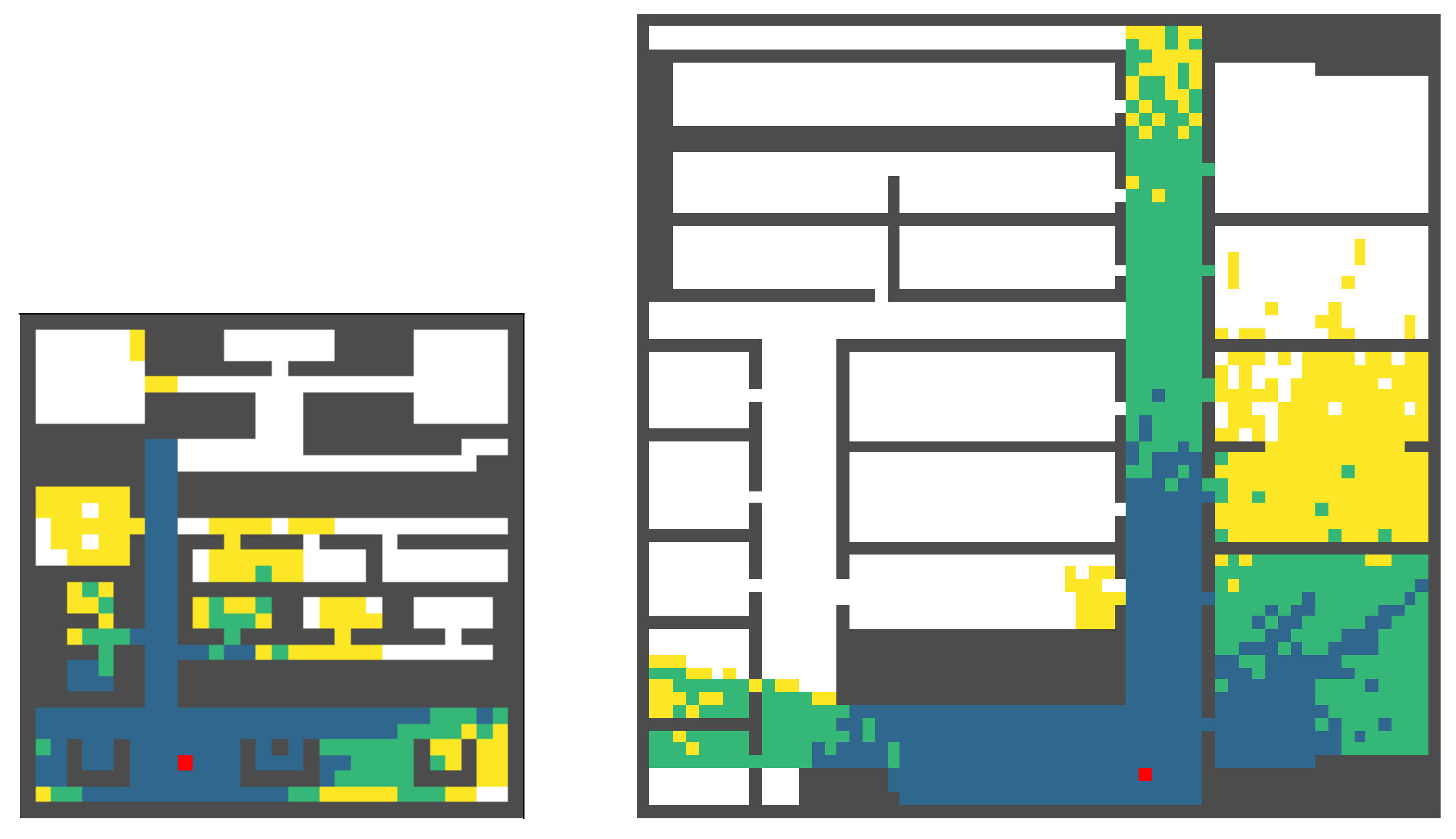
4.4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Garcia, E.; Jimenez, M.A.; De Santos, P.G.; Armada, M. The evolution of robotics research. IEEE Robot. Autom. Mag. 2007, 14, 90–103. [Google Scholar] [CrossRef]
- D’Andrea, R. Guest Editorial: A Revolution in the Warehouse: A Retrospective on Kiva Systems and the Grand Challenges Ahead. IEEE Trans. Autom. Sci. Eng. 2012, 9, 638–639. [Google Scholar] [CrossRef]
- Hönig, W.; Kiesel, S.; Tinka, A.; Durham, J.W.; Ayanian, N. Persistent and Robust Execution of MAPF Schedules in Warehouses. IEEE Robot. Autom. Lett. 2019, 4, 1125–1131. [Google Scholar] [CrossRef]
- Van Henten, E.; Bac, C.; Hemming, J.; Edan, Y. Robotics in protected cultivation. IFAC Proc. Vol. 2013, 46, 170–177. [Google Scholar] [CrossRef]
- Ferrer, A.J.; Marquès, J.M.; Jorba, J. Towards the Decentralised Cloud: Survey on Approaches and Challenges for Mobile, Ad Hoc, and Edge Computing. ACM Comput. Surv. 2019, 51, 1–36. [Google Scholar] [CrossRef]
- Dorigo, M.; Theraulaz, G.; Trianni, V. Reflections on the future of swarm robotics. Sci. Robot. 2020, 5, eabe4385. [Google Scholar] [CrossRef] [PubMed]
- Farinelli, A.; Iocchi, L.; Nardi, D. Distributed on-line dynamic task assignment for multi-robot patrolling. Auton. Robot. 2017, 41, 1321–1345. [Google Scholar] [CrossRef]
- De Lope, J.; Maravall, D.; Quiñonez, Y. Self-organizing techniques to improve the decentralized multi-task distribution in multi-robot systems. Neurocomputing 2015, 163, 47–55. [Google Scholar] [CrossRef]
- Sharon, G.; Stern, R.; Felner, A.; Sturtevant, N.R. Conflict-based search for optimal multi-agent pathfinding. Artif. Intell. 2015, 219, 40–66. [Google Scholar] [CrossRef]
- Reina, A.; Valentini, G.; Fernández-Oto, C.; Dorigo, M.; Trianni, V. A Design Pattern for Decentralised Decision Making. PLoS ONE 2015, 10, e0140950-18. [Google Scholar] [CrossRef]
- Albani, D.; Manoni, T.; Nardi, D.; Trianni, V. Dynamic UAV Swarm Deployment for Non-Uniform Coverage. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Stockholm, Sweden, 10–15 July 2018; pp. 523–531. [Google Scholar]
- Velagapudi, P.; Sycara, K.P.; Scerri, P. Decentralized prioritized planning in large multirobot teams. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4603–4609. [Google Scholar]
- Sabattini, L.; Digani, V.; Secchi, C.; Fantuzzi, C. Optimized simultaneous conflict-free task assignment and path planning for multi-AGV systems. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 1083–1088. [Google Scholar]
- Hönig, W.; Kiesel, S.; Tinka, A.; Durham, J.W.; Ayanian, N. Conflict-Based Search with Optimal Task Assignment. In Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Stockholm, Sweden, 10–15 July 2018; pp. 757–765. [Google Scholar]
- Ma, H.; Koenig, S. Optimal Target Assignment and Path Finding for Teams of Agents. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2016), Singapore, 9–13 May 2016; pp. 1144–1152. [Google Scholar]
- Turpin, M.; Michael, N.; Kumar, V. CAPT: Concurrent assignment and planning of trajectories for multiple robots. Int. J. Robot. Res. 2014, 33, 98–112. [Google Scholar] [CrossRef]
- Ayanian, N.; Kumar, V. Decentralized Feedback Controllers for Multiagent Teams in Environments With Obstacles. IEEE Trans. Robot. 2010, 26, 878–887. [Google Scholar] [CrossRef]
- Panagou, D.; Turpin, M.; Kumar, V. Decentralized goal assignment and trajectory generation in multi-robot networks: A multiple Lyapunov functions approach. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6757–6762. [Google Scholar]
- Bandyopadhyay, S.; Chung, S.; Hadaegh, F.Y. Probabilistic swarm guidance using optimal transport. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; pp. 498–505. [Google Scholar]
- Dias, M.B.; Stentz, A. Opportunistic optimization for market-based multirobot control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Lausanne, Switzerland, 30 September–4 October 2002; pp. 2714–2720. [Google Scholar]
- Castello, E.; Yamamoto, T.; Libera, F.D.; Liu, W.; Winfield, A.F.T.; Nakamura, Y.; Ishiguro, H. Adaptive foraging for simulated and real robotic swarms: The dynamical response threshold approach. Swarm Intell. 2016, 10, 1–31. [Google Scholar] [CrossRef]
- Napp, N.; Klavins, E. A compositional framework for programming stochastically interacting robots. Int. J. Robot. Res. 2011, 30, 713–729. [Google Scholar] [CrossRef]
- Theraulaz, G.; Bonabeau, E.; Denuebourg, J.N. Response threshold reinforcements and division of labour in insect societies. Proc. R. Soc. London Ser. B Biol. Sci. 1998, 265, 327–332. [Google Scholar] [CrossRef]
- Beshers, S.N.; Fewell, J.H. Models of Division of Labor in Social Insects. Annu. Rev. Entomol. 2001, 46, 413–440. [Google Scholar] [CrossRef] [PubMed]
- Miletitch, R.; Dorigo, M.; Trianni, V. Balancing exploitation of renewable resources by a robot swarm. Swarm Intell. 2018, 86, 307–326. [Google Scholar] [CrossRef]
- Stroeymeyt, N.; Robinson, E.J.H.; Hogan, P.M.; Marshall, J.A.R.; Giurfa, M.; Franks, N.R. Experience-dependent flexibility in collective decision making by house-hunting ants. Behav. Ecol. 2011, 22, 535–542. [Google Scholar] [CrossRef]
- Franks, N.R.; Richardson, T.O.; Stroeymeyt, N.; Kirby, R.W.; Amos, W.M.D.; Hogan, P.M.; Marshall, J.A.R.; Schlegel, T. Speed-cohesion trade-offs in collective decision making in ants and the concept of precision in animal behaviour. Anim. Behav. 2013, 85, 1233–1244. [Google Scholar] [CrossRef]
- Reina, A.; Marshall, J.; Trianni, V.; Bose, T. Model of the best-of-N nest-site selection process in honeybees. Phys. Rev. E 2017, 95, 052411. [Google Scholar] [CrossRef]
- Marshall, J.A.R.; Bogacz, R.; Dornhaus, A.; Planqué, R.; Kovacs, T.; Franks, N.R. On optimal decision-making in brains and social insect colonies. J. R. Soc. Interface 2009, 6, 1065–1074. [Google Scholar] [CrossRef]
- Reina, A.; Bose, T.; Trianni, V.; Marshall, J.A.R. Psychophysical Laws and the Superorganism. Sci. Rep. 2018, 8, 4387–4388. [Google Scholar] [CrossRef] [PubMed]
- Reina, A.; Bose, T.; Trianni, V.; Marshall, J.A.R. Effects of Spatiality on Value-Sensitive Decisions Made by Robot Swarms. In Distributed Autonomous Robotic Systems (DARS); Springer: Berlin/Heidelberg, Germany, 2018; pp. 461–473. [Google Scholar]
- Fleming, C.; Adams, J.A. Recruitment-Based Robotic Colony Allocation. In Distributed Autonomous Robotic Systems (DARS); Springer: Berlin/Heidelberg, Germany, 2019; pp. 79–94. [Google Scholar]
- Caleffi, M.; Trianni, V.; Cacciapuoti, A.S. Self-Organizing Strategy Design for Heterogeneous Coexistence in the Sub-6 GHz. IEEE Trans. Wirel. Commun. 2018, 17, 7128–7143. [Google Scholar] [CrossRef]
- De Wilde, B.; Ter Mors, A.W.; Witteveen, C. Push and rotate: A complete multi-agent pathfinding algorithm. J. Artif. Intell. Res. 2014, 51, 443–492. [Google Scholar] [CrossRef]
- Luna, R.; Bekris, K.E. Network-guided multi-robot path planning in discrete representations. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4596–4602. [Google Scholar]
- Gerkey, B.P.; Matarić, M.J. A formal analysis and taxonomy of task allocation in multi-robot systems. Int. J. Robot. Res. 2004, 23, 939–954. [Google Scholar] [CrossRef]
- Khamis, A.; Hussein, A.; Elmogy, A. Multi-robot task allocation: A review of the state-of-the-art. Coop. Robot. Sens. Netw. 2015, 2015, 31–51. [Google Scholar]
- Faria, D.B. Modeling Signal Attenuation in IEEE 802.11 Wireless LANs; Technical Report TR-KP06-0118; Stanford University: Stanford, CA, USA, 2005; Volume 1. [Google Scholar]
- Beuran, R.; Nakata, J.; Okada, T.; Nguyen, L.T.; Tan, Y.; Shinoda, Y. A Multi-Purpose Wireless Network Emulator: QOMET. In Proceedings of the 22nd International Conference on Advanced Information Networking and Applications-Workshops (AINA Workshops 2008), Gino-wan, Japan, 25–28 March 2008; pp. 223–228. [Google Scholar]
- Wang, S.; Krishnamachari, B.; Ayanian, N. The optimism principle: A unified framework for optimal robotic network deployment in an unknown obstructed environment. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 2578–2584. [Google Scholar]
- Dimidov, C.; Oriolo, G.; Trianni, V. Random Walks in Swarm Robotics: An Experiment with Kilobots. In Proceedings of the International Conference on Swarm Intelligence (ANTS), Brussels, Belgium, 7–9 September 2016; Volume 9882, pp. 185–196. [Google Scholar]
- Phillips, M.; Likhachev, M. SIPP: Safe interval path planning for dynamic environments. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 5628–5635. [Google Scholar]
- Ma, H.; Li, J.; Kumar, T.K.S.; Koenig, S. Lifelong Multi-Agent Path Finding for Online Pickup and Delivery Tasks. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems (AAMAS), São Paulo, Brazil, 8–12 May 2017; pp. 837–845. [Google Scholar]
- Smith, R.G. The Contract Net Protocol: High-Level Communication and Control in a Distributed Problem Solver. IEEE Trans. Comput. 1980, 29, 1104–1113. [Google Scholar] [CrossRef]
- Sandholm, T. An implementation of the contract net protocol based on marginal cost calculations. In Proceedings of the AAAI, Washington, DC, USA, 11–15 July 1993; Volume 93, pp. 256–262. [Google Scholar]
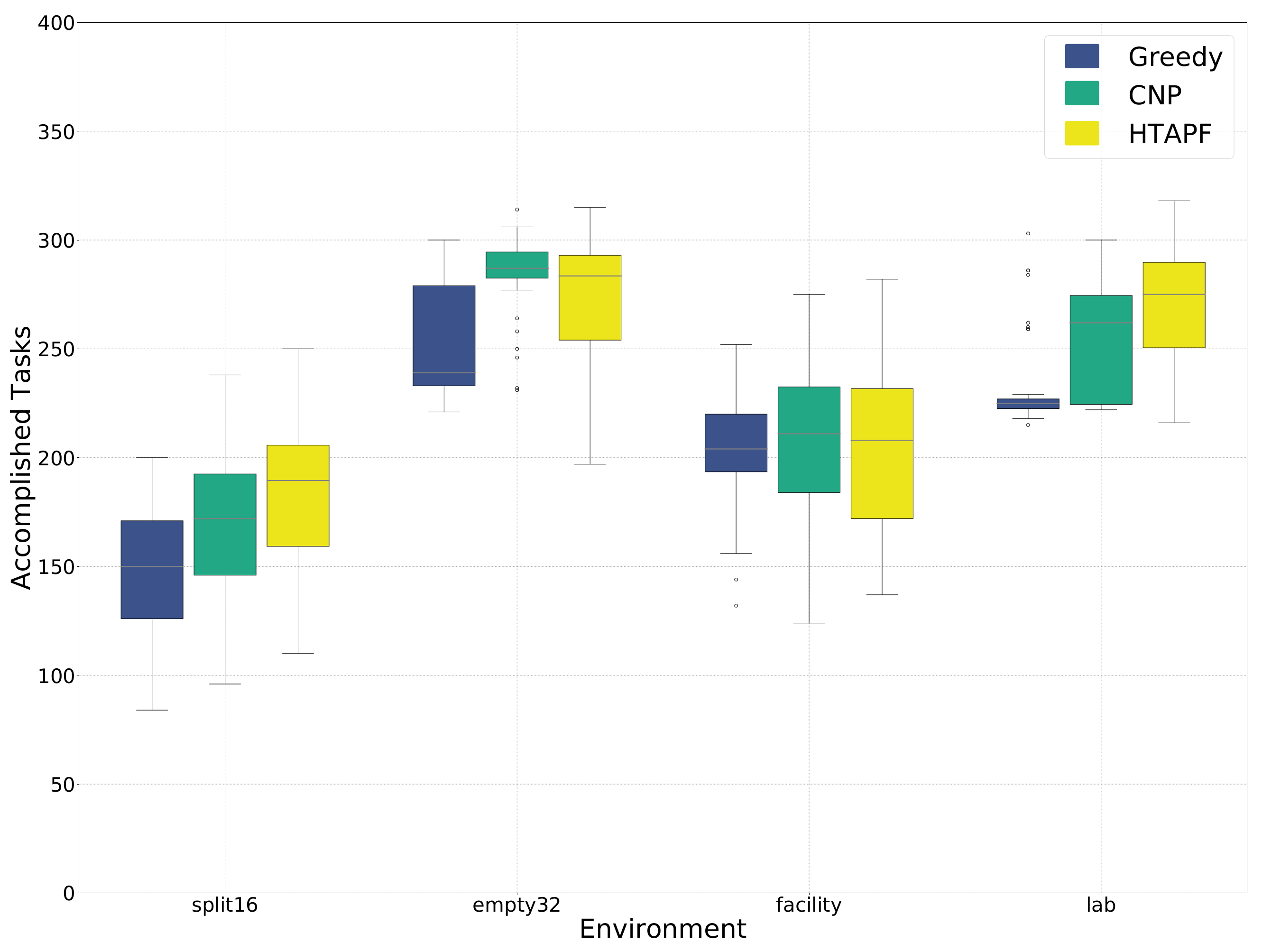
| split16 | empty32 | ||||||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 150 | 172 | 189.5 | 239 | 287 | 283.5 | |
| Kruskal–Wallis | , × 10 | , × 10 | |||||
| p-value | greedy | – | × 10 | × 10 | – | × 10 | × 10 |
| CNP | – | – | × 10 | – | – | × 10 | |
| facility | lab | ||||||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 204 | 211 | 208 | 225 | 262 | 275 | |
| Kruskal–Wallis | , | , | |||||
| p-value | greedy | – | × | × | – | ||
| CNP | – | – | × | – | – | ||
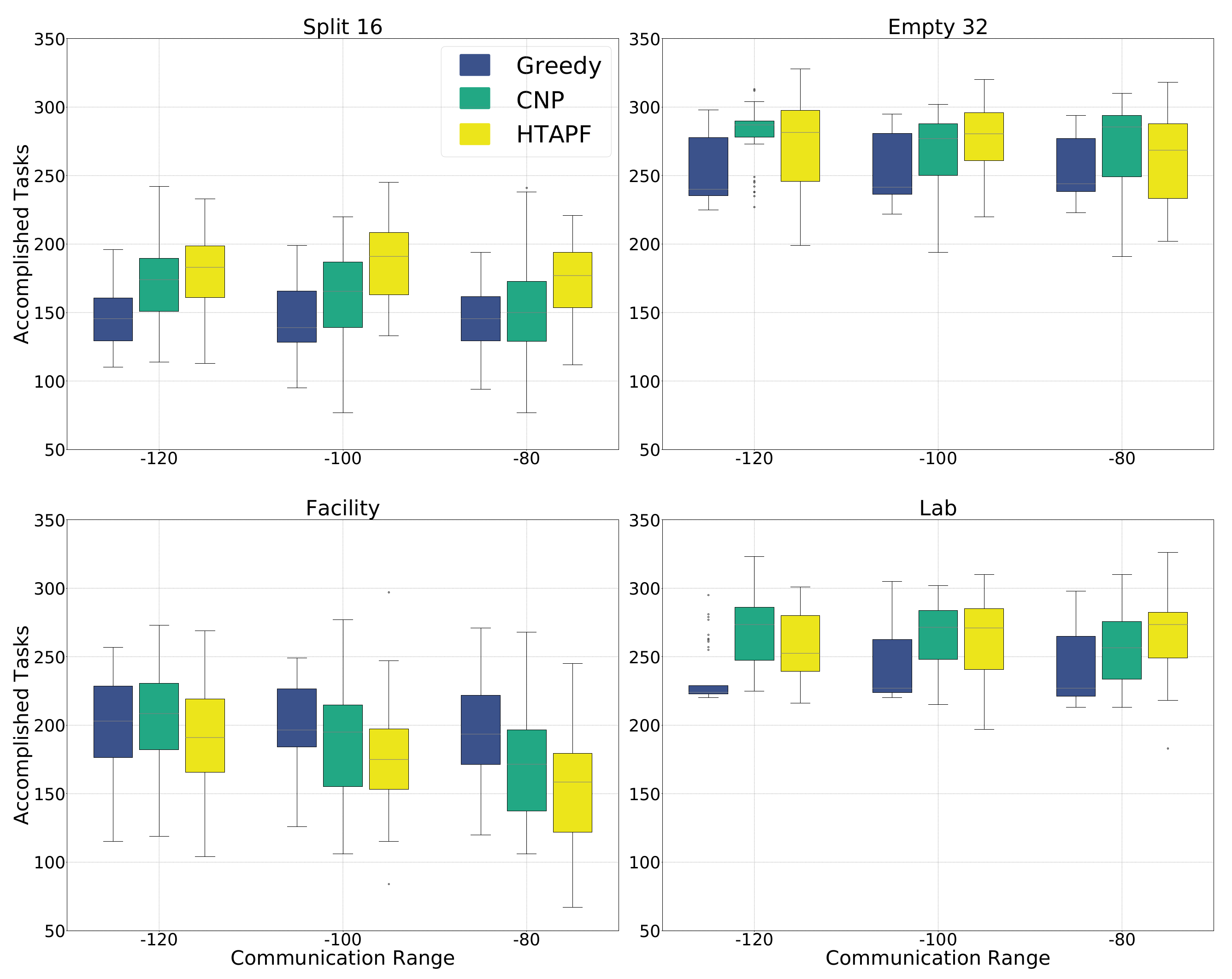
| split16 | empty32 | ||||||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 145.5 | 174 | 183 | 240 | 287 | 281.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 139 | 165.5 | 191 | 241.5 | 277 | 280.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 145.5 | 150 | 177 | 244 | 285.5 | 268.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
| facility | lab | ||||||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 203 | 208.5 | 191 | 224 | 273.5 | 252.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | × | × | – | |||
| CNP | – | – | × | – | – | ||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 196.5 | 195 | 175 | 227 | 271.5 | 271 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
| greedy | CNP | HTAPF | greedy | CNP | HTAPF | ||
| median | 194 | 171.5 | 158.5 | 227 | 256.5 | 273.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
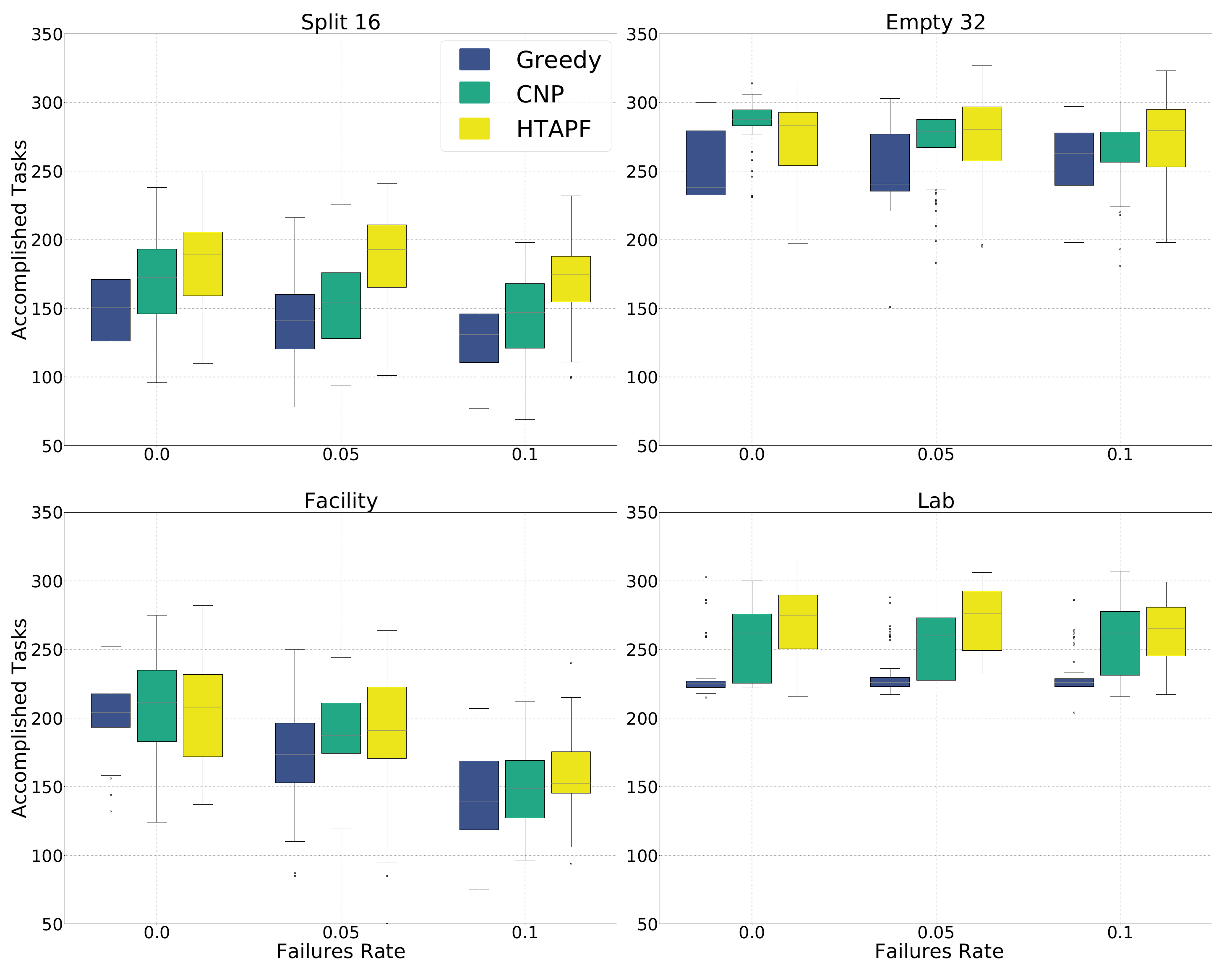
| split16 | empty32 | ||||||
| rate | greedy | CNP | HTAPF | greedy | CNP | HTAPF | |
| median | 141 | 154.5 | 193 | 240.5 | 279.5 | 280.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | 2.2 | 6.4 | – | × | × | |
| CNP | – | – | 4.5 | – | – | × | |
| rate | greedy | CNP | HTAPF | greedy | CNP | HTAPF | |
| median | 131 | 147 | 174.5 | 263 | 269 | 279.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | – | |||||
| CNP | – | – | – | – | |||
| facility | lab | ||||||
| rate | greedy | CNP | HTAPF | greedy | CNP | HTAPF | |
| median | 173.5 | 187.5 | 191 | 226 | 260 | 276 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | × | × | – | |||
| CNP | – | – | × | – | – | ||
| rate | greedy | CNP | HTAPF | greedy | CNP | HTAPF | |
| median | 139.5 | 148.5 | 152.5 | 226 | 262 | 265.5 | |
| Kruskal–Wallis | , | , | |||||
| greedy | – | × | × | – | × | × | |
| CNP | – | – | × | – | – | × | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albani, D.; Hönig, W.; Nardi, D.; Ayanian, N.; Trianni, V. Hierarchical Task Assignment and Path Finding with Limited Communication for Robot Swarms. Appl. Sci. 2021, 11, 3115. https://doi.org/10.3390/app11073115
Albani D, Hönig W, Nardi D, Ayanian N, Trianni V. Hierarchical Task Assignment and Path Finding with Limited Communication for Robot Swarms. Applied Sciences. 2021; 11(7):3115. https://doi.org/10.3390/app11073115
Chicago/Turabian StyleAlbani, Dario, Wolfgang Hönig, Daniele Nardi, Nora Ayanian, and Vito Trianni. 2021. "Hierarchical Task Assignment and Path Finding with Limited Communication for Robot Swarms" Applied Sciences 11, no. 7: 3115. https://doi.org/10.3390/app11073115
APA StyleAlbani, D., Hönig, W., Nardi, D., Ayanian, N., & Trianni, V. (2021). Hierarchical Task Assignment and Path Finding with Limited Communication for Robot Swarms. Applied Sciences, 11(7), 3115. https://doi.org/10.3390/app11073115






