High-Fidelity Fin–Actuator System Modeling and Aeroelastic Analysis Considering Friction Effect
Abstract
Featured Application
Abstract
1. Introduction
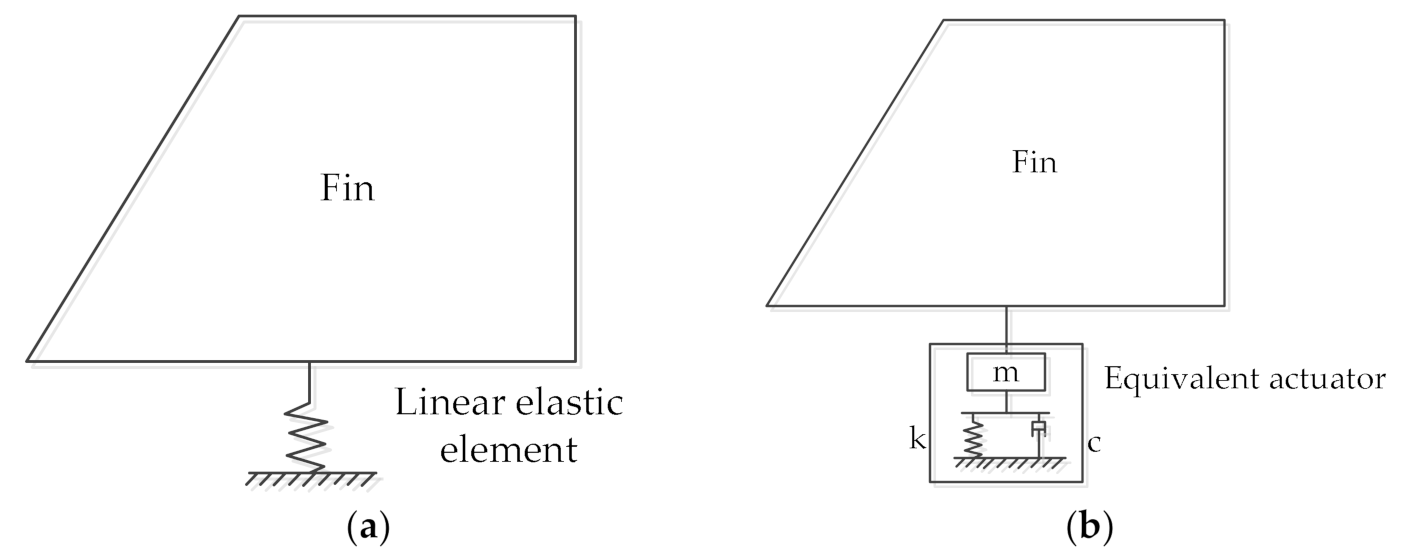
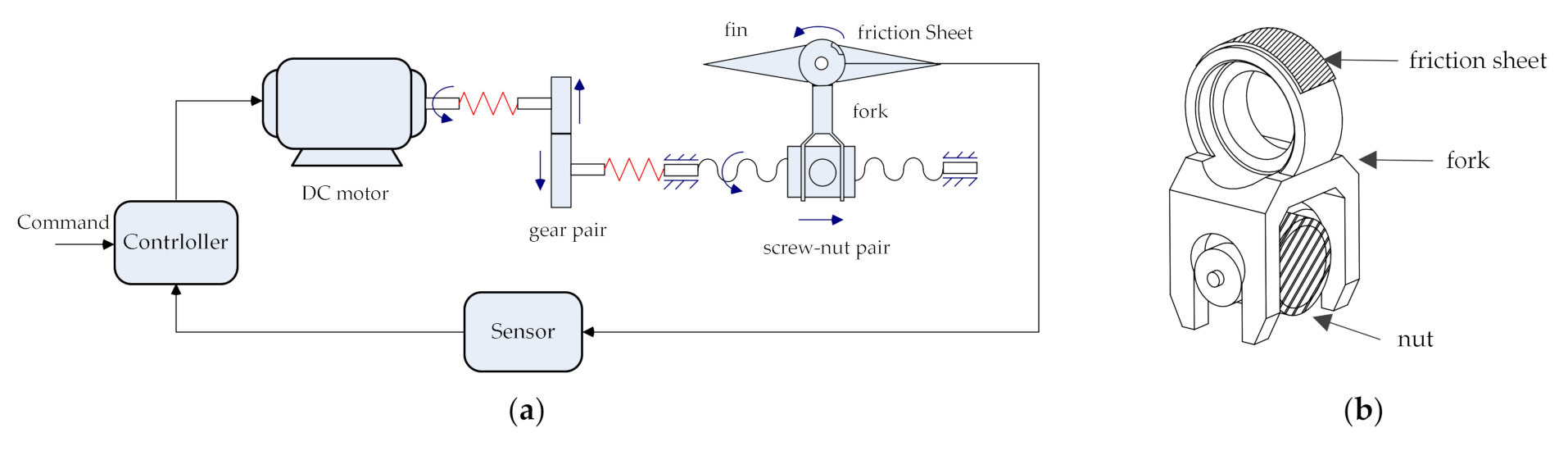
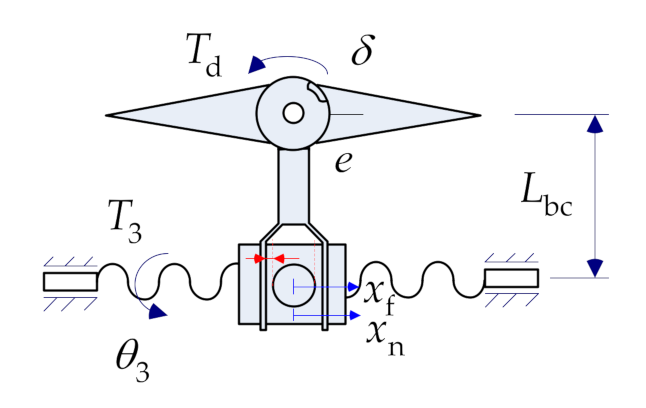
2. Study Object
3. Modeling of the System
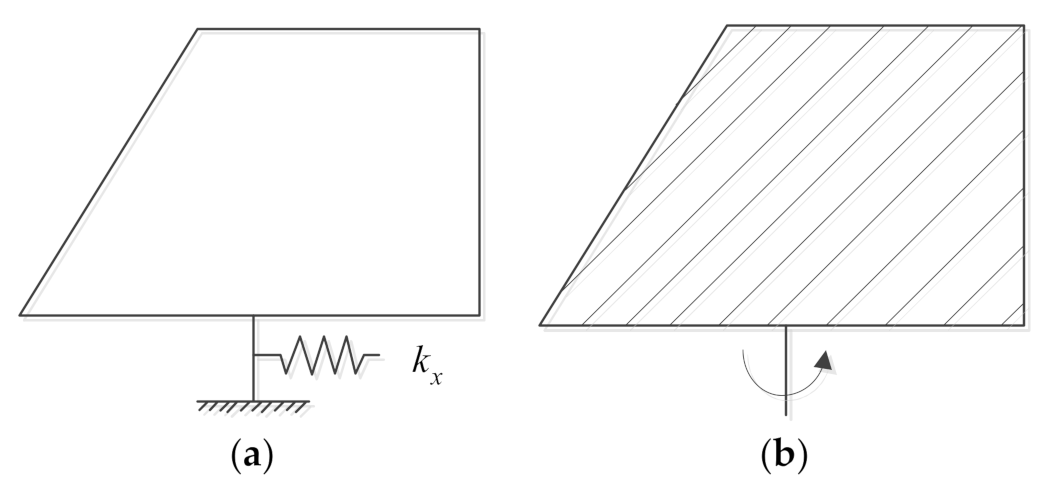
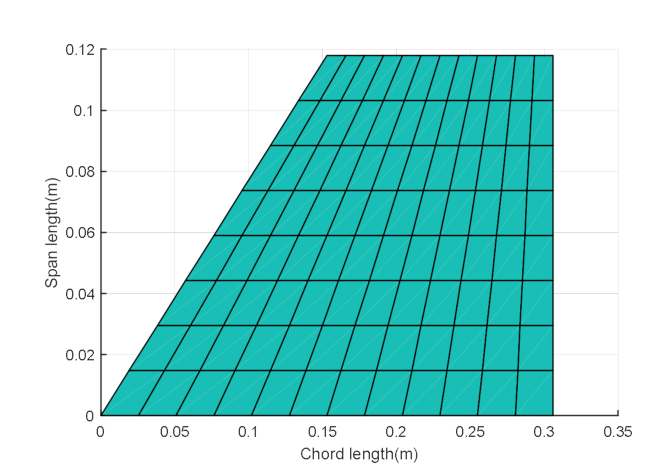
3.1. Modeling of the Fin Structure
3.2. Modeling of the Unsteady Aerodynamics
3.3. State-Space Form of the Fin Model
3.4. Modeling of the Electromechanical Actuator
3.4.1. Model of DC Motor
3.4.2. Model of the Gear Pair
3.4.3. Model of the Screw–Nut Pair and Fork
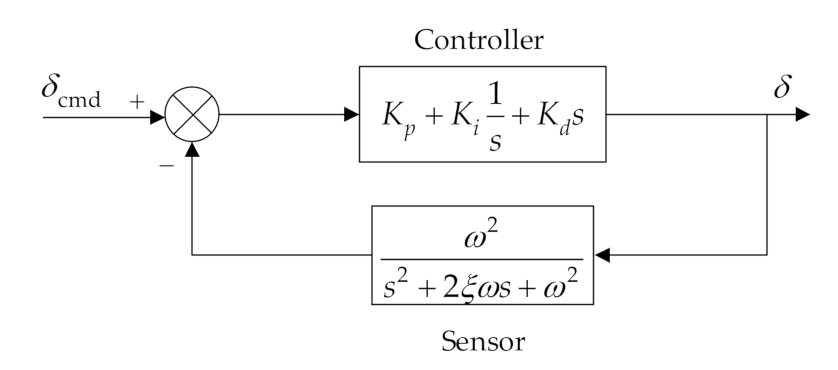
3.4.4. Model of the Controller and Sensor
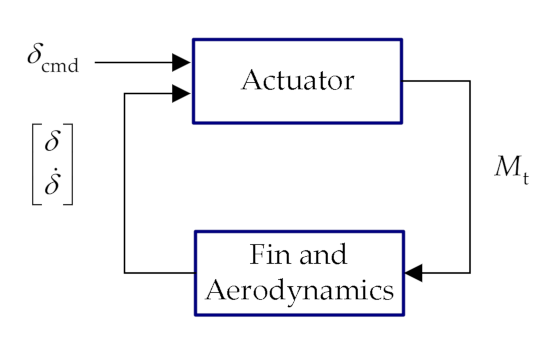
3.4.5. Model of the System
4. Flutter Analysis Method
4.1. Frequency Domain Method
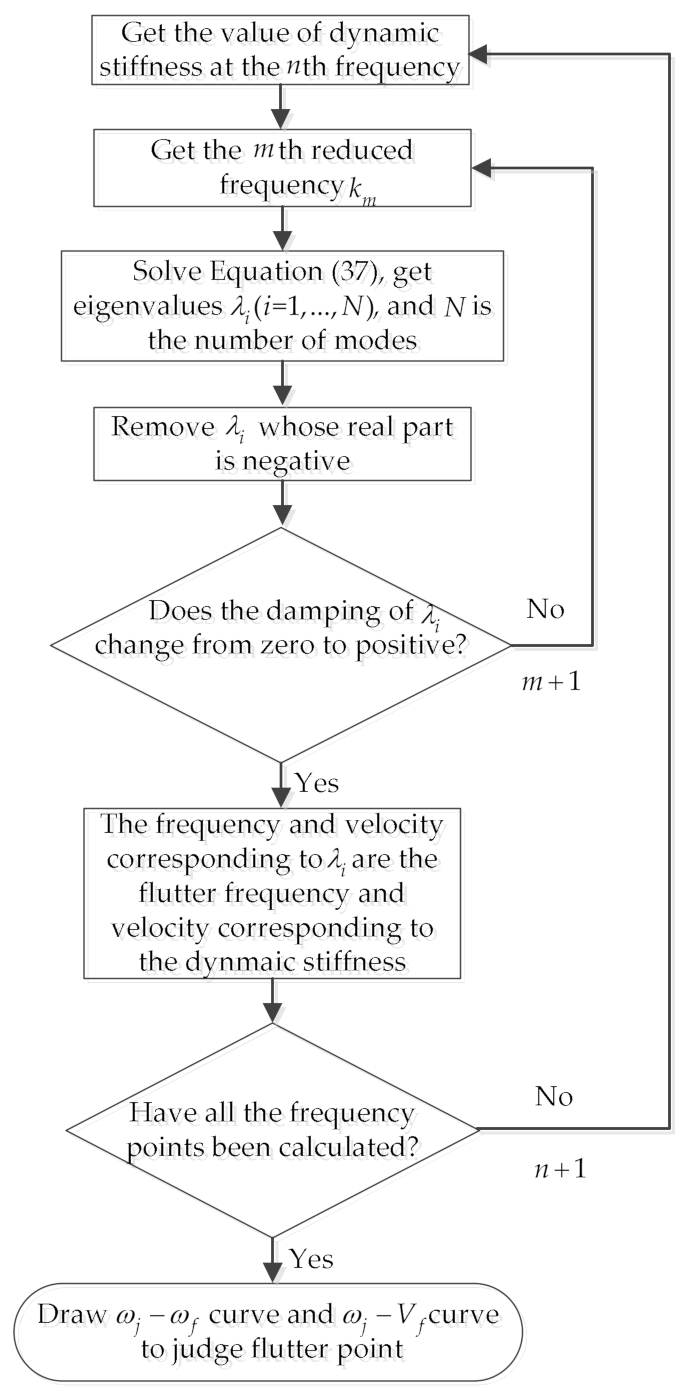
4.1.1. Dynamic Stiffness
4.1.2. Flutter Analysis with V–g Method
4.2. Time Domain Method
5. Aeroelastic Analysis Results and Discussion
5.1. Identification of Actuator Parameters
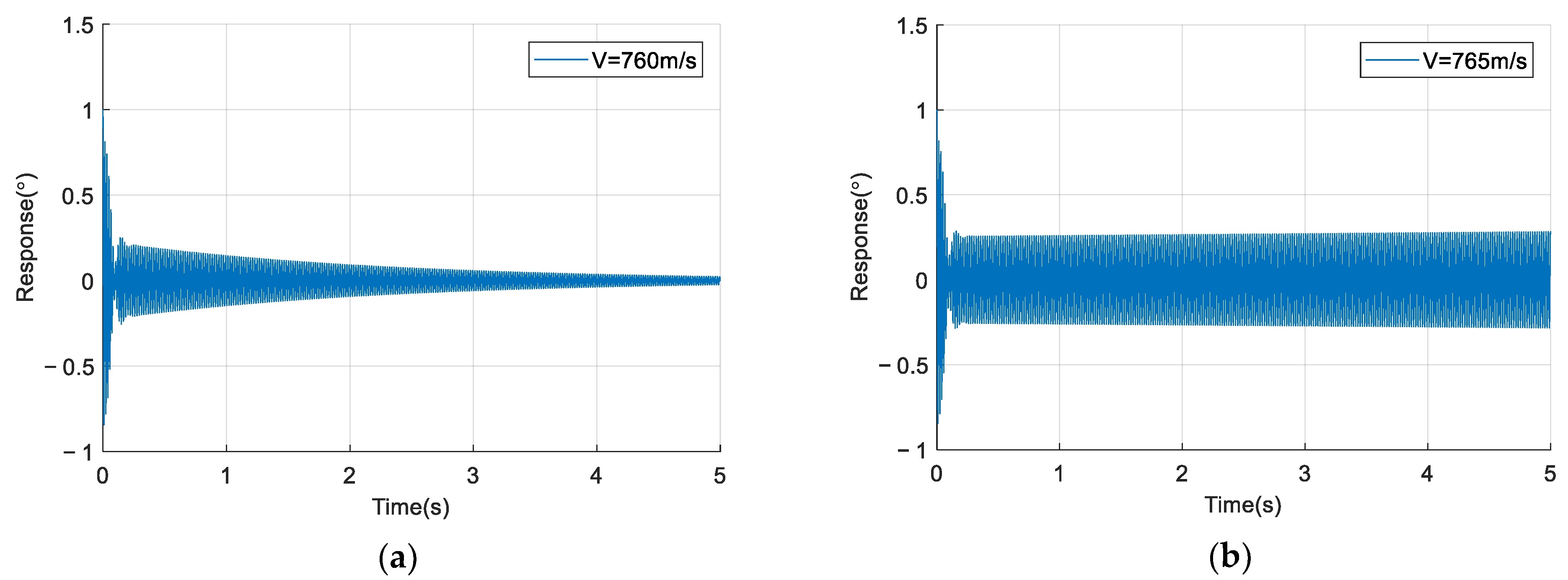
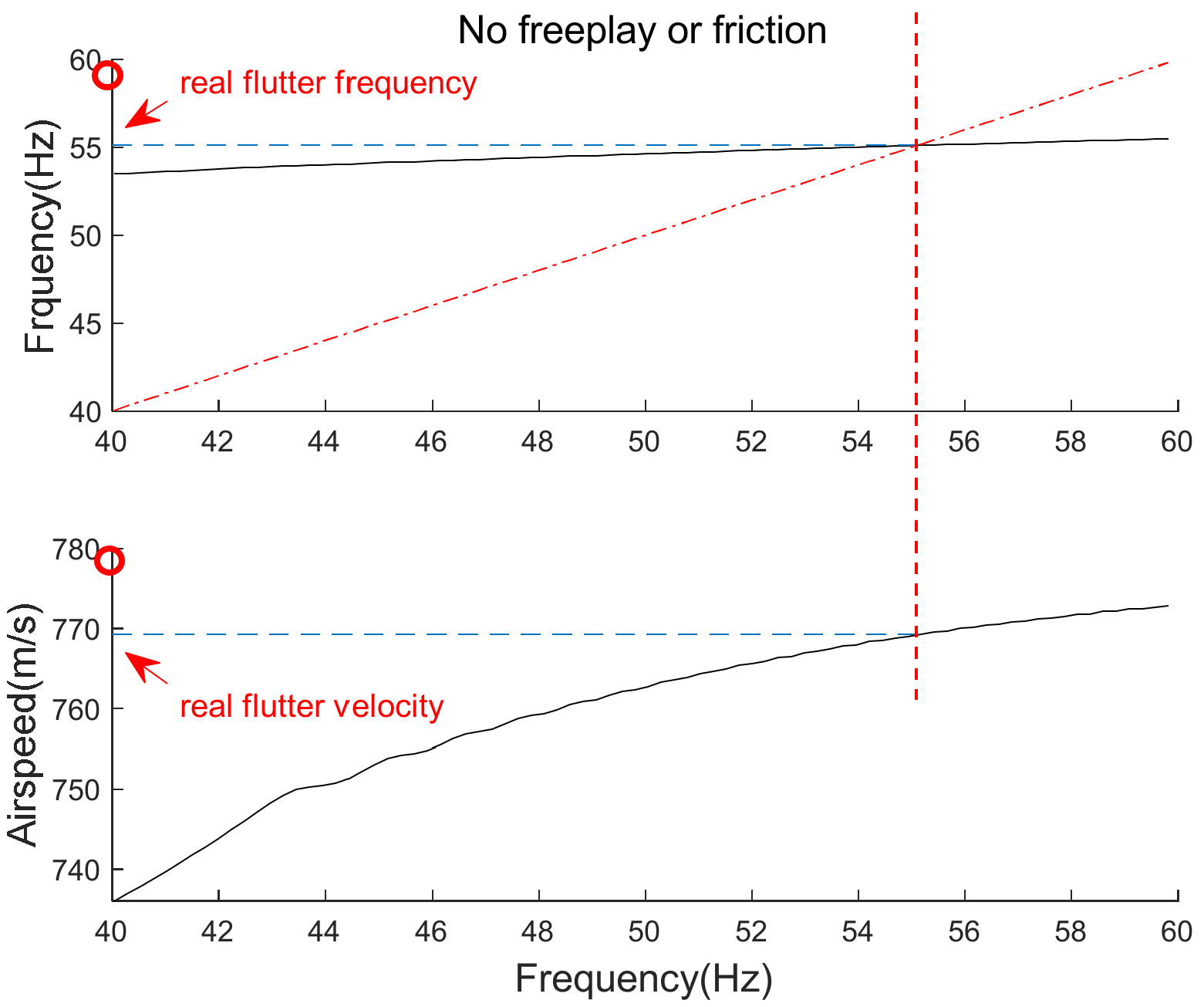
5.2. Preliminary Flutter Results for No-Freeplay Gap () and No-Friction
5.3. Aeroelastic Characteristics of the Fin–Actuator System with Freeplay
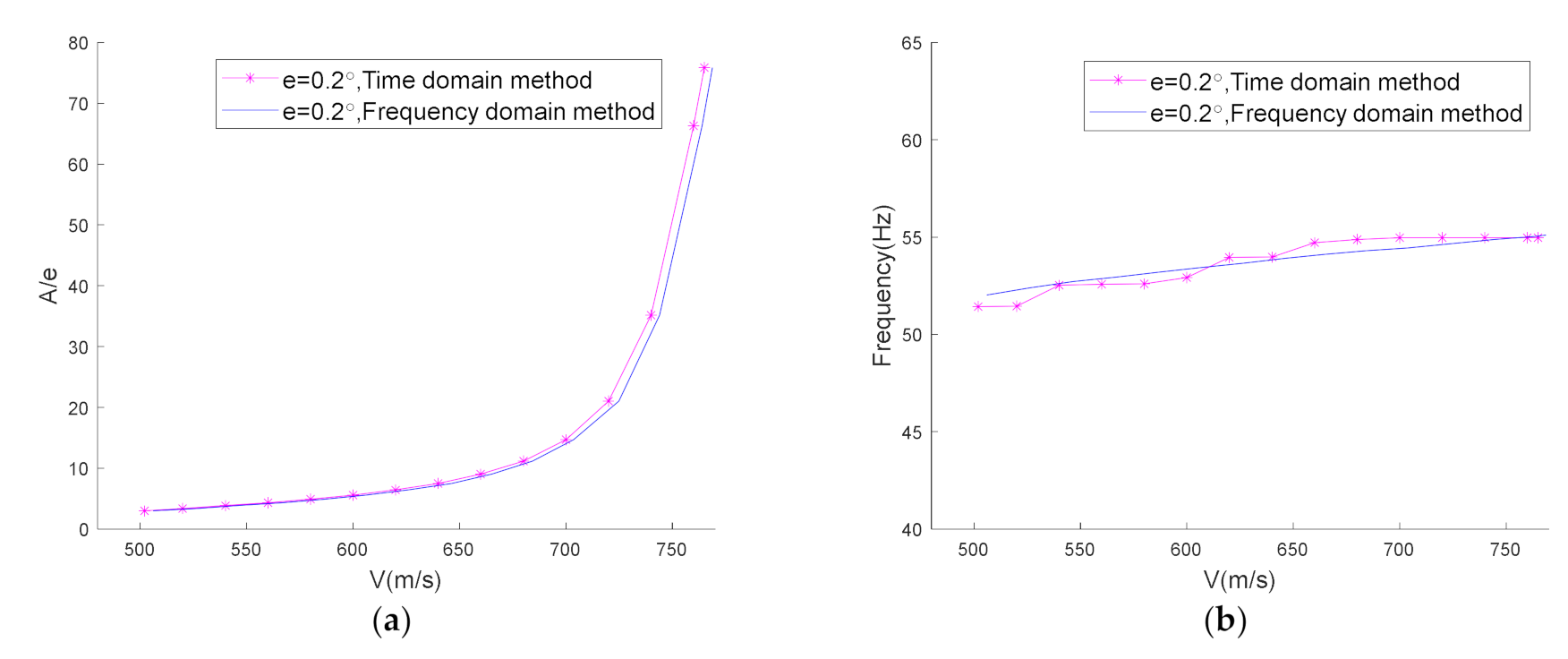
5.3.1. Influence of Different Initial Deflection Angle with
5.3.2. Influence of Different Freeplay with
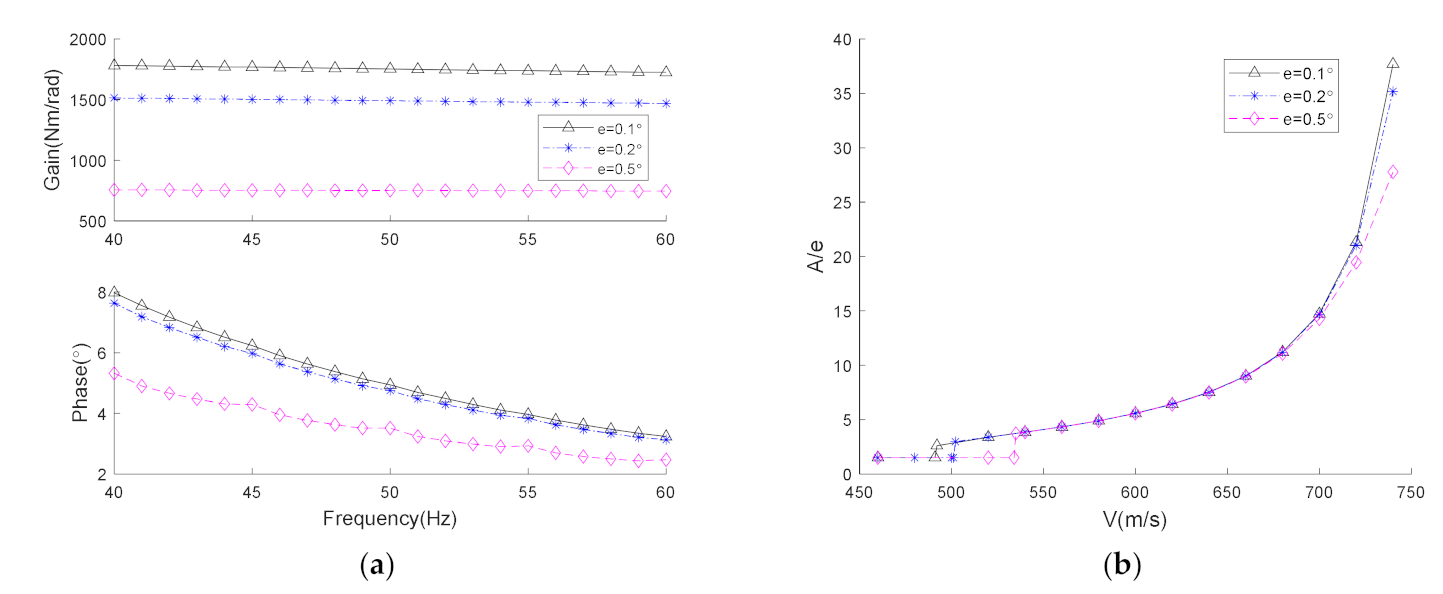
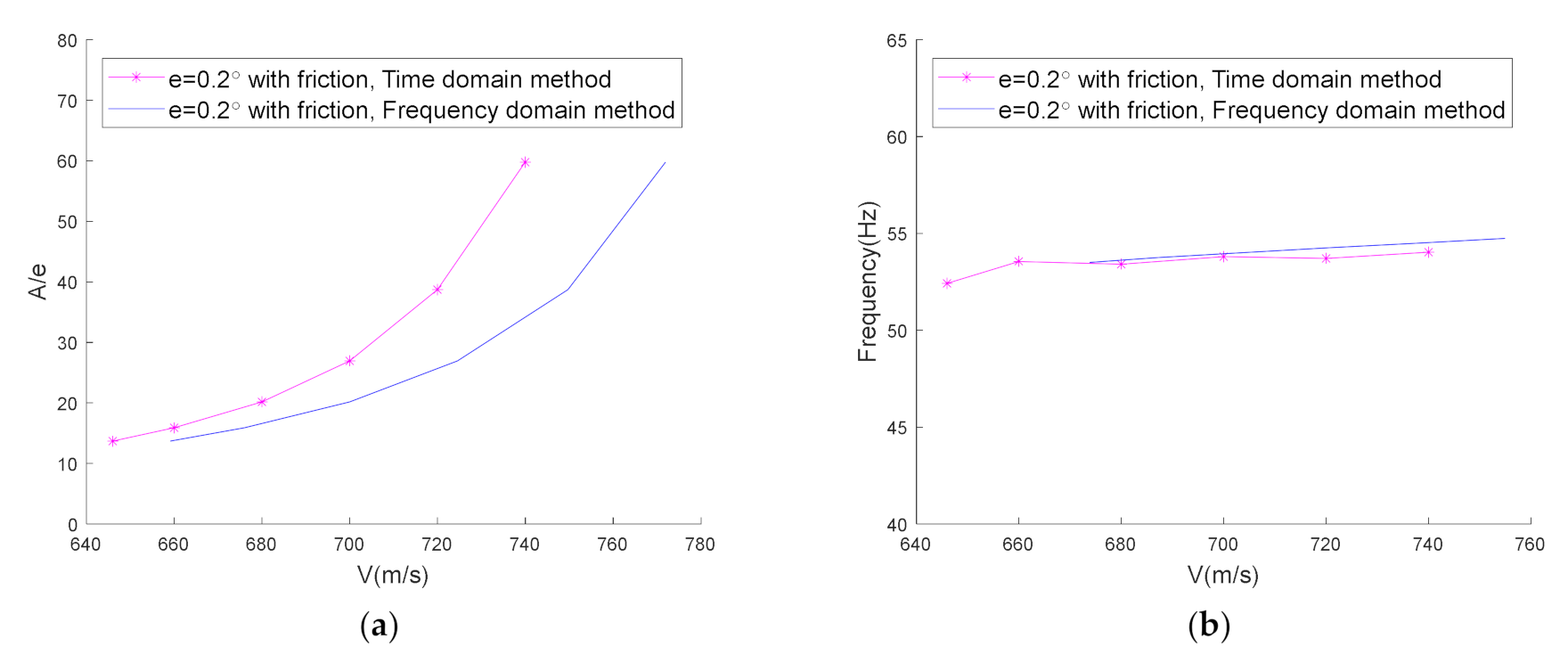
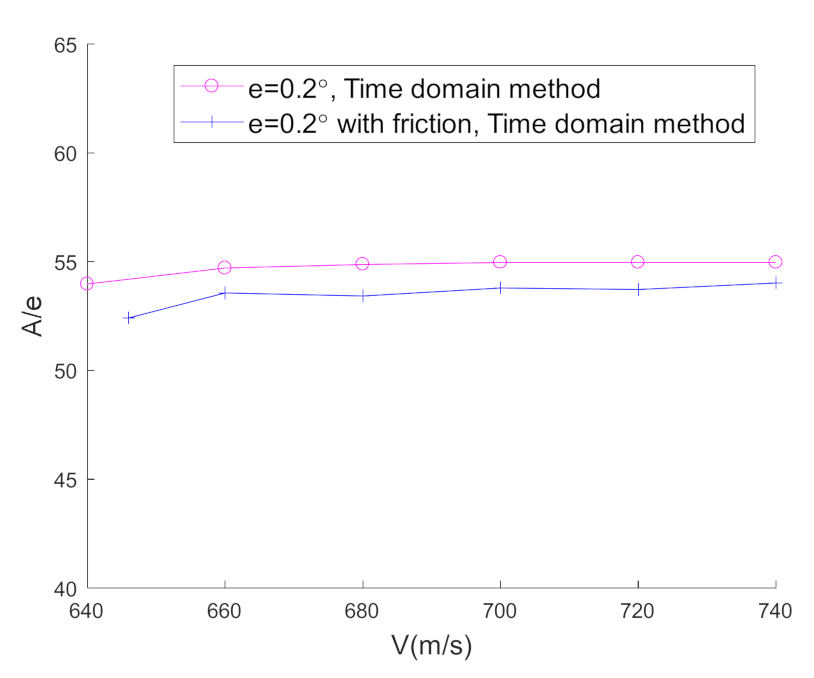
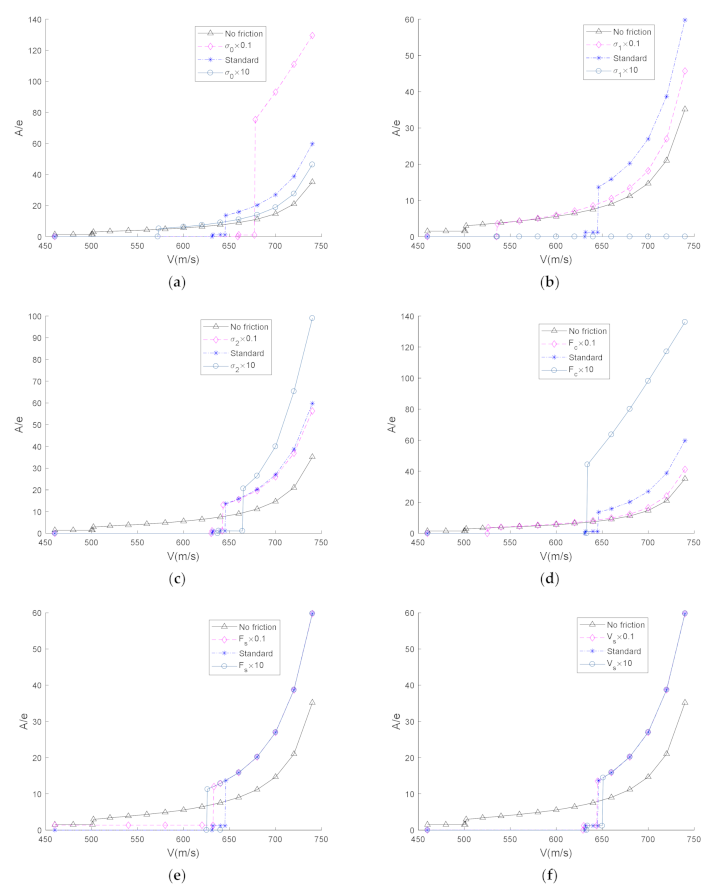
5.4. Aeroelastic Characteristics of the System with Freeplay and Friction
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Matrices and Vectors
References
- Librescu, L.; Marzocca, P. Advances in the Linear/Nonlinear Control of Aeroelastic Structural Systems. Acta Mech. 2005, 178, 147–186. [Google Scholar] [CrossRef]
- Karpel, M. Design for Active and Passive Flutter Suppression and Gust Alleviation. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1981. [Google Scholar]
- Yoo, C.-H.; Lee, Y.-C.; Lee, S.-Y. A Robust Controller for an Electro-Mechanical Fin Actuator. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 5, pp. 4010–4015. [Google Scholar]
- Kim, S.H.; Tahk, M.-J. Dynamic Stiffness Transfer Function of an Electromechanical Actuator Using System Identification. Int. J. Aeronaut. Space Sci. 2018, 19, 208–216. [Google Scholar] [CrossRef]
- Yehezkely, E.; Karpel, M. Nonlinear Flutter Analysis of Missiles with Pneumatic Fin Actuators. J. Guid. Control Dyn. 1996, 19, 664–670. [Google Scholar] [CrossRef]
- Shin, W.-H.; Lee, I.; Shin, Y.-S.; Bae, J.-S. Nonlinear Aeroelastic Analysis for a Control Fin with an Actuator. J. Aircr. 2007, 44, 597–605. [Google Scholar] [CrossRef]
- Yang, N.; Wu, Z.; Yang, C. Structural Nonlinear Flutter Characteristics Analysis for an Actuator-Fin System with Dynamic Stiffness. Chin. J. Aeronaut. 2011, 24, 590–599. [Google Scholar] [CrossRef][Green Version]
- Paek, S.-K.; Lee, I. Flutter Analysis for Control Surface of Launch Vehicle with Dynamic Stiffness. Comput. Struct. 1996, 60, 593–599. [Google Scholar] [CrossRef]
- Shin, W.-H.; Lee, S.-J.; Lee, I.; Bae, J.-S. Effects of Actuator Nonlinearity on Aeroelastic Characteristics of a Control Fin. J. Fluids Struct. 2007, 23, 1093–1105. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, Z.; Yang, C. Dynamic Stiffness Testing-Based Flutter Analysis of a Fin with an Actuator. Chin. J. Aeronaut. 2015, 28, 1400–1407. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, K.; Shen, Y. Research on Nonlinear Mechanical Properties for Actuator Structure. Aero Weapon. 2015, 3, 38–43. [Google Scholar]
- Kingsbury, D.W.; Agelastos, A.M.; Dietz, G.; Mignolet, M.; Liu, D.D.; Schewe, G. Limit Cycle Oscillations of Aeroelastic Systems with Internal Friction in the Transonic Domain—Experimental Results. In Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Austin, TX, USA, 18–21 April 2005; Volume 2, pp. 1412–1422. [Google Scholar]
- Ravanbod-Shirazi, L.; Besancon-Voda, A. Friction Identification Using the Karnopp Model, Applied to an Electropneumatic Actuator. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2003, 271, 123–138. [Google Scholar] [CrossRef]
- Torkaman, A. Flutter Stability of Shrouded Turbomachinery Cascades with Nonlinear Frictional Damping. Electronic Theses and Dissertations, 2004–2019. 2018. Available online: https://stars.library.ucf.edu/etd/6169/ (accessed on 14 January 2019).
- Khalak, A. A Framework for Flutter Clearance of Aeroengine Blades. J. Eng. Gas Turbines Power 2002, 124, 1003–1010. [Google Scholar] [CrossRef]
- Griffin, J.H. Friction Damping of Resonant Stresses in Gas Turbine Engine Airfoils. J. Eng. Power 1980, 102, 329–333. [Google Scholar] [CrossRef]
- Whiteman, W.E.; Ferri, A.A. Suppression of Bending-Torsion Flutter through Displacement-Dependent Dry Friction Damping. AIAA J. 1999, 31, 79–83. [Google Scholar] [CrossRef]
- Mignolet, M.; Agelastos, A.; Liu, D. Impact of Frictional Structural Nonlinearity in the Presence of Negative Aerodynamic Damping. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; p. 1428. [Google Scholar]
- Tan, T.; Li, M.; Liu, B. Stability Analysis of an Aeroelastic System with Friction. Chin. J. Aeronaut. 2013, 26, 624–630. [Google Scholar] [CrossRef]
- Lu, L.; Li, M.; Gan, K. Influence of Coulomb Friction on Two-Dimensional Aeroelastic Airfoils. Eng. Mech. 2015, 5, 250–256. [Google Scholar]
- Wayhs-Lopes, L.D.; Dowell, E.H.; Bueno, D.D. Influence of Friction and Asymmetric Freeplay on the Limit Cycle Oscillation in Aeroelastic System: An Extended Hénon’s Technique to Temporal Integration. J. Fluids Struct. 2020, 96, 103054. [Google Scholar] [CrossRef]
- Sang, Y.; Gao, H.; Xiang, F. Practical Friction Models and Friction Compensation in High-Precision Electro-Hydraulic Servo Force Control Systems. Instrum. Sci. Technol. 2014, 42, 184–199. [Google Scholar] [CrossRef]
- Dahl, P.R. Measurement of Solid Friction Parameters of Ball Bearings; Aerospace Corp El Segundo Ca Engineering Science Operations: El Segundo, CA, USA, 1977. [Google Scholar]
- De Wit, C.C.; Olsson, H.; Astrom, K.J.; Lischinsky, P. A New Model for Control of Systems with Friction. IEEE Trans. Autom. Control 1995, 40, 419–425. [Google Scholar] [CrossRef]
- De Wit, C.C.; Lischinsky, P. Adaptive Friction Compensation with Partially Known Dynamic Friction Model. Int. J. Adapt. Control Signal Process. 1997, 11, 65–80. [Google Scholar] [CrossRef]
- Swevers, J.; Al-Bender, F.; Ganseman, C.G.; Projogo, T. An Integrated Friction Model Structure with Improved Presliding Behavior for Accurate Friction Compensation. IEEE Trans. Autom. Control 2000, 45, 675–686. [Google Scholar] [CrossRef]
- Lampaert, V.; Swevers, J.; Al-Bender, F. Modification of the Leuven Integrated Friction Model Structure. IEEE Trans. Autom. Control 2002, 47, 683–687. [Google Scholar] [CrossRef]
- Lampaert, V.; Al-Bender, F.; Swevers, J. A Generalized Maxwell-Slip Friction Model Appropriate for Control Purposes. In Proceedings of the 2003 IEEE International Workshop on Workload Characterization (IEEE Cat. No. 03EX775), Saint Petersburg, Russia, 20–22 August 2003; Volume 4, pp. 1170–1177. [Google Scholar]
- Al-Bender, F.; Lampaert, V.; Swevers, J. The Generalized Maxwell-Slip Model: A Novel Model for Friction Simulation and Compensation. IEEE Trans. Autom. Control 2005, 50, 1883–1887. [Google Scholar] [CrossRef]
- Ruderman, M.; Bertram, T. Two-State Dynamic Friction Model with Elasto-Plasticity. Mech. Syst. Signal Process 2013, 39, 316–332. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S. High Performance Adaptive Control of Mechanical Servo System with LuGre Friction Model: Identification and Compensation. J. Dyn. Syst. Meas. Control 2012, 134, 011021. [Google Scholar] [CrossRef]
- Mate, C.M.; Carpick, R.W. Tribology on the Small Scale: A Modern Textbook on Friction, Lubrication, and Wear; Oxford University Press: New York, NY, USA, 2019. [Google Scholar]
- Tustin, A. The Effects of Backlash and of Speed-Dependent Friction on the Stability of Closed-Cycle Control Systems. J. Inst. Electr. Eng. Part IIA Autom. Regul. Servo Mech. 1947, 94, 143–151. [Google Scholar] [CrossRef]
- Osborne, N.; Rittenhouse, D. The Modeling of Friction and Its Effects on Fine Pointing Control. In Proceedings of the Mechanics and Control of Flight Conference, Anaheim, CA, USA, 5–9 August 1974; p. 875. [Google Scholar]
- Li, L.; Wang, F.Y.; Zhou, Q. Integrated Longitudinal and Lateral Tire/Road Friction Modeling and Monitoring for Vehicle Motion Control. IEEE Trans. Intell. Transp. Syst. 2006, 7, 1–19. [Google Scholar] [CrossRef]
- Brandenburg, G.; Schafer, U. Influence and Compensation of Coulomb Friction in Industrial Pointing and Tracking Systems. In Proceedings of the Conference Record of the 1991 IEEE Industry Applications Society Annual Meeting, Dearborn, MI, USA, 28 September–4 October 1991; pp. 1407–1413. [Google Scholar]
- Olsson, H.; Astrom, K.J. Friction Generated Limit Cycles. IEEE Trans. Control Syst. Technol. 2001, 9, 629–636. [Google Scholar] [CrossRef]
- Canudas, C.; Astrom, K.; Braun, K. Adaptive Friction Compensation in DC-Motor Drives. IEEE Robot Autom. Mag. 1987, 3, 681–685. [Google Scholar] [CrossRef]
- De Wit, C.C. Robust Control for Servo-Mechanisms under Inexact Friction Compensation. Automatica 1993, 29, 757–761. [Google Scholar] [CrossRef]
- Giorgio, I.; Del Vescovo, D. Energy-based trajectory tracking and vibration control for multilink highly flexible manipulators. Math. Mech. Complex Syst. 2019, 7, 159–174. [Google Scholar] [CrossRef]
- Wang, X.; Lin, S.; Wang, S. Dynamic Friction Parameter Identification Method with Lugre Model for Direct-Drive Rotary Torque Motor. Math. Probl. Eng. 2016, 2016, 6929457. [Google Scholar] [CrossRef]
- Feyel, P.; Duc, G.; Sandou, G. LuGre Friction Model Identification and Compensator Tuning Using a Differential Evolution Algorithm. In Proceedings of the 2013 IEEE Symposium on Differential Evolution (SDE), Singapore, 16–19 April 2013; pp. 85–91. [Google Scholar]
- Zhuo, G.; Wang, J.; Zhang, F. Parameter Identification of Tire Model Based on Improved Particle Swarm Optimization Algorithm; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2015. [Google Scholar]
- Saha, A.; Wiercigroch, M.; Jankowski, K.; Wahi, P.; Stefański, A. Investigation of Two Different Friction Models from the Perspective of Friction-Induced Vibrations. Tribol. Int. 2015, 90, 185–197. [Google Scholar] [CrossRef]
- Gladwell, G.M.L. Branch Mode Analysis of Vibrating Systems. J. Sound Vib. 1964, 1, 41–59. [Google Scholar] [CrossRef]
- Wang, W.L. Vibration and Dynamic Sub-Structure Method; Fudan University Press: Shanghai, China, 1985. [Google Scholar]
- Piccardo, G. A Methodology for the Study of Coupled Aeroelastic Phenomena. J. Wind. Eng. Ind. Aerodyn. 1993, 48, 241–252. [Google Scholar] [CrossRef]
- Version 9.3. Theoretical Manual, ZONA Technology. 2017. Available online: https://www.zonatech.com/downloads.html#ProductDocumentation (accessed on 14 January 2019).
- Astrom, K.J.; De Wit, C.C. Revisiting the Lugre Model Stick-Slip Motion and Rate Dependence. IEEE Control Syst. 2008, 28, 101–114. [Google Scholar]
- Liu, J. MATLAB Simulation of Advanced PID Control, 2nd ed.; Electronic Industry Press: Beijing, China, 2004. [Google Scholar]
- Krylov, N.M.; Bogoliubov, N. Introduction to Nonlinear Mechanics; Princeton University Press: Princeton, NJ, USA, 1943. [Google Scholar]
- Blaquiere, A. Nonlinear System Analysis; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Kochenburger, R.J. A Frequency Response Method for Analyzing and Synthesizing Contactor Servomechanisms. Trans. Am. Inst. Electr. Eng. 1950, 69, 270–284. [Google Scholar] [CrossRef]
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Kim, S.H.; Tahk, M.J. Modeling and Experimental Study on the Dynamic Stiffness of an Electromechanical Actuator. J. Spacecr. Rocket. 2016, 53, 708–719. [Google Scholar] [CrossRef]
- Tang, D.; Dowell, E.H. Aeroelastic Response Induced by Free Play, Part 1: Theory. AIAA J. 2011, 49, 2532–2542. [Google Scholar] [CrossRef]
- Hensen, R.H.; van de Molengraft, M.J.; Steinbuch, M. Frequency Domain Identification of Dynamic Friction Model Parameters. IEEE Trans. Control Syst. Technol. 2002, 10, 191–196. [Google Scholar] [CrossRef]
- Rizos, D.D.; Fassois, S.D. Friction Identification Based upon the LuGre and Maxwell Slip Models. IEEE Trans. Control Syst. Technol. 2008, 17, 153–160. [Google Scholar] [CrossRef]
- Tran, X.B.; Yanada, H. Dynamic Friction Characteristics of Pneumatic Actuators and Their Mathematical Model. In Proceedings of the 8th JFPS International Symposium on Fluid Power, Okinawa, Japan, 25–28 October 2011; pp. 657–664. [Google Scholar]
- Xiao, Q.; Jia, H.; Zhang, J.; Han, X.; Xi, R. Identification and Compensation of Nonlinearity for Electromechanical Actuator Servo System. Opt. Precis. Eng. 2013, 21, 2038–2047. [Google Scholar] [CrossRef]
- Yu, W.; Ma, J.; Li, J.; Xiao, J. Friction Parameter Identification and Friction Compensation for Precision Servo Turning Table. Opt. Precis. Eng. 2011, 19, 2736–2743. [Google Scholar] [CrossRef]
- Liu, Q.; Hu, H.; Liu, J.; Er, L. Research on the Parameter Identification of Friction Model for Servo Systems Based on Genetic Algorithms. J. Syst. Eng. Electron. 2003, 77–79. [Google Scholar]
- Armstrong-Hélouvry, B.; Dupont, P.; De Wit, C.C. A Survey of Models, Analysis Tools and Compensation Methods for the Control of Machines with Friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, I.; Shin, W.H. Flutter Characteristics of Aircraft Wing Considering Control Surface and Actuator Dynamics with Friction Nonlinearity. Int. J. Aeronaut. Space Sci. 2007, 8, 140–147. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Z.; Yang, C. New Flutter-Suppression Method for a Missile Fin with an Actuator. J. Aircraft 2013, 50, 989–994. [Google Scholar] [CrossRef]
- Karpel, M. Design for Active Flutter Suppression and Gust Alleviation Using State-Space Aeroelastic Modeling. J. Aircraft 1982, 19, 221–227. [Google Scholar] [CrossRef]





| Viscous | Stribeck Effect | Pre-Sliding | Hysteresis | |
|---|---|---|---|---|
| Coulomb | No | No | No | No |
| Viscous | Yes | No | No | No |
| Stribeck | Yes | Yes | No | No |
| Dahl | No | No | Yes | Yes |
| LuGre | Yes | Yes | Yes | Yes |
| Leuven | Yes | Yes | Yes | Yes |
| GMS | Yes | Yes | Yes | Yes |
| 2SEP | Yes | Yes | Yes | Yes |
| Elastic Branch | Frequency | Modal Shape |
|---|---|---|
| 1st mode | 50.3 Hz | 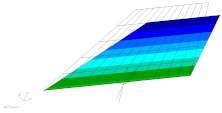 |
| 2nd mode | 593.0 Hz | 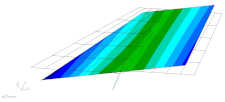 |
| Description | Symbol | Value | Unit |
|---|---|---|---|
| Inductance | mH | ||
| Resistance | 1.1 | ||
| Rotor inertia | |||
| Torque coefficient | 0.0238 | Nm/A | |
| Back EMF coefficient | 0.034 | V/(rad/s) | |
| Connection stiffness | 1000 | Nm/rad | |
| Moment of inertia of gear 1 | |||
| Radius of gear 1 | 0.005 | m | |
| Moment of inertia of gear 2 | |||
| Radius of gear 2 | 0.0225 | m | |
| Meshing stiffness | |||
| Connection stiffness | 1000 | Nm/rad | |
| Screw inertia | |||
| Radius of screw | 0.006 | m | |
| Screw efficiency | 0.85 | ||
| Fork length | 0.0285 | m | |
| Comprehensive stiffness | |||
| Bristle stiffness | 300 | Nm/rad | |
| Bristle damping | 2.5 | Nm/(rad/s) | |
| Viscous damping | 0.02 | Nm/(rad/s) | |
| Coulomb friction | 1.2565 | Nm | |
| Maximum static friction force | 0.774 | Nm | |
| Stribeck velocity | 1 | rad/s |
| Description | Symbol | PARAMETER RANGE | Unit | Parameter Depends Principally upon [26,59,63] |
|---|---|---|---|---|
| Bristle stiffness | Nm/rad | Material properties | ||
| Bristle damping | ~45.2 | Nm/(rad/s) | Contact geometry and lubricant | |
| Viscous damping | ~1.819 | Nm/(rad/s) | Lubricant | |
| Coulomb friction | ~2646.856 | Nm | Lubricant, contact geometry, and pressure | |
| Maximum static friction force | ~8.558 | Nm | Boundary lubrication and pressure | |
| Stribeck velocity | ~88.1 | rad/s | Lubricant and pressure |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wu, Z.; Yang, C. High-Fidelity Fin–Actuator System Modeling and Aeroelastic Analysis Considering Friction Effect. Appl. Sci. 2021, 11, 3057. https://doi.org/10.3390/app11073057
Lu J, Wu Z, Yang C. High-Fidelity Fin–Actuator System Modeling and Aeroelastic Analysis Considering Friction Effect. Applied Sciences. 2021; 11(7):3057. https://doi.org/10.3390/app11073057
Chicago/Turabian StyleLu, Jin, Zhigang Wu, and Chao Yang. 2021. "High-Fidelity Fin–Actuator System Modeling and Aeroelastic Analysis Considering Friction Effect" Applied Sciences 11, no. 7: 3057. https://doi.org/10.3390/app11073057
APA StyleLu, J., Wu, Z., & Yang, C. (2021). High-Fidelity Fin–Actuator System Modeling and Aeroelastic Analysis Considering Friction Effect. Applied Sciences, 11(7), 3057. https://doi.org/10.3390/app11073057





