Nonlinear Dynamics of an Internally Resonant Base-Isolated Beam under Turbulent Wind Flow
Abstract
1. Introduction
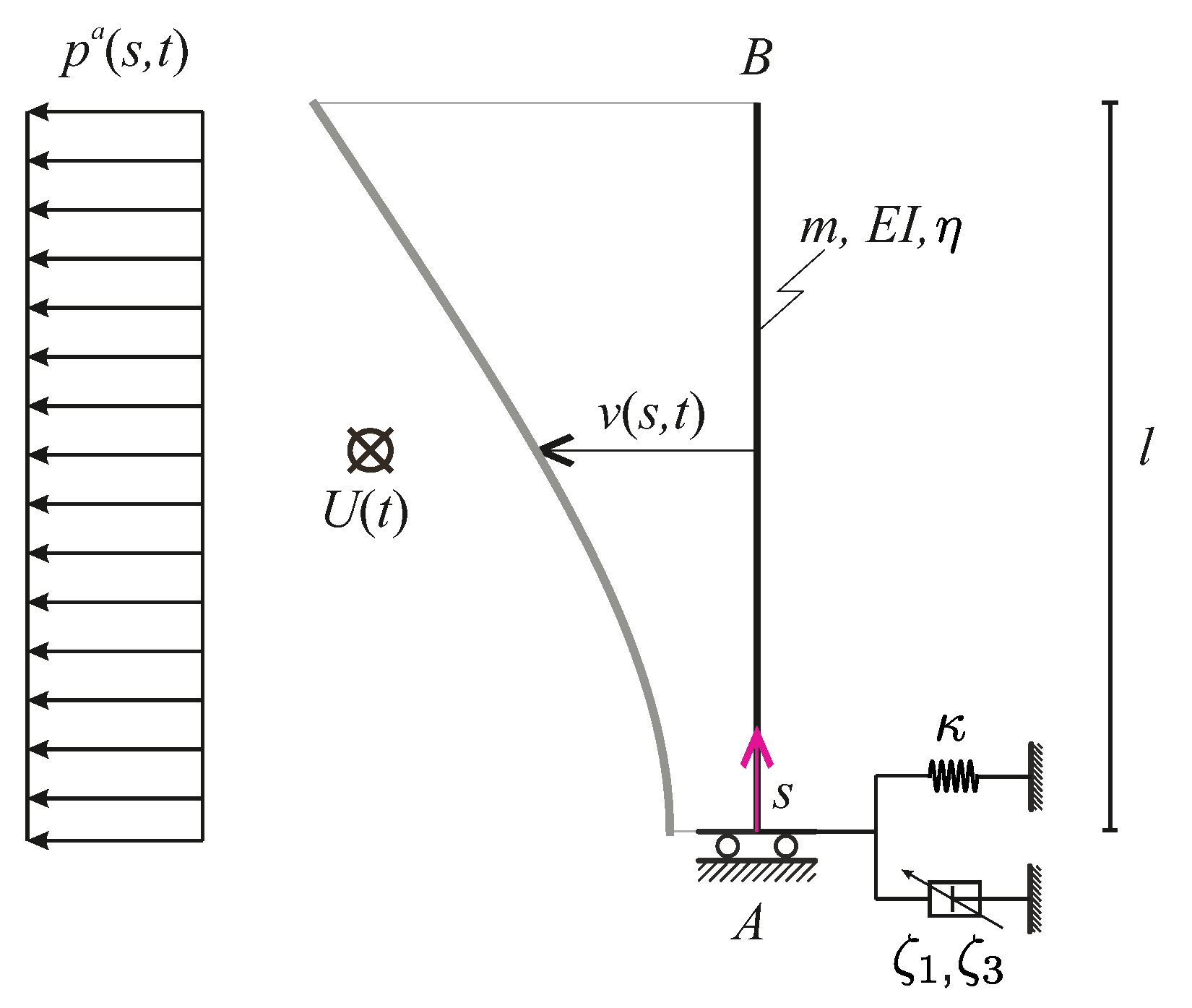
2. Model
2.1. Nonlinear Aeroelastic Model
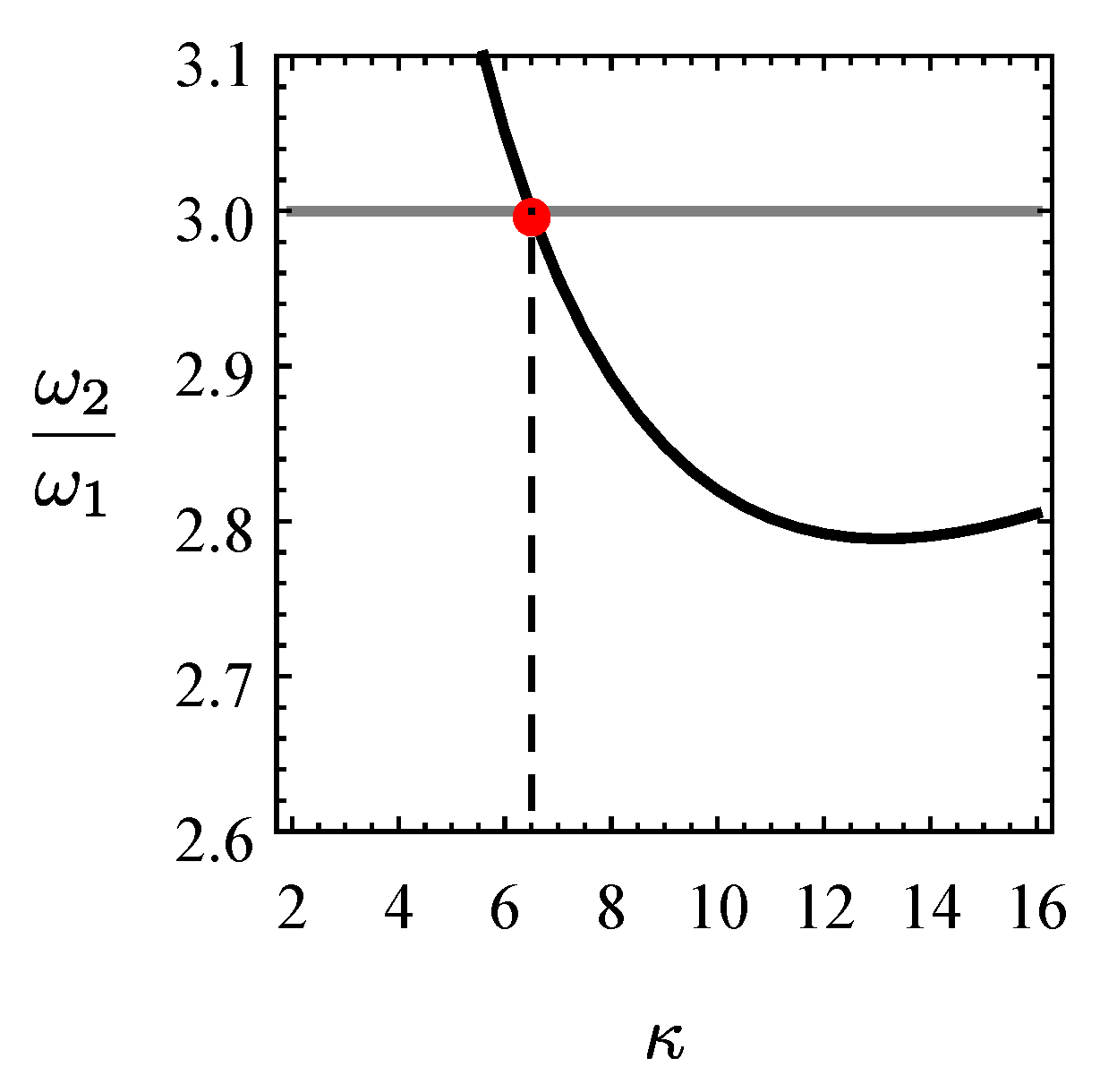
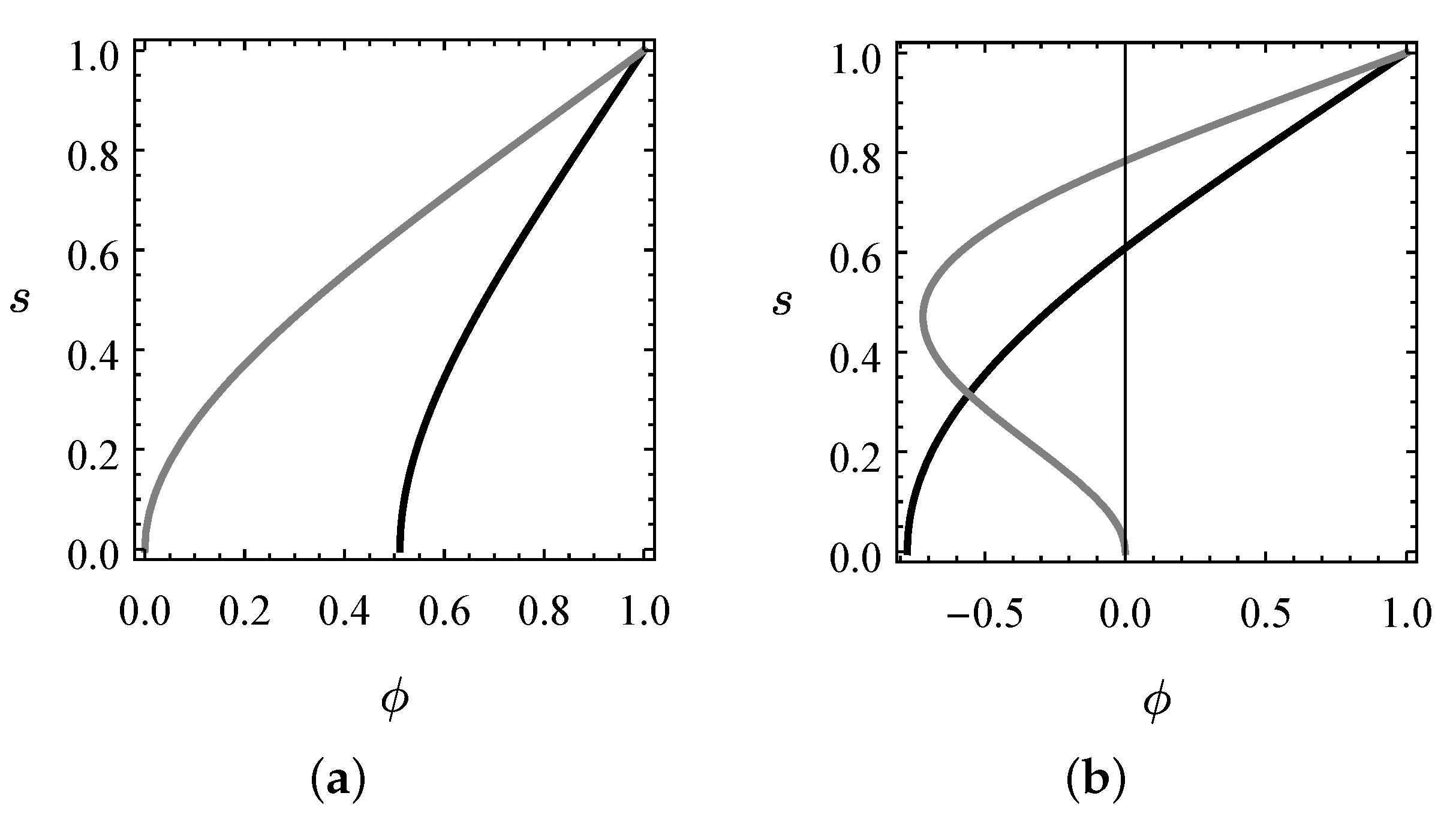
2.2. Modal Proprieties
3. Perturbation Analysis
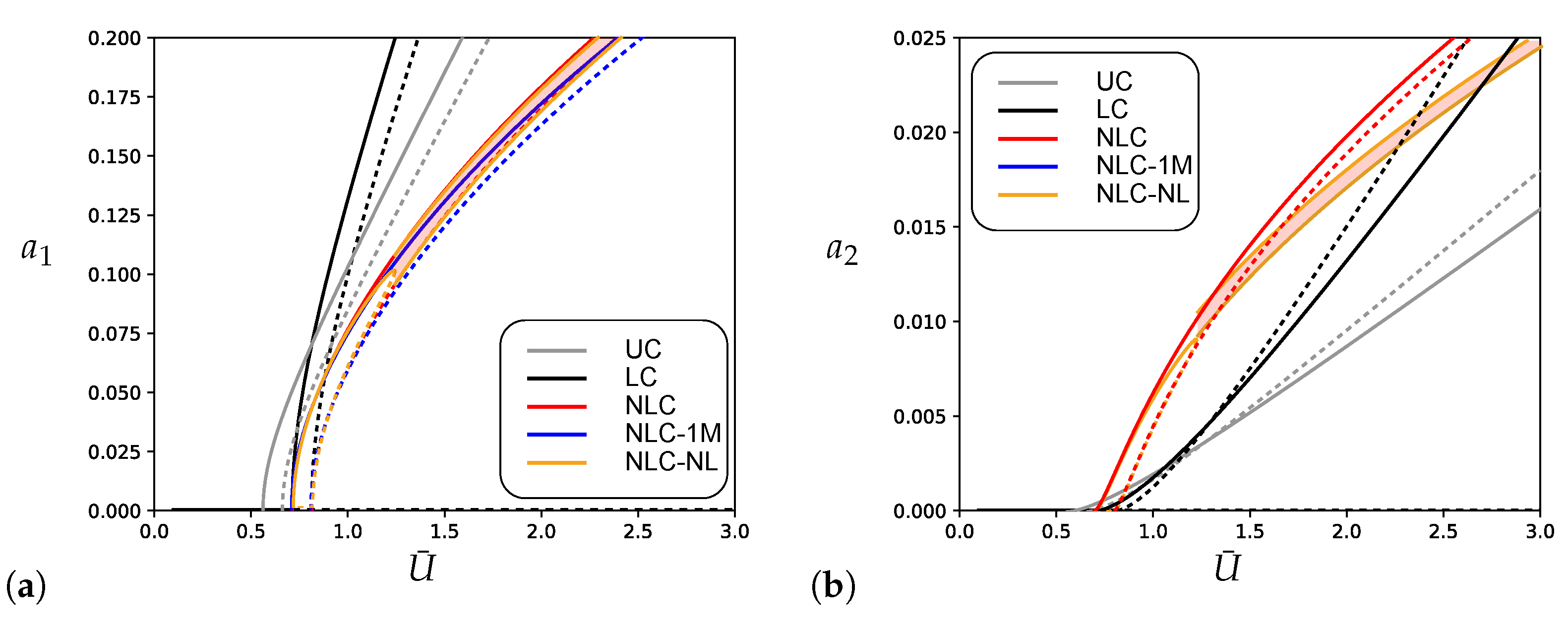
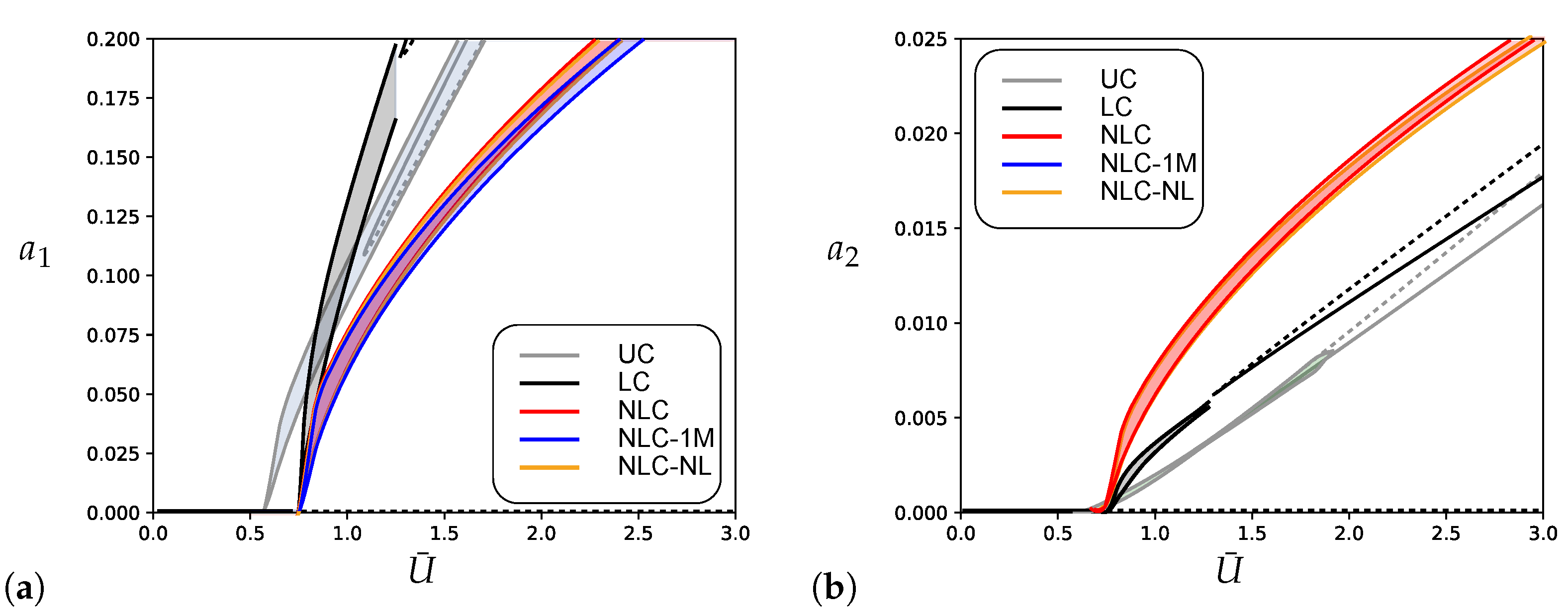
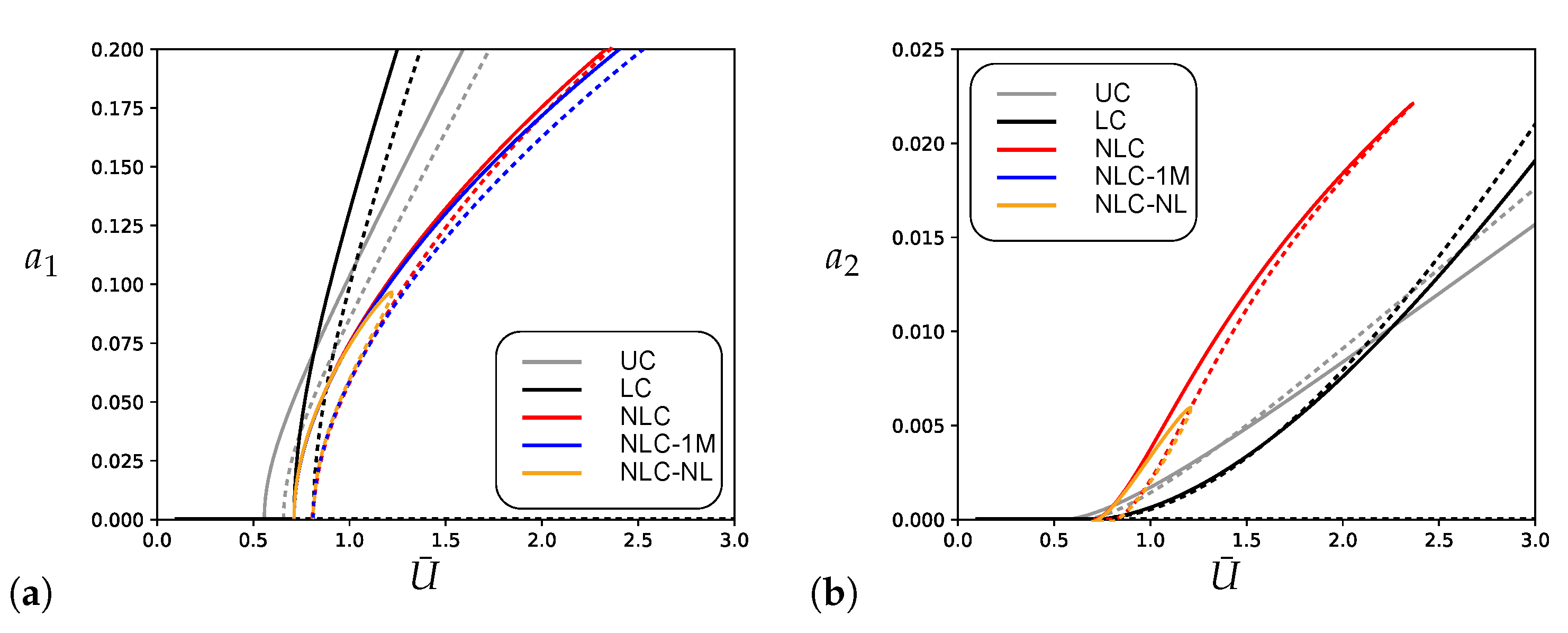
4. Numerical Results
5. Conclusions
- The base device, through its linear viscous component, pushes forward the bifurcation point, as expected;
- The nonlinear viscous term of the device reduces the amplitude of the post-critical evolution, as compared to the use of a purely linear device;
- The galloping induced by the mean wind on the first mode represents the leading phenomenon, being the second mode marginally involved in the motion due to its smaller amplitudes;
- The structural nonlinearities provide weak modification to the response, confirming the almost linear behavior of the cantilever, even when internal resonance occurs.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Nonlinear Equations of Motion
Appendix B. Coefficients of Equations
References
- Tang, D.; Dowell, E.H. Experimental and theoretical study on aeroelastic response of high-aspect-ratio wings. AIAA J. 2001, 39, 1430–1441. [Google Scholar] [CrossRef]
- Afonso, F.; Vale, J.; Oliveira, É.; Lau, F.; Suleman, A. A review on non-linear aeroelasticity of high aspect-ratio wings. Prog. Aerosp. Sci. 2017, 89, 40–57. [Google Scholar] [CrossRef]
- Riziotis, V.; Voutsinas, S.; Politis, E.; Chaviaropoulos, P. Aeroelastic stability of wind turbines: The problem, the methods and the issues. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2004, 7, 373–392. [Google Scholar] [CrossRef]
- Hansen, M.H. Aeroelastic instability problems for wind turbines. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2007, 10, 551–577. [Google Scholar] [CrossRef]
- Tokoro, S.; Komatsu, H.; Nakasu, M.; Mizuguchi, K.; Kasuga, A. A study on wake-galloping employing full aeroelastic twin cable model. J. Wind. Eng. Ind. Aerodyn. 2000, 88, 247–261. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Dynamic instability of inclined cables under combined wind flow and support motion. Nonlinear Dyn. 2012, 67, 71–87. [Google Scholar] [CrossRef]
- Ferretti, M.; Zulli, D.; Luongo, A. A continuum approach to the nonlinear in-plane galloping of shallow flexible cables. Adv. Math. Phys. 2019, 2019, 6865730. [Google Scholar] [CrossRef]
- Larsen, A. Advances in aeroelastic analyses of suspension and cable-stayed bridges. J. Wind. Eng. Ind. Aerodyn. 1998, 74, 73–90. [Google Scholar] [CrossRef]
- Diana, G.; Rocchi, D.; Argentini, T.; Muggiasca, S. Aerodynamic instability of a bridge deck section model: Linear and nonlinear approach to force modeling. J. Wind. Eng. Ind. Aerodyn. 2010, 98, 363–374. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. Nonlinear Aeroelastic in-Plane Behavior of Suspension Bridges under Steady Wind Flow. Appl. Sci. 2020, 10, 1689. [Google Scholar] [CrossRef]
- Kawai, H. Effect of corner modifications on aeroelastic instabilities of tall buildings. J. Wind. Eng. Ind. Aerodyn. 1998, 74, 719–729. [Google Scholar] [CrossRef]
- Braun, A.L.; Awruch, A.M. Aerodynamic and aeroelastic analyses on the CAARC standard tall building model using numerical simulation. Comput. Struct. 2009, 87, 564–581. [Google Scholar] [CrossRef]
- Cluni, F.; Gioffrè, M.; Gusella, V. Dynamic response of tall buildings to wind loads by reduced order equivalent shear-beam models. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 339–348. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F.; Luongo, A. A shear-shear torsional beam model for nonlinear aeroelastic analysis of tower buildings. Z. Angew. Math. Phys. 2015, 66, 1895–1913. [Google Scholar] [CrossRef]
- Piccardo, G.; Tubino, F.; Luongo, A. Equivalent nonlinear beam model for the 3-D analysis of shear-type buildings: Application to aeroelastic instability. Int. J. Non-Linear Mech. 2016, 80, 52–65. [Google Scholar] [CrossRef]
- Zulli, D.; Luongo, A. Nonlinear dynamics and stability of a homogeneous model of tall buildings under resonant action. J. Appl. Comput. Mech. 2020. [Google Scholar] [CrossRef]
- Lu, O.; To, C. Principal resonance of a nonlinear system with two-frequency parametric and self-excitations. Nonlinear Dyn. 1991, 2, 419–444. [Google Scholar] [CrossRef]
- Szabelski, K.; Warmiński, J. Parametric self-excited non-linear system vibrations analysis with inertial excitation. Int. J. Non-Linear Mech. 1995, 30, 179–189. [Google Scholar] [CrossRef]
- El-Bassiouny, A. Principal parametric resonances of non-linear mechanical system with two-frequency and self-excitations. Mech. Res. Commun. 2005, 32, 337–350. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. Nonlinear interaction between self-and parametrically excited wind-induced vibrations. Nonlinear Dyn. 2021, 103, 79–101. [Google Scholar] [CrossRef]
- Abdel-Rohman, M. Effect of unsteady wind flow on galloping of tall prismatic structures. Nonlinear Dyn. 2001, 26, 233–254. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Parametric, external and self-excitation of a tower under turbulent wind flow. J. Sound Vib. 2011, 330, 3057–3069. [Google Scholar] [CrossRef]
- Zulli, D.; Luongo, A. Bifurcation and stability of a two-tower system under wind-induced parametric, external and self-excitation. J. Sound Vib. 2012, 331, 365–383. [Google Scholar] [CrossRef]
- Zulli, D.; Di Egidio, A. Galloping of internally resonant towers subjected to turbulent wind. Contin. Mech. Thermodyn. 2015, 27, 835–849. [Google Scholar] [CrossRef]
- Kirrou, I.; Mokni, L.; Belhaq, M. On the quasiperiodic galloping of a wind-excited tower. J. Sound Vib. 2013, 332, 4059–4066. [Google Scholar] [CrossRef]
- Belhaq, M.; Kirrou, I.; Mokni, L. Periodic and quasiperiodic galloping of a wind-excited tower under external excitation. Nonlinear Dyn. 2013, 74, 849–867. [Google Scholar] [CrossRef]
- Bottasso, C.L.; Croce, A.; Gualdoni, F.; Montinari, P. Load mitigation for wind turbines by a passive aeroelastic device. J. Wind. Eng. Ind. Aerodyn. 2016, 148, 57–69. [Google Scholar] [CrossRef]
- Graham, J.M.R.; Limebeer, D.J.; Zhao, X. Aeroelastic control of long-span suspension bridges. J. Appl. Mech. 2011, 78, 041018. [Google Scholar] [CrossRef]
- Ribeiro, L.P.; de Lima, A.M.G. Robust passive control methodology and aeroelastic behavior of composite panels with multimodal shunted piezoceramics in parallel. Compos. Struct. 2020, 262, 113348. [Google Scholar] [CrossRef]
- Lee, Y.S.; Vakakis, A.F.; Bergman, L.A.; McFarland, D.M.; Kerschen, G. Suppression aeroelastic instability using broadband passive targeted energy transfers, part 1: Theory. AIAA J. 2007, 45, 693–711. [Google Scholar] [CrossRef]
- Lee, Y.S.; Kerschen, G.; McFarland, D.M.; Hill, W.J.; Nichkawde, C.; Strganac, T.W.; Bergman, L.A.; Vakakis, A.F. Suppressing aeroelastic instability using broadband passive targeted energy transfers, part 2: Experiments. AIAA J. 2007, 45, 2391–2400. [Google Scholar] [CrossRef]
- Gendelman, O.V.; Vakakis, A.F.; Bergman, L.A.; McFarland, D.M. Asymptotic analysis of passive nonlinear suppression of aeroelastic instabilities of a rigid wing in subsonic flow. SIAM J. Appl. Math. 2010, 70, 1655–1677. [Google Scholar] [CrossRef]
- Vaurigaud, B.; Manevitch, L.I.; Lamarque, C.H. Passive control of aeroelastic instability in a long span bridge model prone to coupled flutter using targeted energy transfer. J. Sound Vib. 2011, 330, 2580–2595. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Aeroelastic instability analysis of NES-controlled systems via a mixed multiple scale/harmonic balance method. J. Vib. Control 2014, 20, 1985–1998. [Google Scholar] [CrossRef]
- Bichiou, Y.; Hajj, M.R.; Nayfeh, A.H. Effectiveness of a nonlinear energy sink in the control of an aeroelastic system. Nonlinear Dyn. 2016, 86, 2161–2177. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. Nonlinear aeroelastic behavior of a base-isolated beam under steady wind flow. Int. J. Non-Linear Mech. 2020, 119, 103340. [Google Scholar] [CrossRef]
- Di Nino, S.; Luongo, A. Nonlinear dynamics of a base-isolated beam under turbulent wind flow. Nonlinear Dyn. 2021. [Google Scholar] [CrossRef]
- Nayfeh, A.; Chin, C.; Nayfeh, S. On nonlinear normal modes of systems with internal resonance. ASME J. Vib. Acoust. 1996, 118, 340–345. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Lacarbonara, W.; Chin, C.M. Nonlinear normal modes of buckled beams: Three-to-one and one-to-one internal resonances. Nonlinear Dyn. 1999, 18, 253–273. [Google Scholar] [CrossRef]
- Gilliatt, H.C.; Strganac, T.W.; Kurdila, A.J. An investigation of internal resonance in aeroelastic systems. Nonlinear Dyn. 2003, 31, 1–22. [Google Scholar] [CrossRef]
- Luongo, A.; Piccardo, G. A continuous approach to the aeroelastic stability of suspended cables in 1:2 internal resonance. J. Vib. Control 2008, 14, 135–157. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Nonlinear energy sink to control elastic strings: The internal resonance case. Nonlinear Dyn. 2015, 81, 425–435. [Google Scholar] [CrossRef]
- Di Egidio, A.; Zulli, D. Critical and post-critical galloping behavior of base isolated coupled towers. Int. J. Non-Linear Mech. 2021. accepted. [Google Scholar]
- Novak, M. Aeroelastic galloping of prismatic bodies. J. Eng. Mech. Div. 1969, 95, 115–142. [Google Scholar] [CrossRef]
- Luongo, A.; Di Egidio, A. Bifurcation Equations Through Multiple-Scales Analysis for a Continuous Model of a Planar Beam. Nonlinear Dyn. 2005, 41, 171–190. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; John Wiley: New York, NY, USA, 1979. [Google Scholar]
- Pignataro, M.; Rizzi, N.; Luongo, A. Stability, Bifurcation and Postcritical Behaviour of Elastic Structures; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Doedel, E.; Oldeman, B. AUTO-07P: Continuation and Bifurcation Software for Ordinary Differential Equation. 2019. Available online: http://indy.cs.concordia.ca/auto/ (accessed on 22 February 2021).
- Wolfram Research. Mathematica, Version 12.1; Wolfram Research: Champaign, IL, USA, 2020. [Google Scholar]
- Luongo, A.; Zulli, D. A paradigmatic system to study the transition from zero/Hopf to double-zero/Hopf bifurcation. Nonlinear Dyn. 2012, 70, 111–124. [Google Scholar] [CrossRef]
- Luongo, A.; Piccardo, G. Non-Linear Galloping of Sagged Cables in 1:2 Internal Resonance. J. Sound Vib. 1998, 214, 915–940. [Google Scholar] [CrossRef]
- Luongo, A.; Rega, G.; Vestroni, F. On Nonlinear Dynamics of Planar Shear Indeformable Beams. J. Appl. Mech. 1986, 53, 619–624. [Google Scholar] [CrossRef]


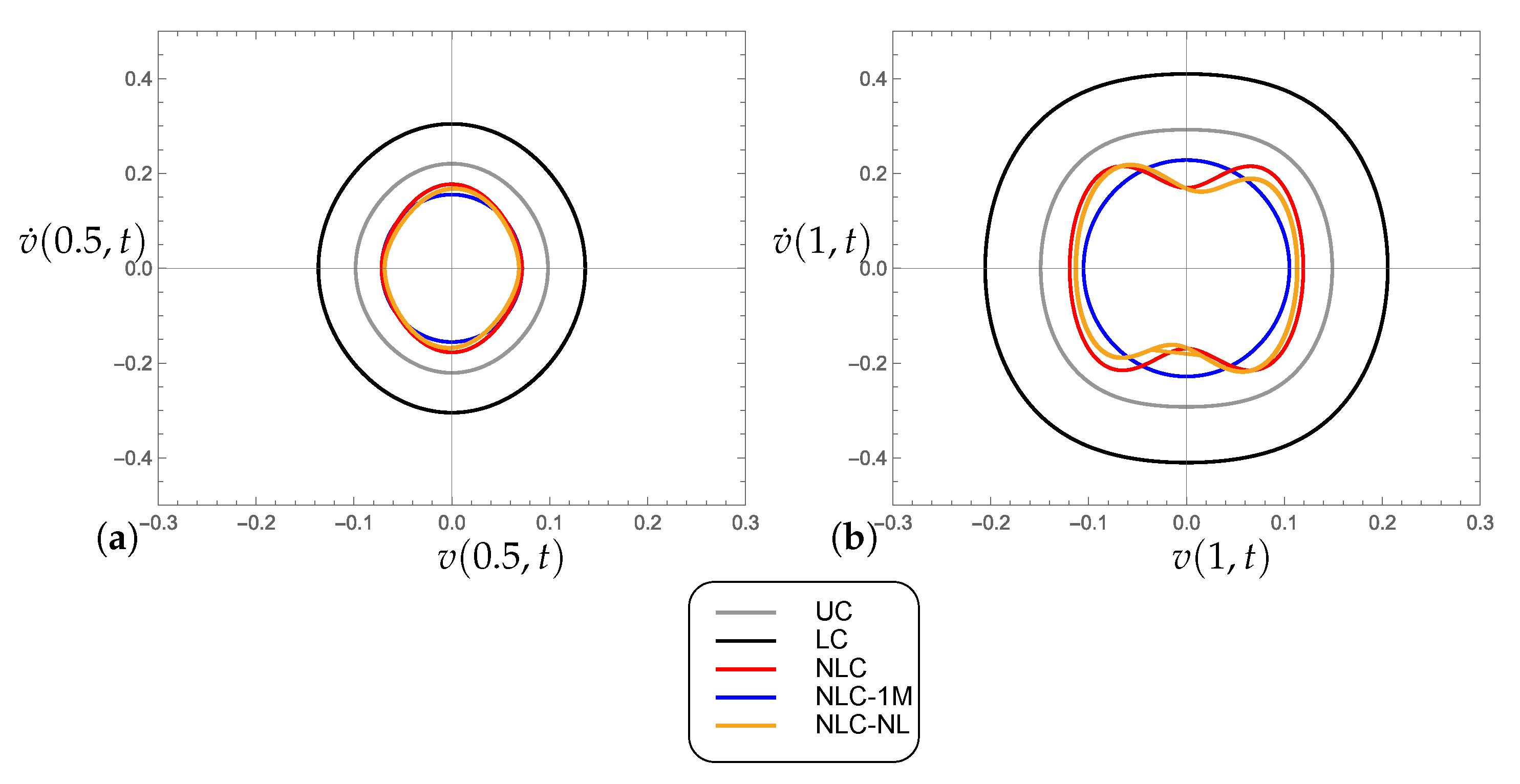
| Uncontrolled (U) | Controlled (C) | ||||
|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 1 | Mode 2 | ||
| 3.52 | 22.03 | 2.17 | 6.51 | ||
| 0.37 | −0.51 | 0.52 | −0.15 | ||
| −0.50 | 0.50 | −0.17 | −0.70 | ||
| −0.37 | 0.51 | −0.52 | 0.15 | ||
| 0.50 | 0.50 | 0.68 | −0.07 | ||
| Case | Control Device | Geometry and Inertia | Number of Modes |
|---|---|---|---|
| UC | No (Fixed base) | Linear | 2 |
| LC | Linear | Linear | 2 |
| NLC | Nonlinear | Linear | 2 |
| NLC-1M [37] | Nonlinear | Linear | 1 |
| NLC-NL | Nonlinear | Nonlinear | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nino, S.; Zulli, D.; Luongo, A. Nonlinear Dynamics of an Internally Resonant Base-Isolated Beam under Turbulent Wind Flow. Appl. Sci. 2021, 11, 3213. https://doi.org/10.3390/app11073213
Di Nino S, Zulli D, Luongo A. Nonlinear Dynamics of an Internally Resonant Base-Isolated Beam under Turbulent Wind Flow. Applied Sciences. 2021; 11(7):3213. https://doi.org/10.3390/app11073213
Chicago/Turabian StyleDi Nino, Simona, Daniele Zulli, and Angelo Luongo. 2021. "Nonlinear Dynamics of an Internally Resonant Base-Isolated Beam under Turbulent Wind Flow" Applied Sciences 11, no. 7: 3213. https://doi.org/10.3390/app11073213
APA StyleDi Nino, S., Zulli, D., & Luongo, A. (2021). Nonlinear Dynamics of an Internally Resonant Base-Isolated Beam under Turbulent Wind Flow. Applied Sciences, 11(7), 3213. https://doi.org/10.3390/app11073213








