A Weighted Linearization Method for Highly RF-PA Nonlinear Behavior Based on the Compression Region Identification
Abstract
1. Introduction
2. Dynamic Modeling Stage
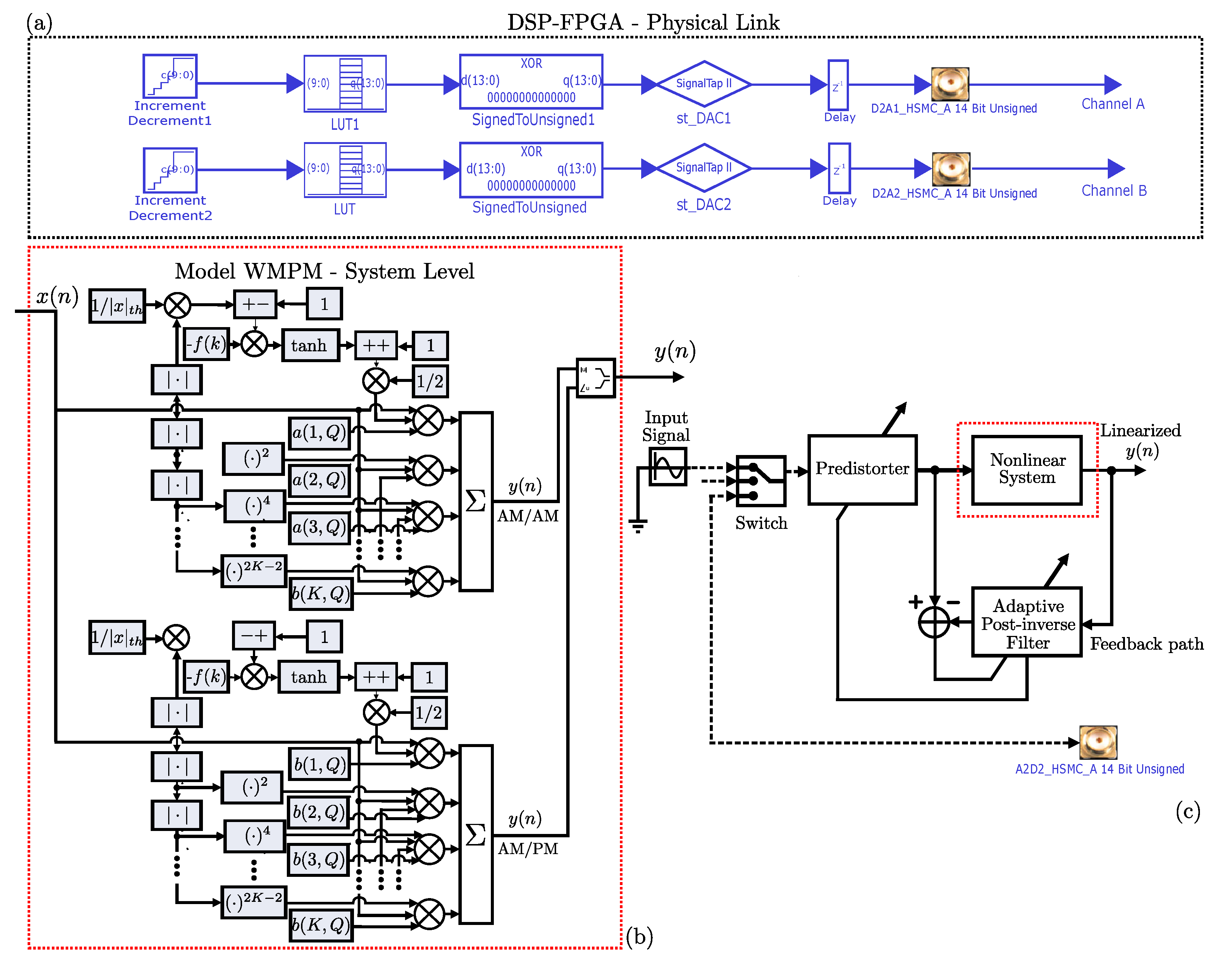
2.1. Memory Polynomial Model (MPM)
2.2. Weighted MPM as Dynamical Modeling and Linearization Stages
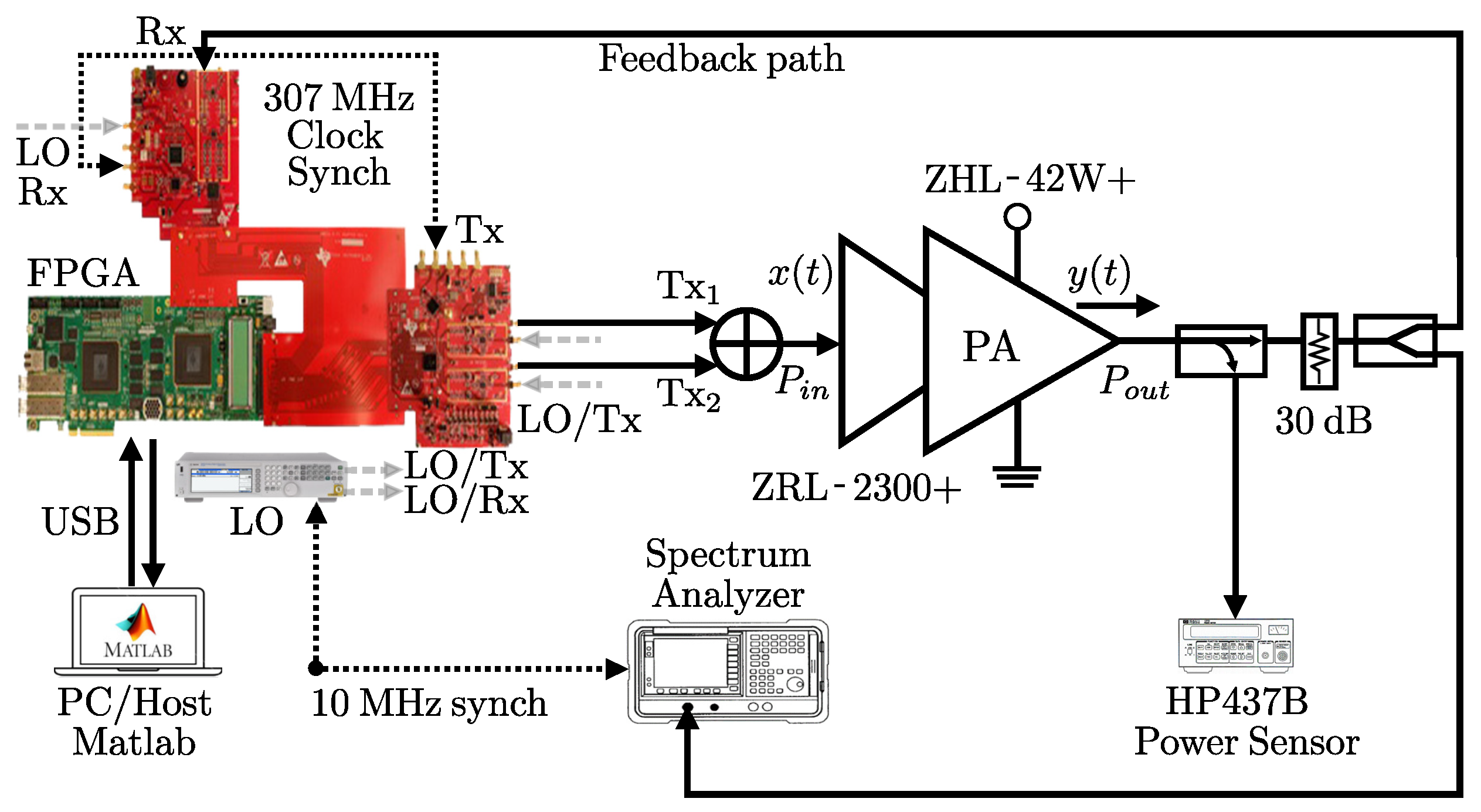
3. Experimental System-Level Setup
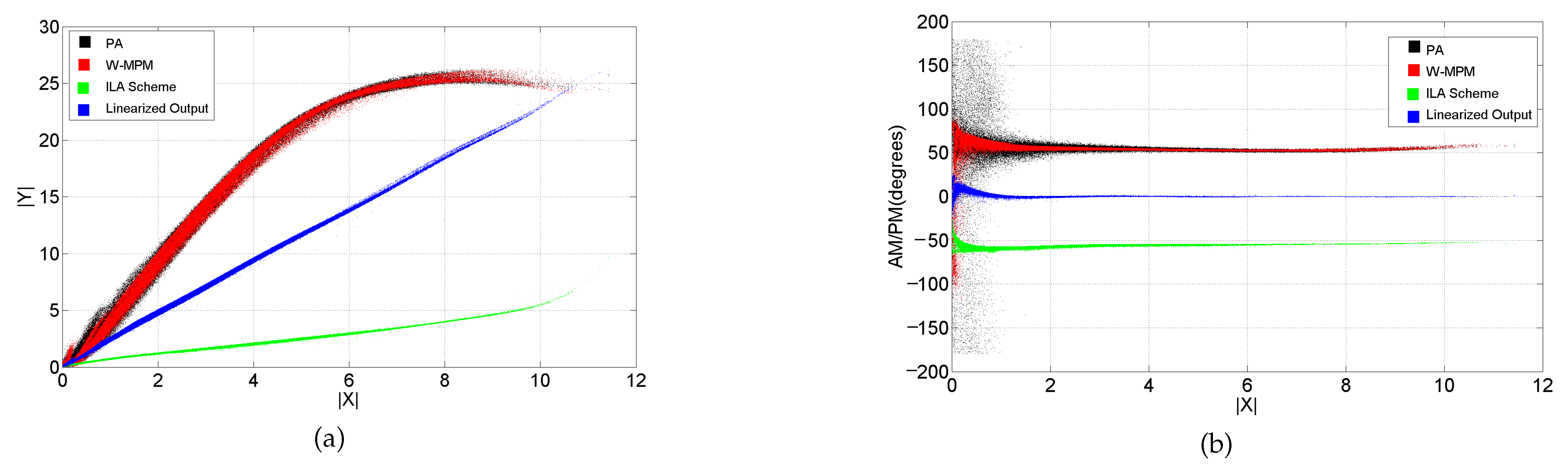
Measurement Procedure
4. Modeling and Linearization Stage Setup
Indirect Learning Approach for the Proposal Modeling Stage
- (i)
- An algorithm is performed for the offline training of the model (PA) and the predistorter (PD) block using the MPM and W-MPM approaches (running on MATLAB-PC with DSP blockset system environment) as defined in the overall block diagram in Figure 2.
- (ii)
- At every iteration, the model searches for a weighting subset of parameters to contribute in the minimization the LSE and NMSE.
- (iii)
- The developed chain through DSP Builder tool allows us to transfer the input signal compared with the amplification process by the DAC of the FPGA development board Cyclone V.
- (iv)
- Both signals are sampled using 10-bit resolution related to the address bus capability; the magnitude signals are sampled for the maximum resolution of the HSMC card with 14 bits.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramella, C.; Piacibello, A.; Quaglia, R.; Camarchia, V.; Pirola, M. High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach. Electronics 2017, 6, 96. [Google Scholar] [CrossRef]
- Lie, D.Y.C.; Mayeda, J.C.; Li, Y.; Lopez, J. A Review of 5G Power Amplifier Design at cm-Wave and mm-Wave Frequencies. Wirel. Commun. Mob. Comput. 2018, 1–17. [Google Scholar] [CrossRef]
- Hallberg, W.; Özen, M.; Gustafsson, D.; Buisman, K.; Fager, C. A Doherty Power Amplifier Design Method for Improved Efficiency and Linearity. IEEE Trans. Microw. Theory Tech. 2016, 64, 4491–4504. [Google Scholar] [CrossRef]
- Raab, F.H.; Asbeck, P.; Cripps, S.; Kenington, P.B.; Popovic, Z.B.; Pothecary, N.; Sevic, J.F.; Sokal, N.O. Power amplifiers and transmitters for RF and microwave. IEEE Trans. Microw. Theory Tech. 2002, 50, 814–826. [Google Scholar] [CrossRef]
- Li, F.; Yan, S.; Yang, X.; Li, X. Spectrum Modeling of Cross-Modulation for Concurrent Dual-Band RF Power Amplifiers in OFDM Modulation. IEEE Trans. Instrum. Meas. 2018, 64, 2772–2784. [Google Scholar] [CrossRef]
- Katz, A.; Wood, J.; Chokola, D. The Evolution of PA Linearization: From Classic Feedforward and Feedback Through Analog and Digital Predistortion. IEEE Microw. Mag. 2016, 17, 32–40. [Google Scholar] [CrossRef]
- Mallouki, N.; Nsiri, B.; Ghanbarisabagh, M.; Hakimi, W.; Ammar, M. Improvement of downlink LTE system performances using nonlinear equalization methods based on SVM and Wiener–Hammerstein. Wirel. Netw. 2017, 23, 2447–2454. [Google Scholar] [CrossRef]
- Belabad, A.R.; Sharifian, S.; Motamedi, S.A. An accurate digital baseband predistorter design for linearization of RF Power amplifiers by a genetic algorithm based Hammerstein structure. Analog. Integr. Circuits Signal Process. 2018, 95, 231–247. [Google Scholar] [CrossRef]
- Mkadem, F.; Islam, A.; Boumaiza, S. Multi-Band Complexity-Reduced Generalized-Memory-Polynomial Power-Amplifier Digital Predistortion. IEEE Trans. Microw. Theory Tech. 2016, 64, 1763–1774. [Google Scholar] [CrossRef]
- Belabad, A.R.; Motamedi, S.A.; Sharifian, S. A Novel Generalized Parallel Two-Box Structure for behavior Modeling and Digital Predistortion of RF Power Amplifiers at LTE Applications. Circ. Syst. Signal Process. 2017, 37, 2714–2735. [Google Scholar] [CrossRef]
- Xu, T.; Jin, C.; Zhang, S.; Jacobsen, G.; Popov, S.; Leeson, M.; Liu, T. Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone. Appl. Sci. 2019, 9, 4717. [Google Scholar] [CrossRef]
- Jayati, A.E.; Suryani, T. Nonlinear Distortion Cancellation using Predistorter in MIMO-GFDM Systems. Electronics 2019, 8, 620. [Google Scholar] [CrossRef]
- Abdulkhaleq, A.M.; Yahya, M.A.; McEwan, N.; Rayit, A.; Abd-Alhameed, R.A.; Ojaroudi Parchin, N.; Al-Yasir, Y.I.; Noras, J. Recent Developments of Dual-Band Doherty Power Amplifiers for Upcoming Mobile Communications Systems. Electronics 2019, 8, 638. [Google Scholar] [CrossRef]
- Abdo, A.S.; Ling, J.; Chen, P. Architecture considerations of LTE/WCDMA wideband power amplifier for efficiency improvement. In Proceedings of the 2019 IEEE 13th International Conference on ASIC (ASICON), Chongqing, China, 29 October–1 November 2019. [Google Scholar]
- Belabad, A.R.; Motamed, S.A.; Sharifian, S. An adaptive digital predistortion for compensating nonlinear distortions in RF power amplifier with memory effects. Integration 2017, 57, 184–191. [Google Scholar] [CrossRef]
- Ehsanian, M.; Askari-Raad, M. A Built-In Self-Test structure for measuring gain and 1-dB compression point of Power Amplifier. Int. J. Electron. Commun. 2018, 86, 47–54. [Google Scholar] [CrossRef]
- Makhsuci, S.; Ehsanian, M. A built-in self-test circuit for measuring 1dB gain compression point of power amplifiers. In Proceedings of the IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, 22 December 2017. [Google Scholar]
- Le, D.H.; Hoang, V.P.; Nguyen, M.H.; Nguyen, H.M.; Nguyen, D.M. Linearization of RF Power Amplifiers in Wideband Communication Systems by Adaptive Indirect Learning Using RPEM Algorithm. Mob. Netw. Appl. 2020, 25, 1988–1997. [Google Scholar] [CrossRef]
- Feng, X.; Wang, Y.; Feuvrie, B.; Descamps, A.S.; Ding, Y.; Yu, Z. Analysis on LUT based digital predistortion using direct learning architecture for linearizing power amplifiers. EURASIP J. Wirel. Commun. Netw. 2016, 132, 1–14. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Quan, X.; Roblin, P.; Rawat, M.; Naraharisetti, N.; Tang, Y.; Kang, K. Multiband Linearization Technique for Broadband Signal with Multiple Closely Spaced Bands. IEEE Trans. Microw. Theory Tech. 2019, 67, 1115–1129. [Google Scholar] [CrossRef]
- Atanasković, A.; Ilić, N.M.; Đoric, A. Controlled coefficient adaptation in linearization of PA by modified baseband signal. In Proceedings of the 13th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS), Nis, Serbia, 18–20 October 2017. [Google Scholar]
- Ren, J. Digital Predistortion Architecture with Feedback Channel Nonlinear Blind Identification and Compensation. IEEE Microw. Wirel. Components Lett. 2020, 30, 1112–1115. [Google Scholar] [CrossRef]
- Ren, J. A New Digital Predistortion Algorithms Scheme of Feedback FIR Cross-Term Memory Polynomial Model for Short-Wave Power Amplifier. IEEE Access 2020, 8, 38327–38332. [Google Scholar] [CrossRef]
- Jung, S.; Kim, Y.; Woo, Y.; Lee, C. A two-step approach for DLA-based digital predistortion using an integrated neural network. Signal Process. 2020, 177, 1–6. [Google Scholar] [CrossRef]
- Galaviz-Aguilar, J.A.; Vargas-Rosales, C.; Tlelo-Cuautle, E. Automated Driving of GaN Chireix Power Amplifier for the Digital Predistortion Linearization. IEEE Trans. Circuits Syst. Express Briefs 2020, 1–5. [Google Scholar] [CrossRef]
- Nuñez-Perez, J.C.; Cardenas-Valdez, J.R.; Gontrand, C.; Reynoso-Hernandez, J.A.; Hirata-Flores, F.I.; Jauregui-Duran, R.; Perez-Pinal, F.J. Flexible test bed for the behavioral modeling of power amplifiers. Int. J. Comput. Math. Electr. Electron. Eng. 2014, 33, 355–375. [Google Scholar] [CrossRef]
- Abdelrahman, A.E.; Hammi, O.; Kwan, A.K.; Zerguine, A.; Ghannouchi, F.M. A Novel Weighted Memory Polynomial for behavioral Modeling and Digital Predistortion of Nonlinear Wireless Transmitters. IEEE Trans. Ind. Electron. 2016, 63, 1745–1753. [Google Scholar] [CrossRef]
- Devi, R.V.S.; Kumar, C.S.P.; Chaitanya, M.K.; Deepak, M.V.; Kurup, D.G. Modeling Broadband RF Power Amplifiers Using A Modified Hammerstein Model. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 3–5 April 2018; pp. 0186–0189. [Google Scholar]
- Dalbah, A.I.; Hammi, O. Enhanced Training Technique for Nested Look-Up Table Based behavioral Modeling of Nonlinear Power Amplifiers. In Proceedings of the 2019 International Conference on Communications, Signal Processing, and their Applications (ICCSPA), Sharjah, United Arab Emirates, 19–21 March 2019. [Google Scholar]
- Cai, J.; Sun, C.Y.L.; Chen, S.; King, J.B. Dynamic behavioral Modeling of RF Power Amplifier Based on Time-Delay Support Vector Regression. IEEE Trans. Microw. Theory Tech. 2019, 67, 533–543. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, L.; Yu, Z.; Zhou, J.; Hong, W. A Modified Canonical Piecewise-Linear Function-Based behavioral Model for Wideband Power Amplifiers. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 195–197. [Google Scholar] [CrossRef]


| PA NXP 10 W @ 2.34 GHz | |
|---|---|
| Parameter | Values |
| Gain | 12.26 dB @ 2.34 GHz |
| PA input Power | 23.84 dBm |
| PA output Power | 36.10 dBm |
| Device biasing | = 50 V, = 54 mA |
| PA ZHL-42W+ @ 2.00 GHz | |
|---|---|
| Parameter | Values |
| Gain | 34 dB @ 2.00 GHz |
| Maximum power | 1.25 W |
| DC Supply | 15 V, 1 A |
| Bandwidth | 10–4200 MHz |
| Description | W-MPM Resource Utilization | MPM Resource Utilization |
|---|---|---|
| Logic Utilization (ALMs) | 340/56,480 (<1%) | 378/56,480 (<1%) |
| Total Registers | 771 | 751 |
| Total Pins I/O | 40/480 (8%) | 40/480 (8%) |
| Total block memory bits | 43,008/7,024,0640 (<1) | 43,008/7,024,0640 (<1) |
| Total PLLs | 1/7 (14%) | 1/7 (14%) |
| Complexity Metric | W-MPM | MPM |
|---|---|---|
| Number of distinct operators | 7 | 7 |
| Number of distinct operands | 7 | 7 |
| Total number of operators | 9 | 11 |
| Total number of operands | 7 | 7 |
| Program vocabulary | 14 | 14 |
| Program length: | 16 | 18 |
| Calculated estimated program length | 39.30 | 39.30 |
| Volume | 60.92 | 68.53 |
| Difficulty | 3.50 | 3.50 |
| Effort | 213.21 | 239.86 |
| Time required to program (s) | 11.85 | 13.33 |
| Number of delivered bugs | 0.07 | 0.08 |
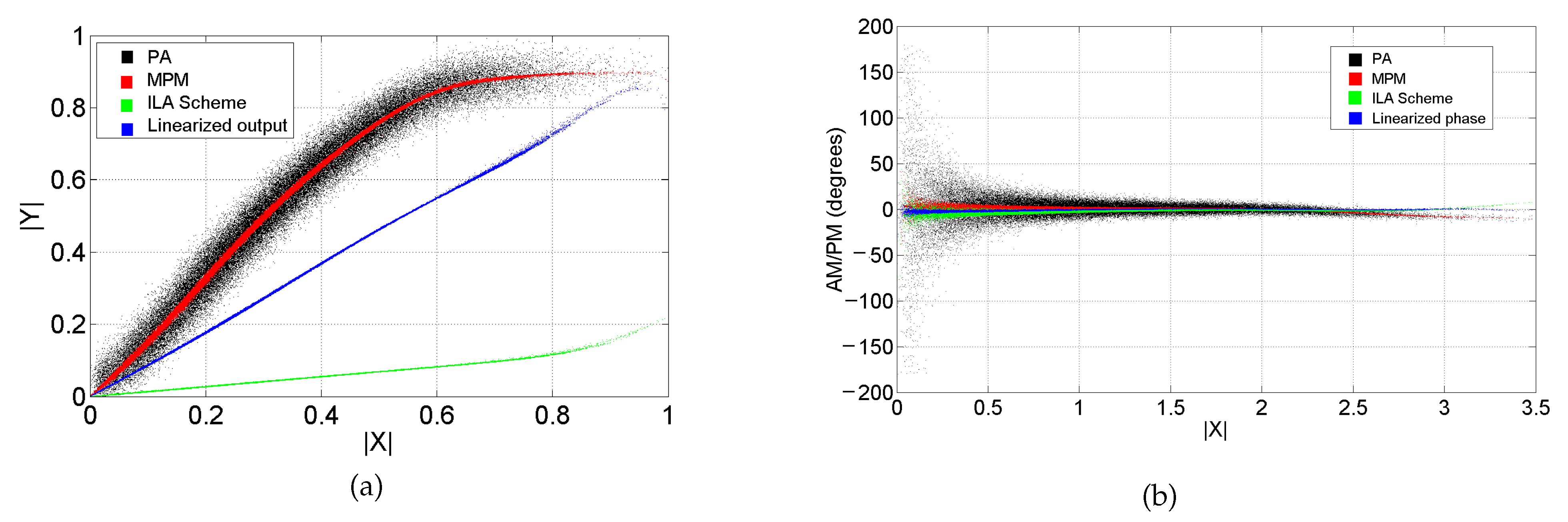
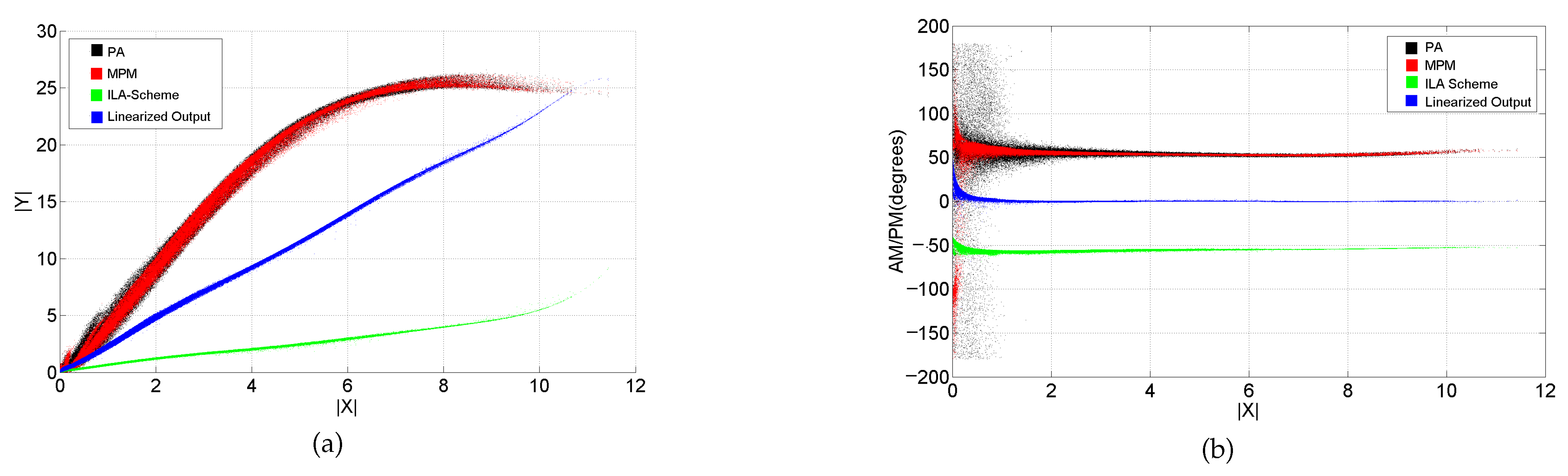
| Model Stage | RF-PA Linearity | Technology | Nonlinearity and Memory Effects | Coefficients Number | Accuracy NMSE (dB) |
|---|---|---|---|---|---|
| Proposed work, Device: PA NXP 10 W @ 2.34 GHz | |||||
| W-MPM model | Nonlinear | GaN HEMT | High order | 55 | −38.03 and −44.9028 |
| MPM model | Nonlinear | GaN HEMT | High order | 67 | −32.72 and −44.349 |
| Proposed work, Device: ZHL-42W+ @2000 MHz 32.24 dBm | |||||
| W-MPM model | Nonlinear | CMOS+LVDS | High order | 55 | −27.8946 |
| MPM model | Nonlinear | CMOS+LVDS | High order | 67 | −24.8707 |
| Related works | |||||
| Hammerstein , [28] | Nonlinear | GaN | High order | N/A | −33.55 |
| Hammerstein , [28] | Nonlinear | GaN | High order | N/A | −35.72 |
| MP, [29] | Nonlinear | GaN Doherty | High order | N/A | −32.2 |
| EMP, [29] | Nonlinear | GaN Doherty | High order | N/A | −24.9 |
| SVR, [30] | Nonlinear | LDMOS | High order | 256 | −36.5 |
| DVR, [31] | Nonlinear | GaN Doherty | High order | 99 | −31 |
| Device NXP 10 W @ 2.34 GHz | Estimated EVM | EVM with ILA |
| MPM | ||
| W-MPM | ||
| Device ZHL-42W+ @ 2000 MHz 32.24 dBm | Estimated EVM | EVM with ILA |
| MPM | ||
| W-MPM |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galaviz-Aguilar, J.A.; Vargas-Rosales, C.; Cárdenas-Valdez, J.R.; Martínez-Reyes, Y.; Inzunza-González, E.; Sandoval-Ibarra, Y.; Núñez-Pérez, J.C. A Weighted Linearization Method for Highly RF-PA Nonlinear Behavior Based on the Compression Region Identification. Appl. Sci. 2021, 11, 2942. https://doi.org/10.3390/app11072942
Galaviz-Aguilar JA, Vargas-Rosales C, Cárdenas-Valdez JR, Martínez-Reyes Y, Inzunza-González E, Sandoval-Ibarra Y, Núñez-Pérez JC. A Weighted Linearization Method for Highly RF-PA Nonlinear Behavior Based on the Compression Region Identification. Applied Sciences. 2021; 11(7):2942. https://doi.org/10.3390/app11072942
Chicago/Turabian StyleGalaviz-Aguilar, Jose Alejandro, Cesar Vargas-Rosales, José Ricardo Cárdenas-Valdez, Yasmany Martínez-Reyes, Everardo Inzunza-González, Yuma Sandoval-Ibarra, and José Cruz Núñez-Pérez. 2021. "A Weighted Linearization Method for Highly RF-PA Nonlinear Behavior Based on the Compression Region Identification" Applied Sciences 11, no. 7: 2942. https://doi.org/10.3390/app11072942
APA StyleGalaviz-Aguilar, J. A., Vargas-Rosales, C., Cárdenas-Valdez, J. R., Martínez-Reyes, Y., Inzunza-González, E., Sandoval-Ibarra, Y., & Núñez-Pérez, J. C. (2021). A Weighted Linearization Method for Highly RF-PA Nonlinear Behavior Based on the Compression Region Identification. Applied Sciences, 11(7), 2942. https://doi.org/10.3390/app11072942











