1. Introduction
Modern cryptography provides four functions, namely, confidentiality, authentication, integrity, and nonrepudiation [
1,
2]. Therefore, as a substitution candidate for next-level secure cryptography, quantum cryptography should also have the ability to offer these four functions. Remarkable progress has been made in the area of confidentiality because the quantum key distribution (QKD) protocol that provides confidentiality has been considerably improved [
3,
4,
5,
6]. QKD aims to enable communication partners, e.g., Alice and Bob, to share secret keys and ultimately perform a one-time pad communication. Those protocols provide unconditional confidentiality based on the principle that an arbitrary unknown quantum state cannot be copied and that quantum measurement is irreversible [
7,
8,
9,
10]. On the other hand, many researchers have also studied how to use these secret keys in quantum message authentication [
11,
12,
13], arbitrated quantum signature [
14,
15,
16,
17,
18,
19], or quantum digital signature [
20,
21,
22,
23,
24,
25,
26,
27,
28,
29], providing authentication, integrity, and non-repudiation.
In this paper, we introduce a simple and practical quantum message authentication protocol with a quantum three-pass protocol [
30,
31,
32,
33] and a quantum encryption scheme [
19,
34]. This protocol is a lightweight to simplify the implementation by removing an arbitrator from our proposed quantum signature protocol [
19]. Here, the quantum three-pass protocol is the quantum version of Shamir’s three-pass protocol [
1,
35], and quantum encryption scheme is to prevent existential forgery, called Gao’s forgery. More specifically, the core elements of the proposed protocol, such as the quantum three-pass protocol and the quantum encryption scheme, are implemented with only single qubit unitary operators. In other words, these can be implemented easily by using linear combinations of wave plates [
36,
37]. Additionally, the swap test that checks the correspondence of the original message and quantum message authentication code (QMAC) can be implemented using a Hong–Ou–Mandel interferometer [
38,
39,
40]. In advance, as the Hong-Ou-Mandel interferometer is a destructive swap test [
40], more resources are needed to implement a controlled swap test.
In
Section 2, we briefly explain the concept of the proposed scheme.
Section 3 presents a security analysis of the proposed protocol for Alice’s private key, the forgery of QMAC pair, and the origin authentication of quantum message.
Section 4 describes the experimental setup and measurement results. We conducted three experiments with the proposed protocol. First, we implemented a quantum three pass protocol, which is a method of conveying information in the proposed quantum message authentication. Second, we implemented a quantum encryption scheme with a single qubit unitary operator to prevent forgery. Finally, we confirmed that the QMAC pair with the quantum encryption scheme is robust to Gao’s forgery. In
Section 5, after a thorough discussion that includes the possibility of expanding the scheme to quantum signature and quantum entity authentication, we present the conclusions of this work.
2. Quantum Message Authentication Protocol
Quantum message authentication, which is similar to conventional message authentication, should provide message integrity and origin authentication. What differentiates quantum message authentication from conventional message authentication [
41,
42] is that the former uses quantum states
and
as a message represented by a sequence of “0” and “1” bits. In addition, using arbitrary quantum states as a message enables more information to be delivered at once [
43,
44]. Moreover, there is a significant difference that is described below. In modern cryptography, asymmetric key cryptography easily provides message integrity, message origin authentication, and nonrepudiation. Unfortunately, a quantum asymmetric key cryptosystem based on the quantum trapdoor one-way function do not exist, making the design of quantum authentication and quantum signature protocols difficult. To overcome this difficulty, we propose a new quantum message authentication protocol based on Shamir’s three-pass protocol [
1,
35]. Shamir’s three pass protocol has the advantage that two parties, e.g., Alice and Bob, can share information without exposing their own private keys. In the implementation, the central idea is that the commutative property [
19] of exponential operation in Shamir’s three-pass protocol is implemented using single-qubit rotation operators consisting of linear combinations of wave plates. To our knowledge, this is the first time a quantum message authentication protocol has been proposed using the quantum three-pass protocol, though other applications of the quantum three-pass protocol, such as direct communication [
32], quantum key distribution [
30], and quantum signature [
19], have been proposed theoretically.
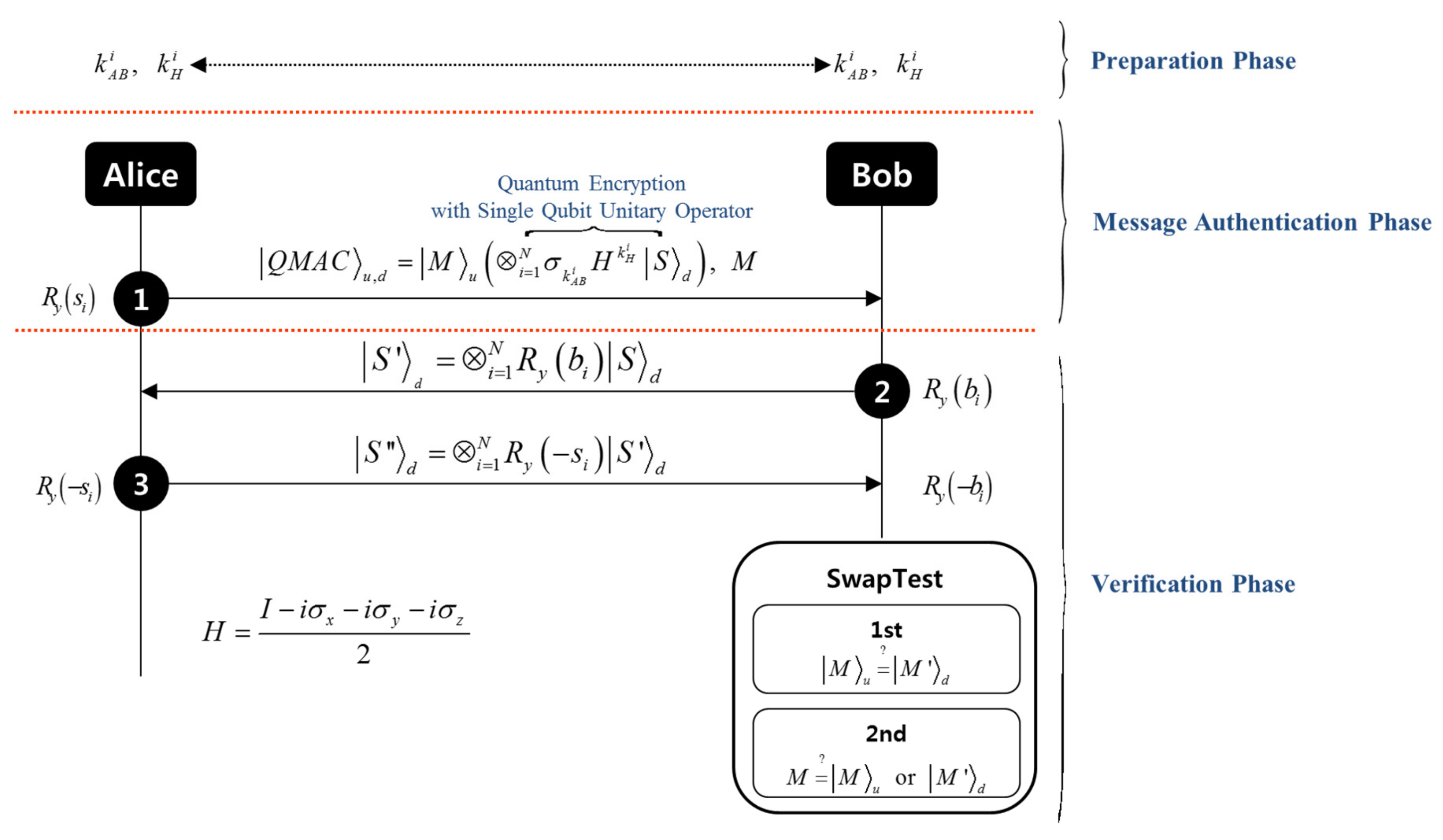
Figure 1 schematically shows the quantum message authentication protocol that we implemented. Our quantum message authentication protocol consists of preparation, quantum message authentication, and verification phase.
2.1. Preparation Phase
In the preparation phase, Alice and Bob pre-share secret key sequences
and
that determine which single-qubit operation is chosen. The sequences
and
are a classical bit sequence with the size of
and
respectively, where
. The secret keys
and
correspond to the Pauli operators
and the operator
. Here, operator is a linear combination of the Pauli operators
and unitary operator
.
2.2. Quantum Message Authentication Phase
The quantum message authentication phase is composed of two stages: quantum message generation, QMAC generation, and quantum encryption. In the quantum message generation stage, Alice generates a quantum message state pair
by applying a single qubit rotation operator
where
is a rotation angle sequence,
, and
are the logical states
or
, corresponding to horizontally polarized photons
and vertically polarized photons
, respectively. The superscript
denotes the
th qubit, and subscripts
and
denote up and down, corresponding to the up-line and down-line, respectively, of the experimental setup used for our protocol. The rotation angle sequence
is a bit message sequence, and we assume that it has already been published in public as in the case of a contract or an official document. The reason for publishing
is to prevent Alice from attempting to forge using a modulated QMAC pair, which is discussed in detail in
Section 3.2 impossibility of forgery.
In the QMAC generation stage, Alice encrypts the quantum message pair
of Equation (2) by using a single qubit rotation operator
;
Here, is a rotation angle sequence, . In addition, is a private key known only to Alice. Furthermore, we call to a QMAC state pair.
In the quantum encryption stage, Alice applies quantum encryption
to the QMAC state pair
of Equation (4);
Here, is an encrypted QMAC state pair, and then she sends it to Bob. This quantum encryption is an essential function for verifying that the entity sending the QMAC pair is Alice and for protecting against forgery.
The rotation angles and are the elements of the finite discrete variable set. For applying them to real protocols, Alice and Bob must preset the range of the finite discrete variable set and pre-decide how to divide the set range. For example, if Alice and Bob split the rotation angle from in intervals of , then the finite discrete variable set becomes . Here, the size of the discrete variable set is determined by the performance of the experimental apparatus. Therefore, as the performance of experimental apparatus improves, the size of the discrete variable set increases. Increasing the size of the discrete variable set means that the rotation angle can be subdivided, and this can lead to authenticating more information compared with using the four states of the BB84 protocol. On the other hand, If the performance of the experimental apparatus is poor, the size of the discrete variable set decreases. Then, the rotation angle cannot be subdivided, and information that can be authenticated decreases. Additionally, in this situation, if the communication members use the subdivided rotation angles to such an extent that the experimental apparatus cannot distinguish, detecting the malicious behavior of Eve is impossible.
2.3. Verification Phase
The verification phase is divided into five stages: “quantum decryption”, “Bob’s encryption”, “QMAC recovery”, “Bob’s decryption”, and “swap test”. In Stage 1, for quantum decryption, Bob uses secret key sequences and , which were pre-shared with Alice to decrypt the encrypted QMAC state pair in Equation , received from Alice to obtain the QMAC state pair of Equation . In Stage 2, Bob’s encryption, Bob generates his own private key sequence and re-encrypts quantum state with it to obtain quantum state . Then, he sends to Alice while keeping the other quantum message state . In Stage 3, QMAC recovery, Alice uses her own private key sequence to apply rotation operator to quantum state and sends quantum state to Bob. In Stage 4, Bob’s decryption, Bob uses his own private key sequence and applies rotation operator to quantum state to obtain quantum message state . Because the proposed quantum message authentication based on the quantum three-pass protocol operates Alice’s private key , there is a need for a method to verify the encrypted QMAC pair described thus far. This is an important element that the proposed protocol can guarantee the origin of quantum message. In addition, to avoid counterfeiting, it is assumed that quantum encryption such as in Equation is applied to Alice and Bob in every process of exchanging quantum states.
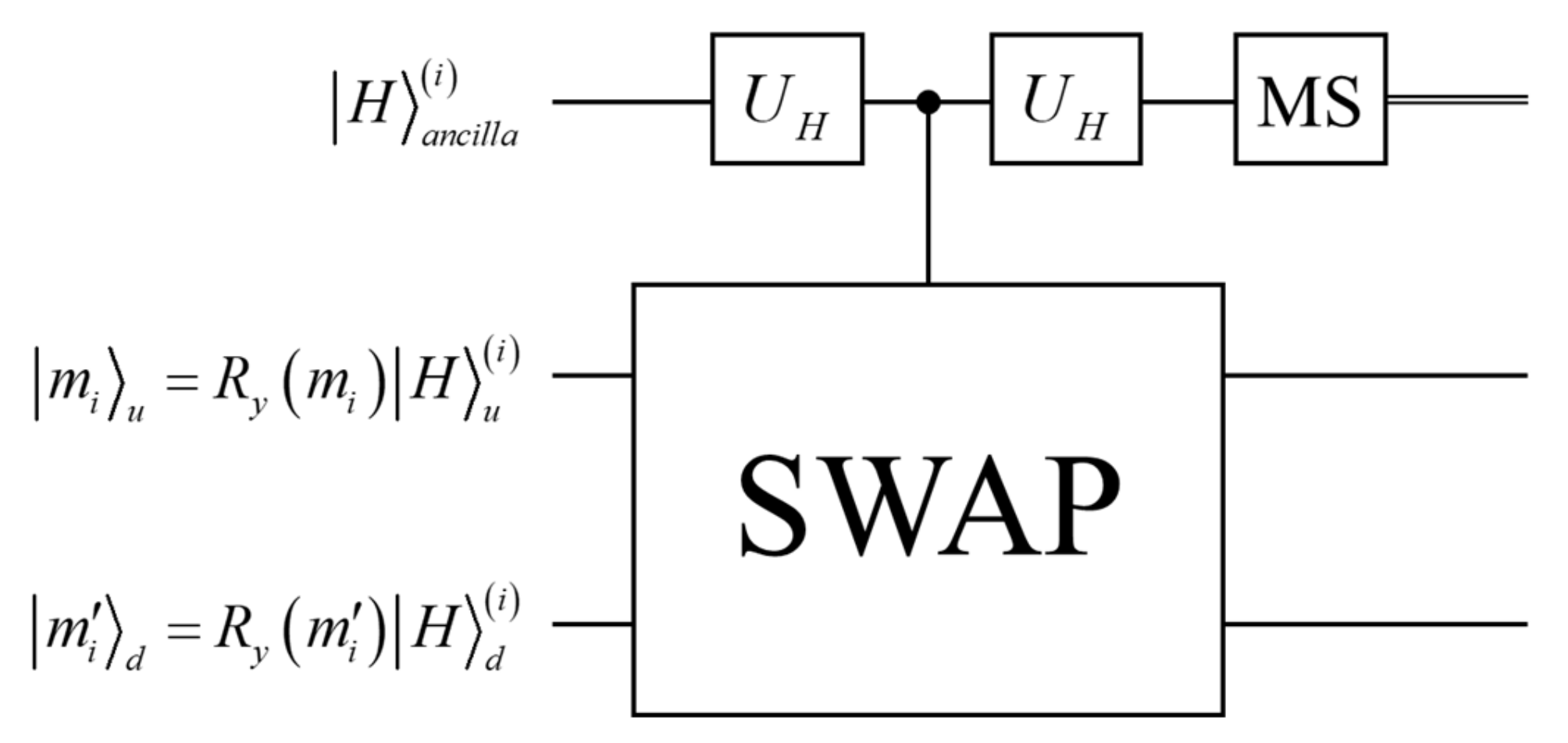
In the final stage, Bob performs the swap test [
42,
45] twice to verify the QMAC state pair. In the first swap test, Bob verifies whether quantum message state
and quantum message state
are the same. If the test result reveals that
and
agree, Bob accepts QMAC state pair
sent by Alice. Otherwise, he does not accept it. In the second swap test, Bob generates quantum state
corresponding to the public bit message sequence
and verifies that it matches quantum message state
or
. If the test result reveals that (
,
) or (
,
) agree, then the integrity of QMAC state pair
is verified completely. For the second swap test, it is noted that the first swap test requires a non-demolition swap test.
Figure 2 shows the swap test in the circuit, and the result of inputting
and
in the second and third lines of the circuit is expressed as follows:
If
and
agree, the above equation becomes
, which makes the measurement outcome of the ancilla state to always be
. However, if
and
do not agree, the measurement outcome becomes
with a probability
or becomes
with a probability
, where
and
. Therefore, if the swap test result of the measurement is
, we know that
and
are different. If the result is
, we cannot guarantee that
and
are the same. The parameter
is determined by the arbitrary quantum state components
of Equation
and
of Equation
. If the two rotation angles
and
are the same, i.e.,
, then the value of parameter
is
. On the other hand, if the difference between
and
is
, i.e.,
, then the parameter
is
. As a result, according to rotation angles
and
, the parameter
has a value between 0 and 1,
. Further, the probability of failure in the verification phase is the total error probability
for
qubits as follows:
Therefore, it is expected that the swap test will work well even though the quantum state sequence is finite. Hence, the probability of failure in the verification phase becomes lower, approaching
as the size of the quantum state sequence
becomes considerably larger [
42,
45]. For an arbitrary
, a random choice for
on the
—rotation circle, the average of
is
. In this case, the upper bound of the total error probability
is
. If the size of the quantum state sequence is
, then the upper bound of the total error probability
is only approximately
. Therefore, it is expected that the swap test will work well even though the quantum state sequence is finite.
4. Experiment Setup and Measurement Results
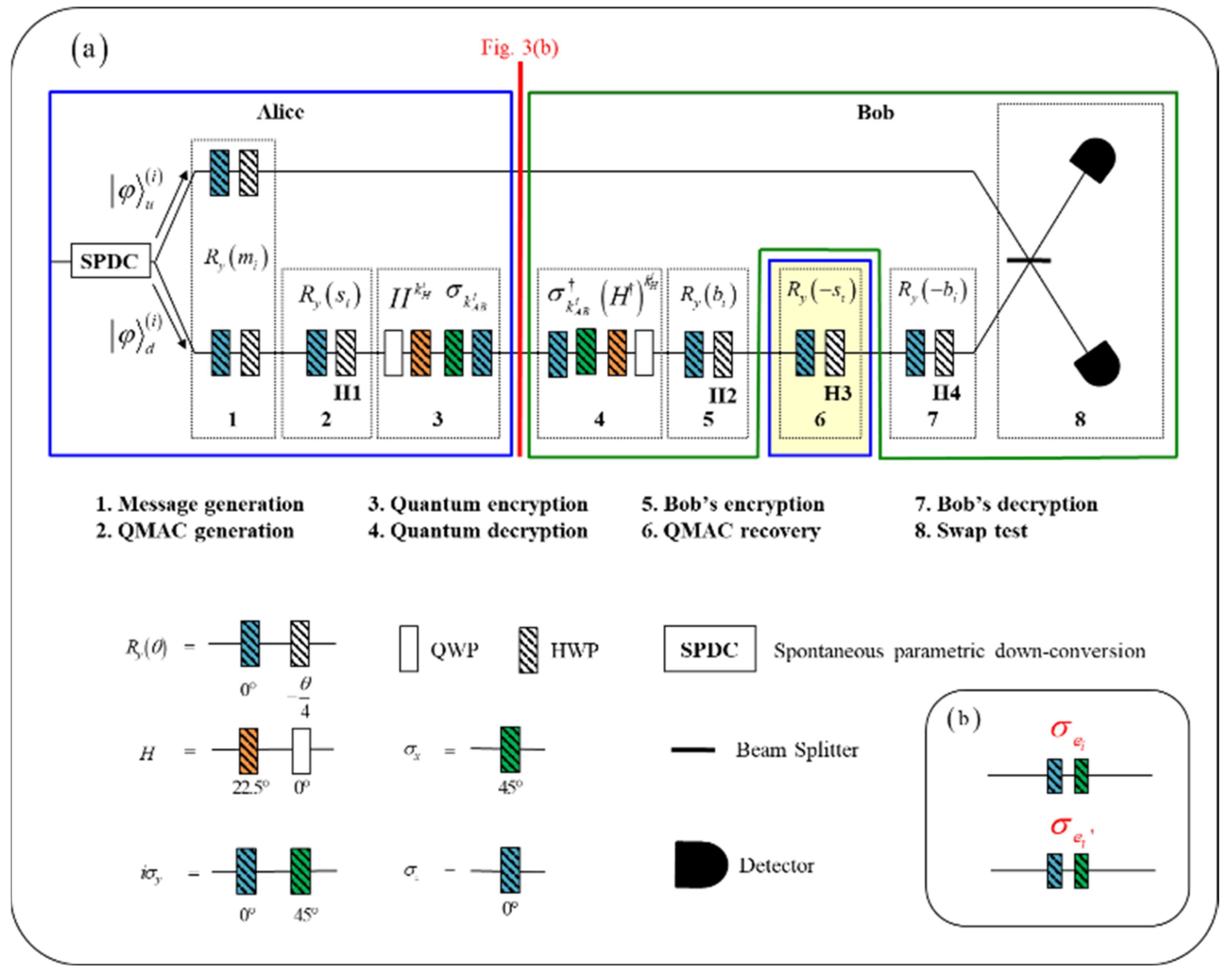
Figure 3a shows the implementation setup of our proposed quantum message authentication protocol. With this setup, we have experimentally proved that the proposed QMAC is robust against existential forgery. Each stage is implemented with a linear combination of wave plates; that is, the
y-axis rotation operator
, the unitary operator
, and the Pauli operators are implemented by combinations of half-wave plates (HWPs) and quarter-wave plates (QWPs).
Figure 3b schematically shows a possible forgery attack that Eve can try. Eve can attempt a forgery attack using the same Pauli operators
[
46], or she can attempt a forgery attack using different Pauli operators
[
49,
50]. We define these two approaches as an original and improved Gao’s Forgeries, respectively. To prevent Gao’s forgeries, we need to choose unitary operator
randomly. We explain this in detail at the end of this section.
We assume that Alice and Bob have already pre-shared the secret key sequences in the preparation phase. For the message authentication phase, we implemented message generation, QMAC generation, and quantum encryption using wave plates on Alice’s side. To create correlated photon pairs, Type-I spontaneous parametric down-conversion (SPDC) photon pairs were generated in a beta barium borate (BBO) crystal pumped by a multimode diode laser with a 408-nm wavelength. The SPDC photon pairs have the same H-polarization and an 816-nm wavelength. The photon pairs are emitted with a noncollinear angle of
. One of the photons goes through only the rotation operator for message generation, and the other experiences the sequence of operations from message generation through the quantum encryption scheme with a single qubit unitary operator. Then, they are delivered to Bob. For the verification phase, one photon is kept on Bob’s side, and the other photon experiences quantum decryption and Bob’s encryption implemented by the wave plate, after which Bob sends it to Alice. Alice then decrypts it by using QMAC recovery. In our experiment, we installed the QMAC recovery stage between Bob’s encryption and Bob’s decryption for convenience of implementation; it is marked by yellow shading in
Figure 3a. Finally, after Bob’s decryption, the swap test that verifies the agreement of the two photon sequences is performed using the Hong–Ou–Mandel interferometer. The Hong–Ou–Mandel dip confirms the similarity between the two photons, which is the last step of the implementation of the proposed quantum message authentication protocol.
In other words, the realization of the quantum three-pass protocol, quantum encryption scheme, and the robustness of Gao’s forgery can be confirmed by the Hong–Ou–Mandel Dip. Hong–Ou–Mandel interference is the same as the destructive swap test [
40]. Because the destructive swap test does not have an ancilla qubit unlike the controlled swap test, the two quantum states that are compared are directly measured and collapsed. For this reason, we performed only the first swap test in the two swap tests shown in
Figure 1. To implement the second swap test in
Figure 1 using Hong–Ou–Mandel interference, there is a need for more resources (e.g., single photons and wave plates) than the current experimental setup. There are other ways to implement a second swap test by using an experimental controlled swap gate that was recently implemented [
51].
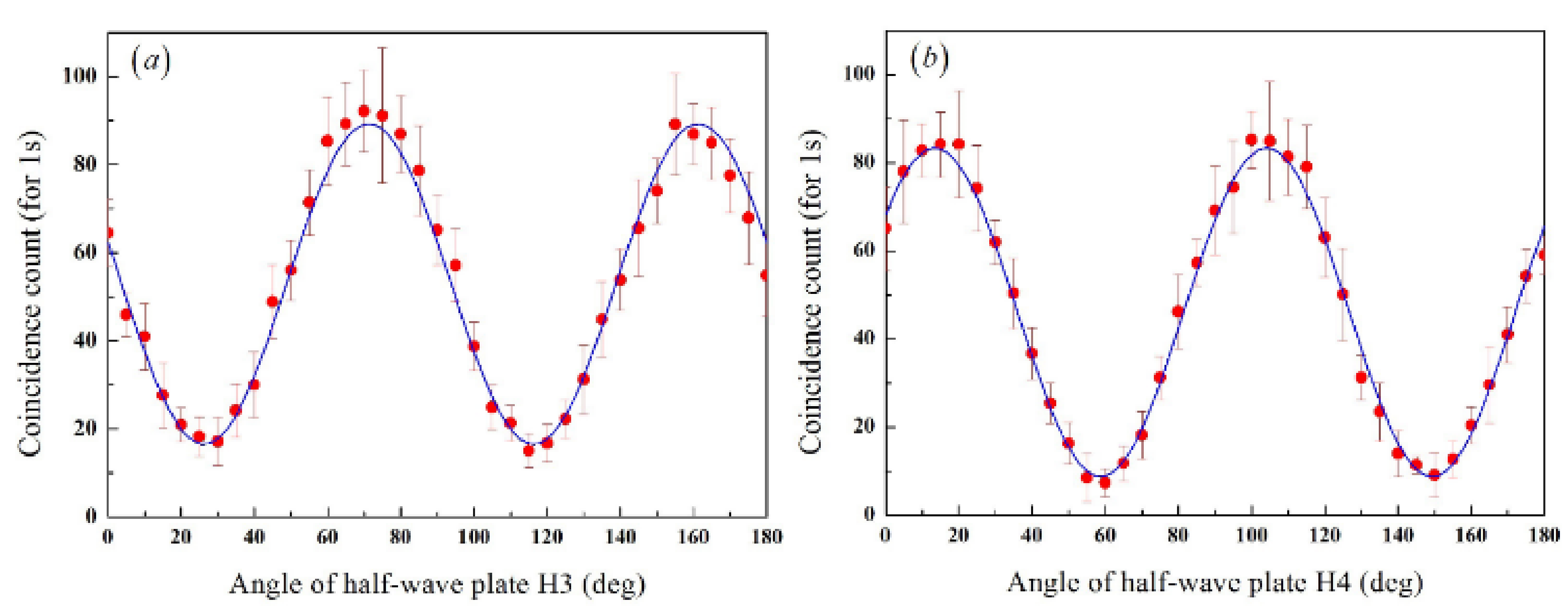
We tested the feasibility of our protocol with the experimental setup for the case without Gao’s forgery. First, we verified that the quantum three-pass protocol (
Figure 3) was working correctly. As shown in
Figure 4a, when the half-wave plate
s angle
is
, the coincidence count reaches its minimum at the half-wave plate
s angles
as expected. This indicates that Alice generates the QMAC state by applying rotation operator
and then uses rotation operator
to recover the QMAC state, where
is an integer, because the period of the half-wave plate is
. The red plots represent the averages of the coincidence counts over one second. In
Figure 4b, we recognize that Bob’s encryption and decryption also work well. When the half-wave plate
s angle
is
, the Hong–Ou–Mandel dip occurs at the half-wave plate
s angles
. Bob uses rotation operator
to re-encrypt the QMAC state, and then he decrypts the re-encrypted QMAC state by applying rotation operator
, where
is an integer. In
Figure 4, the experimental data are the average of
measurements per
s.
During this time, the averages of single counts were and , respectively, and coincidence windows are ns; the maximum value of the coincidence counts after accidental coincidences were removed was , and the minimum value was .
Second, we tested the quantum encryption and decryption. If Alice and Bob are proper users who previously shared secret key sequences
and
then the quantum message states
and
should be identical. Bob can check the correspondence of these states using the Hong–Ou–Mandel interferometer [
38,
39].
Figure 4 shows the experimental results for Alice’s quantum encryption and Bob’s quantum decryption.
is the coincidence probability of Hong–Ou–Mandel interference, and
represents the probability of two quantum message states matching.
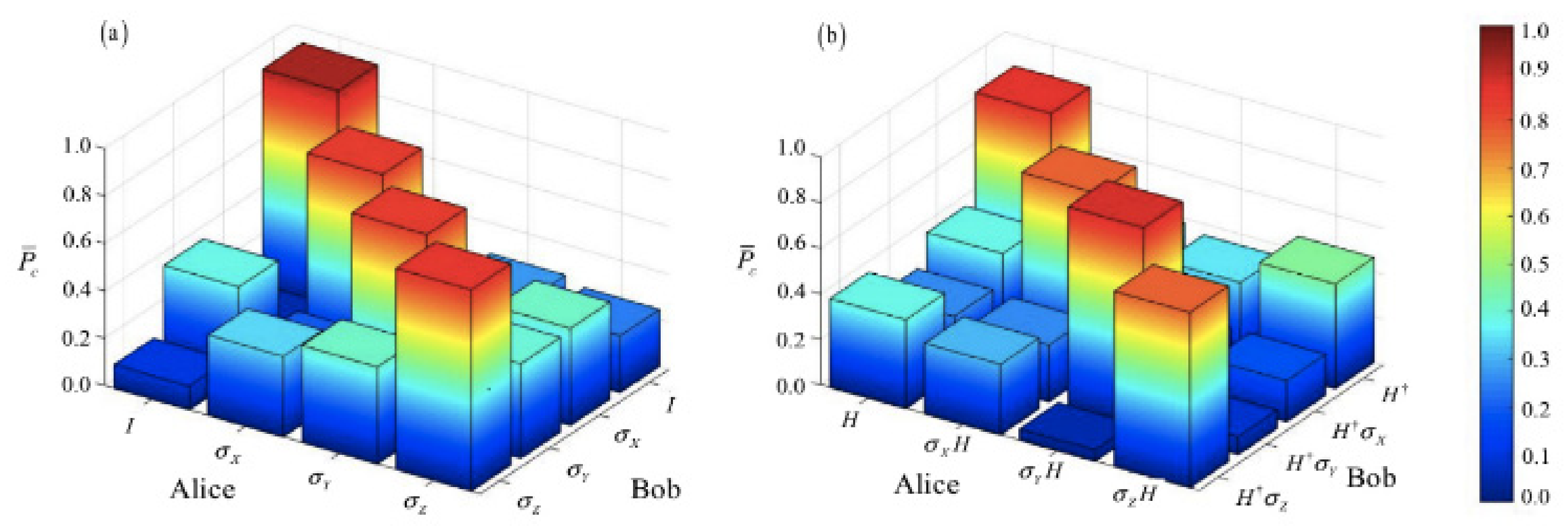
Figure 5a,b represents whether operator
exists or not, respectively. Although theoretically, the red blocks on the diagonal in both cases should be
, experimentally they are greater than
and
, respectively. On the other hand, the blue blocks off the diagonal, when Alice and Bob share different secret keys
and
,
and
have different quantum states, and the respective probabilities are less than
and less than
. Considering that theoretically
can only have less than
, the measurement results prove that our scheme works well. From these results, we can conclude that the encryption operates properly because
is greater than
in the case of the same operators and
is less than
in the case of different operators regardless of the existence of operator
. The above theoretical values are derived from the success probability
of the swap test, with
,
,
, and
. Errors in the experiment shown in
Figure 5 could be due to an inherent error of the swap test, birefringence in the beam splitter, and/or systematic errors in the wave-plate setting [
38,
39,
42,
45].
From the measurement results given in
Figure 4 and
Figure 5, we have demonstrated that our implementation succeeds in realizing the proposed protocol. Although there are some errors due to unavoidable imperfections of the realization, our practical implementation still performs message integrity and message origin authentication successfully only if our protocol is applied to multiple bits sequentially and analyzed statistically.
Gao et al. demonstrated the possibility of existential forgery in the case of quantum message authentication that includes a swap test [
34,
46,
48]. In other words, if the QMAC state pair that Alice generates is not encrypted, Alice cannot detect Eve’s intervention. In the quantum encryption
in Equation
, the secret key
and
correspond to the Pauli operator
and the operator
of quantum encryption with a single qubit unitary operator, respectively. The two bits information
corresponds to the Pauli operator
for Gao’s Attack. For example, if
,
, an encrypted QMAC state pair is
In addition, the forged QMAC state pair by Eve’s Pauli operator
is
The forged QMAC state pair of Equation
transforms into the following state after a decryption process:
Assuming that
and
of Equation
are the same, Eve succeeded in attacking because the Pauli operator
remained in the first and second qubits of Equation
. This is the first method to forge the quantum message code or quantum signature pair proposed by Gao et al. [
34,
46,
48].
As another example, if
, an encrypted QMAC state pair is
The forged QMAC state pair by Eve’s Pauli operator
is
The forged QMAC state pair transforms into the following state after a decryption process:
Despite the assumption that
and
of Equation
are the same, Eve’s attack is unsuccessful. The reason is that the Pauli operators
and
remained in the first and second qubits of Equation
, respectively. This is the (I, H)-type quantum encryption proposed to overcome Gao’s forgery [
47]. Zhang et al., however, showed that the (I, H)-type quantum encryption is not secure for improved Gao’s forgery [
49,
50]. We [
19,
34] overcome the original Gao’s forgery [
46] or the improved Gao’s forgery [
49,
50] with quantum encryption
, which randomly uses operator
Here, the number of all possible cases of quantum encryption
is 8. Furthermore, except
, there are three possible ways that Eve can attack with
. Therefore, there are a total of 24 forgery cases using the Pauli operator
in the encrypted QMAC state pair
of Equation
in the manuscript,
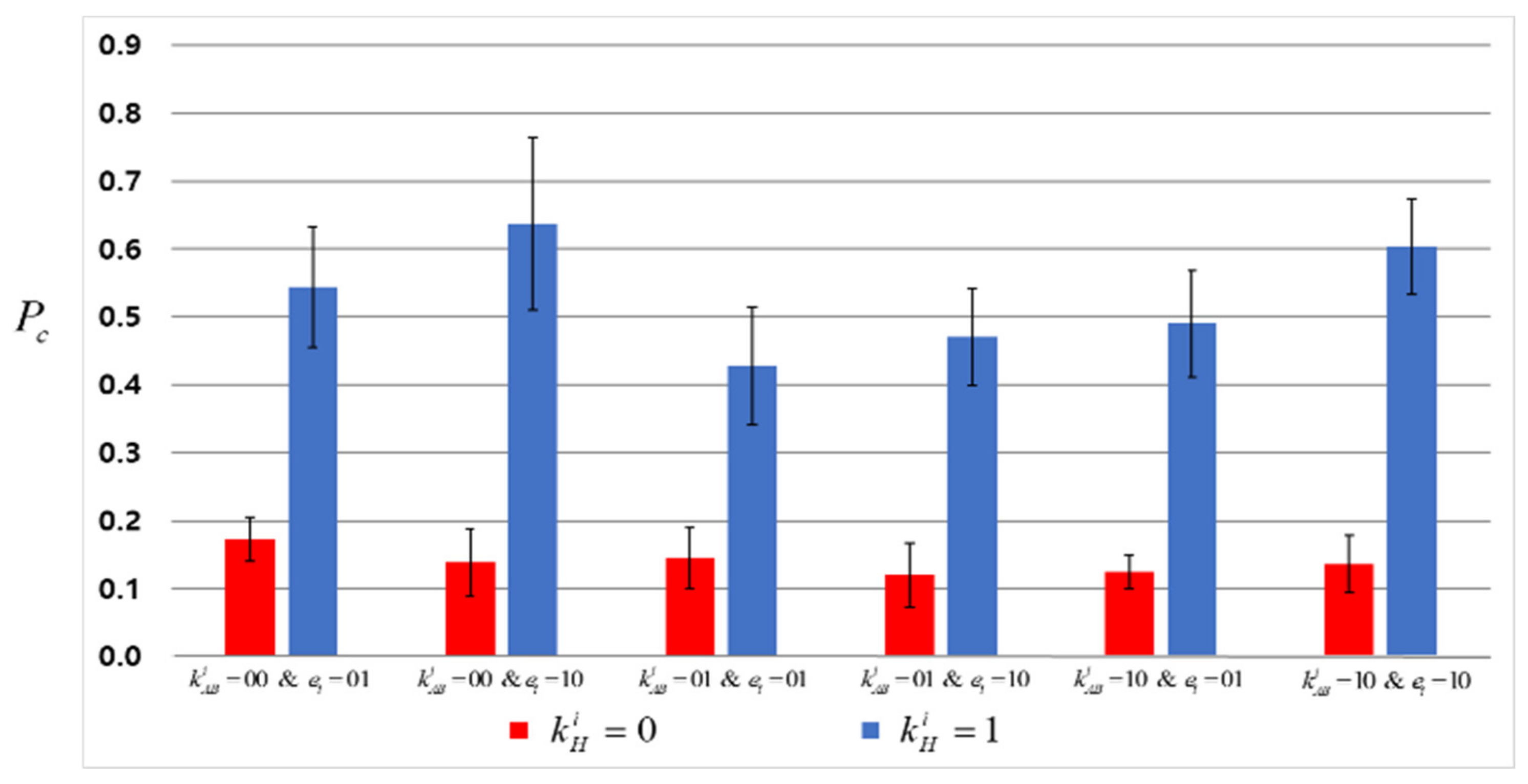
Table 1 lists these 24 cases, and
Figure 6 shows the results of the experiment with the existential forgery using the Pauli operator for 12 cases in
Table 1.