Experimental Analysis of Friend-And-Native Based Location Awareness for Accurate Collaborative Filtering

Abstract

Location-based recommender systems have gained a lot of attention in both commercial domains and research communities where there are various approaches that have shown great potential for further studies. However, there has been little attention in previous research on location-based recommender systems for generating recommendations considering the locations of target users. Such recommender systems sometimes recommend places that are far from the target user’s current location. In this paper, we explore the issues of generating location recommendations for users who are traveling overseas by taking into account the user’s social influence and also the native or local expert’s knowledge. Accordingly, we have proposed a collaborative filtering recommendation framework called the Friend-And-Native-Aware Approach for Collaborative Filtering (FANA-CF), to generate reasonable location recommendations for users. We have validated our approach by systematic and extensive experiments using real-world datasets collected from Foursquare ^TM. By comparing algorithms such as the collaborative filtering approach (item-based collaborative filtering and user-based collaborative filtering) and the personalized mean approach, we have shown that our proposed approach has slightly outperformed the conventional collaborative filtering approach and personalized mean approach.

1. Introduction

Ever since traveling has become more accessible, people have been relying a lot on the location-based recommender system for places to visit during their voyage. As a result, location-based recommender system has gained much attention in the areas of commercial and in the research communities in recent years. Researchers have investigated new approaches to develop novel systems that are able to generate high-quality and personalized recommendations for users. However, in most previous research, location-based recommender system have generated recommendations without considering the current location of the target user. Such systems could recommend places that are far from the location of the target user, and thereby it can be impossible for the user to reach the places at that moment. There are only a handful of state-of-art research that have been proposed to incorporate geographical and social influence into collaborative filtering approach when generating location recommendations [1,2,3,4,5,6,7]. However, those research have not seriously regarded the location of the target user. Suppose a case of one user, for example, who lives in Malaysia and travels abroad to Singapore for vacation. From the original intention of collaborative filtering, users who exhibit similar location visiting behavior to the target user (also known as similar users) are chosen to provide clues for making a recommendation. Since human mobility exhibits geographical locality, most of the similar users are probably living in Malaysia because they have visited various locations that the target user has. As recommendations are generated considering the locations visited by the similar users (who may have never been in Singapore), the recommended locations may be very far from the target user current location and may also not be reachable by the target user at that particular moment. In summary, those previous collaborative filtering approaches may recommend the same location, no matter where the user is currently located in the world. Thus, the systems with those approaches might fail to consider the social aspects that influence a user in the location-based recommender system. In this paper, we study the issues of generating location recommendations for users who travels abroad (users who are far away from their home region) by taking into account the user preferences, social connections, and geographical proximity.

Recently, many studies have explored the application of social relationship amongst the users in recommender systems to enhance the effectiveness of recommendation techniques [1,4,6,7,8,9,10,11,12,13,14,15]. The main ideas of those research are incorporating the trust and interest similarity carried along in social relationships amongst friends to improve personalized search and recommendations. However, as aforementioned, these prior works mainly focus on conventional ways for recommendations. There are only a handful of studies that have explored the use of local experts (natives) in a geospatial range which matches the user’s preferences by a preference-aware candidate selection algorithm and then infer a score of the candidate locations based on the opinions of the selected local experts which offers good efficiency of providing location recommendations.

By exploring the strong social ties between friends and natives, we have proposed a location-based recommender system called Friend-And-Native-Aware Approach For Collaborative Filtering (FANA-CF) for location-based recommendation based on collaborative ratings of commonly visited places made by social friends and the local experts of a certain range of geospatial location, and we perform extensive and systematic experimental analysis on FANA-CF. The evaluation results from benchmark datasets have shown that FANA-CF holds comparable recommendation effectiveness against the compared algorithms.

2. Related Work

The collaborative filtering (CF) technique is widely used for recommender systems and many CF recommendation approaches [16] have been proposed. The CF can be classified into two categories, memory-based CF and model-based CF. Memory-based CF methods can be further classified as user-based collaborative filtering (UBCF) and item-based collaborative filtering (IBCF). UBCF first finds similar users based on their ratings of items, using a similarity measurement such as the Pearson correlation coefficient shown as follows:

$$\begin{array}{c}\hfill w_{a,u}=\frac{{\sum }_{i\in I}\left(r_{a,i}-{\overline{r}}_a\right)\left(r_{u,i}-{\overline{r}}_u\right)}{\sqrt{{\sum }_{i\in I}{\left(r_{a,i}-{\overline{r}}_a\right)}^2}\sqrt{{\sum }_{i\in I}{\left(r_{u,i}-{\overline{r}}_u\right)}^2}}\end{array}$$

(1)

where $w_{a,u}$ is the similarities between user a and user u. $i\in I$ represents the summation of the items that both user a and user u have rated, ${\overline{r}}_a$ is the average rating of the co-rated items of the user a, and ${\overline{r}}_u$ is the average rating of the co-rated items of the user u.

Then the recommendation score for an item is computed by a weighted combination of historical ratings on the items from the similar users shown as follows:

$$\begin{array}{c}\hfill P_{a,i}={\overline{r}}_a+\frac{{\sum }_{u\in U}\left(r_{u,i}-{\overline{r}}_u\right)w_{a,u}}{{\sum }_{u\in U}\left|w_{a,u}\right|}\end{array}$$

(2)

where $P_{a,i}$ represents the prediction for the user a on a certain item i. ${\overline{r}}_a$ and ${\overline{r}}_u$ are the average ratings for the user a and user u respectively. The summation of all the users $u\in U$ who have rated the item i.

In contrast, IBCF works by finding items that are similar to other items that the target user has liked or rated. The formula is shown as follows:

$$\begin{array}{c}\hfill w_{i,n}=\frac{{\sum }_{u\in U}\left(r_{u,i}-{\overline{r}}_i\right)\left(r_{u,n}-{\overline{r}}_n\right)}{\sqrt{{\sum }_{u\in U}{\left(r_{u,i}-{\overline{r}}_i\right)}^2}\sqrt{{\sum }_{u\in U}{\left(r_{u,n}-{\overline{r}}_n\right)}^2}}\end{array}$$

(3)

Note that $u\in U$ denotes the set of users who rated both item i and item n, where i and n are indices for items. $r_{u,i}$ is the rating of user u on item i, $r_{u,n}$ is the rating of user u on item n, ${\overline{r}}_i$ is the average rating of item i by all users.

$$\begin{array}{c}\hfill p_{u,i}=\frac{{\sum }_{n\in N}{r}_{u,n}·w_{i,n}}{{\sum }_{n\in N}\left|w_{i,n}\right|}\end{array}$$

(4)

where $p_{u,i}$ is the prediction of user u on item i. $n\in N$ is the summations of other rated items by user u. $w_{i,n}$ is the weight between item i and item n. $r_{u,n}$ is the rating of user u on item n.

Model-based CF builds models using data mining techniques, such as Bayesian networks, clustering models, and others on user ratings where the models are used to generate recommendations [17]. The model building algorithms are usually computationally expensive.

Personalized mean (PersMean) is one of the techniques used in recommender system to generate recommendations. This technique operates by computing the users and the items average offsets from the global rating. It implements the prediction rule $p_{u,i}=\mu +b_i+b_u$, where $\mu$ is the global mean rating, $b_i$ is the difference between the item’s mean rating and the global mean, and $b_u$ is the mean of the differences between the user’s ratings for each items and the item’s mean.

To the best of our knowledge, there has never been any work supported by detailed experimental analysis on mixing both friends and natives based recommender system. However, there are only a handful of research that have been carried out on friend-based or native-based recommender systems.

Ye et al. [1] have proposed the friend-based collaborative filtering (FCF) approach and the geo-measured friend-based collaborative filtering (GM-FCF) approach. Through the authors’ analysis on the dataset collected from Foursquare (a local search-and-discovery mobile app with location data service platform), they have observed a strong social and geospatial ties among users and their favorite locations or places in the system. The authors have validated the proposed ideas and have evaluated the FCF family techniques through comprehensive experimentation. The evaluation results showed that the family of FCF approaches has comparable recommendation effectiveness against other state-of-the-art recommendation approaches, while incurring significantly lower computational overheads.

Location-based and Preference-Aware Recommendation Using Sparse Geo-social Networking Data by Bao et al. [12] has presented a location-based and preference-aware recommender system that offers users a set of venues within a geospatial range with the consideration of: (a) users’ personal preferences which were learned automatically from users’ location history, and (b) social opinions, which were mined from the location histories of the local experts. This recommender system can facilitate users with information on not only the areas they reside but also the places that are completely unfamiliar to them. Since a user can only visit a limited number of locations within a limited amount of time and the user location matrix is very sparse, thus leading to a big challenge for traditional collaborative filtering-based location recommender system. The problem becomes even more challenging when people travel to a new city in which they have not visited before. The authors have evaluated their system with a large-scale real dataset collected from Foursquare. Following that, the results have confirmed that the method offers more effective recommendations than baselines, while having efficiency in providing the location recommendations.

Cai et al. [10] exploited the idea of object typicality from cognitive psychology and proposed a novel typicality-based collaborative filtering recommendation method named TyCo. TyCo finds “neighbours” of users based on user typicality degrees in user groups.

User Preference, Proximity and Social-Based Collaborative Filtering (UPS-CF) by Ference et al. [4], has incorporated users’ preferences, social connections, and geographical proximity to give location recommendations for mobile users which for most location-based recommender system generates recommendations without considering where the target user is currently located which may generate recommendations that are far from the target user currently located. The authors have conducted extensive experiment to evaluate their proposal and have compared it with CF variants and the baseline approaches using the dataset from Foursquare and Gowalla. The authors have shown that UPS-CF outperformed all other comparing approaches. The authors have also proven that the effectiveness does not degrade for out-of-town users. They have also found that for in-town users, similar users are important, while social friends become even more important for out-of-town users.

Yi and Kang [13] proposed the idea of using recommendations from friends and natives. Their idea of using $\alpha$ for balancing between two measures is inspired from elastic net regularization [18]. In this paper, we extend their idea to design a collaborative filtering recommendation framework, the Friend-And-Native-Aware Approach for Collaborative Filtering (FANA-CF). We have validated our approach by comprehensive experiments using real datasets collected from Foursquare.

Liu et al. [6] presented a new user similarity model to improve the recommendation performance. Their model considers the local context information of user ratings and the global preference of user behavior. They demonstrated their model on three real data sets and showed the superiority of their model.

The Geographical Sparse Additive Generative Model for Spatial Item Recommendation, Geo-SAGE, proposed by [19] for out-of-town and home-town recommendations. It considers both the user’s personal interests and the preferences of the crowd in the target location, by exploiting both the co-occurrence pattern of spatial items and the content of spatial items. To overcome the sparsity problem, Geo-SAGE exploits the geographical correlation by smoothing the crowd’s preferences over a well-designed spatial index structure called spatial pyramid. The authors have conducted extensive experiments to evaluate the performance of the Geo-SAGE model on two real large-scale datasets. The experimental results have demonstrated that the Geo-SAGE model outperforms other state-of-the-art recommender algorithms in the two tasks of both out-of-town and home-town recommendations.

Guo et al. [14] proposed a trust-based matrix factorization technique (TrustSVD) to resolve data sparsity and cold start problems. From the analysis of the social trust data from four real-world data sets, they incorporate the implicit influence of both ratings and trust into a recommendation model.

Jiang et al. [7] proposed an author topic model-based collaborative filtering (ATCF) method for accommodating comprehensive points of interest (POIs) recommendations for social users. Their method extracts user preference topics, such as cultural, cityscape, or landmark, from the geo-tag constrained textual description of photos via the author topic model. They demonstrated their approach by extensive experiments on a large collection of data.

Yang et al. [15] introduced a novel method that works to improve the performance of collaborative filtering recommendations by integrating sparse rating data given by users and sparse social trust network among these same users. Their method adopts matrix factorization technique that maps users into low-dimensional latent feature spaces in terms of their trust relationship. From this adoption, their proposed method accurately reflect the users reciprocal influence on the formation of their own opinions to learn better preferential patterns of users for high-quality recommendations.

Again, our algorithm is different from their approach in that it considers not only the user’s social influence but also the natives’ or local experts’ knowledge. Summarizing the above related work, we present the following

Table 1. A comparison of related work and our approach in terms of using social influence from friends and local experts’ knowledge (natives). 

Research Work	Social Influence	Native’s Knowledge
TrustSVD [14], ATCF [7], Yang et al. [15]	Fully Used	Not Used
UPS-CF [4], Bao et al. [12], Liu et al. [6], Geo-SAGE [19]	Not Used	Fully Used
FCF and GM-FCF. [1]	Fully Used	Partially Used
Yi and Kang [13]	Partially Used	Partially Used
TyCo [10]	Not Used	Partially Used
Our approach	Fully Used	Fully Used

.

3. Proposed Approach

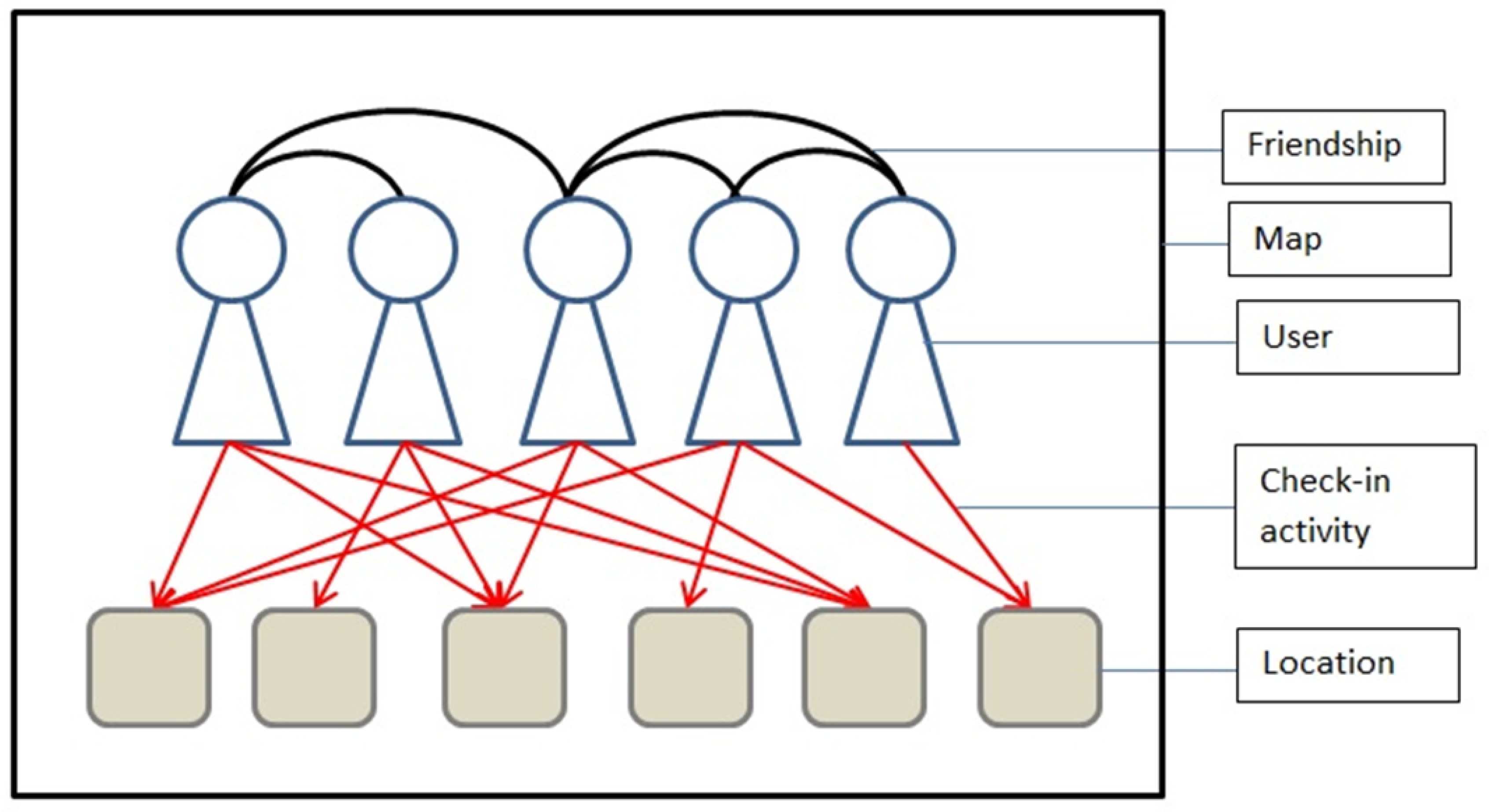
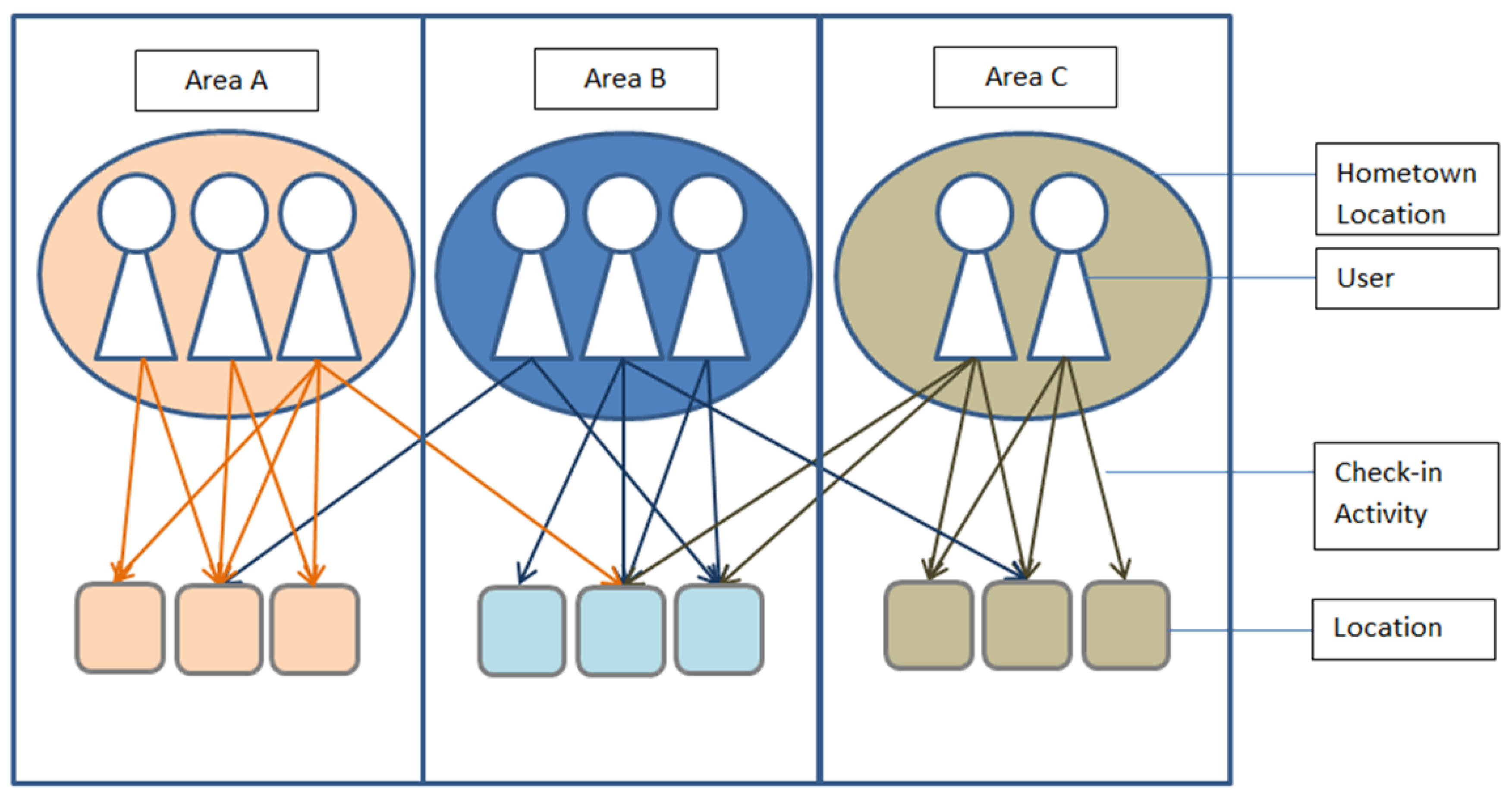
The proposed recommender system approach, the Friend-And-Native-Aware Approach For Collaborative Filtering (FANA-CF), essentially focuses on two groups of users who are the friends (as illustrated in Figure 1) and the natives/local experts (as illustrated in Figure 2) to generate recommendations to the target user. As mentioned earlier, the reason we only use these two groups of users is because we believe that friends have the same preferences, while natives can recommend high-quality recommendations to the target user.

We directly define friends from the social relations of users, and we define natives simply from the clustering of users’ residential addresses. More precisely, in our implementation, we exploited a given social graph structure (in socialgraph.dat described in

Table 2. The content and the usage of the data files.

Datafile	Description
users.dat	Consist of a set of users whereby each user has a unique ID and a geospatial location (latitude and longitude) that represents the user’
venues.dat	Consist of a set of venues whereby each venue has a unique ID and a geospatial location (latitude and longitude)
socialgraph.dat	Consist of social graph edges that exist between users. Each social connections consists of two users (friends) represented by two unique IDs (first_user_id and second_user_id).
checkins.dat	Show the check-ins activities of users at venues. Each check-in has a unique ID, the user ID, and and the venue ID.
ratings.dat	Consist of implicit ratings that quantify how much that particular user like that specific venue.

) prepared by domain experts. Note that our notion of friends and natives is different from the trust metric [20] in a trust aware system. The trust metrics is a more abstract concept which can be expressed as the trustworthiness of “unknown” users. A trust weight is estimated from the propagation of trust over the trust network. The resulting trust weight can be used in place of the similarity weight. Therefore, trust can be considered as an elaborated form induced from social relation; however, it is different from our notion of friends, because we directly measure friend relationships from the social network. Nativeness is different from trust because it is a concept that can be established from one user.

By combining both groups, we believe that this proposed recommender system approach will produce personalized and high-quality recommendations. In this section, we will explain the overall system, each process inside it in terms of an algorithmic description, and modus operandi of the system in detail.

In order to obtain the recommendations, ratings of a given item need to be calculated. The recommendation, $\widehat{r}$, for the given item of the target user, is calculated as follows:

$$\begin{array}{c}\hfill \widehat{r}=\alpha ·{\widehat{p}}_{af}+(1-\alpha )·{\widehat{p}}_{an}\end{array}$$

(5)

${\widehat{p}}_{af}$ represents the prediction of recommendations based on target user a and friend users f. ${\widehat{p}}_{an}$ represents the prediction of recommendations based on target user a and native users, n. Both predictions are calculated using collaborative filtering (CF) method. $\alpha$ is the weights that are given to each of the relative prediction ${\widehat{p}}_{af}$ and ${\widehat{p}}_{an}$.

In UBCF, the prediction ${\widehat{p}}_{af}$ and ${\widehat{p}}_{an}$ are obtained through weighted sum of others’ rating method, FANA-UBCF. The equations for both predictions in UBCF are as follows:

$$\begin{array}{c}\hfill {\widehat{p}}_{af}=\frac{{\sum }_{f\in FNN}\left(r_{fx}-{\overline{r}}_f\right)\times si{m}_{af}}{{\sum }_{f\in FNN}si{m}_{af}}\end{array}$$

(6)

$$\begin{array}{c}\hfill {\widehat{p}}_{an}=\frac{{\sum }_{n\in NNN}\left(r_{nx}-{\overline{r}}_n\right)\times si{m}_{an}}{{\sum }_{n\in NNN}si{m}_{an}}\end{array}$$

(7)

In Equation (6), $f\in FNN$ represents user f as one of the elements in the set of friend’s nearest neighbour (FNN). $r_{fx}$ represents the rating of user f on item x. ${\overline{r}}_f$ is the mean rating of user f. $si{m}_{af}$ represents the similarities between target user a and friend user f.

In Equation (7), $n\in NNN$ represents user n as one of the elements in the set of native’s nearest neighbour (NNN). $r_{nx}$ represents the rating of user n rates on item x. ${\overline{r}}_n$ is the mean rating of user n. $si{m}_{an}$ represents the similarities between target user a and native user n.

In IBCF, the prediction ${\widehat{p}}_{af}$ and ${\widehat{p}}_{an}$ are obtained through the weighted sum method (FANA-IBCF). The equations for both predictions in IBCF are as follows:

$$\begin{array}{c}\hfill {\widehat{p}}_{af}=\frac{{\sum }_i^{I_f}\left(si{m}_{i,I_f}\times r_{a,I_f}\right)}{{\sum }_i^{I_f}\left(\left|si{m}_{i,I_f}\right|\right)}\end{array}$$

(8)

$$\begin{array}{c}\hfill {\widehat{p}}_{an}=\frac{{\sum }_i^{I_n}\left(si{m}_{i,I_n}\times r_{a,I_n}\right)}{{\sum }_i^{I_n}\left(\left|si{m}_{i,I_n}\right|\right)}\end{array}$$

(9)

In Equation (8), $I_f$ represents all similar items among target user a and friend users f. $si{m}_{i,I_f}$ represents the similarity between item i and all the similar items among target user a and friend users f. $r_{a,I_f}$ is the rating of target user a on all the similar items among target user a and friend user f.

In Equation (9), $I_n$ represents all the similar items among target user a and native users n. $si{m}_{i,I_n}$ represents the similarity between item i and all the similar items rated by the target user a and native user n. $r_{a,I_n}$ is the rating of target user a with that of the native users n.

The users’ similarities (similarities between the target user and the friend user, $si{m}_{af}$, and similarities between the target user and the native user, $si{m}_{an}$) and items’ similarities (similarities between the target item and the friend item, $si{m}_{i,I_f}$, and similarities between the target item and native item, $si{m}_{i,I_n}$) are computed using the Pearson correlation coefficient (PCC) method. The reason the PCC method was chosen in this approach is because it has been proven by Herlocker et al. [16] that the PCC method is one of the effective methods to form the nearest neighbourhood in k-NN method. The following equations show the calculations of the similarities between the target user and the friend user, $si{m}_{af}$; similarities between the target user and the native user, $si{m}_{an}$; similarities between the target item and the friend item, $si{m}_{i,I_f}$; and similarities between the target item and the native user, $si{m}_{i,I_n}$ used in the PCC method.

$$\begin{array}{c}\hfill si{m}_{af}=\frac{{\sum }_{i\in I}\left(r_{ai}-{\overline{r}}_a\right)\left(r_{fi}-{\overline{r}}_f\right)}{\sqrt{{\sum }_{i\in I}{\left(r_{ai}-{\overline{r}}_a\right)}^2}\sqrt{{\sum }_{i\in I}{\left(r_{fi}-{\overline{r}}_f\right)}^2}}\end{array}$$

(10)

$$\begin{array}{c}\hfill si{m}_{an}=\frac{{\sum }_{i\in I}\left(r_{ai}-{\overline{r}}_a\right)\left(r_{ni}-{\overline{r}}_n\right)}{\sqrt{{\sum }_{i\in I}{\left(r_{ai}-{\overline{r}}_a\right)}^2}\sqrt{{\sum }_{i\in I}{\left(r_{ni}-{\overline{r}}_n\right)}^2}}\end{array}$$

(11)

$$\begin{array}{c}\hfill si{m}_{i,I_f}=\frac{{\sum }_{f\in F}\left(r_{f,i}-{\overline{r}}_i\right)\left(r_{f,I_f}-{\overline{r}}_{I_f}\right)}{\sqrt{{\sum }_{f\in F}{\left(r_{f,i}-{\overline{r}}_i\right)}^2}\sqrt{{\sum }_{f\in F}{\left(r_{f,I_f}-{\overline{r}}_{I_f}\right)}^2}}\end{array}$$

(12)

$$\begin{array}{c}\hfill si{m}_{i,I_n}=\frac{{\sum }_{n\in N}\left(r_{n,i}-{\overline{r}}_i\right)\left(r_{n,I_n}-{\overline{r}}_{I_n}\right)}{\sqrt{{\sum }_{n\in N}{\left(r_{n,i}-{\overline{r}}_i\right)}^2}\sqrt{{\sum }_{n\in N}{\left(r_{n,I_n}-{\overline{r}}_{I_n}\right)}^2}}\end{array}$$

(13)

In Equation (10), $i\in I$ represents a single item of a set of element I. $r_{ai}$ represents the rating of target user a given on the item i; meanwhile, $r_{fi}$ represents the mean rating of friend user f given on the item i. ${\overline{r}}_a$ represents the mean rating of target user a. ${\overline{r}}_f$ represents the mean rating of friend user f.

In Equation (11), $r_{ni}$ represents the rating that the native user, n, given to the item i. ${\overline{r}}_n$ represents the mean rating of the native user n.

In Equation (12), $f\in F$ represents a single friend user f of a set of the friend users F. $r_{f,i}$ represents the rating that friend user f given on target item i; meanwhile, $r_{f,I_f}$ represents the rating that friend user f given on friend item $I_f$. ${\overline{r}}_i$ represents the mean rating of target item i. ${\overline{r}}_{I_f}$ represents the mean rating of friend item $I_f$.

In Equation (13), $n\in N$ represents a single native user n of a set of native users N. $r_{n,i}$ represents the rating that the native user n given on target item i; meanwhile, $r_{n,I_n}$ represents the rating that native user n given on native item $I_n$. ${\overline{r}}_i$ represents the mean rating of target item i. ${\overline{r}}_{I_n}$ represents the mean rating of native item $I_n$.

3.1. Algorithm

FANA-CF algorithm is very straightforward, as is described in Figure 3. FANA-CF takes inputs from a target user ($u_t$) and a location ($l_d$) that the target user wishes to go to and returns the list ($R_{fn}$) of top-k recommended items.

The algorithm starts by classifying the two groups of users, friends and natives. The system will then check on the hometown location ($l_i$) of every user ($u_i$). If the hometown location ($l_i$) of the user ($u_i$) equals the destination ($l_d$) the target user ($u_t$) wishes to go to, then the user ($u_i$) will be classified as a native. If user ($u_i$) is linked to the target user ($u_t$) through a social graph; then the user ($u_i$) will be classified as a friend.

Next, the system will check the rating’s location (rating${}_f$) through friends. If the location of rating${}_f$ is equal to the location ($l_d$) that the target user ($u_t$) wishes to go, then rating${}_f$ will be assigned to the friends’ rating ($r_f$). The system will then check on the location’s rating (rating${}_n$) by natives. If the location of rating${}_n$ is equal to the location ($l_d$) that the target user ($u_t$) wishes to go to, then rating${}_n$ will be assigned to the friends’ rating ($r_n$).

Friends’ rating, $r_f$, and natives’ rating, $r_n$, will use collaborative filtering to obtain friends’ recommendations, $R_f$, and natives’ recommendations, $R_n$ respectively. User supplied weights ($\alpha$) will then be applied on $R_f$ and $R_n$, in order to obtain a new recommendation rating through the combination of weights with recommendations of friends and recommendations of natives, $R_{fn}$.

Finally, the system will return top $R_{fn}$.

3.2. Complexity Analysis

As for the complexity of the algorithm, first of all, it takes a constant time for line 1 in Figure 3.

Constructing “natives” and “friends” data structures in line 2 and 3 takes $O\left(\right|U\left|\right)$, where $U\ni u_i$ is the set of users. It takes linear time in terms of the total number of users, $\left|U\right|$, because we initially have constructed an index structure between the user data (user.dat) and the social graph (socialgraph.dat), which is commonly used in the database systems.

Since the resulting sizes of the “natives” and “friends” data structures are less than or equal to $\left|U\right|$ in the worst case, lines 4 and 5 asymptotically take $O\left(\right|U\left|\right)$ using the index structure among the user data (user.dat), the venue data (venues.dat), and the ratings data (ratings.dat).

As for the “collaborative filtering” in lines 6 and 7, the asymptotic running time for line 6 (between the target user and the friend user) and the running time for line 7 (between the target user and the native user) are the same, because “natives” and “friends” are subsets of the users U. Therefore, without loss of generality, it suffices to show the running time for the target user and the friend user (line 6). For UBCF, we need to calculate ${\widehat{p}}_{af}$ (in Equation (6)), and for calculating ${\widehat{p}}_{af}$, we need to calculate $si{m}_{af}$ (in Equation (10)). Calculating $si{m}_{af}$ takes $O\left(\right|I\left|\right)$ where I means the items, and thus calculating ${\widehat{p}}_{af}$ takes $O\left(\right|I|\times |U\left|\right)$. Similarly, for IBCF, $si{m}_{i,I_f}$ (in Equation (12)) takes $O\left(\right|U\left|\right)$, and thus ${\widehat{p}}_{af}$ takes $O\left(\right|U|\times |I\left|\right)$, which is the same as that of UBCF.

As $O\left(\right|U|\times |I\left|\right)$ dominates $O\left(\right|U\left|\right)$, the overall running time of the algorithm is the same as that of the baseline collaborative filtering algorithm with extra B+ tree-like data structure.

Another advantage of our proposed algorithm is that it can be applied to any memory-based collaborative filtering algorithm. That is, we can substitute any memory-based collaborative filtering algorithm with “collaborative filtering” in lines 6 and 7 of our algorithm in Figure 3.

4. Experiments

In this section we evaluate the performance of our proposed approach, the Friend-And-Native-Aware Approach For Collaborative Filtering (FANA-CF), and compare our proposal with existing collaborative filtering approaches (item-based collaborative filtering and user-based collaborative filtering) and PersMean using a real-world dataset, the University of New Mexico(UMN)/Sarwat Foursquare dataset. In order to evaluate our FANA-CF, we have chosen several commonly-used CF metrics which are the mean absolute error (MAE), root mean squared error (RMSE), and normalized discounted cumulative gain (nDCG).

4.1. Dataset

We performed experiments on a real large-scale location-based social network (LBSN) dataset, UMN/Sarwat Foursquare [3,5]. This dataset contains 2,153,471 users, 1,143,092 venues, 27,098,480 social connections, 1,021,970 check-ins, and 2,809,581 ratings that the users have assigned to the venues. All this information was extracted from the Foursquare application through the public API. The information of all users has been anonymized according to users’ geolocations; ID is used to represent each user and his geospatial location. The same process has been conducted for the venues’ information. The data consist of five files—user.dat, venues.dat, socialgraph.dat, checkins.dat, and ratings.dat. The content details and the usage of the files are described in Table 2.

Before running the algorithm, reverse geocoding was performed on both users.dat and venues.dat in order to find the natives. Reverse geocoding is a process of reversing the coding of a certain location (latitude and longitude) to a readable address or place name. This process permits the identification of a nearby street address, place, or area subdivision, such as a neighbourhood, state, or country. After implementing the reverse geocoding process, users who originate from the same venue or hometown will be classified as the natives of that location. Users who are linked by the socialgraph.dat will be classified as friends. For this case study, we chose users from Malaysia, Singapore, and Indonesia.

4.2. Evaluation Metrics

The quality of a recommender system can be known based on the evaluation results. There are several types of metrics used depending on the types of collaborative filtering applications. According to Herlocker et al. [16], the recommender systems’ evaluation metrics can be generally classified into three general categories: predictive accuracy metrics, classification accuracy metrics, and rank accuracy metrics.

In order to evaluate our FANA-CF, we have chosen several commonly used collaborative filtering metrics: mean absolute error (MAE), root mean squared error (RMSE), and normalized discounted cumulative gain (nDCG).

4.2.1. Mean Absolute Error (MAE):

MAE is most widely used evaluation metric in CF research literature [16]. MAE computes the average of absolute difference between the prediction ratings and the true ratings.

$$\begin{array}{c}\hfill MAE=\frac{{\sum }_{i=1}^N\left|p_i-r_i\right|}{n}\end{array}$$

(14)

where n represents the total number of ratings over all users, $p_i$ is the predicted rating of item i, and $r_i$ is the actual rating of item i.

4.2.2. Root Mean Squared Error (RMSE):

Root mean squared error (RMSE) can be calculated as follows:

$$\begin{array}{c}\hfill RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^N{\left(p_i-r_i\right)}^2}\end{array}$$

(15)

where n is the total number of ratings over all users, and $p_i$ is the predicted rating for item i, whereas $r_i$ represents the actual rating of item i. RMSE amplifies the contributions of the absolute errors between the predictions and the true values.

Although the accuracy metrics have greatly helped in the field of the recommender systems, accurate recommendations are sometimes not the ones that are most useful to users. For example, users may prefer to be recommended with items that are unfamiliar to them, rather than the old favorites that they may not want.

4.2.3. Normalized Discounted Cumulative Gain (nDCG):

$nDCG$ measures the performance of a recommender system based on the graded relevance of the recommended entities that varies from 0.0 to 1.0, with 1.0 representing the ideal ranking of the entities. This metric is commonly used in information retrieval and also to evaluate the performance of Web search engines. Cumulative gain ($CG$) is the sum of the graded relevance values in the results. Discounted cumulative gain ($DCG$) considers the position of the result penalized in logarithmic factor [21]. Since the lengths of query results can vary, $DCG$ is normalized by dividing with the maximum possible $DCG$ to produce $nDCG$ [22].

$$\begin{array}{c}\hfill C{D}_k=\sum _{i=1}^{k}re{l}_i\end{array}$$

(16)

$$\begin{array}{c}\hfill DC{G}_k=\sum _{i=1}^k\frac{2^{re{l}_i}-1}{{log}_2\left(i+1\right)}\end{array}$$

(17)

$$\begin{array}{c}\hfill nDC{G}_k=\frac{DC{G}_k}{IDC{G}_k}\end{array}$$

(18)

where k represents the maximum number of entities that can be recommended. $re{l}_i$ represents the relevance of item i. $IDC{G}_k$ is the maximum possible (ideal) $DCG$ for a given set of queries, documents, and relevance.

4.3. Evaluation Results

We have evaluated the performance of our proposed approach, FANA-CF, which uses two groups of users’ ratings (friends and natives) in order to generate recommendations, by comparing it with existing item-based collaborative filtering, user-based collaborative filtering, and the personalized mean approach, which uses every user’s rating to generate recommendations. The Foursquare dataset has been used to test the recommendation quality. We randomly selected 20% of ratings from the evaluation dataset as the test set and used the remaining 80% as the training set. We also conducted the cross validation in terms of k-fold cross validation (5-fold) on the training set, by randomly selecting the different test and training sets each time, and taking the average of the results. The evaluation metrics that we used to test the recommendations’ quality were mean absolute error (MAE), root mean squared error (RMSE), and normalized discounted cumulative gain (nDCG).

Table 3. Comparison of mean absolute error (MAE) performance among item-based collaborative filtering (IBCF), user-based collaborative filtering (UBCF), personalized mean (PersMean), and our proposed approach, FANA-CF, using 5-fold cross validation. We have calculated the average of MAE value and the standard deviation for each approach. 

Experiment #	IBCF	UBCF	PersMean	FANA-IBCF	FANA-UBCF
1	16.780	14.723	20.304	16.630	14.720
2	15.274	13.741	20.896	15.233	13.721
3	17.419	15.097	21.816	16.259	15.097
4	13.787	13.201	20.189	13.774	13.201
5	16.566	14.194	20.778	16.568	14.173
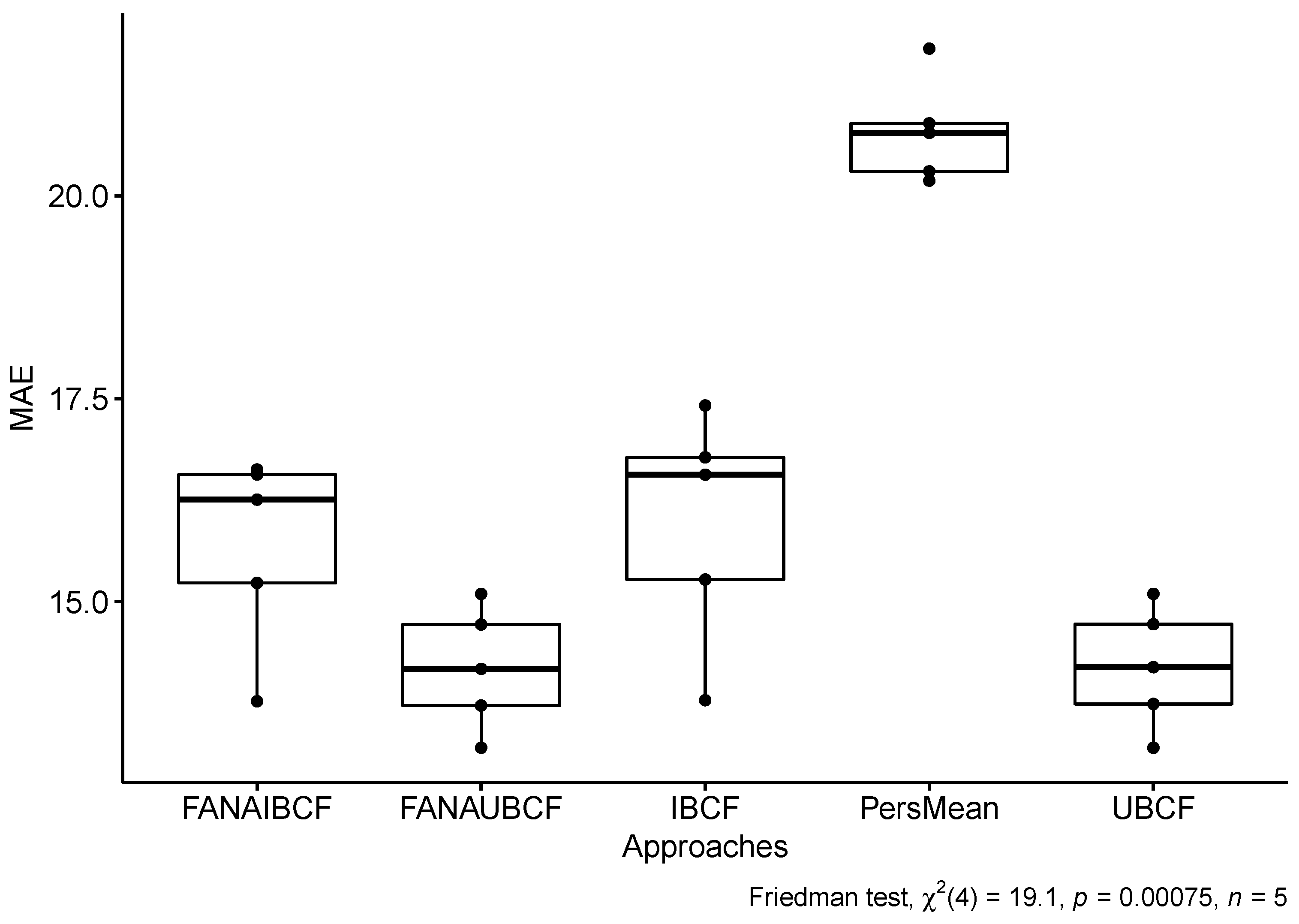
Average	15.965 ± 1.293	14.191 ± 0.676	20.797 ± 0.576	15.693 ± 1.082	14.182 ± 0.679

shows the comparison of MAE performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF, using 5-fold cross validation. We also calculated the average of MAE values and the standard deviation for each approach. The MAE evaluation metric is used to evaluate the average magnitude of errors in a set of prediction ratings. For this evaluation, a lower value indicates that the approach scores better in terms of accuracy. From the evaluation, it can be seen that our proposed approach (FANA-UBCF), which uses two groups of users’ ratings, friends and natives, to generate recommendations, scored an average of 14.182 ± 0.679, slightly outperforming the existing IBCF, UBCF, and PersMean approaches that use every user’s rating to generate recommendations. This shows that by using two groups of users’ ratings to generate recommendations instead of just using every user’s ratings to generate recommendations will have a lower error rate (i.e., higher accuracy). as friends have more commonly rated items (i.e., the same preferences). For further analysis of the results, we show a box and whisker plot in Figure 4 with Friedman test results [23]. Note that a p value < 0.05 means the experimental result in Table 3 is statistically significant.

We performed pairwise Wilcoxon signed-rank tests [24] to identify which pairs were significant.

Table 4. Pairwise Wilcoxon signed-rank test of MAE performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF. The results in bold are statistically significant with a 90% confidence level. 

	UBCF	PersMean	FANA-IBCF	FANA-UBCF
IBCF	0.062	0.062	0.125	0.062
UBCF	-	0.062	0.062	0.181
PersMean	-	-	0.062	0.062
FANA-IBCF	-	-	-	0.062

shows the pairwise Wilcoxon signed-rank test of MAE. It can be seen that our proposed algorithms mostly outperformed other algorithms.

Table 5. Comparison of root mean squared error (RMSE) performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF, using 5-fold cross validation. We have calculated the average RMSE and the standard deviation for each approach. 

Experiment #	IBCF	UBCF	PersMean	FANA-IBCF	FANA-UBCF
1	19.119	17.200	22.692	18.927	17.199
2	17.773	16.389	23.267	17.695	16.381
3	19.780	17.715	24.193	18.776	17.715
4	16.841	16.367	23.162	16.824	16.367
5	18.782	16.820	23.210	18.779	16.796
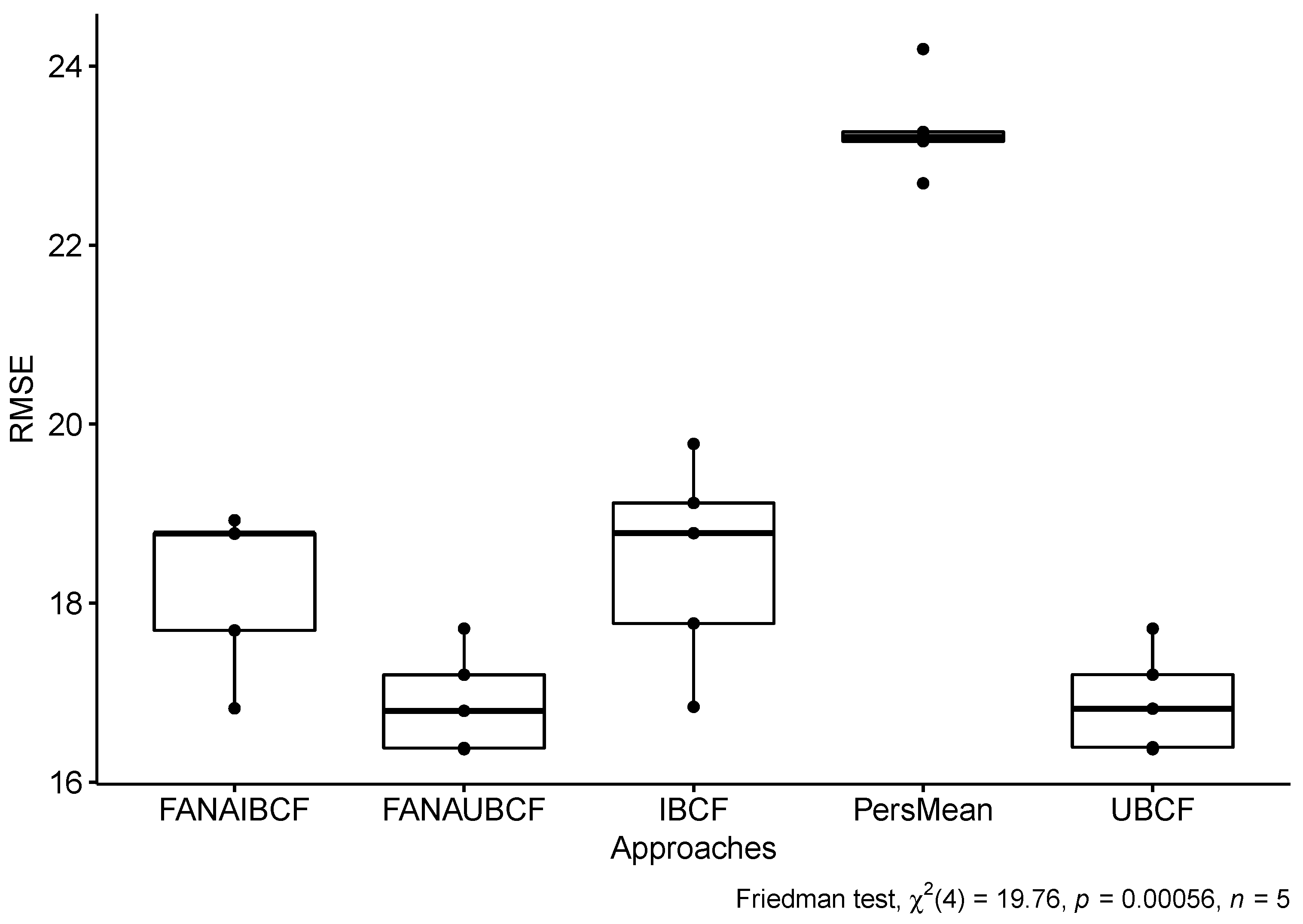
Average	18.459 ± 1.037	16.898 ± 0.511	23.3045 ± 0.489	18.200 ± 0.818	16.892 ± 0.513

shows the comparison of RMSE performance among our proposed approach (FANA-CF), IBCF, UBCF, and PersMean using 5-fold cross validation. We have calculated the average RMSE and the standard deviation for each approach. RMSE evaluation metric is a quadratic scoring rule which measures the average magnitude of the error. For this evaluation, our proposed approach, FANA-UBCF, with the average of 16.892 ± 0.513, slightly outperformed IBCF, UBCF, and PersMean approaches. This has shown that user-based collaborative filtering that uses two groups of users’ ratings (friends and natives) to generate recommendations can achieve a lower error rate(i.e., higher accuracy) than IBCF, UBCF, and PersMean approaches. For further analysis of the results, we show a box and whisker plot in Figure 5 with Friedman test results. Note that a p value <0.05 means the experimental result in Table 5 is statistically significant.

Again, we applied pairwise Wilcoxon signed-rank tests to identify which pairs were significant.

Table 6. Pairwise Wilcoxon signed-rank test of RMSE performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF. The results in bold are statistically significant with a 90% confidence level. 

	UBCF	PersMean	FANA-IBCF	FANA-UBCF
IBCF	0.062	0.062	0.062	0.062
UBCF	-	0.062	0.062	0.181
PersMean	-	-	0.062	0.062
FANA-IBCF	-	-	-	0.062

shows the pairwise Wilcoxon signed-rank test of RMSE. It can be seen that FANA-IBCF significantly outperformed all other algorithms.

Table 7. Comparison of normalized discounted cumulative gain (nDCG) performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF, using 5-fold cross validation. We have calculated the average of nDCG values and the standard deviation for each approach. 

Experiment #	IBCF	UBCF	PersMean	FANA-IBCF	FANA-UBCF
1	99.404	99.373	99.401	99.407	99.374
2	99.410	99.343	99.408	99.413	99.343
3	99.589	99.537	99.492	99.589	99.537
4	99.431	99.404	99.041	99.431	99.408
5	99.490	99.348	99.417	99.490	99.348
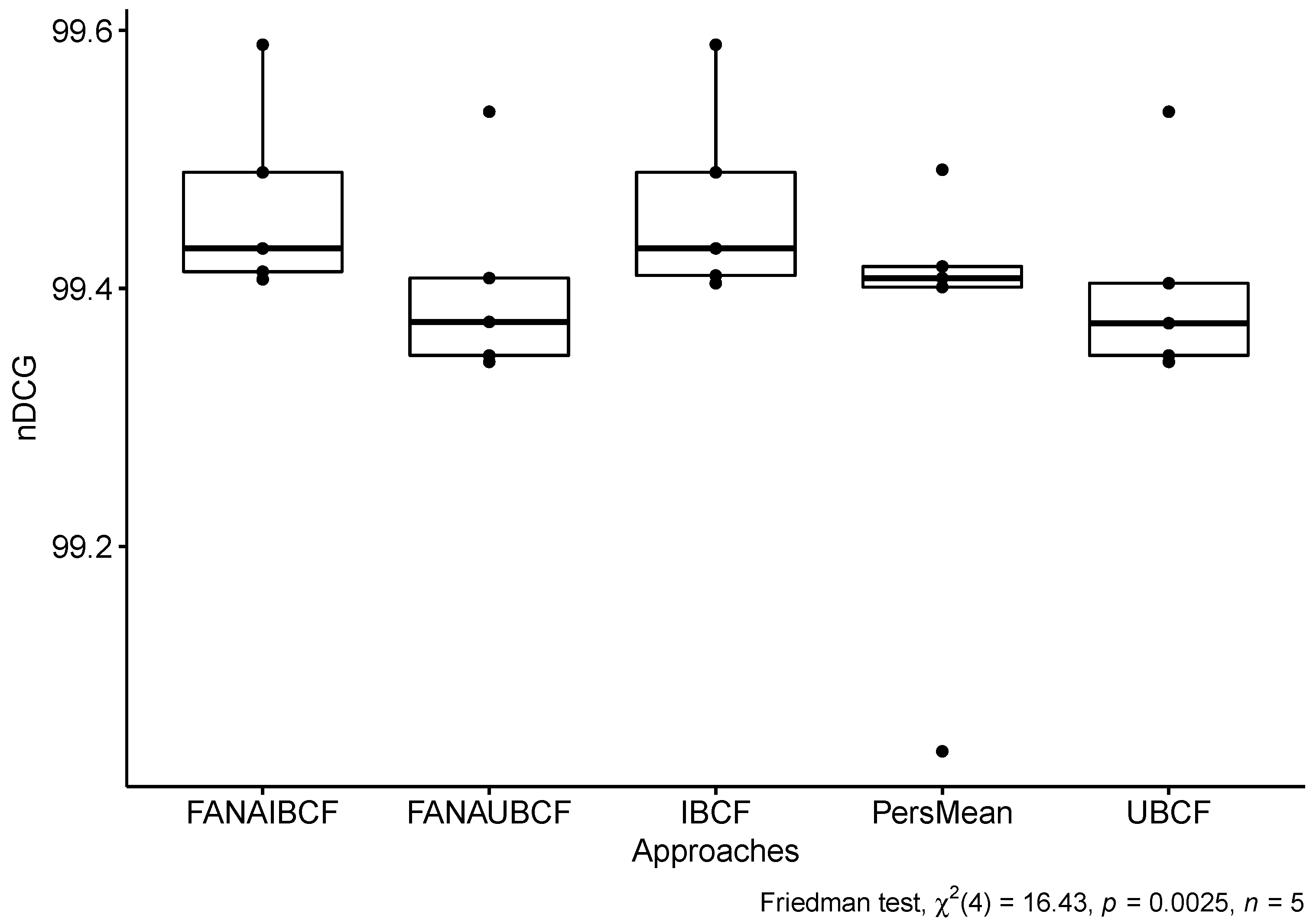
Average	99.465 ± 0.069	99.401 ± 0.071	99.352 ± 0.159	99.466 ± 0.068	99.402 ± 0.071

shows the nDCG performance evaluations for our proposed approach (FANA-CF), IBCF, UBCF, and PersMean using 5-fold cross validation. We have calculated the average of nDCG value and the standard deviation for each approach. nDCG is a measurement for ranking the quality of the recommended items. For this evaluation, our proposed approach FANA-IBCF, with the average of 99.466 ± 0.068, slightly outperformed IBCF, UBCF, and PersMean approaches. This shows that item-based collaborative filtering that uses only items’ ratings by two groups of users (friends and natives) manages to generate higher quality item recommendations than IBCF, UBCF, and PersMean approaches. In order to further analyze the results, we show a box and whisker plot in Figure 6 with Friedman test results. Note that a p value $<0.05$ means the experimental result in Table 7 is statistically significant.

Table 8. Pairwise Wilcoxon signed-rank test of nDCG performance among IBCF, UBCF, PersMean, and our proposed approach, FANA-CF. The results in bold are statistically significant with a 90% confidence level. 

	UBCF	PersMean	FANA-IBCF	FANA-UBCF
IBCF	0.062	0.062	0.346	0.062
UBCF	-	1.000	0.062	0.371
PersMean	-	-	0.062	1.000
FANA-IBCF	-	-	-	0.062

shows the pairwise Wilcoxon signed-rank test of nDCG. We can see that our algorithms (FANA-IBCF and FANA-UBCF) are still comparable to other algorithms.

4.4. Summary

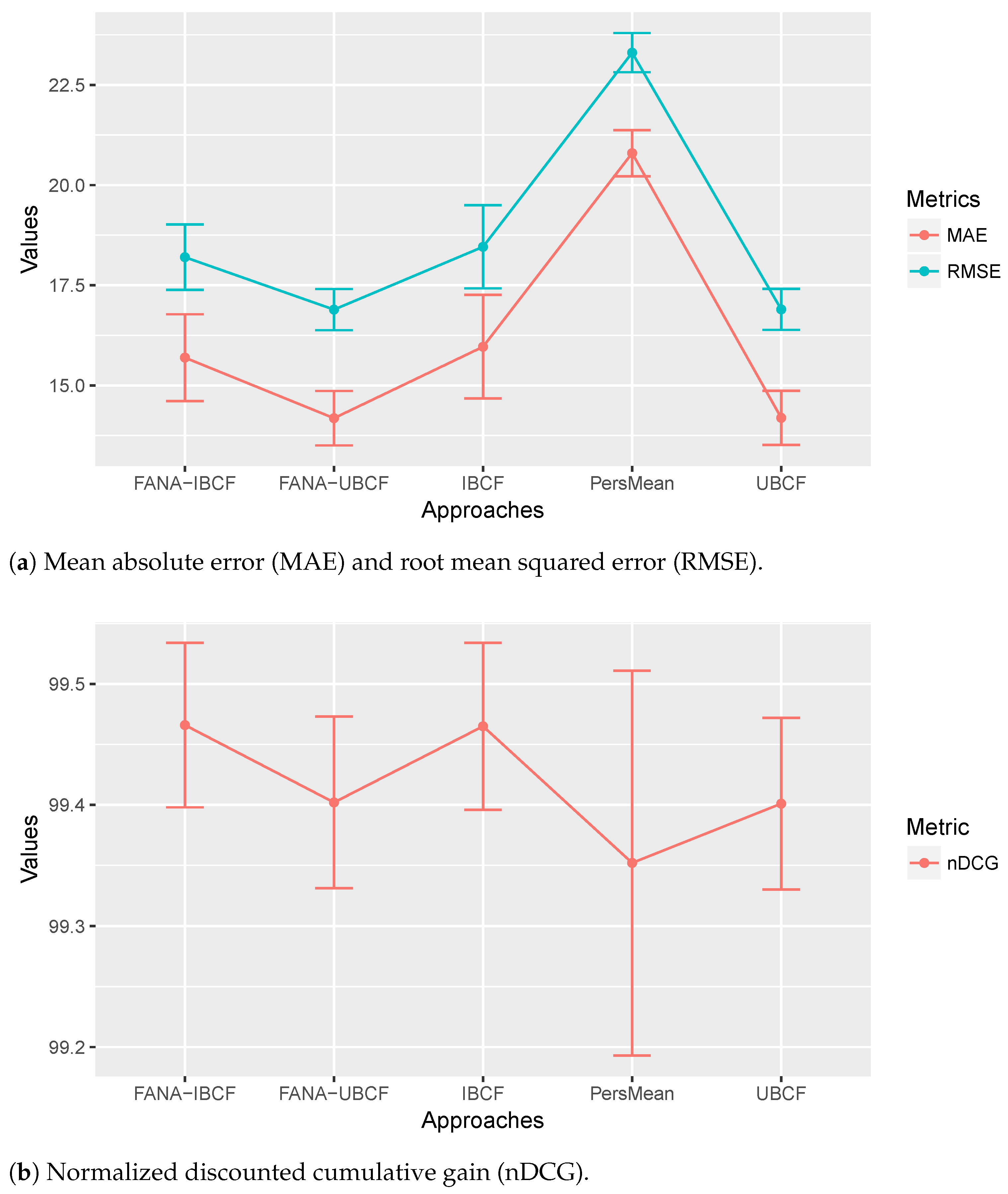
In the evaluations, we compared our proposed approaches, FANA-IBCF and FANA-UBCF, which use two groups of users’ ratings (friends and natives) to generate recommendations, with existing IBCF, UBCF, and PersMean approaches, which use every user’s rating to generate recommendations. As shown in Figure 7, our proposed approach managed to outperform or be on par with IBCF, UBCF, and PersMean approaches in MAE, RMSE, and nDCG performance evaluations. It can be seen that our approaches achieved relatively lower MAE/RMSE and higher nDCG than other approaches. This shows that our proposed approach produces a lower error rate and generates higher quality recommendations.

5. Conclusions and Future Work

Nowadays, recommender systems can be found in various modern applications [25], and the location-based recommender system is one of the applications that has gained popularity amongst modern applications [26]. In this paper, we have proposed a location-based recommender system, the Friend-And-Native-Aware Approach For Collaborative Filtering (FANA-CF) which contains two approaches, FANA-IBCF and FANA-UBCF.

This proposed approach mainly focuses on two groups of users’ ratings in order to generate recommendations to the target user. The two groups of users are the friends (users who are linked to the target user socially) and the natives (users who originate from the location that the target user wishes to go to).

The reason why we have chosen to use friends is because we believe that users that are linked to the target user have the same preferences, whereas the reason why we have chosen natives is because we believe that users originating from the location that the target user wishes to go know the best places to visit.

Although recommender systems have been popular in both industry and academia, there are only a handful of studies that were carried out on a recommender system that focuses on these two groups of users, which we strongly believe to be able to give personalized and high-quality recommendations.

The implementation was carried out in order to test the performance, and the performance evaluations were conducted for the existing approaches and our proposed approach. The result of the performance evaluations showed that our proposed approach that uses two groups of users’ ratings (friends and natives) to generate recommendations has a slightly lower error rate (higher accuracy) in generating recommendations and also manages to generate slightly higher-quality recommendations than the existing IBCF, UBCF, and PersMean approaches that use every user’s rating to generate recommendations.

The future work will be focused on implementing other recommender methods in order to generate even higher quality recommendations, including those with deep learning techniques [27]. Besides that, we also plan to add more attributes, such as time, in order to generate high-quality recommendations. Finally, we want to investigate theoretically and empirically the effect of dataset size on efficiency of collaborative filtering recommender systems [28].