Abstract
Many of the works conducted on algorithm selection strategies—methods that choose a suitable solving method for a particular problem—start from scratch since only a few investigations on reusable components of such methods are found in the literature. Additionally, researchers might unintentionally omit some implementation details when documenting the algorithm selection strategy. This makes it difficult for others to reproduce the behavior obtained by such an approach. To address these problems, we propose to rely on existing techniques from the Machine Learning realm to speed-up the generation of algorithm selection strategies while improving the modularity and reproducibility of the research. The proposed solution model is implemented on a domain-independent Machine Learning module that executes the core mechanism of the algorithm selection task. The algorithm selection strategies produced in this work are implemented and tested rapidly compared against the time it would take to build a similar approach from scratch. We produce four novel algorithm selectors based on Machine Learning for constraint satisfaction problems to verify our approach. Our data suggest that these algorithms outperform the best performing algorithm on a set of test instances. For example, the algorithm selectors Multiclass Neural Network (MNN) and Multiclass Logistic Regression (MLR), powered by a neural network and linear regression, respectively, reduced the search cost (in terms of consistency checks) of the best performing heuristic (KAPPA), on average, by 49% for the instances considered for this work.
1. Introduction
There is no single strategy that can adequately solve all instances from a particular problem domain. This statement is, give or take a few words, the “No Free Lunch Theorem” coined by Wolpert and Macready [1]. Hence, a common practice today is to use strategies that automatically decide which technique to apply for each specific situation. Unfortunately, this selection is not straightforward, since it requires, for instance, mapping the problem’s characterization to one or more suitable solution methods.
The literature commonly refers to the scenario described above as the algorithm-selection problem [2]. Examples of some ideas developed for addressing such a problem include algorithm portfolios [3,4,5,6,7], selection hyper-heuristics [8,9,10,11,12], and Instance-Specific Algorithm Configuration (ISAC) [13,14]. In general, these methods manage a set of algorithms and apply the most suitable to the current problem state for improving the overall performance. Some examples of developments related to algorithm selection include, but are not limited to, ASlib [15], which proposes a format for representing algorithm selection scenarios; HyFlex [16], which provides a framework for constructing hyper-heuristics for different problem domains by hiding the details of particular heuristics; and SATzilla [17], which is a portfolio-based algorithm selection for boolean satisfiability problems. Algorithm selectors can be implemented through different techniques, but it is common to use metaheuristics. Once produced, algorithm selectors tend to be generic since they can control heuristics, solvers, parameters, or any other aspect of the solving process. However, there are many names used to indicate these methods. To unify terms, we refer to them as algorithm selectors or algorithm-selection strategies. Before moving further, it is important to stress the difference between heuristics and metaheuristics in the context of this investigation. Heuristics refer to a set of low-level strategies that guide the search towards promising search areas. Heuristics are usually easy to implement but are problem-dependent. Their inspiration is usually common sense or expertise in the problem domain. Conversely, metaheuristics refer to problem-independent strategies, some of which have existed for more than 30 years, such as Genetic Algorithms [18] and Simulated Annealing [19]. The inspiration for such approaches is usually a natural process, such as the natural evolution or the reorganization of crystalline structures, as is the case in our previous examples. Metaheuristics can be applied to many different domains with few or no adaptations at all.
Algorithm-selection strategies have successfully tackled different hard-to-solve optimization problems [20,21], which include boolean satisfiability [17], bin packing [22], traveling salesman [23,24], and vehicle routing [25]. Particularly, these strategies have been extensively implemented on the Constraint Satisfaction Problem (CSP), which can be found in diverse practical applications in operations research and artificial intelligence [26,27,28]. A crucial component in the algorithm selectors is the one that adequately discriminates between instances to recommend a suitable algorithm to solve them. Thus, having tools for quickly assessing a given selector is paramount. Moreover, several ideas for improving algorithm selectors can be generated with relative ease. Implementing and testing such ideas are usually more complex tasks. The lack of a common framework is, perhaps, one of the main reasons for this situation since each algorithm must be implemented from scratch for each new idea. Adding to this is the accompanying development time required to properly test and debug said implementation. Therefore, having a third-party application, which handles some of the core mechanics that a researcher wishes to try out, may save valuable time resources. Relying on reusable and domain-independent components from the Machine Learning realm allows for rapid prototyping and, so, a researcher can focus on polishing an idea instead of worrying about its implementation.
Machine Learning (ML) has been used in the process of solving a wide range of combinatorial optimization problems, such as the Quadratic Assignment Problem (QAP), Bin Packing Problem (BPP), Vehicle Routing Problem (VRP), and Supply Chain (SC) [29,30,31,32]. With the extraction of essential information from data using ML tools, we can obtain useful descriptions of optimization instances and, more importantly, we can select competent solvers from a particular instance. In this paper, we propose using ML classifiers for solver selection to improve the results obtained by traditional approaches that rely on metaheuristics. With these tools, we can reduce the implementation as well as the running time of such selectors, as we show in the experiments. To test our idea, we chose four well-known classifiers: neural network [33], logistic regression [34], decision forests [35], and decision jungles [36]. However, any other classifiers could be incorporated with ease and based on user preference.
The solution approach described in this document provides two main advantages concerning other existing approaches for developing algorithm selection strategies. First, our solution approach speeds up the development phase of the methods, as it reuses existing ML algorithms available from a third-party provider. The developer does not need to worry about the actual implementation of these algorithms or how to integrate them into the algorithm selection module. One direct benefit of reusing already existing modules is that the developer can try out different Machine Learning algorithms (already implemented and tested) and compare their results before deciding which model to implement for the production phase. The second advantage is that our solution approach encourages reproducibility of the research, as the data (as well as any preprocessing steps), ML algorithms, and output details are available online (since, in our case, the provider is a cloud-based service). Thus, by looking at one single Uniform Resource Locator (URL), anyone can analyze and verify the whole process conducted to achieve a particular algorithm selection strategy, which provides an additional layer of transparency to the research. To the best of the authors’ knowledge, this is the first time the algorithm-selection problem is addressed from this perspective. To verify this proposal, we implement it to solve constraint satisfaction problems, but it can be extended to other problem domains with ease.
The outline of this document is as follows. Section 2 presents the related background, which includes a description of the CSP as well as the features that characterize the instances, the heuristics considered for solving the problem, and some algorithm-selection approaches related to this research. Section 3 provides the insights of the proposed solution approach. In Section 4, we describe the experiments conducted as well as the results obtained with their corresponding analysis. Finally, Section 5 summarizes the conclusion and some future trends derived from this work.
2. Background
Algorithm-selection strategies strive to exploit patterns in a broad spectrum of problem instances to better deal with them. They solve problems indirectly by determining the proper technique for each situation rather than by tackling the problem directly [10,37,38]. The selected algorithm is then applied to solve the instance. In this research as well as in previous studies, an algorithm-selection method defines a mechanism that controls how and when to use specific algorithms throughout the search [37]. Before applying any algorithm-selection approach, the task is to identify the strengths and weaknesses of the available algorithms. Algorithms are chosen based on the current problem state and, ideally, must relate to the best available alternative.
In general, frameworks to generate and deploy algorithm selection strategies should follow a layered architecture. The data flow through these layers in order to generate an algorithm selector and then use it to solve unseen instances. In this architecture, some of the layers may be generic while others may be domain-dependent. The implementations of algorithm selectors available in the literature lack a standardized architecture since each implementation is different from the rest. For this work, we suggest that the algorithm selection process follows a three-layer architecture:
- 1
- The first layer contains the domain-related aspects such as the instances, their characterization, and the available algorithms to choose from.
- 2
- The second layer “learns” which algorithm to apply given the features of the problem at hand.
- 3
- The third layer applies the selected algorithm to solve unseen instances.
In this work, we focus on the second layer, which is the one where the algorithm selection strategies are produced. This layer is domain-independent (if properly implemented). In the past, researchers have relied on different techniques to learn which algorithm to apply given the features of the problem at hand: neural networks [39], genetic algorithms [40], ant-based search [41], principal component and landscape analysis [42,43], among others.
As stated before, most of the research on algorithm selection strategies lack a layered-architecture, making it difficult to change one part of the algorithm selection process without affecting the others. Thus, researchers need to work on many different parts of their model to find whether a change improves the performance of the algorithm selector. Should the performance sit below expectations, more changes must be introduced and tested to improve the algorithm selection strategy. In this work, we propose an alternative where changes to the components of one layer only affect said layer within the algorithm selector. This makes it easier to debug and maintain the algorithm selector.
2.1. Constraint Satisfaction Problems
The definition of CSP comprises a set of variables X, each one taking a value from a specific domain, subject to a set of constraints C. Solving a CSP requires assigning a valid value to each variable while satisfying all the existing constraints. Backtracking-based algorithms start the search with an empty variable assignment and extend it until they either obtain a complete assignment where all constraints are satisfied or prove that such an assignment does not exist [44]. When assigning a variable fails to satisfy one or more constraints, another value is chosen for the variable. When any variable runs out of values, a previously assigned variable must change its value, and the process is repeated from that point onward. Every time a variable is checked to verify that it does not violate a constraint, a consistency check occurs. In general, the fewer the number of consistency checks, the better the search.
The way the former solving strategy explores the search space relies on the assignment ordering of the variables. In this way, poor variable orderings might result in lots of unnecessary operations that would increase the cost of the search. Various heuristics have been proposed to deal with the variable ordering problem in CSPs. However, none of them works well in all instances. Thus, selecting a suitable heuristic based on the features of the instance to be solved may reduce the cost of the search.
The idea of systematically mapping CSP instances to solve algorithms based on the features of such instances dates back to 1995 [45]. In that seminal study, Tsang et al. established a relation between formulation of the CSP and one suitable solving method [45]. After that work, their idea has been implemented through various algorithm-selection approaches. For example, Petrovic and Epstein studied the idea of combining various heuristics to produce ensembles that work well on some sets of CSP instances [46]. Their algorithm-selection model is based on random sets of performance-based weighted criteria, on which different ordering heuristics rely to make their decisions. Other investigations have explored symbolic cognitive architectures to produce small “chunks” of code that serve as components for rules that decide when to apply some variable ordering heuristics for map coloring and job shop scheduling problems represented as CSPs [47]. Autonomous search was applied to rank the ordering heuristics according to their quality to exclude those that exhibit a low performance and to replace them with more promising ones as the search takes place, producing competent variable ordering strategies for CSPs [48,49]. Other works in the field have explored different topologies of neural networks as algorithm selectors for applying heuristics on different sets of CSP instances [39]. More recently, Ortiz-Bayliss et al. described a Genetic Algorithm that discovers rules for applying ordering heuristics to reduce the overall cost of the search [40].
Variable Ordering Heuristics
This study considers three commonly used variable ordering heuristics for CSPs. Although some of them were first described more than two decades ago, they remain useful and competitive nowadays for various benchmark instances [50]. All the heuristics used in this investigation are dynamic: they order the variables as the search takes place and take into consideration the changes made to the instance as the result of previously assigned variables. When a tie is present, the heuristics use the lexical order of the names of the variables to decide which one to assign. The three variable ordering heuristics considered for this work are described as follows:
- Domain (DOM) selects the variable with the smallest number of available values in its domain. The idea consists in taking the most restricted variable from those that have not been instantiated yet and, in doing so, reduces the branching factor of the search [50].
- Kappa (KAPPA) selects the variable in such a way that the resulting subproblem minimizes the value of the parameter of the instance [51]. With this heuristic, the search branches on the variable that is estimated to be the most constrained, yielding the least constrained subproblem—the one with the smallest . For an instance, is calculated aswhere is the fraction of forbidden pairs of values in constraint c and is the domain of variable .
- Weighted Degree (WDEG) captures previous states of the search that have already been exploited [52]. To do so, WDEG attaches a weight to every constraint in the instance. The weights are updated whenever a deadend occurs (no more values are available for the current variable). This heuristic first examines the locally inconsistent, or hard, parts of the instance by prioritizing variables with the largest weighted degrees.
Once the process selects a variable, the Min-conflicts heuristic determines the value assigned to such a variable. Min-conflicts prefer the value involved with the fewest conflicts [53]. This heuristic tries to leave the maximum flexibility for subsequent variable assignments. In case of ties, Min-conflicts will favor the first available value.
2.2. Instance Characterization
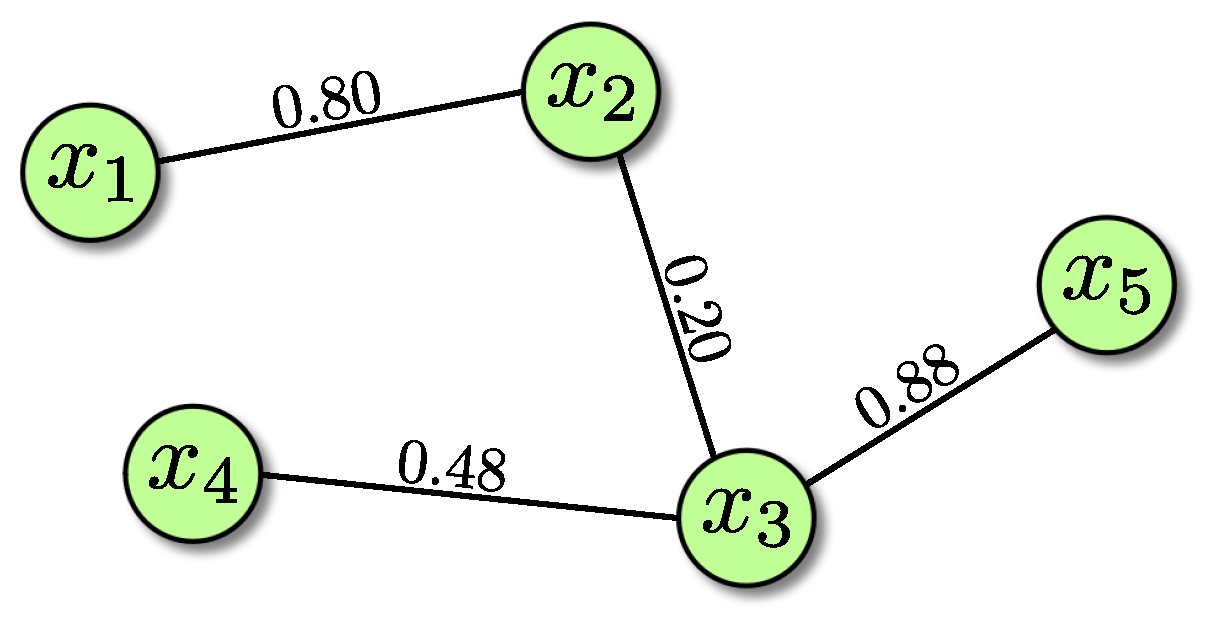
In this investigation, we characterize the instances by using seven simple yet useful binary CSP features. Before describing them, we must introduce three concepts: the constraint density, the constraint tightness, and the clustering coefficient. To help clarify these concepts and features, we use the example CSP instance depicted in Figure 1.
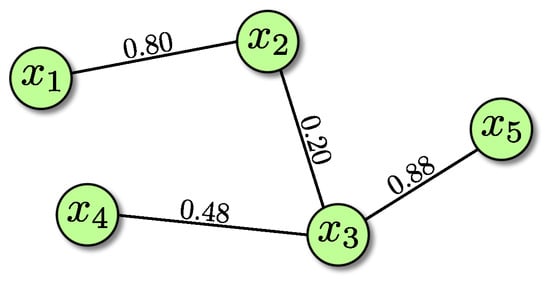
Figure 1.
An example of a Constraint Satisfaction Problem (CSP) instance.
The constraint density of a variable is the number of constraints where it is involved divided by the maximum number of possible constraints for such a variable. In the case of binary constraints, a variable can participate in, at most, constraints (which would mean that such a variable is fully connected to the remaining variables in the instance). In our example, variable participates in three out of four possible constraints. Then, its constraint density is 0.75.
The constraint tightness, on the other hand, applies to constraints, not to variables. The constraint tightness is the fraction of forbidden pairs of values between two variables given a constraint. It estimates how difficult it is to satisfy a constraint. In our example, each variable can take one out of five available values. Then, there are 25 possible combinations of value assignments for each constraint. The constraint between variables and forbids 20 out of those 25 possible assignments. In other words, such a constraint forbids 80% of the possible assignments, which is why tightness of this constraint is 0.8. The lower the tightness of a constraint, the easier it is to satisfy it.
The clustering coefficient is somehow similar to the constraint density, but it takes the analysis a little further. It measures how close the neighbors of one particular variable are to being fully connected. For example, variable is connected to two variables, and . Then, its constraint density is 0.5 (it participates in two out of four possible constraints). By considering a subgraph containing only these three variables ( and its two neighbors and ), we can have, at most, three constraints (assuming a fully connected graph). Since there are two out of three possible constraints in such a subgraph, the clustering coefficient of variable is 0.66.
Now, by using these three concepts, we can define the features used to characterize the instances in this work:
- 1
- Average constraint density is the average of the constraint densities of all the variables within the instance. The constraint density in our example CSP is calculated as
- 2
- Average constraint tightness is the average of the constraint tightnesses of all the constraints within the instance. In our example, the constraint tightness is calculated as
- 3
- Average clustering coefficient is the average of the clustering coefficients of all the variables within the instance. The average clustering coefficient of our example CSP is calculated as
- 4
- Lower quartile of the constraint density is the middle number between the smallest number and the median of the constraint densities of all the variables within the instance. First, we need to sort the constraint densities in our example CSP: 0.25, 0.25, 0.25, 0.5, and 0.75. Based on these values, the median is 0.25 and, in this case, the lower quartile is also 0.25.
- 5
- Upper quartile of the constraint density is the middle number between the median and the largest of the constraint densities of all the variables within the instance. Based on the constraint densities sorted in the previous feature, the upper quartile is 0.50.
- 6
- Lower quartile of the constraint tightness is the middle number between the smallest number and the median of the constraint tightnesses of all the constraints within the instance. After we sort the constraint tightnesses in our example CSP, we obtain 0.20, 0.48, 0.80, and 0.88. Based on these values, the median is 0.64 and the lower quartile is 0.34.
- 7
- Upper quartile of the constraint tightness is the middle number between the median and the largest of the constraint tightnesses of all the constraints within the instance. Based on the constraint tightnesses sorted in the previous feature, the upper quartile is 0.84.
2.3. Benchmark Instances
For this investigation, we considered a total of 400 binary CSP instances—each constraint involves no more than two variables—split into four sets as follows. Sets BQWH15 and BQWH18 contain 200 satisfiable (there is, at least, one solution) balanced quasi-group instances with holes. Set EHI85 contains 100 unsatisfiable (we can confirm that there is no solution at all) 3-SAT instances that have been converted into CSP instances using the dual method as described in [54]. The last set, GEOM, contains 100 kind-of-random instances in which a constraint between two variables can only exist if the distance between the two variables involved is less than . The GEOM generation model assumes that random coordinates are assigned to the variables in order to estimate the distance. GEOM contains both satisfiable and unsatisfiable instances with 50 variables each and a uniform domain size of 20. At this point, we must highlight that there are other instances available at the repository but that these ones were selected because they comprise a variety of representative patterned, quasi-random, and structured CSP instances that are publicly available at http://www.cril.univ-artois.fr/~lecoutre/benchmarks (accessed on 16 March 2021).
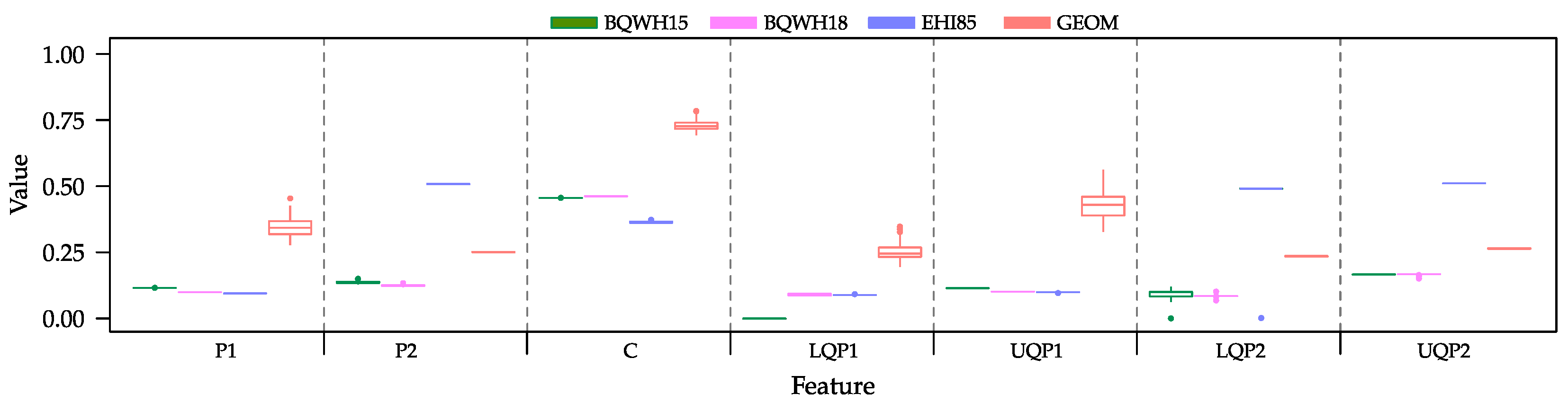
To deepen the characterization of these instances, we provide an overview of the distribution of the features described in Section 2.2 for all 400 CSP instances considered for this work, grouped by set. We can observe from Figure 2 that, in general, these features produce a very narrow range of values inside each set. This suggests that the instances in each set are similar to each other when analyzing each feature in isolation. However, the values for these features vary from set to set, which allows the ML methods to grasp some information to discriminate among instances and to associate them to a suitable solving method.
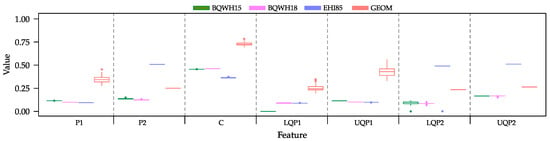
Figure 2.
Distribution of the values of the seven features that characterize the CSP instances, grouped by set.
2.4. Machine Learning Techniques
Throughout this research, we produced four Machine-Learning-based algorithm selection strategies. These algorithm selectors are based on four different classifiers available in Microsoft Azure ML. In all cases, we used the default configuration of each of these techniques as provided by the platform. The four Machine Learning techniques used are briefly described below. For specific details on the implementation of such methods, the reader is welcome to consult Microsoft Azure ML technical documentation (https://docs.microsoft.com/en-us/azure/machine-learning/ accessed on 16 March 2021).
- Multiclass Logistic Regression (MLR) is a well-known method used to predict the probability of an outcome and is particularly famous for classification tasks. The algorithm predicts the probability of occurrence of an event by fitting data to a logistic function.
- Multiclass Neural Network (MNN) is a set of interconnected layers in which the inputs lead to outputs using a series of weighted edges and nodes. A training process takes place to adjust the weights of the edges based on the input data and the expected outputs. The information within the graph flows from inputs to outputs, passing through one or more hidden layers. All the nodes in the graph are connected by the weighted edges to nodes in the next layer.
- Multiclass Decision Forest (MDF) is an ensemble learning method for classification. The algorithm works by building multiple decision trees and then by voting on the most popular output class. Voting is a form of aggregation, in which each tree outputs a non-normalized frequency histogram of labels. The aggregation process sums these histograms and normalizes the result to get the “probabilities” for each label. The trees that have high prediction confidence have a greater weight in the final decision of the ensemble.
- Multiclass Decision Jungle (MDJ) is an extension of decision forests. A decision jungle consists of an ensemble of decision Directed Acyclic Graphs (DAGs). By allowing tree branches to merge, a decision DAG typically has a better generalization performance than a single decision tree, albeit at the cost of a somewhat higher training time. DAGs have the advantage of performing integrated feature selection and classification and are resilient in the presence of noisy features.
It is essential to highlight that, although we used Microsoft Azure ML for this work, the rationale is to separate the Machine Learning algorithms from the rest of the components of the algorithm-selection process. Then, any other application such as IBM Watson Machine Learning Service, Google Cloud Machine Learning, or Weka could be used for this purpose. In our particular case, it was a personal preference, given our previous experience with the platform.
3. Solution Model
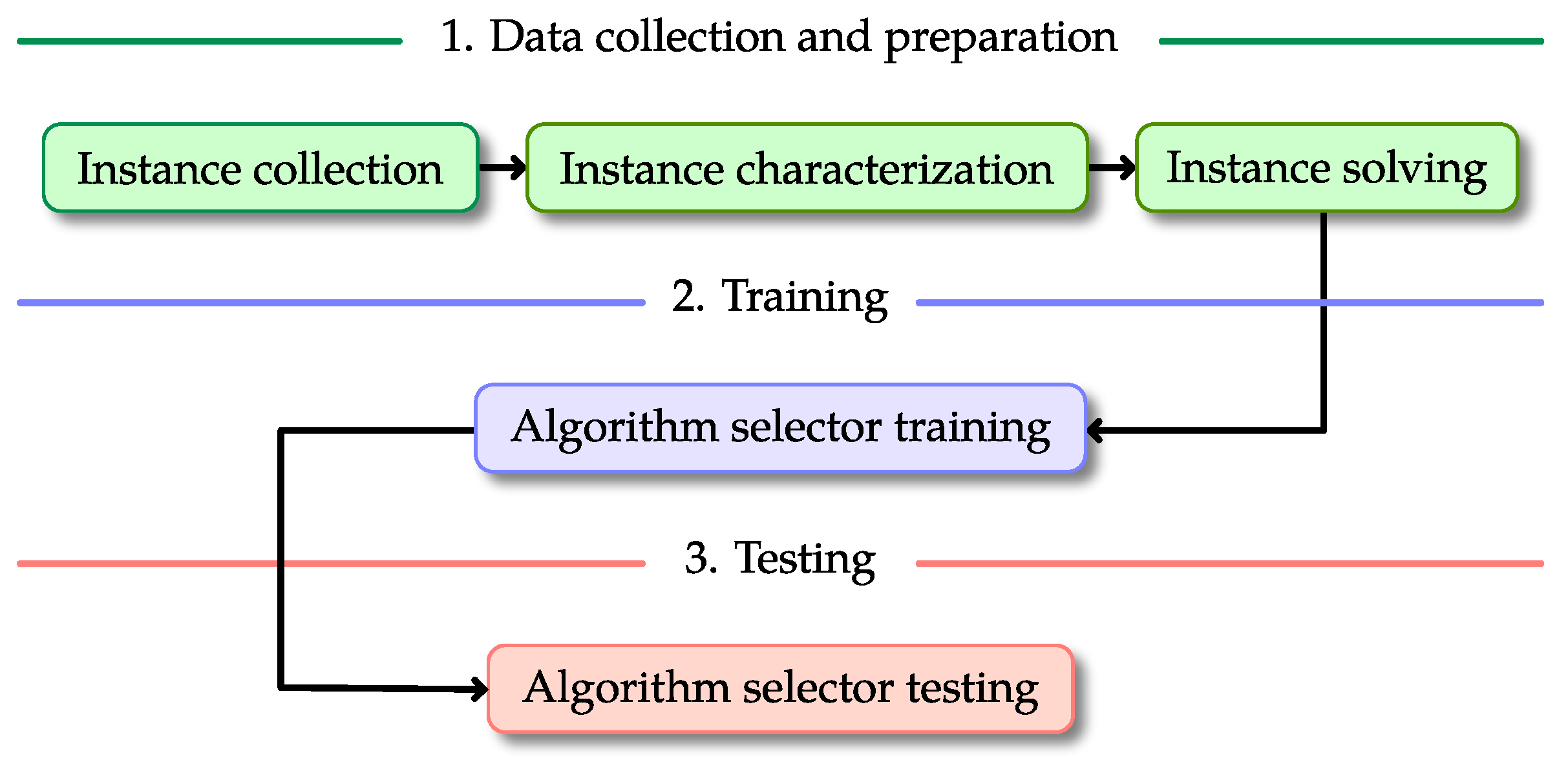
The solution model proposed in this document follows the three-layer architecture described in Figure 3. This solution model is similar to others described in the literature related to algorithm-selection strategies. However, the main difference relies on how the algorithm selection module is implemented, which provides a higher level of independence and flexibility. In our solution approach, the layer where the algorithm selector is produced is clearly apart from the remaining domain-dependent layers. Since this layer is domain-independent, we have great flexibility for using any tool we decide to produce the algorithm selectors. In this particular case, we used some Machine Learning algorithms provided by Microsoft Azure ML. This simple yet important change in the solution model allows us to speed up the process of generating and testing different algorithm selection approaches with no changes to the rest of the modules in the system.
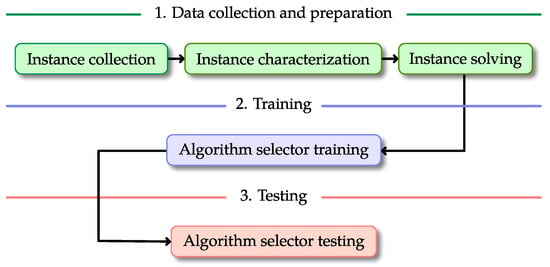
Figure 3.
A graphical description of the proposed solution model.
Moreover, each layer of the proposed model in Figure 3 contains specific steps that were implemented as follows.
- 1
- Data collection and preparation. The first step of the process involves gathering and solving the CSP instances in such a way that we can construct the tables for training and testing. These tables must contain the characterization of each instance as well as the cost of using the heuristics on such instances. Additionally, in our case, a column with a label for the best choice of heuristic is required since we considered supervised Machine Learning methods. However, this column may not be necessary if the methods are unsupervised. The data collection and preparation step is divided into three tasks that are applied sequentially.
- (a)
- Instance collection. The first step of the solution model consists of gathering a set of instances where the methods are trained and tested. It is advisable that these instances contain categories or classes, such that some patterns can be extracted from the instances. For this research, we collected 400 CSP instances, classified into four categories (see Section 2.3 for more details).
- (b)
- Instance characterization. Once the instances have been collected, the model requires characterizing those instances based on the values of some specific features. This characterization allows the algorithm selector to identify patterns that minimize the cost of solving unseen instances. In this work, we considered seven features for characterizing CSPs (see Section 2.2 for more details).
- (c)
- Instance solving. Once the instances have been characterized, the next step consists of solving those instances with each available heuristic (see Section 2.1 for more details). The process requires preserving the result of each heuristic and labelling the best performing one for each individual instance. This information will be used later on to produce the algorithm selector. We estimate heuristic performance by counting the number of consistency checks required to solve each instance.
- 2
- Algorithm selector training. This step generates the mapping from a problem state (defined by the values of the features of the instance) to one suitable algorithm. Once the instances have been solved, the next step is to split the instances (with their corresponding results) into training and test sets. To produce the algorithm selectors described in this work, we first shuffled the instances in each one of the sets described in Section 2.3. Then, we took the first 60% of the instances in each set and merged them into a single training set (the same training set was used for the four algorithm selectors). To avoid biasing the results, we kept the remaining 40% of the instances exclusively for testing purposes. By using the information from the instances and their best performers, we trained four algorithm selectors by using the Machine Learning techniques described in Section 2.4. The result of this process was four mechanisms for discriminating among heuristics for CSPs, based on their problem features. Since we claim that our approach favors the transparency of the research and its reproducibility, we invite the reader to consult the complete process for creating these algorithm selectors. This information is publicly available at https://bit.ly/3hvzwlY (accessed on 16 March 2021).
- 3
- Algorithm selector testing. We used the data from the test set to evaluate the performance of the algorithm selectors (see Section 4 for more details).
4. Experiments and Results
As described in Section 3, we produced four algorithm selectors based on four Machine Learning methods: Multiclass Logistic Regression (MLR), Multiclass Neural Networks (MNN), Multiclass Decision Forest (MDF), and Multiclass Decision Jungle (MDJ). We compared the performance of the Machine-Learning-based algorithm selectors against the one of the variable ordering heuristics applied in isolation as well as two metaheuristic-based algorithm selectors taken from the literature. Later, we tested the performance of the algorithm selectors against the performance of the best possible result from the heuristics: the Oracle—an unrealistic method that would achieve 100% accuracy on the test set.
4.1. Challenging the Heuristics
We compared the performance of the four Machine-Learning-based algorithm selectors against the performance of the individual heuristics and two algorithm selectors from the literature, and we obtained exciting data. The algorithm selectors taken from the literature rely on a Genetic Algorithm (GA) [40] and Simulated Annealing (SA) [11] to produce algorithm selectors for Combinatorial Optimization Problems, including CSPs. In both cases, we used the configurations suggested by their authors:
- GA uses a steady-state genetic algorithm to produce algorithm selectors [40]. The evolutionary process starts with 25 randomly initialized individuals and runs for 150 cycles. The crossover and mutation rates are 1.0 and 0.1, respectively. The crossover and mutation operators are tailored for the task. For selecting the individuals for mating, a tournament selection of size two was used.
- SA relies on simulated annealing to generate an algorithm selector [11]. This selector was originally proposed for solving job-shop scheduling problems, but we adapted it for CSPs. The initial temperature is set to 100 with a cooling schedule defined byThe maximum number of iterations of the process is set to 200. The solution representation as well as the mutation operators were taken from [40].
It is important to stress that, contrary to what happens with our Machine-Learning-based algorithm selectors, both GA and SA may select a different heuristic at different steps of the search process, even for the same instance. This behavior is defined within the solution model, and then, we decided not to change it for this work.
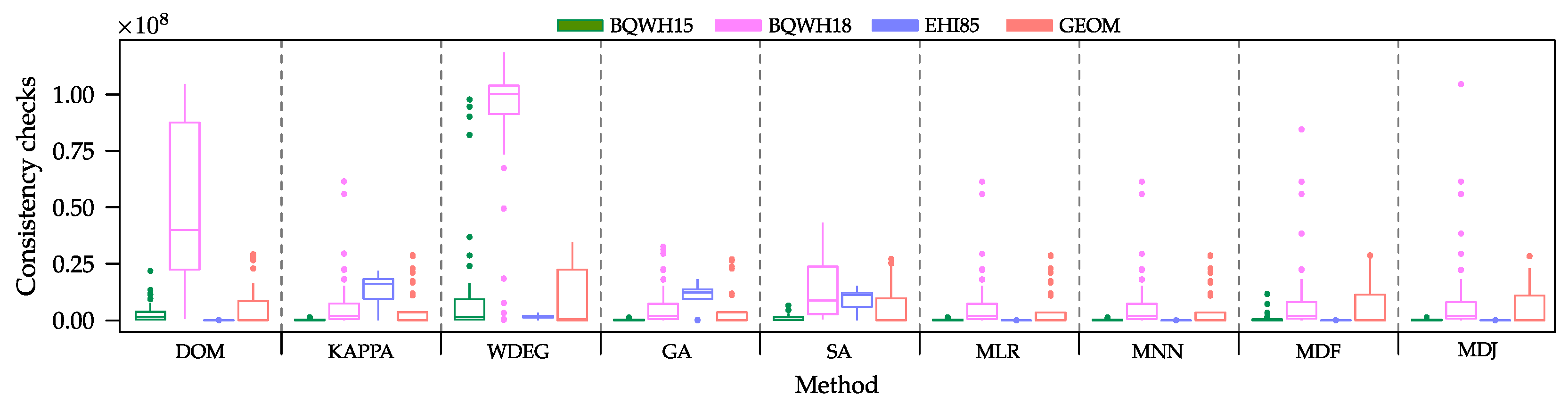
We summarized the data obtained in Table 1. As expected, no heuristic performs best over all instances. DOM performs best on set EHI85, while KAPPA performs best on sets BQWH15, BQWH18, and GEOM. Interestingly, WDEG performed poorly (on average) on the four test subsets, being unable to outperform DOM and KAPPA. A careful revision of the results shows that, for some instances, WDEG can be the right choice. However, none of the Machine-Learning-based algorithm selectors were able to perceive this fact and to use it to their advantage. The graphical analysis of the results through boxplots (Figure 4) shows a huge dispersion of the results obtained by some methods. The larger the dispersion of the consistency checks per set of instances, the less certainty we have on the performance of the method. Based on these results, we can observe some methods that exhibit similar behaviors for some sets—for example, KAPPA, GA, MLR, and MNN in GEOM. The similar performance of different methods is not new, but it confirms the benefit of our approach in our context. In the four cases, the distribution of the results obtained by MLR and MNN is similar to that of the best performing heuristic in each set. Then, two of the ML-based algorithm selectors can replicate the behavior of the best heuristic for each particular set.

Table 1.
Average number of consistency checks for all heuristics and algorithm selectors, operating on the four test subsets of the benchmark instances (the best results are highlighted in bold).
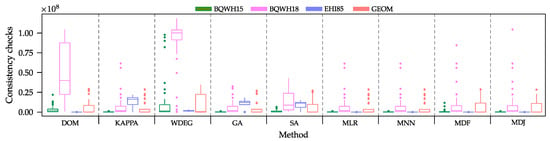
Figure 4.
Boxplots of the consistency checks required by each method on the test set.
It is interesting to note that all the Machine-Learning-based algorithm selectors properly learned to differentiate between heuristics. The ability to differentiate seems to increase when the ratio between weak and best-performing approaches is very high (for example, for the instances in set EHI85). Although MLR and MNN obtained the best results for most of the subsets, there is no significant difference in terms of the performance between the Machine-Learning-based algorithm selectors studied in this work (when considering all the instances in the test set). Even in the worst case, the four Machine-Learning-based algorithm selectors improved the individual results of the heuristics when considering the whole instances in the test set.
By using the Machine-Learning-based algorithm selectors, we achieved critical savings in terms of consistency checks. These savings are the result of selecting the best performing heuristic for each set, as MLR and MNN do. This drastically reduces the overall number of consistency checks with respect to the heuristics applied in isolation. When all instances in the test set are considered, the four Machine-Learning-based algorithm selectors overcome the heuristics as well as the two metaheuristic-based algorithm selectors taken from the literature. Among all the methods, the performances of MLR and MNN are outstanding. These methods solved the test set by using approximately half of the consistency checks required by KAPPA, the best overall performing heuristic.
4.2. Challenging the Oracle
In a more challenging analysis, we compared the Machine-Learning-based algorithm selectors against the Oracle (a method that always chooses the best among the three heuristics for each instance). The average number of consistency checks per instance required by the Oracle is 2,996,917.37, which is still lower than any of the studied methods. In fact, both MRL and MNN require around 9% additional consistency checks compared to the Oracle to solve the whole test set. This means that, although the Machine-Learning-based algorithm selectors are capable solvers, there is still room for improvement. Since the Oracle is a method that would achieve a 100% accuracy on the test set, it seems reasonable to analyze the accuracy of the Machine-Learning-based algorithm selectors as a way to estimate how close such methods are to the best possible decision. Table 2 shows the accuracy of all the methods under analysis on the test set. Although heuristics always apply the same criteria and no selection process is involved, the accuracy reflects the fraction of instances where each heuristic is the best choice. Additionally, it is important to remark that we do not present the accuracy of GA and SA since their application model does not allow us to calculate it properly. GA and SA are allowed to dynamically change the heuristic as the search takes place. Then, such methods do not rely on the accuracy but on their capacity to modify the search so it reduces its cost.

Table 2.
Accuracy of the different methods.
As expected, the good performance of the Machine-Learning-based algorithm selectors, in terms of consistency checks, is supported by a large accuracy of their corresponding classifiers. It is interesting to observe that, a small difference in the accuracy can translate into a huge change in the number of consistency checks required to solve the set. For example, The difference in the accuracies of MNN and MDJ is only 1.875%. However, this represents around 25% additional consistency checks when solving the test set. This finding suggests that, a few poor decisions can tremendously impact the overall performance of the algorithm selectors.
Additional to the accuracy of the methods, in Table 2, we included the p-value of a paired two-sided t-test that compares each method against the Oracle, based on the number of consistency checks per instance. By using 5% significance, the statistical evidence does not allow us to state that any of the generated Machine-Learning-based algorithm selectors is different in performance to the Oracle. However, the statistical evidence suggests that DOM, KAPPA, WDEG, GA, and SA are not equal to the Oracle in performance. Thus, we can conclude that all the Machine-Learning-based algorithm selectors produced as part of this work are statistically equivalent to the Oracle for the instances in the test set. Additionally, we found that there is an improvement concerning individual use of the heuristics and two metaheuristic-based algorithm selectors.
4.3. A Glance at the Classifiers
So far, we analyzed the performance of the Machine-Learning-based algorithm selectors by considering only the number of consistency checks required to solve the instances in the test set. However, we did not dive into the classifiers within them. For this reason, in this section, we analyze the confusion matrices of those classifiers.
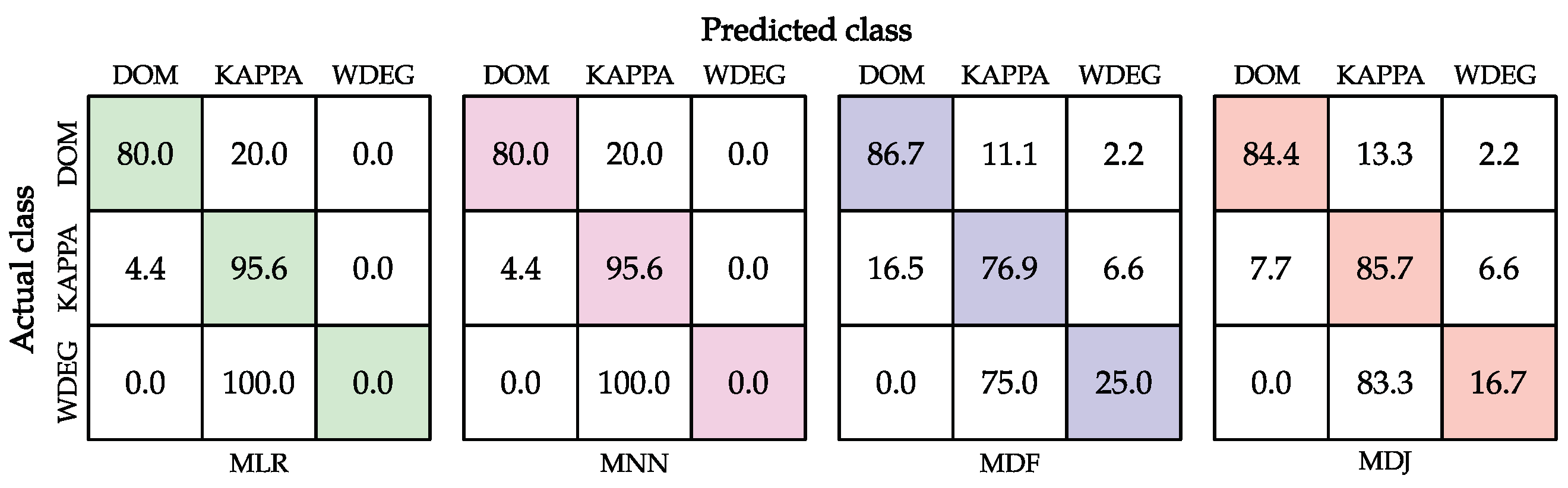
The confusion matrices (Figure 5) show that both MLR and MNN never recommend using WDEG. Instead, they classify all those cases as KAPPA. Although MLR and MNN ignore one of the classes, it seems to be a good strategy since the algorithm selectors based on such techniques obtained the best results on the test set. Conversely, MLR and MNN accurately recommend DOM and KAPPA for most instances, which means that the classifiers properly learned to discriminate among those heuristics given the features that describe the instances.
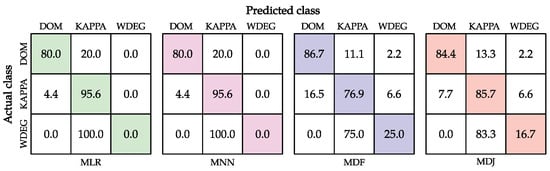
Figure 5.
Confusion matrices for the classifiers within the Machine-Learning-based algorithm selectors on the test set.
MDF and MDJ make some important mistakes when trying to classify KAPPA, since in 6.6% of the cases, they classify those cases as WDEG. These mistakes affect the overall performance, which is observable in Table 1.
4.4. Discussion
At this point, we briefly discuss the training time of the algorithm selectors. Based on our experience, it is usually difficult to justify the extra effort of training an algorithm selector when the results are not considered to “be worth the effort”. In this work, the data suggest that we can cut off the cost of solving the testing set to around a half with respect to the best-performing heuristic on the whole set (which we cannot know in advance). As discussed before, the layered architecture in our model allowed us to execute different parts of the experimental process on different platforms:
- Data collection and preparation. We solved the instances on a Linux Mint 19 PC with 12 GB of RAM, giving the solvers a time-out of 60 s as stopping criterion for each instance. When the time-out was reached, the search stopped and the current consistency checks were reported. The time needed to solve the instances in both the training and testing sets using the three heuristics was 242 min. This information was later used to train the classifiers. We also used this platform to produce the algorithm selectors used for comparison purposes. GA and SA required 485 and 1270 min, respectively, to generate their corresponding algorithm selectors.
- Training and Testing. Training and testing of the classifiers were executed directly on the Microsoft Azure ML platform (free account). With the data gathered from the previous layer, training and testing the four Machine-Learning-based algorithm selectors took less than four minutes. When we compare this time against those of the metaheuristic-based algorithm selectors, we observe a significant difference in the time required to produce such algorithm selectors, and their overall performance was below the ones of the Machine-Learning-based algorithm selectors.
As a final remark, we identified at least two issues representing critiques of our tests. The first issue is the lack of real-world instances. This situation was derived from the fact that only a few binary CSP instances defined in extension are provided for real-world instances in the public repository where the instances were taken. The features used to characterize the instances in this work are limited to binary constraints. Although we can convert any n-ary CSP (where n > 2) to an equivalent binary CSP [55], the conversion is usually avoided, as we have also done in this case. Moreover, the fact that the instances are defined in extension is related to the solver’s technical limitations in this work. The second issue is related to the solvers considered for this work. Many other heuristics or solvers could have been considered, such as impact or activity-based strategies [56,57]. Although including real-world instances and other heuristics would certainly strengthen the results reported in this investigation, at this point, the goal was to present a clear and straightforward approach of how to combine different solvers by using ML and the three-layer architecture proposed. Our results have confirmed not only that the proposed approach works as expected—allowing the execution of different components of the algorithm selection process on its own layer and platform—but also that the approach is faster and obtains better results than the two other metaheuristic-based approaches taken from the literature (GA and SA).
5. Conclusions and Future Work
This paper introduced a procedure to facilitate the task of devising algorithm selection strategies. One of the most remarkable features of this procedure is its reduced training time, which is a bottleneck of these methods. Additionally, the effort needed to collect all the training examples remains the same for both traditional algorithm selection methods and those produced with our approach. The difference lies in the way such instances are used to produce an algorithm selector. We noticed that Machine Learning techniques are a suitable option for this purpose. As a general conclusion, in this work, the proposed approach reduced the time needed to produce algorithm selectors and outperformed other metaheuristic-based approaches taken from the literature (GA and SA).
Our proposed model helps in lightening the load of building a critical element of algorithm selection methods for CSPs: the learning component that maps instances to heuristics. Addditionally, our implementation of the model increases the credibility of the research, since all elements related to the inner selection algorithm are publicly available.
At this point, we consider the importance of highlighting the flexibility of the proposed approach. In this work, we used a few ML methods to implement algorithm selectors for CSP. However, using the layered-architecture proposed, we could easily change the problem domain and maintain the same ML methods. Such a change would allow us to address a different problem domain easily. Conversely, we could modify the layer related to the algorithm selection process, where the ML methods are, and then provide different capabilities to the algorithm selectors. The idea of splitting the logic of the algorithm selection process by layers represents an improvement regarding generality of the algorithm selection process.
We identified two exciting paths for future work. The first one is how the Machine-Learning-based algorithm selectors may deal with making decisions as the search progresses. All the algorithm selectors generated in this work make a decision about which heuristic to use only when the search starts and keeps that decision until the instance is solved, it is proven unsatisfiable, or the process stops due to a time-out. Other methods from the literature are allowed to choose a different heuristic while solving an instance—and not only at the beginning of the search. Some examples include algorithm selectors based on genetic algorithms and simulated annealing. Even so, these methods were, in overall terms, outperformed by those we developed in this work. Nonetheless, the algorithm selector obtained through genetic algorithms showed an outstanding performance for set BQWH18, where it even surpassed the Oracle. Hence, it would be interesting to study options for Machine-Learning-based algorithms selectors to explode this capability while maintaining the already observed benefits. Some ideas for achieving this goal might involve hybrid methods that lie on the intersection of Machine Learning and metaheuristics [58,59]. Another critical path for research might focus on extending the proposed model to cover algorithm generation. In this work, we explored Machine Learning techniques that produce algorithm selectors. However, the community shows a growing interest in methods that automatically generate new solving strategies, such as heuristics [10,38]. In this regard, we find that extending our model to also consider algorithm generation is an exciting idea to explore as part of future work.
Author Contributions
Conceptualization, J.C.O.-B.; methodology, J.C.O.-B., A.E.G.-R. and I.A.; software, J.C.O.-B.; validation, I.A. and J.M.C.-D.; formal analysis, J.C.O.-B., A.E.G.-R., I.A. and J.M.C.-D.; investigation, S.E.C.-P.; resources, J.C.O.-B.; data curation, J.C.O.-B.; writing—original draft preparation, J.C.O.-B., I.A., A.E.G.-R.; writing—review and editing, J.M.C.-D., H.T.-M. and S.E.C.-P.; visualization, J.M.C.-D.; supervision, H.T.-M.; project administration, J.C.O.-B. and I.A.; funding acquisition, I.A. and H.T.-M. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by the CONACyT Basic Science Project under grant 287479.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
All the instances used for this work are available at http://www.cril.univ-artois.fr/~lecoutre/benchmarks accessed on 16 March 2021. A full description of the experiments conducted can be consulted via Microsoft Azure ML, at https://bit.ly/3hvzwlY accessed on 16 March 2021.
Acknowledgments
This research was partially supported by the CONACyT Basic Science Project under grant 287479 and the ITESM Research Group with Strategic Focus on Intelligent Systems.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Rice, J.R. The Algorithm Selection Problem. Adv. Comput. 1976, 15, 65–118. [Google Scholar]
- Epstein, S.L.; Freuder, E.C.; Wallace, R.; Morozov, A.; Samuels, B. The Adaptive Constraint Engine. In Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming (CP ’02), Ithaca, NY, USA, 9–13 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 525–542. [Google Scholar]
- Lindauer, M.; Hoos, H.H.; Hutter, F.; Schaub, T. AutoFolio: An Automatically Configured Algorithm Selector. J. Artif. Int. Res. 2015, 53, 745–778. [Google Scholar] [CrossRef]
- Loreggia, A.; Malitsky, Y.; Samulowitz, H.; Saraswat, V. Deep Learning for Algorithm Portfolios. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (AAAI’16), Phoenix, AZ, USA, 12–17 February 2016; AAAI Press: Palo Alto, CA, USA, 2016; pp. 1280–1286. [Google Scholar]
- Malitsky, Y.; Sabharwal, A.; Samulowitz, H.; Sellmann, M. Non-Model-Based Algorithm Portfolios for SAT. In Theory and Applications of Satisfiability Testing—SAT 2011; Sakallah, K.A., Simon, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 369–370. [Google Scholar] [CrossRef]
- O’Mahony, E.; Hebrard, E.; Holland, A.; Nugent, C.; O’Sullivan, B. Using Case-based Reasoning in an Algorithm Portfolio for Constraint Solving. In Proceedings of the 19th Irish Conference on Artificial Intelligence and Cognitive Science, Dublin, Ireland, 7–8 December 2008; pp. 1–10. [Google Scholar]
- Amaya, I.; Ortiz-Bayliss, J.C.; Rosales-Pérez, A.; Gutiérrez-Rodríguez, A.E.; Conant-Pablos, S.E.; Terashima-Marín, H.; Coello, C.A.C. Enhancing Selection Hyper-Heuristics via Feature Transformations. IEEE Comput. Intell. Mag. 2018, 13, 30–41. [Google Scholar] [CrossRef]
- Branke, J.; Hildebrandt, T.; Scholz-Reiter, B. Hyper-heuristic Evolution of Dispatching Rules: A Comparison of Rule Representations. Evol. Comput. 2015, 23, 249–277. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.H.; Kheiri, A.; Özcan, E.; Burke, E.K. Recent Advances in Selection Hyper-heuristics. Eur. J. Oper. Res. 2020, 285, 405–428. [Google Scholar] [CrossRef]
- Garza-Santisteban, F.; Sanchez-Pamanes, R.; Puente-Rodriguez, L.A.; Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.; Terashima-Marin, H. A Simulated Annealing Hyper-heuristic for Job Shop Scheduling Problems. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 57–64. [Google Scholar] [CrossRef]
- van der Stockt, S.A.; Engelbrecht, A.P. Analysis of selection hyper-heuristics for population-based meta-heuristics in real-valued dynamic optimization. Swarm Evol. Comput. 2018, 43, 127–146. [Google Scholar] [CrossRef]
- Malitsky, Y.; Sabharwal, A.; Samulowitz, H.; Sellmann, M. Algorithm Portfolios Based on Cost-sensitive Hierarchical Clustering. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence (IJCAI’13), Beijing, China, 3–9 August 2013; AAAI Press: Palo Alto, CA, USA, 2013; pp. 608–614. [Google Scholar]
- Malitsky, Y. Evolving Instance-Specific Algorithm Configuration. In Instance-Specific Algorithm Configuration; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 93–105. [Google Scholar] [CrossRef]
- Bischl, B.; Kerschke, P.; Kotthoff, L.; Lindauer, M.; Malitsky, Y.; Fréchette, A.; Hoos, H.; Hutter, F.; Leyton-Brown, K.; Tierney, K.; et al. ASlib: A benchmark library for algorithm selection. Artif. Intell. 2016, 237, 41–58. [Google Scholar] [CrossRef]
- Ochoa, G.; Hyde, M.; Curtois, T.; Vazquez-Rodriguez, J.A.; Walker, J.; Gendreau, M.; Kendall, G.; McCollum, B.; Parkes, A.J.; Petrovic, S.; et al. HyFlex: A Benchmark Framework for Cross-Domain Heuristic Search. In Evolutionary Computation in Combinatorial Optimization; Hao, J.K., Middendorf, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 136–147. [Google Scholar]
- Xu, L.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. SATzilla: Portfolio-based algorithm selection for SAT. J. Artif. Intell. Res. 2008, 32, 565–606. [Google Scholar] [CrossRef]
- Goldberg, D.; Holland, J. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Kotthoff, L. Algorithm Selection for Combinatorial Search Problems: A Survey. In Data Mining and Constraint Programming: Foundations of a Cross-Disciplinary Approach; Bessiere, C., De Raedt, L., Kotthoff, L., Nijssen, S., O’Sullivan, B., Pedreschi, D., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 149–190. [Google Scholar] [CrossRef]
- Lindauer, M.; van Rijn, J.N.; Kotthoff, L. The algorithm selection competitions 2015 and 2017. Artif. Intell. 2019, 272, 86–100. [Google Scholar] [CrossRef]
- Amaya, I.; Ortiz-Bayliss, J.C.; Conant-Pablos, S.; Terashima-Marin, H. Hyper-heuristics Reversed: Learning to Combine Solvers by Evolving Instances. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 1790–1797. [Google Scholar] [CrossRef]
- Aziz, Z.A. Ant Colony Hyper-heuristics for Travelling Salesman Problem. Procedia Comput. Sci. 2015, 76, 534–538. [Google Scholar] [CrossRef]
- Kendall, G.; Li, J. Competitive travelling salesmen problem: A hyper-heuristic approach. J. Oper. Res. Soc. 2013, 64, 208–216. [Google Scholar] [CrossRef]
- Sabar, N.R.; Zhang, X.J.; Song, A. A math-hyper-heuristic approach for large-scale vehicle routing problems with time windows. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 830–837. [Google Scholar] [CrossRef]
- Amaya, I.; Ortiz-Bayliss, J.C.; Gutierrez-Rodriguez, A.E.; Terashima-Marin, H.; Coello, C.A.C. Improving hyper-heuristic performance through feature transformation. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 2614–2621. [Google Scholar] [CrossRef]
- Berlier, J.; McCollum, J. A constraint satisfaction algorithm for microcontroller selection and pin assignment. In Proceedings of the IEEE SoutheastCon 2010 (SoutheastCon), Concord, NC, USA, 18–21 March 2010; pp. 348–351. [Google Scholar]
- Bochkarev, S.V.; Ovsyannikov, M.V.; Petrochenkov, A.B.; Bukhanov, S.A. Structural synthesis of complex electrotechnical equipment on the basis of the constraint satisfaction method. Russ. Electr. Eng. 2015, 86, 362–366. [Google Scholar] [CrossRef]
- Smith-Miles, K.A. Cross-disciplinary perspectives on meta-learning for algorithm selection. ACM Comput. Surv. CSUR 2009, 41, 6. [Google Scholar] [CrossRef]
- Smith-Miles, K.; Lopes, L. Measuring instance difficulty for combinatorial optimization problems. Comput. Oper. Res. 2012, 39, 875–889. [Google Scholar] [CrossRef]
- Gutierrez-Rodríguez, A.E.; Conant-Pablos, S.E.; Ortiz-Bayliss, J.C.; Terashima-Marín, H. Selecting meta-heuristics for solving vehicle routing problems with time windows via meta-learning. Expert Syst. Appl. 2019, 118, 470–481. [Google Scholar] [CrossRef]
- Makkar, S.; Devi, G.N.R.; Solanki, V.K. Applications of Machine Learning Techniques in Supply Chain Optimization. In Proceedings of the International Conference on Intelligent Computing and Communication Technologies, Hyderabad, India, 9–11 January 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 861–869. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Wright, R.E. Logistic regression. In Reading & Understanding Multivariate Statistics; American Psychological Association: Washington, DC, USA, 1995; pp. 217–244. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis And Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Shotton, J.; Sharp, T.; Kohli, P.; Nowozin, S.; Winn, J.; Criminisi, A. Decision jungles: Compact and rich models for classification. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 234–242. [Google Scholar]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Pillay, N.; Qu, R. Hyper-Heuristics: Theory and Applications; Natural Computing Series; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Ortiz-Bayliss, J.C.; Terashima-Marín, H.; Conant-Pablos, S.E. Learning vector quantization for variable ordering in constraint satisfaction problems. Pattern Recogn. Lett. 2013, 34, 423–432. [Google Scholar] [CrossRef]
- Ortiz-Bayliss, J.C.; Terashima-Marín, H.; Conant-Pablos, S.E. Combine and conquer: An evolutionary hyper-heuristic approach for solving constraint satisfaction problems. Artif. Intell. Rev. 2016, 46, 327–349. [Google Scholar] [CrossRef]
- Kiraz, B.; Etaner-Uyar, A.Ş.; Özcan, E. An Ant-Based Selection Hyper-heuristic for Dynamic Environments. In Proceedings of the Applications of Evolutionary Computation: 16th European Conference, EvoApplications 2013, Vienna, Austria, 3–5 April 2013; Esparcia-Alcázar, A.I., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 626–635. [Google Scholar] [CrossRef]
- Bischl, B.; Mersmann, O.; Trautmann, H.; Preuß, M. Algorithm Selection Based on Exploratory Landscape Analysis and Cost-sensitive Learning. In Proceedings of the 14th Annual Conference on Genetic and Evolutionary Computation, GECCO ’12, Philadelphia, PA, USA, 7–11 July 2012; ACM: New York, NY, USA, 2012; pp. 313–320. [Google Scholar] [CrossRef]
- López-Camacho, E.; Terashima-Marín, H.; Ochoa, G.; Conant-Pablos, S.E. Understanding the structure of bin packing problems through principal component analysis. Int. J. Prod. Econ. 2013, 145, 488–499. [Google Scholar] [CrossRef]
- Jussien, N.; Lhomme, O. Local Search with Constraint Propagation and Conflict-Based Heuristics. Artif. Intell. 2012, 139, 21–45. [Google Scholar] [CrossRef]
- Tsang, E.P.K.; Borrett, J.E.; Kwan, A.C.M.; Sq, C.C. An Attempt to Map the Performance of a Range of Algorithm and Heuristic Combinations. In Proceedings of Adaptation in Artificial and Biological Systems (AISB’95); IOS Press: Amsterdam, The Netherlands, 1995; pp. 203–216. [Google Scholar]
- Petrovic, S.; Epstein, S.L. Random Subsets Support Learning a Mixture of Heuristics. Int. J. Artif. Intell. Tools 2008, 17, 501–520. [Google Scholar] [CrossRef]
- Bittle, S.A.; Fox, M.S. Learning and using hyper-heuristics for variable and value ordering in constraint satisfaction problems. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers; ACM: New York, NY, USA, 2009; pp. 2209–2212. [Google Scholar]
- Crawford, B.; Soto, R.; Castro, C.; Monfroy, E. A hyperheuristic approach for dynamic enumeration strategy selection in constraint satisfaction. In Proceedings of the 4th International Conference on Interplay Between Natural and Artificial Computation: New Challenges on Bioinspired Applications—Volume Part II (IWINAC’11), Mallorca, Spain, 10–14 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 295–304. [Google Scholar]
- Soto, R.; Crawford, B.; Monfroy, E.; Bustos, V. Using Autonomous Search for Generating Good Enumeration Strategy Blends in Constraint Programming. In Computational Science and Its Applications—ICCSA 2012, Proceedings of the 12th International Conference, Salvador de Bahia, Brazil, 18–21 June 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 607–617. [Google Scholar]
- Moreno-Scott, J.H.; Ortiz-Bayliss, J.C.; Terashima-Marín, H.; Conant-Pablos, S.E. Experimental Matching of Instances to Heuristics for Constraint Satisfaction Problems. Comput. Intell. Neurosci. 2016, 2016, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Gent, I.; MacIntyre, E.; Prosser, P.; Smith, B.; Walsh, T. An empirical study of dynamic variable ordering heuristics for the constraint satisfaction problem. In Proceedings of the International Conference on Principles and Practice of Constraint Programming (CP’96), Cambridge, MA, USA, 19–22 August 1996; pp. 179–193. [Google Scholar]
- Boussemart, F.; Hemery, F.; Lecoutre, C.; Sais, L. Boosting Systematic Search by Weighting Constraints. In Proceedings of the European Conference on Artificial Intelligence (ECAI’04), Valencia, Spain, 23–27 August 2004; pp. 146–150. [Google Scholar]
- Minton, S.; Johnston, M.D.; Phillips, A.; Laird, P. Minimizing Conflicts: A Heuristic repair Method for CSP and Scheduling Problems. Artif. Intell. 1992, 58, 161–205. [Google Scholar] [CrossRef]
- Bacchus, F. Extending Forward Checking. In Proceedings of the International Conference on Principles and Practice of Constraint Programming (CP’00), Louvain-la-Neuve, Belgium, 7–11 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 35–51. [Google Scholar]
- Rossi, F.; Petrie, C.; Dhar, V. On the Equivalence of Constraint Satisfaction Problems. In Proceedings of the 9th European Conference on Artificial Intelligence, Stockholm, Sweden, 6–10 August 1990; pp. 550–556. [Google Scholar]
- Refalo, P. Impact-Based Search Strategies for Constraint Programming. In Principles and Practice of Constraint Programming—CP 2004; Wallace, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 557–571. [Google Scholar]
- Michel, L.; Van Hentenryck, P. Activity-Based Search for Black-Box Constraint Programming Solvers. In Integration of AI and OR Techniques in Contraint Programming for Combinatorial Optimzation Problems; Beldiceanu, N., Jussien, N., Pinson, É., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 228–243. [Google Scholar]
- Al-Obeidat, F.; Belacel, N.; Spencer, B. Combining Machine Learning and Metaheuristics Algorithms for Classification Method PROAFTN. In Enhanced Living Environments: Algorithms, Architectures, Platforms, and Systems; Ganchev, I., Garcia, N.M., Dobre, C., Mavromoustakis, C.X., Goleva, R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 53–79. [Google Scholar] [CrossRef]
- Talbi, E. Machine Learning for Metaheuristics—State of the Art and Perspectives. In Proceedings of the 2019 11th International Conference on Knowledge and Smart Technology (KST), Phuket, Thailand, 23–26 January 2019; p. XXIII. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).