Abstract
Large scale computational models are important for studying impact cratering events that are prevalent both on Earth and, more broadly, in this solar system. To address these problems, models must reliably account for both large length scales (e.g., kilometers) and relatively long time scales (hundreds of seconds). This work benchmarks two such approaches, a more traditional hydrodynamics approach and a finite-discrete element method (FDEM), for impact cratering applications. Both 2D and 3D results are discussed for two different impact velocities, 5 km/s and 20 km/s, striking normal to the target and, for 3D simulations, 45° from vertical. In addition, comparisons to previously published data are presented. Finally, differences in how these methods model damage are discussed. Ultimately, both approaches show successful modeling of several different impact scenarios.
1. Introduction
Impact cratering is a phenomenon that happens across a wide range of spatial scales, from large geological scales which encompass examples such as asteroid impacts to very small scales such as microparticle impacts. Particularly on the largest scales, experimental data become limited as kilometer scales cannot be reached in the laboratory environment, and many impact craters of interest are extraterrestrial. Thus, models operative at larger spatial scales become critical for studying and understanding these impact craters. Consequently, validation and verification of these models is important for the generation of reliable results. In lieu of experimental data, code-to-code comparisons can be informative for understanding differences in modeling approaches and the overall effect on results.
Impact cratering is a complex process that can be divided into three stages: contact and compression; excavation; crater modification [1,2]. The initial stage, contact and compression, occurs as the impactor strikes the target, transferring momentum and resulting in a shock wave [1,2,3]. During this stage, target and impactor materials behave as fluids, with hydrodynamics governing the motion of material [1,2,3]. The second stage, excavation, occurs as material is ejected from the forming crater. This ejected material may be in the form of solid particles or in the form of vapor [1,2]. During the final stage, crater modification, strength and/or gravity dominate the crater formation, depending on the cratering regime of the impact [1,2]. As excavation ends and modification begins, material begins to settle into the crater floor, and other processes such as slumping and the overturned flap occur [1,2]. For this final stage especially, more accurate modeling of solid materials, including material strength and damage, is essential to better understanding impact crater formation through computational models.
This work presents a code-to-code comparison between a hydrodynamics code (hydrocode) and a finite-discrete element method (FDEM) code. The hydrocode approach is a more traditional approach for addressing impact cratering problems [4,5,6,7,8,9], while the FDEM approach has been traditionally used for brittle fracture in geomaterials [10,11,12]. These approaches are operative on similar spatial scales, but the underlying formulation, particularly in how each approach accounts for damage, is very different.
Hydrocodes solve the equations for conservation of mass, momentum, and energy, along with constitutive relations describing the response of different materials. Hydrocode approaches have been under development for decades [13,14,15] and thus have many attractive features for addressing impact cratering problems. One such feature is the ability of these models to employ Eulerian, Lagranian, or a combination of these two descriptions of the equations of motion [15,16]. In Eulerian codes, material is allowed to freely move or ‘flow’ through a spatially fixed mesh [15]. Such methods have advantages because simulations are not limited by the consequences of excessive grid or element deformation, though they are not without drawbacks. For example, tracking the interfaces between materials presents a challenge in the form of mixed material cells, in which multiple materials exist in a single cell. In this case, material properties are often averaged [15,16]. Conversely, in Lagrangian approaches, the mesh deforms with the material, making the tracking of interfaces between materials trivial. Thus, this approach has advantages particularly for problems considering solid materials. However, these formulations are subject to stability issues and/or inaccuracies when elements experience significant deformation, and mesh tangling can result [13,15]. In order to capitalize on the advantages of both Lagrangian and Eulerian approaches, hybrid methods, or arbitrary Lagrangian–Eulerian (ALE) methods, have emerged [16]. ALE methods use a mix of Lagrangian and Eulerian schemes in which the solution from a distorted Lagrangian mesh is remapped to a spatially fixed Eulerian mesh. In addition, adaptive mesh refinement (AMR) techniques have been developed to provide dynamic mesh resolution in regions where material interfaces or shock fronts exist [17].
While hydrocodes can capture a wide range of multiphysics, they typically do not discretely resolve many features important to material deformation. Examples include cracks, fragmentation, or grains/particles within polycrystalline or granular microstructures. While such limitations may seem like a disadvantage from a physical standpoint, from the computational standpoint, this type of homogenization often makes this formulation more computationally efficient than other approaches, which allows for the ability to study very large systems in reasonable amounts of times.
FDEMs operate on similar spatial scales as hydrocodes. FDEMs were introduced by Munjiza in the late 1980s/early 1990s for the simulation of “transient dynamics on fragmenting solids” [18,19]. As the name indicates, FDEM merges the advancements achieved by both the Finite-Element Method (FEM) and the Discrete-Element Method (DEM). From the start, FDEM’s FEM portion was designed to be able to handle finite displacements, finite rotations, and finite strain-based deformation of the solid [20,21]. The FEM approach was then combined with contact detection, contact interaction, and objective discrete crack initiation and crack propagation solutions that were inherited from the DEM [20,22]. FDEM provides a framework for representing the transition from continuum to discontinuum (i.e., fracture) of solid materials when they are subjected to loads that exceed the material’s strength. This transition is allowed to occur at the boundaries of the finite elements. The first implementations of FDEMs were mainly focused on the simulation of fracture and fragmentation processes for cementitious materials [23]. These models used assumptions that the material inside the finite elements behaves elastically and that the localization process (fractures) was limited to the boundaries of the finite elements. More recently, a growing need for the simulation of problems where the aforementioned assumptions were no longer valid because of the large extent of permanent deformation mechanisms has led to the incorporation of plasticity models inside of the finite elements [24]. Traditional FDEM-based simulations involve the resolution of fracture, fragmentation, and contact problems. A typical solution for contact is via the implementation of penalty methods [25], which are computationally robust but require the use of relatively high values of contact stiffness (i.e., penalty coefficients), which in turn require smaller time step sizes. Combined with the fact that contact problems also require a spatial search for contacts every certain number of time steps [26,27], the result is that FDEM is more computationally expensive than traditional continuum-based models. Another drawback of the FDEM, because it is a Lagrangian-based method, is the time-step size restrictions imposed by highly deformed elements [13,15]. This type of situation usually occurs in areas located close to impacts or around high strain sources, such as explosions.
As mentioned previously, this work is focused on a code-to-code comparison of a hydrocode and an FDEM code, with the goal of benchmarking both numerical methods for impact cratering simulations and also evaluating the effects that the different numerical methods have on the overall solutions. In this work, hydrocode simulations use the ALE code Free LAGrange (FLAG), and FDEM simulations use the Hybrid Optimization Software Suite (HOSS). Both codes are developed and maintained by Los Alamos National Laboratory [28,29,30,31,32,33]. The following section contains brief summaries of each approach. Section 3 describes the test problem and model setups for both FLAG and HOSS simulations. Section 4 presents the comparisons for both 2D and 3D simulation results between FLAG and HOSS. In addition, this section includes comparison with previously published results from a wide range of hydrocodes. Finally, Section 5 presents a final summary and key conclusions of this work.
2. Computational Methods
This section presents more specific details about the underlying formulations between the two codes studied in this work, FLAG and HOSS. A summary of each code focuses on key aspects of the approaches that are of relevance to this study.
2.1. FLAG—Hydrodynamics Approach
The FLAG hydrocode uses a second-order finite-volume approach [30,31,32] to solving the Euler equations for conservation laws:
where is density, is velocity, P is pressure, E is energy per unit mass, V is volume, and is the Lagrangian differential [3]. FLAG is massively parallel and supports fully unstructured grids in 1–3 spatial dimensions [30,31,32,33].
FLAG has been used for a variety of physics applications at temporal and spatial scales that vary by several orders of magnitude [17,34,35,36]. It has the capability to run simulations in Eulerian, Lagrangian, and ALE frameworks [33]. FLAG has a variety of meshing tools for problem initialization as well as AMR capabilities [17,33].
In addition to a selection of computational approaches and meshing strategies, FLAG also offers a variety of options for equations of state (EOS) and material models, including failure and damage models [30,31,32,33]. These features are vital for modeling crater formation from high-velocity impacts into solid materials [1,2,3]. FLAG has been verified and validated for impact cratering simulations in both the strength-dominated and gravity-dominated cratering regimes [4] and has been used to study impact structures in the strength regime on extraterrestrial bodies [6].
2.2. HOSS—Finite-Discrete Element Method
FDEM combines aspects of both discrete- and finite-element methods. FDEM simulations consist of continuous, solid domains that are discretized into finite elements. Individual solid domains are allowed to interact with one another and, upon meeting some failure criterion, may develop new discontinuities or undergo fragmentation, resulting in the creation of new discrete domains. The governing equations for FDEM can be expressed as
where and are the lumped mass and damping matrices, respectively, is the displacement vector, and is the equivalent nodal force load. Equation (2) is solved using a second-order central difference time integration scheme to obtain the temporal evolution of the system.
A formal introduction to the FDEM formulation and descriptions of the contact detection and interaction algorithms are presented in detail elsewhere [20,22]. The material behavior is represented through a large-strain adaptation of the continuum-based constitutive law [21], which includes material non-linearities such as plasticity. The material can deform elastically and/or inelastically until surpassing either its tensile or shear strengths (or some combination of the two), resulting in the onset of damage [37,38]. Once the strength of the material is surpassed, the strain-softening behavior of the material is governed by a stress-displacement formulation that is incorporated into the constitutive law [39].
HOSS has been used to simulate a diverse array of problems, ranging from lab-scale experiments [10,40,41] to earthquake rupture [42,43]. Although HOSS has been used to model small-scale, high strain-rate impact problems in the past [44,45,46], this is the first time it has been used in the context of large-scale impact modeling.
3. Code Verification Problem
The code verification simulations were based on the problem initially introduced by Pierazzo et al. in a multi-code benchmarking study [5]. The verification problem consists of a 1 km diameter sphere of aluminum (Al-6061) impacting an aluminum target at 5 km/s and 20 km/s [5]. A schematic of this test problem is shown in Figure 1. Most of the results do not consider material strength, as in the initially proposed test problem, which allows for focus on the early stages of crater formation as well as for direct comparison to previously published results. In addition to modeling the materials as strengthless, simulations of this same verification problem using models for both material strength and damage are discussed later in Section 4.4. Relevant material parameters are included in the problem setup discussions for each code.
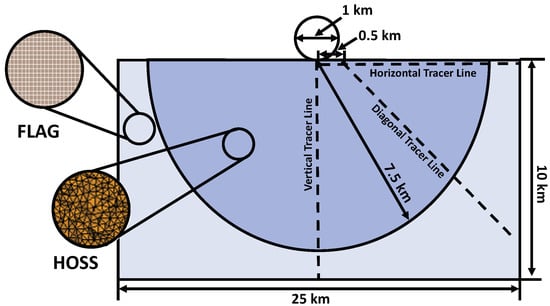
Figure 1.
2D schematic of the Al-Al (Al-6061) test problem. The Al target can be modeled either as a rectangular block, as in FLAG, or as a semicircle, as in HOSS. Both configurations are shown in this schematic. The insets show examples of the different meshes employed by the two methods. The dashed lines show lines in which pressure decay data were taken in 2D and 3D runs for comparison in Section 4.1 and Section 4.3.
Several simulations were completed using this test problem configuration, many of which are consistent with those performed by Pierrazzo et al. [5] so that comparisons between results could be made. These simulations included a mesh resolution study in 2D, which tested mesh resolutions in the range of 5–40 cells per projectile radius (cppr). For the mesh resolution study, shock pressure decay was recorded at tracer particles along the impactor trajectory from the point of impact to 10 km into the target, shown with a dashed line in Figure 1 (labeled as the vertical tracer). 3D simulations included both normal impacts and impacts 45° from vertical (also referred to as the oblique impact). Shock pressure decay was recorded in 3D simulations, but a mesh resolution study was not performed because of the significant computational cost of 3D simulations. Similar to the 2D case, the shock pressure decay was measured at different tracers from the impact point, including a vertical, horizontal, and 45° from vertical (i.e., diagonal) tracer line, all of which are indicated with dashed lines in Figure 1. Note that for the diagonal tracers, data were taken at approximately one projectile radius (∼0.5 km) downrange from the impact. This tracer placement is consistent with data presented previously by Pierazzo et al., which also reported diagonal tracer data originating from one projectile radius downrange [5].
Because the target and impactor had the same material composition, the theoretical maximum pressure can be calculated for a 1D impact:
where P is the maximum pressure, is the initial density, is the reference sound velocity (at 0 pressure), S is the linear EOS coefficient, and is the particle velocity, equal to half of the impact velocity when target and impactor have the same material [3]. S can also be expressed in terms of shock velocity with the following relationship: [3]. Substituting the values for the verification problem into Equation (3) yields a maximum pressure of 58.725 GPa for the 5 km/s impact and 506.25 GPa for the 20 km/s impact.
3.1. FLAG Setup
The 2D FLAG setup included a circular impactor with diameter 1 km, a 10 km × 25 km target block, and surrounding air with dimension 23.5 km × 25 km. The simulation ran until the shock wave reached the back of the target, 10 km from the point of impact. The mesh was uniform rectilinear with zone sizes corresponding to 5, 10, 20, and 40 cppr. The schematic shown in Figure 1 is representative of this setup.
In 3D, the computational domain included an impactor sphere with diameter 1 km, a target box with dimension 10 km × 25 km × 10 km, and surrounding air with dimension 23.5 km × 25 km × 10 km. Figure 2 shows the initial 3D configuration used in FLAG.
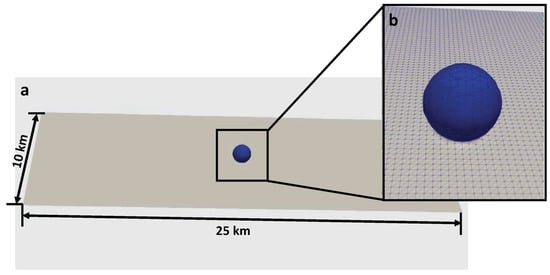
Figure 2.
Initialization of 3D FLAG simulations of an aluminum impactor (blue) striking an aluminum target (grey). (a) shows the impactor and surface of the 3D target, and (b) presents a close-up of the impactor and mesh.
FLAG simulations used a SESAME tabular EOS [47] and a Barton artificial viscosity model [48]. The Al-6061 in the problem was initialized with a density of 2700 kg/m3 and specific internal energy of 0 J. The air was modeled as a -law gas with = 1.4 and was initialized at 273 K with density 1.2922 kg/m3. FLAG simulations had free boundary conditions. The ALE strategy was by geometry. Shock pressure decay data came from 20 ∼ equally spaced tracer particles along the line of impact. In the 3D oblique simulations, tracers were placed along the diagonal impact trajectory as well as the vertical and horizontal directions from the point of impact, illustrated in Figure 1. Although 2D simulations showed FLAG converged at resolutions between 10 cppr and 20 cppr depending on impact velocity, the computational cost of running such resolutions in 3D is prohibitively expensive. Thus, the resolution for 3D simulations was 5 cppr, consistent with the 3D resolution used by the codes in the Pierazzo et al. study [5]. The computational domain consisted of about 8.6 million zones, divided across 360 cores. For comparison, a resolution of 10 cppr in 3D would have 67.6 million zones and would require 2815 cores for comparable load sharing. 40 cppr would have more than 4.29 billion zones and would require nearly 179,000 cores for comparable load sharing. The 5 cppr resolution has the additional benefit of allowing for a fair comparison to results presented by Pierazzo et al. [5]. Simulations used Cartesian geometry.
3.2. HOSS Setup
The 2D HOSS set up consisted of a circular impactor with diameter 1 km and a 7.5 km radius semicircular target (Figure 1). The simulations concluded shortly after the shock wave reflected off of the boundary of the target domain, 7.5 km from the point of impact. The mesh consisted of evenly sized triangular elements that varied with the cppr of interest (5, 10, 20).
Figure 3 illustrates the 3D HOSS simulation domain that consisted of a spherical aluminum impactor with diameter 1 km and a 7.5 km radius hemispherical target. Both the aluminum impactor and target were considered to be strengthless, and a Tillotson EOS [49] was used to describe the aluminum’s bulk response. The HOSS implementation of the Tillotson EOS, which follows the procedure outlined by Melosh [2], is shown in Equation (4).
where E is the energy density, is the density, , and . Relevant parameters for the EOS are included in Table 1. Tracer points were equally spaced throughout the domain to record the temporal evolution of displacement, velocity, and pressure as functions of distance and time. A resolution of ∼5 cppr was selected for consistency in the code comparison. The computational cost for HOSS is also prohibitively expensive for high-resolution 3D simulations. For 5 cppr, the HOSS computational domain consisted of 2.8 million tetrahedral elements divided across 1961 cores. If the resolution were 40 cppr, the same computational domain would have roughly 4.5 billion tetrahedral elements and would require 3 million cores assuming the same load balancing.
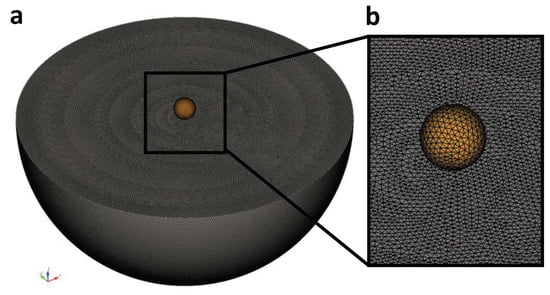
Figure 3.
HOSS 3D Simulation domain for an aluminum on aluminum impact, where (a) shows the full simulation domain, and (b) displays a zoomed in region where the impactor is initialized.

Table 1.
Tillotson equation of state parameters for aluminum.
4. Results and Discussion
4.1. 2D Mesh Resolution Study
2D simulations are advantageous because the computation time is sufficiently reduced to accommodate studying the effects of mesh resolution on the results. Figure 4 shows the effect of mesh resolution on shock pressure decay, varying from 5–40 cppr, for normal impacts of 5 km/s and 20 km/s for both FLAG and HOSS. Overall, both codes showed similar shock pressure decay trends among the resolutions tested. For the lower velocity, the FLAG results show some dependence in the pressure decay regime, with a notable difference in decay from the 5 cppr resolution compared to the more aligned results from the 10, 20 and 40 cppr simulations. At the higher impact velocity, FLAG results were well matched and seemed to converge in the 10–20 cppr range. Conversely, HOSS results show the same dependence in the maximum pressure calculated at the point of impact, with the higher resolution showing a slightly lower maximum pressure.
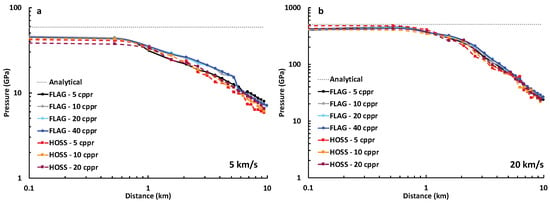
Figure 4.
2D mesh resolution study for FLAG and HOSS for (a) 5 km/s normal impact and (b) 20 km/s normal impact.
4.2. 3D Impact Cratering Simulations
This section presents qualitative comparisons of the 3D simulations from both FLAG and HOSS. Figure 5 shows the particle velocity evolution in both codes at 0.5 s and 1.0 s after impact from a normal impact with a velocity of 20 km/s. Overall, the shock wave propagates similarly; however, there are some distinct differences. Within the target itself, both FLAG and HOSS simulations show the highest velocity occurs at the front of the shock, as expected. In both codes, the highest particle velocities in the entire system appear in the crater ejecta. While both codes capture the ejecta, the ability for discrete elements to break away from the mesh in the FDEM approach allows for much more ejecta to appear within the crater in the HOSS simulations. However, it is worth noting that a considerable part of the material located inside the crater, shown in Figure 5b,d, corresponds to the impactor material. Also for consideration, the SESAME EOS used in the FLAG simulations allows for material vaporization. The resulting vapor plume of ejected material is significantly underdense and thus not visible in these figures, which have been thresholded on density to remove the surrounding air. The FLAG simulations appear to show interactions between waves, resulting in some variations in the velocity profiles. This behavior can be attributed to the shock reflection, regions of compression and tension, and the pressure differential between the target and ambient air. These effects, while visible in the velocity plots, do not affect the crater formation in a significant way.
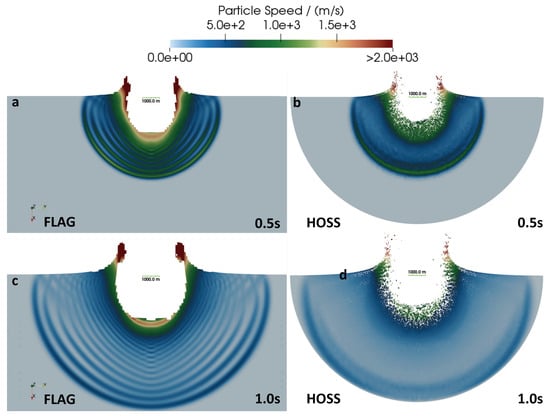
Figure 5.
Particle velocity from a m/s normal impact at 0.5 s (a,b) and 1.0 s (c,d) as calculated from 3D simulations from FLAG and HOSS. (a,c) show particle velocity from 3D FLAG simulations, and (b,d) show particle velocity from HOSS simulations. The length of the horizontal green bar shown inside the crater represents a distance of 1000 m.
Figure 6 presents similar particle velocity plots for an oblique impact with a velocity of 5 km/s. Similar to the normal impact case, the highest velocities occur in the crater ejecta. Figure 7a,b and Figure 8a,b directly overlay the crater profiles for both the normal and oblique impacts just discussed. The HOSS target is shown in green, on top of the FLAG target, which is shown in orange. The impactors themselves are also distinguished, where red indicates the FLAG impactor and dark green indicates the HOSS impactor. Overall, the HOSS simulations tend to predict slightly deeper craters than FLAG. In general, this is a result of the higher amount of ejecta/fragmentation accounted for within the crater in HOSS. Some of this ejecta will not leave the crater, but rather settle into the bottom, producing a crater depth closer to what FLAG predicts. The predicted crater diameters are similar between FLAG and HOSS.
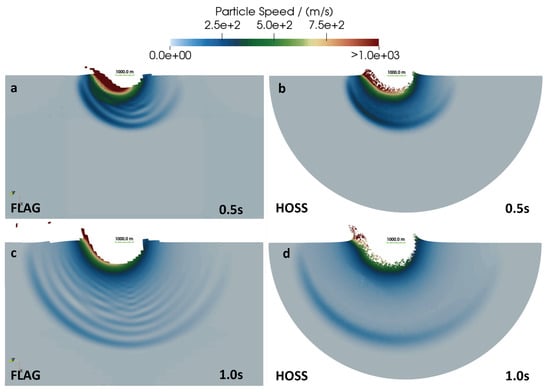
Figure 6.
Particle velocity from a m/s 45° oblique impact at 0.5 s (a,b) and 1.0 s (c,d) as calculated from 3D simulations from FLAG and HOSS. (a,c) show particle velocity for 3D FLAG simulations, and (b,d) show particle velocity for 3D Hoss simulations. The length of the horizontal green bar shown inside the crater represents a distance of 1000 m.
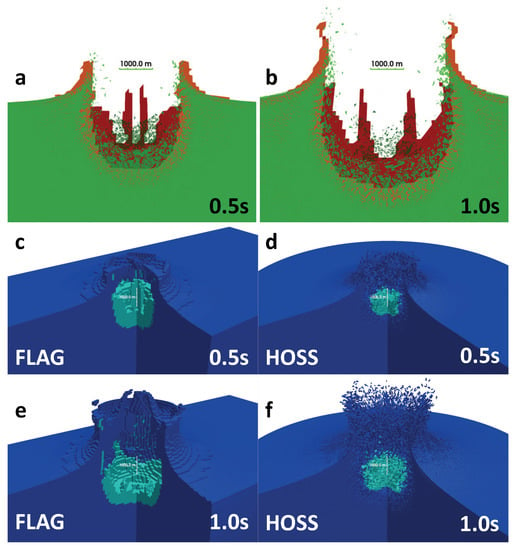
Figure 7.
FLAG and HOSS simulations overlaid to show differences in the crater profiles from a 20 km/s normal impact (a,b) at 0.5 s and 1.0 s. The FLAG simulations are represented with an orange target material and red impactor. HOSS simulations are shown with a green target material and dark green impactor. (c–f) show 3D cross-sections of the impact scenario at 0.5 s and 1.0 s, where dark blue and cyan represent the target and impactor, respectively. The length of the horizontal green bar (a,b) and of the vertical white bar (c–f) shown represents a distance of 1000 m.
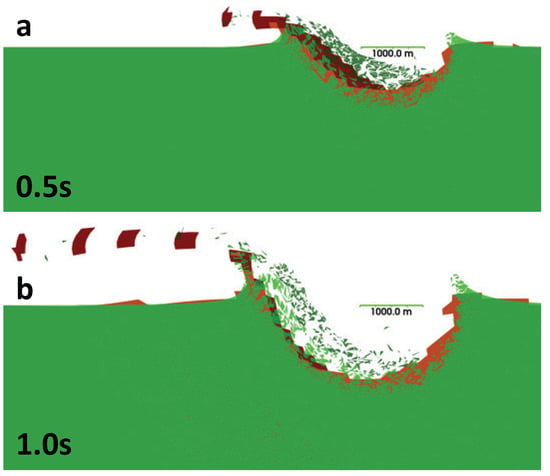
Figure 8.
FLAG and HOSS simulations overlaid to show differences in the crater profiles from a 5 km/s oblique impact at (a) 0.5 s and (b) 1.0 s. The FLAG simulations are represented with an orange target material and red impactor. HOSS simulations are shown with a green target material and dark green impactor. The length of the horizontal green bar shown inside the crater represents a distance of 1000 m.
In the case of an oblique impact, as shown in Figure 8, both codes capture ejecta. In FLAG, the ejecta is predominately the impactor material, whereas the ejecta in HOSS is comprised of both impactor and target material. In both cases, material appears as though it is being ejected in discrete segments; however, it is important to consider the different meshing strategies. In FLAG, the ejected material moves through a deformed, but connected, mesh, while in HOSS, individual, and also deformed, elements can separate and move away from their original positions. Both approaches result in ejected material, but the manner in which the codes handle ejected material is quite different.
Figure 7c–f also shows 3D cross-sections of the impact event in both FLAG and HOSS. In these figures, the target is represented as dark blue, and the impactor is represented as cyan. In these figures, the effect that the different mesh strategies have on the shape of the ejected material can be clearly seen. It is more apparent that the material is moving through a connected mesh in FLAG, resulting in less distributed impact ejecta. Conversely, the ejected material in HOSS is more distributed, spraying outward because of the ability of discrete elements to move apart from the initial mesh.
As mentioned previously, the inclusion of discrete elements and the Lagrangian framework in HOSS often comes at a cost of increased run times in comparison to the more traditional hydrocodes such as FLAG. Table 2 compares the computational resources required for the 3D normal and oblique simulations completed. The HOSS simulations were all run for a specified number of time steps, resulting in uniform run times and simulated times. FLAG required fewer cores and ran for less time than HOSS to reach the same or longer simulated times. The one exception was the oblique 20 km/s simulation, which suffered from mesh tangling and did not fully complete in FLAG. However, even with this enhanced computational efficiency, FLAG still requires high performance computing capabilities to complete these 3D simulations.

Table 2.
Computational resources required for the 3D impact simulations.
4.3. Benchmarking against Other Hydrocodes
In this section, the FLAG and HOSS results are compared to those reported in the benchmarking study by Pierazzo et al. [5]. The study used multiple hydrodynamic/shock codes: ALE3D, AUTODYN, CTH, iSALE, RAGE, SOVA, SPH, and ZEUS-MP. These codes span a variety of approaches, including Eulerian, ALE, and smooth-particle hydrodynamics [5]. ALE3D is a hybrid (finite-element + finite-volume) multiphysics code developed at Lawrence Livermore National Laboratory and is based on ALE solutions. ALE3D has been used to simulate asteroid impacts, atmospheric entry, and breakup [51]. AUTODYN is part of the ANSYS Workbench package that was specifically designed to resolve the material response under high strain-rate loading conditions. For solid modeling, AUTODYN uses Lagrangian elements, while for fluid modeling, there is an option of using Eulerian formulations or smooth-particle hydrodynamics solvers. Researchers have used AUTODYN to simulate hypervelocity impacts of asteroids on the surface of the Earth [52]. CTH is a solid mechanics code that was developed at Sandia National Laboratories with a special focus on strong shock applications. CTH has been used to simulate many types of impact problems, such as those conducted for the Federal Emergency Management Agency [53] and for the National Aeronautics and Space Administration [54]. iSALE is an open-source hydrocode widely used by the planetary science community. It was developed for modeling fluid flows across a variety of speeds. However, it is largely serial and primarily used in 2D simulations [55,56]. The RAGE hydrodynamics code, developed and maintained by Los Alamos National Laboratory, is an Eulerian hydrocode with capabilities for radiation hydrodynamics and AMR [57]. SOVA uses an Eulerian approach and models multi-material problems and dusty flows [58]. SPH has no underlying grid and can model solid materials [59]. Finally, ZEUS-MP is an Eulerian code that can model radiative and magnetized materials [60]. These codes are discussed in more detail in the benchmarking paper by Pierazzo et al. [5], but clearly this collection of shock codes represents a wide range of model formulations that can be used for impact cratering studies.
Table 3 first compares the results from FLAG and HOSS to the theoretical maximum pressures for normal 5 km/s and 20 km/s impact velocities for the most resolved simulations. Note that the theoretical maximum pressure is derived from impedance matching in 1D for strengthless materials [3]. This table also includes the mean value, determined from all codes tested by Pierazzo et al. and their corresponding relative errors for comparison [5]. Note that the theoretical value applies only to the maximum pressure and not the shock pressure decay throughout the target. In addition, because the original comparison of Pierazzo et al. was published more than a decade ago, it is also expected that FLAG and HOSS would both show improvements from advances in numerical methods, model development, etc., that were not present in the other codes during the original study but may have since been implemented.

Table 3.
Maximum pressures from 2D simulations in FLAG and HOSS compared to the theoretical maximum. These values are also compared to the mean of the values reported in Pierazzo et al. [5] by various codes. The relative error is reported with respect to the 1D analytical solution.
Overall, the Pierazzo et al. results show relative errors of ∼25–30% [5]. Indeed, the FLAG and HOSS results both show improvement on these values, particularly in the 5 km/s case. In the 20 km/s case, the relative errors for FLAG and HOSS are somewhat larger than for the simulations with a 5 km/s impact velocity, consistent with the codes tested in the original study.
The pressure decay from FLAG and HOSS obtained for several impact cases, including 5 km/s normal and oblique impacts and 20 km/s normal and oblique impacts, are compared against other hydrocodes. Unless otherwise noted, all subsequent comparisons are for 3D simulations. To compare the pressure decay for 3D normal and oblique impact angles, pressure values are recorded along vertical, diagonal (45° from vertical), and horizontal lines extending outward from the impact point. These lines are shown schematically as dashed lines in Figure 1.
In the case of the normal impacts, the results can also be compared to the analytical solutions in Table 3, shown as a constant dotted line in Figure 9. This figure, which includes digitized results from Pierazzo et al. [5], shows that all of the codes tested produce pressure values at the impact point that underpredict the analytical solution. The degree to which the codes underpredict the analytical solution varies highly in the 5 km/s impact velocity case. In the 20 km/s impact velocity case, the codes in general come very close to the analytical prediction, although most predictions are just under the analytical value. In this case, HOSS shows the best match to the analytic value close to the point of impact. However, it also shows some subsequent oscillations before the shock decay regime, whereas hydrocode simulations resulted in a slightly lower maximum pressure but a smoother decay curve.
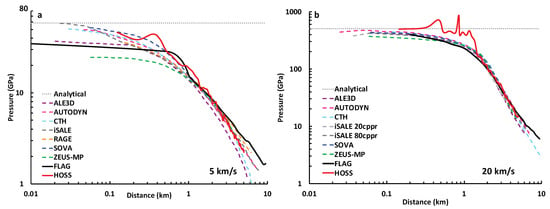
Figure 9.
3D normal impact, vertical tracers from FLAG and HOSS simulations, plotted with data from Pierazzo et al. [5] for (a) 5 km/s impact and (b) 20 km/s impact.
It is worth noting that for the 5 km/s normal impact case, the 2D FLAG simulations slightly overpredict the analytic value (see Table 3), while the 3D simulations underpredict the analytic value (see Figure 9a). This dimensional difference can be attributed to to the increased number of directions in which shocks can travel and dissipate in 2D versus 3D as well as the 1D calculation of the analytic solution.
Figure 10, Figure 11 and Figure 12 show the shock decay computed with FLAG and HOSS for oblique impact scenarios in comparison to the data presented by Pierrazzo et al. [5]. Overall, the results from the HOSS and FLAG simulations have similar shock pressure decay to the codes tested by Pierrazo et al. [5]. The FDEM simulations exhibit a fair amount of variability in the region directly below the impact point. Farther from the impact point (roughly 1 km), the pressures calculated by both HOSS and FLAG exhibit stable, power-law decay with distance. Overall, the FLAG results are fairly smooth in the shock decay region, which is somewhat in contrast to the variations seen in the particle velocity profiles (see Figure 5a,c and Figure 6a,c). However, because the shock pressure decay is based on the maximum pressure at each point over all time, rather than the value at each point for one specific time, the smooth decay is expected. Plotting pressure rather than velocity does not show the same variations.
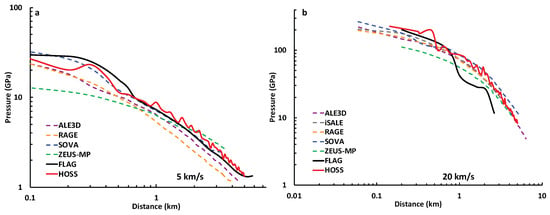
Figure 10.
3D oblique impact (45° from vertical), vertical tracers from FLAG and HOSS simulations, plotted with data from Pierazzo et al. [5] for (a) 5 km/s impact and (b) 20 km/s impact.
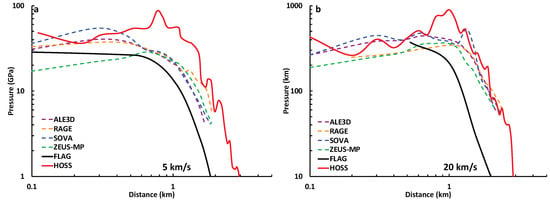
Figure 11.
3D oblique impact (45° from vertical), horizontal tracers from FLAG and HOSS simulations, plotted with data from Pierazzo et al. [5] for (a) 5 km/s impact and (b) 20 km/s impact.
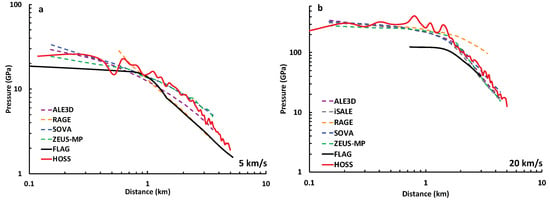
Figure 12.
3D oblique impact (45° from vertical), diagonal tracers from FLAG and HOSS simulations, plotted with data from Pierazzo et al. [5] for (a) 5 km/s impact and (b) 20 km/s impact.
4.4. Implications for Modeling Fracture
For impact cratering cases in the strength-dominated regime, strength and damage also play a role in the crater formation process [1,2]. Thus, modeling the 5 km/s normal impact simulations, which lie in the strength regime, with the inclusion of strength and damage models can provide additional insight into simulating cratering processes.
The FLAG simulations used a constant yield stress with linear hardening behavior to model both target and impactor, and damage was modeled using the Johnson–Cook model [61]. The yield stress was 276 MPa, and the hardening parameter was 0.1 [62]. The HOSS simulations also used a constant yield stress with linear hardening. This simulation used a yield stress of 276 MPa and a linear hardening of 113.3 MPa. In addition, the properties of cohesive bonds between the elements were assigned such that fracture occurred once the stress in the material surpassed its ultimate tensile strength (310 MPa).
The particle velocity and damage metrics are presented in Figure 13 and Figure 14, respectively. Snapshots are shown at 0.4 s and 0.8 s. Because of the difference in damage formulations, it is difficult to directly compare across codes. Thus, the damage in FLAG is termed ‘continuum damage,’ as it indicates damage incurred within a cell/zone. Damage in HOSS is termed ‘discrete damage,’ as it indicates damage incurred between two cells/zones. In both cases, a damage value of 0 represents completely undamaged material while 1 represents a fully damaged region. In HOSS, fully damaged regions directly correspond to fractures or cracks evolving within the material. Damage in FLAG is more homogenized, so there is not a direct correlation with a discrete crack network.
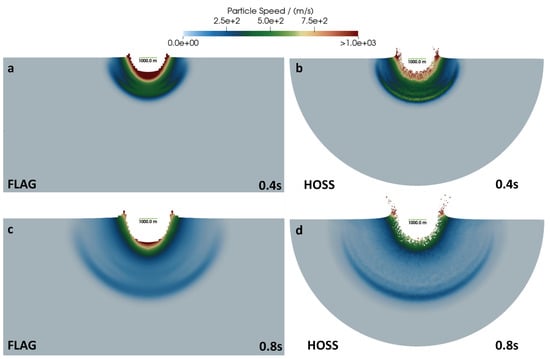
Figure 13.
Particle velocity from a m/s normal impact in which strength and damage are considered in the material models. Snapshots are shown at 0.4 s (a,b) and 0.8 s (c,d) and are calculated from 3D simulations from FLAG and HOSS. (a,c) show particle speed from 3D FLAG simulations, and (b,d) show particle speed from 3D HOSS simulations. The length of the horizontal green bar shown inside the crater represents a distance of 1000 m.
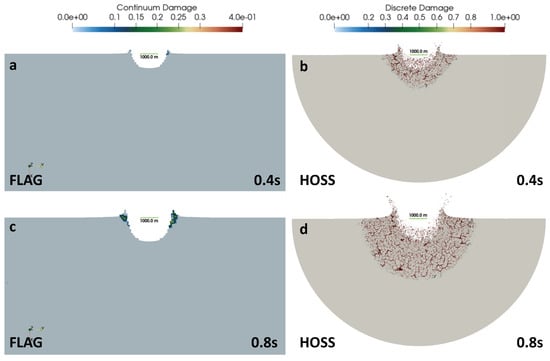
Figure 14.
Continuum and discrete damage measures from a m/s normal impact in which strength and damage are considered in the material models. Snapshots are shown at 0.4 s (a,b) and 0.8 s (c,d) and are calculated from 3D simulations from FLAG and HOSS. (a,c) show continuum damage from 3D FLAG simulations, and (b,d) show discrete damage from 3D HOSS simulations. The length of the horizontal green bar shown inside the crater represents a distance of 1000 m.
While the FLAG and HOSS particle velocities shown in Figure 13 are relatively similar, the damage from both codes, shown in Figure 14, is very different. HOSS shows a significant amount of damage developing and evolving in the wake of the shockwave as it travels through the medium. In FLAG, however, only highly damaged regions in the crater ejecta are visible at these early times. The FLAG simulation did continue to run to 3.0 s, and more damage is evident at later simulation times, below the crater floor and surrounding the crater walls, similar to the shape of the damaged region in HOSS at early times (see Appendix A).
5. Conclusions
This work presented a code-to-code comparison between a modern hydrodynamics code, FLAG, and an FDEM code, HOSS. This study successfully benchmarked both numerical methods for impact cratering simulations. This work explored multiple Al-Al impact scenarios, in both 2D and 3D, in order to evaluate the differences each numerical method had on the overall solution obtained. Both numerical methods produced qualitatively similar velocity contours and predicted similarly sized craters in the early stages of crater formation. From a quantitative point of view, both codes produced maximum pressures with lower relative errors than previously published results of the same simulations using different hydrocodes. In addition, both FLAG and HOSS demonstrated abilities to incorporate strength and damage processes into impact simulations, key components to modeling strength-dominated crater formation.
One notable difference in these two approaches is the meshing strategies used. FLAG employs an ALE strategy that allows for deformation of the mesh and also transport of material through the mesh, but ultimately the mesh remains connected and cannot break apart. Conversely, HOSS allows for elements in the mesh to both deform and break away from the initial configuration, disconnecting along element edges. Partially as a result of these mesh strategies, primary differences in results are apparent in damage evolution and computational expense. HOSS shows more damage evolution in the system, particularly at early times, resolved to a level in which individual cracks can form and evolve. This meshing strategy also allows for more distributed ejecta coming from the impact crater. While FLAG does not have the ability to resolve damage in the same way at early simulation times, it is more computationally efficient, requiring fewer cores and less computation time to achieve the similar if not longer simulation times. At later times, the extent of damage in FLAG simulations more closely resembles the extent of damage in HOSS simulations, as shown in Appendix A.
Overall, both approaches appropriately capture the impact cratering process at different impact velocities and impact trajectories. Major aspects of the cratering process, including shock wave propagation, shock pressure decay, and crater profiles, are captured with reasonable accuracy determined through comparison between the codes and to previous published simulated data.
Author Contributions
Conceptualization, W.K.C., B.E., C.S.P., C.L., Z.L., E.E.K., E.R. and A.H.; methodology, W.K.C. and B.E.; software, W.K.C. and B.E.; validation, W.K.C. and B.E.; formal analysis, W.K.C., B.E., C.S.P., C.L., Z.L., E.E.K., E.R. and A.H.; writing—original draft preparation, W.K.C., B.E., E.R. and A.H.; writing—review and editing, W.K.C., B.E., C.S.P., C.L., Z.L., E.E.K., E.R. and A.H.; visualization, W.K.C., B.E., E.R. and A.H.; supervision, C.S.P., E.R. and A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are subject to release restrictions and are not publicly available. Requests for these data can be made to the corresponding author(s).
Acknowledgments
W.K.C. acknowledges the Advanced Simulation and Computing (ASC)— Integrated Codes (IC) program through the Lagrangian Applications Project (LAP) at Los Alamos National Laboratory (LANL) and the ASC—Threat Reduction (TR) program at LANL. B.E. would like to thank the LANL Institutional Computing program for their support in generating these data. C.S.P. acknowledges the ASC—Verifcation and Validation program at LANL. A.H. gratefully acknowledges support from the ASC—IC program through LAP at LANL. C.L., Z.L., E.E.K. and E.R. acknowledge the Laboratory Directed Research and Development program of LANL under project number 20170109ER. Los Alamos National Laboratory, an affirmative action/equal opportunity employer, is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the Department of Energy under contract 89233218NCA000001.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| 2D | two-dimensional |
| 3D | three-dimensional |
| Al | aluminum |
| ALE | arbitrary Lagrangian Eulerian |
| cppr | cells per projectile radius |
| DEM | discrete-element method |
| EOS | equation of state |
| FDEM | finite-discrete element method |
| FEM | finite-element method |
| FLAG | Free LAGrange |
| HOSS | Hybrid Optimization Software Suite |
Appendix A. FLAG Damage Figures
As mentioned in Section 4.4, the FLAG simulation ran to a stopping time of 3.0 s. Figure A1 shows damage in the FLAG simulation about 1.0 s after impact, and Figure A2 shows damage in the FLAG simulation at the simulation stopping time of 3.0 s.
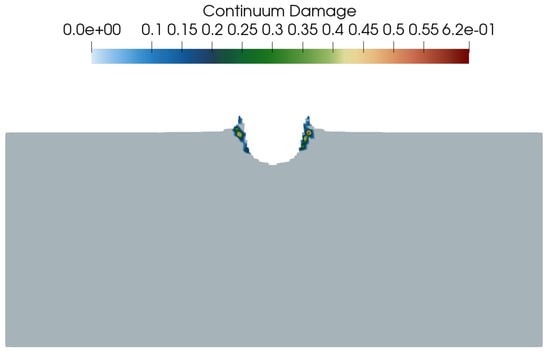
Figure A1.
FLAG simulation of m/s Al-Al (Al-6061) normal impact, 1 s after impact, colored by damage.
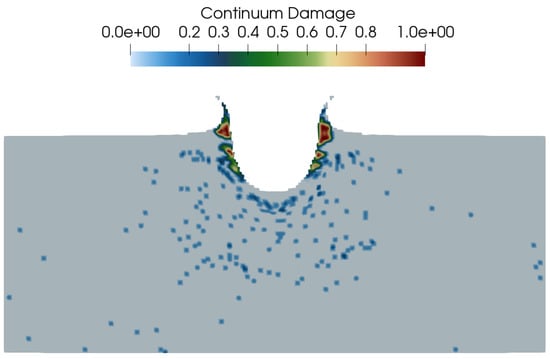
Figure A2.
FLAG simulation of m/s Al-Al (Al-6061) normal impact, 3 s after impact, colored by damage.
References
- Melosh, H.J. Planetary Surface Processes; Cambridge University Press: Cambridge, UK, 2011; Volume 13. [Google Scholar]
- Melosh, H.J. Impact Cratering: A Geologic Process; Research supported by NASA; Oxford Monographs on Geology and Geophysics, No. 11; Oxford University: New York, NY, USA, 1989; Volume 11, 253p. [Google Scholar]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons: New York City, NY, USA, 1994. [Google Scholar]
- Caldwell, W.K.; Hunter, A.; Plesko, C.S.; Wirkus, S. Verification and Validation of the FLAG Hydrocode for Impact Cratering Simulations. J. Verif. Valid. Uncertain. Quantif. 2018, 3, 031004. [Google Scholar] [CrossRef]
- Pierazzo, E.; Artemieva, N.; Asphaug, E.; Baldwin, E.; Cazamias, J.; Coker, R.; Collins, G.; Crawford, D.; Davison, T.; Elbeshausen, D.; et al. Validation of numerical codes for impact and explosion cratering: Impacts on strengthless and metal targets. Meteorit. Planet. Sci. 2008, 43, 1917–1938. [Google Scholar] [CrossRef]
- Caldwell, W.K.; Hunter, A.; Plesko, C.S.; Wirkus, S. Understanding Asteroid 16 Psyche’s composition through 3D impact crater modeling. Icarus 2020, 351, 113962. [Google Scholar] [CrossRef]
- Sherburn, J.A.; Horstemeyer, M.F. Hydrodynamic modeling of impact craters in ice. Int. J. Impact Eng. 2010, 37, 27–36. [Google Scholar] [CrossRef]
- Suetsugu, R.; Tanaka, H.; Kobayashi, H.; Genda, H. Collisional disruption of planetesimals in the gravity regime with iSALE code: Comparison with SPH code for purely hydrodynamic bodies. Icarus 2018, 314, 121–132. [Google Scholar] [CrossRef]
- Pierazzo, E.; Collins, G. A Brief Introduction to Hydrocode Modeling of Impact Cratering. In Cratering in Marine Environments and on Ice; Springer: Berlin/Heidelberg, Germany, 2004; pp. 323–340. [Google Scholar] [CrossRef]
- Euser, B.; Rougier, E.; Lei, Z.; Knight, E.E.; Frash, L.P.; Carey, J.W.; Viswanathan, H.; Munjiza, A. Simulation of Fracture Coalescence in Granite via the Combined Finite–Discrete Element Method. Rock Mech. Rock Eng. 2019, 52, 3213–3227. [Google Scholar] [CrossRef]
- Okubo, K.; Rougier, E.; Lei, Z.; Bhat, H.S. Modeling earthquakes with off-fault damage using the combined finite-discrete element method. Comput. Part. Mech. 2020, 7, 1057–1072. [Google Scholar] [CrossRef]
- Fukuda, D.; Mohammadnejad, M.; Liu, H.; Zhang, Q.; Zhao, J.; Dehkhoda, S.; Chan, A.; Kodama, J.; Fujii, Y. Development of a 3D Hybrid Finite-Discrete Element Simulator Based on GPGPU-Parallelized Computation for Modelling Rock Fracturing Under Quasi-Static and Dynamic Loading Conditions. Rock Mech. Rock Eng. 2020, 53, 1079–1112. [Google Scholar] [CrossRef]
- Anderson, C.E., Jr. An overview of the theory of hydrocodes. Int. J. Impact Eng. 1987, 5, 33–59. [Google Scholar] [CrossRef]
- Johnson, W.E.; Anderson, C.E., Jr. History and application of hydrocodes in hypervelocity impact. Int. J. Impact Eng. 1987, 5, 423–439. [Google Scholar] [CrossRef]
- Collins, G.S. An Introduction to Hydrocode Modeling; Applied Modelling and Computation Group, Imperial College London: London, UK, 2002; pp. 2–11. [Google Scholar]
- Benson, D.J. Computational methods in Lagrangian and Eulerian hydrocodes. Comput. Methods Appl. Mech. Eng. 1992, 99, 235–394. [Google Scholar] [CrossRef]
- Burton, D.; Morgan, N.; Charest, M.; Kenamond, M.; Fung, J. Compatible, energy conserving, bounds preserving remap of hydrodynamic fields for an extended ALE scheme. J. Comput. Phys. 2018, 355, 492–533. [Google Scholar] [CrossRef]
- Munjiza, A. Discrete Elements in Transient Dynamics of Fractured Media. Ph.D. Thesis, Swansea University, Swansea, UK, 1992. [Google Scholar]
- Munjiza, A.; Owen, D.; Bicanic, N. A combined finite-discrete element method in transient dynamics of fracturing solids. Eng. Comput. 1995, 12, 145–174. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; Knight, E.E. Large Strain Finite Element Method: A Practical Course; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Munjiza, A.; Knight, E.E.; Rougier, E. Computational Mechanics of Discontinua; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Aliabadi, M. Fracture of Rock, 1st ed.; Computational Mechanics; WIT Press: Southampton, UK, 1999. [Google Scholar]
- Rougier, E.; Munjiza, A.; Lei, Z.; Chau, V.T.; Knight, E.E.; Hunter, A.; Srinivasan, G. The combined plastic and discrete fracture deformation framework for finite-discrete element methods. Int. J. Numer. Methods Eng. 2020, 121, 1020–1035. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F. Penalty function method for combined finite–discrete element systems comprising large number of separate bodies. Int. J. Numer. Methods Eng. 2000, 49, 1377–1396. [Google Scholar] [CrossRef]
- Munjiza, A.; Rougier, E.; John, N.W.M. MR linear contact detection algorithm. Int. J. Numer. Methods Eng. 2006, 66, 46–71. [Google Scholar] [CrossRef]
- Rougier, E.; Munjiza, A. MRCK_3D contact detection algorithm. In Proceedings of the 5th International Conference on Discrete Element Methods, London, UK, 25–26 August 2010; Queen Mary, University of London: London, UK, 2010; pp. 37–45. [Google Scholar]
- Knight, E.E.; Rougier, E.; Lei, Z.; Euser, B.; Chau, V.; Boyce, S.H.; Gao, K.; Okubo, K.; Froment, M. HOSS: An implementation of the combined finite-discrete element method. Comput. Part. Mech. 2020, 7, 765–787. [Google Scholar] [CrossRef]
- Boyce, S.H.S.; Knight, E.E.; Rougier, E.; Lei, Z.; Euser, B. HOSS –The Hybrid Optimization Software Suite. 2021. Available online: www.lanl.gov/hoss (accessed on 30 January 2021).
- Burton, D. Connectivity Structures and Differencing Techniques For Staggered-Grid Free-Lagrange Hydroynamics; Technical Report UCRL-JC-110555; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1992. [Google Scholar]
- Burton, D. Multidimensional Discretization of Conservation Laws for Unstructured Polyhedral Grids; Technical Report UCRL-JC-118306; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1994. [Google Scholar]
- Burton, D. Consistent Finite-Volume Discretization of Hydrodynamic Conservation Laws for Unstructured Grids; Technical Report UCRL-JC-118788; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1994. [Google Scholar]
- Hill, J.L. User’s Manual for FLAG Version 3.6.0. The Lagrangian Applications Project; LA-CP-17-20057; Los Alamos National Laboratory: Livermore, CA, USA, 2017. [Google Scholar]
- Fung, J.; Harrison, A.K.; Chitanvis, S.; Margulies, J. Ejecta source and transport modeling in the FLAG hydrocode. Comput. Fluids 2013, 83, 177–186. [Google Scholar] [CrossRef]
- Larkin, K.; Hunter, A.; Abdelkefi, A. Comparative investigations of multi-fidelity modeling on performance of electrostatically-actuated cracked micro-beams. Int. J. Mech. Sci. 2021, 192, 106139. [Google Scholar] [CrossRef]
- Larkin, K.; Rougier, E.; Chau, V.T.; Srinivasan, G.; Abdelkefi, A.; Hunter, A. Scale bridging damage model for quasi-brittle metals informed with crack evolution statistics. J. Mech. Phys. Solids 2020, 138, 103921. [Google Scholar] [CrossRef]
- Godinez, H.C.; Rougier, E.; Osthus, D.; Lei, Z.; Knight, E.; Srinivasan, G. Fourier amplitude sensitivity test applied to dynamic combined finite-discrete element methods–based simulations. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 30–44. [Google Scholar] [CrossRef]
- Osthus, D.; Godinez, H.C.; Rougier, E.; Srinivasan, G. Calibrating the stress-time curve of a combined finite-discrete element method to a Split Hopkinson Pressure Bar experiment. Int. J. Rock Mech. Min. Sci. 2018, 106, 278–288. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.; White, J. Combined single and smeared crack model in combined finite-discrete element analysis. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Carey, J.W.; Lei, Z.; Rougier, E.; Mori, H.; Viswanathan, H. Fracture-permeability behavior of shale. J. Unconv. Oil Gas Resour. 2015, 11, 27–43. [Google Scholar] [CrossRef]
- Gao, K.; Guyer, R.; Rougier, E.; Ren, C.X.; Johnson, P.A. From Stress Chains to Acoustic Emission. Phys. Rev. Lett. 2019, 123, 048003. [Google Scholar] [CrossRef] [PubMed]
- Klinger, Y.; Okubo, K.; Vallage, A.; Champenois, J.; Delorme, A.; Rougier, E.; Lei, Z.; Knight, E.E.; Munjiza, A.; Satriano, C.; et al. Earthquake Damage Patterns Resolve Complex Rupture Processes. Geophys. Res. Lett. 2018, 45, 10279–10287. [Google Scholar] [CrossRef]
- Okubo, K.; Bhat, H.S.; Rougier, E.; Marty, S.; Schubnel, A.; Lei, Z.; Knight, E.E.; Klinger, Y. Dynamics, Radiation, and Overall Energy Budget of Earthquake Rupture With Coseismic Off-Fault Damage. J. Geophys. Res. Solid Earth 2019, 124, 11771–11801. [Google Scholar] [CrossRef]
- Rougier, E.; Knight, E.; Broome, S.; Sussman, A.; Munjiza, A. Validation of a three-dimensional Finite-Discrete Element Method using experimental results of the Split Hopkinson Pressure Bar test. Int. J. Rock Mech. Min. Sci. 2014, 70, 101–108. [Google Scholar] [CrossRef]
- Chau, V.; Rougier, E.; Lei, Z.; Knight, E.E.; Gao, K.; Hunter, A.; Srinivasan, G.; Viswanathan, H. Numerical analysis of flyer plate experiments in granite via the combined finite–discrete element method. Comput. Part. Mech. 2020, 7, 1005–1016. [Google Scholar] [CrossRef]
- Froment, M.; Rougier, E.; Larmat, C.; Lei, Z.; Euser, B.; Kedar, S.; Richardson, J.E.; Kawamura, T.; Lognonné, P. Lagrangian-based Simulations of Hypervelocity Impact Experiments on Mars Regolith Proxy. Geophys. Res. Lett. 2020, 47, e2020GL087393. [Google Scholar] [CrossRef]
- Lyon, S.P.; Johnson, J.D. SESAME: The Los Alamos National Laboratory Equation of State Database; Technical Report; LA-UR-92-3407; Los Alamos National Laboratory: Livermore, CA, USA, 1992. [Google Scholar]
- Margolin, L. A centered artificial viscosity for cells with large aspect ratio. NASA STI/Recon Tech. Rep. N 1988, 89, 13748. [Google Scholar]
- Tillotson, J.H. Metallic Equations of State for Hypervelocity Impact; Technical Report; General Atomics: San Diego, CA, USA, 1962. [Google Scholar]
- O’Keefe, J.D.; Ahrens, T.J. Cometary and Meteorite Swarm Impact on Planetary Surfaces. J. Geophys. Res. Solid Earth 1982, 87, 6668–6680. [Google Scholar] [CrossRef]
- Robertson, D.K.; Gisler, G.R. Near and far-field hazards of asteroid impacts in oceans. Acta Astronaut. 2019, 156, 262–277. [Google Scholar] [CrossRef]
- Saito, T.; Kaiho, K.; Abe, A.; Katayama, M.; Takayama, K. Hypervelocity impact of asteroid/comet on the oceanic crust of the earth. Int. J. Impact Eng. 2008, 35, 1770–1777. [Google Scholar] [CrossRef]
- Boslough, M.; Jennings, B.; Carvey, B.; Fogleman, W. FEMA Asteroid Impact Tabletop Exercise Simulations. Procedia Eng. 2015, 103, 43–51. [Google Scholar] [CrossRef][Green Version]
- Stickle, A.; Atchison, J.; Barnouin, O.; Cheng, A.; Crawford, D.; Ernst, C.; Fletcher, Z.; Rivkin, A. Modeling Momentum Transfer from Kinetic Impacts: Implications for Redirecting Asteroids. Procedia Eng. 2015, 103, 577–584. [Google Scholar] [CrossRef]
- Amsden, A.; Ruppel, H.; Hirt, C. SALE: A Simplified ALE Computer Program for Fluid Flow at All Speeds; Technical Report; Los Alamos Scientific Lab.: Livermore, CA, USA, 1980. [Google Scholar]
- Ivanov, B.; Deniem, D.; Neukum, G. Implementation of dynamic strength models into 2D hydrocodes: Applications for atmospheric breakup and impact cratering. Int. J. Impact Eng. 1997, 20, 411–430. [Google Scholar] [CrossRef]
- Gittings, M.; Weaver, R.; Clover, M.; Betlach, T.; Byrne, N.; Coker, R.; Dendy, E.; Hueckstaedt, R.; New, K.; Oakes, W.R.; et al. The RAGE radiation-hydrodynamic code. Comput. Sci. Discov. 2008, 1, 015005. [Google Scholar] [CrossRef]
- Shuvalov, V. Multi-dimensional hydrodynamic code SOVA for interfacial flows: Application to the thermal layer effect. Shock Waves 1999, 9, 381–390. [Google Scholar] [CrossRef]
- Benz, W.; Asphaug, E. Simulations of brittle solids using smooth particle hydrodynamics. Comput. Phys. Commun. 1995, 87, 253–265. [Google Scholar] [CrossRef]
- Hayes, J.C.; Norman, M.L.; Fiedler, R.A.; Bordner, J.O.; Li, P.S.; Clark, S.E.; Mac Low, M.M. Simulating Radiating and Magnetized Flows in Multiple Dimensions with ZEUS-MP. Astrophys. J. Suppl. Ser. 2006, 165, 188. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Steinberg, D.J. Equation of State and Strength Properties of Selected Materials; Technical Report UCRL-MA-106439; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1996. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).