Abstract
The registration between images is a crucial part of the 3-D tooth reconstruction model. In this paper, we introduce a registration method using our proposed statistical randomization-based particle swarm optimization (SR-PSO) algorithm with the iterative closet point (ICP) method to find the optimal affine transform between images. The hierarchical registration is also utilized in this paper since there are several consecutive images involving in the registration. We implemented this algorithm in the scanned commercial regular-tooth and orthodontic-tooth models. The results demonstrated that the final 3-D images provided good visualization to human eyes with the mean-squared error of 7.37 micrometer2 and 7.41 micrometer2 for both models, respectively. From the results compared with the particle swarm optimization (PSO) algorithm with the ICP method, it can be seen that the results from the proposed algorithm are much better than those from the PSO algorithm with the ICP method.
1. Introduction
A 3-D tooth model reconstruction is a very crucial part of orthodontics. It is a helpful tool in diagnostic or examination and also problem identification in the treatment planning process in other dental caries in adults and children [1]. This is especially true in children in which dental caries are one of the most children chronic diseases [2]. Nowadays, the most powerful tools are image reconstructions from sophisticated devices, for example, CT or laser. There are several research works on CT image reconstruction [3] and the reconstruction from multimodal images [4,5,6]. Unfortunately, oral healthcare is not sufficient and dental care access is limited, particularly in rural areas [7]. In Thailand, the dental innovation foundation under royal patronage has provided dental care access in rural communities for a long time. However, one of the difficulties in providing dental care to children in those areas is how to take a 3-D tooth image inside their mouths. It is not easy to use any sophisticated imaging devices when the units are applied in the countryside due to the distance or the location limitation.
Therefore, a 3-D reconstruction system from optical images is needed. Still, one of the essential processes in 3-D image reconstruction is image registration. In the literature, there exist some 2-D medical image registration research works [8,9,10,11,12]. However, in our case, the 3-D registration is more suitable. There exist some 3-D medical image registration methods [13,14] that utilize several features in the registration process including point-cloud coordinates representing the 3-D shapes of objects. These coordinates have also been used in the registration process shown in [15,16,17,18,19,20]. All the mentioned research works utilize a variation of the particle swarm optimization (PSO) to find the matching location between the source and target images. Most of the existing registration methods find the matching locations/points based on rotation and/or translation only. However, in the 3-D affine transform, there are other types of transform, e.g., scaling, shearing, and reflection.
In this paper, we develop a system that can create a 3-D image from optical images. However, it is not easy to use real images taken from children due to a research ethical approval requirement. Therefore, we postulate scanned images from two commercial tooth models and then create point-cloud images. We propose the statistical randomization-based particle swarm optimization (SR-PSO) algorithm to find an appropriate affine transform (shearing, rotation, scaling and translation) between images for the registration purpose. The proposed SR-PSO algorithm is based on a modification of the particle swarm optimization [21] to cope with the premature convergence [22] and to improve exploration and exploitation of the algorithm [23]. After that, the iterative closet point (ICP) method [24,25] is used to refine the resulting registration because the ICP method has been proved in several research works [8,17] that it can help to refine registered results. Finally, the 3-D tooth models are reconstructed.
2. Registration Method
In a 3-D registration problem, the geometry transform can be calculated from the relation between two point-cloud images. The more they are related, the higher quality of the transformation. The highest quality transformation corresponds to the minimization of the following statement:
where P is the target point-cloud matrix ([pi]M×4, M is the number of target point-cloud points), Q is the source point-cloud matrix ([qj]N×4, N is the number of source point-cloud points), and H is the geometry transform. Finally, O(⋅) is an objective function. Since the transformation H is estimated by finding the nearest neighbor [26] between a set of point-pairs (pj, qj), the minimum error of the distance between two corresponding points can be considered [27]. Using the mean squared error (MSE), hence, the minimization problem, in this case, is calculated as
The transformation H is the 3-D transformation with 15 unknown parameters, i.e., 3 parameters from scaling (S), 3 parameters from translation (T), 3 parameters from rotation (R), and 6 parameters from shearing (SH) [28]. The matrix H is computed as
where , , and , and
H= T × S × R × SH,
Hence,
where
It is worthwhile noting that a through j are non-rigid transformations resulting from the combination of scaling, shearing, and rotation properties. Meanwhile, l, m, and n are simply tx, ty, and tz, respectively. Moreover, p, q, and r are set to 0 since they are perspective property values. Finally, s is always set to 1 because of the scaling factor.
The proposed statistical randomization-based particle swarm optimization (SR-PSO) algorithm described in the following section is used to find the optimal H. Each individual in the swarm has 15 dimensions. The search space is defined as shown in Table 1.

Table 1.
Parameters boundaries in optimization process.
Statistical Randomization-Based PSO (SR-PSO) Algorithm
In this research, we modify the particle swarm optimization [21,29,30,31] following [22,23] to cope with the premature convergence, low accuracy, and to improve exploration and exploitation of the algorithm. In particular, we modify and combine the methods in [22] and [23] to exploit both of their advantages.
Let X = be a set of N particles in the swarm in d-dimensional feature space. and xg are the individual best of the ith particle and the global best of the swarm, respectively. The update equations for velocity and position of each particle are
where r1 and r2 are randomly generated numbers from the uniform distribution within [0, 1]. c1 and c2 are the acceleration coefficients, and w is the inertia weight calculated by [29,30,31]
where wmax = χ, T is the number of iterations, α = 1 (normally 0 < α ≤ 2), and
In our case, we also set the velocity limit to [vmin, vmax] where
In the experiment, we set k = 0.1.
We modify the method in [22] by introducing an extra intermediate particle by randomizing the particle’s position using Gaussian distribution in each dimension in order to increase the chance of premature convergence avoidance. The details of intermediate particles are as follows:
For the jth dimension of intermediate particle with K being the number of particles in the swarm,
- −
- Calculated from an average of all individual best :
- −
- Calculated from a median of all individual best :
- −
- Calculated by random generate number from Gaussian distribution with mean and standard deviation computed from individual best positions:
- −
- Calculated from the larger absolute value of the maximum and the minimum in that dimension:
- −
- Calculated from the smaller absolute value of the maximum and the minimum in that dimension:
If the lth intermediate particle (xtml) is the best particle among the intermediate particles and it is better than the global particle, then the global best particle will be replaced by xtml.
To increase the chance of exploration and exploitation of xg, we randomly select the individual best () from all particles (instead of randomly selecting a particle except the best one as in [23]) using
For each dimension (), if a randomly generated number (∈ [0, 1]) is bigger than or equal to a certain thresholding value, we reinitialize by randomizing the number within [lbi, ubi], where lbi and ubi are the lower and upper bounds in the search space in the ith dimension. That is
In this case, we set the thresholding value to 1 − (1/d), where d is the number of dimensions of a particle. If is better than xg, it is then updated using
The SR-PSO algorithm is summarized as followings:


In our experiment, the optimal solution is the global best in the last population. To fine tune the registration results from the SR-PSO algorithm, after we find the optimized parameters, we utilize the iterative closest point algorithm (ICP) method as in [24,25] with the Nelder–Mead simplex method [32].
3. Experimental Results
The 3-D tooth model reconstruction system is shown in Figure 1. The SR-PSO algorithm is used to find the optimal transformation matrix H−1 (transform from source point-cloud to target point-cloud). The ICP method is used to fine-tune the resultant H−1. Finally, the 3-D tooth models are reconstructed based on the registered source and target point-clouds.
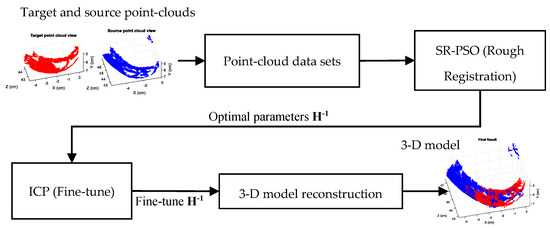
Figure 1.
Diagram of the proposed 3-D tooth model reconstruction system.
To test the algorithm, we ran the experiment of the generated original shape and its 3-D transformation as shown in Figure 2.
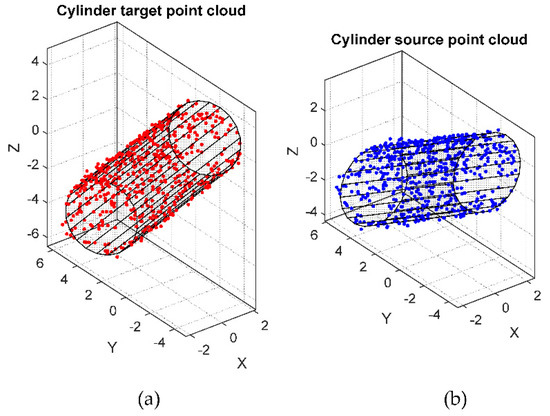
Figure 2.
(a) The original shape (Target point-cloud) and (b) the 3-D transformation (Source point-cloud).
The transformation matrix used to transform the original shape described by the target point-cloud (Figure 2a) to the transformed shape described by the source point-cloud (Figure 2b) is
Hence, the transform matrix from the source point-cloud (Figure 2b) to the target point-cloud (Figure 2a) is
In the experiment, the parameters for the SR-PSO algorithm were set as shown in Table 2. To demonstrate how the SR-PSO algorithm works in each step, we provide an example as follows:

Table 2.
Statistical randomization-based particle swarm optimization (SR-PSO) algorithm’s parameters settings in the experiment.
Suppose an initialized particle is , then after the velocity and position are updated, the transformation is . The individual best of this particle is and the global best in this iteration is . Then, all five intermediate particles are ,
,
,
, and
. The best of intermediate particles is and it is better than , hence . Then from Equation (20) is . After comparing with , is better, hence . Figure 3 depicts the registration mean-squared error (MSE) of the global best of the SR-PSO algorithm. We can see that, as the iteration proceeds, the MSE decreases and moves towards 3.22 × 10−31 at the 2000th iteration. Figure 4 shows the registration progress image of the global best particle in the 1st, 50th, 500th, and 2000th iterations. It can be seen that the registration result in the last iteration is an almost perfect match.
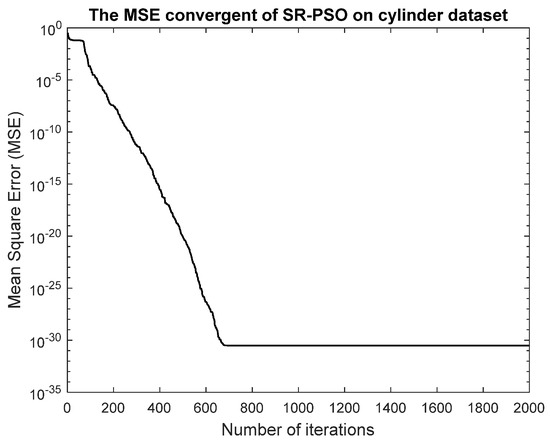
Figure 3.
Mean−squared error (MSE) of SR−PSO algorithm.
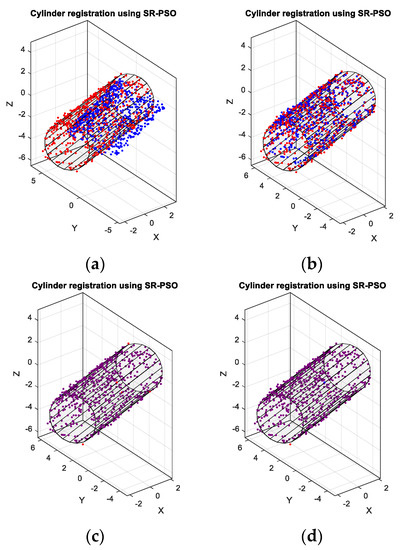
Figure 4.
Registration results from the global best particle at the (a) 1st, (b) 50th, (c) 500th, and (d) 2000th iterations.
The registration mean-squared errors (MSEs) using the SR-PSO algorithm with and without refining with the ICP method are shown in Table 3. The best result is when α = 1.5 with an extremely tiny error of 3.22 × 10−31. The best final registration result is also shown in Figure 5.

Table 3.
The registration mean-squared error (MSE) in pixels2 (the best value is in bold).
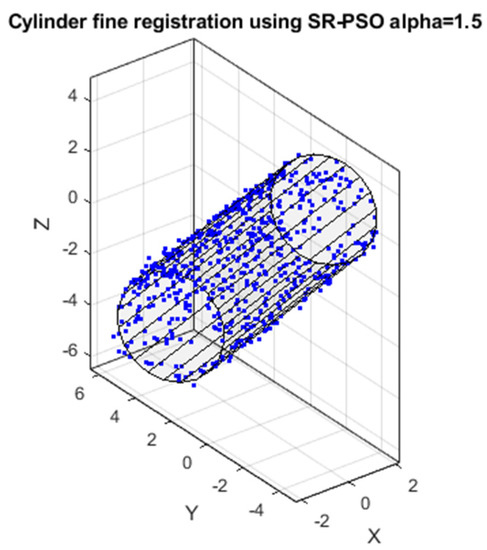
Figure 5.
The best final registration.
The best final transformation matrix is
Although the MSEs of the final registration with the other values of α are not as good, the final registration images are almost aligned as shown in Figure 6. The reason for this mistake might be because the SR-PSO algorithm does not find the correct global minimum.
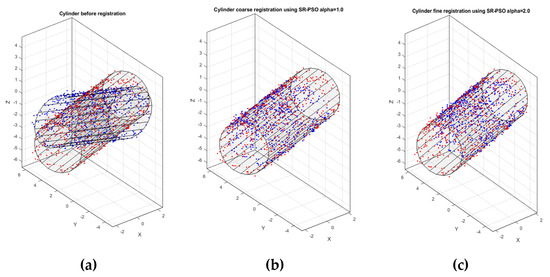
Figure 6.
(a) The superimposed image before registration, the final registration with α is equal to (b) 1.0, and (c) 2.0.
Now, we are ready to implement this algorithm on tooth reconstruction. We used the EinScan series, a commercial 3-D scanner, to collect a point-cloud data set in several consecutive views from two commercial tooth models. Examples of data acquisition setup and the point-cloud data are shown in Figure 7.

Figure 7.
(a) Hardware setup and (b) point-cloud view.
We implemented this system on two different tooth models, i.e., a regular tooth model and an orthodontic tooth model. We used only six consecutive point-cloud coordinate (x, y, z) views with an interval of 30 degrees in each model. The information of the tooth point-cloud data is shown in Table 4.

Table 4.
Tooth dataset information.
In this dataset, we randomly sampled each view into 60% of the original view. We also assumed that there was overlapping between each consecutive view. We also selected representative points inside the overlapping area using the voxel hull method [33,34,35] before we implemented the registration process with the parameter setting shown in Table 2. Since there were six consecutive views, we utilized the hierarchical registration to increase the registration performance as shown in Figure 8 with F = 6. At each level, we selected the best final registration result (SR-PSO algorithm with the ICP method) to survive to the next level of the hierarchical registration.
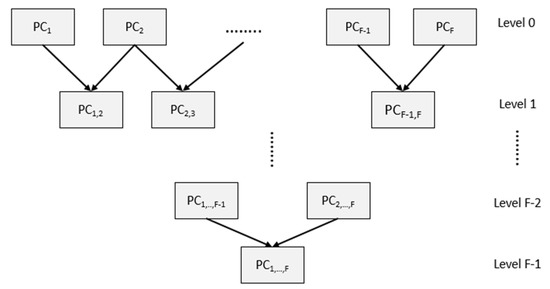
Figure 8.
Hierarchical multiple-views registration.
We also compared the results with those from the regular particle swarm optimization (PSO) algorithm with the ICP method. The registration process from the PSO algorithm with the ICP method is the same as the SR-PSO algorithm with the ICP method. However, the inertia weight update equation in PSO [29] is
The parameter setting was similar to those used in the SR-PSO algorithm except that wmin, wmax, c1, and c2 were set to 0.4, 0.9, 2, and 2, respectively.
For the regular-tooth model, the registration MSEs for the SR-PSO algorithm and the PSO algorithm for each registration pair are shown in Table 5. Meanwhile, the registration MSEs for each of the two algorithms with the ICP method for each registration pair are shown in Table 6. Figure 9 and Figure 10 show the best registration image of each consecutive pair from the SR-PSO algorithm without and with the ICP method, respectively. Again, the local optima are the cause of high MSE in pair-wise registration. Although Table 6 shows that the PSO algorithm with the ICP method is a little bit better than the SR-PSO algorithm with the ICP method in some pair-wise registrations, i.e., 1 vs. 2, 2 vs. 3, and 3 vs. 4, the difference is only in the order of 0.002 to 0.05 micrometer2. When considering the final registration results of six consecutive views shown in Table 7, we find that the best result from the SR-PSO algorithm with the ICP method and α = 1.5 is 7.3666 micrometer2 whereas that from the PSO algorithm with the ICP method is 17.1150 micrometer2. The result from the SR-PSO algorithm with the ICP method is better than that from the PSO algorithm with the ICP method. The final registration result of the regular-tooth model is shown in Figure 11. We can see that the final registration image provides a good visualization to human eyes.

Table 5.
MSE from SRPSO and PSO for the regular-tooth model (the best value is in bold and the worst value is underlined).

Table 6.
MSE from SR−PSO with iterative closet point (ICP) and PSO with ICP for the regular-tooth model (the best value is in bold).
Figure 9.
The best SR-PSO registration results for the pairs (a) 1 and 2; (b) 2 and 3; (c) 3 and 4; (d) 4 and 5; (e) 5 and 6 of the regular-tooth model.
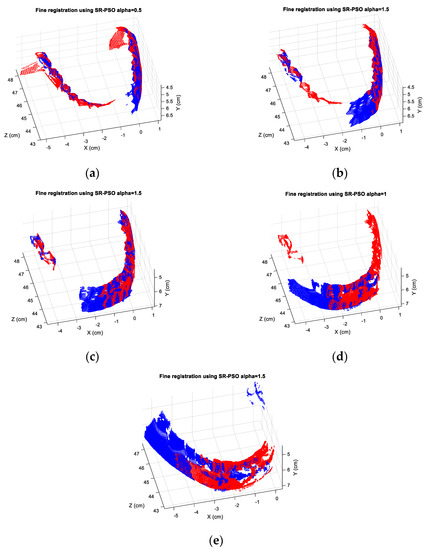
Figure 10.
The best SR-PSO with the ICP registration results for the pairs (a) 1 and 2; (b) 2 and 3; (c) 3 and 4; (d) 4 and 5; (e) 5 and 6 of the regular-tooth model.

Table 7.
MSE of the final registration of six consecutive views (micrometer2) for the regular-tooth model (the best value is in bold).
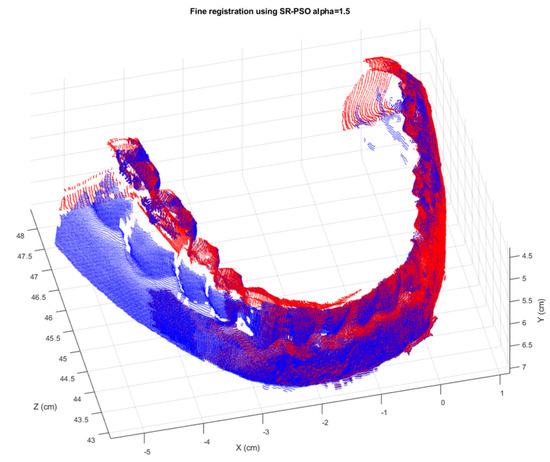
Figure 11.
The final registration result of six consecutive views of the regular-tooth model from the SR-PSO with the ICP.
For the orthodontic-tooth model, the registration MSEs for the SR-PSO algorithm and the PSO algorithm for each registration pair are shown in Table 8. Figure 12 shows the best registration images of different pairs from the SR-PSO algorithm. Meanwhile, the registration MSEs for the SR-PSO algorithm with the ICP method and the PSO algorithm with the ICP method for each registration pair are shown in Table 9. The best registration images of different pairs from the SR-PSO algorithm with the ICP method are shown in Figure 13. We can see that using only the SR-PSO algorithm provides better results than using only the PSO algorithm. However, the PSO algorithm with the ICP method is better than the SR-PSO algorithm with the ICP method in one of the pair-wise registrations (4 vs. 5) with a little difference. The final registration MSEs of the six consecutive views are shown in Table 10. The best final 3-D registration image is from the SR-PSO algorithm with the ICP method and α = 0.5. It has an MSE of 7.4130 micrometer2 whereas the comparable error of 7.4672 micrometer2 is achieved by the PSO algorithm with the ICP method. We can also see in Figure 14 that the final 3-D registration image of the orthodontic-tooth model also provides a good visualization to human eyes.

Table 8.
MSE from SR-PSO and PSO for the orthodontic-tooth model (the best value is in bold).
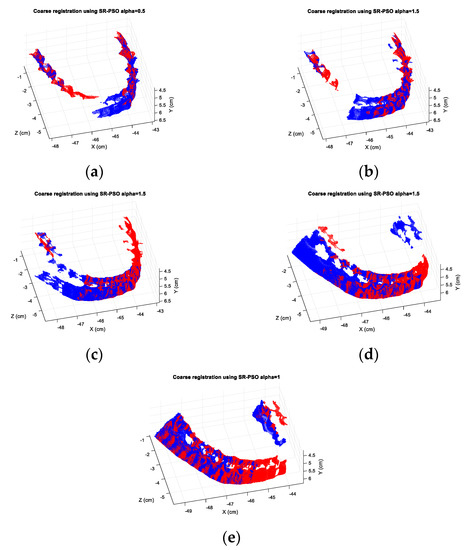
Figure 12.
The best SR-PSO registration results for the pairs (a) 1 and 2; (b) 2 and 3; (c) 3 and 4; (d) 4 and 5; (e) 5 and 6 of the orthodontic-tooth model.

Table 9.
MSE from SR-PSO with ICP and PSO with ICP for the orthodontic-tooth model (the best value is in bold).
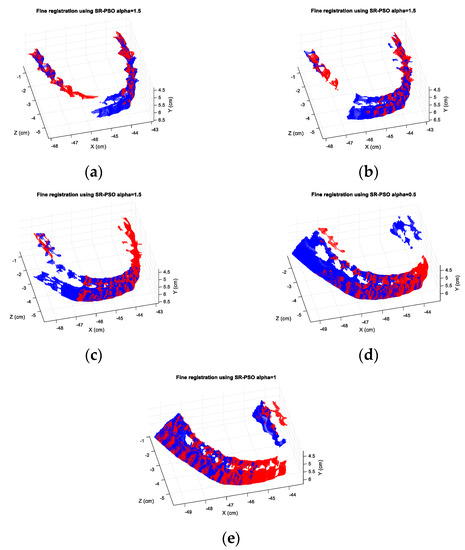
Figure 13.
The best SR-PSO with ICP registration results for the pairs (a) 1 and 2; (b) 2 and 3; (c) 3 and 4; (d) 4 and 5; (e) 5 and 6 of the orthodontic-tooth model.

Table 10.
MSE of the final registration of six consecutive views (micrometer2) for the orthodontic-tooth model (the best value is in bold).
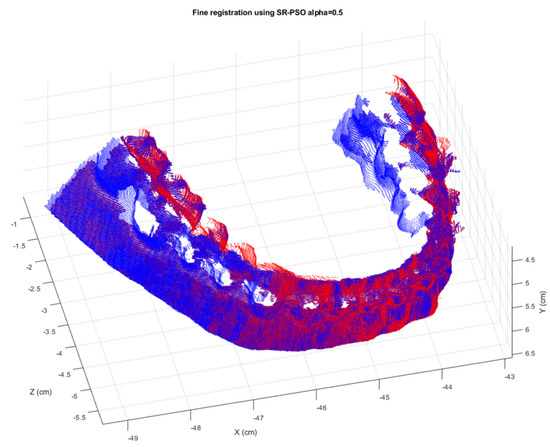
Figure 14.
The final registration result of six consecutive views of the orthodontic-tooth model from the SR-PSO with the ICP.
4. Conclusions
To aid in orthodontics or the diagnostic and treatment planning process in dental caries, a 3-D tooth model reconstruction is one of the important parts. In this paper, we introduce a registration process using our proposed statistical randomization-based particle swarm optimization (SR-PSO) algorithm with the iterative closet point (ICP) method to determine the optimal affine transform between images in 3-D. Because there were several consecutive images scanned from a commercial tooth model, we implemented a hierarchical registration process to produce the final registration image. We also compared the results with those from the particle swarm optimization (PSO) method with the ICP method. The best results from the SR-PSO algorithm with the ICP method for the regular-tooth model and the orthodontic-tooth model yielded the mean-squared error (MSE) of 7.3666 micrometer2 and 7.4130 micrometer2, respectively. For the sake of comparison, the MSEs from the PSO algorithm with the ICP method for the two tooth models were 17.115 micrometer2 and 7.4672 micrometer2, respectively. The SR-PSO algorithm with the ICP method provided better results than that of the PSO algorithm with the ICP method. Moreover, the resulting 3-D images from the SR-PSO algorithm with the ICP method are also viewable by human eyes and are useful for experts. In future work, we will implement this algorithm for the tooth models with defections in order to simulate dental caries in real situations.
Author Contributions
All authors conceived and designed the experiments; R.W. performed the experiments; and all authors contributed to the writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Royal Golden Jubilee Ph.D. Program (Grant No. PHD-0170-2558).
Institutional Review Board Statement
Not applicable.
Acknowledgments
The authors would like to thank the Royal Golden Jubilee PhD Program (RGJ-PhD) for support under grant No. PHD-0170-2558 for financial funding.
Conflicts of Interest
The authors of the paper do not have any conflict of interest with any companies or institutions. This work was supported by the Thailand Research Fund under the Royal Golden Jubilee Ph.D. Program (Grant No. PHD-0170-2558). This article does not contain any studies with human participants or animals performed by any of the authors.
References
- Sivakumar, A.; Thangaswamy, V.; Ravi, V. Treatment planning in conservative dentistry. J. Pharm. Bioallied Sci. 2012, 4, S406–S409. [Google Scholar] [CrossRef] [PubMed]
- Hugar, S.M.; Sogi, H.P.S.; Nalawade, T.M.; Sinha, A.; Hugar, S.; Mallikarjuna, R.M. Knowledge, attitude, and practices of oral health care in prevention of early childhood caries among parents of children in Belagavi city: A Questionnaire study. J. Fam. Med. Prim. Care 2016, 5, 286–290. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, R.; Sugaya, Y.; Kasahara, S.; Omachi, S. Tooth shape reconstruction from dental CT images with the region-growing method. Dentomaxillofacial Radiol. 2014, 43, 20140080. [Google Scholar] [CrossRef]
- Zhou, X.; Gan, Y.; Xiong, J.; Zhang, D.; Zhao, Q.; Xia, Z. A Method for Tooth Model Reconstruction Based on Integration of Multimodal Images. J. Heal. Eng. 2018, 2018, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Gan, Y.; Xiong, J.; Xia, Z. Three-dimensional tooth model reconstruction based on fusion of dental computed tomography images and laser-scanned images (Chineses Article). Shengwu Yixue Gongchengxue Zazhi 2017, 34, 7–14. (In Chinese) [Google Scholar] [PubMed]
- Yau, H.-T.; Yang, T.-J.; Chen, Y.-C. Tooth model reconstruction based upon data fusion for orthodontic treatment simulation. Comput. Biol. Med. 2014, 48, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Srisilapanan, P.; Nirunsittirat, A.; Roseman, J. Trends over Time in Dental Caries status in Urban and Rural Thai Children. J. Clin. Exp. Dent. 2017, 9, e1201–e1206. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Fakhry, A.E.; El-henawy, I.; Qiu, T.; Sangaiah, A.K. Feature and Intensity Based Medical Image Registra-tion Using Particle Swarm Optimization. J. Med. Syst. 2017, 41, 197. [Google Scholar] [CrossRef]
- Sarvamangala, D.R.; Kulkarni, R.V. Swarm Intelligence Algorithms for Medical Image Registration: A Comparative Study. Commun. Comput. Inf. Sci. 2017, 776, 451–465. [Google Scholar] [CrossRef]
- Khan, M.K.; Nystrom, I. A Modified Particle Swarm Optimization Applied in Image Registration. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; IEEE: Piscataway Township, NJ, USA, 2010; pp. 2302–2305. [Google Scholar]
- Jara, R.I.; Imbachí; Buchelly, F.J.; Meschino, G.; Ballarin, V.L. Improved Particle Swarm Optimization algorithm applied to rigid registration in medical images. In VII Latin American Congress on Biomedical Engineering CLAIB, Proceedings of the VII Latin American Congress on Biomedical Engineering CLAIB 2016, Bucaramanga, Santander, Colombia, 26–28 October 2016; Torres, I., Bustamante, J., Sierra, D., Eds.; IFMBE Proceedings; Springer: Singapore, 2016; Volume 60, pp. 161–164. [Google Scholar]
- Yonghong, Y.; Jiying, L.; Qiang, W.; Tao, Z. Improved Particle Swarm Optimization Image Registration Based on Mutual Information. In Proceedings of the 2019 11th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Qiqihar, China, 28–29 April 2019; IEEE: Piscataway Township, NJ, USA, 2019; pp. 450–453. [Google Scholar]
- Wachowiak, M.P.; Smolíková, R.; Zheng, Y.; Zurada, J.M.; Elmaghraby, A.S. An Approach to Multimodal Biomedical Im-age Registration Utilizing Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 289–301. [Google Scholar] [CrossRef]
- Chen, Y.-W.; Mimori, A. Hybrid Particle Swarm Optimization for Medical Image Registration. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjian, China, 14–16 August 2009; IEEE: Piscataway Township, NJ, USA, 2009; Volume 6, pp. 26–30. [Google Scholar]
- Zhan, X.; Cai, Y.; He, P. A three-dimensional point cloud registration based on entropy and particle swarm optimization. Adv. Mech. Eng. 2018, 10, 1–13. [Google Scholar] [CrossRef]
- Zhan, X.; Cai, Y.; Li, H.; Li, Y.; He, P. A point-cloud registration algorithm based on normal vector and particle swarm optimization. Meas. Control. 2019, 53, 1–11. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, B.; Nie, J.; Sun, B. A point cloud registration method combining enhanced particle swarm optimization and iterative closest point method. In Proceedings of the 2016 Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; IEEE: Piscataway Township, NJ, USA, 2016; pp. 2810–2815. [Google Scholar]
- Yousry, M.; Youssef, B.A.B.; El Aziz, M.A.; Sidky, F.I. 3D Point-cloud Registration Using Particle Swarm Optimization Based on Different Descriptors. Int. J. Sci. Eng. Res. 2017, 8, 558–564. [Google Scholar]
- John, V.; Xu, Y.; Mita, S.; Long, Q.; Liu, Z.; Tan, Y.; Takagi, H.; Shi, Y. Registration of GPS and Stereo Vision for Point Cloud Localization in Intelligent Vehicles Using Particle Swarm Optimization. In Lecture Notes in Computer Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 10385, pp. 209–217. [Google Scholar]
- Zhang, L.; Yang, B.; Wang, L.; Zhao, X.; Zhou, J.; Li, M.; Han, Y. Three-dimensional Cement Image Registration Based on Multi-layer PSO and Mutual Information. In Proceedings of the 2016 3rd International Conference on Informative and Cybernetics for Computational Social Systems (ICCSS), Jinzhou, China, 26–29 August 2016. [Google Scholar]
- Kennedy, J.; Eberhart, E. Particle swarm optimization. In International Conference on Neural Networks (ICNN); IEEE: Perth, WA, Australia, 1995; pp. 1942–1948. [Google Scholar]
- Sun, L.; Song, X.; Chen, T. An Improved Convergence Particle Swarm Optimization Algorithm with Random Sampling of Control Parameters. J. Control. Sci. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Fajr, R.; Bouroumi, A. An Improved Particle Swarm Optimization Algorithm for Global Multidimensional Optimization. J. Intell. Syst. 2017, 29, 127–142. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, Z. A survey of iterative closest point algorithm. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 4395–4399. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification, 2nd ed.; John Willey & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vision Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- FitzGibbon, A.W. Robust registration of 2D and 3D point sets. Image Vis. Comput. 2003, 21, 1145–1153. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, CEC00 (Cat. No.00TH8512), La Jolla, CA, USA, 16–19 July 2000; pp. 84–88. [Google Scholar]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia Weight strategies in Particle Swarm Optimization. In Proceedings of the Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- Rathore, A.; Sharma, H. Review on Inertia Weight Strategies for Particle Swarm Optimization. In Proceedings of the Advances in Intelligent Systems and Computing; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Volume 547, pp. 76–86. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder—Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Briese, C.; Ressl, C. A Correspondence Framework for ALS Strip Adjustments based on Variants of the ICP Algorithm. Photogramm. Fernerkund. Geoinformation 2015, 2015, 275–289. [Google Scholar] [CrossRef]
- Glira, P.; Pfeifer, N.; Ressl, C.; Briese, C. Rigorous Strip Adjustment of Airborne Laserscanning Data Based on the ICP Algorithm. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 73–80. [Google Scholar] [CrossRef]
- Point-Cloud Tools for Matlab. Available online: www.geo.tuwien.ac.at/downloads/pg/pctools/pctools.html (accessed on 10 December 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).