Abstract
In order to select the optimal transportation route among alternative transportation routes more accurately and objectively, the choice of urban oversize cargo transportation routes was studied by taking the optimization weight–TOPSIS combination method for specific calculations. This model, based on an entropy weight method, cloud model, and TOPSIS method, combines the superiority of the cloud model for reflecting the randomness and discreteness of subjective evaluation with the advantages of the TOPSIS method in dealing with the problem of multi-objective programming. Through selecting and classifying several the main road influencing factors of urban oversize cargo transportation, based on the data of four urban roads, the entropy weight method is used to initially determine the weights of each influencing factor, the cloud model is used to optimize weights, the TOPSIS method is used to compare and evaluate the paths, and the optimal transportation route is selected on this basis. The results showed that the optimization weight–TOPSIS method is scientific and accurate for the multi-objective planning of oversize cargo transportation route selection, and solves the problem of the impact of subjective factors in existing methods and the difficulty of processing multiple influencing factors. The Pearson consistency test results show that the Pearson correlation coefficient between the proposed method and the actual oversize cargo transportation route selection is 0.995, which is higher than the calculation results without using the combination weight.
1. Introduction
As an important part of modern logistics, oversize cargo transportation refers to a series of applications of suitable vehicles, ships, and other transportation tools, using the corresponding safety measures and the necessary administrative permission, via roads, waterways, railways, and other transportation methods, from the place of departing to the place of delivery. A series of professional operations such as moving, loading and unloading, transportation, and storage of oversize cargos with non-dismantling characteristics is carried out.
Due to the development of infrastructure construction, the number and scale of construction projects are increasing, and the large-scale equipment supporting them is becoming bigger, heavier, and of higher value. The demand for the oversize cargo logistics market continues to increase.
Due to actual transportation demands, there are situations where oversize cargoes are transported through cities. This kind of transportation has caused great problems for urban traffic. Generally, it is necessary to block roads in advance and carry out necessary demolition operations. At the same time, because the transportation speed of oversize cargoes is generally slow, it will also cause long-term lane occupation over time. Furthermore, the inability to select a suitable transportation route quickly and accurately is an unsolved problem of current oversize cargo transportation. In order to minimize the interference of oversize cargo transportation on urban traffic from the space dimension and the time dimension, as well as make the route selection of oversize cargo transportation faster and more reasonable, this paper proposes a model of oversize cargo transportation route selection based on the optimization weight–technique for order preference by similarity to an ideal solution (TOPSIS) method. The purpose of the research is to construct a calculation and grade division method for urban oversize cargo transportation routes.
Our research uses the entropy weight method for initial weight calculation, the cloud model for weight optimization, and the TOPSIS method for route selection. Since the entropy weight method can fully reflect the objectivity of the weights, it is selected as the initial weight calculation. Since the cloud model can perform a good conversion between subjective and objective expressions, the cloud model is introduced to optimize the weights of the entropy weight method. Since the TOPSIS method has a good application effect for multi-objective planning problems, it is used to calculate the final result. In the summary section, the calculations of the TOPSIS method, entropy weight–TOPSIS method, and the optimization method used in our research are compared and analyzed with the actual transportation selections in the past five years.
This paper is divided into five parts for writing, as shown in Figure 1:
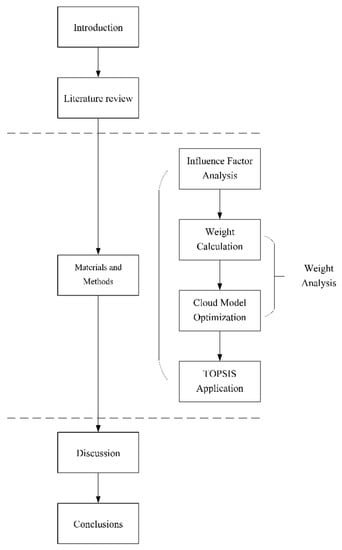
Figure 1.
Research route.
2. Literature Review
In the field of oversize cargo transportation, Meng has conducted research on a route selection method based on the turns of road intersections [1]. Petraška suggested an algorithm for the assessment of heavy-weight and oversize cargo transportation routes [2]. Bazaras developed a route selection criteria system for oversize goods transportation [3]. Wolnowska performed research on the multi-criterial analysis of oversize cargo transport through a city [4]. Luo tried to find a route planning method of multimodal transportation for oversize and heavy cargo based on reconstruction [5].
Additionally, some scholars have conducted research on route selection in recent years. Koohathongsumrit used Functional Resonance Analysis Method (FRAM), data envelopment analysis (DEA), and multi-criteria decision-making (MCDM) methods to conduct research on transportation route selection and used a real-world multimodal freight transportation route selection between Thailand and Cambodia to verify them [6]. Pamucar proposed an adaptive neuro fuzzy inference guidance system, which can provide actual routing advice to the driver in light of the real-time traffic conditions [7]. Ma presented a multi-objective robust optimization model for transportation by taking robust control parameters into consideration [8]. In the area of modelling, Herrera contrasted the Sequentially Timed Events Plotting (STEP) method and the Functional Resonance Analysis Method (FRAM) for accident analysis and modelling [9]. Zhu introduced the novel integration of a Super efficiency SBM model of data envelopment analysis (DEA) and Partial Least Squares Structural Equation Modeling (PLS-SEM) in a land use study [10]. Campisi researched the benefits of including a small underpass in a city through Analytical Hierarchy Process (AHP), which prioritized a number of decision-making alternatives [11].
At present, scholars from various countries have conducted a lot of research on the use of the entropy weight method. Its application fields and scenarios have become wider, and it has been widely used in agriculture, industry, economy, computer, energy, transportation, and other fields. In traffic and transportation, Huang used the entropy weight method to evaluate the transportation of dangerous cargos; the results show that the unsafe actions and behaviors of humans are the most dangerous factors that influence the normal and safe operations of transportation [12]. Guo used the entropy weight method to determine the weight of each evaluation metric to analyze the impact of reticulation community, which is open to the surrounding road traffic [13]. In other fields, researchers have used the entropy weight method to study a series of environmental issues, mainly focusing on many evaluations, such as the impact of floods [14,15,16], the water quality of groundwater and surface water [17,18], the impact of environmental pollution, the vulnerability of building landslides [19], the impact of climate disasters [20], and the analysis of the interaction between population and environment [21], etc. The entropy weight method also had many applied types of research in economics. In recent years, research has mainly focused on the selection of suppliers and order distribution [22], enterprise product quality evaluation [23], soft power analysis [24], community sustainability assessment of public rental housing [25], user behavior analysis [26], social development analysis [27], and social impact evaluation [28], etc. In the research of energy and related fields, scholars used the entropy weight method to optimize the design of the hybrid energy system [29], comprehensive evaluation of power grid planning [30], evaluation of park energy utilization [31], comprehensive risk assessment of electricity [32], calculation of petroleum standard indicators [33], and diesel engine emission evaluation [34], etc. In other practical application fields, scholars also used the entropy weight method to determine weight coefficients in ionospheric combination prediction [35], construction project management evaluation [36], decision support for heavy machine remanufacturing [37], etc. There have been many studies on the entropy weight method itself, such as a study on Shannon entropy [38], studies on the combination of AHP and the entropy weight method [39,40], a study on the combination of the entropy weight method and fuzzy algorithm [41], and research on the combination of the ideal point method and the entropy weight method [42,43]. At the same time, Kumar et al. systematically reviewed and sorted the development process of the entropy weight method [44].
Cloud models study fuzziness and randomness and the relationship between them, which can improve the deficiency of probability theory and fuzzy mathematics in dealing with uncertainty. Therefore, it is applied in risk control, trust evaluation, and other aspects of research. Zhao and Li proposed a hybrid risk evaluation model based on a cloud model and fuzzy comprehensive evaluation (FCE) method to evaluate the risk of Ultra High Voltage projects and find out the key risk factors [45]. Liu applied a novel integrated FMEA model based on cloud model theory and a hierarchical TOPSIS method to assess and rank the risk of failure modes [46]. Wang developed a new quantifiable subjective trust evaluation approach based on the cloud model, which can effectively support subjective trust decisions and provide a helpful exploitation for subjective trust evaluation [47]. Zhang suggested a trust evaluation method for clustered wireless sensor networks based on the cloud model, which implements the conversion between the qualitative and quantitative of sensor nodes’ trust metrics [48]. Li used the cloud model in a smart distribution grid to achieve mutual combination and conversion between the qualitative evaluation system and the quantitative study [49]. Wang proposed a decision-making method based on a cloud model in order to solve multicriteria group decision-making problems in situations where the criteria weights are known completely, but the decision-makers’ weights are unknown and the criteria values are interval linguistic variables [50].
In the application of the TOPSIS method, some scholars used it in the research of logistics and transportation. Li used TOPSIS to determine the location of the logistics center and verify the applicability of TOPSIS in the field of transportation and logistics [51] and supplier selection [52]. Rostamzadeh used TOPSIS to conduct research on risk management in the supply chain and transportation fields, and these research results have been well applied in enterprises [53]. Sirisawat used TOPSIS to study reverse logistics in the electronics industry and illustrated the robustness of the method [54]. In other fields, the TOPSIS method is often used—e.g., in management research, such as the analysis of corporate driving factors [55], the selection of device location [56], the selection of personnel [57], the selection of information technology solutions [58], and the problem of location selection [59], etc. The main research achievements for the environment are earthquake disaster analysis [60], environmental indicator evaluation [61], solid waste management [62], and drought assessment [63], etc. Over recent years, improvement of the TOPSIS method has been in progress. Yoon introduced the behavior tendency of decision-makers to improve the TOPSIS method [64]. Akram explored the application of the TOPSIS method in group decision making [65], Zhang introduced grey relational analysis [66], Hanif introduced the CBR method [67], and Sangaiah integrated fuzzy DEMATEL, TOPSIS, and ELECTRE methods [68].
It can be summed up from the literature review that there is currently no research on the route selection of oversize cargo transportation passing through a city. However, there are research foundations of oversize cargo transportation and route selection. From the method perspective, the literature review introduces the current research status of the entropy weight method, cloud model, and the usage of the TOPSIS method in recent years. These three methods have not been combined and applied in the research and practical application of oversize cargo transportation, and will be further explored and discussed in this paper.
3. Materials and Methods
3.1. Influence Factor Analysis
Many influence factors need to be considered in urban oversize cargo transportation. Some key factors play an important role in transportation. Some directly affect whether the transportation route can be used, and others have a great impact on the cost and time of transportation operations. Through the actual operation of large cargo transportation, and the opinions of practitioners in a logistics company, this paper selects the following factors as the basic influence factors for evaluating the urban transportation of oversize cargo: total mileage, number of horizontal curves with a turning radius less than 20 m, number of switch-back curves, road mileage with a longitudinal gradient greater than 5%, road mileage with a width of less than 15 m, road mileage with a width greater than 25 m, and the number of bridges with headroom less than 5 m.
There are many types of attribute, including benefit attributes, cost attributes, and interval attributes. The benefit attribute has a positive influence on the result, the cost attribute has a negative influence on the result, and the interval attribute can be accepted in a certain interval.
This section is divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.
3.1.1. Total Mileage
In a general sense, the increase in total mileage of a road section will increase the transportation cost and transportation time, which is a factor to be considered in path comparison. It is defined as a cost attribute, denoted as TM, and its unit is kilometers.
3.1.2. Horizontal Curves
In urban transportation, inevitably, there will be intersection turns; the length and width of the oversize cargos are larger than the ordinary cargos and the trajectory deviation is greater than that of ordinary vehicles when passing through the curve. In the general urban road design process, ordinary vehicles are used as a design reference, and the transportation of oversize cargo is rarely considered. Therefore, transportation bottlenecks are often formed in the curvature radius of the turning radius, which is too small, and the general reconstruction method is to widen the roadbed and pavement at the curve.
In this paper, the number of horizontal curves with a radius less than 20 m and the number of switch-back curves, which mainly affect the transportation of oversize cargos, are taken as the important influence factors for the judgment of transportation channels. In actual transportation, the smaller the curve of the small radius curvature, the higher the passing capacity of the oversize cargo; therefore, it is defined as a cost attribute. The number of horizontal curves with a radius less than 20 m is denoted as FC and the unit is quantity. The number of switch-back curves is denoted as TC and the unit is quantity.
3.1.3. Longitudinal Gradient
The value of urban road longitudinal gradient directly affects a series of problems such as driving speed, transportation cost, and transportation safety. For oversize cargo, the impact of longitudinal gradient on transportation will increase compared to ordinary cargo due to the expansion of the weight and volume of the cargo. Therefore, the longitudinal gradient is an influencing factor that must be considered. Based on the influence of the actual urban transportation process, this paper introduces one influence factor—road mileage with a longitudinal gradient of more than 5%. The longitudinal gradient is defined as a cost attribute. The road mileage with a longitudinal gradient greater than 5% is denoted as LG and the unit is kilometers.
3.1.4. Road Width
Road width is also one of the influencing factors affecting the urban transportation path of oversize cargo. The level of urban roads, the number of two-way lanes, and whether or not there are partitions will affect the width of the passable roads. Branch roads with narrow road widths or roads with partitions will restrict urban oversize cargo transportation. In this paper, road mileage with a width less than 15 m and road mileage with a width greater than 25 m are regarded as important factors in determining the transportation path. The shorter the road mileage with a width less than 15 m, the higher the passing capacity of the oversize cargos, which is defined as a cost attribute, denoted as RN, with the unit being kilometers. The longer the road mileage with a width greater than 25 m, the higher the passing capacity of the oversize cargos, which is defined as a benefit attribute, and denoted as RW, with the unit being kilometers.
3.1.5. Bridges
Due to the intersection of roads and overpass bridges and pedestrian bridges in urban roads, the available headroom of the road changes. This research counts the number of overpass bridges and pedestrian bridges in each route and uses the 5 m clearance height usually required for oversize cargos as the demarcation point to count the number of flyovers with a clearance height of less than 5 m.
Many intersections use overpass bridges to reduce the conflict of traffic flow lines. Due to the existence of overpass bridges, the usable road headroom changes. This paper counts the number of overpass bridges on each road and counts the number of bridges with a headroom less than 5 m. The number of bridges with a headroom less than 5 m is a cost attribute, denoted as BN, and the unit is quantity.
Based on the road design drawings and on-site measurements, the data of four routes through Suzhou are selected as alternative route sections for urban oversize cargo transportation. The attribute values of the four routes are in Table 1:

Table 1.
Alternative routes attribute values.
- In all Tables of this paper:
- FC is the number of horizontal curves with a radius less than 20 m.
- TC is the number of switch-back curves.
- TM is the total mileage.
- LG is the road mileage with a longitudinal gradient greater than 5%.
- RW is the road mileage with a width greater than 25 m.
- RN is the road mileage with a width less than 15 m.
- BN is the number of bridges with headroom less than 5 m.
3.2. Weight Calculation
3.2.1. Standardize
First, the data are standardized and non-quantitatively strengthened, and the original road parameter data are scaled to make them fall into a small specific interval. To remove the unit restriction of the data, the original data are transformed into a dimensionless value, so that the factors of different units can be compared and weighed. The original data matrix is set as:
In this paper, the Z-score method is used to standardize the original data, and the conversion formula of the Z-score method standardization is as follows:
where indicates the original data, indicates the mean value of the original data, indicates the standard deviation of the original data, and is the standardized value of the original data.
After standardized calculation, the descriptive statistics of the original data are in Table 2:

Table 2.
Descriptive statistics of original data.
After the standardization, each datum retains two decimal places, and the matrix is recorded as:
3.2.2. Determine the Weight of Influencing Factor
In this paper, the entropy weight method is used to determine the weight of each influencing factor. According to the explanation of basic principles of information theory, information is a measure of system order and entropy is a measure of system disorder. According to the definition of information entropy, for a certain item factor, the entropy value can be used to measure the degree of a certain factor’s discreteness. The smaller the information entropy value of the factor, the greater the degree of the factor’s discreteness, and the greater the impact of the factor on the comprehensive evaluation (i.e., weight); if the value of the factor is all equal, the factor does not play a role in the comprehensive evaluation. Therefore, the tool of information entropy can be used to calculate the weight of each factor and provide a basis for a comprehensive evaluation of multiple factors.
Based on standardized data, a factor data matrix is constructed with the information entropy. Setting the information entropy of each factor to , its calculation formula is:
where indicates the number of alternative routes, and in this paper, this is 4. If , then define . According to the calculation formula of information entropy, the information entropy of eight factors is calculated as . Based on the information entropy, the weights of the seven factors are calculated as:
The result of the calculation is shown in Table 3:

Table 3.
Information entropy and weight.
3.3. Cloud Model Optimization
The entropy in the cloud model reflects the degree of value divergence. Our research uses cloud entropy to optimize the weights obtained by the entropy weight method, and proposes an improved factors weight calculation method. The subjective scores of oversize cargo transportation practitioners in a Suzhou logistics company are processed through the cloud model, and then, the improved calculation method is used to obtain a weight distribution that takes into account both subjective and objective weights, and reflects the importance of each factor as accurately as possible.
3.3.1. Definition of Cloud Model
Set U as a quantitative target interval with clear upper and lower bounds, and C as a qualitative subinterval of U with fuzzy upper and lower bounds. For a certain value in the target interval U, denote it as . The membership degree of for the qualitative subinterval C is recorded as . For all , the distribution of the membership degree in the target interval is defined as the membership cloud. The value range of is [0,1]. The membership cloud is the insinuation from U to the value range of in the target interval, denoted as .
3.3.2. Descriptive Statistics of Cloud Model
Cloud models are generally characterized by three descriptive statistics, which are mean value (), entropy (), and hyper-entropy (). The cloud model can be expressed as .
: The mean value in the cloud model is the same as the mean value in statistics. It is the average value of all cloud droplets and the basic characteristic value of the cloud model, which can reflect the central position of the model.
: The entropy of the cloud model is defined by the randomness of the cloud droplets set in the model. It is a representation of the uncertainty of the cloud droplets set, as well as the dispersion and ambiguity between cloud droplets. The magnitude of entropy reflects the breadth of the subinterval C. The larger the entropy, the wider the coverage of C.
: Hyper-entropy is a secondary statistic based on entropy, which is a representation of the uncertainty of entropy and also a manifestation of the randomness of the cloud model. In the cloud model, the greater the hyper-entropy, the larger the cloud thickness and the greater the degree of dispersion between cloud droplets.
3.3.3. Backward Cloud Generator
The backward cloud generator (BCG), as shown in Figure 2, is the process of transforming a certain number of accurate numerical values into qualitative relations , and further analysis and calculations are carried out according to the three descriptive statistics, , , and , of the generated cloud model. This is the basic transformation principle of BCG. In this case, we input the exact score, analyze the discreteness of the score through BCG from , , and , and use the result of the analysis as an important reference for weights. Our research uses the backward cloud generator as the tool of weight optimization.

Figure 2.
Backward cloud generator.
Our research invites Suzhou oversize cargo logistics practitioners to give scores to factors and use a backward cloud generator to analyze the score table.
The mean of the data is calculated as:
The center distance of the data is calculated as:
The variance of the data is calculated as:
The cloud entropy of the data is calculated as:
According to the calculation result of cloud entropy, combined with the entropy weight method, calculate the optimized weight according to Formula (9). The mean values are processed on the basis of the degree of dispersion , and the weights of the factors in this part are calculated and adjusted, and then the result is combined with in Section 3.2.
The judgement is based on two aspects: the mean value and the cloud entropy. The larger the mean cloud value, the more important a factor is. If the cloud entropy is larger, it means that the practitioners have greater disagreement on the factor, and the weight of the factor should be reduced. The smaller the cloud entropy, the smaller the disagreement among practitioners on this factor, and the weight of the factor should be increased.
The subjective scores of oversize cargo transportation practitioners in a Suzhou logistics company are shown in Table 4. The research conducted this investigation with practitioners and asked them to score the impact of factors on the actual transportation process based on work experience and actual cases. The score range is 0–100, and the score is an integer multiple of 5. The higher the importance, the higher the score.

Table 4.
The scores given by practitioners.
The score is calculated by the backward cloud generator, and the cloud images obtained are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9:
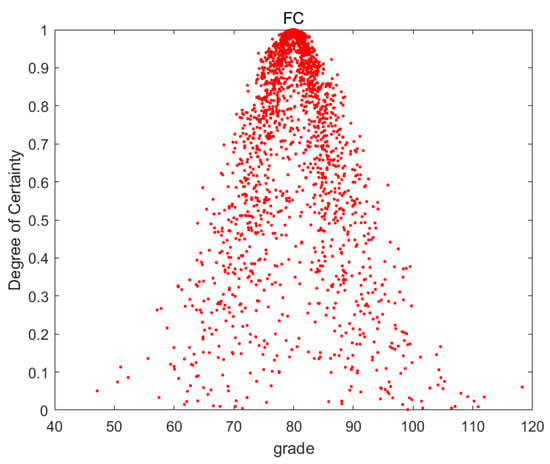
Figure 3.
Cloud image of FC.
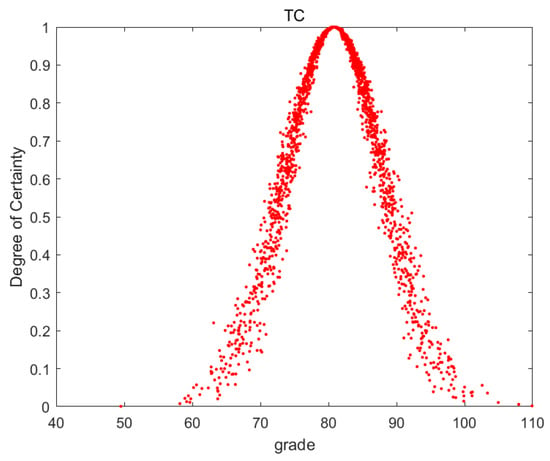
Figure 4.
Cloud image of TC.
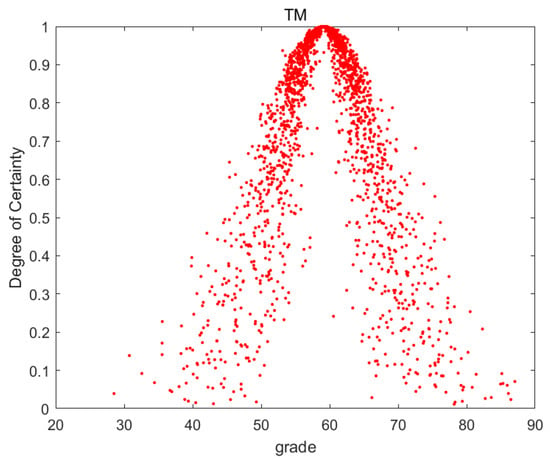
Figure 5.
Cloud image of TM.
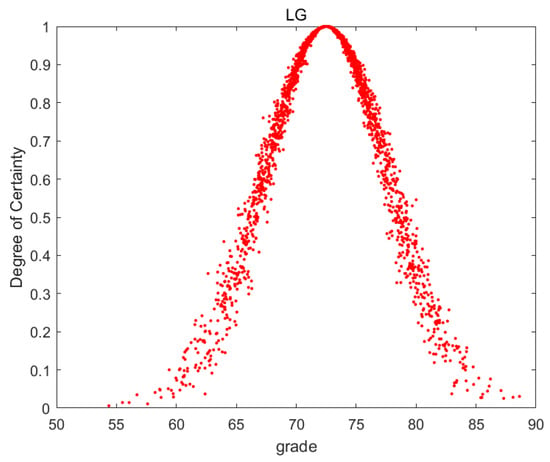
Figure 6.
Cloud image of LG.
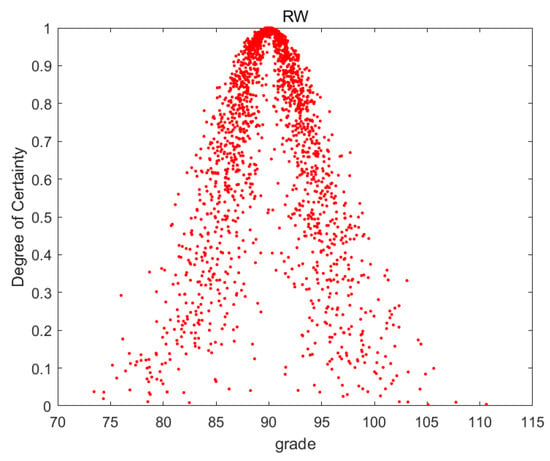
Figure 7.
Cloud image of RW.
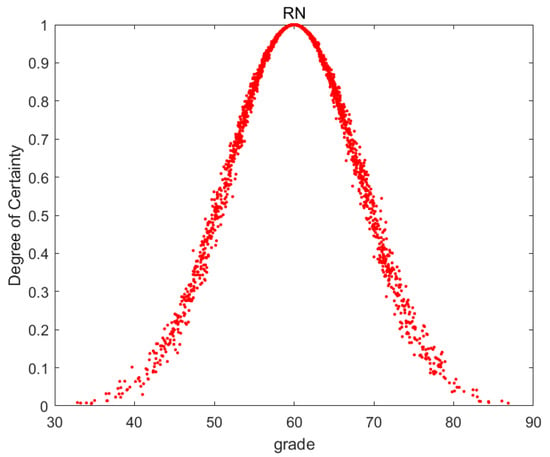
Figure 8.
Cloud image of RN.
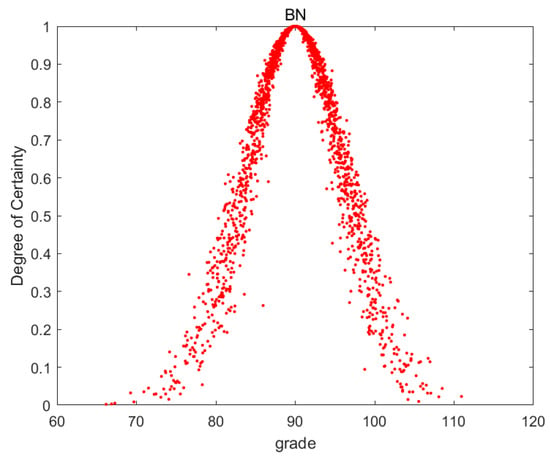
Figure 9.
Cloud image of BN.
The degree of dispersion of the droplets in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 indicates the inconsistency of individual scores for this indicator. It can be seen from the figures that the degree of dispersion of RN, LG, TC, and BN is significantly smaller, indicating that the score trends for these indicators are consistent. The middle line of the images in the figures represents the mean value of the indicators. The mean value of the indicators is adjusted according to the degree of dispersion. The higher the degree of dispersion, the greater the divergence of individual scores on this indicator, which should be reduced on the basis of the mean value.
The mean value (), entropy (), and hyper-entropy () of the eight factors are shown in Table 5:

Table 5.
The descriptive statistics of cloud models.
According to Formula (9), using the mean value and the cloud entropy to optimize the weight obtained by the entropy weight method in Section 3, the optimized weights are shown in Table 6:

Table 6.
The factors weight.
3.4. TOPSIS Application
3.4.1. Step 1
The same trend processing can make any scheme with the better standardized attribute value have a larger attribute value after processing.
Normalize benefit attributes and cost attributes and establish a corresponding matrix. Convert the values in the table to the interval [0,1].
The standardized decision matrix is recorded as: .
The transformed decision matrix is recorded as: .
Set as the maximum value in j column of the decision matrix, and as the minimum value in j column of the decision matrix.
If is a benefit attribute, then:
In this paper, road mileage with a width greater than 25 m is a benefit attribute.
If is a cost attribute, then:
In this paper, cost attribute includes: total mileage, number of horizontal curves with a turning radius less than 20 m, number of switch-back curves, road mileage with a longitudinal gradient greater than 5%, road mileage with a width of less than 15 m, and the number of bridges with a headroom less than 5 m.
Although this paper does not involve interval attributes, for the completeness of theoretical system, supplementary explanations on interval attributes are provided.
If there are interval attributes, set the optimal attribute interval be ; is the intolerable lower bound and is the intolerable upper bound.
The worst attribute value after transformation is 0, and the best attribute value is 1. After same trend processing, each datum retains two decimal places, and the matrix is recorded as:
3.4.2. Step 2
Normalize the data matrix after the same trend processing and establish the corresponding matrix. The data are subjected to secondary standardization processing and the matrix is set after secondary standardization processing as: .
In this matrix,
Then, construct a weighted normalization matrix:
After weighted normalization, the factor data characteristics of the four alternative routes are as Figure 10:
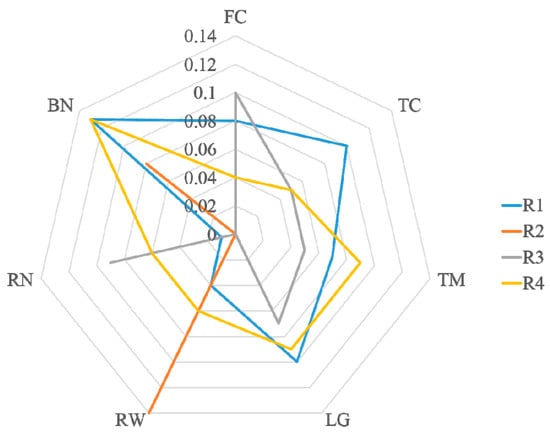
Figure 10.
Factor data characteristics.
3.4.3. Step 3
Determine the positive and negative ideal solution. The positive ideal solution plane is formed by the maximum value in matrix V of the benefit factors and the minimum value in matrix V of the cost factor from all alternative routes. The negative ideal solution plane is formed by the minimum value in matrix V of the benefit factors and the maximum value in matrix V of the cost factor from all alternative routes.
where indicates the benefit attribute and indicates the cost attribute. The positive ideal solution plane and the negative ideal solution plane, as shown in Figure 11, can be obtained.
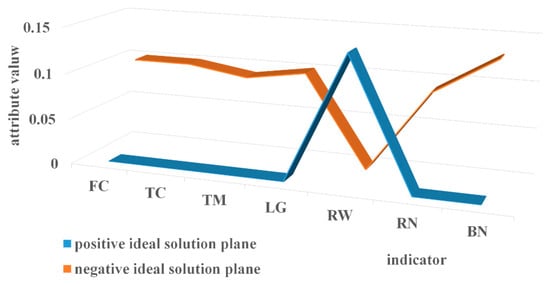
Figure 11.
Positive and negative ideal solution planes.
3.4.4. Step 4
For all the alternative routes, the better route is closer to the positive ideal point plane and further away from the negative ideal point plane. Therefore, the factors’ comprehensive distance between the positive ideal solution plane and the negative ideal solution plane in each alternative route should be calculated. The calculation method is:
where indicates the distance between each oversize cargo transportation route and the positive ideal solution plane. indicates the distance between each urban oversize cargo transportation route and the negative ideal solution plane.
The calculated results are shown in Table 7:

Table 7.
Distance to positive and negative ideal solution planes.
3.4.5. Step 5
Calculate the relative proximity and make a judgment; the route with the higher relative proximity is the better one.
where indicates the relative proximity. The calculation result is: , , , .
It can be summarized from the calculation result that the priority ranking of the four alternative routes is .
4. Discussion
As a comparison, this article compares the calculation results using only the TOPSIS method and the entropy weight–TOPSIS method with the calculation results used in our research. The calculation results of the three methods are shown in Table 8:

Table 8.
Relative proximity of three methods.
It can be seen that when only the TOPSIS method is used, the ranking of four routes is . When the entropy weight–TOPSIS method is used, the ranking of four routes is . In order to verify the feasibility of the proposed method, we selected the transportation of oversize cargo across Suzhou in the last 5 years for comparison as shown in Table 9.

Table 9.
Actual route selections of oversize cargo transportation.
It can be seen that in the actual route selections of oversize cargo transportation in the past five years, 22 transportations have occurred. Among them, there are three selections for route 1, nine selections for route 2, five selections for route 3, and four selections for route 4. The percentages are 0.136, 0.409, 0.227, and 0.182. The Pearson correlation coefficients between the three methods and the actual transportation route selections were checked; the Pearson correlation coefficients are shown in Table 10:

Table 10.
Pearson correlation coefficient.
According to the analysis, it can be concluded that the matching degree between the optimization weight–TOPSIS method proposed in this research and the actual transportation route selections is significantly higher than the TOPSIS method, and slightly higher than the entropy weight–TOPSIS method. In the actual urban transportation of oversize cargo, in addition to objective conditions, the subjective route choice is also very important. Therefore, subjective judgment should be appropriately introduced in the design of the route selection algorithm to make the calculation results more realistic.
Regarding the calculation of the TOPSIS, the authors believe that the calculation method used in this paper is effective for the situation discussed in this case. In some special cases, such as when the solution plane is difficult to reach, the positive ideal solution plane and the negative ideal solution plane can be adjusted to meet the requirements of variables and practical applications.
5. Conclusions
Based on the optimization for entropy weight–TOPSIS with the cloud model, this paper constructs a calculation method for the selection of oversize cargo transportation routes, which can improve the reasonability and accuracy of route selection. The entropy method is used to objectively weight the seven main transportation influence factors, and on this basis, the cloud model is used to optimize weight with a subjective score and the TOPSIS method is used to divide alternative transportation routes. Using four routes through Suzhou which are capable of oversize cargo transportation for empirical analysis and calculations, reasonable calculation results could be obtained. In the actual transportation of oversize cargos, the calculation results of this method could be used to provide the decision-making basis for the rapid selection of oversize cargos through the city.
This method could comprehensively consider subjective and objective weights. Furthermore, because the urban oversize cargo transportation route choice problem is a multi-target plan, the accuracy and scientificity of the evaluation results are guaranteed by introducing the cloud model into the entropy weight method to distinguish the attributes of each factor. Based on the characteristics of the cloud model that can reasonably handle subjective evaluation, it can be used to optimize the weight; the objective distribution of the weight is ensured and the subjective opinions of the practitioners are fully considered.
For different types of oversize cargos, adjusting factors in the actual transportation process could be considered. For example, for ultra-high cargos, the decision maker could introduce more height-related factors, such as traffic lights and overhead wires. For ultra-wide cargos, more factors related to width could be introduced, such as bus stops.
The main contributions of this study can be summarized as follows:
- It summarizes the factors that need to be generally considered in urban oversize cargo transportation.
- Based on the characteristics of the cloud model that can reasonably handle subjective evaluation, it can be used to optimize the weight; the objective distribution of the weight is ensured and the subjective opinions of the practitioners are fully considered.
- The weight optimization method combined with TOPSIS is introduced into the field of oversize cargo transportation passing through a city for the first time, providing a new route selection solution. Its Pearson correlation coefficient for actual transportation is 0.018 higher than the entropy weight–TOPSIS method and 0.057 higher than the TOPSIS method.
This research can be used for the selection of large cargo transportation routes within cities but there is no discussion on whether large cargo can be split and transported, which can be improved upon in future research. However, since the selected survey objects are all from urban large-cargo transportation cases, the method can be used in intercity large-cargo transportation—but it needs to be adjusted according to the characteristics of intercity transportation.
Author Contributions
Conceptualization, D.H. and M.H.; Formal analysis, D.H.; Funding acquisition, M.H.; Investigation, M.H.; Methodology, D.H.; Project administration, M.H.; Validation, D.H.; Writing—original draft, D.H. and M.H.; Writing—review and editing, D.H. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data and analyses from the current study are available from the corresponding authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meng, L.; Hu, Z.; Huang, C.; Zhang, W.; Jia, T. Optimized Route Selection Method based on the Turns of Road Intersections: A Case Study on Oversized Cargo Transportation. ISPRS Int. J. Geo-Inf. 2015, 4, 2428–2445. [Google Scholar] [CrossRef]
- Petraška, A.; Čižiūnienė, K.; Jarašūnienė, A.; Maruschak, P.; Prentkovskis, O. Algorithm for the assessment of heavyweight and oversize cargo transportation routes. J. Bus. Econ. Manag. 2017, 18, 1098–1114. [Google Scholar] [CrossRef][Green Version]
- Bazaras, D.; Batarlienė, N.; Palsaitis, R.; Petraška, A. Optimal road route selection criteria system for oversize goods transportation. Balt. J. Road Bridg. Eng. 2013, 8, 19–24. [Google Scholar] [CrossRef]
- Wolnowska, A.E.; Konicki, W. Multi-criterial analysis of oversize cargo transport through the city, using the AHP method. Transp. Res. Procedia 2019, 39, 614–623. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Y.; Huang, J.; Yang, H. Multi-route planning of multimodal transportation for oversize and heavyweight cargo based on reconstruction. Comput. Oper. Res. 2021, 128, 105172. [Google Scholar] [CrossRef]
- Koohathongsumrit, N.; Meethom, W. An integrated approach of fuzzy risk assessment model and data envelopment analysis for route selection in multimodal transportation networks. Expert Syst. Appl. 2021, 171, 114342. [Google Scholar] [CrossRef]
- Pamucar, D.; Ćirović, G. Vehicle route selection with an adaptive neuro fuzzy inference system in uncertainty conditions. Decis. Mak. Appl. Manag. Eng. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- Ma, C.; Hao, W.; He, R.; Moghimi, B. A Multiobjective Route Robust Optimization Model and Algorithm for Hazmat Transportation. Discret. Dyn. Nat. Soc. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Herrera, I.A.; Rogier, W. Comparing a multi-linear (STEP) and systemic (FRAM) method for accident analysis. Reliab. Eng. Syst. Saf. 2010, 95, 1269–1275. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, P.; Wei, Y.; Li, Y.; Zhao, H. Measuring the efficiency and driving factors of urban land use based on the DEA method and the PLS-SEM model—A case study of 35 large and medium-sized cities in China. Sustain. Cities Soc. 2019, 50, 101646. [Google Scholar] [CrossRef]
- Campisi, T.; Socrates, B.; Tesoriere, G.; Trouva, M.; Papas, T.; Mrak, I. How to Create Walking Friendly Cities. A Multi-Criteria Analysis of the Central Open Market Area of Rijeka. Sustainability 2020, 12, 9470. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Yu, Y.; Xu, Y.; Xu, M.; Zhang, R.; De Dieu, G.J.; Yin, D.; Liu, Z. Historical data-driven risk assessment of railway dangerous goods transportation system: Comparisons between Entropy Weight Method and Scatter Degree Method. Reliab. Eng. Syst. Saf. 2021, 205, 107236. [Google Scholar] [CrossRef]
- Guo, S. Application of Entropy Weight Method in the Evaluation of the Road Capacity of Open Area; MEP: Hangzhou, China, 2017; Volume 1839, p. 20120. [Google Scholar]
- Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. J. Hydrol. 2018, 563, 975–986. [Google Scholar] [CrossRef]
- Gorgij, A.D.; Kisi, O.; Moghaddam, A.A.; Taghipour, A. Groundwater quality ranking for drinking purposes, using the entropy method and the spatial autocorrelation index. Environ. Earth Sci. 2017, 76, 269. [Google Scholar] [CrossRef]
- Lianxiao; Morimoto, T. Spatial Analysis of Social Vulnerability to Floods Based on the MOVE Framework and Information Entropy Method: Case Study of Katsushika Ward, Tokyo. Sustainability 2019, 11, 529. [Google Scholar] [CrossRef]
- Islam, A.R.M.T.; Ahmed, N.; Doza, B.; Chu, R. Characterizing groundwater quality ranks for drinking purposes in Sylhet district, Bangladesh, using entropy method, spatial autocorrelation index, and geostatistics. Environ. Sci. Pollut. Res. 2017, 24, 26350–26374. [Google Scholar] [CrossRef]
- Sahoo, M.M.; Patra, K.; Swain, J.; Khatua, K.K. Evaluation of water quality with application of Bayes’ rule and entropy weight method. Eur. J. Environ. Civ. Eng. 2016, 21, 730–752. [Google Scholar] [CrossRef]
- Zhao, H.; Yao, L.; Mei, G.; Liu, T.; Ning, Y. A Fuzzy Comprehensive Evaluation Method Based on AHP and Entropy for a Landslide Susceptibility Map. Entropy 2017, 19, 396. [Google Scholar] [CrossRef]
- Fang, R.; Shang, R.; Wang, Y.; Guo, X. Identification of vulnerable lines in power grids with wind power integration based on a weighted entropy analysis method. Int. J. Hydrogen Energy 2017, 42, 20269–20276. [Google Scholar] [CrossRef]
- Romero, I.; Delgado, A. Applying grey systems and shannon entropy to social impact assessment and environmental conflict analysis. Int. J. Appl. Eng. Res. 2017, 12, 14327–14337. [Google Scholar]
- Feng, J.; Gong, Z. Integrated linguistic entropy weight method and multi-objective programming model for supplier selection and order allocation in a circular economy: A case study. J. Clean. Prod. 2020, 277, 122597. [Google Scholar] [CrossRef]
- Ren, Z. Evaluation Method of Port Enterprise Product Quality Based on Entropy Weight TOPSIS. J. Coast. Res. 2020, 103, 766–769. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J. Comprehensive Evaluation and Analysis of Maritime Soft Power Based on the Entropy Weight Method (EWM); CISAT: Daqing, China, 2019; Volume 1168, p. 032108. [Google Scholar]
- Duan, K.; Zuo, J.; Zhao, X.; Tang, D. Integrated Sustainability Assessment of Public Rental Housing Community Based on a Hybrid Method of AHP-Entropy Weight and Cloud Model. Sustainability 2017, 9, 603. [Google Scholar] [CrossRef]
- Gong, Y.; Chen, L. Trust Evaluation of User Behavior Based on Entropy Weight Method; CENet: Xi’an, China, 2020; pp. 670–675. [Google Scholar]
- Delgado, A.; Ayala, B.; Carbajal, C. An Approach to Analyse Social Development in South America by Shannon Entropy Theory; CHILECON: Valparaiso, Chile, 2019; pp. 1–5. [Google Scholar]
- Delgado, A.; Carbajal, C.; Reyes, H.; Romero, I. Social Impact Assessment on a Mining Project in Peru Using the Grey Clustering Method and the Entropy-Weight Method; ColCACI: Barranquilla, Colombia, 2019; pp. 116–128. [Google Scholar]
- Lu, J.; Wang, W.; Zhang, Y.; Cheng, S. Multi-Objective Optimal Design of Stand-Alone Hybrid Energy System Using Entropy Weight Method Based on HOMER. Energies 2017, 10, 1664. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, D. Comprehensive evaluation of AC/DC hybrid microgrid planning based on analytic hierarchy process and entropy weight method. Appl. Sci. 2019, 9, 3843. [Google Scholar] [CrossRef]
- Zhou, S.-J.; Tan, M.; Wang, X.-D.; Yang, Y.-B.; Zhang, X.-X. Comprehensive Effectiveness Evaluation Based on Entropy Weight Method for Energy Utilization Schemes of Smart Parks; EEA: Hong Kong, China, 2017; pp. 326–332. [Google Scholar]
- Liao, X.; Xue, M.; Mao, X.; Pan, Y.; Sun, G.; Wei, Z. Risk Assessment of Integrated Electricity--Heat Energy System with Cross Entropy and Objective Entropy Weight Method; ACPEE: Chengdu, China, 2020; pp. 94–99. [Google Scholar]
- Xu, T.; Qin, C.; Zhang, H.; Qu, Y.; Fang, W. Study on Petroleum Standard Attention Index Calculation based on the Entropy Weight Method. IOP Conf. Ser. Earth Environ. Sci. 2020, 514, 514. [Google Scholar] [CrossRef]
- Muqeem, M.; Sherwani, A.F.; Ahmad, M.; Khan, Z.A. Application of the Taguchi based entropy weighted TOPSIS method for optimisation of diesel engine performance and emission parameters. Int. J. Heavy Veh. Syst. 2019, 26, 69. [Google Scholar] [CrossRef]
- Bai, H.; Feng, F.; Wang, J.; Wu, T. A Combination Prediction Model of Long-Term Ionospheric foF2 Based on Entropy Weight Method. Entropy 2020, 22, 442. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wu, D.; Zhang, Y.; Wang, M. Extension evaluation of green building Project Management performance based on entropy weight method. J. Eng. Manag. 2018, 32, 125–130. [Google Scholar]
- Du, Y.; Zheng, Y.; Wu, G.; Tang, Y. Decision-making method of heavy-duty machine tool remanufacturing based on AHP-entropy weight and extension theory. J. Clean. Prod. 2020, 252, 119607. [Google Scholar] [CrossRef]
- Song, M.; Zhu, Q.; Peng, J.; Gonzalez, E.D.S. Improving the evaluation of cross efficiencies: A method based on Shannon entropy weight. Comput. Ind. Eng. 2017, 112, 99–106. [Google Scholar] [CrossRef]
- Han, Y.M.; Fang, D.; Zhang, H.Y.; Li, Y. Efficiency Evaluation of Intelligent Swarm Based on AHP Entropy Weight Method; CISAI: Inner Mongolia, China, 2020; p. 012072. [Google Scholar]
- Qi, X.; Zhou, M. Integrated Energy Service Demand Evaluation Based on AHP and Entropy Weight Method; ICEEB: Xi’an, China, 2020; Volume 185, p. 01046. [Google Scholar]
- Wu, Z.; Chen, G.; Yao, J. The Stock Classification Based on Entropy Weight Method and Improved Fuzzy C-Means Algorithm; ICBDC: Guangzhou, China, 2019; pp. 130–134. [Google Scholar]
- Lu, J.; Wei, C.; Wu, J.; Wei, G. TOPSIS Method for Probabilistic Linguistic MAGDM with Entropy Weight and Its Application to Supplier Selection of New Agricultural Machinery Products. Entropy 2019, 21, 953. [Google Scholar] [CrossRef]
- Dos Santos, B.M.; Godoy, L.P.; Campos, L.M. Performance evaluation of green suppliers using entropy-TOPSIS-F. J. Clean. Prod. 2019, 207, 498–509. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.S.; Jatin, K.; Singh, J.; Singh, S.; Scutaru, M.-L.; Pruncu, C.I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Zhao, H.; Li, N. Risk Evaluation of a UHV Power Transmission Construction Project Based on a Cloud Model and FCE Method for Sustainability. Sustainability 2015, 7, 2885–2914. [Google Scholar] [CrossRef]
- Liu, H.-C.; Wang, L.-E.; Li, Z.; Hu, Y.-P. Improving Risk Evaluation in FMEA with Cloud Model and Hierarchical TOPSIS Method. IEEE Trans. Fuzzy Syst. 2019, 27, 84–95. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Ma, N.; Wang, S. An Evaluation Approach of Subjective Trust Based on Cloud Model; CSSE: Wuhan, China, 2008; pp. 1062–1068. [Google Scholar]
- Zhang, T.; Yan, L.; Yang, Y. Trust evaluation method for clustered wireless sensor networks based on cloud model. Wirel. Netw. 2018, 24, 777–797. [Google Scholar] [CrossRef]
- Li, L.; Liu, L.; Yang, C.; Li, Z. The Comprehensive Evaluation of Smart Distribution Grid Based on Cloud Model. Energy Procedia 2012, 17, 96–102. [Google Scholar] [CrossRef]
- Wang, J.-Q.; Peng, J.-J.; Zhang, H.-Y.; Liu, T.; Chen, X.-H. An Uncertain Linguistic Multi-criteria Group Decision-Making Method Based on a Cloud Model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Chen, Y. Selection of logistics center location using Axiomatic Fuzzy Set and TOPSIS methodology in logistics management. Expert Syst. Appl. 2011, 38, 7901–7908. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A novel plithogenic TOPSIS-CRITIC model for sustainable supply chain risk management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Rostamzadeh, R.; Ghorabaee, M.K.; Govindan, K.; Esmaeili, A.; Nobar, H.B.K. Evaluation of sustainable supply chain risk management using an integrated fuzzy TOPSIS- CRITIC approach. J. Clean. Prod. 2018, 175, 651–669. [Google Scholar] [CrossRef]
- Sirisawat, P.; Kiatcharoenpol, T. Fuzzy AHP-TOPSIS approaches to prioritizing solutions for reverse logistics barriers. Comput. Ind. Eng. 2018, 117, 303–318. [Google Scholar] [CrossRef]
- Gandhi, N.S.; Thanki, S.J.; Thakkar, J.J. Ranking of drivers for integrated lean-green manufacturing for Indian manufacturing SMEs. J. Clean. Prod. 2018, 171, 675–689. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Gamal, A.; Smarandache, F. A Group Decision Making Framework Based on Neutrosophic TOPSIS Approach for Smart Medical Device Selection. J. Med Syst. 2019, 43, 38. [Google Scholar] [CrossRef] [PubMed]
- Kelemenis, A.; Askounis, D. A new TOPSIS-based multi-criteria approach to personnel selection. Expert Syst. Appl. 2010, 37, 4999–5008. [Google Scholar] [CrossRef]
- Oztaysi, B. A decision model for information technology selection using AHP integrated TOPSIS-Grey: The case of content management systems. Knowl. Based Syst. 2014, 70, 44–54. [Google Scholar] [CrossRef]
- Fu, Z.; Liao, H. Unbalanced double hierarchy linguistic term set: The TOPSIS method for multi-expert qualitative decision making involving green mine selection. Inf. Fusion 2019, 51, 271–286. [Google Scholar] [CrossRef]
- Nyimbili, P.H.; Erden, T.; Karaman, H. Integration of GIS, AHP and TOPSIS for earthquake hazard analysis. Nat. Hazards 2018, 92, 1523–1546. [Google Scholar] [CrossRef]
- Mi, Z.-F.; Wei, Y.-M.; He, C.-Q.; Li, H.-N.; Yuan, X.-C.; Liao, H. Regional efforts to mitigate climate change in China: A multi-criteria assessment approach. Mitig. Adapt. Strateg. Glob. Chang. 2017, 22, 45–66. [Google Scholar] [CrossRef]
- Coban, A.; Ertis, I.F.; Cavdaroglu, N.A. Municipal solid waste management via multi-criteria decision making methods: A case study in Istanbul, Turkey. J. Clean. Prod. 2018, 180, 159–167. [Google Scholar] [CrossRef]
- SafarianZengir, V.; Sobhani, B.; Asghari, S. Modeling and Monitoring of Drought for forecasting it, to Reduce Natural hazards Atmosphere in western and north western part of Iran, Iran. Air Qual. Atmos. Health 2019, 13, 119–130. [Google Scholar] [CrossRef]
- Yoon, K.P.; Kim, W.K. The behavioral TOPSIS. Expert Syst. Appl. 2017, 89, 266–272. [Google Scholar] [CrossRef]
- Akram, M.; Adeel, A. TOPSIS Approach for MAGDM Based on Interval-Valued Hesitant Fuzzy N-Soft Environment. Int. J. Fuzzy Syst. 2018, 21, 993–1009. [Google Scholar] [CrossRef]
- Zhang, M.; Li, G.-X. Combining TOPSIS and GRA for supplier selection problem with interval numbers. J. Central South Univ. 2018, 25, 1116–1128. [Google Scholar] [CrossRef]
- Hanif, M.; Nishikant, M.; Sameer, K. A novel TOPSIS–CBR goal programming approach to sustainable healthcare treatment. Ann. Oper. Res. 2018, 1–23. [Google Scholar] [CrossRef]
- Sangaiah, A.K.; Gopal, J.; Basu, A.; Subramaniam, P.R. An integrated fuzzy DEMATEL, TOPSIS, and ELECTRE approach for evaluating knowledge transfer effectiveness with reference to GSD project outcome. Neural Comput. Appl. 2017, 28, 111–123. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).