Abstract
In current Proof-of-Work (PoW) blockchain systems, miners usually form mining pools to compete with other pools/miners in the mining competition. Forming pools can give miners steady revenues but will introduce two critical issues. One is mining pool selection, where miners select the pools to join in order to maximize their revenues. The other is a Block WithHolding (BWH) attack, where pools can inject part of their hash/mining power into other pools to obtain additional revenues without contributing to the mining process of the attacked pools. Reasoning that the BWH attack will have significant impacts on the pool selection, we therefore investigate the mining pool selection issue in the presence of a BWH attack in this paper. In particular, we model the pool selection process of miners as an evolutionary game and find the Evolutionarily Stable States (ESSs) of the game (i.e., stable pool population states) as the solutions. Previous studies investigated this problem from the perspective of pool managers and neglected the revenues from attacked pools (attacking revenues), leading to less accurate and insightful findings. This paper, however, focuses on the payoffs of miners and carefully takes the attacking revenues into consideration. To demonstrate how the problem is solved, we consider the scenario with two mining pools and further investigate the case where one pool attacks the other and the case where the two pools attack each other. The results in this paper show that pools can attract more miners to join by launching a BWH attack and the attack power significantly affects the stable pool populations.
1. Introduction
Blockchain, at its core, is a distributed ledger based on the technologies of encryption and Peer-to-Peer networking. Different from traditional centralized ledgers that reliably manage transactions in a central server, all participants in blockchain systems are synchronized to maintain the same copies of the transactions in order to guarantee the tamper-proof feature. Such a feature renders blockchain a highly promising technology for cryptocurrency platforms, such as Bitcoin [1] and Ethereum [2], as well as other applications like cyber–physical systems [3], access control [4,5,6,7,8], supply chain management [9], data sharing [10] and storage [11], healthcare [12,13,14], real estate [15] and media digital right [16].
Blockchain uses a data structure called block to store transactions. Each block has a hash value, which uniquely identifies the block. A block contains a timestamp, which records the time when the block was created, a difficulty, which is the system-wide difficulty requirement of generating the block (i.e., the leading n bits of the hash must be zeros), a nonce, which is some random number used to calculate the hash value of the block, and the hash of its previous block. Blocks are limited in size [17]. For example, in the current Bitcoin, the block size is limited to about 1 MB [18]. Blockchain, usually Proof-of-Work (PoW) blockchain, relies on a process called mining to create blocks and ensure the tamper-proof feature of the transactions inside. Mining is a competition among the participants of the blockchain system, whose goal is to find the latest valid block (called full PoW). Valid blocks have hash values satisfying the system-wide difficulty requirement. In a mining competition, only the first participant that finds the latest valid block is the winner and will be rewarded. For example, in Bitcoin, the winner will be given some bitcoins as the reward, which includes a fixed Coinbase reward about bitcoins [19] and a varying reward coming from the residual transaction fees.
Mining requires a huge amount of hash calculations, because the only way to find the valid hash is guessing and trying. The system-wide difficulty requirement is difficult to meet, which means that miners have to try a huge amount of different hash values until they find a valid one. This is why blockchain is considered tamper-proof, because an extremely huge amount of calculations are needed to alter the blocks, which is computationally impossible.
Since mining is computationally expensive, it is difficult for solo miners, especially those with low computation powers, to win the mining competition. Therefore, in practical blockchain systems, like Bitcoin, miners prefer to form groups called mining pools to compete with other miners or pools in the mining competition. In a mining pool, each miner contributes his/her computation power to the pool in exchange for rewards. A pool has a manger, who sets another pool-wide difficulty, which is easier to satisfy than the system-wide difficulty. All miners in the pool are required to find the blocks that meet the pool-wide difficulty (called partial PoW) and report them to the manager. The number of partial PoWs (PPoWs) will be used to measure the contributions of the miners. There are several functions to distribute rewards according to miners’ contributions, like proportional reward function, Pay-Per-Share (PPS) reward function and Pay-Per-Last-N-Share (PPLNS) reward function [20]. This paper focuses on the proportional reward function, where the rewards of miners are proportional to their contributions.
Forming pools shortens the average waiting time of miners for upcoming rewards, leading to steady mining revenues for miners. When multiple mining pools exist, miners face the problem of selecting which pool to join in order to maximize its revenues. We call this problem the mining pool selection of miners.
In addition, the existence of multiple mining pools causes another problem, i.e., the Block WithHolding (BWH) attack [21,22], where pools can inject part of their hash/mining power to other pools to obtain additional revenues while not contributing to the mining process of the attacked pools. Figure 1 illustrates the details of the BWH attack in the case of two pools, where one pool (say Pool 1) attacks the other (say Pool 2). Suppose Pool 1, i.e., the attacking pool, dispatches some of its miners as spies to Pool 2, i.e., the attacked pool. When the spies find full PoWs (FPoWs), they discard them, while they still report PPoWs to the manager of Pool 2. In this way, the spies can obtain revenues/rewards from Pool 2 by reporting PPoWs, while they actually contribute nothing to the mining of Pool 2. The revenues of the spies can be sent back to Pool 1, which will be re-distributed to the miners in Pool 1 including the spies. The study in [23] shows that a pool can obtain more revenues by launching the BWH attack to other pools.
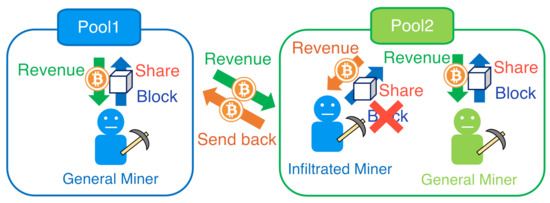
Figure 1.
Illustration of a Block WithHolding (BWH) attack.
Reasoning that the BWH attack will have significant impacts on the pool selection, we therefore aim to investigate the mining pool selection issue in the presence of BWH attack in this paper. The mining pool selection problem without considering the BWH attack was investigated in [24] based on the evolutionary game theory. The mining pool selection issue in the presence of BWH attack has also been addressed in [25] from the perspective of evolutionary game as well. The authors solved the problem from the viewpoint of pool managers and investigated how pool managers can change strategies to attract miners, which differs from the objective of this paper. In addition, the authors neglected the revenues from attacked pools, which may lead to less accurate and insightful findings. Motivated by these observations, our research objective is to investigate the mining pool selection issue under the BWH attack from the perspective of miners. Like [24,25], this paper also applies the evolutionary game theory to model the mining pool selection process and find the Evolutionarily Stable States (ESSs) (i.e., stable population states) of the game as the solutions. To achieve this goal, we first derive the expected revenue densities of all pools to determine the expected payoffs of miners in the pools. Based on the expected payoffs, we formulate replicator dynamics to represent the growth rates of the populations in all pools. With the help of the replicator dynamics, we obtain the Nash Equilibria (NE) of the game, i.e., rest points where the population growth rates are zeros, and discuss their stability to identify the ESSs of the game. To demonstrate the process of solving the game, we consider the scenario with two mining pools (Note that the two-pool scenario has been widely adopted in the analysis of mining pool selection [24,25], because this scenario is easy to analyze yet powerful enough to reveal the fundamental findings. In addition, the analysis and results obtained from this scenario can serve as the building blocks for those of more general scenarios with more mining pools.) and further investigate the case where one pool attacks the other and the case where the two pools attack each other. Simulation and numerical results are also provided to corroborate our analysis and to illustrate the theoretical findings. The results in this paper show that pools can attract more miners to join by launching the BWH attack and the attack power significantly affects the stable pool populations.
The conference version of this paper was published in [26], which focused only on the case where one pool attacks the other. This paper extends [26] by including the analysis and numerical results for the case where the two pools attack each other. Compared with the previous work in [25], this paper has the following two main contributions. First, the previous work studied the problem from the viewpoint of pool managers and focused on the payoffs of mining pools, while this paper investigates the mining pool selection problem from the viewpoint of miners and formulates the payoffs of individual miners. To do this, we propose a new concept called revenue density to characterize the revenue per unit hash power of a pool. Second, this paper carefully takes the revenues from attacked pools (i.e., attacking revenue) into consideration, while the previous work neglected the attacking revenue to simplify the analysis. The results in this paper show that neglecting the attacking power may give us inaccurate results and less insightful findings.
The rest of the paper is organized as follows. Section 2 introduces the related work. In Section 3, we model the mining pool selection problem in the presence of BWH attack as an evolutionary game and conduct analysis to solve the game. The case study with two mining pools is presented in Section 4. We provide simulations and numerical results in Section 5 and finally conclude this paper in Section 6.
2. Related Work
Game theory is a widely used method for analyzing the interactions (i.e., competition and cooperation) among rational decision makers, which choose their strategies to maximize their payoffs inside a game. Game models include non-cooperative game, extensive-form game, stochastic game, coalition formation game and evolutionary game, which have found various applications in blockchain to address the security issues and mining management. For example, the non-cooperative game model was applied to investigate the BWH attack [23,27,28,29,30,31]. The stochastic game model was adopted to study the selection between honest mining and selfish mining [32]. The coalition formation game model was chosen to solve the mining pool formation problem [33,34]. The evolutionary game model was used for modeling the mining pool selection behaviors of miners [24,25]. In this section, we focus on the studies of applying the evolutionary game to solve the mining pool selection problem. For a detailed survey on the application of game theory in blockchain, please refer to [35].
2.1. Mining Pool Selection without BWH Attack
The authors in [24] formulated the process of mining pool selection as an evolutionary game, while they focused on the case without the BWH attack. Each pool adopts different strategies, which are the size of blocks to be mined by the pool and the minimum hash power required for joining the pool. Miners select pools based on these parameters. To obtain the ESSs (i.e., stable population states), where the population of each pool remains unchanged, they investigated the time variation of population fractions for the special case with two pools. This work was later extended to various scenarios. For instance, the authors in [36] extended [24] by considering different reward sharing strategies (i.e., PPS strategy and PPLNS strategy) rather than the proportional reward sharing strategy in [24]. The authors in [37] extended [24] by additionally considering the impact of temporary fork on the revenues of miners and pools.
2.2. Mining Pool Selection under BWH Attack
The authors in [25] investigated the process of mining pool selection under BWH attack. In this study, they also used the evolutionary game theory to model the mining pool selection process of miners. However, they focused on this problem from the perspective of mining pool managers and formulated the rewards of mining pools instead of miners, which is quite different from this paper. In addition, the authors did not consider the revenues from attacked pools in the formulation, which may result in less accurate and convincing insights into the problem and make the incentive of launching the BWH arguable. In addition to the minimum required hash power and the size of blocks to be mined, the authors also considered the population of attackers as an additional strategy parameter. They investigated the properties of the population states and described how pool managers can change the mining strategies to drive the population of miners to stable states. The authors in [38] considered a scenario where miners can select to join an attacking pool to perform honest mining or the BWH attack to another pool, and modeled the selections between miners and attacking pools by indicator variables. A novel anti-attack mining revenue optimization algorithm was proposed to determine the pool selection so as to improve the group revenue of the attacking pools. In [39], the BWH game among multiple mining pools was modeled as a stochastic game and the reinforcement learning techniques were applied to analyzed the game. During the game analysis, the pool selection of miners was also considered, where each miner randomly chooses the pool to join based on the attractiveness of the pools. In [40], the authors investigated the power splitting problem of a miner under the BWH attack from the game-theoretic perspective, where a miner can choose to devote its mining power to one pool or split its mining power among multiple pools to maximize its payoff. The power splitting game can be regarded as one variant of the mining pool selection problem.
3. Evolutionary Game for Mining Pool Selection
Similar to [24], we also applied the evolutionary game theory to model the mining pool selection process of miners in the presence of BWH attack. Our goal was to obtain the ESSs and investigate the impact of the BWH attack on the ESSs. The analysis flow to solve the game is as follows. First, we define the game and parameters. We then determine the expected payoffs of miners in all the pools, which will be further used to obtain the replicator dynamics, i.e., the growth rates of population fractions of all pools. Based on the replicator dynamics, we obtain the NEs of the population fractions, where the replicator dynamics of all pools are zeros, i.e., the populations of all pools remain unchanged. Finally, we analyze the stability of the NEs to identify the ESSs.
3.1. Game Definition
We consider a blockchain network consisting of N miners and M pools. The game can be defined as . The details of the game parameters are shown in Table 1.

Table 1.
Game parameters.
Each pool i uses , and as its parameters in the game. As in [24], we assume that all miners in pool i adopt the same hash power for mining. Thus, the total hash power of pool i is . We assume that pools can not detect the existence of infiltrated hash power. All the parameters are pre-fixed before the game and will remain unchanged during the playing of the game.
3.2. Expected Payoff
We first derive the expected payoff of a miner in pool i, which is the revenue of the miner minus the cost for mining. The revenue can be given by the product of the miner’s hash power and the revenue density of pool i (i.e., the revenue obtained per unit hash power). The cost comes from the power consumption (e.g., electricity fee) for mining. We use p to denote the power charge required for unit hash power and use to denote the revenue density of pool i, which is a function of , , and as will be shown in Section 3.2.1. The expected payoff of miners in pool i can be expressed as
3.2.1. Revenue Density
Next, we consider the revenue density , which is calculated as the total revenue of pool i divided by the total hash power seen by pool i. As pools can not detect the existence of infiltrated hash power, the total hash power seen by pool i includes the hash power of pool i and those from other pools that attack pool i. Letting be the total revenue of pool i and be the total hash power of pool i, we can formulate the revenue density of pool i as
The total revenue of pool i consists of the revenue obtained from honest mining (i.e., winning the mining competition) and that obtained by attacking other pools. We call the former mining revenue and the latter attacking revenue. The mining revenue consists of the residual transaction fees and a fixed amount of revenue from the coinbase of the new block. Let C denote the fixed revenue from the coinbase and denote the transaction fee per unit block size. The mining revenue is thus given by . Since pool i can obtain the mining revenue only when it wins the mining competition, we need to consider the winning probability. Defining the winning probability by , we obtain the expected mining revenue of pool i as .
Attacking revenues are the revenues obtained from attacking other pools. Suppose pool i attacks pool j with an attack size , i.e., pool i injects a fraction of its own hash power into pool j for launching the BWH attack. The attacking revenue from pool j is the product of attacking hash power and the revenue density of pool j, which is given by , where is the hash power of pool i and is the revenue density of pool j. Summing up the attacking revenues from all the attacked pools gives the total attacking revenue of pool i, which is . Finally, combining the expected mining revenue and the total attacking revenue yields the following expression of the total revenue of pool i:
For the case without considering the attacking revenue as in [25], we can simplify the total revenue of pool i to
by simply ignoring the second term in the right-hand side of (3).
The total hash power seen by Pool i can easily be given by
3.2.2. Probability of Wining Mining Competition
We can see from Section 3.2.1 that the probability of pool i wining the mining competition is essential to determine the expected mining revenue of pool i. In the mining competition, each pool aims to mine a block with a valid hash (i.e., an FPoW). Finding such a block is a random event, because the only way is just to try different hash values relentlessly. Since all pools and solo miners join the competition, the probability that pool i mines a valid block is proportional to the ratio between its effective hash power to the network total effective hash power [34]. By effective, we mean the hash power used for mining (excluding those for BWH attack). We use to denote the probability of pool i mining a valid block, which is given by
After finding a new block, pool i broadcasts the block to its adjacent mining pools and solo miners, which will verify the block, append it to their local blockchains and further broadcast it inside the network until the block is received by the majority of the network. This is the situation when other pools and solo miners did not find valid blocks. In this situation, pool i is the winner of the competition. However, when some other pool or miner also finds valid a block, the block mined by pool i may be discarded or orphaned by most pools and miners, since the other block may arrive at these pools and miners earlier. In this situation, pool i will lose the competition. The main cause of orphaning blocks is the propagation time of blocks, which is dependent on the average block propagation delay of network links and average verification time of blocks [24]. According to [24], the propagation delay of a block of size s can be modeled as , where is a parameter related to the scale of the network and c is the average effective channel capacity of each link. The verification time of a block of size s can be modeled as a linear function , where b is a parameter determined by the scale of the network and average verification time of each node [41,42]. Thus, the average propagation time of a block of size s is given by
Suppose that the average block generation interval is a constant T. The occurrence of block orphaning due to the propagation time of blocks can be modeled as a Poisson process with mean rate [43]. Thus, the probability that the block found by pool i (i.e., of size ) is not orphaned is
Pool i wins the competition if and only if it finds a valid block and the block is not orphaned. Thus, the probability of wining the competition for pool i is
3.3. Game-Theoretic Analysis
In this section, using the results of the previous section, we analyze the game to obtain the ESSs. First, we formulate the replicator dynamics, i.e., the growth rates of the population fractions of all pools. We then find the NEs where the population fractions remain unchanged, i.e, the replicator dynamics are all zeros. Finally, we analyze the stability of the obtained NEs to identify the ESSs.
3.3.1. Replicator Dynamics
The growth rate of the miner population in a pool can be described by the replicator dynamics [44]. Based on the pairwise proportional imitation protocol [45], the replicator dynamics of pool i is given by the following Ordinary Differential Equation (ODE):
where is the population fraction of pool i at time t, is the expected payoff of miners in pool i at time t and is the average expected payoff of all the miners at time t, i.e., network average payoff. We can see that the replicator dynamics represents the growth rate of the population of pool i at time t, which is related to the difference between the miner payoff of pool i and the network average payoff. If the payoff of pool i is larger than the network payoff, its population will increase. Otherwise, its population will decrease.
3.3.2. Nash Equilibria (NE)
The population states can be interpreted as mixed strategies that each miner may choose, where each denotes the probability of selecting pool i. An NE is then a mixed strategy that is a best reply to itself. That means under the condition that other miners choose , a miner cannot gain more revenue by choosing any other rather than . Formally, an NE satisfies the following inequality [46]:
where with given by (1). According to [47], an NE is actually a rest point of the following equation system of the ODEs:
for . This means that, in an NE, the temporal growth rate of the population fraction of each pool i is zero. That is, holds [48]. By solving the above equation system, we can find the NEs of the game.
3.3.3. Evolutionary Stability of NEs
Generally, ESSs are NEs, while NEs are not necessarily ESSs. Thus, we need to analyze the stability of NEs to identify the ESSs of the game. Again, we interpret the population states as mixed strategies. Suppose the entire population adopts the strategy and there is another mutant strategy that attempts to invade a fraction of the population. If the following inequality holds, then is an ESS:
More precisely, is an ESS if the following two conditions are met [46]:
- If , then holds.
The first condition means that an ESS must be an NE. The second condition indicates that if a miner choosing strategy can earn as much revenue as a miner who chooses the NE strategy when other miners choose the NE, then a miner who chooses the NE must earn more revenue than a miner who chooses when other miners choose .
4. Case Study with Two Mining Pools
In this section, we focus on the special case with two mining pools to show how the game is analyzed.
4.1. One-Side Attack Case
We first consider the one-side attack case, where one pool attacks the other. Suppose that pool 1 attacks pool 2, i.e., and . According to (2), the revenue densities of the two pools are given by
Substituting (16) and (15) into (1), we can obtain the following expected payoffs of miners in both pools:
When pool 2 attacks pool 1, similar to (14) and (15), the revenue densities are expressed as follows:
The expected payoffs are given by
According to (10), the equation system of the ODEs for the replicator dynamics can be expressed as follows:
where is
Since , letting and , we can simplify the system of ODEs to the following equation:
Thus, the population state can be expressed as .
For the case where pool 1 attacks pool 2, substituting (17) and (18) into (26) and solving the equation yields rest points in the form of , where is given by
with
When pool 2 attacks pool 1, is also expressed as
but with
Next, we proceed to analyze the evolutionary stability of the above rest points to find the ESSs. However, this is very difficult in our game model. We therefore discuss the evolutionary stability of the rest points based on the phase portrait of the replicator dynamics, which is a geometric representation of the trajectories of the population states, as shown in Figure 2. The condition for rest points to be stable is that for a rest point, any path starting from the neighborhood (red circle in Figure 2) of that point will finally converge to that point.
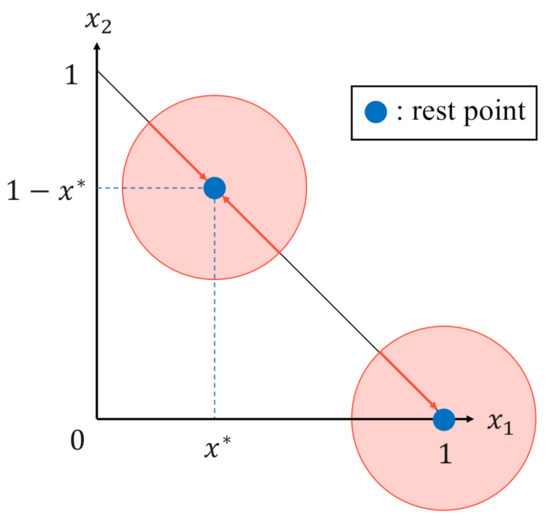
Figure 2.
Stable rest points.
4.2. Both-Side Attack Case
Next, we consider the both-side attack case, where the two pools attack each other. According to (2), the revenue densities of both pools can be expressed as follows:
Note that (29) and (30) form an equation system in terms of and . Solving this equation system, we obtain the expressions of and , which are given by (31) and (32).
However, in the both-side attack case, the expressions of the rest points are difficult to obtain due to the complexity of the replicator dynamics. Thus, we resort to numerical calculations to obtain the values of the rest points.
5. Numerical Results
In this section, we conduct simulations to show the evolution of population states in the two-pool case. The simulation results can be used to verify the correctness of our analysis in Section 3 and Section 4. We also plot the phase portraits of the replicator dynamics to show the stability of the obtained NEs. We consider three cases, i.e., the case without BWH attack (no-attack case), the one-side attack case and the both-attack case. Based on these results, we investigate the impacts of the BWH attack size on the stable population states.
5.1. Simulation Algorithm
We simulate the pool selection process based on Algorithm 1. This algorithm shows how each miner selects the pool to join based on the pairwise proportional imitation protocol. At the beginning of the simulation, each miner joins a pool randomly. After the initialization, each miner i randomly chooses a pool j () for payoff comparison and decides to move to pool j from its current pool k () with a certain probability , if the expected payoff of pool j is larger than the expected payoff of pool k. Otherwise, the miner will stay in its current pool k. These steps will be repeated until the population states converges.
| Algorithm 1 Mining Pool Selection Algorithm | ||
| 1: | Initialize: | |
| 2: | while is not converged and do | |
| 3: | for all do | |
| 4: | ||
| 5: | ▹ Choose a pool j for payoff comparison at random | |
| 6: | Move from pool k to j with probability | |
| 7: | ||
| 8: | end for | |
| 9: | ||
| 10: | end while | |
5.2. Results and Discussions
In this section, we verify the correctness of the analysis by simulations and also show the impacts of BWH attack on the population states of the mining pools. In the simulations, we execute Algorithm 1 to obtain the population states after convergence. The parameter settings used in the simulations are shown in Table 2.

Table 2.
Parameter settings.
5.2.1. No-Attack Case
First, we consider the case without BWH attack (i.e., ). In this case, we set the minimum required hash powers of the two pools as and and the block sizes of both pools as . Under this parameter setting, we obtain an NE by calculating (27) with . Figure 3a shows the corresponding phase portraits. The figure shows that all paths converge to the point , indicating the stability of the NE obtained from theoretical analysis. This result is consistent with the simulation results in Figure 3b and the results in [24], indicating the correctness of the theoretical analysis. In addition, the ratio of the population of pool 1 to that of pool 2 in the stable population state is the inverse ratio of the hash powers of pool 1 to that of pool 2. This means that the revenue of a miner depends only on the required hash power of the pool to which he or she belongs in this case.
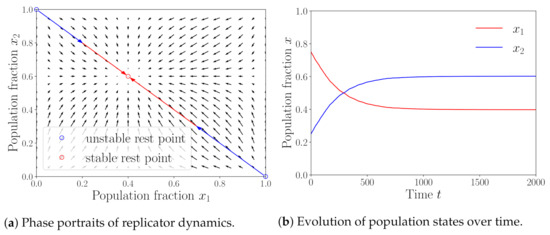
Figure 3.
No-attack case.
5.2.2. One-Side Attack Case
Next, we consider the one-side attack case, where pool 1 attacks pool 2 with attack size . Other parameters are set to the same as those in Figure 3. Under this setting, we obtain four NEs: , , and by calculating (27). Figure 4a shows the phase portrait of the replicator dynamics. We can see from Figure 4a that the population states converge to from the initial state with and converge to from . This means that only and are stable, i.e., they are ESSs. We consider three initial population states for simulations, i.e., , and . Figure 4b shows the simulation results of the evolution of population states over time. We can see from Figure 4b that the population state converges to different points from different initial states, indicating the existence of two stable population states, which are and . The simulation results are consistent with the theoretical ones, verifying the correctness of our analysis. Comparing the stable population states with those in the no-attack case, we can see that the population fraction of pool 1 increases from (no-attack case) to or to (one-side attack). This indicates that pools can attracts miners to join by launching the BWH attack.
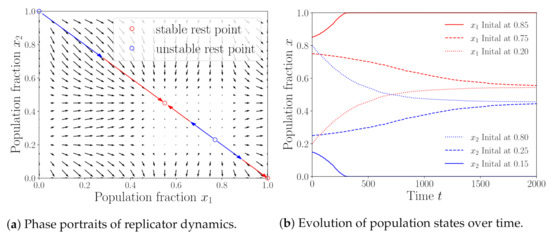
Figure 4.
One-side attack case with .
We proceed to investigate the impacts of attack size on the stable population states, for which we fix the initial population state at . Figure 5a,b show the simulation results for small attack size (i.e., in the region ) and large attack size (i.e., in the region ), respectively. From Figure 5a, we can see that as the attack size increases, the population of the attacking pool (i.e., pool 1) increases, while that of the attacked pool (i.e., pool 2) decreases. The results show that using more hash power for BWH attack attracts more miners to join, when the attack size is small. However, this is not the case when the attack size is sufficiently large, as shown in Figure 5b. We can see from Figure 5b that, for the case of the large attack size, the population of the attacking pool decreases as the attack size increases, while that of the attacked pool increases. The reason is that the larger the attack size is, the less hash power is used for mining, leading to decreased mining revenue, which dominates the trend of the total revenue of the pool. This indicates that devoting too much hash power for BWH attack may discourage miners to join the attacking pool. Similar observations have also been reported in [25].
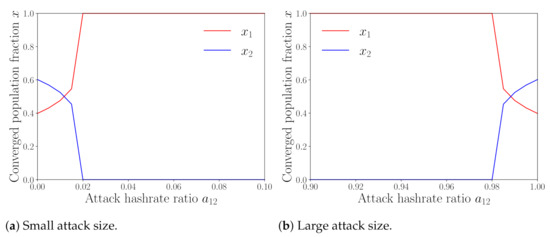
Figure 5.
Stable population states vs. attack size .
We now examine the importance of the attacking revenue (i.e., revenue from the attacked pool) in the pool selection, for which we show in Figure 6 how the attack size of pool 1 affects the stable population states for both the case with attacking revenue (this paper) and without attacking revenue ([25]). We fix the initial population state as and also consider two regions, i.e., small attack size (i.e., to ) and large attack size (i.e., to ). We can see from Figure 6a that, for the case without considering the attacking revenue, miners prefer to join the attacked pool (i.e., pool 2) as the attack size increases. This is unreasonable, since intuitively joining the attacked pool will earn less revenues than joining the attacking pool, due to the advantage brought by BWH attack. We can see from Figure 6a that increasing the attack size to a sufficiently large (or even to 1) has no impact on the mining selection of miners in the case without considering the attacking revenue. This is also unreasonable, because the advantage of the attacking pool decreases due to the reduction of mining revenue in this situation, making the attacking pool less attractive for miners. The results in both figures show that ignoring the attacking revenue as in [25] may provide us with less accurate and convincing insights into the pool selection problem.
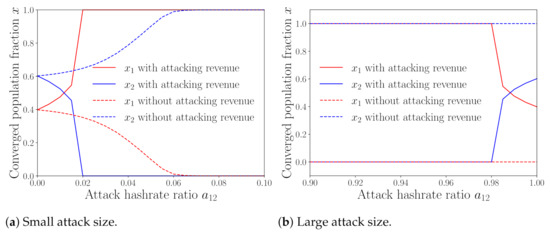
Figure 6.
Impact of considering the attacking revenue.
We also investigate the case where pool 2 attacks pool 1 with attack size . Other parameters are the same as those in Figure 3. Under this setting, we obtain two NEs and by calculating (28). Figure 7a plots the phase portrait of the replicator dynamics. We can see from Figure 7a that the population states converge to from any initial state, implying that the NE (i.e., the state where all miners join pool 2) is stable and thus the only ESS. We also show in Figure 7b the simulation results for three initial population states . The results show that all the population states finally converge to the state , which agree with the theoretical results. Note that the minimum hash powers required to join pool 1 and pool 2 are and in Figure 4 and Figure 7. Comparing the results in these two figures, we can see that a pool with lower hash power requirement is more likely to attract miners when launching the BWH attack.
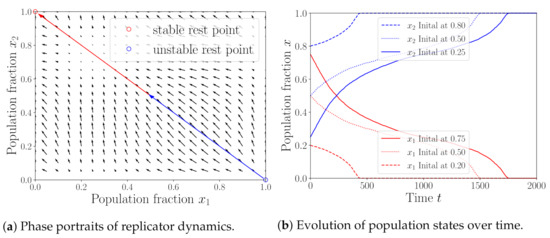
Figure 7.
One-side attack case with .
5.3. Both-Side Attack Case
Finally, we focus on the both-side attack case with attack sizes of and . Other parameters are set as those in Figure 3. Under this parameter setting, we obtain five NEs: and based on numerical calculations. We show in Figure 8a the phase portrait of the replicator dynamics. We can see from Figure 8a that the population states converge to for initial states with , converge to for initial states with and converges to for initial states with . This implies that the ESSs in this case are , and . To verify the correctness of the analysis, we conducted simulations with three initial states and summarize the results in Figure 8b. The results show that all the population states finally converge to the state from initial state , converge to from initial state and converge to from initial state , which agree with the theoretical results. Comparing the results with those of the no-attack case, we can see that the pool with sufficiently large initial population fraction (e.g., more than ) will attract more miners to join. In addition, when the initial population fraction of either pool is not sufficiently large, attack has no impacts if the two pools attack with the same size, which can also be observed from Figure 5a.
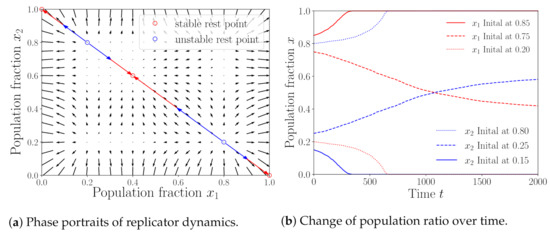
Figure 8.
Both-side attack case with and .
Next, we investigate the impacts of attack sizes and on the converged population states. Figure 9 shows how the stable population state changes when the attack size of pool 1 () increases from 0 to under various values of the attack size of pool 2 (). In Figure 9a, the initial state is fixed as and the attack size of pool 2 is set as . This figure shows that, as the attack size of pool 1 (resp. pool 2) increases, the stable population fraction of pool 1 (resp. pool 2) increases. This means that using more hash powers for attack will attract more miners to join the pool after convergence. Furthermore, we can see that when the two pools use the same attack size, the populations converge to nearly the stable state without attack , which means that attack has no impacts in this case. The results with initial states and are also shown in Figure 9b,c. We can see the same phenomenon from these two figures that mining pools can attract more miners to join after convergence by increasing their attack sizes, implying that attack can give mining pools advantages.
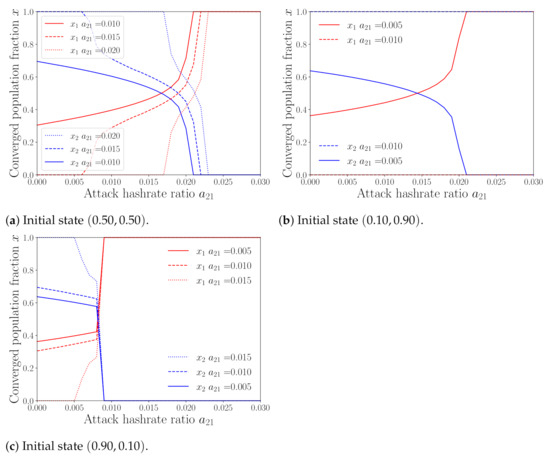
Figure 9.
Stable population states vs. attack sizes and .
6. Conclusions
In this paper, we have investigated the mining pool selection problem in the presence of a Block WithHolding (BWH) attack and obtained the stable population states from the perspective of evolutionary game theory. In particular, we have focused on the scenario with two mining pools and provided simulation and theoretical results to show the correctness of the analysis. The results in this paper have shown that pools can attract miners to join by launching the BWH attack, and devoting more hash power (computation power) for attack attracts more miners, when the attack power is small. However, too large of an attack power will discourage miners to join. These observations indicate the significant impacts of BWH attack on the mining pool selection of miners. Note that this paper considered the two-pool scenario as the case study, which is good enough for us to obtain fundamental findings but may provide less insights to the general case with more mining pools. Therefore, we will focus on the general scenario in the future work. In addition, we will also consider conducting experiments with more practical parameter settings or in real-world blockchain networks like Bitcoin to help us understand the problem more deeply.
Author Contributions
Scheme design, K.F., Y.Z., M.S. and S.K.; implementation, K.F.; writing—original draft preparation, K.F.; writing—review and editing, Y.Z., M.S. and S.K.; supervision, S.K.; project administration, S.K.; funding acquisition, Y.Z., M.S. and S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by KAKENHI (A) under Grant 19H01103, SCAT Research Grant and The Telecommunications Advancement Foundation.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Bitcoin Whitepaper. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 25 December 2020).
- Wood, G. Ethereum: A Secure Decentralised Generalised Transaction Ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- Skowroński, R. The open blockchain-aided multi-agent symbiotic cyber–physical systems. Future Gener. Comput. Syst. 2019, 94, 430–443. [Google Scholar] [CrossRef]
- Zhang, Y.; Kasahara, S.; Shen, Y.; Jiang, X.; Wan, J. Smart Contract-Based Access Control for the Internet of Things. IEEE Internet Things J. 2019, 6, 1594–1605. [Google Scholar] [CrossRef]
- Yutaka, M.; Zhang, Y.; Sasabe, M.; Kasahara, S. Using Ethereum Blockchain for Distributed Attribute-Based Access Control in the Internet of Things. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nakamura, Y.; Zhang, Y.; Sasabe, M.; Kasahara, S. Capability-Based Access Control for the Internet of Things: An Ethereum Blockchain-Based Scheme. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nakamura, Y.; Zhang, Y.; Sasabe, M.; Kasahara, S. Exploiting Smart Contracts for Capability-Based Access Control in the Internet of Things. Sensors 2020, 20, 1793. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yutaka, M.; Sasabe, M.; Kasahara, S. Attribute-Based Access Control for Smart Cities: A Smart Contract-Driven Framework. IEEE Internet Things J. 2020, 1. [Google Scholar] [CrossRef]
- Saberi, S.; Kouhizadeh, M.; Sarkis, J.; Shen, L. Blockchain Technology and Its Relationships to Sustainable Supply Chain Management. Int. J. Prod. Res. 2019, 57, 2117–2135. [Google Scholar] [CrossRef]
- Xia, Q.I.; Sifah, E.B.; Asamoah, K.O.; Gao, J.; Du, X.; Guizani, M. MeDShare: Trust-Less Medical Data Sharing Among Cloud Service Providers via Blockchain. IEEE Access 2017, 5, 14757–14767. [Google Scholar] [CrossRef]
- Jiang, S.; Cao, J.; Wu, H.; Yang, Y. Fairness-based Packing of Industrial IoT Data in Permissioned Blockchains. IEEE Trans. Ind. Inform. 2020, 1. [Google Scholar] [CrossRef]
- Mettler, M. Blockchain Technology in Healthcare: The Revolution Starts Here. In Proceedings of the IEEE 18th International Conference on E-Health Networking, Applications and Services (Healthcom), Munich, Germany, 14–17 September 2016; pp. 1–3. [Google Scholar]
- Griggs, K.N.; Ossipova, O.; Kohlios, C.P.; Baccarini, A.N.; Howson, E.A.; Hayajneh, T. Healthcare Blockchain System Using Smart Contracts for Secure Automated Remote Patient Monitoring. J. Med Syst. 2018, 42, 130. [Google Scholar] [CrossRef]
- Jiang, S.; Cao, J.; Wu, H.; Yang, Y.; Ma, M.; He, J. BlocHIE: A BLOCkchain-Based Platform for Healthcare Information Exchange. In Proceedings of the 2018 IEEE International Conference on Smart Computing (SMARTCOMP), Taormina, Italy, 18–20 June 2018; pp. 49–56. [Google Scholar] [CrossRef]
- Karamitsos, I.; Papadaki, M.; Al Barghuthi, N.B. Design of the Blockchain Dmart Contract: A Use Case for Real Estate. J. Inf. Secur. 2018, 9, 177–190. [Google Scholar]
- Xu, R.; Zhang, L.; Zhao, H.; Peng, Y. Design of Network Media’s Digital Rights Management Scheme Based on Blockchain Technology. In Proceedings of the IEEE 13th International Symposium on Autonomous Decentralized System (ISADS), Bangkok, Thailand, 22–24 March 2017; pp. 128–133. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. In Proceedings of the IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar]
- Tschorsch, F.; Scheuermann, B. Bitcoin and Beyond: A Technical Survey on Decentralized Digital Currencies. IEEE Commun. Surv. Tutor. 2016, 18, 2084–2123. [Google Scholar] [CrossRef]
- Gjermundrød, H.; Chalkias, K.; Dionysiou, I. Going Beyond the Coinbase Transaction Fee: Alternative Reward Schemes for Miners in Blockchain Systems. In Proceedings of the 20th Pan-Hellenic Conference on Informatics, Patras, Greece, 10–12 November 2016; pp. 1–4. [Google Scholar]
- Schrijvers, O.; Bonneau, J.; Boneh, D.; Roughgarden, T. Incentive Compatibility of Bitcoin Mining Pool Reward Functions. In Proceedings of the International Conference on Financial Cryptography and Data Security, Christ Church, Barbados, 22–26 February 2016; pp. 477–498. [Google Scholar]
- Saad, M.; Spaulding, J.; Njilla, L.; Kamhoua, C.; Shetty, S.; Nyang, D.; Mohaisen, D. Exploring the Attack Surface of Blockchain: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2020, 22, 1977–2008. [Google Scholar] [CrossRef]
- Dong, X.; Wu, F.; Faree, A.; Guo, D.; Shen, Y.; Ma, J. Selfholding: A combined attack model using selfish mining with block withholding attack. Comput. Secur. 2019, 87, 101584. [Google Scholar] [CrossRef]
- Eyal, I. The Miner’s Dilemma. In Proceedings of the IEEE Symposium on Security and Privacy, San Jose, CA, USA, 18–20 May 2015; pp. 89–103. [Google Scholar]
- Liu, X.; Wang, W.; Niyato, D.; Zhao, N.; Wang, P. Evolutionary Game for Mining Pool Selection in Blockchain Networks. IEEE Wirel. Commun. Lett. 2018, 7, 760–763. [Google Scholar] [CrossRef]
- Kim, S.; Hahn, S.G. Mining Pool Manipulation in Blockchain Network Over Evolutionary Block Withholding Attack. IEEE Access 2019, 7, 144230–144244. [Google Scholar] [CrossRef]
- Fujita, K.; Zhang, Y.; Sasabe, M.; Kasahara, S. Mining Pool Selection Problem in the Presence of Block Withholding Attack. In Proceedings of the IEEE International Conference on Blockchain (IEEE Blockchain), Rhodes Island, Greece, 2–6 November 2020; pp. 321–326. [Google Scholar]
- Alkalay-Houlihan, C.; Shah, N. The Pure Price of Anarchy of Pool Block Withholding Atacks in Bitcoin Mining. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1724–1731. [Google Scholar]
- Wang, Y.; Tang, C.; Lin, F.; Zheng, Z.; Chen, Z. Pool Strategies Selection in PoW-Based Blockchain Networks: Game-Theoretic Analysis. IEEE Access 2019, 7, 8427–8436. [Google Scholar] [CrossRef]
- Wu, D.; Liu, X.D.; Yan, X.B.; Peng, R.; Li, G. Equilibrium Analysis of Bitcoin Block Withholding Attack: A Generalized Model. Reliab. Eng. Syst. Saf. 2019, 185, 318–328. [Google Scholar] [CrossRef]
- Tang, C.; Li, C.; Yu, X.; Zheng, Z.; Chen, Z. Cooperative Mining in Blockchain Networks With Zero-Determinant Strategies. IEEE Trans. Cybern. 2020, 50, 4544–4549. [Google Scholar] [CrossRef]
- Chen, Z.; Li, B.; Shan, X.; Sun, X.; Zhang, J. Discouraging Pool Block Withholding Attacks in Bitcoins. arXiv 2020, arXiv:2008.06923. [Google Scholar]
- Yang, Z.; Miao, Y.; Chen, Z.; Tang, C.; Chen, X. Zero-Determinant Strategy for the Algorithm Optimize of Blockchain PoW Consensus. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 1441–1446. [Google Scholar]
- Lewenberg, Y.; Bachrach, Y.; Sompolinsky, Y.; Zohar, A.; Rosenschein, J.S. Bitcoin Mining Pools: A Cooperative Game Theoretic Analysis. In Proceedings of the International Conference on Autonomous Agents and Multiagent Systems, Istanbul, Turkey, 4–8 May 2015; pp. 919–927. [Google Scholar]
- Brünjes, L.; Kiayias, A.; Koutsoupias, E.; Stouka, A.P. Reward Sharing Schemes for Stake Pools. In Proceedings of the IEEE European Symposium on Security and Privacy (EuroS&P), Genoa, Italy, 7–11 September 2020; pp. 256–275. [Google Scholar]
- Liu, Z.; Luong, N.C.; Wang, W.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. A Survey on Applications of Game Theory in Blockchain. arXiv 2019, arXiv:1902.10865. [Google Scholar]
- Xu, C.; Zhu, K.; Wang, R.; Xu, Y. Dynamic Selection of Mining Pool with Different Reward Sharing Strategy in Blockchain Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.; Chen, X.; Yu, J.; Wu, W.; Wu, D. Impact of Temporary Fork on the Evolution of Mining Pools in Blockchain Networks: An Evolutionary Game Analysis. IEEE Trans. Netw. Sci. Eng. 2020, 1. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Han, M.; Liu, B.; Chen, Q.; Ma, Z. A Novel Anti-attack Revenue Optimization Algorithm in the Proof-of-Work Based Blockchain. In Wireless Algorithms, Systems, and Applications; Springer International Publishing: Cham, Switzerland, 2020; pp. 40–50. [Google Scholar]
- Toroghi Haghighat, A.; Shajari, M. Block Withholding Game among Bitcoin Mining Pools. Future Gener. Comput. Syst. 2019, 97, 482–491. [Google Scholar] [CrossRef]
- Luu, L.; Saha, R.; Parameshwaran, I.; Saxena, P.; Hobor, A. On Power Splitting Games in Distributed Computation: The Case of Bitcoin Pooled Mining. In Proceedings of the IEEE 28th Computer Security Foundations Symposium, Verona, Italy, 13–17 July 2015; pp. 397–411. [Google Scholar]
- Biais, B.; Bisiere, C.; Bouvard, M.; Casamatta, C. The Blockchain Folk Theorem. Rev. Financ. Stud. 2019, 32, 1662–1715. [Google Scholar] [CrossRef]
- Houy, N. The Bitcoin Mining Game. 2014. SSRN 2407834. Available online: http://dx.doi.org/10.2139/ssrn.2407834 (accessed on 25 December 2020).
- Garay, J.; Kiayias, A.; Leonardos, N. The Bitcoin Backbone Protocol: Analysis and Applications. In Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques, Sofia, Bulgaria, 26–30 April 2015; pp. 281–310. [Google Scholar]
- Schuster, P.; Sigmund, K. Replicator Dynamics. J. Theor. Biol. 1983, 100, 533–538. [Google Scholar] [CrossRef]
- Machida, M.; Kanazawa, T. Population-Independent Pairwise Proportionally Imitative Dynamics for Multipopulation Games. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Hong Kong, China, 9–12 October 2015; pp. 852–857. [Google Scholar]
- Hofbauer, J.; Sandholm, W.H. Stable Games and Their Dynamics. J. Econ. Theory 2009, 144, 1665–1693. [Google Scholar] [CrossRef]
- Weibull, J.W. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Game Dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).