1. Introduction
The condition of train wheels has an impact on the passengers’ comfort, the rolling noise generation and the deterioration of railway infrastructure and, hence, the safety of railway operations. Severe wheel defects cause high dynamical load, which can damage the railway track and shorten the life span of railway bridges [
1]. There are several types of wheel defects and wear mechanisms. An overview of different wheel tread irregularities is given in [
2]. Prominent examples are isolated wheel flats, polygonal wheels, corrugation, spalling, shelling and roughness. All these defects have different amplitudes and wavelengths but all increase the dynamic wheel–rail contact forces. Additionally, permanent wheel wear leads to a constant reduction of the wheel diameter that amount to several centimeters over the wheel’s life span. In several studies, the effects of wheel defects on the dynamic wheel–rail interaction have been investigated, e.g., Bian et al. [
3] used a finite element model to analyze the impact induced by a wheel flat. Bogacz and Frischmuth [
4] studied the rolling motion of a polygonalized railway wheel and in [
5], a method for the computation of the wheel–rail surface degradation in a curve is explained. Casanueva et al. [
6] address the issues of model complexity, accuracy and the input needed for wheel and track damage prediction using vehicle–track dynamic simulations.
The traditional maintenance strategies of wheelsets are based on the removal of the wheelset at given intervals. However, from a safety, environmental and economic point of view, the early detection of wheel defects is important. Wayside monitoring systems are commonly used to detect faulty wheelsets in service. Mosleh et al. [
7] investigated an envelope spectral analysis approach to detect wheel flats with wayside sensors using a range of 3D simulations based on a train–track interaction model. In contrast to wayside systems, on-board monitoring systems have traditionally been focused on the detection of track defects [
8,
9,
10,
11,
12] but are more and more considered for vehicle monitoring [
13]. The advantage of on-board monitoring systems is that the wheel is monitored continuously and not only when the vehicle passes a track side monitoring site. This allows for the timely detection of emerging wheel defects [
14]. Furthermore, if the on-board monitoring system provides positioning, the occurrence of a wheel defect can be linked to a position on the track. The track at this position can then be inspected and in case a track defect is identified, appropriate maintenance actions can be issued to avoid further damage to the rail and other passing vehicles.
Previous studies have also shown that train-borne accelerometers can be used to monitor the wheel. In [
15] a methodology is proposed to monitor the wheel diameter by means of onboard vibration measurements. Jia and Dhanasekar [
16] used wavelet approaches for monitoring rail wheel flat damage from bogie vertical acceleration signatures. Several methods based on the analysis of axle-box acceleration (ABA) have been proposed. Bosso et al. [
14] used vertical ABA to detect wheel flat defects. In [
17], a data driven approach to estimate the length of a wheel flat is proposed. Bai et al. [
18] presented a frequency-domain image classification method to analyze wheel flats.
In general, a trend can be noticed in sensor data analysis and condition monitoring towards analysis techniques based on data driven machine learning approaches. They can be used to find patterns, i.e., clusters and for outlier and novelty detection in an unsupervised manner. Furthermore, supervised machine learning can be used to predict class memberships and their probabilities and to estimate relationships between independent variables, e.g., health status indices, and features extracted from the data. These methodologies are quite powerful. They can approximate complex and non-linear relationships and need little or no a priori information. Therefore, they are often preferred over model-based approaches. However, since machine learning techniques make use of the underlying statistics in the data, they rely on the fact that sufficient data are available. In addition, supervised machine learning approaches need sufficient labeled data for training. A strong focus on machine learning techniques bears the risk that powerful traditional signal processing techniques are overseen, even when they might be the right choice for a specific data analysis problem. One example of such a powerful but uncommonly used tool is the cepstrum analysis. It dates back to the 1960s and 1970s, when it was introduced to analyze, e.g., echoes and reverberations in radar, sonar, speech and seismic data. For a detailed overview see [
19,
20] and the references therein. The power cepstrum was first defined by Bogert et al. [
21] as the power spectrum of the logarithm of the power spectrum of a signal. In contrast to the complex cepstrum it does not consider any phase information and therefore only involves the logarithm of real, positive numbers. Bracciali and Cascini [
22] used cepstrum analysis of rail acceleration to detect wheel flats of railway wheels. They identified the power cepstrum as the best instrument to reveal periodic acceleration peaks as those excited by wheel flats. Here, we adapt this methodology to the analysis of ABA data for wheel condition monitoring. Specifically, and in analogy to the estimation of the arrival times of echoes and their relative amplitudes, we use the power cepstrum to estimate the wheel circumference and the relative contribution of the wheel imperfections to the excited wheel vibrations.
The main contribution of this research is to introduce a simple, robust and yet precise methodology to extract wheel wear related features from the ABA signals without relying on a priori knowledge or training data. This methodology relies on the processing of ABA data in the distance domain. That is, the ABA time series need to be transformed using speed information so as to obtain spatial acceleration signatures. Hence, the vehicle speed must be estimated using further onboard sensors, namely a global navigation satellite system (GNSS) receiver [
23] and an inertial measurement unit (IMU) [
24]. The estimation relies on Kalman filter methods [
25].
The remainder of the paper is structured as follows.
Section 2 provides the theoretical background by reviewing the calculation of the power cepstrum and introducing the term navewumber. In
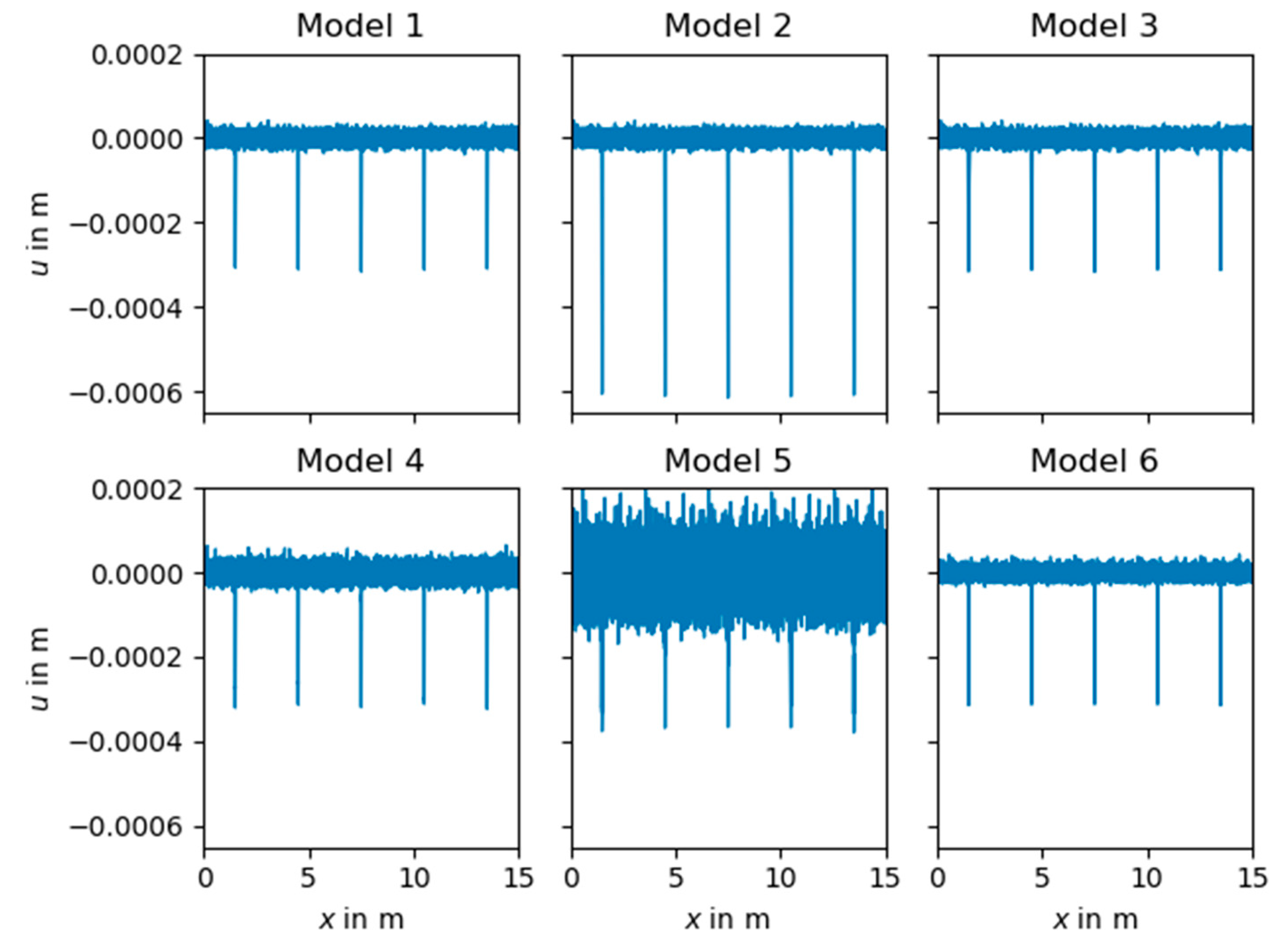
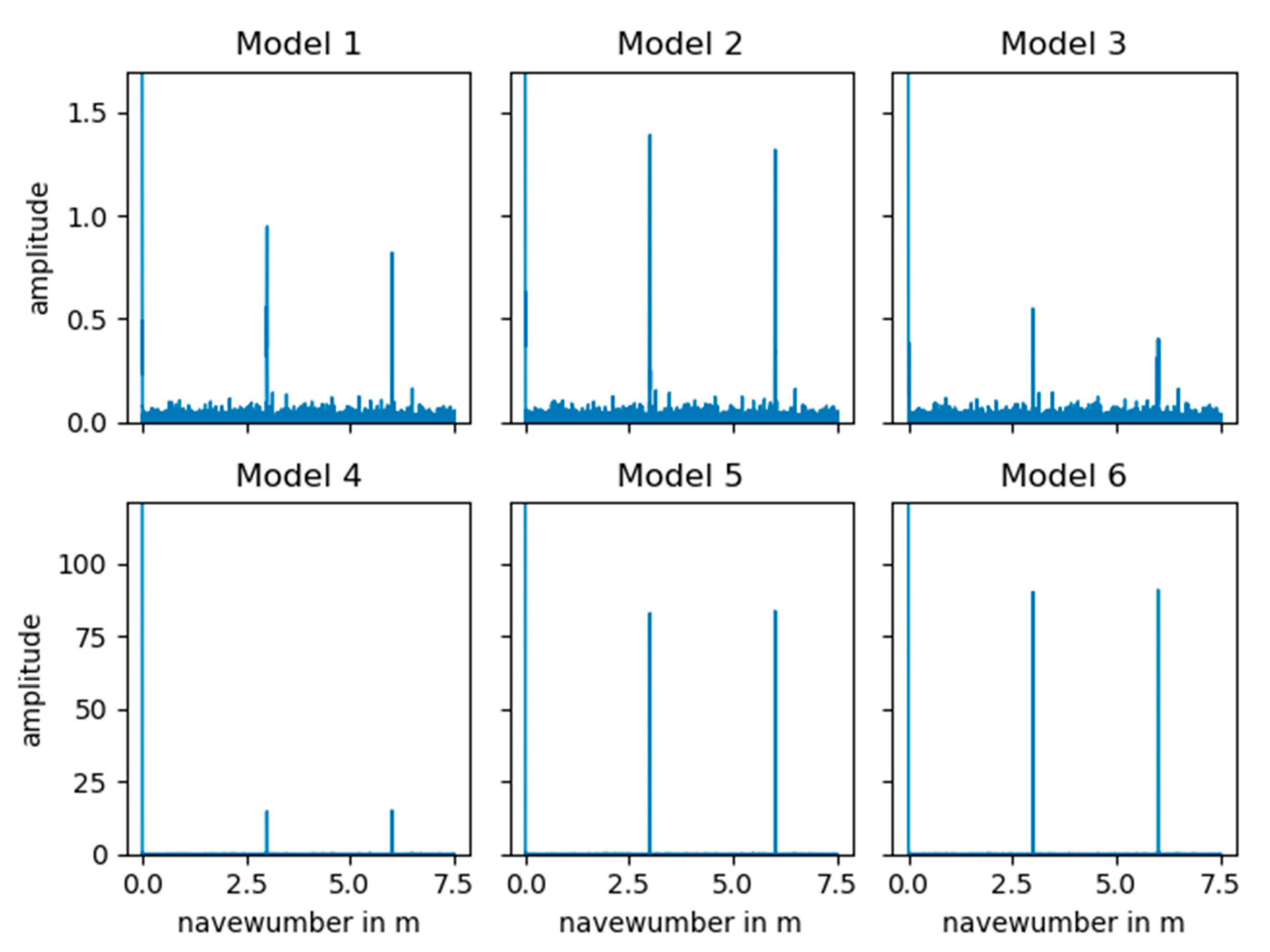
Section 3, the sensitivity of the cepstral analysis to different wheel surface defects is tested by means of simple synthetic data. In
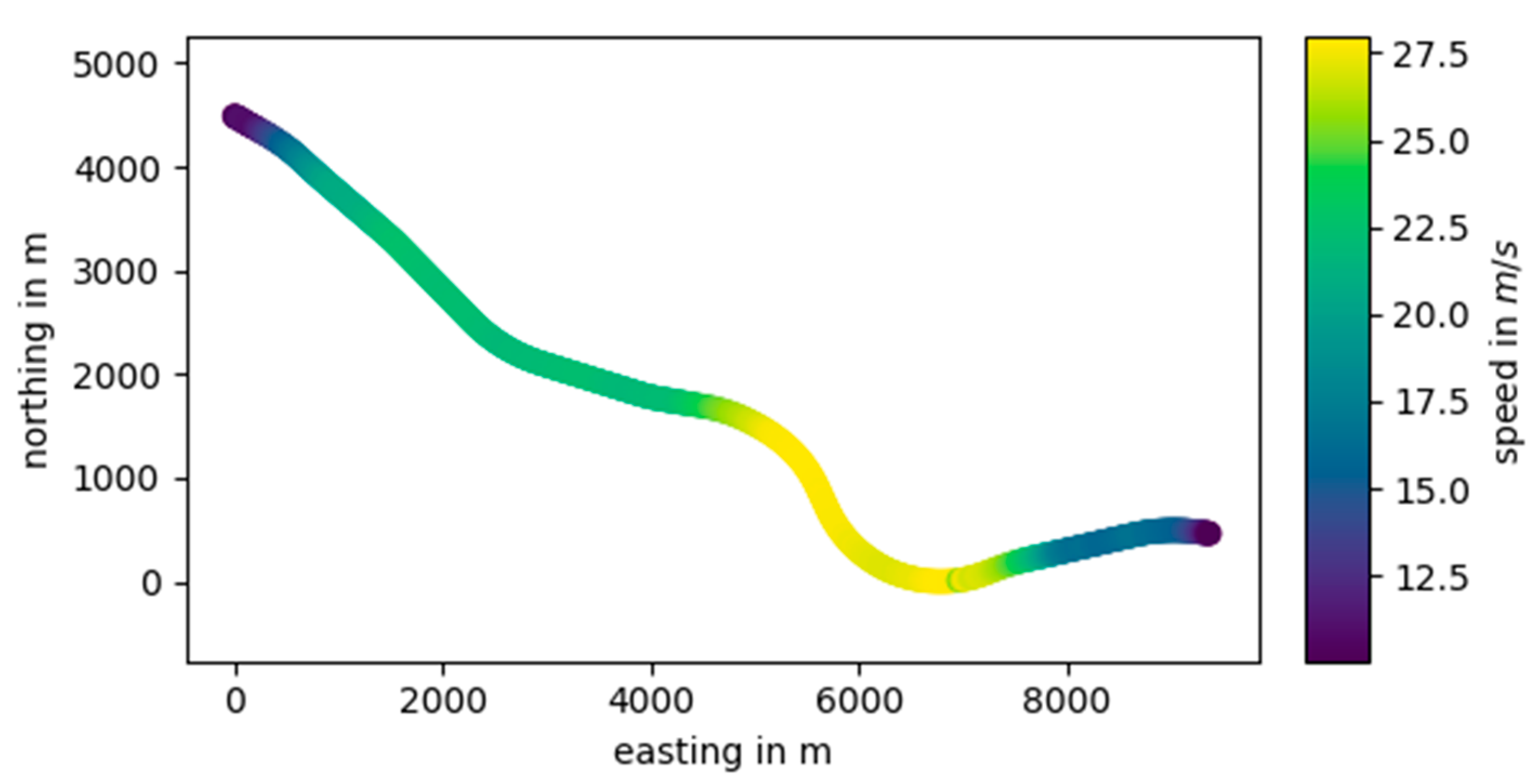
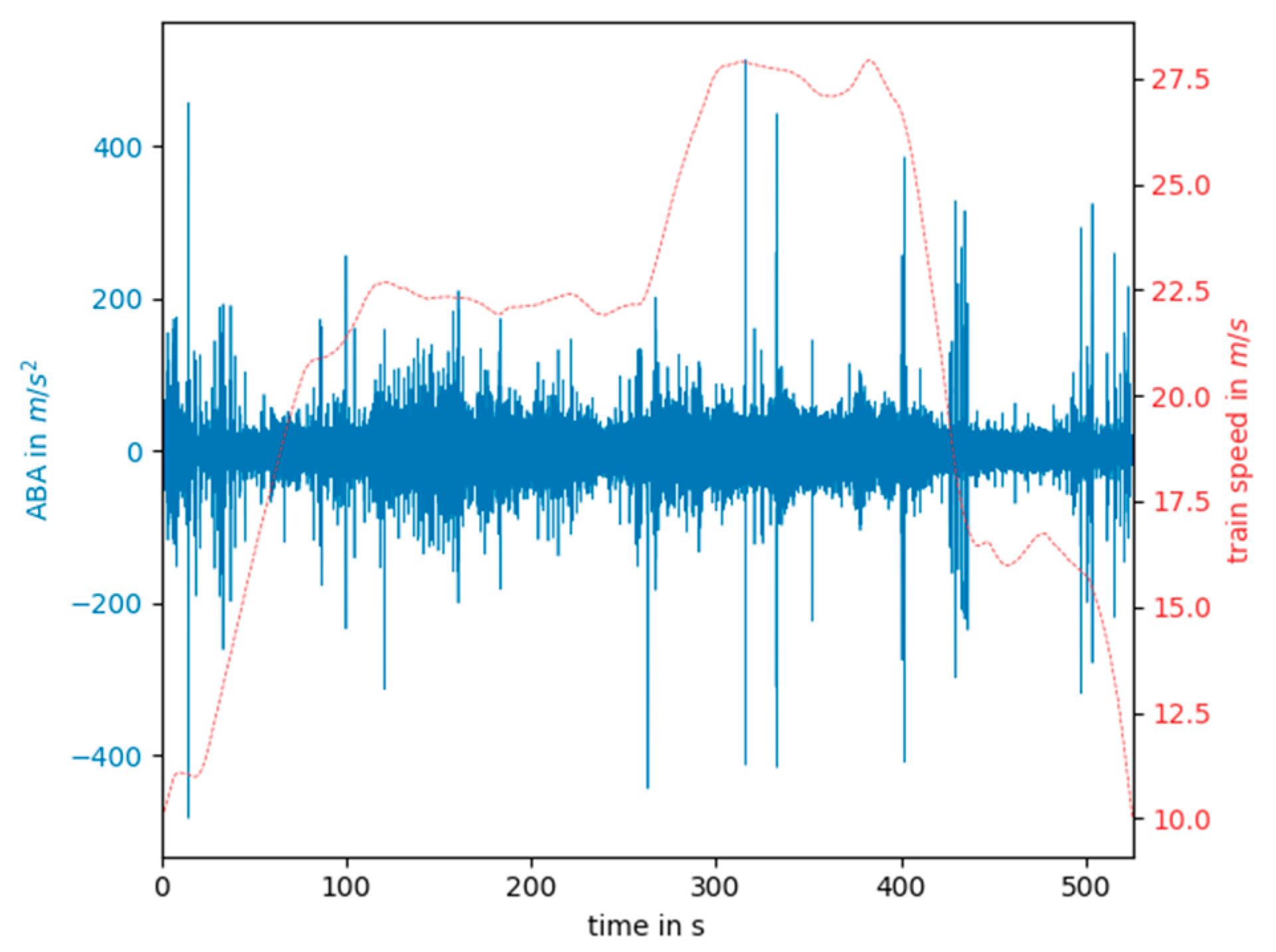
Section 4, experimental data are used to test the performance of the cepstrum under real-world conditions. Data pre-processing and vehicle speed estimation is also explained in this section. In
Section 5, the results are discussed and
Section 6 provides a final conclusion.
2. Cepstral Analysis and Navewumber Domain
The power cepstrum
can be defined as the power spectrum of the logarithm of the power spectrum of a function
:
Here, the Fourier transform
is calculated by using the fast Fourier transform (FFT) algorithm. The application of the forward FFT or the inverse FFT to the logarithm of the power spectrum in Equation (1) provides the same result apart from a scaling factor. The independent variable
has the same dimension as
and is originally called quefrency to indicate that it is the inverse of the frequency, which is the case for the cepstrum of a time series. Accordingly, the independent variable of the cepstrum of data in the spatial domain is dimensionally a distance. Following the nomenclature introduced by Borgert et al. [
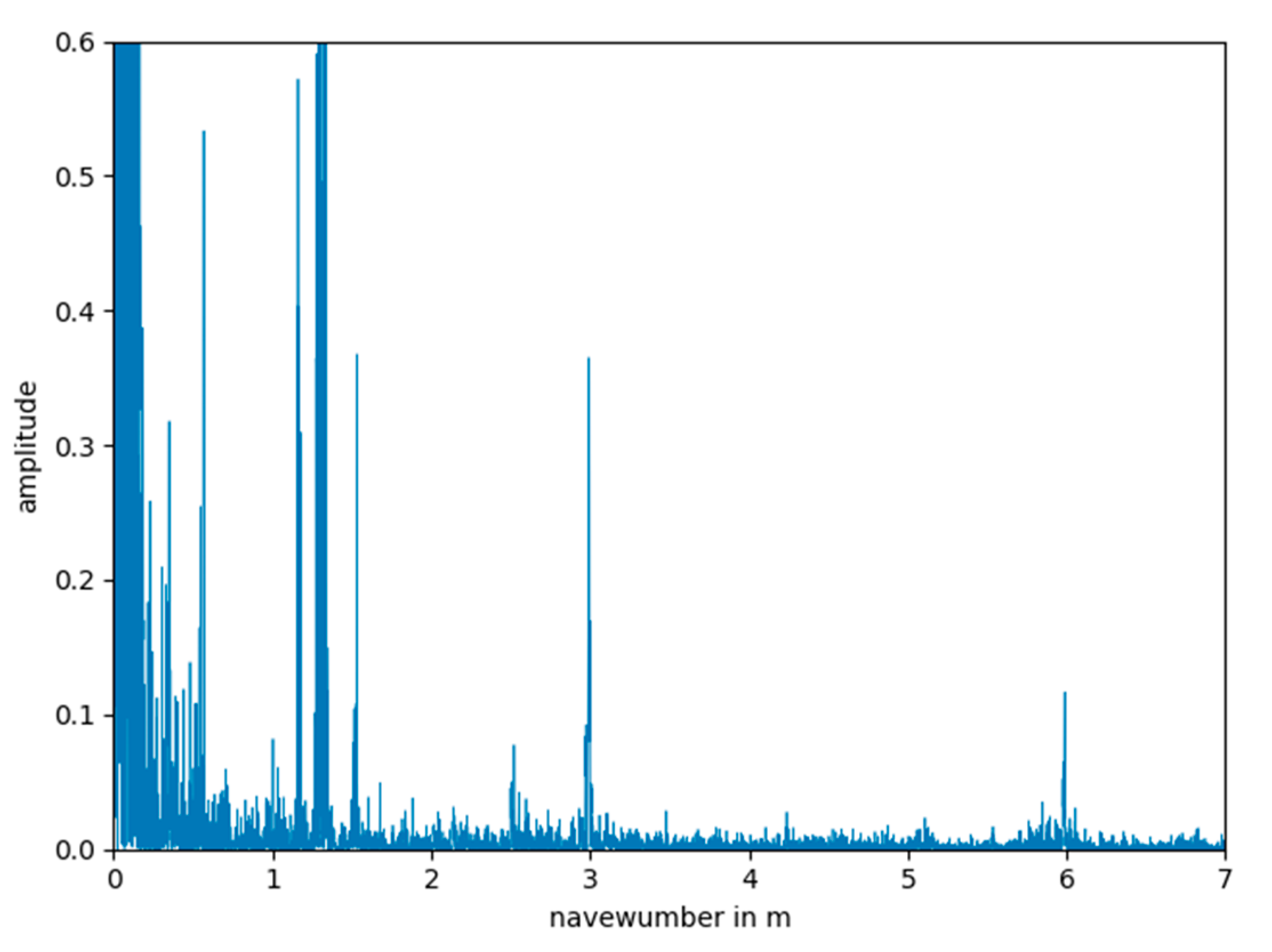
21], we call the independent variable of the cepstrum navewumber when its dimension is a distance, since in this case it is the inverse of the wavenumber. Furthermore, we call the cepstral domain navewumber domain. In the following the term cepstrum is always used for the power cepstrum.
The cepstrum can be used to convert a convolution into the addition of the individual components and thus a complicated deconvolution procedure can be performed by simply subtracting the undesired components in the cepstral domain. This procedure is called homomorphic deconvolution [
26]. According to Equation (1), the cepstrum of a continuous function
consisting of two components
and
coupled via convolution
can be calculated by the following sequence of mathematical operations:
Due to the linearity of the Fourier transform, the components in the cepstrum are still coupled by addition. The final squaring operation produces a cross product term. However, if the cepstra of
and
occupy different navewumber ranges, this term can be omitted [
27] and Equation (5) becomes
The cross-terms can also be avoided if the final squaring operation is not included in Equation (1).
Periodic components of the logarithmic power spectrum are reduced to series of spikes (Dirac delta functions) in the cepstral domain. Ulrych [
27] found out that if the spectrum of a signal is smooth it maps around the origin in the navewumber domain, while the cepstrum of a periodic impulse sequence, as excited by a wheel irregularity, is also an impulse sequence with the same period. This means that in the cepstrum of ABA data, the component of a wheel defect can simply be separated from the component of the transmission path, i.e., the cepstra of the impulse responses of the track, wheel and sensor. Hence, bypassing the transmission path makes trend analyses robust towards changes of the mechanical structures of the components, which influence the signal transmission. This property makes the cepstrum a promising tool for wheel monitoring.
5. Discussion
5.1. Wheel Condition Monitoring with ABA Sensors
Wheel monitoring with train-borne sensors means that each wagon needs to be equipped with sensors. In contrast, wayside measurement systems are able to measure conditions of all wheelsets of each passing train with one measurement system. However, on-board systems provide a quasi-continuous monitoring of the wagon, while wayside systems only provide data in certain time intervals, when the train passes. Another advantage of train-borne measurement systems is that they can be used to monitor the track as well, which could justify the high number of sensors. Using broad-band accelerometers below the suspension, in contrast to sensors installed at the bogie or car body, allows to monitor the wheel diameter with very high resolution, which is beneficial for wheel-wear trend analysis. A comprehensive cost-benefit study of available wheel monitoring systems for condition-based and predictive maintenance was not part of this work but should be dealt with in future studies.
5.2. Navewumber Analysis
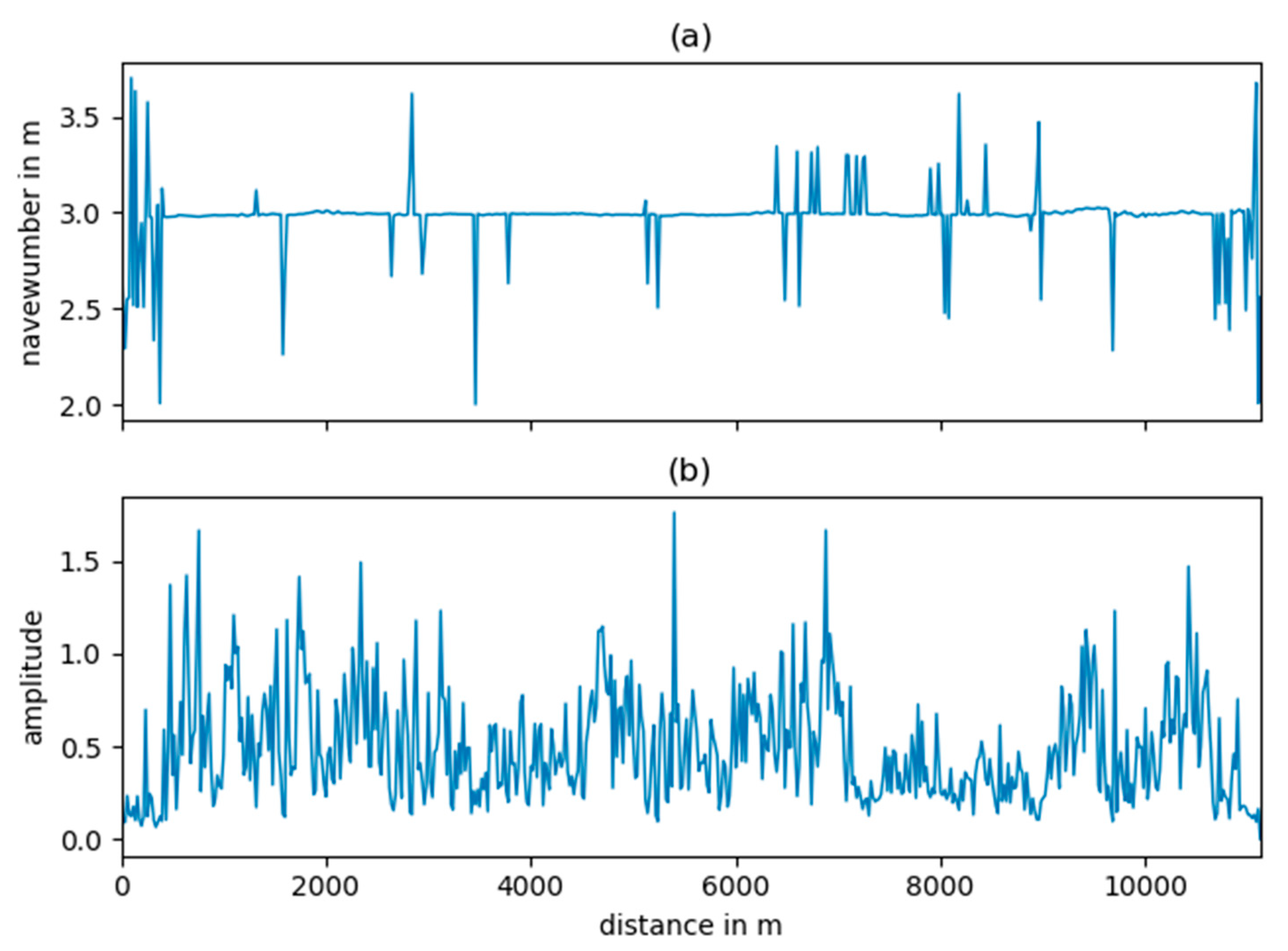
The navewumber analysis provides a robust tool to extract the wheel circumference from the ABA data. It can be recovered with a resolution equal to the distance between two measurement points, which depends on the train speed and sampling frequency. At a speed of 20 m/s and sampling frequency of 20 kHz the cepstral resolution is 0.001. We could show that between 80 and 90 percent of the calculated wheel circumferences were within a range of two millimeters along the whole train journey.
The high resolution and accuracy allow precise monitoring of the wheel diameter and therefore enable wheel-wear trend analysis. The approach provides reliable results under varying operational conditions. We found out that a minimal train speed of 15 m/s is sufficient to allow the estimation of the wheel circumference. Above this speed, the navewumber analysis is not affected by the train speed but its accuracy directly depends on the accuracy of the speed estimation that is used to transform the data from the time to distance domain. Thus, short-term variations of the estimated wheel diameter most likely relate to speed estimation errors. These Gaussian distributed errors can be estimated by the positioning algorithms introduced in
Section 4.2.
It is especially noteworthy that the track condition only has a minor effect on the estimation of the wheel circumference. Even at track segments, where high wheel vibrations were excited, the wheel circumference could be determined accurately.
Due to the conicity of the wheels, the gauge and curve radius might have an influence on the estimated wheel circumference. However, the data analyzed in this study were not affected by the track geometry. Furthermore, the wear-related reduction of the wheel diameter is monotonic, while track-geometry changes only occur at certain track segments. Therefore, trend analysis of the wheel wear is not influenced by the track geometry. The influence of the track conditions can be further reduced by averaging over several track segments or taking longer track segments into account.
The synthetic data analysis has shown that the absolute amplitude of the cepstral peak can be similarly influenced by the track as well as wheel conditions. A mildly defected wheel running on a track with low roughness can produce a peak similar to that produced by a more severely defected wheel on a track with higher roughness. More generally, the amplitudes of the peaks in the navewumber domain provide a measure of the repeatability of the ABA signal and hence a measure of the relative contribution of the wheel condition to the dynamic wheel rail interaction.
The discrimination of different wheel defects using cepstral peak position and amplitude alone seems to be impracticable. Nevertheless, the cepstral features might complement other data driven approaches for wheel defect diagnosis.
It should be noticed that the measurement campaign, which builds the data base for this study did not focus on wheel monitoring but rather on testing the performance of the multi-sensor system. Therefore, no ground truth on the actual condition of the wheel exists. Nevertheless, no severe wheel defects were observed during operation. Hence, further tests including ground truth measurements and calibration by means of direct wheel profile measurements are required to determine thresholds for wheel defect detection. In principal, the methodology provided here, could be similarly used for the on-board detection of bearing defects, which should be subject of future studies.
6. Conclusions
The early detection of wheel defects is an important asset management and maintenance task. Wheel vibrations are excited by the imperfections of the wheel and rail and hence contain information on the health status of both assets. These vibrations can be measured by means of ABA sensors.
In this paper, a promising methodology, the cepstrum analysis, was tested for the application to wheel condition monitoring. The cepstrum is powerful in revealing periodic signals and separating them from the rest of the signal. This makes the cepstrum particularly interesting for wheel monitoring. The vibration signal excited by the wheel profile is periodic with respect to the wheel circumference. This periodicity changes with the rotational frequency of the wheel and hence depends on the speed of the train. This dependency can be compensated for by transforming the ABA data from the time to the spatial domain. To accomplish that, accurate speed information is necessary, which was obtained by fusing IMU and (E)GNSS data. The cepstral analysis was then performed in the spatial domain. The obtained cepstrum itself is then in a spatial domain, which we called navewumber domain to highlight the inverse relation to the wavenumber. The periodicity of the ABA signal excited by the wheel is then represented by a peak in the cepstrum at a wavenumber equal to the wheel circumference. The position of the peak precisely indicates the wheel circumference and can therefore be used to monitor the wheel diameter. The amplitude of this peak provides a measure of the relative contribution of the wheel to the combined wheel–rail roughness. The cepstral wheel monitoring approach presented here requires neither extensive hyperparameter testing nor training data. Ground truth data might be used to define hard thresholds for the detection of certain track defects. However, we think that it is more reasonable and also sufficient to monitor changes in the cepstral features and thus detect deviations from the normal behavior that can be related to wheel defects.
Through the analysis of experimental data, we could show that the cepstrum analysis is robust under varying operating conditions.
From these findings we conclude that cepstral analysis of ABA data is a powerful methodology to monitor the wear-related reduction of the wheel circumference and to detect and monitor the evolution of wheel surface defects.