Abstract
The management of industrial systems is done through different levels, ranging from strategic (designing the system), to tactical (planning the activities and assigning the resources) and operational (scheduling the activities). In this paper, we focus on the latter level by considering a real-world scheduling problem from a plastic injection company, where the production process combines parallel machines and a set of resources. We present a scheduling algorithm that combines a metaheuristic and a list algorithm. Two metaheuristics are tested and compared when used in the proposed scheduling approach: the stochastic descent and the simulated annealing. The method’s performances are analyzed through an experimental study and the obtained results show that its outcomes outperform those of the scheduling policy conducted in a case-study company. Moreover, besides being able to solve large real-world problems in a reasonable amount of time, the proposed approach has a structure that makes it flexible and easily adaptable to several different planning and scheduling problems. Indeed, since it is composed by a reusable generic part, the metaheuristic, it is only required to develop a list algorithm adapted to the objective function and constraints of the new problem to be solved.
1. Introduction
Industry is changing rapidly and is facing the fourth industrial revolution. In this new context, industrial systems need to be more flexible and intelligent to deal with an ever-growing data availability, real time decisions and increasing customization. With Internet of Things, which allows various objects in the company or on the shop-floor to communicate with each other, industrial systems will become more intelligent and able to anticipate shortage of materials, the need for maintenance operations or to respond to urgent commands. This will imply the use of more efficient tools for planning and re-planning shop-floor operations.
Such decision support tools will be important at all decision levels: For example, at a strategic level, they can be used to decide which activities must be performed during a given planning horizon and to estimate the resources needed. At this level they can also be useful to model and test new shop-floor configurations and anticipate the impact of these changes on the system performance. Considering the tactical level, decision tools will allow to allocate resources to each activity planned to occur during a given time horizon. Finally, at the operational level they can be used to schedule the activities, determining the time allocation of each resource and to re-schedule them to respond to emergencies (new activities that have to be done as soon as possible). Table 1 summarizes the problems encountered at the different levels.

Table 1.
Levels of decision.
In this paper, we present a hybrid optimization method to solve a lot sizing and scheduling problem encountered in a plastic injection facility that produces components for electronic products. The proposed method was first introduced in [1] and concisely used to solve optimization problems from different areas: healthcare systems, as well as textile and plastic injection industries, with promising preliminary results. In the current work, the method’s application to plastic injection molding is further developed and its performance analyzed with a comparison to optimal and heuristic solutions.
Injection molding can be considered as a single-stage manufacturing process where parts are produced by injecting a molten material, typically a thermoplastic polymer, like in our case study company, into a custom-made mold. In the injection machine, the material is molten, mixed and injected into the mold, acquiring, after cooling, the shape imposed by the configuration of the cavity and being then ejected. The obtained part usually have the finished shape, not requiring further operations. In general, the shop-floor is composed by several injection machines which are shared by different products necessitating different molds. A setup time occurs each time a new product has to be manufactured. This setup time consists in the time required to dismount the mold used for the previous part and to mount the new mold on the machine. Obtaining a good schedule for such a constrained problem can be a real challenge.
The above described problem can be stated as follows: n jobs have to be processed on parallel machines, using their needed mold. These jobs have to be scheduled, considering their given processing time and due date before they have to be completed. When two jobs consecutively processed on one machine need two different molds, a sequence dependent setup time is recorded. Jobs have to be processed at once (non-preemptive constraint). To save setup costs, jobs using the same mold may be scheduled one after another. There are compatibility constraints between the molds and the machines: Each mold can only be assigned to some specific machines. Each mold exists in a single copy, thus the same mold cannot be used by more than one machine during the same time period. The objective is to find the suitable allocation of the jobs to the machines as well as the schedule of jobs on each machine so that minimizing the total tardiness.
This paper is structured as follows—Section 2 provides a literature review on the problems that present some analogies with the scheduling issue considered in this paper, such as batching and lot-sizing. A mathematical formulation modelling the problem and its constraints is detailed in Section 3. Then, in Section 4, we present an optimization method to solve the problem, consisting in a list algorithm and a metaheuristic. The different results of the experimental study are then presented in Section 5. The article ends with a Conclusion and some proposals for further work.
2. Literature Review
Several papers from the literature addressed the injection molding planning and scheduling problems. Dastidar and Nagi [2] studied a parallel machine scheduling problem in an injection molding facility, where different products require different types of resources. The authors provide a mathematical formulation and a decomposition based approach to minimize the setup and the inventory holding costs. A decomposition strategy is also used in [3,4] where the compatibility constraints between injection molds and machines are taken into account. In both articles, the problem is decomposed into sub-problems by grouping the machines by sets according to their compatible molds. Each sub-problem is then dealt with as a Capacitated Lot-Sizing Problem (CLSP). Van Wassenhove and De Bodt [3] used two heuristic procedures while [4] provides a goal programming formulation and a heuristic to minimize the production’s costs. The obtained results are shown to outperform the planning and scheduling procedures currently used in their case-study injection plants.
The problem we study in this paper also shares some features with the CLSP. Indeed, the lot-sizing issue reflects the fact that companies usually have to manufacture several types of products with limited production capacity. It is a very popular subject in the field of combinatorial optimization and has been defined since the early 1900s with the EOQ Economic Order Quantity [5]. Lot-sizing problems have been widely studied since then; a recent literature review can be found in [6]. Different lot-sizing models have been developed, depending on the characteristics of the production process. Although most of the lot-sizing studies focus on “product lots” (i.e., determining the right period and the quantity to produce for each type of product), some of them can also be related to “process lots”; in other words, to the decision of how many times or how long each process should be used and how the processes should be scheduled, given that each process can lead to a set of products. Such a feature appears in several industrial problems [7,8,9], including injection molding [10], for which a mixed integer programming model is proposed and tested on real data from a Brazilian molded pulp plant.
CLSP has many extensions, including the consideration of parallel production machines per period and setup times between products of different types. However, the scheduling is not part of this issue and is traditionally made as a second step. Therefore there is a significant difference between CLSP and the problem we study. Indeed, separating assignment and scheduling or decomposing a problem can immediately eliminate several good solutions from the searching space. In this work, we take the problem as a whole and this issue may thus be referred to as a batching problem. Batching is indeed the decision of whether or not to schedule similar jobs contiguously, to avoid setup times or setup costs [11].
Drexl and Kimms [12] draw an analogy between the batching and lot-sizing problems. In the continuous time lot sizing and scheduling problem, each demand is characterized by its deadline and its size. Demands are interpreted as jobs and the demand size determines the processing time of a job. An important assumption is that the capacity (e.g., the speed of the machine) is constant over time and thus the processing time of a job does not depend on the schedule. Another fundamental assumption is that jobs are not allowed to be split, which means that a certain demand must always be processed from the beginning to the end. Of course, several demands for the same item may be grouped together and processed by lots to save setup costs. Problems with these assumptions can thus be referred to as a batching and scheduling problem (BSP) rather than a lot sizing and scheduling problem. The relationship between batching and lot-sizing is also analyzed in [13], where the studied lot sizing problem is solved as a batch sequencing problem.
Potts and Kovalyov [14] review the literature on scheduling with batching, in the particular case of parallel machines. In this paper, parallel machines are classified as: identical, when the processing times depend only of the jobs, regardless of the machine on which they are processed; uniform, if the processing times depend on the jobs and the machines’ speed; or unrelated, when the processing time is a function of both the job and the machine where it is allocated. One of the specificities of our problem is that the processing time of the jobs depends only on the jobs. But because of the incompatibility between some molds and some machines, not all the machines can process all the jobs. To the best of our knowledge, this aspect has not been considered in batching problems but [15,16] solved some scheduling problems with eligibility restrictions using constructive heuristics. The eligibility aspect can also be found in [17] but in the flowshop case. Nevertheless, our problem can be seen as a problem with parallel unrelated machines, where the processing time will be: (1) the time required to process the job if the mold is compatible with the selected machine or (2) infinite if the mold is not compatible with the selected machine. A batch-scheduling problem with parallel unrelated machines is dealt with in [18], where the authors compare the performances of four heuristics to minimize the total weighted tardiness. Their study showed the superiority of a two-level batching heuristic and a simulated annealing approach over heuristics that use priority rules such as earliest weighted due date or shortest weighted processing time. Reference [19] also addressed a parallel unrelated batch scheduling problem with sequence dependent setup times and developed a GRASP metaheuristic to minimize the makespan. Reference [20] provide a constructive algorithm and a simulated annealing to portion and schedule batches in a multi-stages semi-conductor manufacturing plant where the parallel machines per stage are non-identical.
Because the weighted tardiness minimization in an unrelated parallel machine scheduling problem, , is already NP-hard [21], our problem is also NP-hard. Indeed, the is a particular case of our problem when the jobs have equal weights, the setup-times are null and each mold is required by only one job. As seen in this literature review, whether for solving the lot-sizing or batching problems, the developed methods are quite sophisticated constructive approaches or optimization approaches. Our aim in this paper is to provide a high performing optimization method which is easy to develop and use. Although in this article the proposed method will only be tested in a case study company, injection molding is a common industrial activity and several plants may share the same features. Our solving method will thus not be limited to a single use-case and this work may be considered as a first step toward a final objective which is to generalize the optimization tool to other scheduling problems with new characteristics.
In the following section, we provide a mathematical model that will be useful to spot the limit of the exact resolution for this NP-hard problem in terms of solving times and to ensure the quality of our method for the small-sized instances. The method itself is described and implemented in Section 4 and then experimented in a real plastic injection case.
3. Mathematical Model
The mathematical model of the problem we intend to solve, described in this section, was inspired by a model proposed by [22], although there are some significant differences between them. In the original model both earliness and tardiness were to be minimized. In our case study company, earliness is not considered as an issue, thus only tardiness is considered leading to a difference in the objective function. Furthermore, in the original model changeover occur whenever two jobs from different families are sequenced one after the other but this time is constant. In our case, when a setup time occur, this time depends of the sequence of jobs i and j, considering the time required to dismount the mold to produce i plus the time necessary to mount the mold to process j. Thus, unlike the original model we consider a sequence dependent setup time, which lead to a difference in the way the setups are considered in the model, specifically in the equations used to determine the completion time of a given job. Finally and this is probably the main difference between the models, in [22] the model is developed for identical parallel machines, which means that any job can be processed in any machine. In our case study company, a job can only be processed in a subset of the available machines. This has led to the introduction of a new constraint (3) to ensure that a job is always allocated to a compatible machine.
Below, we provide the inputs of our model:
- Number of molds
- Number of jobs
- Number of machines
- Mold for job
- Due date of job
- Processing time of job
- Time to mount the mold of job on the machine
- Time to dismount the mold of job
- : The setup time when job follows job on a machine. This setup time is equal to the time to dismount the mold used by () plus the time to mount the mold used by (), if and require different molds. Thus:if0 otherwise
- : Binary variable denoting if job is compatible with machine :
- : “Big M,” sufficiently large number to make the problem solvable by linear programming. In our case, should be much higher than the ending time of any job.
The decision variables of our model are the following:
- Completion time of job
- Tardiness of job
- : Binary variable denoting if is the first job to be processed on machine :
- : Binary variable denoting if job is scheduled right after job :
- : Binary variable denoting if job is processed on machine but not in the first place:
The mathematical model can be stated as follows:
Minimize:
Restricted to:
Equation (1) represents the objective function, which is to minimize the sum of all tardiness. A job is considered tardy if its completion time is higher than its due date; and in that case, the difference between its completion time and its due date is added to the sum. Equation (2) ensures that each job must be assigned to one machine. Equation (3) checks compatibility, which means that a job can only be scheduled on a compatible machine. Equation (4) enforces a job and its direct successor in the processing sequence to both be produced on the same machine. Equation (5) ensures that, for each machine, there can only be one job scheduled first. Equation (6) states that if a job is not the first to be scheduled on any machines, then it must have a predecessor. Equation (7) says that for each job, there can only be one other scheduled immediately before it or none in case it is the first job. Equation (8) forces the completion time of a certain task to be bigger than its processing time plus the setup and the completion time of its predecessor.
Equation (9) computes the completion time of the first job processed by each machine as its processing time plus the setup time. Equation (10) provides the completion time of a job smaller or equal to the sum of its due date and the tardiness. Equation (11) is the non-negativity constraint.
4. Proposed Solution Approach
Since the studied problem is NP-hard, solving our model with a mathematical solver is not expected to be efficient for the large-sized industrial problems. Therefore, we provided a solving algorithm that can quite rapidly reach good solutions. We propose a hybrid method, which combines a constructive heuristic (a list algorithm) with a metaheuristic. The problem characteristics are specified in the list algorithm while the metaheuristic is more generic and can be adapted to other scheduling problems without changes. The principle of the method is given in Figure 1. It can be seen as a master/slave resolution scheme, where the metaheuristic handles the searching process and the list-algorithm performs the quality assessment of the solutions [23,24].
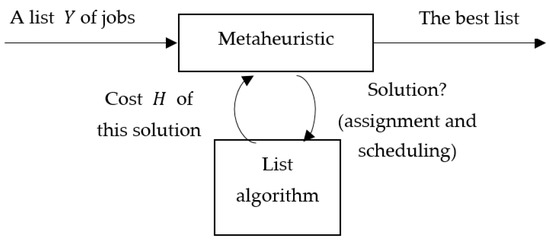
Figure 1.
Hybridization metaheuristic—List algorithm.
The encoding scheme of the proposed metaheuristic is a list of jobs, which is the order in which they will be selected by the algorithm to be assigned to the machines. The move between neighbor solutions is performed by jobs’ permutation. The jobs are selected one by one by list algorithm , following their order as given in List and assigned to the requested resources, building a scheduling that takes into account the problem constraints. From this scheduling emerges Solution , which will be evaluated by objective function . On the basis of this assessment, the metaheuristic decides if the solution should be selected or not. At the end of its run, the proposed method gives the scheduling sequence that gives the best value of objective function.
The general encoding scheme can be represented by Equation (12). is the set of all lists ; the set of all admissible assignments of the jobs to the machines. An assignment is considered admissible if all constraints are respected. More details about the encoding are given in [25].
4.1. List Algorithm
List algorithms are greedy heuristics that are widely used to solve scheduling problems. The standard list algorithm iteratively constructs a schedule by considering the jobs in a listed order and assigning each one of them to the first machine that becomes idle [26]. Examples of list algorithms applied to and activity planning and resource allocation in a hospital are presented in [27].
In the injection molding problem described in this paper, we propose a list scheduling algorithm to schedule jobs and assign them to the machines and dates considering tool compatibility. One of the advantages of using a list algorithm is to provide a simple neighborhood structure for metaheuristics, which can browse the set of solutions by permutations between two items in a list, as we will see in the next subsection. The details of the list algorithm is described by Algorithm 1. The algorithm takes as input the number of machines, the number of molds, as well as a sorted list of jobs which states the order in which they will be selected to be assigned to the machines. Of course, the jobs’ durations and their associated molds are part of the input. The algorithm gives as output the assignation of the jobs to the machines.
| Algorithm 1 List algorithm for the injection problem |
| Data: List of jobs |
| forallJobdo |
| Order the machines according to their release date: |
| j: = 0 |
| while Job not assigned AND do |
| if Job and machine compatible with the mold then |
| if Needed mold available then |
| Release date machine : = Release date machine + processing time of Job + setup time |
| Release date needed mold: = Release date machine |
| Assign Job to machine |
| else |
| Find on which machine the needed mold is used: MachineUsing |
| If the mold currently used in MachineUsing is the one needed by Job then |
| Release date MachineUsing: = Release date MachineUsing + processing time of Job |
| else |
| Release date MachineUsing: = Release date MachineUsing + processing time of Job + setup time |
| Release date needed mold: = Release date machine MachineUsing |
| Assign Job to machine MachineUsing |
| else |
| Next machine: |
Figure 2 shows an example of the algorithm’s assignment rule for a 3-machines instance. At iteration , the mold required by the next job on the list is not being used on any machine. is thus assigned to the less loaded machine with a setup time. Next, job needs a mold that is currently used on machine that has the lowest release time. will therefore be assigned to without setup. For job however, the required mold is currently used on the most-loaded machine and therefore the job has to wait for its release time before being processed. is assigned to without setup time.
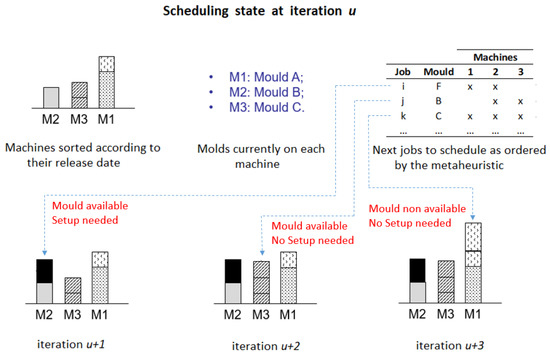
Figure 2.
Illustration of the List Algorithm’s assignment rule.
4.2. Metaheuristic
The proposed list algorithm is combined with a metaheuristic. We chose to use two single solution-based metaheuristics: stochastic descent and simulated annealing.
4.2.1. Tuning
The metaheuristic performs in the set of all jobs’ permutations. Given that is the number of jobs, cardinal of Ω is . One solution is a list of jobs.
Solutions are compared according to an objective function which characterizes their quality. In our case, the objective function is the total tardiness: the sum of the tardiness of all jobs. After having assigned the jobs to the molds and to the machines using the list algorithm described in the previous section, the value of the objective function is computed as follows: for each job, it is the difference between the completion time and the due date. All positive values are added.
The neighborhood system is the exchange of two jobs’ positions in List : job at position permutes with the one at position . checks accessibility and reversibility properties. An initial solution is randomly computed, based on a randomly sorted list of jobs.
4.2.2. Stochastic Descent
Stochastic descent is one of the oldest metaheuristics. Its principle is to compute a solution which is a neighbor of the current solution , according to the neighborhood system . After applying the list algorithm , a solution is obtained. If the value of the objective function is lower or equal to the current one , then the solution of the list is accepted. Stochastic descent converges to a local minimum. This method is easy to implement but the quality of the results may be insufficient. Algorithm 2 describes stochastic descent.
| Algorithm 2 Principle algorithm of stochastic descent |
| Data: Initial solution |
| whilenecessarydo |
| choose uniformly and randomly |
| if then |
4.2.3. Simulated Annealing
This metaheuristic comes from process used in metallurgy. That process alternates cycles of slow cooling and heating [28] used inhomogeneous simulated annealing to emulate this process. Applied to the optimization field, the algorithm consists of executing a local search with a computed probability to choose a worse solution than the current one, allowing thus to escape local optimum. This probability progressively decreases throughout the running process of the algorithm. If neighborhood system satisfies the accessibility and reversibility properties, simulated annealing converges in probability to the set of optimal solutions [29]. Algorithm 3 describes the principle algorithm of simulated annealing.
| Algorithm 3 Principle algorithm of simulated annealing |
| Data: Initial solution , Temperature , Decreasing factor |
| whilenecessarydo |
| choose uniformly and randomly |
| if then |
| else |
| if rand[0, 1]then |
| Compute the new temperature |
Two parameters have to be chosen:
- The initial temperature is chosen to be big enough so that most of the transitions are accepted at the beginning: .
- The decreasing factor is chosen in such a way that the final temperature would be close to zero.
5. Experiments
In this section, we carry out an experimental study to assess the performance of the proposed method. The outcomes are compared with an exact resolution performed by a mathematical solver for small-sized instances and with the results obtained with a heuristic presented in [30] for bigger ones. This benchmark heuristic is the scheduling method currently used in the molding company and it consists of a two-phase algorithm: first it assigns molds to machines and then it schedules jobs on each machine. Each mold is thus assigned to only one machine throughout the scheduling, with no possibility to move to another one. This method has thus he advantage to ensure a small number of setups throughout the production process.
5.1. Instances Generation
The case study company can produce more than 500 different parts, each one requiring its own mold. 25 injection machines are available in the shop-floor. An average of 200 production orders are received each week. The production planner needs to generate a weekly plan for the received orders, considering the items to be produced, their required quantities and the due date negotiated with the costumer. To execute this plan, the production planner must decide which job will be processed in each machine and the sequence by which they will be produced.
To test the proposed approach, 11 instances were randomly generated. The characteristics of these instances (number of machines available, number of molds required and number of jobs to be planned) are presented in Table 2. To correctly replicate the case study company problem, real data (jobs processing times and setup times) were collected on the shop-floor. The following statistical distributions fitting the collected data were used to generate the instances:

Table 2.
Generated instances.
- (1)
- Jobs’ processing times: Exponential with an average of 10.75 h.
- (2)
- Due dates: Uniform with a minimum of 24 and a maximum of 312 h.
- (3)
- Setup times:
- ○
- Time required to dismount a mold: Uniform with a minimum of 15 and a maximum of 45 min
- ○
- Time required to mount a mold: Uniform with a minimum of 20 and a maximum of 60 min.
The big M value of our mathematical model (i.e., variable ) has been chosen as equal to 10.000. Let us note that this value has no impact on the model’s solving times, since there is no loop or sum that depends on it.
5.2. Results
The computer that was used in the experiments is powered by an i7 CPU running at 2.6 GHz. First, to validate the quality of our method, we compared its results to those of the mathematical model. The solver used to solve the mathematical model is CPLEX 12.6.3. Table 3 summarizes results obtained by both methods. Results represent tardiness. Computational times are also given. In case the solver does not find any solution in a reasonable computational time, the upper and lower bounds are reported.

Table 3.
Comparison of results between the solver and the hybrid method.
As we can see in Table 3, for the 10 and 15 jobs instances, our method finds an optimal solution in less time than the solver. For larger instances, the solver does not reach any optimal solution for hours while our method finds a good solution (actually the upper bound found by the solver) in a few seconds. Since the CPLEX solver ran for more than 30 h without finding a solution for the 32 jobs instance, we decided not to continue the exact resolution for larger instances, for which we propose a comparison between our method and the scheduling heuristic currently used by the company.
Table 4 presents the results obtained for the big-sized instances with this benchmark heuristic and with our method. The comparison considers the tardiness and the number of setups. Over several replication, the shortest time needed to find one best solution is reported in the last column of the table.

Table 4.
Comparison of results between the benchmark method and the proposed approach.
The results show that besides being easy to develop, the proposed method is effective, giving good results in reasonable computational time. In comparison with the benchmark method proposed by [30], an average reduction of 35% is achieved in tardiness. For some instances, the reduction of tardiness is as high as 65%. This can be explained by the fact that the proposed method is less constraining, as the molds are not fixed and can switch from a machine to another throughout the scheduling. Nevertheless, the proposed method leads to an increase in the number of setups. It is important to note that, since the main objective of the company was to reduce the tardiness, the number of setups was not considered in the objective function of the proposed method but for other problems or future studies, an objective function considering tardiness and number of setups, with different weights, can be considered.
From the experimental study conducted in this section, we can thus conclude that our proposed approach brings a significant improvement in terms of tardiness when compared to the company current approach. Therefore, it is expected that the proposed approach will be implemented by the company as part of their production planning and scheduling system.
6. Conclusions and Perspectives
In this paper, a real world scheduling problem from a plastic injection company has been studied and solved. This problem considers sequence dependent setup time, parallel machines and compatibility constraints between machines and resources (molds). The considered objective is to minimize the jobs’ tardiness (i.e., the difference between the completion time of the jobs and their due date). First, a mathematical formulation of the problem has been provided. Then, an optimization method aiming to solve the big-sized instances has been developed. The proposed tool consists of a hybridization of a list-algorithm and a metaheuristic and can be seen as a master/slave approach. The obtained results show that the method provides high quality results for the proposed problem, outperforming a two-stage heuristic previously developed for the same problem [30] and currently used by the case-study injection plant.
This hybridization has been proposed instead of a classical metaheuristic because it is easier to develop. Indeed, using a classical metaheuristic needs to define a neighborhood system to browse the solution space. This neighborhood system can be complex: the neighbor solution needs to respects all constraints of the specific problem. In our approach, the neighbor is a swap between two jobs in the list of jobs and then the application of the list algorithm ensure the constraints respect. This has two interests. Our tool aims to solve industrial applications, so an easy, friendly tool may have more chance to be used by a company. Plus, we intend to solve others industrial applications, using the same tool, only adapting the list algorithm and the objective function (see [1] for other implementation of this tool). Ultimately, a generic tool that could be used to solve several different operational management problems could be developed. A strong point of the proposed method is that the metaheuristic can be used without any change for a large portfolio of problems. The intended tool would thus have a generic part composed of this metaheuristic and a library of list algorithms, which will allow rapid implementation by different companies, facing different planning, scheduling and assignment issues.
Several ways of improvement are considered to go deeper in the development of our tool. Within the hybridization, new metaheuristics could be used for the proposed method, including other single solution-based methods as iterated local search or population-based metaheuristics, such as particle swarm optimization using parallel computation with GPU. This will make it possible to assess the effectiveness of the proposed tool under different metaheuristic approaches. New list algorithms are currently proposed for different industrial problems. We are currently collecting data in companies with lot-sizing, scheduling and assignment problems. These problems take into account new constraints, as precedencies between jobs. Moreover, new objective function are considered: for instance improving the ergonomic and not only the economic aspect. Thus, our tool could face more realistic industrial problems from Industry 4.0, which deals with new markets and new technologies.
Author Contributions
Methodology, L.P. and N.K.; Supervision, C.S.; Writing—review & editing, N.K. and M.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by FEDER Hauts de France and CEA Tech.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study were generated on the basis of information provided by a case-study company and are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klement, N.; Silva, C. A generic decision support tool to planning and assignment problems: Industrial applications and industry 4.0. In Scheduling in Industry 4.0 and Cloud Manufacturing; Sokolov, B., Ivanov, D., Dolgui, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 167–192. [Google Scholar] [CrossRef]
- Dastidar, S.G.; Nagi, R. Scheduling injection molding operations with multiple resource constraints and sequence dependent setup times and costs. Comput. Oper. Res. 2005, 32, 2987–3005. [Google Scholar] [CrossRef]
- Van Wassenhove, L.N.; De Bodt, M.A. Capacitated lot sizing for injection moulding: A case study. J. Oper. Res. Soc. 1983, 34. [Google Scholar] [CrossRef]
- Nagarur, N.; Vrat, P.; Duongsuwan, W. Production planning and scheduling for injection molding of pipe fittings a case study. Int. J. Prod. Econ. 1997, 53. [Google Scholar] [CrossRef]
- Erlenkotter, D. Ford whitman harris and the economic order quantitymodel. Oper. Res. 1990, 38, 937–946. [Google Scholar] [CrossRef]
- Copil, K.; Wörbelauer, M.; Meyr, H.; Tempelmeier, H. Simultaneous lotsizing and scheduling problems: A classification and review of models. OR Spectr. 2016, 1–64. [Google Scholar] [CrossRef]
- Gramani, M.C.N.; França, P.M. The combined cutting stock and lot-sizing problem in industrial processes. Eur. J. Oper. Res. 2006, 174, 509–521. [Google Scholar] [CrossRef]
- Luche, J.R.D.; Morabito, R.; Pureza, V. Combining process selection and lot sizing models for production scheduling of eletrofused grains. Asia-Pac. J. Oper. Res. 2009, 26, 421–443. [Google Scholar] [CrossRef]
- Gaudreault, J.; Frayret, J.M.; Rousseau, A.; Amours, S.D. Combined planning and scheduling in a divergent production system with co-production:A case study in the lumber industry. Comput. Oper. Res. 2011, 38, 1238–1250. [Google Scholar] [CrossRef]
- Martinez, K.Y.P.; Toso, E.A.V.; Morabito, R. Production planning in the molded pulp packaging industry. Comput. Ind. Eng. 2016, 98, 554–566. [Google Scholar] [CrossRef]
- Potts, C.N.; Van Wassenhove, L. Integrating scheduling with batching and lot-sizing: A review of algorithms and complexity. J. Oper. Res. Soc. 1992, 395–406. [Google Scholar] [CrossRef]
- Drexl, A.; Kimms, A. Lot sizing and scheduling: Survey and extensions. Eur. J. Oper. Res. 1997, 99, 221–235. [Google Scholar] [CrossRef]
- Jordan, C. Discrete lot-sizing and scheduling by batch sequencing. In Batching and Scheduling; Springer: Berlin/Heidelberg, Germany, 1996; pp. 95–119. [Google Scholar] [CrossRef]
- Potts, C.N.; Kovalyov, M.Y. Scheduling with batching: A review. Eur. J. Oper. Res. 2000, 120, 228–249. [Google Scholar] [CrossRef]
- Centeno, G.; Armacost, R.L. Parallel machine scheduling with release time and machine eligibility restrictions. Comput. Ind. Eng. 1997, 33, 273–276. [Google Scholar] [CrossRef]
- Centeno, G.; Armacost, R.L. Minimizing makespan on parallel machines with release time and machine eligibility restrictions. Int. J. Prod. Res. 2004, 42, 1243–1256. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C. A genetic algorithm for hybrid flowshops with sequence dependent setup times and machine eligibility. Eur. J. Oper. Res. 2006, 169, 781–800. [Google Scholar] [CrossRef]
- Kim, D.-W.; Na, D.-G.; Chen, F.F. Unrelated parallel machine scheduling with setup times and a total weighted tardiness objective. Robot. Comput.-Integr. Manuf. 2003, 19, 173–181. [Google Scholar] [CrossRef]
- Sáenz-Alanís, C.A.; Jobish, V.D.; Salazar-Aguilar, M.A.; Boyer, V. A parallel machine batch scheduling problem in a brewing company. Int. J. Adv. Manuf. Technol. 2016, 87, 65–75. [Google Scholar] [CrossRef]
- Yugma, C.; Dauzère-Pérès, S.; Artigues, C.; Derreumaux, A.; Sibille, O. A batching, and scheduling algorithm for the diffusion area in semiconductor manufacturing. Int. J. Prod. Res. 2012, 50, 2118–2132. [Google Scholar] [CrossRef]
- Lenstra, J.K.; Rinnooy Kan, A.H.G.; Brucker, P.J. Complexity of machine scheduling problems. Ann. Discret. Math. 1977, 1, 343–362. [Google Scholar] [CrossRef]
- Omar, M.K.; Teo, S.C. Minimizing the sum of earliness/tardiness in identical parallel machines schedule with incompatible job families: An improved MIP approach. Appl. Math. Comput. 2006, 181, 1008–1017. [Google Scholar] [CrossRef]
- Toutouh, J.; Nesmachnow, S.; Alba, E. Fast energy-aware olsr routing invanets by means of a parallel evolutionary algorithm. Clust. Comput. 2012, 16. [Google Scholar] [CrossRef]
- Afsar, H.M.; Lcomme, P.; Ren, L.; Prodhon, C.; Vigo, D. Resolution of a job-shop problem with transportation constraints: A master/slave approach. In Proceedings of the 8th IFAC Conference on Manufacturing Modelling, Management and Control MIM, Troyes, France, 28 June 2016. [Google Scholar] [CrossRef]
- Gourgand, M.; Grangeon, N.; Klement, N. An analogy between bin packing problem and permutation problem: A new encoding scheme. In Advances in Production Management Systems. Innovative and Knowledge-Based Production Management in a Global-Local World; Springer: Berlin/Heidelberg, Germany, 2014; Volume 438, pp. 572–579. [Google Scholar] [CrossRef]
- Zhu, X.; Wilhelm, W.E. Scheduling and lot sizing with sequence-dependent setup: A literature review. IIE Trans. 2006, 38, 987–1007. [Google Scholar] [CrossRef]
- Klement, N.; Gourgand, M.; Grangeon, N. Medical imaging: Exams planning and resource assignment: Hybridization of a metaheuristic and a list algorithm. In Proceedings of the 10th International Conference on Health Informatics, Porto, Portugal, 21–23 February 2017. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Aarts, E.; van Laarhoven, P. Simulated Annealing: Theory and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Silva, C.; Ferreira, L.M. Microplano—A scheduling support system for the plastic injection industry. In E-Manufacturing: Business Paradigms and Supporting Technologies; Springer: Berlin/Heidelberg, Germany, 2004; pp. 81–89. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).