Shadow Estimation for Ultrasound Images Using Auto-Encoding Structures and Synthetic Shadows
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Datasets
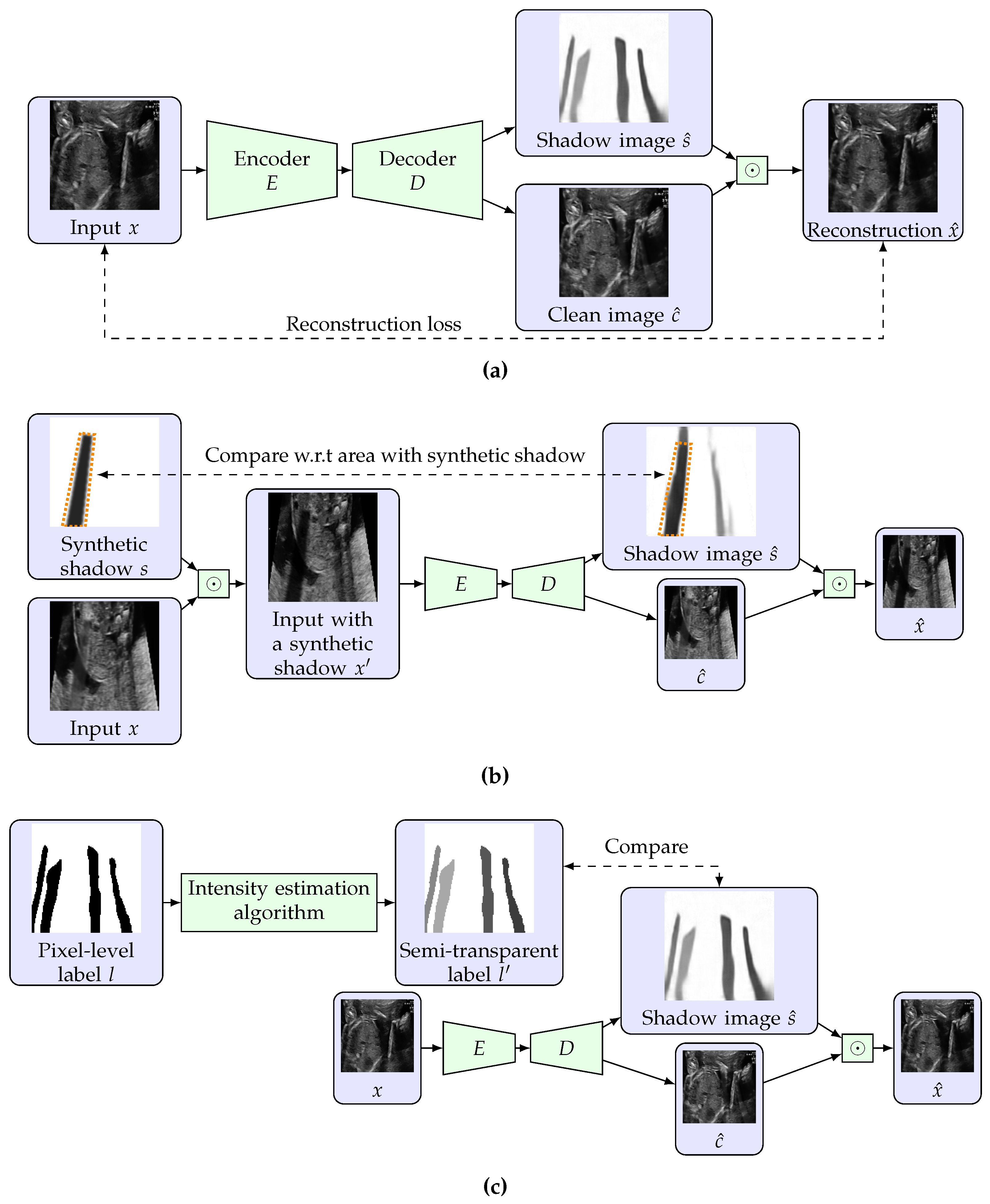
3.2. Restricted Auto-Encoding Structure for Shadow Estimation
3.3. Training Using Unlabeled Data with Synthetic Shadows
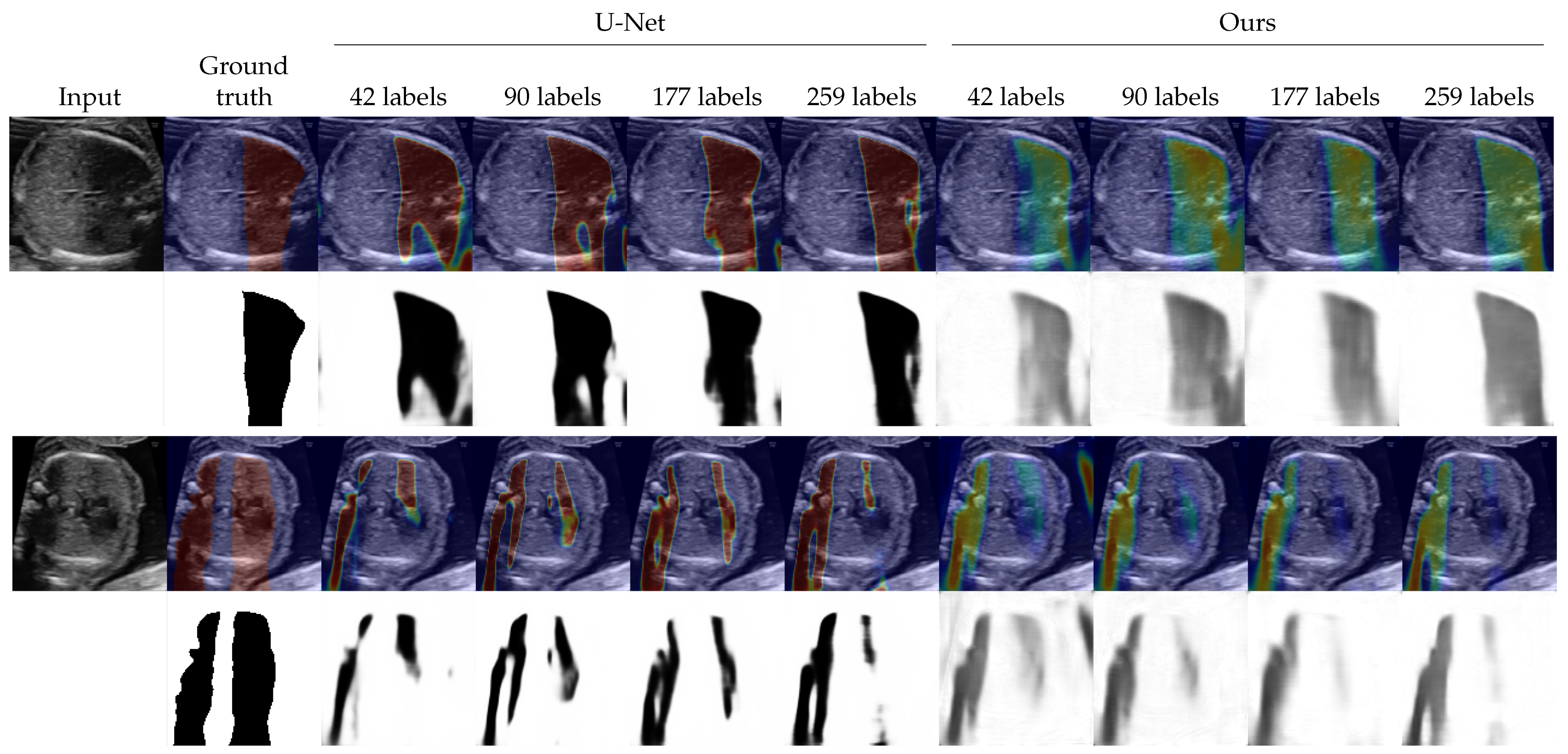
3.4. Use of Pixel-Level Labels and Extension to Semi-Supervised Learning
| Algorithm 1 Estimation of shadow intensities using a pixel-level binary label. |
| Input: A US image , a pixel-level label of shadows , and a threshold T. |
| Output: Semi-transparent label |
| 1: |
| 2: |
| 3: |
| 4: for each labeled shadow in l (i.e., each connected component in l with a value 0) do |
| 5: for each coordinate that corresponds to do |
| 6: |
| 7: end for |
| 8: end for |
4. Results
4.1. Setting
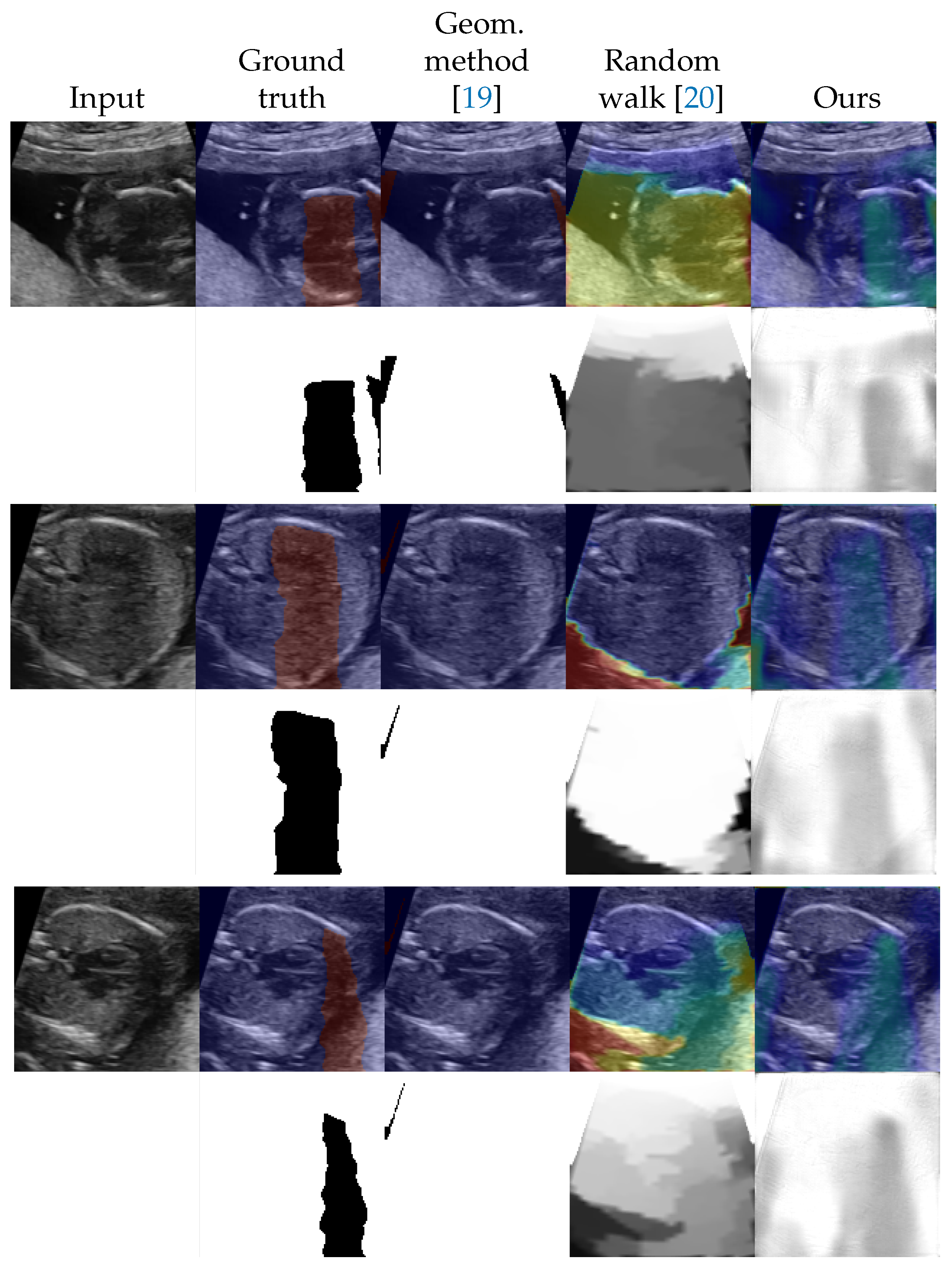
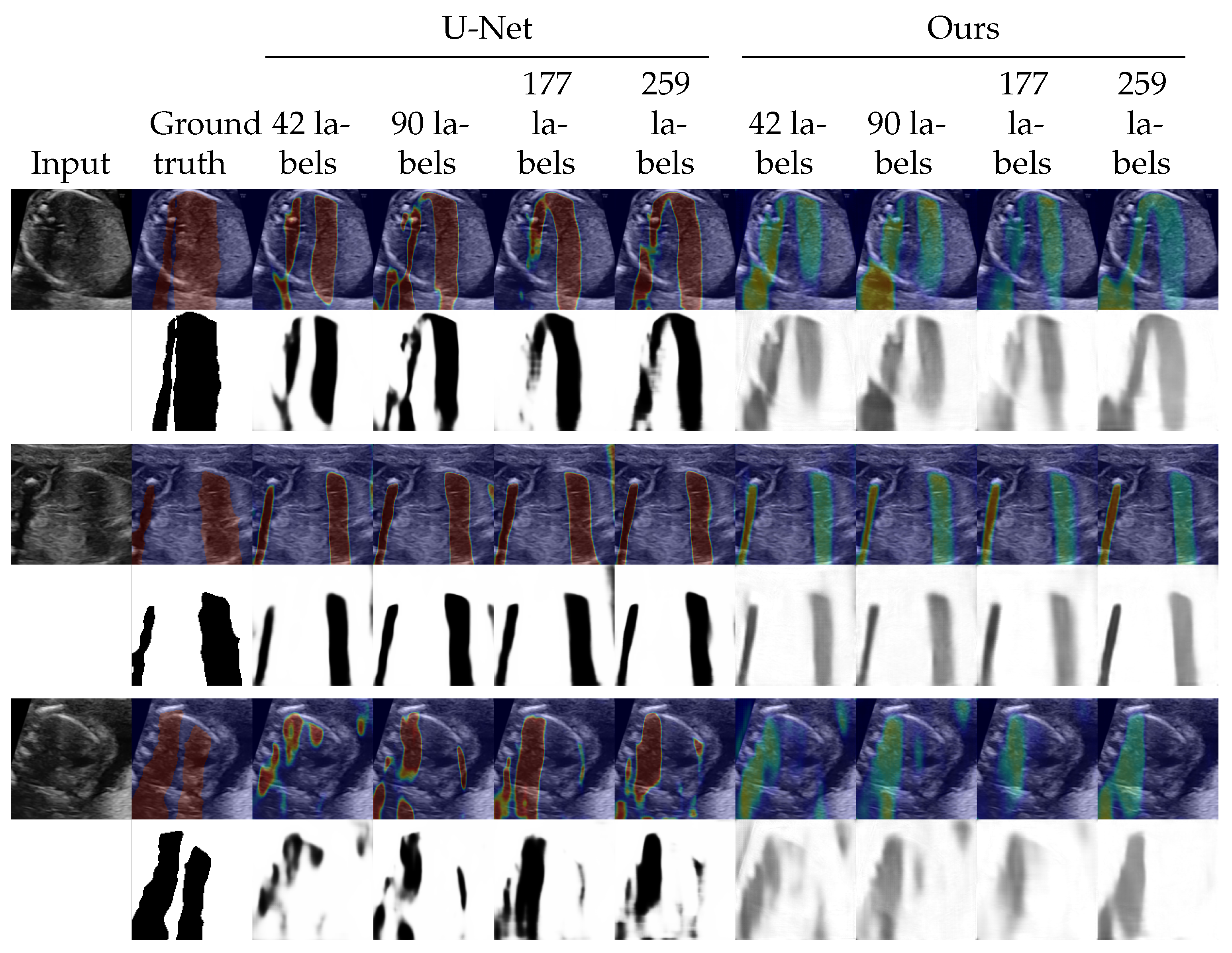
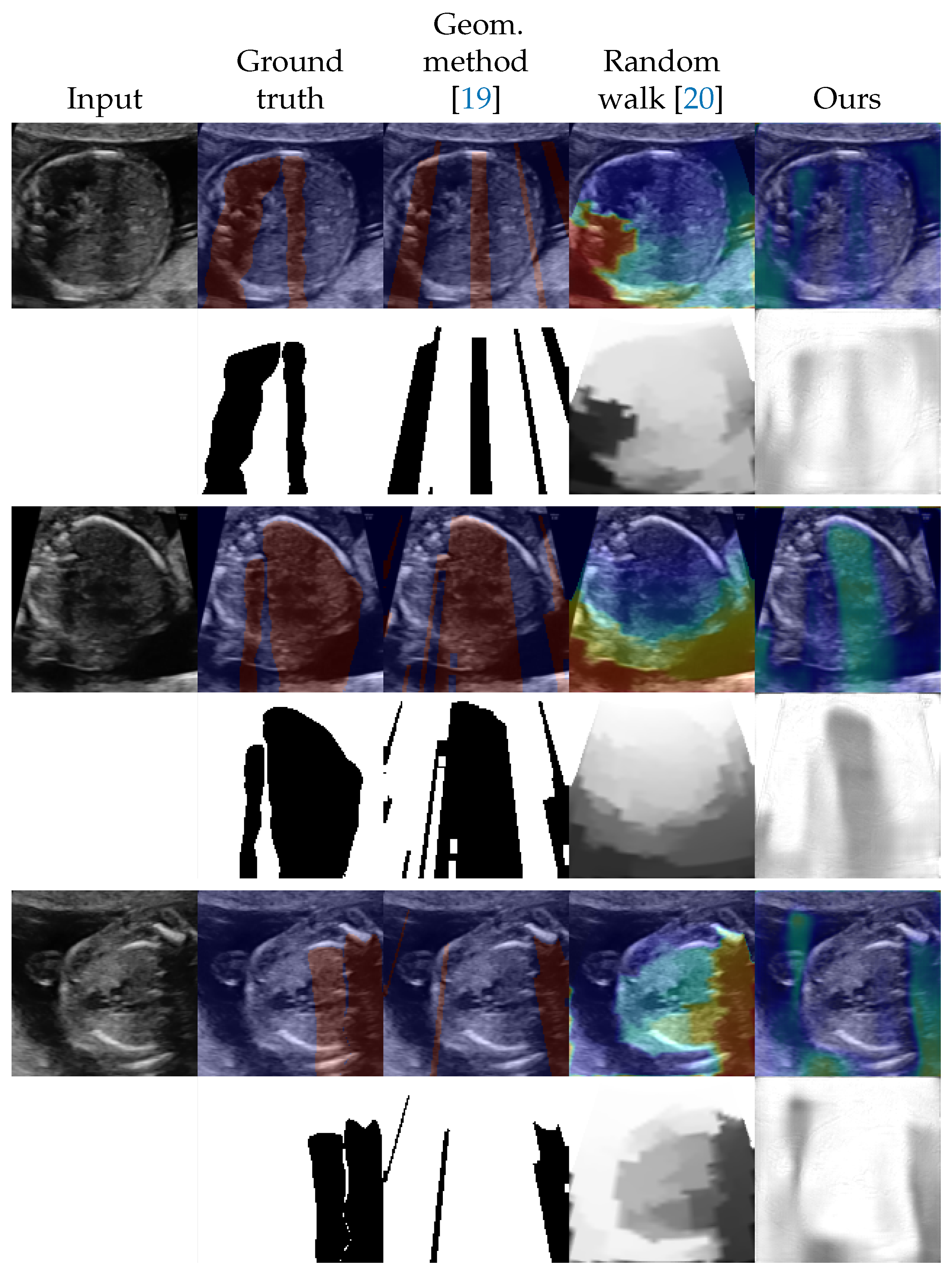
4.2. Shadow Detection
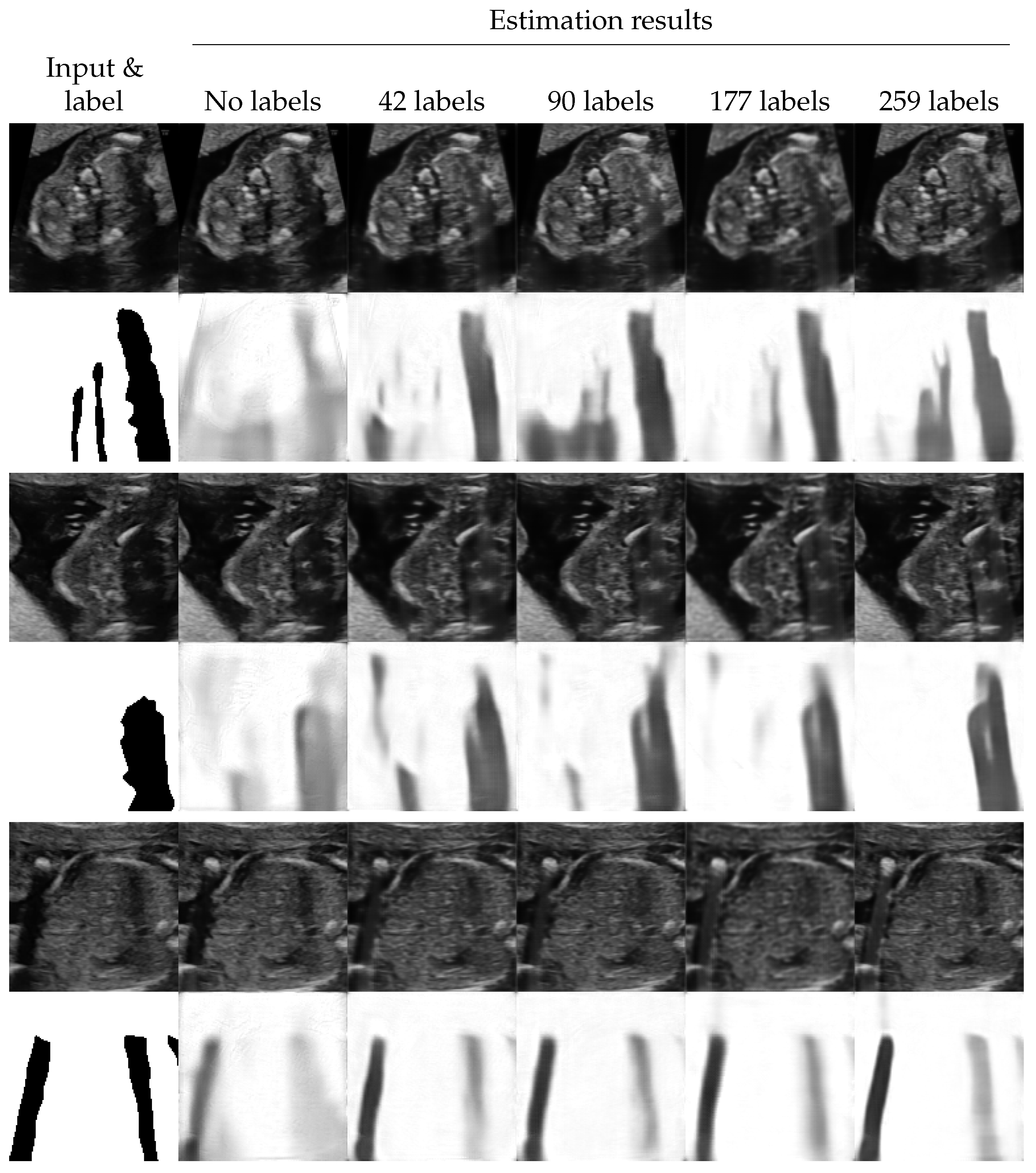
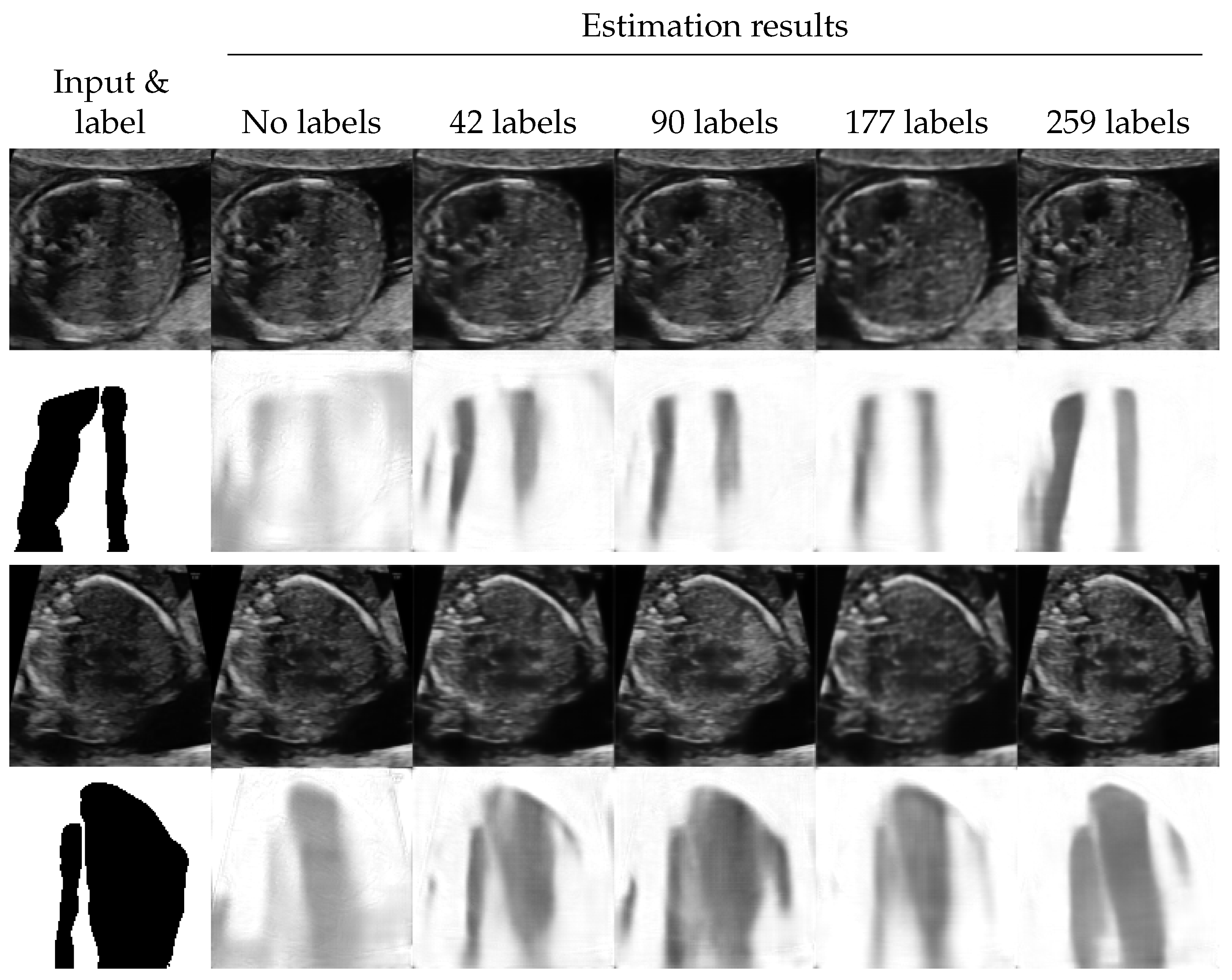
4.3. Shadow Intensity Estimation
4.4. Shadow Removal
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Algorithm for Generating Synthetic Shadows
| Algorithm A1 Generation of annular sector shaped synthetic shadows. A function draws a sample from a uniform distribution. |
| Input: Parameters for annular sectors (center coordinate , range of direction , range of angle , range of outer radius , and minimum inner radius ), blurring parameters , and range of shadow intensity . |
| Output: Image of a synthetic shadow . |
| 1: . |
| 2: . |
| 3: . |
| 4: . |
| 5: . |
| 6: (a zero matrix shaped ). |
| 7: for do |
| 8: Let be a image that filled with 1 inside an annular sector which center is p, outer radius is r, angle is , and direction is , and 0 otherwise. |
| 9: . |
| 10: end for |
| 11: . |
| 12: . |
| 13: Apply Gaussian blur with variance to s. |
Appendix B. Details of DNNs

Appendix C. Selected Hyperparameters
| Number of Labeled Images | |||||
|---|---|---|---|---|---|
| Hyperparameter | 0 | 42 (5 Videos) | 90 (10 Videos) | 177 (20 Videos) | 259 (30 Videos) |
| Threshold for random walk [20] | 0.996 | - | - | - | - |
| Threshold for the proposed method | 0.865 | 0.870 | 0.890 | 0.894 | 0.885 |
| 0.996 | 1 | 1 | 10 | 10 | |
| 0.996 | 0 | 0 | 0 | ||
| 0.996 | 0.1 | 0.5 | 0.1 | 0.5 | |
Appendix D. Additional Results
| Number of Labeled Images | |||||
|---|---|---|---|---|---|
| Method | 0 | 42 (5 Videos) | 90 (10 Videos) | 177 (20 Videos) | 259 (30 Videos) |
| Geometric method [19] | 0.201 (±0.213) | - | - | - | - |
| Random walk [20] | 0.349 (±0.151) | - | - | - | - |
| U-Net [30] | - | 0.539 (±0.220) | 0.575 (±0.215) | 0.636 (±0.176) | 0.657 (±0.181) |
| Ours | 0.491 (±0.180) | 0.615 (±0.176) | 0.640 (±0.201) | 0.676 (±0.157) | 0.692 (±0.172) |
| Number of Labeled Images | |||||
|---|---|---|---|---|---|
| Method | 0 | 42 (5 Videos) | 90 (10 Videos) | 177 (20 Videos) | 259 (30 Videos) |
| Geometric method [19] | 0.194 (±0.131) | - | - | - | - |
| Random walk [20] | −0.054 (±0.295) | - | - | - | - |
| U-Net [30] | - | 0.282 (±0.170) | 0.267 (±0.158) | 0.262 (±0.168) | 0.210 (±0.187) |
| Ours | 0.353 (±0.190) | 0.426 (±0.131) | 0.420 (±0.140) | 0.338 (±0.153) | 0.310 (±0.168) |
References
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Moran, C.M.; Pye, S.D.; Ellis, W.; Janeczko, A.; Morris, K.D.; McNeilly, A.S.; Fraser, H.M. A Comparison of the Imaging Performance of High Resolution Ultrasound Scanners for Preclinical Imaging. Ultrasound Med. Biol. 2011, 37, 493–501. [Google Scholar] [CrossRef]
- Sassaroli, E.; Crake, C.; Scorza, A.; Kim, D.S.; Park, M.A. Image Quality Evaluation of Ultrasound Imaging Systems: Advanced B-Modes. J. Appl. Clin. Med. Phys. 2019, 20, 115–124. [Google Scholar] [CrossRef]
- Entrekin, R.R.; Porter, B.A.; Sillesen, H.H.; Wong, A.D.; Cooperberg, P.L.; Fix, C.H. Real-Time Spatial Compound Imaging: Application to Breast, Vascular, and Musculoskeletal Ultrasound. Semin. Ultrasound CT MRI 2001, 22, 50–64. [Google Scholar] [CrossRef]
- Desser, T.S.; Jeffrey, R.B., Jr.; Lane, M.J.; Ralls, P.W. Tissue Harmonic Imaging: Utility in Abdominal and Pelvic Sonography. J. Clin. Ultrasound 1999, 27, 135–142. [Google Scholar] [CrossRef]
- Ortiz, S.H.C.; Chiu, T.; Fox, M.D. Ultrasound Image Enhancement: A Review. Biomed. Signal Process. Control 2012, 7, 419–428. [Google Scholar] [CrossRef]
- Perdios, D.; Vonlanthen, M.; Besson, A.; Martinez, F.; Arditi, M.; Thiran, J. Deep Convolutional Neural Network for Ultrasound Image Enhancement. In Proceedings of the 2018 IEEE International Ultrasonics Symposium, Kobe, Japan, 22–25 October 2018. [Google Scholar]
- Feldman, M.K.; Katyal, S.; Blackwood, M.S. US Artifacts. RadioGraphics 2009, 29, 1179–1189. [Google Scholar] [CrossRef] [PubMed]
- Ziskin, M.C.; Thickman, D.I.; Goldenberg, N.J.; Lapayowker, M.S.; Becker, J.M. The Comet Tail Artifact. J. Ultrasound Med. 1982, 1, 1–7. [Google Scholar] [CrossRef]
- Noble, J.A.; Boukerroui, D. Ultrasound Image Segmentation: A Survey. IEEE Trans. Med. Imaging 2006, 25, 987–1010. [Google Scholar] [CrossRef]
- Brattain, L.J.; Telfer, B.A.; Dhyani, M.; Grajo, J.R.; Samir, A.E. Machine Learning for Medical Ultrasound: Status, Methods, and Future Opportunities. Abdom. Radiol. 2018, 43, 786–799. [Google Scholar] [CrossRef]
- Liu, S.; Wang, Y.; Yang, X.; Lei, B.; Liu, L.; Li, S.X.; Ni, D.; Wang, T. Deep Learning in Medical Ultrasound Analysis: A Review. Engineering 2019, 5, 261–275. [Google Scholar] [CrossRef]
- Drukker, L.; Noble, J.A.; Papageorghiou, A.T. Introduction to Artificial Intelligence in Ultrasound Imaging in Obstetrics and Gynecology. Ultrasound Obstet. Gynecol. 2020, 56, 498–505. [Google Scholar] [CrossRef] [PubMed]
- Dozen, A.; Komatsu, M.; Sakai, A.; Komatsu, R.; Shozu, K.; Machino, H.; Yasutomi, S.; Arakaki, T.; Asada, K.; Kaneko, S.; et al. Image Segmentation of the Ventricular Septum in Fetal Cardiac Ultrasound Videos Based on Deep Learning Using Time-Series Information. Biomolecules 2020, 10, 1526. [Google Scholar] [CrossRef] [PubMed]
- Shozu, K.; Komatsu, M.; Sakai, A.; Komatsu, R.; Dozen, A.; Machino, H.; Yasutomi, S.; Arakaki, T.; Asada, K.; Kaneko, S.; et al. Model-Agnostic Method for Thoracic Wall Segmentation in Fetal Ultrasound Videos. Biomolecules 2020, 10, 1691. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, M.; Sakai, A.; Komatsu, R.; Matsuoka, R.; Yasutomi, S.; Shozu, K.; Dozen, A.; Machino, H.; Hidaka, H.; Arakaki, T.; et al. Detection of Cardiac Structural Abnormalities in Fetal Ultrasound Videos Using Deep Learning. Appl. Sci. 2021, 11, 371. [Google Scholar] [CrossRef]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Hellier, P.; Coupé, P.; Morandi, X.; Collins, D.L. An Automatic Geometrical and Statistical Method to Detect Acoustic Shadows in Intraoperative Ultrasound Brain Images. Med. Image Anal. 2010, 14, 195–204. [Google Scholar] [CrossRef][Green Version]
- Karamalis, A.; Wein, W.; Klein, T.; Navab, N. Ultrasound Confidence Maps Using Random Walks. Med. Image Anal. 2012, 16, 1101–1112. [Google Scholar] [CrossRef]
- Hacihaliloglu, I. Enhancement of bone shadow region using local phase-based ultrasound transmission maps. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 951–960. [Google Scholar] [CrossRef]
- Meng, Q.; Baumgartner, C.; Sinclair, M.; Housden, J.; Rajchl, M.; Gomez, A.; Hou, B.; Toussaint, N.; Zimmer, V.; Tan, J.; et al. Automatic Shadow Detection in 2D Ultrasound Images. In Data Driven Treatment Response Assessment and Preterm, Perinatal, and Paediatric Image Analysis, Granada, Spain, 16 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 66–75. [Google Scholar]
- Meng, Q.; Sinclair, M.; Zimmer, V.; Hou, B.; Rajchl, M.; Toussaint, N.; Oktay, O.; Schlemper, J.; Gomez, A.; Housden, J.; et al. Weakly Supervised Estimation of Shadow Confidence Maps in Fetal Ultrasound Imaging. IEEE Trans. Med. Imaging 2019, 38, 2755–2767. [Google Scholar] [CrossRef]
- Hu, R.; Singla, R.; Yan, R.; Mayer, C.; Rohling, R.N. Automated Placenta Segmentation with a Convolutional Neural Network Weighted by Acoustic Shadow Detection. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Berlin, Germany, 23–27 July 2019; pp. 6718–6723. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial Autoencoders. arXiv 2016, arXiv:1511.05644. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-Supervised Learning with Ladder Networks. In Advances in Neural Information Processing Systems, Montréal, Canada, 7–10 December 2015; Curran Associates, Inc.: Red Hook, NY, USA, 2015; Volume 28, pp. 3546–3554. [Google Scholar]
- Garcia-Garcia, A.; Orts-Escolano, S.; Oprea, S.; Villena-Martinez, V.; Martinez-Gonzalez, P.; Garcia-Rodriguez, J. A Survey on Deep Learning Techniques for Image and Video Semantic Segmentation. Appl. Soft Comput. 2018, 70, 41–65. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In International Conference on Medical Image Computing and Computer-Assisted Intervention, Proceedings of the MICCAI 2015: Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chen, C.; Qin, C.; Qiu, H.; Tarroni, G.; Duan, J.; Bai, W.; Rueckert, D. Deep Learning for Cardiac Image Segmentation: A Review. Front. Cardiovasc. Med. 2020, 7, 25. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.W.; Siu, W.C.; Liu, Z.S.; Li, C.T.; Lun, D.P.K. Deep Relighting Networks for Image Light Source Manipulation. In Proceedings of the the 2020 European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Yasutomi, S.; Arakaki, T.; Hamamoto, R. Shadow Detection for Ultrasound Images Using Unlabeled Data and Synthetic Shadows. arXiv 2019, arXiv:1908.01439. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Carass, A.; Roy, S.; Gherman, A.; Reinhold, J.C.; Jesson, A.; Arbel, T.; Maier, O.; Handels, H.; Ghafoorian, M.; Platel, B.; et al. Evaluating White Matter Lesion Segmentations with Refined Sørensen-Dice Analysis. Sci. Rep. 2020, 10, 8242. [Google Scholar] [CrossRef] [PubMed]
- Lane, D.; Scott, D.; Hebl, M.; Guerra, R.; Osherson, D.; Zimmer, H. Introduction to Statistics; Rice University: Houston, TX, USA, 2003; Available online: https://open.umn.edu/opentextbooks/textbooks/459 (accessed on 10 December 2020).
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-To-Image Translation With Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In ICML Workshop on Deep Learning for Audio, Speech and Language Processing, Atlanta, USA, 16–21 June 2013; PMLR: Cambridge, MA, USA, 2013. [Google Scholar]
| Number of Labeled Images | |||||
|---|---|---|---|---|---|
| Method | 0 | 42 (5 Videos) | 90 (10 Videos) | 177 (20 Videos) | 259 (30 Videos) |
| Geometric method [19] | 0.193 (±0.210) | - | - | - | - |
| Random walk [20] | 0.450 (±0.142) | - | - | - | - |
| U-Net [30] | - | 0.610 (±0.184) | 0.655 (±0.170) | 0.681 (±0.136) | 0.698 (±0.137) |
| Ours | 0.578 (±0.164) | 0.666 (±0.142) | 0.686 (±0.148) | 0.707 (±0.113) | 0.720 (±0.151) |
| Number of Labeled Images | |||||
|---|---|---|---|---|---|
| Method | 0 | 42 (5 Videos) | 90 (10 Videos) | 177 (20 Videos) | 259 (30 Videos) |
| Geometric method [19] | 0.152 (±0.182) | - | - | - | - |
| Random walk [20] | −0.047 (±0.290) | - | - | - | - |
| U-Net [30] | - | 0.308 (±0.150) | 0.267 (±0.144) | 0.262 (±0.158) | 0.247 (±0.172) |
| Ours | 0.351 (±0.155) | 0.388 (±0.150) | 0.414 (±0.159) | 0.358 (±0.149) | 0.349 (±0.162) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasutomi, S.; Arakaki, T.; Matsuoka, R.; Sakai, A.; Komatsu, R.; Shozu, K.; Dozen, A.; Machino, H.; Asada, K.; Kaneko, S.; et al. Shadow Estimation for Ultrasound Images Using Auto-Encoding Structures and Synthetic Shadows. Appl. Sci. 2021, 11, 1127. https://doi.org/10.3390/app11031127
Yasutomi S, Arakaki T, Matsuoka R, Sakai A, Komatsu R, Shozu K, Dozen A, Machino H, Asada K, Kaneko S, et al. Shadow Estimation for Ultrasound Images Using Auto-Encoding Structures and Synthetic Shadows. Applied Sciences. 2021; 11(3):1127. https://doi.org/10.3390/app11031127
Chicago/Turabian StyleYasutomi, Suguru, Tatsuya Arakaki, Ryu Matsuoka, Akira Sakai, Reina Komatsu, Kanto Shozu, Ai Dozen, Hidenori Machino, Ken Asada, Syuzo Kaneko, and et al. 2021. "Shadow Estimation for Ultrasound Images Using Auto-Encoding Structures and Synthetic Shadows" Applied Sciences 11, no. 3: 1127. https://doi.org/10.3390/app11031127
APA StyleYasutomi, S., Arakaki, T., Matsuoka, R., Sakai, A., Komatsu, R., Shozu, K., Dozen, A., Machino, H., Asada, K., Kaneko, S., Sekizawa, A., Hamamoto, R., & Komatsu, M. (2021). Shadow Estimation for Ultrasound Images Using Auto-Encoding Structures and Synthetic Shadows. Applied Sciences, 11(3), 1127. https://doi.org/10.3390/app11031127








