Rail Diagnostics Based on Ultrasonic Guided Waves: An Overview
Abstract
1. Introduction
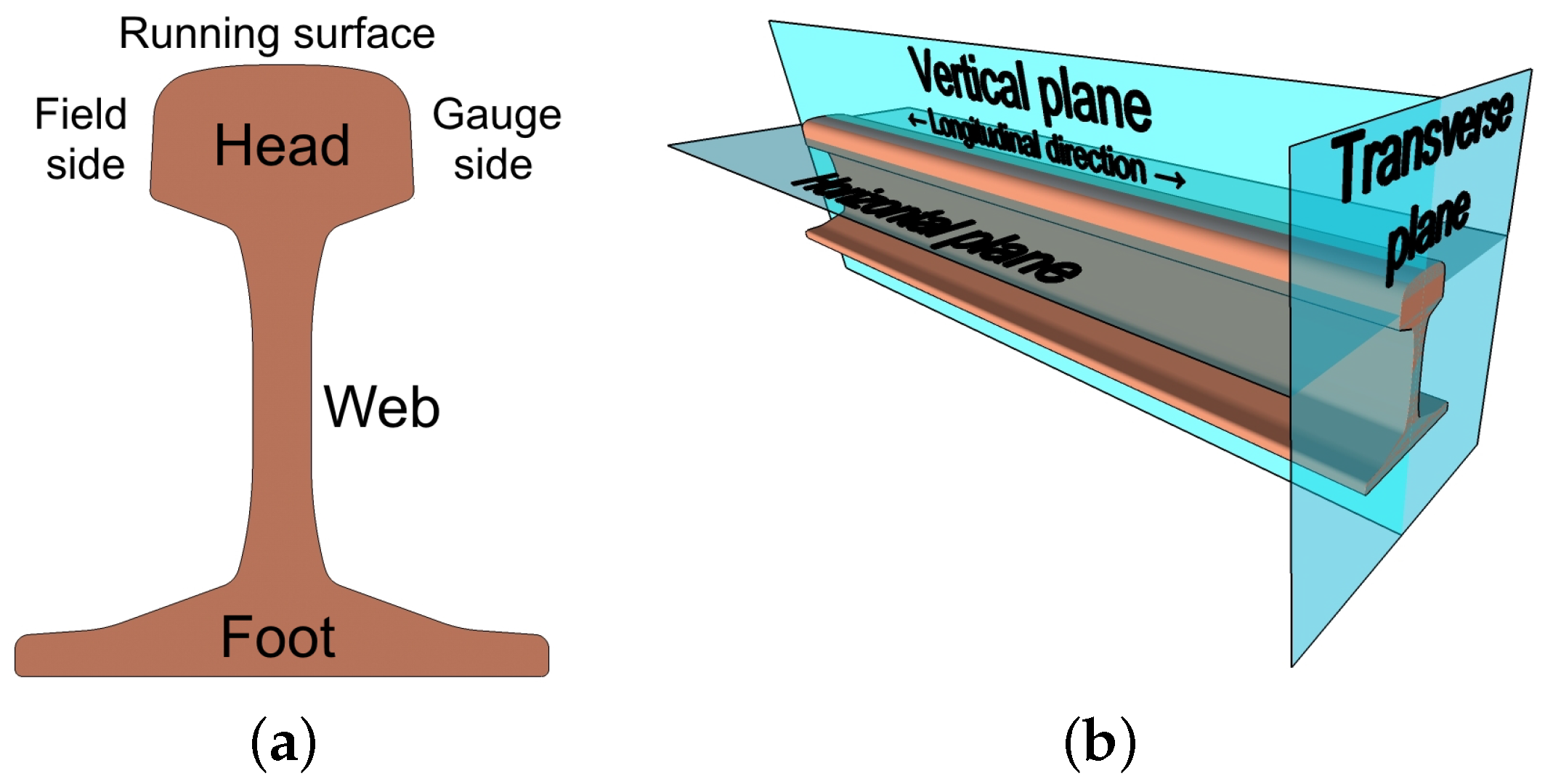
2. An Overview of Rail Defects and of the Techniques for Their Detection
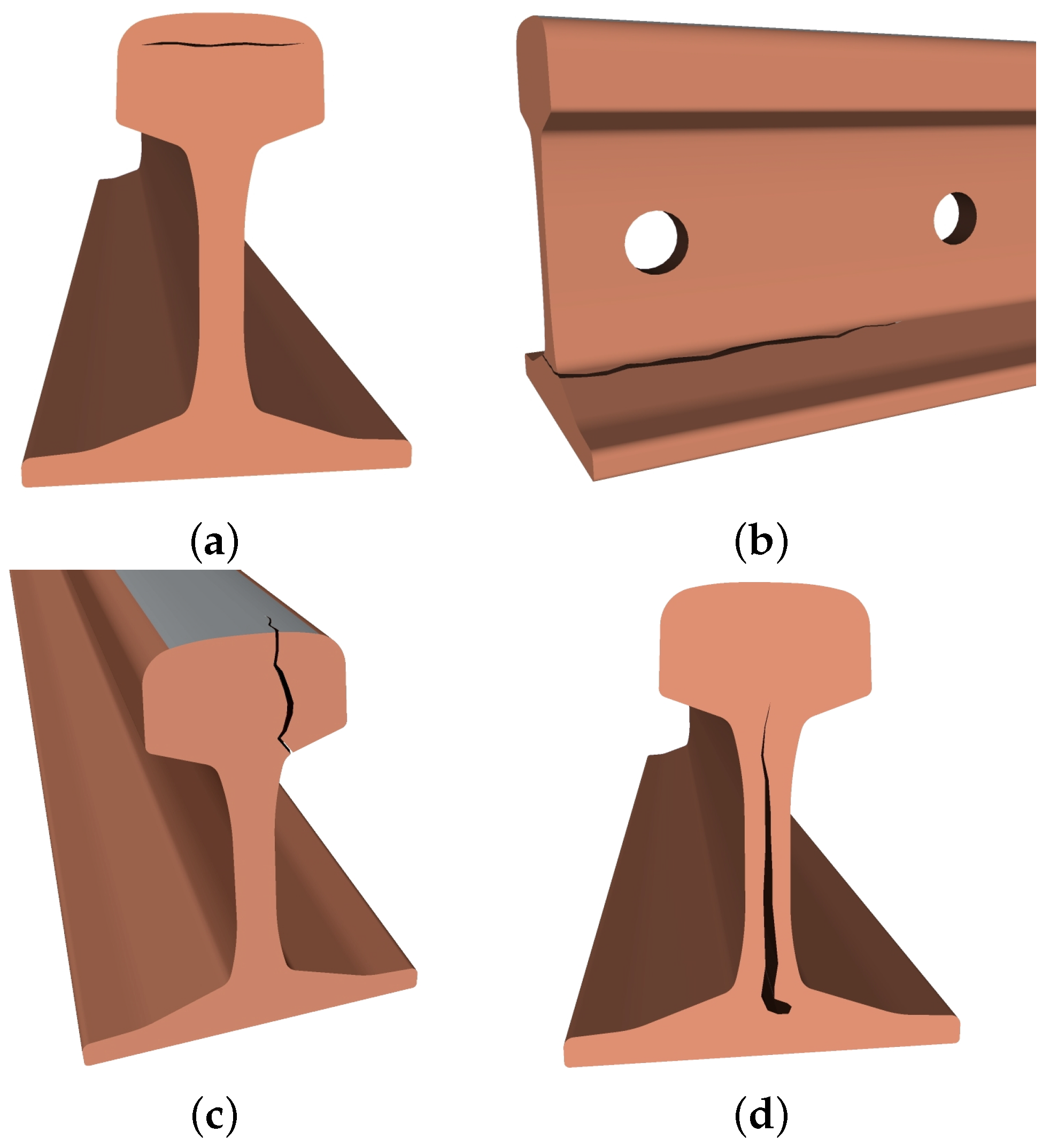
2.1. Rail Defects
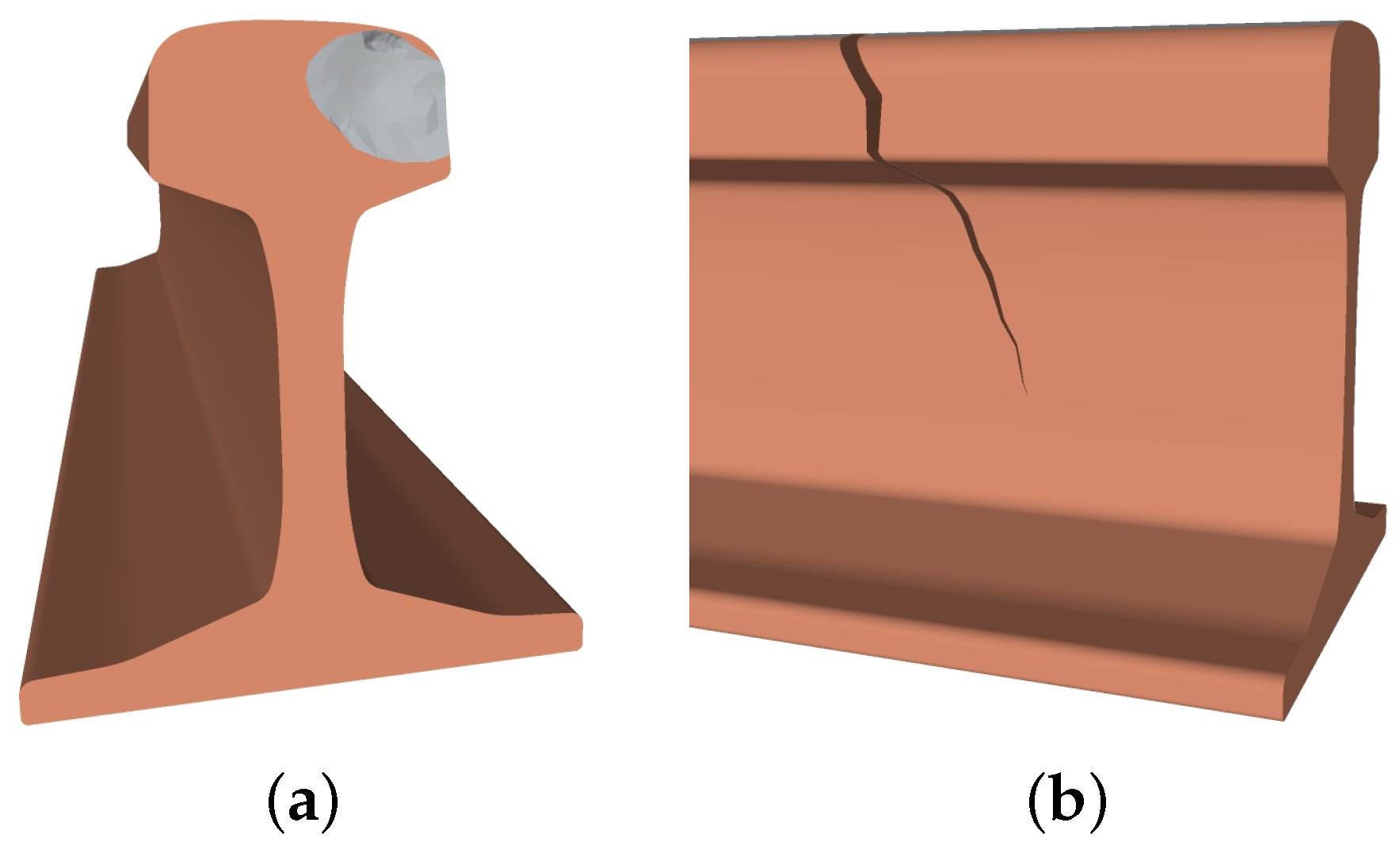
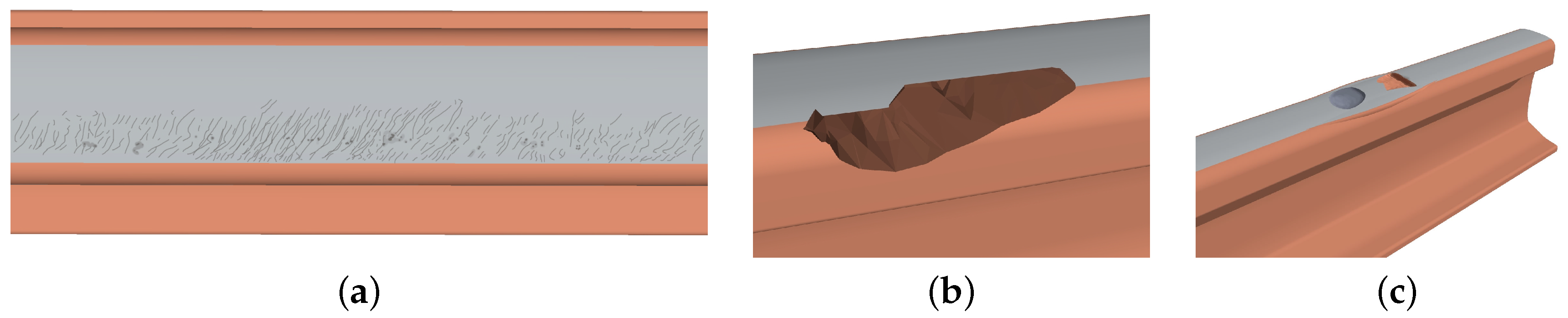
2.1.1. Rail Manufacturing Defects
2.1.2. Defects Due to Improper Use or Handling of Rails
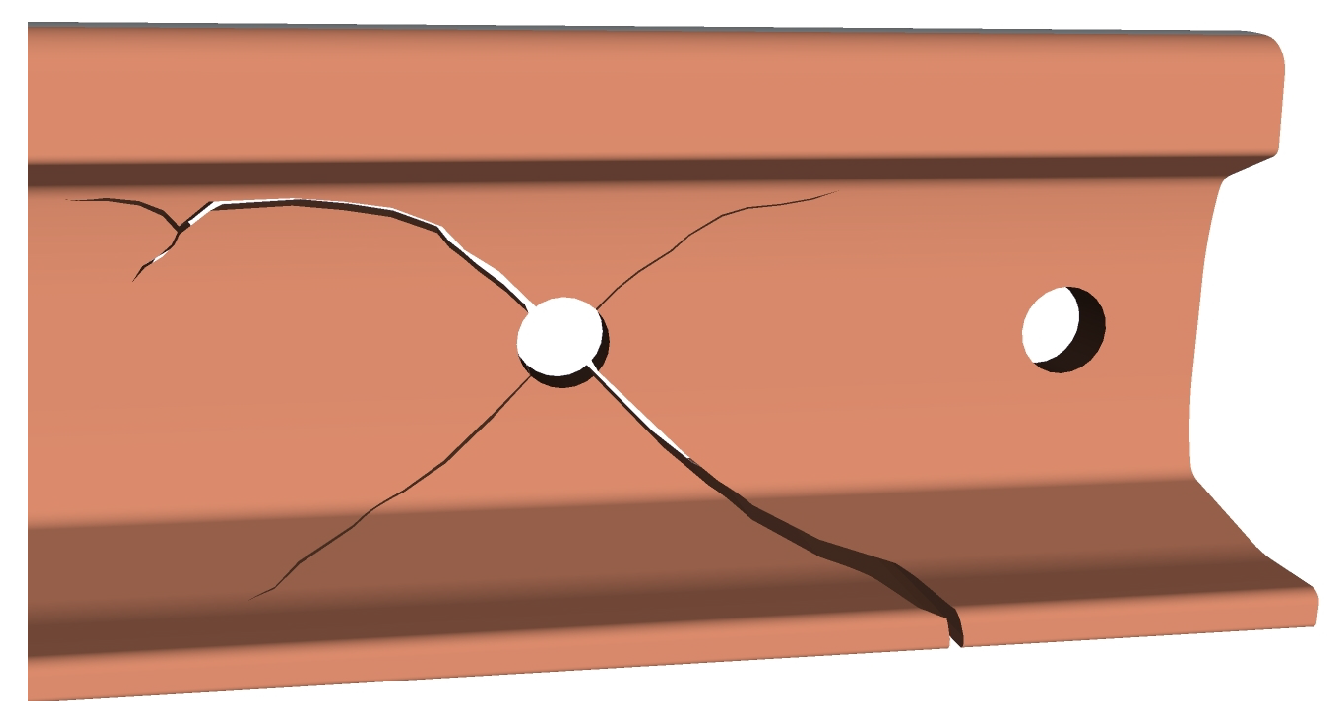
2.1.3. Defects Due to Rail Wear and Fatigue
2.1.4. Defect Growth
2.2. Rail Diagnostics Techniques
2.2.1. EC-Based Methods
2.2.2. Ultrasonic Techniques
2.2.3. Visual Inspection
2.2.4. Thermal Techniques
2.2.5. Radiographic Techniques
2.2.6. Track Circuits
2.3. Defect Detection Techniques Based on Ultrasonic Waves
2.3.1. Conventional Ultrasonic Techniques
2.3.2. Phased Arrays
2.3.3. Guided Waves
3. Systems for Rail Defect Detection Based on Ultrasonic Guided Waves: Classification
- On-board systems [40,45,46,47,48,49]-The measurement equipment is embarked on board a moving vehicle (e.g., an inspection cart), allowing for scanning the head of the rails on which it is riding. The detection of defects in the scanned rails is achieved through a pitch–catch mechanism. Initial implementations were based on an active approach, in which a source of ultrasounds was used to inject UGW into the rails, and sensing was accomplished through an array of transducers. More recent implementations adopt a passive approach, in which the ultrasonic excitation is generated by the rolling wheels of the moving vehicle. The approaches based on on-board systems have been promoted, among others, by the Experimental Mechanics & NDE Laboratory of the University of California, San Diego, USA.
- Land-based systems [9,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]-The employed equipment is placed on the ground near to the railway infrastructure, and its actuators and sensors are attached to the rails under test. The detection of defects in the rails is achieved through a pulse-echo approach. A lot of contributions about this topic have been published by the Sensor Science and Technology Department of the Council for Scientific and Industrial Research, South Africa. The ultrasonic broken rail detection (UBRD) system has been developed by this institution and put in use on the Oreline in South Africa to detect the presence of a fully broken rail; the system is evolved to implement an early defect detection system. In recent years, important results in this research field have been achieved by two Chinese research groups. In fact, significant contributions about the best methods to excite and detect propagation modes in a rail, and about feasible methods for rail defect location have been published by various researchers working at the Beijing Jiaotong University (School of Mechanical, Electronic, and Control Engineering, and Key Laboratory of Vehicle Advanced Manufacturing, Measuring and Control Technology). Moreover, an electronic system able to efficiently excite ultrasonic guided waves in rails has been developed by various researchers working at the Xi’an University of Technology (Department of Electronic Engineering).
4. Systems for Rail Defect Detection Based on Ultrasonic Guided Waves: Architecture
4.1. On-Board Systems
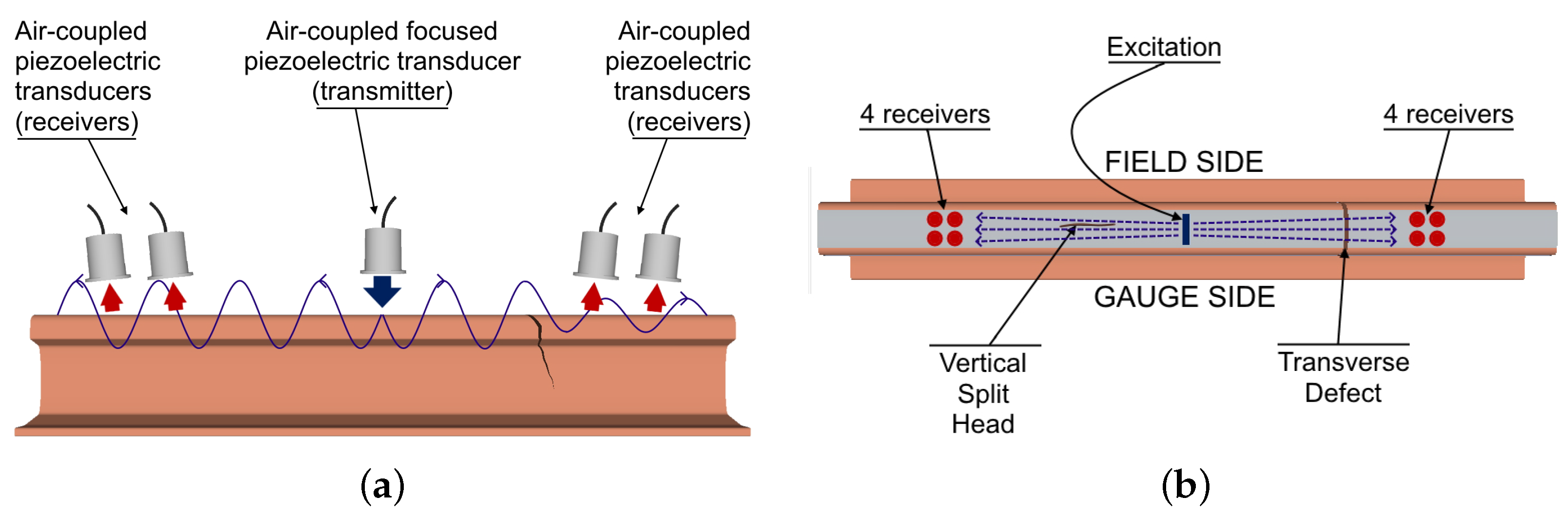
- An active rail inspection system is able to detect surface-breaking cracks and internal defects located in the railhead. It is based on UGWs and air-coupled contactless probing. Both the transmission of test signals and their reception are accomplished by means of air-coupled piezoelectric transducers arranged in a pitch–catch configuration. The use of a laser transmitter has been also investigated [40]; however, this option has been judged too costly and is potentially hard to maintain. In an active system, receivers are arranged in pairs and placed at the two sides of the transmitter: this allows for implementing a differential detection scheme. The system output, after data analysis, is represented by the so-called damage index (DI), exhibiting peaks in correspondence of discontinuities (i.e., of potential defects) in rails. In recent years, the use of laser technology for both exciting UGWs in rails and sensing them has been investigated [68,69]. In this case, non-ablative laser sources are used to generate a guided tensional wave system in the rail; the response to such a system can be sensed by means of a rotational laser vibrometer.
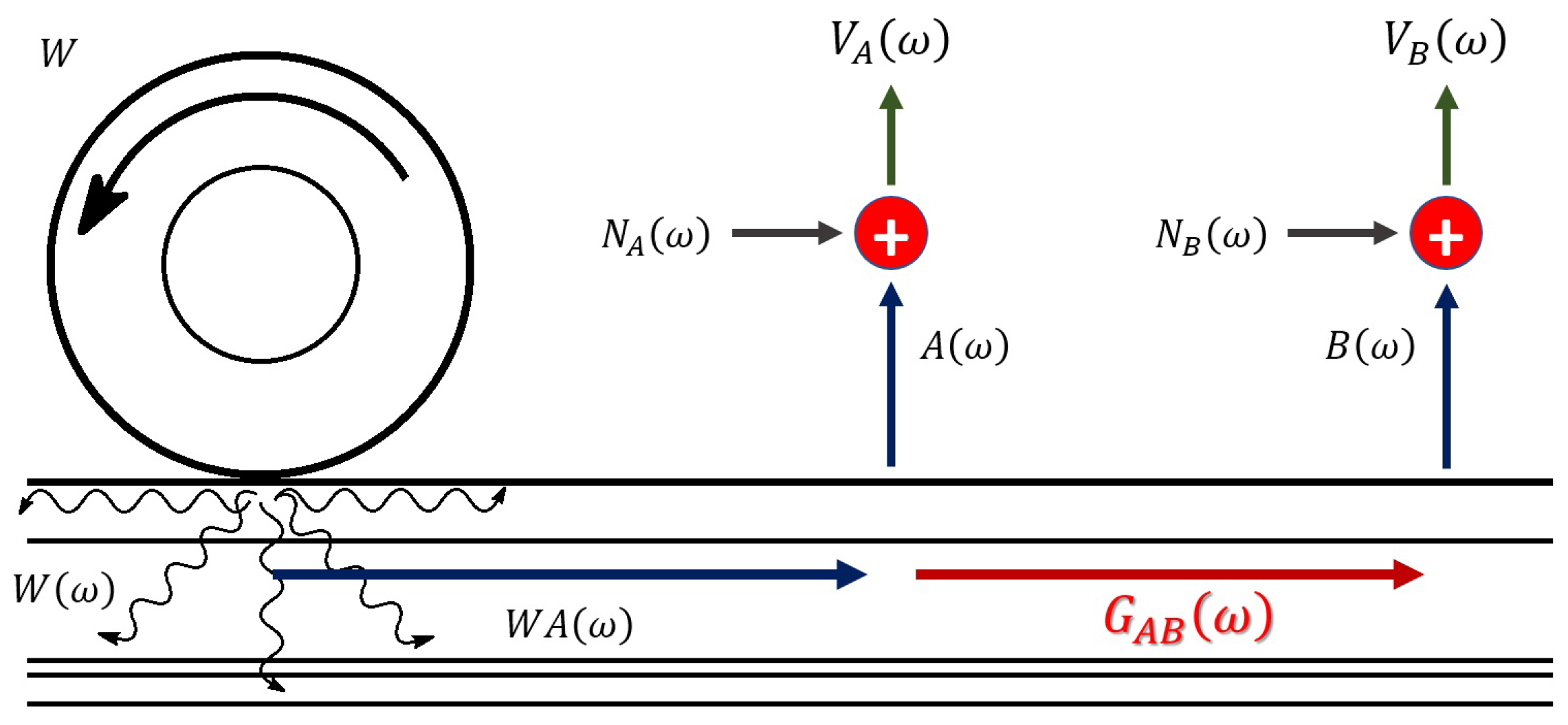
- A passive rail inspection system aims at estimating the acoustic transfer function of rails; the excitation is represented by the rolling wheels of the moving instrumented train [48]. When a train is in motion, its rotating wheels generate a continuous dynamic excitation of the rail. Such an excitation is uncontrolled, non-stationary, and difficult to characterize [48]. Therefore, in this case, the challenge to be faced is to generate a stable rail transfer function that is not affected by the excitation [49]. The presence of a discontinuity in the rail can be inferred from the estimated transfer function, using again the DI indicator.
4.2. Land-Based Systems
5. Implementation of On-Board Systems
5.1. Active Approach
5.1.1. Hardware Configuration
5.1.2. Defect Detection Principles
5.1.3. Signal Processing
5.1.4. Reverberation of Airborne Signals Caused by an Acoustic Mismatch
5.2. Passive Approach
5.2.1. Hardware Configuration
5.2.2. Defect Detection Principle
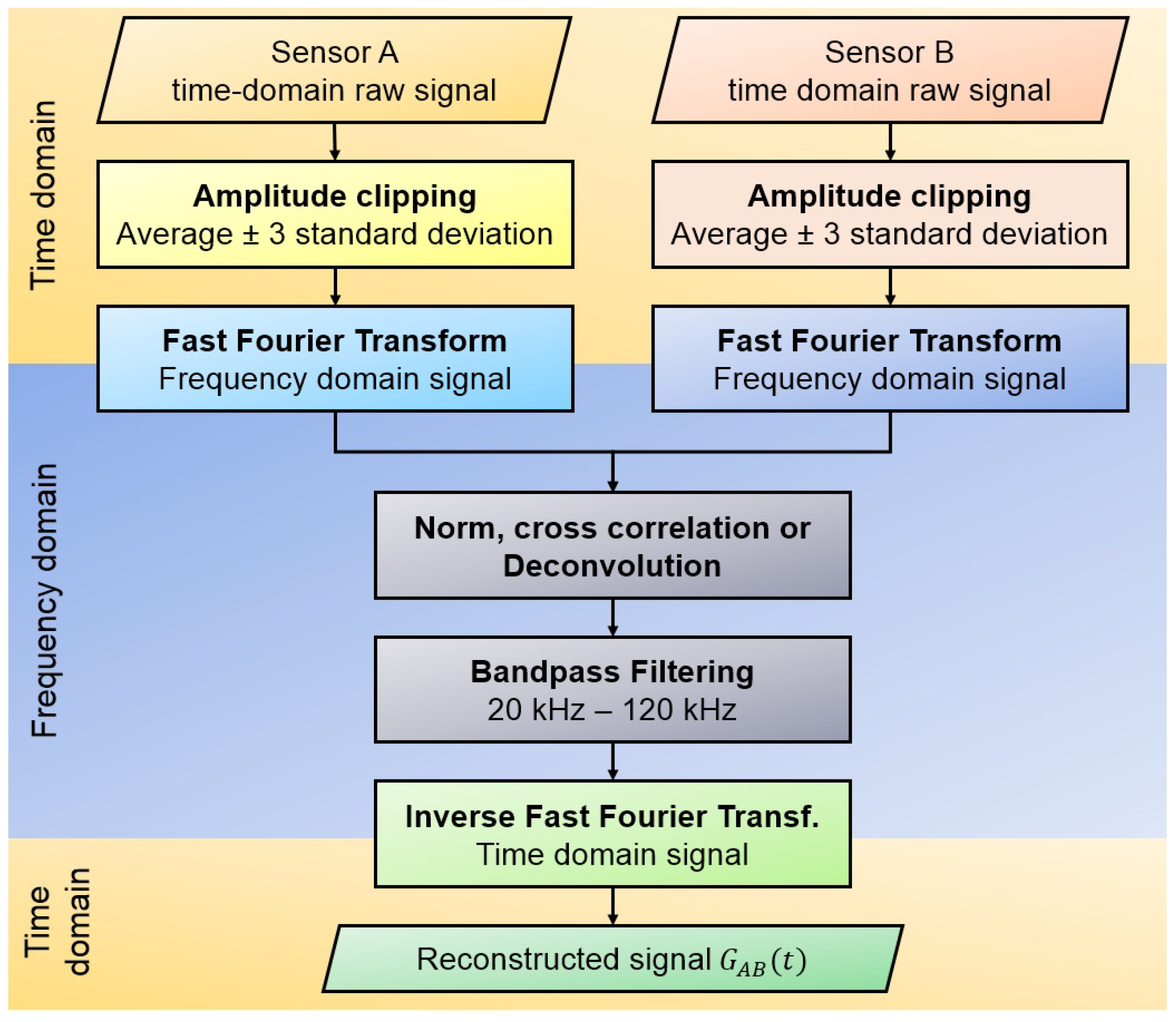
5.2.3. Data Processing
5.2.4. Trade-Offs
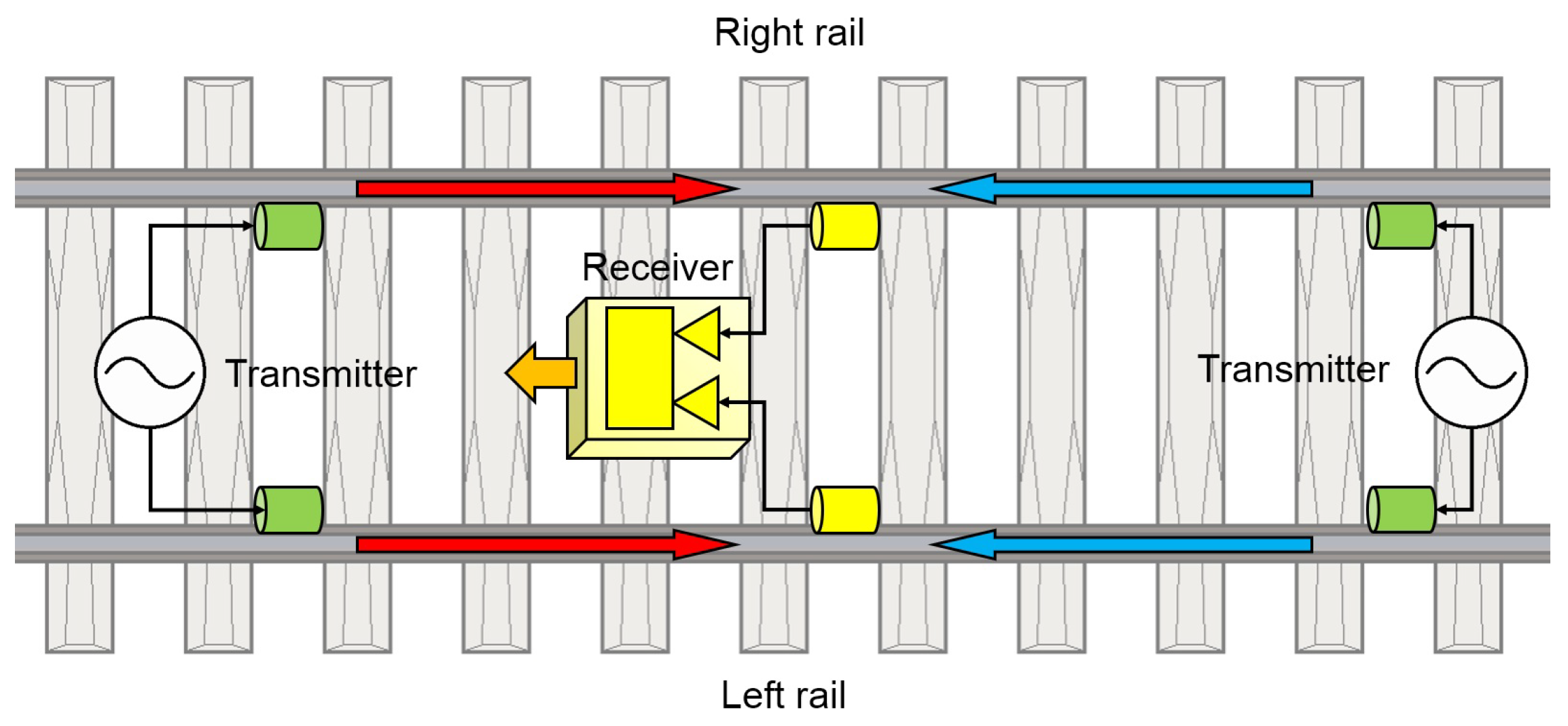
6. Land-Based Systems Implementation-Premise: Ultrasonic Broken Rail Detector (UBRD)
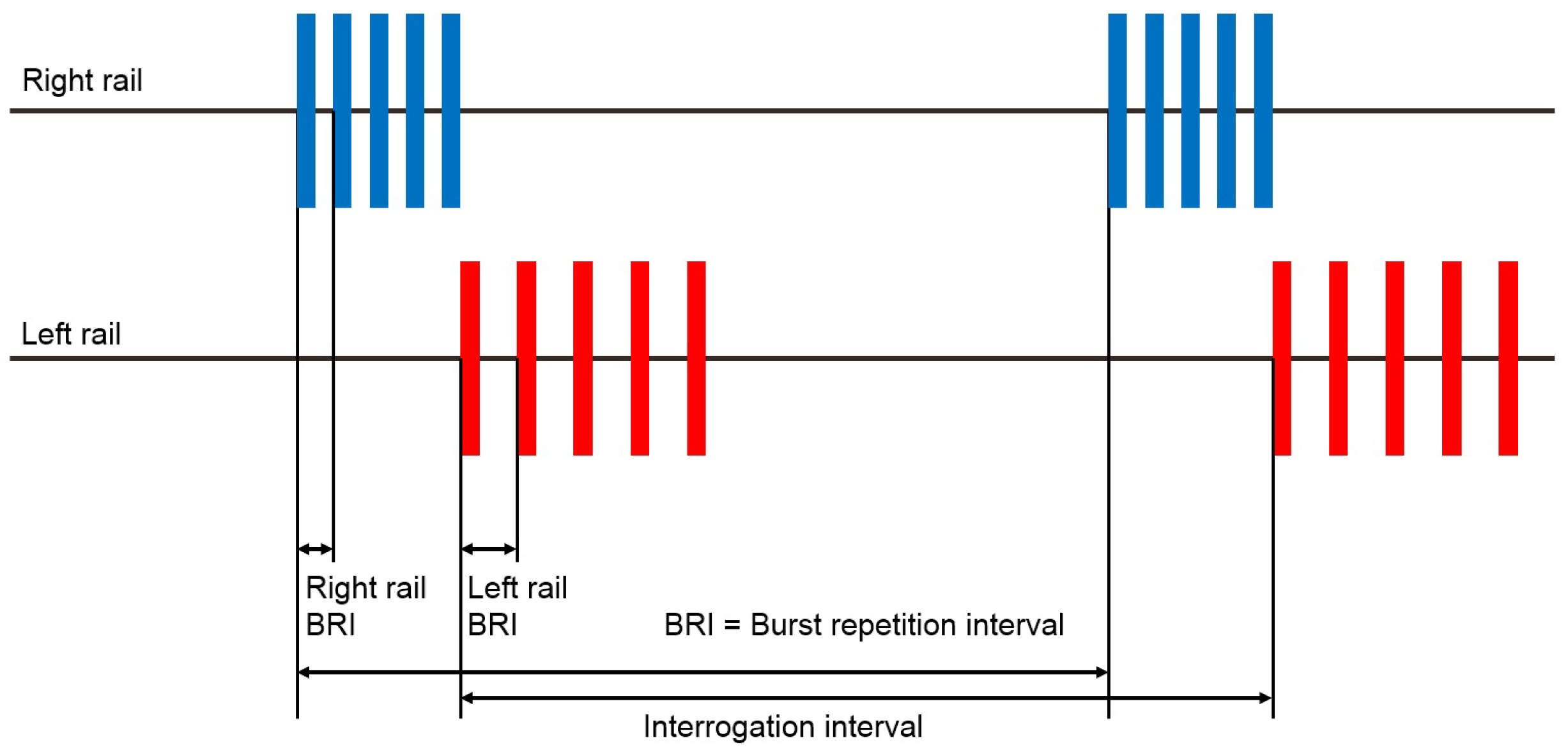
6.1. UBRD Hardware Configuration and Generated Signals
6.2. Defect Detection Principle and Employed Signal Processing Method
6.3. UBRD Updates
7. Land-Based Systems Implementation-Evolution: Early Rail Defect Detection Capability
7.1. Introduction
7.2. Monitoring Set-Up
7.2.1. Selected Modes for Guided Wave Propagation
7.2.2. Monitoring System Hardware and Software
7.2.3. Behavior of a Defect during Time
7.3. Signal Pre-Processing
7.3.1. Acquired Signals
7.3.2. Phased Array Processing
7.3.3. Dispersion Compensation
7.3.4. Signal Stretching and Scaling
7.3.5. Signal Reordering to Simulate the Monotonic Growth of a Defect
7.4. Defect Detection
Data-Driven Defect Detection Techniques
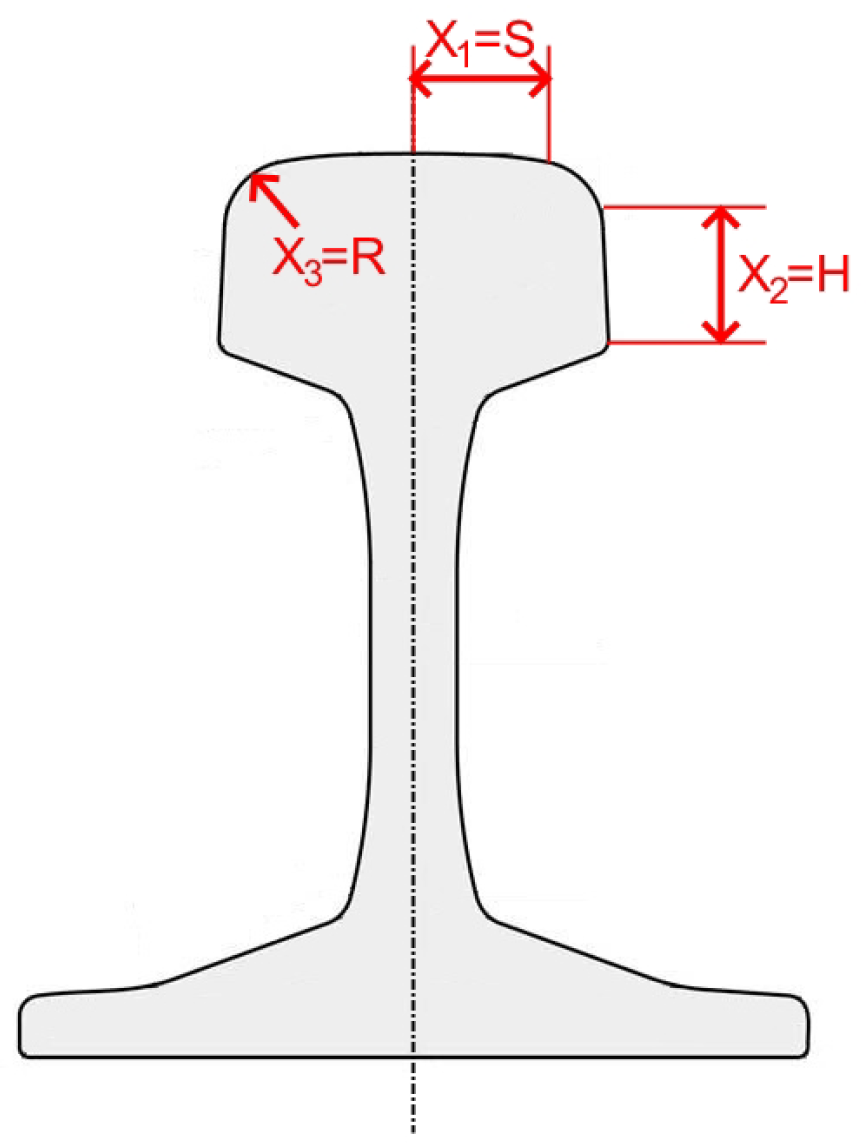
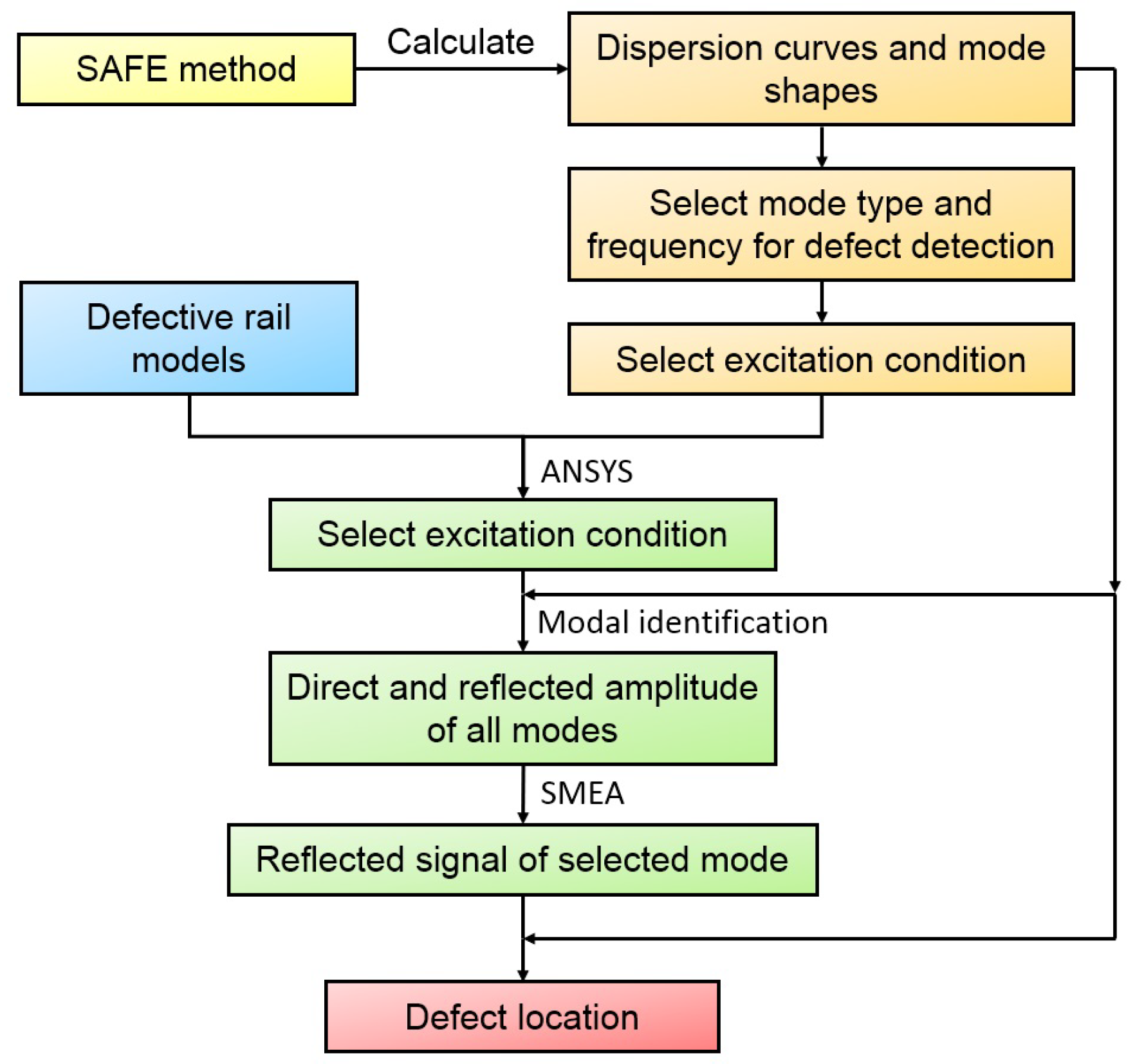
7.5. Adaptive SAFE Model for Rail Parameter Estimation
7.5.1. Problem Statement
7.5.2. Possible Solutions
7.5.3. Conclusions
8. Land-Based Systems Implementation—Other Projects
8.1. RailAcoustic by Enekom
8.2. Technical Contributions Provided by the Beijing Jiaotong University
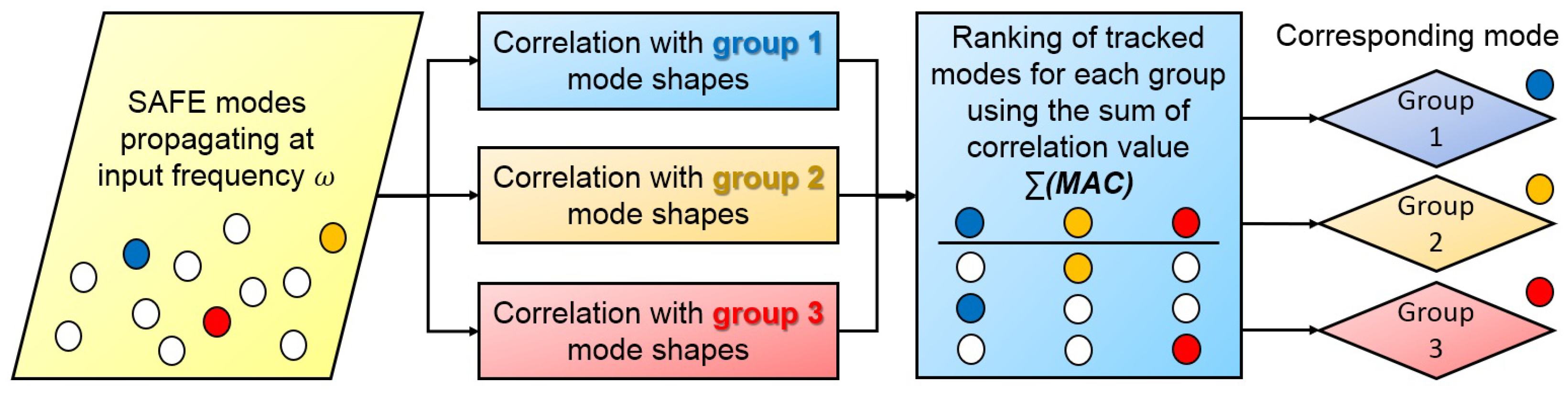
Single Modal Extraction Algorithm
8.3. Technical Contributions Provided by the Xi’an University of Technology
- The design of a high-voltage pulser achieving an improved transmission efficiency [63].
- The development of a tracking method able to estimate the optimal excitation frequency, i.e., the one maximizing the received signal power [64].
- The use of Baker coded UGW signals for enhancing the SNR of the received signal and the development of an adaptive peak detection algorithm [78].
9. Performance Analysis
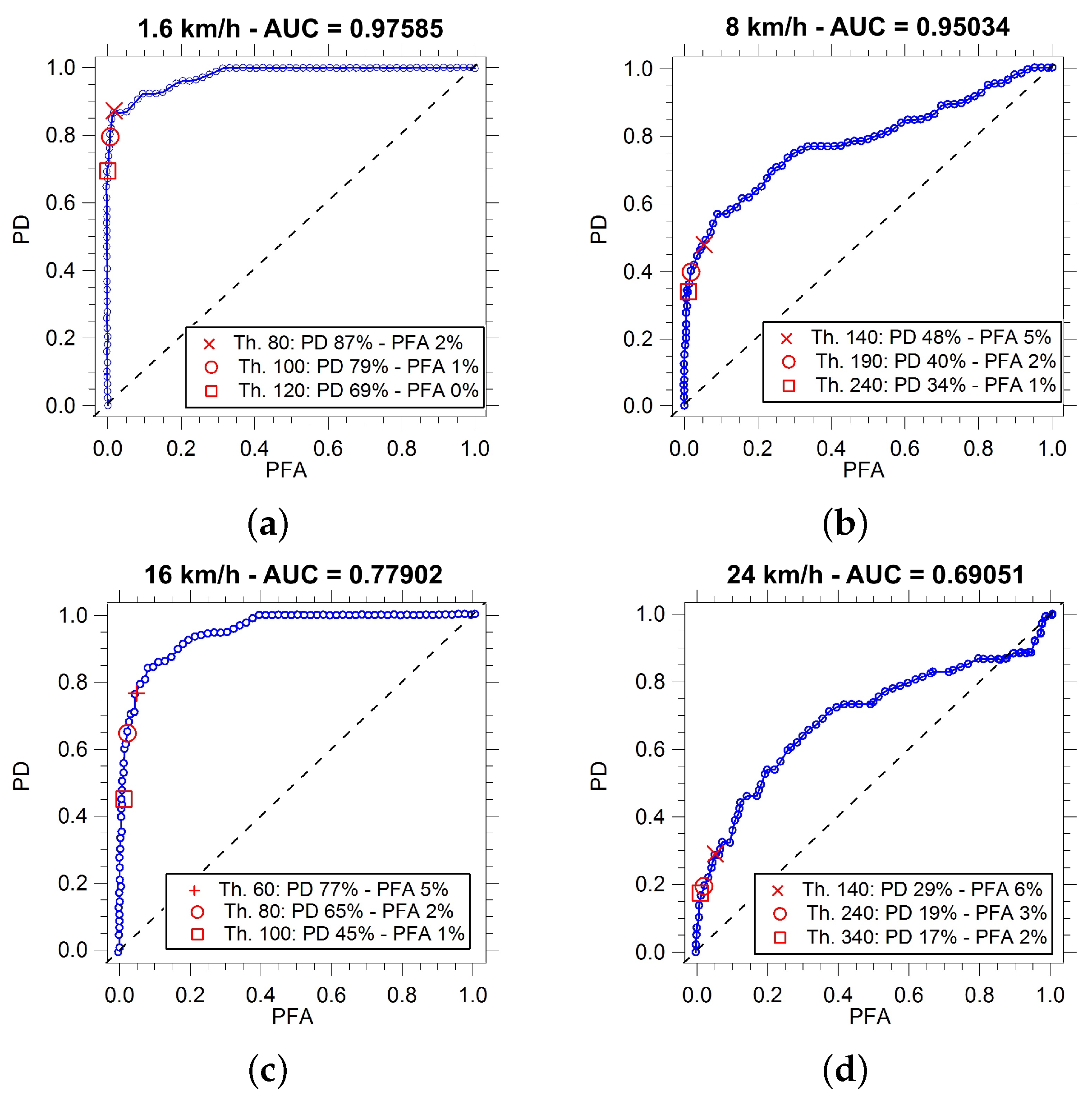
9.1. On-Board Active System: Performance Analysis
9.2. On-Board Passive System: Performance Analysis
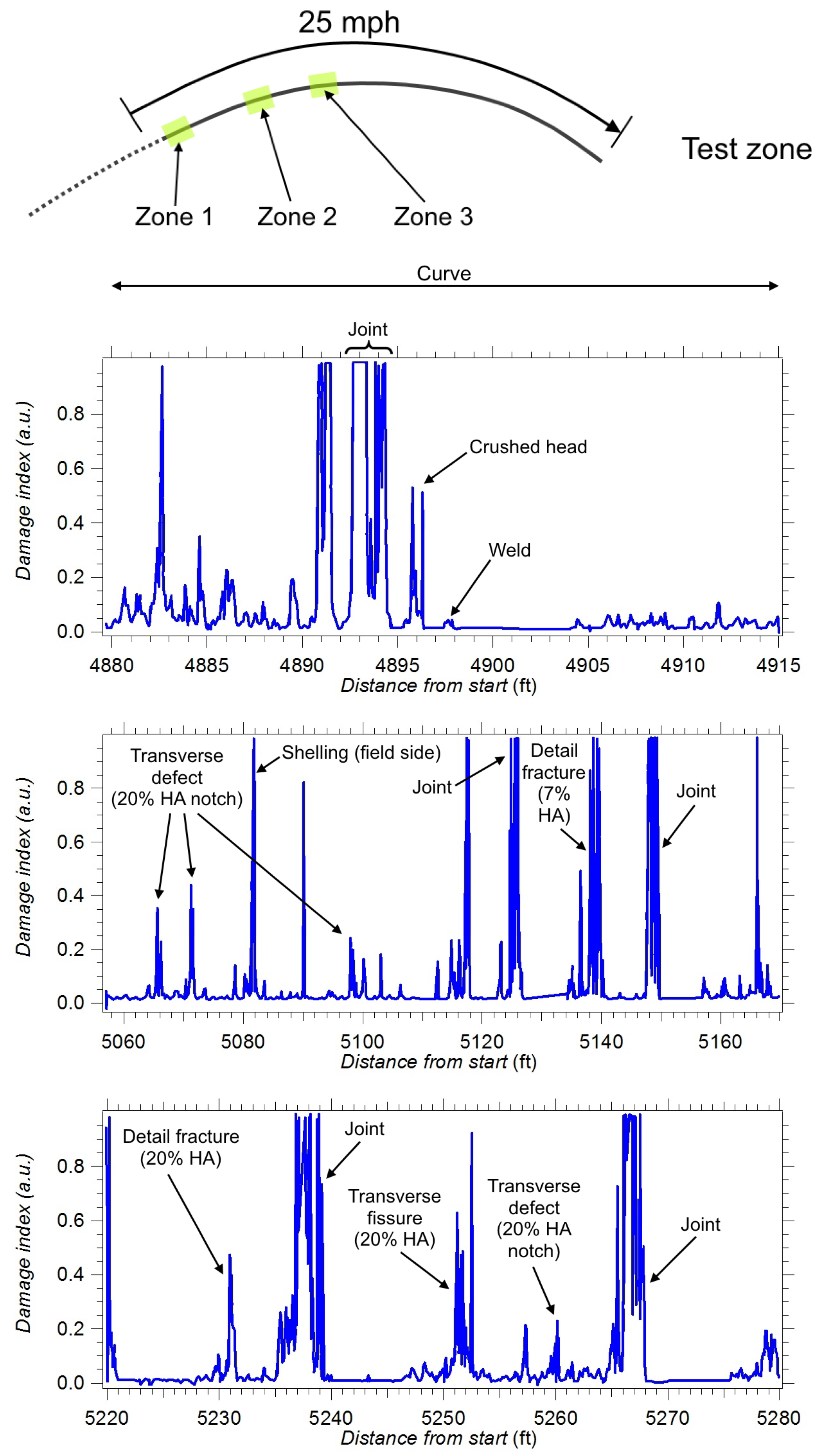
- The zones in which the received signal was strong enough for defect detection were primarily localized in sections of curved tracks, where wheels were flanging, so generating stronger excitation signals.
- As speed decreases, a larger portion of the run becomes sub-optimal, since the presence of a defect cannot be easily detected.
- At high speeds (say, higher than 96 km/h), an optimal source excitation energy is generated; this allows for achieving a stable Green’s function.
- Poor results were found in areas where the source excitation energy was too low to be detected by the receivers, e.g., in most of the tangent portion of the track. affecting the performance of the defect detection algorithms (and, in particular, of the ICA; see Section 7.4).
9.3. Land-Based Ultrasonic Broken Rail Detection System Test Results and Performance Analysis
9.4. Land-Based UBRD System with Early Rail Defect Detection Capability: Performance Analysis
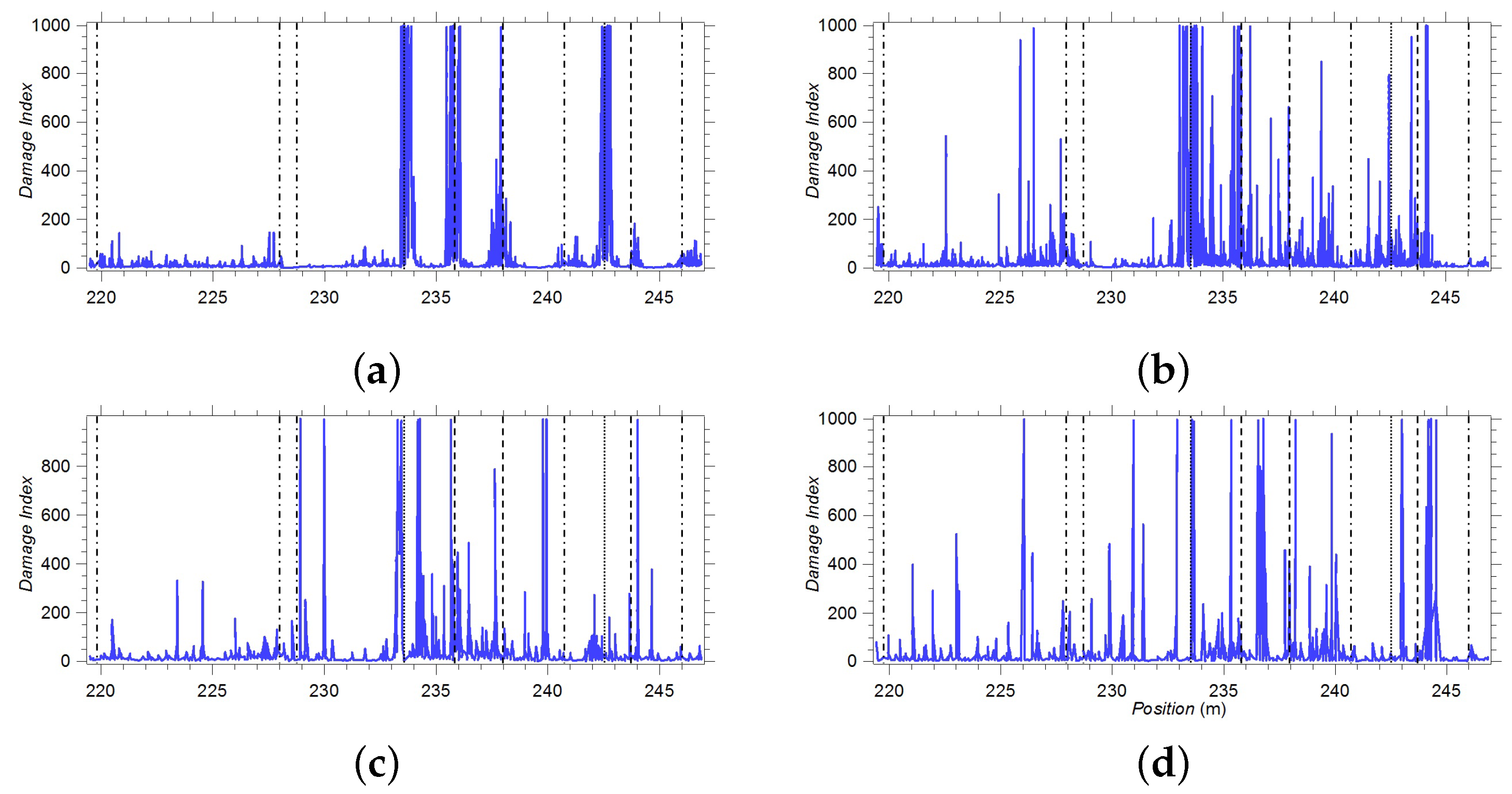
9.4.1. Defect Detection in the Presence of Large Defects
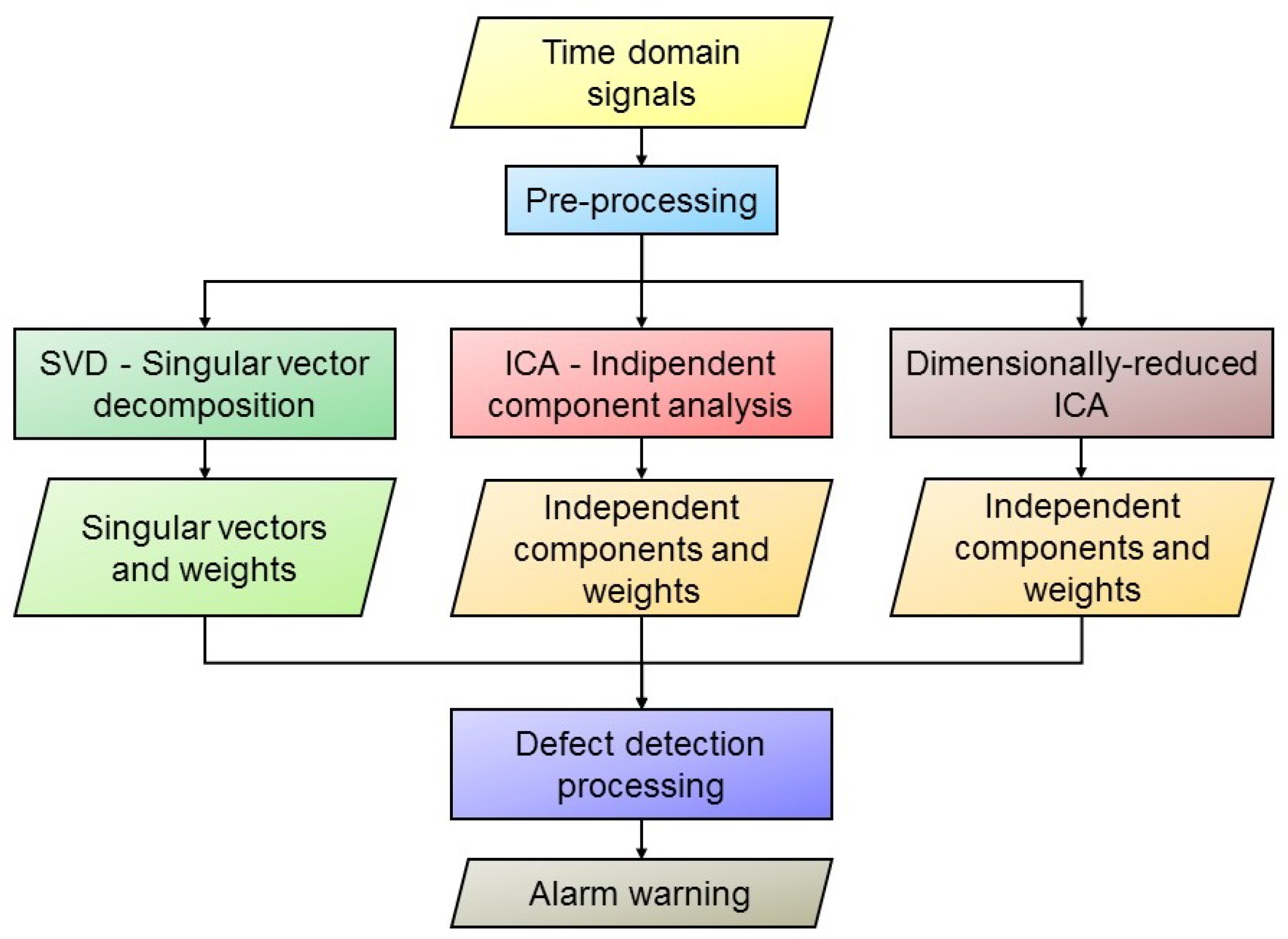
- The SVD, ICA, and dimensionally-reduced ICA techniques are able to separate the signature of artificial defects from the baseline.
- Their performance is appreciably affected by the EOCs and the multi-mode nature of ultrasonic guided waves propagation in rails. As far as the last issue is concerned, it is important to stress that mode conversion is one of the possible causes of phantom reflections appearing when ultrasonic guided waves impinge on a defect; the multi-mode nature of propagation may cause the defect signature to spread over different components. Moreover, the EOCs can have a different influence on each mode.
- In general, the independent components produced by the ICA algorithm appear to be less noisy than the singular vectors generated by the SVD technique.
- The presence of relatively large monotonic trends is confirmed by the analysis of the M–K test scores over the component weights.
- A good match between the components achieving a large M–K test score and the components related to the defect signature is found in the SVD, ICA, and dimensionally-reduced ICA techniques.
9.4.2. Defect Detection in the Presence of Small Defects
- From the outcomes of SVD analysis, it has been inferred that the presence of an artificial defect cannot be easily detected. Moreover, selecting the singular values characterized by the highest M–K score does not guarantee defect detection; furthermore, in these conditions, the defect cannot be located by analyzing the components of the singular vectors.
- The analysis of the results generated by the ICA have proven that the defect signature is spread over multiple independent components, whose associated weights exhibit a monotonic increase, proportional to defect growth.
9.4.3. Concluding Analysis on the Evolved UBRD System
10. Discussion and Conclusions
10.1. Advantages and Disadvantages of the Considered Systems
10.2. Future Developments
10.3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Guided Waves
Appendix B. Characteristics of Guided Waves in Rails
- Dispersion—If different modes are excited, they travel at different (frequency-dependent) velocities in both directions. Consequently, each mode takes a different time to travel along the employed waveguide, so compromising spatial resolution (for instance, a given reflector can generate multiple echoes). This problem can be mitigated by resorting to dispersion compensation.
- Coherent noise—This noise is observed in the same frequency band of the signal of interest. It is due to: (a) the excitation and reception of unwanted modes; (b) the transmission of waves in the wrong direction along the waveguide and the reception of echoes from that direction. Therefore, mitigating coherent noise requires exciting and sensing only the selected modes. This can be accomplished by using a proper transducer or excitation signal, and by suppressing unwanted modes.
- Changes in temperature or in material properties with age—These changes, even if small, affect the above-mentioned dispersion phenomenon. This problem has to be taken into account when comparing signals received at different instants.
Appendix B.1. Excitation of Guided Modes
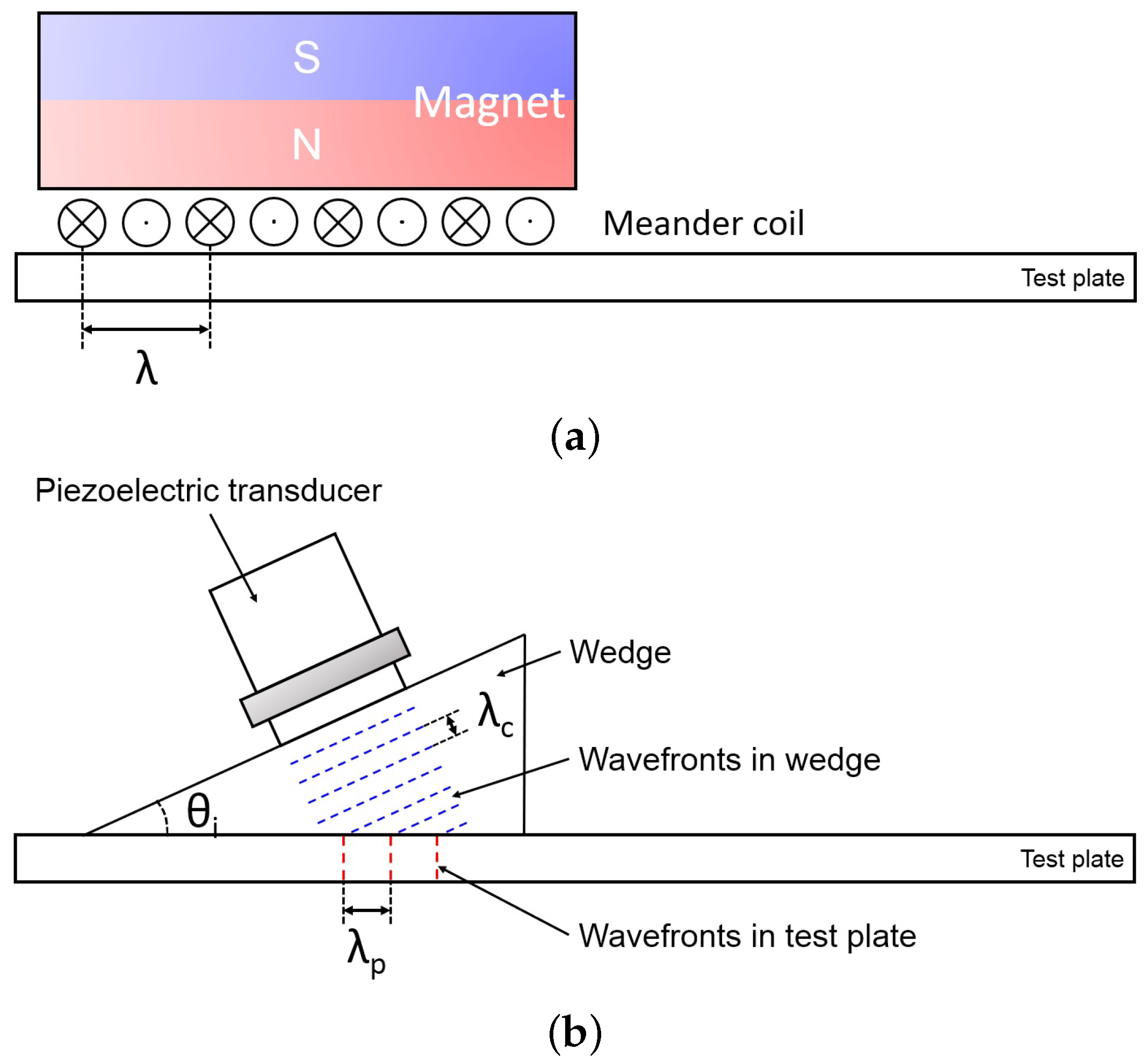
Appendix B.2. Selection of Guided Modes
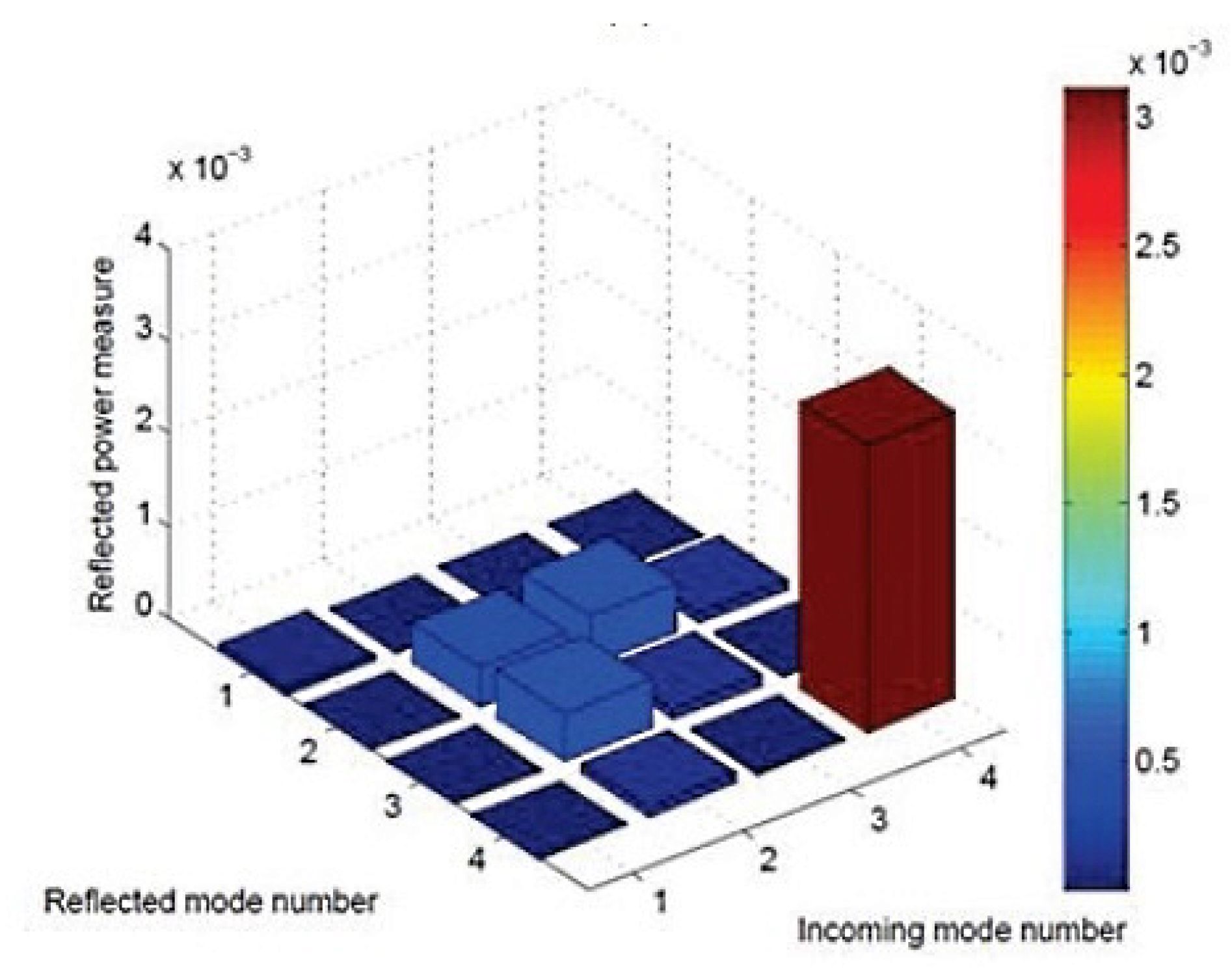
References
- Zumpano, G.; Meo, M. A new damage detection technique based on wave propagation for rails. Int. J. Solids Struct. 2006, 43, 1023–1046. [Google Scholar] [CrossRef]
- Ferreira, L.; Murray, M. Modelling rail track deterioration and maintenance: Current practices and future needs. Transp. Rev. 1997, 17, 207–221. [Google Scholar] [CrossRef]
- European Union Agency of Railways. Railway Safety in the European Union-Safety Overview 2017; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar]
- Papaelias, P.; Roberts, M.C.; Davis, C.L. A Review on Non-Destructive Evaluation of Rails: State-of-the-Art and Future Development. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2008, 222, 367–384. [Google Scholar] [CrossRef]
- Rizzo, P. Sensing solutions for assessing and monitoring railroad tracks. In Sensor Technologies for Civil Infrastructures; Wang, M.L., Lynch, J.P., Sohn, H., Eds.; Woodhead Publishing: Cambridge, UK, 2014; Volume 56, pp. 497–524. [Google Scholar]
- Fadaeifard, F.; Toozandehjani, M.; Mustapha, F.; Matori, K.; Mohd Ariffin, M.K.A.; Zahari, N.; Nourbakhsh, A. Rail inspection technique employing advanced nondestructive testing and Structural Health Monitoring (SHM) approaches—A review. In Proceedings of the Malaysian International NDT conference and Exhibition (MINDTCE 13), Kualalampur, Malaysia, 16–18 June 2013. [Google Scholar]
- Cawley, P.; Lowe, M.J.S.; Alleyne, D.N.; Pavlakovic, B.; Wilcox, P. Practical long range guided wave testing: Applications to pipes and rail. Mater. Eval. 2003, 61, 66–74. [Google Scholar]
- Ghofrani, F.; Pathak, A.; Mohammadi, R.; Aref, A.; He, Q. Predicting rail defect frequency: An integrated approach using fatigue modeling and data analytics. Comput. Aided Civ. Infrastruct. Eng. 2019, 35, 1–15. [Google Scholar] [CrossRef]
- Loveday, P.; Taylor, R.M.C.; Long, C.; Ramatlo, D. Monitoring the reflection from an artificial defect in rail track using guided wave ultrasound. AIP Conf. Proc. 2018, 1949, 090003. [Google Scholar]
- Sadeghi, J.M.; Askarinejad, H. Development of track condition assessment model based on visual inspection. Struct. Infrastruct. Eng. 2011, 7, 895–905. [Google Scholar] [CrossRef]
- Muravev, V.V.; Boyarkin, E.V. Nondestructive testing of the structural-mechanical state of currently produced rails on the basis of the ultrasonic wave velocity. Russ. J. Nondestruct. Test. 2003, 39, 24–33. [Google Scholar] [CrossRef]
- Abbaszadeh, K.; Rahimian, M.; Toliyat, H.A.; Olson, L.E. Rails defect diagnosis using wavelet packet decomposition. IEEE Trans. Ind. Appl. 2003, 39, 1454–1461. [Google Scholar]
- Jeffrey, B.D.; Peterson, M.L.; Gutkowski, R.M. Assessment of rail flaw inspection data. AIP Conf. Proc. 2000, 509, 789–796. [Google Scholar]
- Vadillo, E.G.; Tarrago, J.A.; Zubiaurre, G.G.; Duque, C.A. Effect of sleeper distance on rail corrugation. Wear 1998, 217, 140–146. [Google Scholar] [CrossRef]
- Bohmer, A.; Klimpel, T. Plastic deformation of corrugated rails—A numerical approach using material data of rail steel. Wear 2002, 253, 150–161. [Google Scholar] [CrossRef]
- Cannon, D.F.; Edel, K.O.; Grassie, S.L.; Sawley, K. Rail defects: An overview. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 865–886. [Google Scholar] [CrossRef]
- Cannon, D.F.; Pradier, H. Rail rolling contact fatigue research by the European Rail Research Institute. Wear 1996, 191, 1–13. [Google Scholar] [CrossRef]
- Grassie, S.; Nilsson, P.; Bjurstrom, K.; Frick, A.; Hansson, L.G. Alleviation of rolling contact fatigue on Swedens heavy haul railway. Wear 2002, 253, 42–53. [Google Scholar] [CrossRef]
- Australian Rail Track Corporation. Rail Defects Handbook-Some Rail Defects, Their Characteristics, Causes and Control. Document RC2400; Australian Rail Track Corporation: Mile End, Australia, 2006. [Google Scholar]
- Shull, P.J. Nondestructive Evaluation: Theory, Techniques, and Applications, 1st ed.; CRC Press: New York, NY, USA, 2002. [Google Scholar]
- Bray, D.E.; Stanley, R.K. Nondestructive Evaluation. A Tool in Design, Manufacturing, and Service, 2nd ed.; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Mix, P. Introduction to Nondestructive Testing, A Training Guide, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Clark, R. Rail flaw detection: Overview and need for future developments. NDT&E Int. 2004, 37, 111–118. [Google Scholar]
- Rajamäki, J.; Vippola, M.; Nurmikolu, A.; Viitala, T. Limitations of eddy current inspection in railway rail evaluation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 121–129. [Google Scholar] [CrossRef]
- Xu, P.; Zhu, C.; Zeng, H.; Wang, P. Rail crack detection and evaluation at high speed based on differential ECT system. Measurement 2020, 166, 108152. [Google Scholar] [CrossRef]
- Wang, J.; Dai, Q.; Lautala, P. Real-Time Rail Defect Detection with Eddy Current (EC) Technique: Signal Processing and Case Studies of Rail Samples; Final Rep. of the Project NURail2020-MTU-R18; National University Railway Center: Urbana, IL, USA, 2020. [Google Scholar]
- Nichoha, V.; Storozh, V.; Matiieshyn, Y. Results of the development and research of information-diagnostic system for the magnetic flux leakage defectoscopy of rails. In Proceedings of the 2020 IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 25–29 February 2020; pp. 852–857. [Google Scholar]
- Deutschl, E.; Gasser, C.; Niel, A.; Werschonig, J. Defect detection on rail surfaces by a vision based system. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 507–511. [Google Scholar]
- Singh, M.; Singh, S.; Jaiswal, J.; Hempshall, J. Autonomous rail track inspection using vision based system. In Proceedings of the IEEE International Conference on Computational Intelligence for Homeland Security and Personal Safety, Alexandria, VA, USA, 16–17 October 2006; pp. 56–59. [Google Scholar]
- Molina, L.F.; Resendiz, E.; Edwards, J.R.; Hart, J.M.; Barkan, C.P.L.; Ahuja, N. Condition monitoring of railway turnouts and other track components using machine vision. In Proceedings of the Transportation Research Board 90th Annual Meeting, Washington, DC, USA, 23–27 January 2011; pp. 11–1442. [Google Scholar]
- Molina, L.F.; Edwards, J.R.; Barkan, C.P.L. Emerging condition monitoring technologies for railway track components and special trackwork. In Proceedings of the 2011 Joint Rail Conference, Pueblo, CO, USA, 16–18 March 2011; pp. 151–158. [Google Scholar]
- Oukhellou, L.; Côme, E.; Bouillaut, L.; Aknin, P. Combined use of sensor data and structural knowledge processed by Bayesian network: Application to a railway diagnosis aid scheme. Transp. Res. Part C 2008, 16, 755–767. [Google Scholar] [CrossRef]
- Rete Ferroviaria Italiana. Diagnostics Services Catalogue 2018; Rete Ferroviaria Italiana: Rome, Italy, 2018. [Google Scholar]
- Vandone, A.; Rizzo, P.; Vanali, M. Two-stage algorithm for the analysis of infrared images. Res. Nondestruct. Eval. 2012, 23, 69–88. [Google Scholar] [CrossRef]
- Peng, D.; Jones, R. Lock-in thermographic inspection of squats on rail steel head. Infrared Phys. Technol. 2013, 57, 89–95. [Google Scholar] [CrossRef]
- Usamentiaga Fernández, R.; Sfarra, S.; Fleuret, J.; Yousefi, B.; García Martínez, D.F. Rail inspection using active thermography to detect rolled-in material. In Proceedings of the 14th Quantitative InfraRed Thermography (QIRT) Conference, Berlin, Germany, 25–29 June 2018. [Google Scholar]
- Bayissa, W.L.; Dhanasekar, M. High speed detection of broken rails, rail cracks and surface faults. In Advanced Project Management Training Needs; CRC for Rail Innovation: Brisbane, Australia, 2011. [Google Scholar]
- Marais, J.J.; Mistry, K.C. Rail integrity management by means of ultrasonic testing. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 931–938. [Google Scholar] [CrossRef]
- Olympus. Advances in Phased Array Ultrasonic Technology Applications; Olympus: Waltham, MA, USA, 2011; p. 280. [Google Scholar]
- Mariani, S.; Nguyen, T.; Phillips, R.R.; Kijanka, P.; Lanza di Scalea, F.; Staszewski, W.J.; Fateh, M.; Carr, G. Noncontact ultrasonic guided wave inspection of rails. Struct. Health Monit. 2013, 12, 539–548. [Google Scholar] [CrossRef]
- Coccia, S.; Bartoli, I.; Salamone, S.; Phillips, R.; Lanza di Scalea, F.; Fateh, M.; Carr, G. Noncontact Ultrasonic Guided Wave Detection of Rail Defects. Transp. Res. Rec. 2009, 2117, 77–84. [Google Scholar] [CrossRef]
- Wilcox, P.; Pavlakovic, B.; Evans, M.; Vine, K.; Cawley, P.; Lowe, M.; Alleyne, D. Long Range Inspection of Rail Using Guided Waves. AIP Conf. Proc. 2003, 657, 236–243. [Google Scholar]
- Ryue, J.; Thompson, D.J.; White, P.R.; Thompson, D.R. Wave Propagation in Railway Tracks at High Frequencies. In Noise and Vibration Mitigation for Rail Transportation Systems. Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Schulte-Werning, B., Thompson, D., Gautier, P.-E., Hanson, C., Hemsworth, B., Nelson, J., Maeda, T., de Vos, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 99, pp. 440–446. [Google Scholar]
- Long, C.; Loveday, P. Prediction of Guided Wave Scattering by Defects in Rails Using Numerical Modelling. AIP Conf. Proc. 2014, 1581, 240–247. [Google Scholar]
- Rizzo, P.; Cammarata, M.; Bartoli, I.; Lanza di Scalea, F.; Salamone, S.; Coccia, S.; Phillips, R. Ultrasonic Guided Waves-Based Monitoring of Rail Head: Laboratory and Field Tests. Adv. Civ. Eng. 2010, 2010, 1–13. [Google Scholar] [CrossRef]
- Mariani, S.; di Scalea, F.L. Predictions of defect detection performance of air-coupled ultrasonic rail inspection system. Struct. Health Monit. 2018, 17, 684–705. [Google Scholar] [CrossRef]
- Mariani, S.; Nguyen, T.; Zhu, X.; Lanza di Scalea, F. Field Test Performance of Noncontact Ultrasonic Rail Inspection System. J. Transp. Eng. Part A Syst. 2017, 143, 04017007. [Google Scholar] [CrossRef]
- Lanza Di Scalea, F.; Zhu, X.; Capriotti, M.; Liang, A.; Mariani, S.; Sternini, S. Passive Extraction of Dynamic Transfer Function From Arbitrary Ambient Excitations: Application to High-Speed Rail Inspection From Wheel-Generated Waves. ASME J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2018, 1, 011005. [Google Scholar] [CrossRef]
- Liang, A.; Sternini, S.; Capriotti, M.; Lanza di Scalea, F. High-Speed Ultrasonic Rail Inspection by Passive Noncontact Technique. Mater. Eval. 2019, 77, 941–950. [Google Scholar]
- Ultrasonic Broken Rail Detector Overview. Available online: http://www.railsonic.co.za/pdf_files/UBRD_Overview_V1.pdf (accessed on 25 December 2020).
- Loveday, P.W.; Burger, F.A.; Long, C.S. Rail Track Monitoring in SA using Guided Wave Ultrasound. In Proceedings of the Conference & Exhibition of the South African Institute for NDT (SAINT-2018), Johannesbourg, South Africa, 17–18 February 2018. [Google Scholar]
- Setshedi, I.; Long, C.; Loveday, P.; Wilke, D. Adaptive SAFE model of a rail for parameter estimation. In Proceedings of the South African Conference on Computational and Applied Mechanics (SACAM), Vaal University of Technology, Vanderbijlpark, South Africa, 17–19 September 2018. [Google Scholar]
- Steyn, B.M.; Pretorius, J.F.W.; Burger, F. Development, testing and operation of an Ultrasonic Broken Rail Detector System. In Computers in Railways IX; Allan, J., Brebbia, C.A., Hill, R.J., Sciutto, G., Sone, S., Eds.; WIT Press: Ashurst Lodge, UK; Southampton, UK, 2004; Volume 74, pp. 351–358. [Google Scholar]
- Yuan, L.; Yang, Y.; Hernández, Á.; Shi, L. Feature Extraction for Track Section Status Classification Based on UGW Signals. Sensors 2018, 18, 1225. [Google Scholar] [CrossRef] [PubMed]
- Loveday, P.W.; Dhuness, K.; Long, C.S. Experimental development of electromagnetic acoustic transducers for measuring ultraguided waves. In Proceedings of the Eleventh South African Conference on Computational and Applied Mechanics (SACAM 2018), Vanderbijlpark, South Africa, 17–19 September 2018; pp. 693–702. [Google Scholar]
- Loveday, P.; Long, C. Influence of resonant transducer variations on long range guided wave monitoring of rail track. AIP Conf. Proc. 2016, 1706, 150004-1–150004-6. [Google Scholar]
- Setshedi, I.; Loveday, P.; Long, C.; Wilke, D. Estimation of rail properties using semi-analytical finite element models and guided wave ultrasound measurements. Ultrasonics 2019, 96, 240–252. [Google Scholar] [CrossRef]
- Enekom. Enekom RCFSS UsersManual V4; Enekom: Ankara, Turkey, 2019. [Google Scholar]
- Xining, X.; Lu, Z.; Bo, X.; Zujun, Y.; Liqiang, Z. An Ultrasonic Guided Wave Mode Excitation Method in Rails. IEEE Access 2018, 6, 60414–60428. [Google Scholar] [CrossRef]
- Shi, H.; Zhuang, L.; Xu, X.; Yu, Z.; Zhu, L. An Ultrasonic Guided Wave Mode Selection and Excitation Method in Rail Defect Detection. Appl. Sci. 2019, 9, 1170. [Google Scholar] [CrossRef]
- Xu, X.; Xing, B.; Zhuang, L.; Shi, H.; Zhu, L. A Graphical Analysis Method of Guided Wave Modes in Rails. Appl. Sci. 2019, 9, 1529. [Google Scholar] [CrossRef]
- Xing, B.; Yu, Z.; Xu, X.; Zhu, L.; Shi, H. Research on a Rail Defect Location Method Based on a Single Mode Extraction Algorithm. Appl. Sci. 2019, 9, 1107. [Google Scholar] [CrossRef]
- Wei, X.; Yang, Y.; Yao, W.; Zhang, L. Design of full bridge high voltage pulser for sandwiched piezoelectric ultrasonic transducers used in long rail detection. Appl. Acoust. 2019, 149, 15–24. [Google Scholar] [CrossRef]
- Wei, X.; Yang, Y.; Yao, W.; Zhang, L. An automatic optimal excitation frequency tracking method based on digital tracking filters for sandwiched piezoelectric transducers used in broken rail detection. Measurement 2019, 135, 294–305. [Google Scholar] [CrossRef]
- Loveday, P.W.; Long, C.S.; Ramatlo, D.A. Ultrasonic guided wave monitoring of an operational rail track. Struct. Health Monit. 2019, 19, 1666–1684. [Google Scholar] [CrossRef]
- Liang, A.; Sternini, S.; Capriotti, M.; Zhu, P.X.; Lanza di Scalea, F.; Wilson, R. Passive extraction of Green’s function of solids and application to high-speed rail inspection. In Proceedings of the SPIE 10970, Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems, SPIE Smart Structures + Nondestructive Evaluation, Denver, CO, USA, 27 March 2019; Lynch, J.P., Huang, H., Sohn, H., Wang, K.-W., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 10970, pp. 109700R-1–109700R-10. [Google Scholar]
- Yuan, L.; Yang, Y.; Alonso, I.H.; Li, S. Application of VMD Algorithm in UGW-based Rail Breakage Detection System. In Proceedings of the IEEE International Conference on Vehicular Electronics and Safety (ICVES), Madrid, Spain, 12–14 September 2018; pp. 1–6. [Google Scholar]
- Benzeroual, H.; Khamlichi, A.; Zakriti, A. Detection of Transverse Defects in Rails Using Noncontact Laser Ultrasound. Proceedings 2020, 42, 43. [Google Scholar] [CrossRef]
- Teidj, S. Defect Indicators in a Rail Based on Ultrasound Generated by Laser Radiation. Procedia Manuf. 2020, 46, 863–870. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Wilcox, P.D. Guided-Wave Array Methods. In Encyclopedia of Structural Health Monitoring; Boller, C., Chang, F.-K., Fujino, Y., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wilcox, P.D. A rapid signal processing technique to remove the effect of dispersion from guided wave signals. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 419–427. [Google Scholar] [CrossRef]
- Moustakidis, S.; Kappatos, V.; Karlsson, P.; Selcuk, C.; Gan, T.H.; Hrissagis, K. An intelligent methodology for railways monitoring using ultrasonic guided waves. J. Nondestruct. Eval. 2014, 33, 694–710. [Google Scholar] [CrossRef]
- Liu, C.; Harley, J.B.; Bergés, M.; Greve, D.W.; Oppenheim, I.J. Robust ultrasonic damage detection under complex environmental conditions using singular value decomposition. Ultrasonics 2015, 58, 75–86. [Google Scholar] [CrossRef]
- Dobson, J.; Cawley, P. Independent component analysis for improved defect detection in guided wave monitoring. Proc IEEE 2016, 104, 1620–1631. [Google Scholar] [CrossRef]
- Liu, C.; Dobson, J.; Cawley, P. Efficient generation of receiver operating characteristics for the evaluation of damage detection in practical structural health monitoring applications. Proc. R. Soc. 2017, 437, 1–26. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Wei, X.; Yang, Y.; Ureña, J.; Yan, J.; Wang, H. An Adaptive Peak Detection Method for Inspection of Breakages in Long Rails by Using Barker Coded UGW. IEEE Access 2020, 8, 48529–48542. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, Y.; Hernández, Á.; Shi, L. Novel adaptive peak detection method for track circuits based on encoded transmissions. IEEE Sens. J. 2018, 18, 6224–6234. [Google Scholar] [CrossRef]
- Burger, F.A.; Loveday, P.; Long, C. Large scale implementation of guided wave based broken rail monitoring. AIP Conf. Proc. 2015, 1650, 771–776. [Google Scholar]
- Ihara, I. Ultrasonic Sensing: Fundamentals and its Applications to Nondestructive Evaluation. In Sensors. Lecture Notes Electrical Engineering; Mukhopadhyay, S., Huang, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 21, pp. 287–305. [Google Scholar]
- Mazzoldi, P.; Nigro, M.; Voci, C. Fisica Vol. 1-Meccanica-Termodinamica, 1st ed.; EdiSES: Napoli, Italy, 1991; Chapter 8; pp. 215–232. [Google Scholar]
- Rose, J.L. A Baseline and Vision of Ultrasonic Guided Wave Inspection Potential. ASME. J. Press. Vessel Technol. 2002, 124, 273–282. [Google Scholar] [CrossRef]
- Loveday, P.; Long, C.; Ramatlo, D. Mode Repulsion of Ultrasonic Guided Waves in Rails. Ultrasonics 2018, 84, 341–349. [Google Scholar] [CrossRef]
- Ryue, J.; Thompson, D.; White, P.; Thompson, D.R. Investigations of propagating wave types in railway tracks at high frequencies. J. Sound Vib. 2008, 315, 157–175. [Google Scholar] [CrossRef]
- Ryue, J.; Thompson, D.; White, P.; Thompson, D.R. Decay rates of propagating waves in railway tracks at high frequencies. J. Sound Vib. 2009, 320, 955–976. [Google Scholar] [CrossRef]



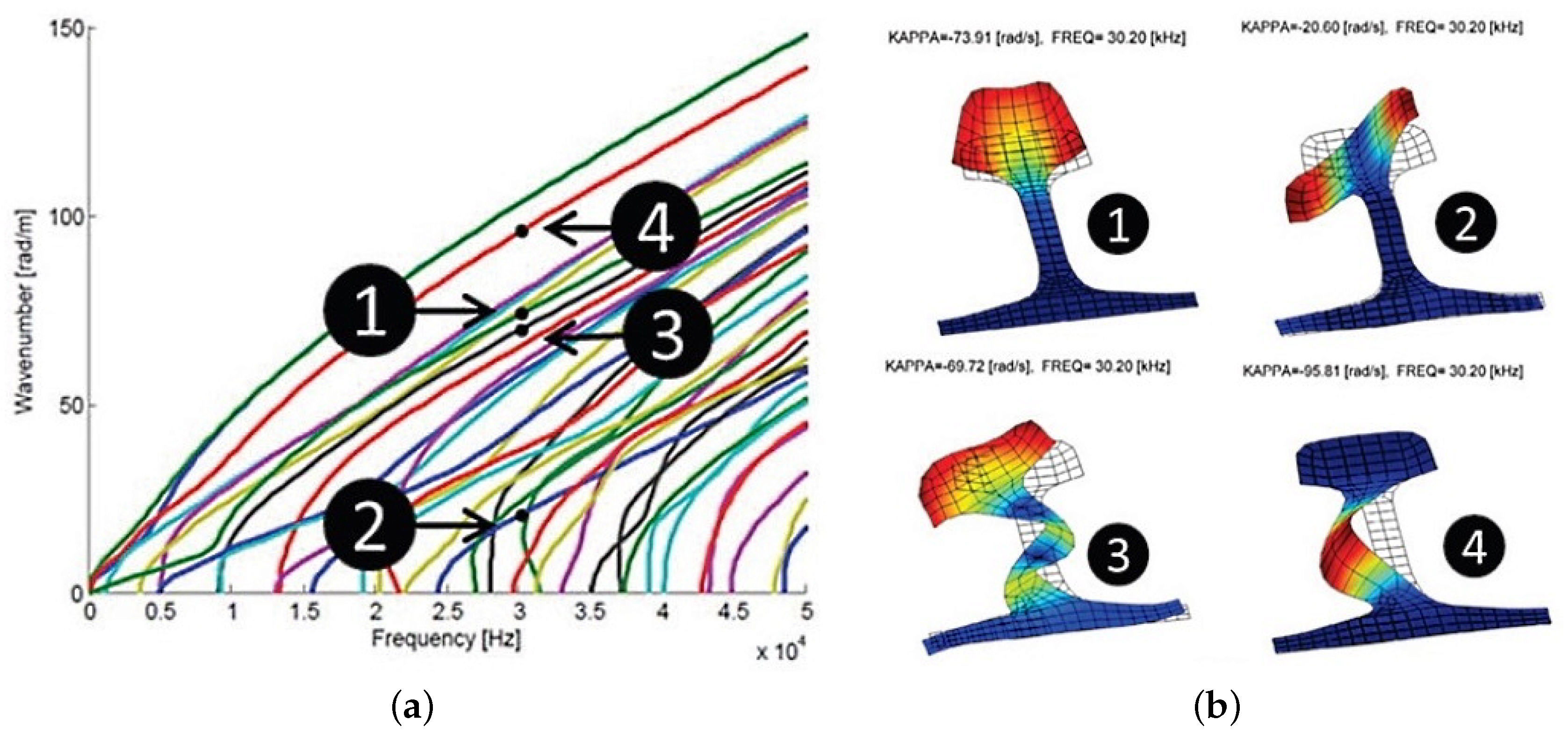


| Feature # | Feature Content |
|---|---|
| 1 | |
| 2 | |
| 3 |
| Test Speed (km/h) | PD (%) Achievable for Specific PFAs | AUC (%) | |||
|---|---|---|---|---|---|
| 0% PFA | 1% PFA | 5% PFA | 10% PFA | ||
| 1.6 | 65.38 | 76.92 | 86.54 | 92.31 | 97.58 |
| 8 | 7.08 | 47.79 | 78.76 | 85.84 | 95.03 |
| 16 | 0.00 | 29.23 | 47.69 | 56.92 | 77.90 |
| 24 | 1.92 | 9.62 | 28.85 | 32.69 | 69.05 |
| Test Speed | Recording Time Window | SNR of Reconstructed Transfer Function |
|---|---|---|
| 30 mph (48.28 km/h) | ~15.25 ms | ~12 |
| 50 mph (80.46 km/h) | ~9.15 ms | ~9 |
| 80 mph (128.75 km/h) | ~5.7 ms | ~4.5 |
| Technique | Approach | Detected Defects | Scanning Speed | Performance | Open Problems |
| Eddy current (EC) | Manual inspection, on-board, non-contact | Surface defects and near-surface internal railhead defects. | ≤70 km/h | Reliable detection of surface defects; adversely affected by grinding marks. It is sensitive to probe lift-off. | Mature technology |
| Magnetic flux leakage (MFL) | On-board, non-contact | Surface defects and near-surface internal railhead defects. Unsuitable for longitudinal fissures. | ≤35 km/h | Reliable detection of surface and near-surface defects in the railhead. Cracks smaller than 4 mm are not detected. Performance degradation observed at high speeds. | Mature technology, research aims at increasing its scanning speed |
| Visual inspection | Manual inspection, on-board, non-contact | Surface breaking defects, rail head profile, corrugation, missing parts, defective ballast. No internal defects. | From 4 to 320 km/h | Reliable detection on the surface of the rail and track. Internal cracks are not detected. Sensitive to lighting conditions (these require proper compensation). | Mature technology |
| Radiography | Manual system | Welds and all types of known internal defects. | Static | Reliable detection of internal defects in rails and welds that are difficult to inspect by means of other techniques. Some transverse defects can be missed. Safety hazard, costly and time-consuming. | Mature technology |
| Conventional ultrasound | Manual inspection, on-board, contact | Surface defects, railhead, web and foot internal defects. | <70 km/h in tests; in practice around 15 km/h | Reliable manual inspection, but rail foot defects can be missed. In high-speed inspection, surface defects smaller than 4 mm, as well as internal defects (especially in the rail foot) can be missed. Limit on the maximum speed achievable. Surface shallow RCF defects can mask severe internal cracks. | Mature technology |
| Active on-board guided waves ultrasound | Active on-board, non-contact | Surface defects and rail head web and foot internal defects. Best for transverse and mixed mode defects. | ≤16 km/h laser; ≤24 km/h air-coupled piezoelectric | Reliable on-board system able to detect surface and internal defects. Affected by sensors lift-off variations. Difficult to be deployed at high speeds. The employed laser is costly and hard to maintain. | In case of piezoelectric excitation, the airborne signal reverberation limits the achievable test speed because of acoustic mismatch between air and steel. |
| Passive on-board guided waves ultrasound | Passive, on-board | Surface defects and rail head web and foot internal defects. Best for transverse and mixed mode defects. | >96 km/h | The system reliably detects defects when the signal strength is high, i.e., where the rail-wheel interaction is stronger (e.g., in curves). As long as the quality of the received signal is good, its strength is not so important. System under development. | Quantification and improvement of defect detection reliability by selecting appropriate thresholds. Improvement of source excitation signals at low speeds or in tangent tracks. |
| Technique | Approach | Detected Defects | Scanning Speed | Performance | Open Problems |
| Ultrasonic broken rail detector (UBRD) | Active, land-based | Broken rails | Fixed system (1 km sections), quasi real-time operation | The system is designed to reliably detect clean breakages in rails. It is already working in operating conditions. | Mature technology. Evolution to reliably detect defects in rails and to increase section length. |
| Land-based guided waves ultrasound rail defect detection | Active, land-based | Transverse and mixed mode internal defects | Fixed system (1 km sections), quasi real-time operation | The technology is under development. The aim is to detect and monitor a growing defect, and raise an alarm when it reaches a critical size. | Study of the behavior of a defect during time, compensation of resonant transducers variations, compensation of varying environmental and operating conditions which modify the propagation of guided waves. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bombarda, D.; Vitetta, G.M.; Ferrante, G. Rail Diagnostics Based on Ultrasonic Guided Waves: An Overview. Appl. Sci. 2021, 11, 1071. https://doi.org/10.3390/app11031071
Bombarda D, Vitetta GM, Ferrante G. Rail Diagnostics Based on Ultrasonic Guided Waves: An Overview. Applied Sciences. 2021; 11(3):1071. https://doi.org/10.3390/app11031071
Chicago/Turabian StyleBombarda, Davide, Giorgio Matteo Vitetta, and Giovanni Ferrante. 2021. "Rail Diagnostics Based on Ultrasonic Guided Waves: An Overview" Applied Sciences 11, no. 3: 1071. https://doi.org/10.3390/app11031071
APA StyleBombarda, D., Vitetta, G. M., & Ferrante, G. (2021). Rail Diagnostics Based on Ultrasonic Guided Waves: An Overview. Applied Sciences, 11(3), 1071. https://doi.org/10.3390/app11031071





