Abstract
The miniaturization of electronic devices and the inefficiency of CMOS technology due to the development of integrated circuits and its lack of responsiveness at the nanoscale have led to the acquisition of nanoscale technologies. Among these technologies, quantum-dot cellular automata (QCA) is considered one of the possible replacements for CMOS technology because of its extraordinary advantages, such as higher speed, smaller area, and ultra-low power consumption. In arithmetic and comparative circuits, XOR logic is widely used. The construction of arithmetic logic circuits using AND, OR, and NOT logic gates has a higher design complexity. However, XOR gate design has a lower design complexity. Hence, the efficient and optimized XOR logic gate is very important. In this article, we proposed a new XOR gate based on cell-level methodology, with the expected output achieved by the influence of the cells on each other; this design method caused less delay. However, this design was implemented without the use of inverter gates and crossovers, as well as rotating cells. Using the proposed XOR gate, two new full adder (FA) circuits were designed. The simulation results indicate the advantage of the proposed designs compared with previous structures.
1. Introduction
In today’s world, digital systems, and especially computer systems, play an important role in human life, and they are widely used. As a result, scientists and researchers have focused all of their efforts, both orbital and economic, on the development, improvement, and optimization of these systems. Moreover, the miniaturization of day-to-day electronic devices and components and the lack of responsiveness of common technology (CMOS), due to the appearance of problems at the nanoscale, have led to the acquisition of nanoscale devices. These devices have led to the coming existence of new nanoscale technologies. This field of electronics is called nanoelectronics or nanotechnology.
Among these technologies, quantum-dot cellular automata (QCA) is one of them, which has introduced a new landscape with unique features. QCA technology is considered as a new communication and computing technology due to its unique features, such as small size, high operating speed, and ultra-low power consumption. This technology has drawn the attention of many researchers and scientists. As a result, QCA can be considered as a potential solution to the scale limitations of complementary metal–oxide–semiconductor (CMOS) technology [1].
As previously mentioned, QCA technology is a novel nanoscale computational paradigm that may significantly enhance electronic circuit design technology [2]. It uses nano-level interactions to implement digital logic with low energy consumption and high clocking frequency. The advancements in the fabrication [3,4] and simulation [5,6] of QCA circuits have enabled researchers to design complete computational circuits [7]. Moreover, adders are one of the most basic and main computational circuits of digital logic, and as the most common and most widely used arithmetic digital circuits, they are the subject of many research studies [8].
However, with the appearance of new technologies to operate these technologies, it is necessary to create well-known tools needed for use in more complex applications, which, in the digital field, leads to the design of basic and main logic gates. The optimization of logic gates is very important because the improvement and optimization of these gates, due to their many uses in larger and more complicated circuits of the cause, improve and optimize these circuits. One of the most important and widely used logic gates is the XOR gate. The improvement and optimization of the XOR gate are very important. Adders are constituent and also one of the main and basic blocks of many VLSI systems, such as microprocessors and other various processors. One of the factors leading to optimizing the relevant blocks is the presentation of new designs in proportion to the development of new technologies. Designing a full adder with a simple structure and limited power consumption can play an essential role in simplifying digital circuits.
There are certain factors for a better design of full adder circuits. The most important criterion is the usage in more complex and larger circuits. Other criteria include low power consumption, high speed, and simplex circuits; these criteria themselves can be considered as components of the usage criterion. Among the most important items used are full adders, which are used in more complex and larger computing circuits and communication devices. Given that mass media is portable and fully available today, the main concern is an increase in battery life, which reduces the need for recharging. In other words, the main concern is reducing power consumption. Increasing the performance of the full adder is directly related to improving orbital parameters and improving system performance. Thus, many researchers are looking for ways to reduce power consumption. Adders are widely used in mobile digital devices, and they are the main element in many computing circuits. Nowadays, with the increasing use of electronic devices, the need for the optimal design of adders has become very important. The better the quality and parametric characteristics of the adders, the more direct their effect on the device used, and as a result, the device will be more popular. For this reason, the presentation of new structures for these circuits is of interest to integrated circuit designers. The main goal in designing digital adders is to increase speed and reduce power consumption.
One of the factors indicating the efficiency and good performance of the adder block is its use in larger and more practical circuits. Among the challenges in the design of the composite layout and cells is the challenge of designing the crossovers of wires in the best way to reduce costs [9,10,11]. Nowadays, non-adjacent clock phases are used to design the crossover of passing wires in a single layer [9,12], and the presence of crossover in the design increases the delay.
As a result, we did not use any crossovers in our designs in the present research, which in turn reduced the number of cells, the consumption area, and delay; therefore, the designs are coplanar due to the lack of need for crossovers. Therefore, we designed a new XOR gate, and we designed and implemented two full adder (FA) circuits with this proposed XOR gate, which was designed without an inverter gate (NOT gate); with a reduced number of cells, reduced consumption area, less delay, and reduced cost function; without crossovers and rotated cells (cell-45); and with the coplanar method.
The remainder of this article is organized as follows: an overview of QCA and previous works is given in Section 2. In Section 3, the design of the XOR gate is proposed, and then the architecture of the circuits of the full adder proposed by this research is presented. In Section 4 and Section 5, we compare the proposed designs with previous architectures. In Section 6, we conclude the article.
2. Background
The QCA Basics
The main component of QCA technology is the QCA cell. Each QCA cell contains two electrons, which, based on the coulombic interactions created between the two electrons [9], create two logical values, “0” and “1” [13]. Every QCA cell contains four holes, in which two electrons are trapped inside. By placing two electrons in four holes, due to the coulombic interactions between the electrons, two electrons are always positioned diagonally [14]. As a result, two stable states are created, and the electrons are diagonally placed inside the cavities to keep the maximum distance from each other and to establish the coulombic interaction law. By placing electrons in the diameter, two structures are created, which we attribute to the polar structures +1 and −1 with the logical values “1” and “0”, respectively; the poles 1+ and 1− are the same poles of the square cells shown in Figure 1 [15].
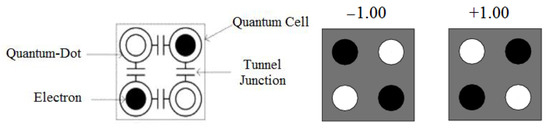
Figure 1.
The QCA cell.
The clocked QCA maintains four clocking phases (switch, hold, release, and relax) to transmit a signal [8], as shown in Figure 2. During the switch phase, the interdot barriers become lower, and the data propagation happens through electron tunneling. The potential barrier is raised gradually, and the cell becomes polarized according to the modes of the input drives. At the end of this phase, the barriers are high enough to prevent electronic tunneling. During the hold phase, the barriers remain high, and the cell retains the polarization state. In this state, the cell maintains a steady state and transmits data to the neighboring cells. Indeed, the outputs can be used as inputs to the next stage. During the release phase, the barriers gradually decrease, and the QCA cells start to lose their polarization by lowering the barriers. During the relaxation state, cell barriers stay on the lowest level and in an unpolarized state [9,10].
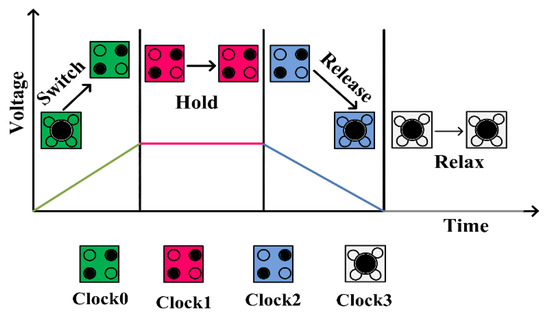
Figure 2.
Clock phases in QCA.
The most simple gate in a logic circuit is the inverter gate (NOT gate). Figure 3 shows these gates [16]. In QCA logic circuit design, the majority gate (MV) is the most commonly used logic gate. This gate has three inputs and one output cell. The majority vote of the inputs determines the output. As a result, the majority of the logical values of the inputs specify the polarization and the value of the output cell [14,16]. Figure 4 shows different samples of this gate.

Figure 3.
QCA representation of NOT gate.
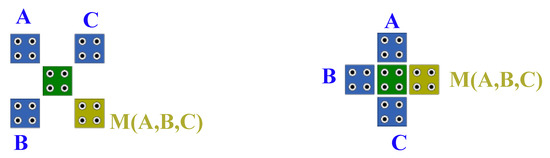
Figure 4.
Original QCA majority gate and rotated QCA majority gate.
By stabilizing one of the inputs of the majority gate and valuing the logical “0” (polarization −1), the AND gate is constructed [16,17]. Figure 5 shows the AND gate of two inputs. The OR gate is also created by fixing one of the inputs of the majority gate and value logical “1” (polarization +1) [16,17]. Figure 6 also shows the OR gate of two inputs.
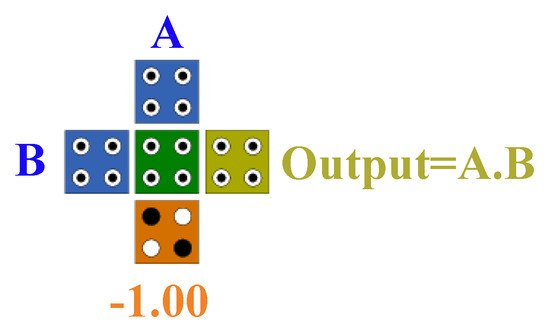
Figure 5.
The QCA implementation of the two-input AND gate.
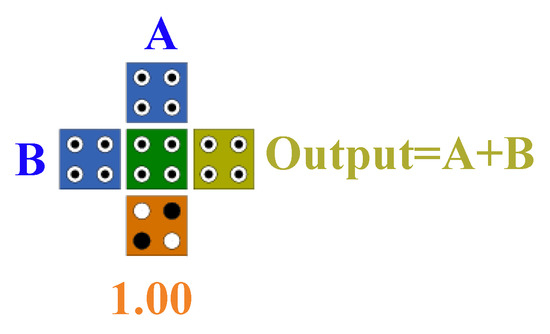
Figure 6.
The QCA implementation of the two-input OR gate.
3. The Proposed Circuits
Adders are one of the main and most basic computational circuits in digital logic, which is the most common and most widely used digital arithmetic circuit.
Among the adder circuits, the full adder circuit is one of the most important and main computational circuits because this circuit is used in all arithmetic and computational circuits. In the present article, we first design and implement a new XOR gate. Then, by inverting the fixed cells of this proposed XOR gate, we implement the XNOR gate. Finally, using the same proposed XOR gate, we implement two new full adder (FA) circuits. These are designed to have a reduced cost function, and the implementations are performed without the use of rotational cells, without the use of crossovers and NOT gates, and in a coplanar manner (single layer) compared to the best previous models.
3.1. The XOR Gate Design
The XOR gate is one of the most momentous and main logic gates. Moreover, the XOR gate is the fundamental logic gate, plays an important role in digital circuit design, and is the core of several reversible gates. The proposed XOR gate in this research has the following advantages over the previous best design:
- -
- Reduced number of cells consumed;
- -
- Reduced consumption area;
- -
- Reduced cost function;
- -
- Less delay;
- -
- No use of NOT gates;
- -
- No use of crossovers;
- -
- No use of rotary cells (45-degree cells).
Figure 7 shows the implementation of the proposed XOR gate design, and Figure 8 shows the simulator output of this gate. Equation (1) shows the logical relationship of this gate:
A⊕B = A.B’ + A’.B
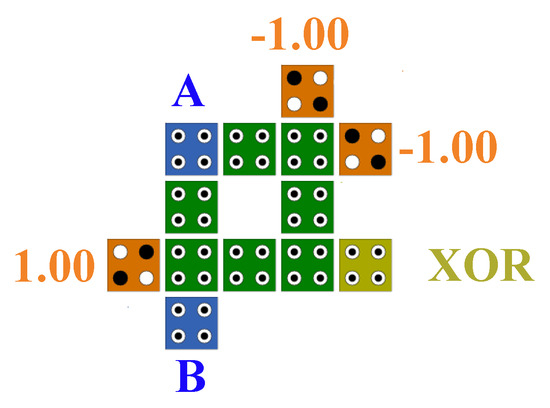
Figure 7.
The proposed XOR gate.
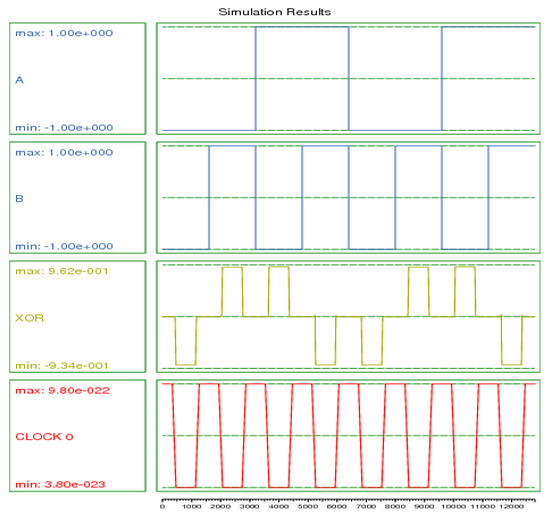
Figure 8.
Simulation results for the proposed XOR gate.
To design a large circuit using smaller units, the area and delay of the small units are crucial because these smaller units are used multiple times. Hence, our main goal is to design an efficient XOR block. The proposed structure for a two-input XOR gate (with a 0.25 clock cycle delay) can be effectively utilized as a building block in designing multi-input XOR gates. Similarly, a three-input XOR gate can be designed using only two two-input XOR gates with a 0.5 clock cycle delay. A four-input XOR gate can be designed using only three cascaded two-input XOR gates with a 0.75 clock cycle. In the same way, an ultra-high-speed five-input XOR can be effectively designed using four cascaded gates working in one clock cycle as shown in Figure 9 and Figure 10, which show, respectively, a block diagram and implementation. Following the proposed five-input XOR gate, we also provided cost function, complexity and delay diagrams in Section 4 to illustrate the application of the cost function for L, K, P = 2. Equation (2) below describes this important criterion. As can be seen in cost function diagram in Section 4, in evaluating the comparison of the cost function parameter [18] for QCA XOR, the highest value is related to the designs [19,20], and the lowest value is related to our proposed design.
Cost Function = (MK + I + CL) × TP
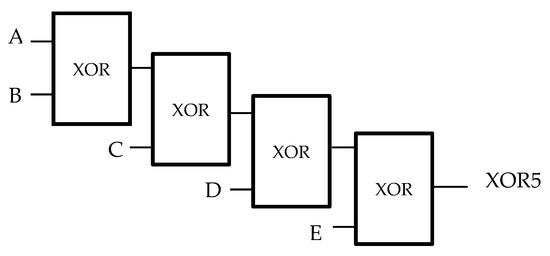
Figure 9.
Logical diagram of the proposed 5-input XOR gate.
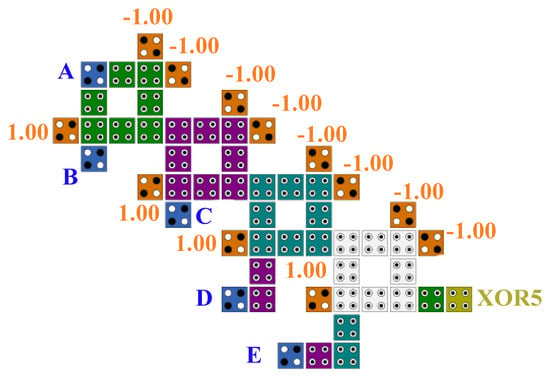
Figure 10.
Logical diagram of the proposed 5-input XOR gate.
3.2. The XNOR Gate Design
The XNOR gate is achieved by inverting (NOT) the proposed XOR gate fixed cells. Figure 11 shows the implementation of the XNOR gate, and Figure 12 shows the simulator output of this gate. Equation (3) shows the logical relationship of this gate:
(A⊕B)’ = A’.B’ + A.B
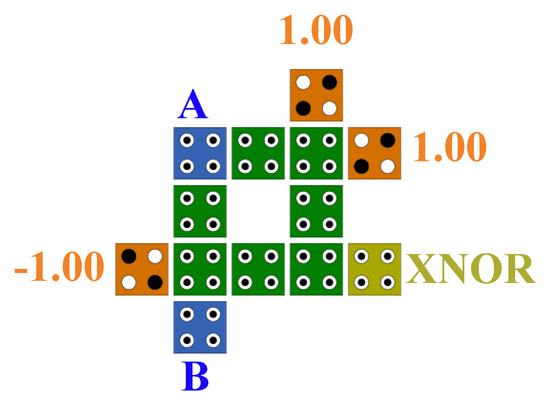
Figure 11.
The proposed XNOR gate.
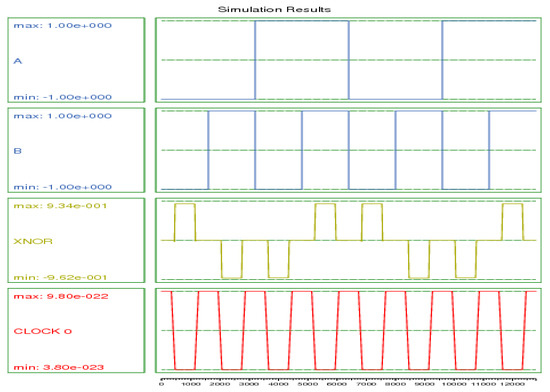
Figure 12.
Simulation results for the proposed XNOR gate.
3.3. The Full Adder (FA) Circuits’ Design
In this section, we designed and implemented two full adder (FA) circuits using the proposed XOR gate. The design was carried out with a delay of only three clock phases (0.75 clocks). The FA circuits proposed in this research are among the best samples ever designed. This is because they are designed without the use of a NOT gate, rotational cells, and crossovers, and they are designed to be coplanar. Equations (4) and (5) below are relationships related to the full adder circuits; Table 1 is its truth table; Figure 13 and Figure 14 present, respectively, a block diagram and implementation of the a and b proposed FA circuits with QCA technology; and Figure 15 shows the simulator output of these FA circuits.
S = A⊕B⊕Cin = ABCin + A’B’Cin + AB’Cin’ + A’BCin’
Cout = M (A, B, Cin) = A.B + A.Cin + B.Cin

Table 1.
Truth table of the full adder/subtractor.
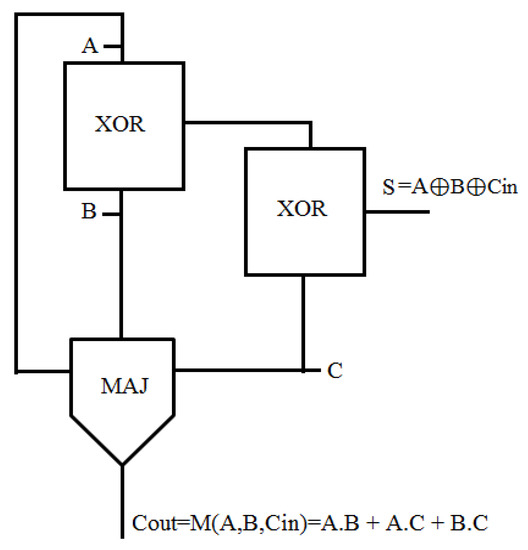
Figure 13.
Logical diagram of the proposed full adder (FA) circuits.
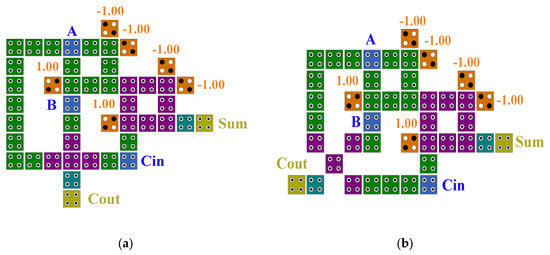
Figure 14.
The proposed full adder (FA) (a) FA design-1 (b) FA design-2 circuits.
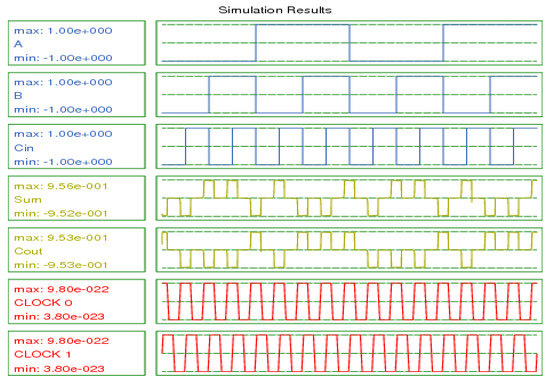
Figure 15.
Simulation results for the proposed XOR gate.
4. Performance Evaluation
This section evaluates the proposed circuits for the QCA implementation of the XOR gate and the FA circuits and compares them to those of previous works. For this evaluation, the number of cells, the area, and the delay obtained with the QCA Designer tool are considered. In Table 2, the simulation parameters used by the QCA Designer tool are listed. The simulation results of the proposed full adder (FA) circuits are shown in Table 3. As can be seen, the proposed full adder (FA) circuits in this research were compared with the best previous examples. As can be seen, the proposed collectors of this research have a better advantage than the previous designs due to the lack of any crossovers and inverter gate (NOT gate), as well as the reduced use of the majority gate number.

Table 2.
Simulation parameters for the QCA Designer.

Table 3.
Relative evaluation of the proposed full adder (FA) circuits in comparison with the state of the art.
As can be seen in Table 3, the consumption area of the proposed FA design-2 circuit is less than that of all the compared works. Regarding the consumption area of the proposed FA design-1 circuit, as shown in the table, the consumption area of this proposed design is equal to that of the design in [27]; however, the delay of our proposed design is better. Moreover, compared to the design in [23], the consumption area of our proposed design is higher, but in the design in [23], a 45-degree cell was used to implement the FA circuit.
Comparing the parameter of the number of cells used, as can be seen, the number of cells in the proposed circuit design of FA design-2 is less than that of all previous works, and in the case of the number of cells in the circuit of FA design-1, it can be said that compared to the design in [27], one more cell is used for implementation; however, our proposed FA design-1 circuit is designed using three clock phase (0.75 clock cycle).
Regarding the comparison of the proposed designs’ delay compared to the previous works, as can be seen, the delay of both of our proposed circuits is the same, and the delay of these two designs is less (superior) than that of all previous designs, except those in [23,26]. The delay of our proposed circuit designs is equal to that of the design in [22], but, instead, the number of its cells is more than that of our proposed designs, and also, in this design [23], 45-degree cells have been used to implement the circuit. Moreover, the delay of the proposed circuits compared to that of the design in [26] is more than one clock phase (0.25); however, the consumption area and the number of cells in this design are much higher than those of our proposed designs, and most importantly, in this design, not only is the crossover used, but also 45-degree cells are used to implement it, and this reduces the delay of this design, which instead has less cost function and strength and stability.
Regarding the parameters of the number of crossing intersections, the number of inverter gates, and the number of 45-degree cells, it can be said that none of these circuit parameters were used in the proposed design, which made the cost function of the proposed designs superior to that of previous works. It should be noted that the three-input majority gate used in the proposed FA design-2 is realized by four inverter gates; however, this majority gate is considered as one gate.
In this paper, the coefficients of L, K, and P are considered equal to one (L, K, P = 2); to evaluate the performance of the proposed XOR gate and compare the performance of the previous work, an evaluation was carried out. The diagram in Figure 16 shows the evaluation and comparison of the cost function criterion for L, K, P = 2. As can be seen in this diagram, the evaluation criterion of cost function for our proposed XOR gate design and that of the design in [24] is significantly superior to that of all previous designs. The reasons for this superiority are the lack of use of NOT gates and crossovers and the reduced number of majority gates used in the implementation of the proposed designs. These results and this comparison were carried out in the size range of 1≤ n ≤ 128. Figure 17 also shows a comparison diagram of the complexity parameter. In this evaluation, the number of majority gates, the number of inverter gates, and the number of crossovers were compared. To measure the complexity of the proposed XOR gate (nbit-input) with previous designs, this evaluation was performed in the range of 1≤ n ≤ 128. As can be seen in the review of this evaluation criterion, our proposed XOR gate design and the design in [24] are significantly superior to all previous designs. The diagram in Figure 18 also shows the delay parameter. This parameter is also used to measure the speed of the XOR gate. This comparison is also carried out in the range of 1≤ n ≤ 128, and as can be seen, the fastest XOR gate is related to our proposed design, [19,20,24,28,29,30,31,32,33,34,35]; our proposed design is coplanar, and crossovers are not used in any of the designs.
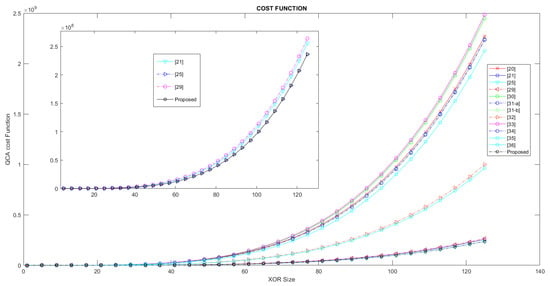
Figure 16.
Comparison of QCA XOR with cost function.
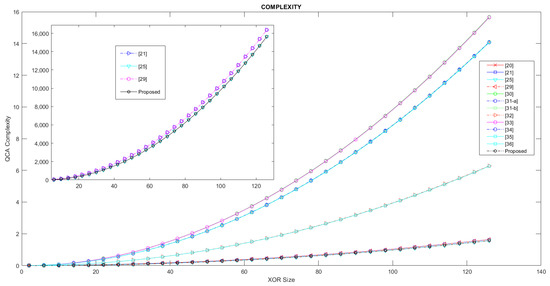
Figure 17.
Comparison of QCA XOR with complexity.
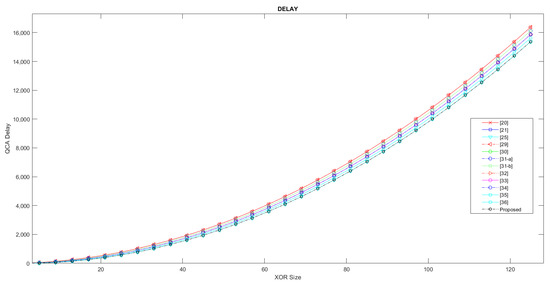
Figure 18.
Comparison of QCA XOR with delay.
5. Power Delay Product (PDP) Analysis
The QCADesignerE was used to estimate the energy dissipation of the proposed FA, as well as the previous FA [21,22,23,24,25,26,27]. Here, we considered the default parameters of QCADesignerE, and this simulation tool provides energy dissipation data as shown in Table 4. For power delay product (PDP) calculation, the standard theoretical clock frequency of 1 THz was considered.
Power Delay Product (PDP) = Power × Delay

Table 4.
Energy and power dissipation analysis of the proposed full adder (FA) circuits in comparison with the state of the art.
6. Conclusions
The many FA designs in QCA technology use at least three layers for the crossovers; there are also a number of designs that use rotation cells or the design of the coplanar crossover with the utilization of non-adjacent clock phases. That is why we did not use any crossovers in our designs. As a result, they were designed not only to be coplanar but also to be designs without the use of any NOT gates, crossovers, and rotation cells, which creates a more stable and robust circuit. Our proposed designs are superior to the previous designs; the number of cells in design-2 is superior to that in all compared designs, with 29.51% and 2.27% reductions when compared to the smallest and largest previous examples, respectively, [26,27]. Moreover, the area consumption of design-2 is superior to that of all the compared designs, with reductions of 10.53% and 51.32% when compared to the most compact previous sample [23] and the largest previous sample [26], respectively. In the case of the delay parameter, the delay in our proposed design-1 and design-2 is shorter than that of any of the previous designs, except for the design in [26]. This design uses rotation cells, and both the number of cells and the area of consumption are higher than those of design-1 and design-2. The proposed XOR circuit can be implemented in QCA technology, which employs reversible logic for its implementation, including Feynman gate, Toffoli gate, Peres gate, and other reversible circuits where the XOR gate is the most important element for the design of these circuits.
Author Contributions
Conceptualization, M.V.; methodology, M.V.; validation, M.V., P.L. and A.N.B.; formal analysis, M.V.; investigation, M.V., P.L. and A.N.B.; writing—original draft preparation, M.V.; writing—review and editing, P.L., A.N.B. and K.A.W.; supervision, P.L., A.N.B. and K.A.W. All authors have read and agreed to the published version of the manuscript.
Funding
Pavel Lyakhov would like to acknowledge the financial support of this work by the Ministry of Science and Higher Education of the Russian Federation under assignment No. FSEE-2020-0002.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roohi, A.; DeMara, R.F.; Khoshavi, N. Design and evaluation of an ultra-area-efficient fault-tolerant QCA full adder. Microelectron. J. 2015, 46, 531–542. [Google Scholar] [CrossRef]
- Babaie, S.; Sadoghifar, A.; Bahar, A.N. Design of an efficient multilayer arithmetic logic unit in quantum-dot cellular automata (QCA). IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 963–967. [Google Scholar] [CrossRef]
- Liu, W.; Swartzlander, E.E., Jr.; O’Neill, M. Design of Semiconductor QCA Systems; Artech House: Norwood, MA, USA, 2013. [Google Scholar]
- Macucci, M. Quantum Cellular Automata; Imperial College Press: London, UK, 2006. [Google Scholar]
- Walus, K.; Dysart, T.J.; Jullien, G.A.; Budiman, R. A QCADesigner: A rapid design and simulation tool for quantum-dot cellular automata. IEEE Trans. Nanotechnol. 2004, 3, 26–31. [Google Scholar] [CrossRef]
- Teodosio, T.; Sousa, L. QCA-LG: A tool for the automatic layout generation of QCA combinational circuits. In Proceedings of the IEEE Norchip, Aalborg, Denmark, 19–20 November 2007; pp. 1–5. [Google Scholar]
- Swartzlander, E.E.; Cho, H.; Kong, I.; Kim, S.W. Computer arithmetic implemented with QCA: A progress report. In Proceedings of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–7 November 2010. [Google Scholar]
- Vahabi, M.; Lyakhov, P.; Bahar, A.N. Design and Implementation of Novel Efficient Full Adder/Subtractor Circuits Based on Quantum-Dot Cellular Automata Technology. Appl. Sci. 2021, 11, 8717. [Google Scholar] [CrossRef]
- Tougaw, P.D.; Lent, C.S. Logical devices implemented using quantum cellular automata. J. Appl. Phys. 1994, 75, 1818–1825. [Google Scholar] [CrossRef]
- Cho, H.; Swartzlander, E.E. Adder designs and analyses for quantum-dot cellular automata. IEEE Trans. Nanotechnol. 2007, 6, 374–383. [Google Scholar] [CrossRef]
- Huang, J.; Momenzadeh, M.; Tahoori, M.B.; Lombardi, F. Design and characterization of an and-or-inverter (AOI) gate for QCA implementation. In Proceedings of the 14th ACM Great Lakes Symposium on VLSI 2004, Boston, MA, USA, 26–28 April 2004; pp. 426–429. [Google Scholar]
- Shin, S.-H.; Jeon, J.-C.; Yoo, K.-Y. Wire-crossing technique on quantum-dot cellular automata. In Proceedings of the NGCIT2013: 2nd International Conference on Next Generation Computer and Information Technology, Las Vegas, NV, USA, 15–17 April 2013; Volume 27, pp. 52–57. [Google Scholar]
- Lent, C.S.; Tougaw, P.D.; Porod, W. Quantum cellular automata: The physics of computing with arrays of quantum dot molecules. In Proceedings of the PhysComp 94: Workshop on Physics and Computing, Dallas, TX, USA, 17–20 November 1994; pp. 5–13. [Google Scholar]
- Frost, S.E.; Rodrigues, A.F.; Janiszewski, A.W.; Rausch, R.T.; Kogge, P.M. Memory in motion: A study of storage structures in QCA. In Proceedings of the First Workshop on Non-Silicon Computing, Cambridge, MA, USA, 3 February 2002. [Google Scholar]
- Wang, W.; Walus, K.; Jullien, G.A. Quantum-dot cellular automata adders. In Proceedings of the 2003 Third IEEE Conference on Nanotechnology, San Francisco, CA, USA, 12–14 August 2003; pp. 461–464. [Google Scholar]
- Beigh, M.R.; Mustafa, M.; Ahmad, F. Performance evaluation of efficient XOR structures in quantum-dot cellular automata (QCA). Sci. Res. Circuits Syst. 2013, 4, 29850. [Google Scholar] [CrossRef] [Green Version]
- Modi, S.; Tomar, A.S. Logic gate implementations for quantum dot cellular automata. In Proceedings of the 2010 International Conference on IEEE Computational Intelligence and Communication Networks (CICN), Bhopal, India, 26–28 November 2010. [Google Scholar]
- Liu, W.; Lu, L.; O’Neill, M.; Swartzlander, E.E. A first step toward cost functions for quantum-dot cellular automata designs. IEEE Trans. Nanotechnol. 2014, 13, 476–487. [Google Scholar]
- Chabi, A.M.; Sayedsalehi, S.; Angizi, S.; Navi, K. Efficient QCA exclusive-or and multiplexer circuits based on a nanoelectronic-compatible designing approach. Int. Sch. Res. Not. 2014, 2014, 63967. [Google Scholar] [CrossRef]
- Mohammadi, H.; Navi, K. Energy-efficient single-layer QCA logical circuits based on a novel XOR gate. J. Circuits Syst. Comput. 2018, 27, 1850216. [Google Scholar] [CrossRef]
- Abedi, D.; Jaberipur, G.; Sangsefidi, M. Coplanar full adder in quantum-dot cellular automata via clock-zone-based crossover. IEEE Trans. Nanotechnol. 2015, 14, 497–504. [Google Scholar] [CrossRef]
- Sandhu, A.; Gupta, S. Performance Evaluation of an Efficient Five-Input Majority Gate Design in QCA Nanotechnology. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 8, 194–205. [Google Scholar]
- Sarvaghad-Moghaddam, M.; Orouji, A.A. New symmetric and planar designs of reversible full-adders/subtractors in quantum-dot cellular automata. Eur. Phys. J. D 2019, 73, 125. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Xie, G. A Novel XOR/XNOR Structure for Modular Design of QCA Circuits. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3327–3331. [Google Scholar] [CrossRef]
- Safoev, N.; Jeon, J.-C. Design of high-performance QCA incrementer/decrementer circuit based on adder/subtractor methodology. Microprocess. Microsyst. 2020, 72, 102927. [Google Scholar] [CrossRef]
- Erniyazov, S.; Jeon, J.-C. Carry save adder and carry look ahead adder using inverter chain based coplanar QCA full adder for low energy dissipation. Microelectron. Eng. 2019, 211, 37–43. [Google Scholar] [CrossRef]
- Zoka, S.; Gholami, M. A novel efficient full adder–subtractor in QCA nanotechnology. Int. Nano Lett. 2019, 9, 51–54. [Google Scholar] [CrossRef] [Green Version]
- Sasamal, T.N.; Singh, A.K.; Ghanekar, U. Design and Analysis of Ultra-Low Power QCA Parity Generator Circuit. In Advances in Power Systems and Energy Management; Springer: Singapore, 2018; pp. 347–354. [Google Scholar]
- Raj, M.; Kumaresan, R.S.; Gopalakrishnan, L. Optimized Multiplexer and Exor gate in 4-dot 2-electron QCA using Novel Input Technique. In Proceedings of the 2019 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), Kanpur, India, 6–8 July 2019; pp. 1–4. [Google Scholar]
- Khakpour, M.; Gholami, M.; Naghizadeh, S. Parity generator and digital code converter in QCA nanotechnology. Int. Nano Lett. 2020, 10, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Deng, F.; Cheng, X.; Xie, G. A Coplanar XOR Using NAND-NOR-Inverter and Five-Input Majority Voter in Quantum-Dot Cellular Automata Technology. Int. J. Theor. Phys. 2020, 59, 484–501. [Google Scholar] [CrossRef]
- Raj, M.; Gopalakrishnan, L.; Ko, S.-B. Fast Quantum-Dot Cellular Automata Adder/Subtractor Using Novel Fault Tolerant Exclusive-or Gate and Full Adder. Int. J. Theor. Phys. 2019, 58, 3049–3064. [Google Scholar] [CrossRef]
- Karkaj, E.T.; Heikalabad, S.R. Binary to gray and gray to binary converter in quantum-dot cellular automata. Opt. Int. J. Light Electron Opt. 2017, 130, 981–989. [Google Scholar] [CrossRef]
- Safoev, N.; Jeon, J.-C. A novel controllable inverter and adder/subtractor in quantum-dot cellular automata using cell interaction based XOR gate. Microelectron. Eng. 2020, 222, 111197. [Google Scholar] [CrossRef]
- Chabi, A.M.; Roohi, A.; Khademolhosseini, H.; Sheikhfaal, S.; Angizi, S.; Navi, K.; DeMara, R.F. Towards ultra-efficient QCA reversible circuits. Microprocess. Microsyst. 2017, 49, 127–138. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).