Development of Dynamics for Design Procedure of Novel Grating Tiling Device with Experimental Validation
Abstract
:1. Introduction
2. Kinematics of Grating Device as a Multibody System
2.1. Kinematics Grating Device
2.2. System of Equations of Motion
- An estimate of the preliminary situations that outline the preliminary configuration of the multibody model is formed. The preliminary situations that constitute the preliminary coordinates and velocities should be an excellent approximation of the precise preliminary configuration:
- Using the preliminary coordinates, the constraint Jacobian matrix is constructed, assemble the global mass matrix and other equation of motion items;
- Solve the linear set of the equations of motion Equation (3) for a constrained multibody system in order to obtain the accelerations at instant time and the Lagrange multipliers;
- Integrate the accelerations determined the coordinates and velocities. The vector of Lagrange multipliers can be used to determine the generalized reaction forces using Equation (4);
- This process is maintained until the preferred give up of the simulation time is reached.
2.3. Design of Grating Device
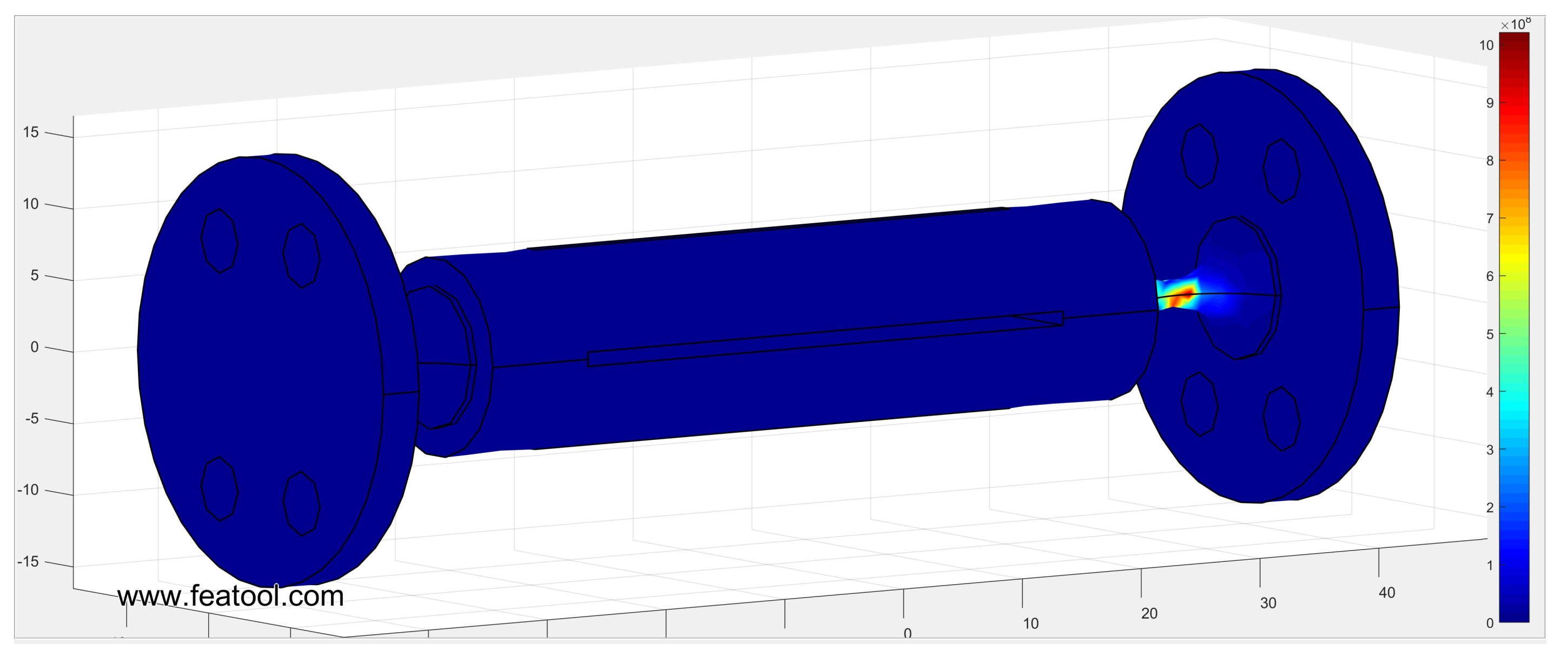
3. Multibody Model of Grating Device
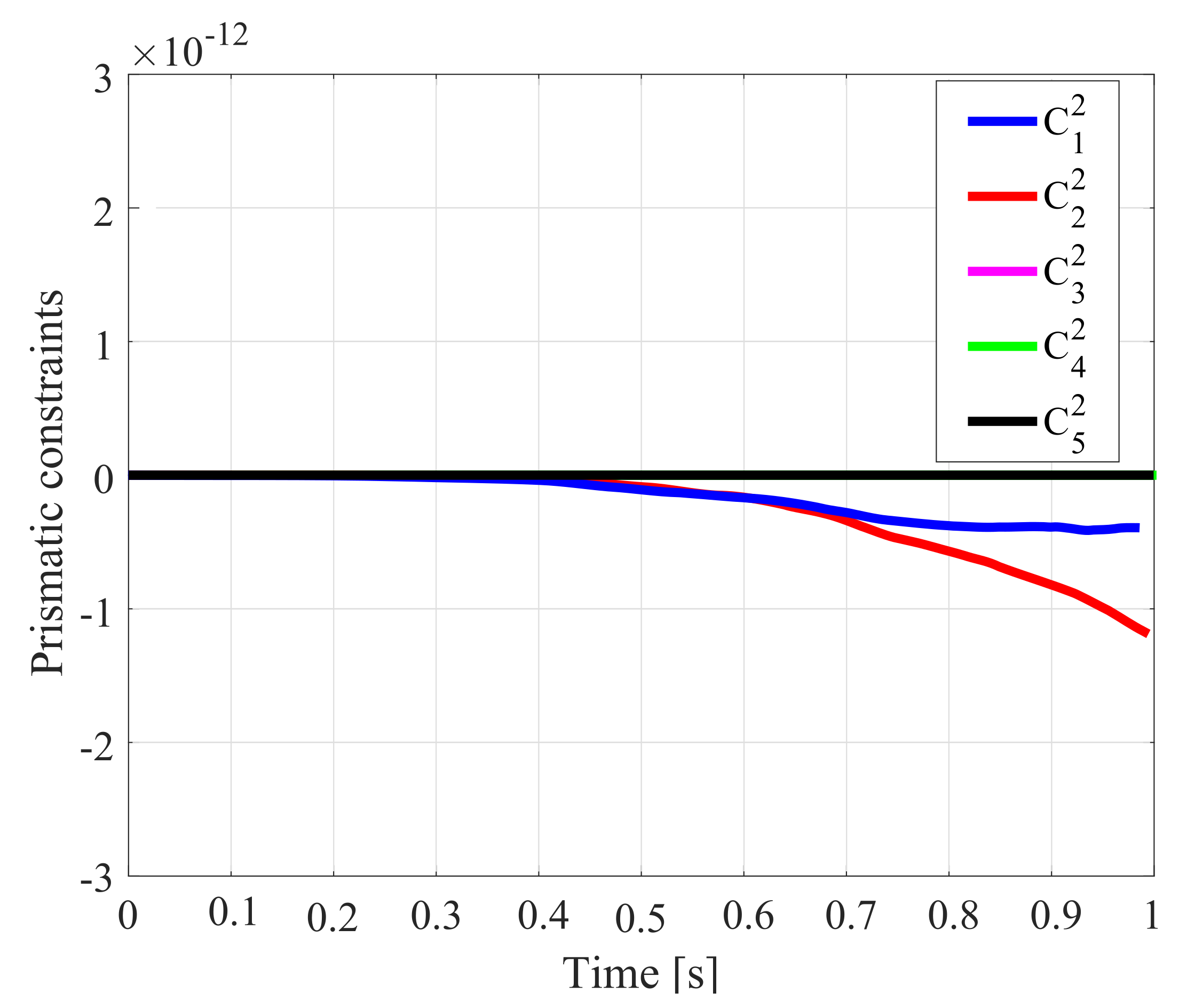
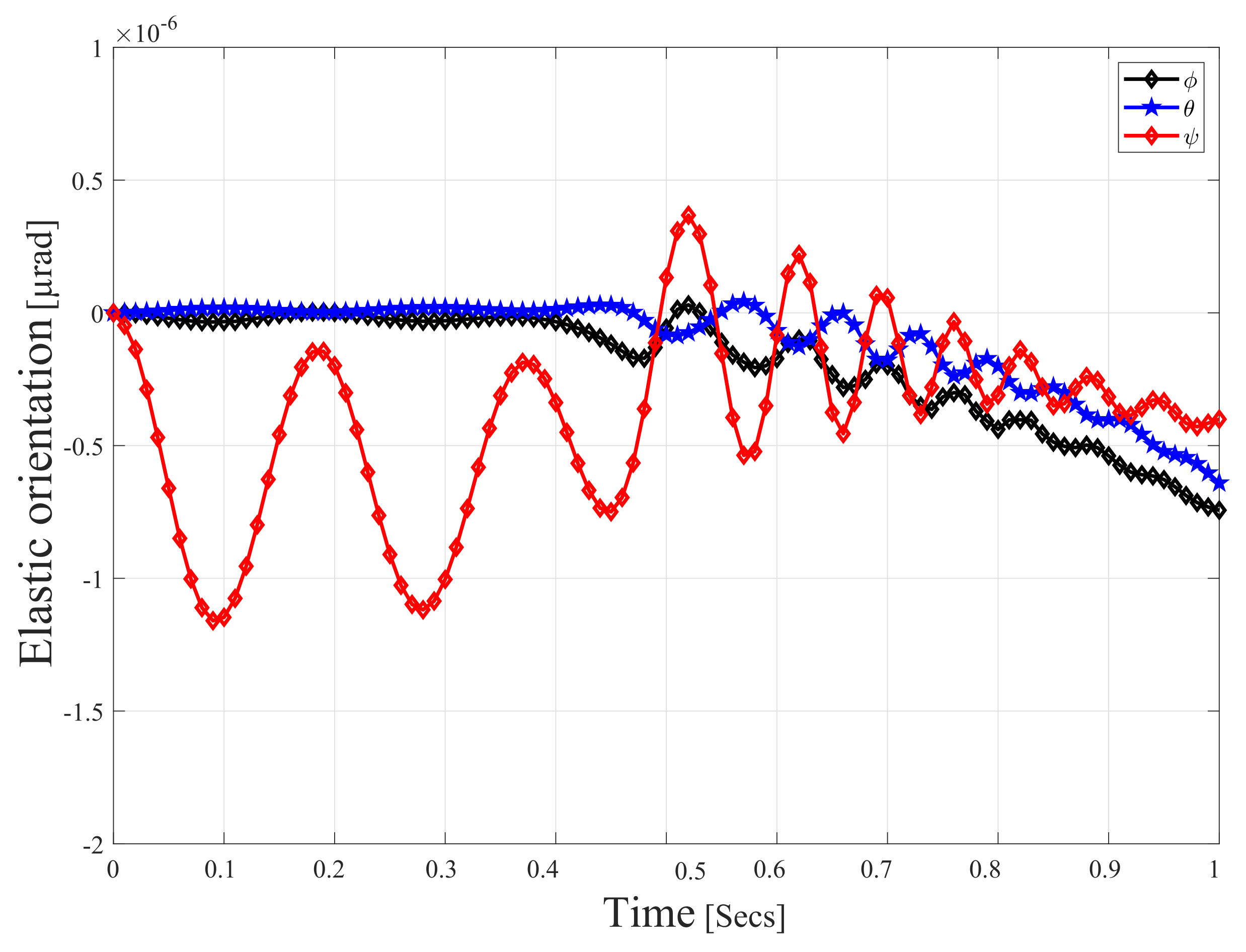
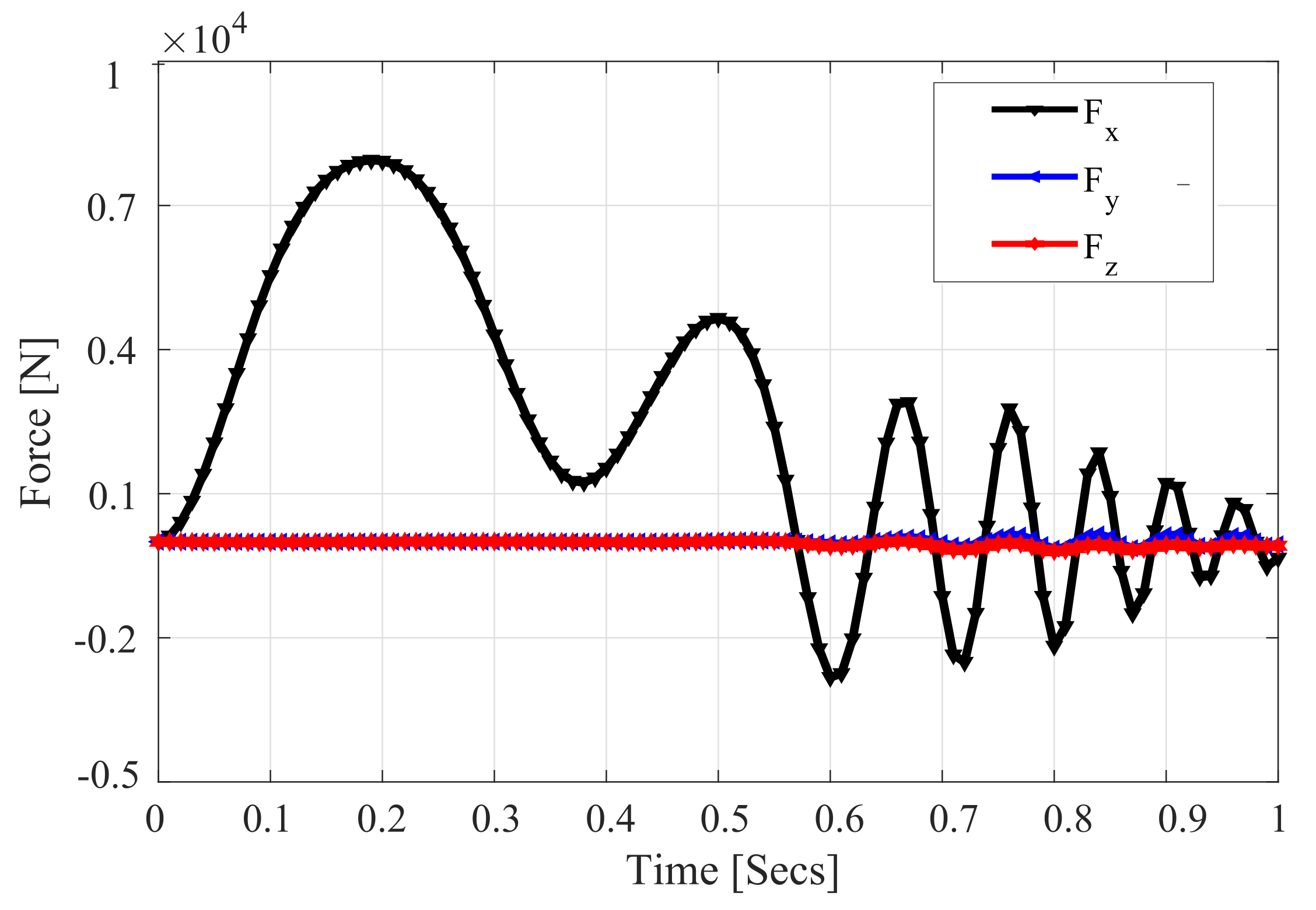
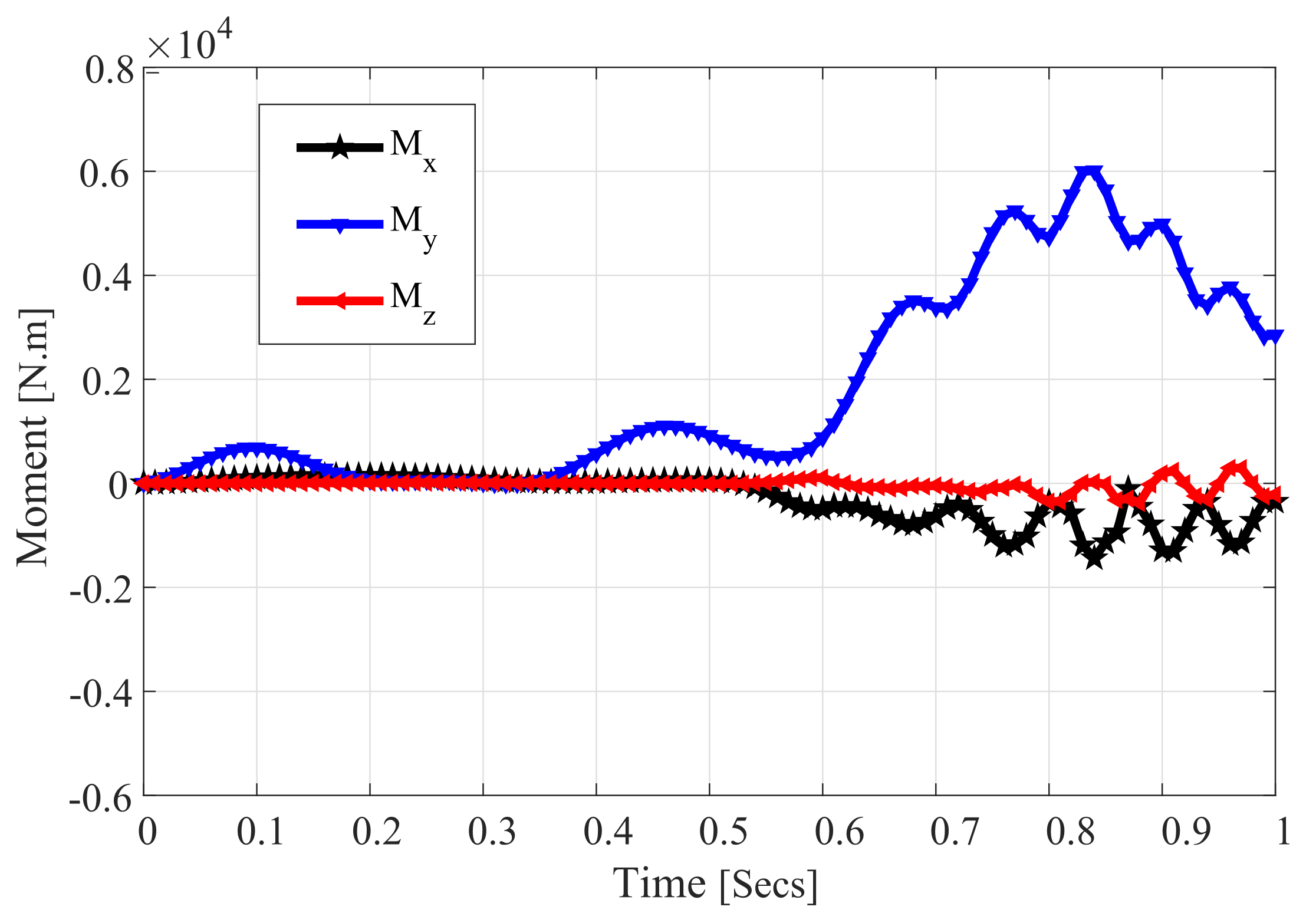
4. Numerical Results and Discussion
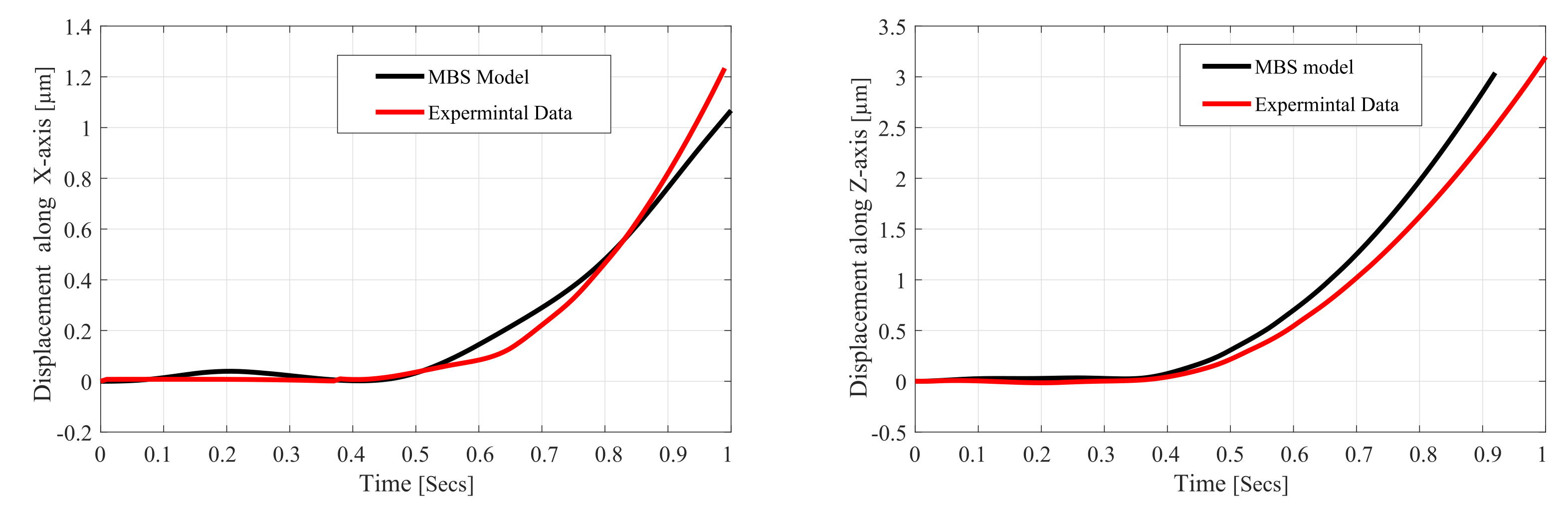
5. Experimental Validation
6. Conclusions
- (1)
- The grating device model was successfully implemented in a simulation tool entirely elaborated in MATLAB including symbolic and computational work. Equation of motion solution included system coordinates and Lagrange multipliers are obtained. These multipliers are used to estimate the reaction forces utilized in the design procedure of the grating system.
- (2)
- From the results presented in the preceding sections, the optimal design of such a grating device is carried out for maximum ranges of grating movements. The design procedure proposed in this work is systematic and oriented for grating devices to realize the positioning and attitude adjustment of the moving grating.
- (3)
- The design was constructed in real life and the movement was verified experimentally, which confirms the effectiveness of the proposed procedure. The design method of the grating device system based on the DFD procedure proposed in this paper provides new ideas and methods for the design of large load, and high-precision grating systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DFD | Dynamics For Design |
| MBS | Multibody System Dynamics |
| FFR | Floating Frame Of Refferences |
| ANCF | Absolute Nodal Coordinate Formulation |
| DAE | Differential-Algebraic Equations |
| DOF | Degree Of Freedom |
| PZT | piezoelectric ceramic actuator |
References
- Shao, Z.X.; Zhang, Q.C.; Bai, Q.S.; FU, H.Y. Design method of controlling device for tiling high precision and large aperture grating. Opt. Precis. Eng. 2009, 1, 158–165. [Google Scholar]
- Wu, J.; Luo, Z.; Zhang, N.; Zhang, Y.; Walker, P.D. Uncertain dynamic analysis for rigid-flexible mechanisms with random geometry and material properties. Mech. Syst. Signal Process. 2017, 85, 487–511. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Zhang, Y.; Qian, J.; Sun, L. Precision analysis of a large aperture tiled-gratings device. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO 2014), Bali, Indonesia, 5–10 December 2014; pp. 1175–1179. [Google Scholar]
- Yunfei, L.; Yi, Z.; Mingjun, M.; Ke, C. Structural stability of large-size grating tiling device based on dynamic stiffness. J. Softw. Eng. 2015, 9, 287–297. [Google Scholar] [CrossRef]
- Bai, Q.; Liang, Y.; Cheng, K.; Long, F. Design and analysis of a novel large-aperture grating device and its experimental validation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1349–1359. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, S.; Wu, J.; Fu, H. A novel 5-DOF high-precision compliant parallel mechanism for large-aperture grating tiling. Mech. Sci. 2017, 8, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Bai, Q.; Shehata, M.; Nada, A. Efficient Modeling Procedure of Novel Grating Tiling Device Using Multibody System Approach. In International Symposium on Multibody Systems and Mechatronics; Springer: Córdoba, Argentina, 12–15 October 2020; pp. 168–176. [Google Scholar]
- Saleh, M.; Nada, A.; El-Betar, A.; El-Assal, A. Computational Design Scheme for Wind Turbine Drive-Train Based on Lagrange Multipliers. J. Energy 2017, 2017, 16. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, D.; Shi, L.; Liu, J. Multi-Body Dynamics Modeling and Control for Strapdown Inertially Stabilized Platforms Considering Light Base Support Characteristics. Appl. Sci. 2020, 10, 7175. [Google Scholar] [CrossRef]
- Nada, A.A.; Bishiri, A.H. Multibody system design based on reference dynamic characteristics: Gyroscopic system paradigm. Mech. Based Des. Struct. Mach. 2021, 1–23. [Google Scholar] [CrossRef]
- Wasfy, T.M.; Noor, A.K. Computational strategies for flexible multibody systems. Appl. Mech. Rev. 2003, 56, 553–613. [Google Scholar] [CrossRef]
- Zahariev, E.V. Generalized finite element approach to dynamics modeling of rigid and flexible systems. Mech. Based Des. Struct. Mach. 2006, 34, 81–109. [Google Scholar] [CrossRef]
- Nada, A.; Hussein, B.; Megahed, S.; Shabana, A. Use of the floating frame of reference formulation in large deformation analysis: Experimental and numerical validation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2010, 224, 45–58. [Google Scholar] [CrossRef]
- Sharma, H.; Patil, M.; Woolsey, C. A review of structure-preserving numerical methods for engineering applications. Comput. Methods Appl. Mech. Eng. 2020, 366, 113067. [Google Scholar] [CrossRef]
- Shabana, A.A. Definition of ANCF finite elements. J. Comput. Nonlinear Dyn. 2015, 10, 054506. [Google Scholar] [CrossRef]
- Si, H.; Guo, Y.B.; Liang, Y.C. Application and Developing Trends of Mechanical Tiling Technology in the Laser Fusion Device. In Key Engineering Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2014; Volume 621, pp. 57–62. [Google Scholar]
- Rui, X.; Gu, J.; Zhang, J.; Zhou, Q.; Yang, H. Visualized simulation and design method of mechanical system dynamics based on transfer matrix method for multibody systems. Adv. Mech. Eng. 2017, 9, 1687814017714729. [Google Scholar] [CrossRef] [Green Version]
- Korkealaakso, P.; Mikkola, A.; Rantalainen, T.; Rouvinen, A. Description of joint constraints in the floating frame of reference formulation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2009, 223, 133–145. [Google Scholar] [CrossRef]
- Pappalardo, C.M.; Lettieri, A.; Guida, D. Stability analysis of rigid multibody mechanical systems with holonomic and nonholonomic constraints. Arch. Appl. Mech. 2020, 90, 1961–2005. [Google Scholar] [CrossRef]
- O’Shea, J.J.; Jayakumar, P.; Mechergui, D.; Shabana, A.A.; Wang, L. Reference conditions and substructuring techniques in flexible multibody system dynamics. J. Comput. Nonlinear Dyn. 2018, 13, 041007. [Google Scholar] [CrossRef]
- El-Ghandour, A.; Foster, C. Coupled finite element and multibody systems dynamics modelling for the investigation of the bridge approach problem. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 1097–1111. [Google Scholar] [CrossRef]
- Kim, H.W.; Yoo, W.S. MBD applications in design. Int. J. Non-Linear Mech. 2013, 53, 55–62. [Google Scholar] [CrossRef]
- Ziegler, P.; Humer, A.; Pechstein, A.; Gerstmayr, J. Generalized component mode synthesis for the spatial motion of flexible bodies with large rotations about one axis. J. Comput. Nonlinear Dyn. 2016, 11, 041018. [Google Scholar] [CrossRef]
- Sugiyama, H.; Escalona, J.L.; Shabana, A.A. Formulation of three-dimensional joint constraints using the absolute nodal coordinates. Nonlinear Dyn. 2003, 31, 167–195. [Google Scholar] [CrossRef]
- Yoo, W.S.; Kim, K.N.; Kim, H.W.; Sohn, J.H. Developments of multibody system dynamics: Computer simulations and experiments. Multibody Syst. Dyn. 2007, 18, 35–58. [Google Scholar] [CrossRef]
- Wallin, M.; Hamed, A.M.; Jayakumar, P.; Gorsich, D.J.; Letherwood, M.D.; Shabana, A.A. Evaluation of the accuracy of the rigid body approach in the prediction of the dynamic stresses of complex multibody systems. Int. J. Veh. Perform. 2016, 2, 140–165. [Google Scholar] [CrossRef]
- Elshami, M.; Shehata, M.; Bai, Q.; Zhao, X. Multibody Dynamics Modeling of Delta Robot with Experimental Validation. In International Symposium on Multibody Systems and Mechatronics; Springer: Córdoba, Argentina, 12–15 October 2021; pp. 94–102. [Google Scholar]
- Bauchau, O. On the modeling of prismatic joints in flexible multi-body systems. Comput. Methods Appl. Mech. Eng. 2000, 181, 87–105. [Google Scholar] [CrossRef]

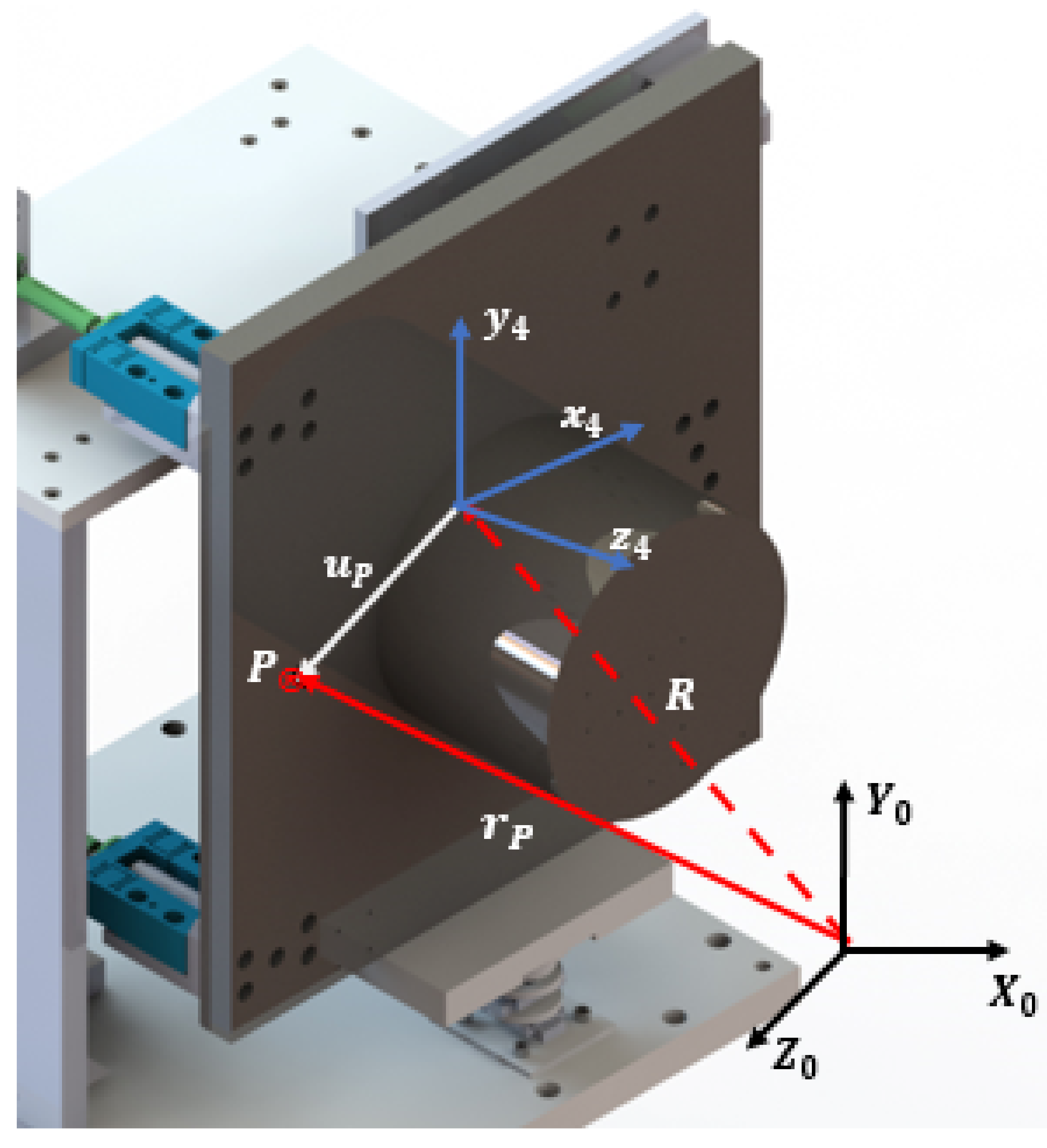

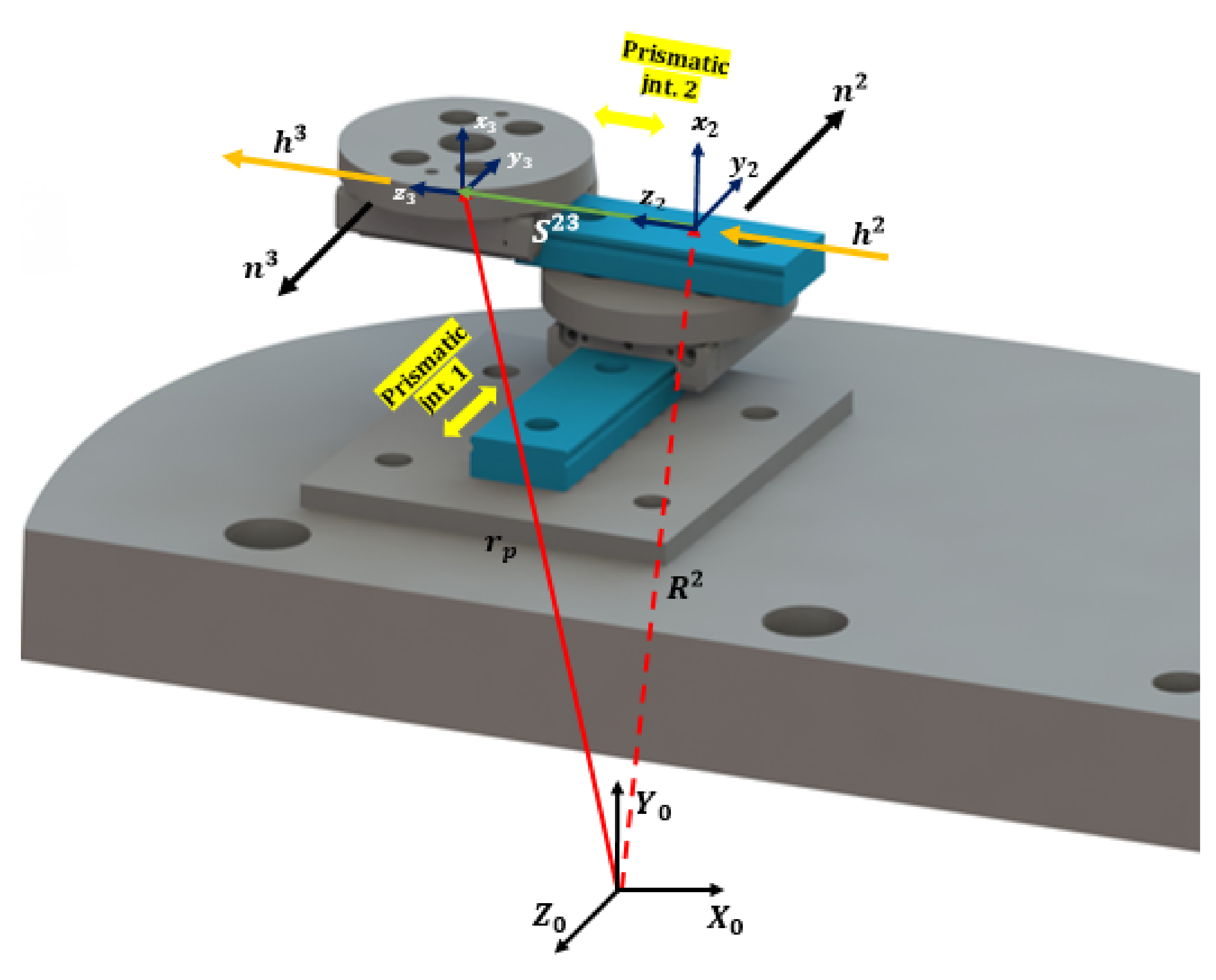

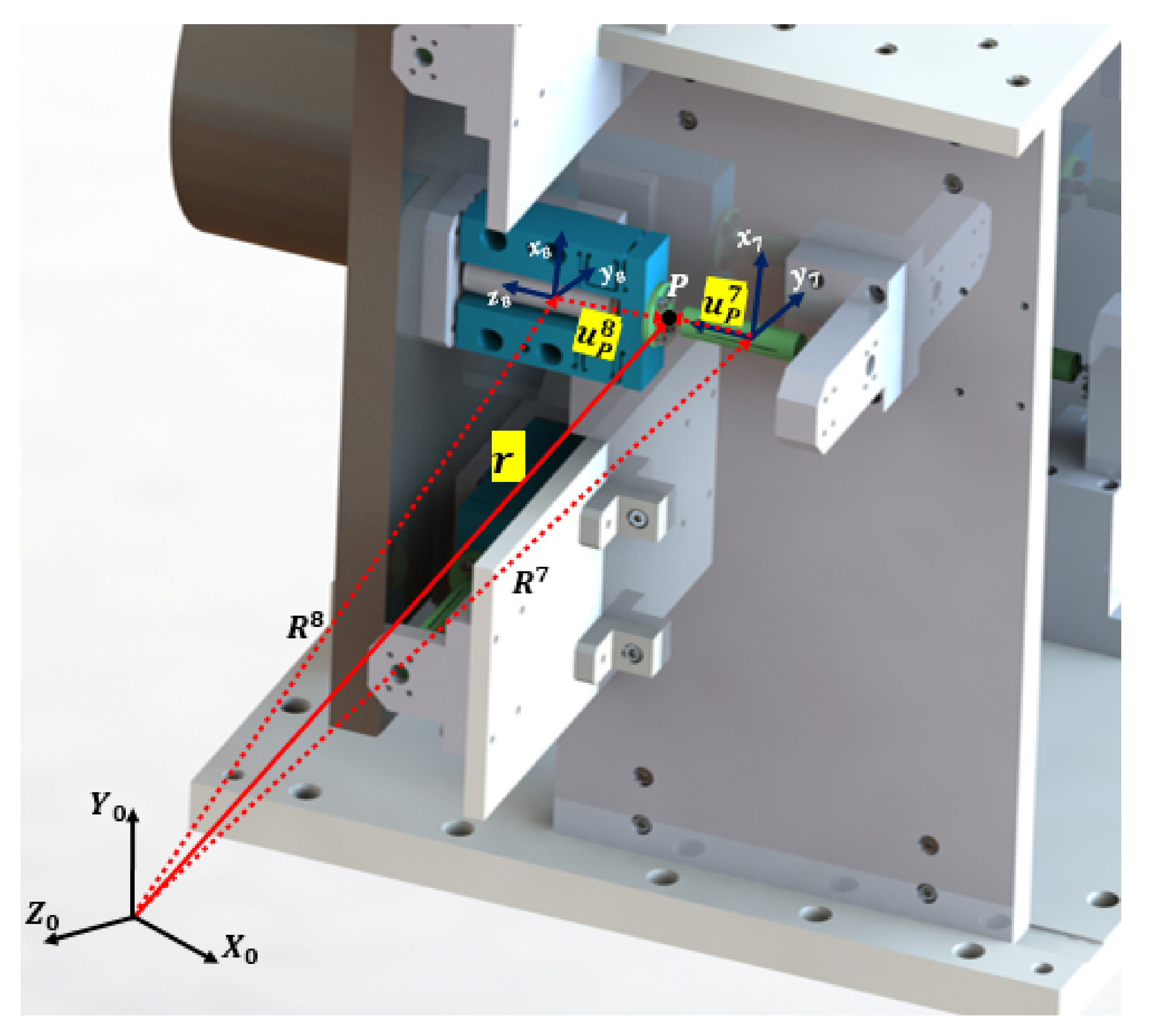
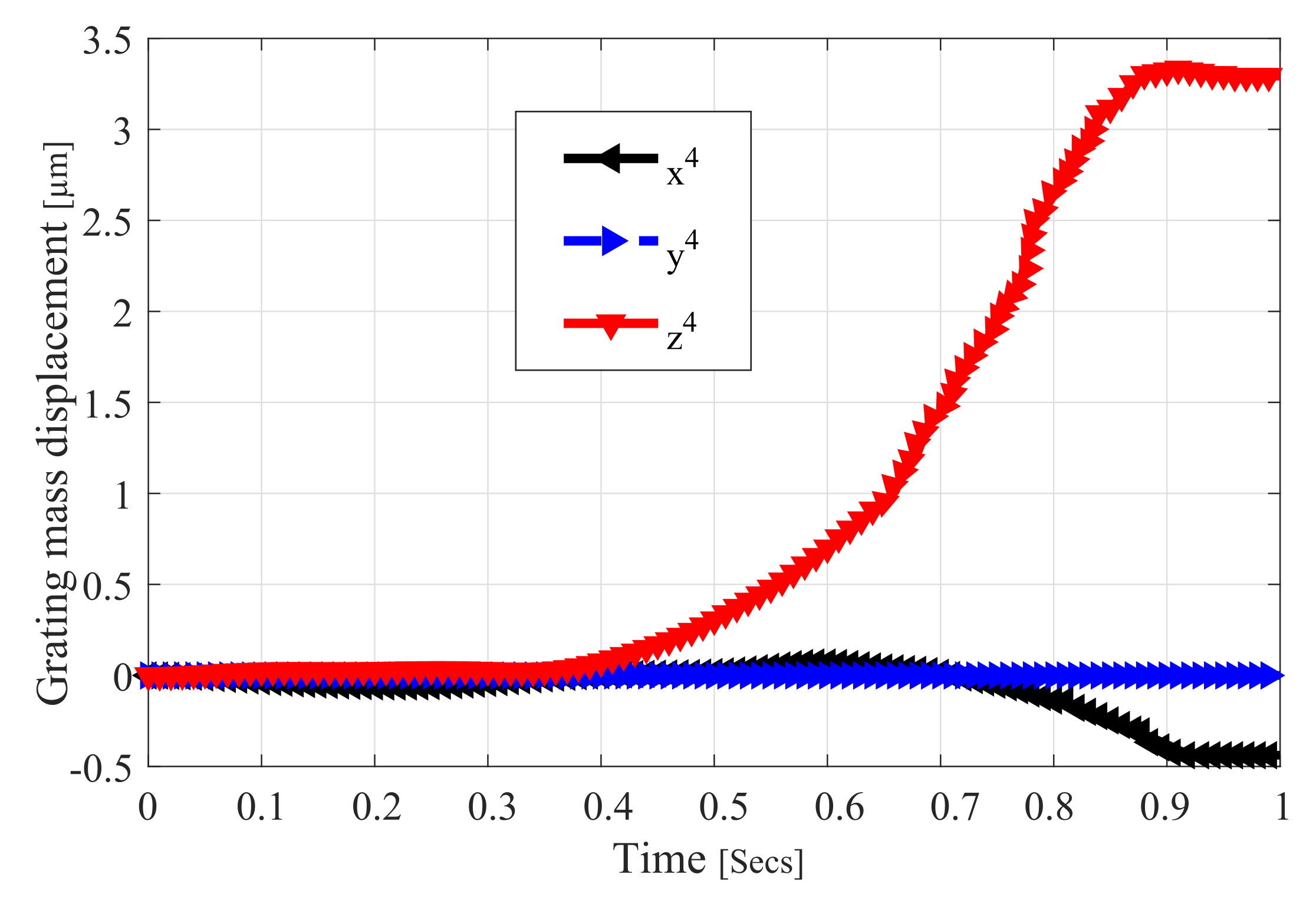
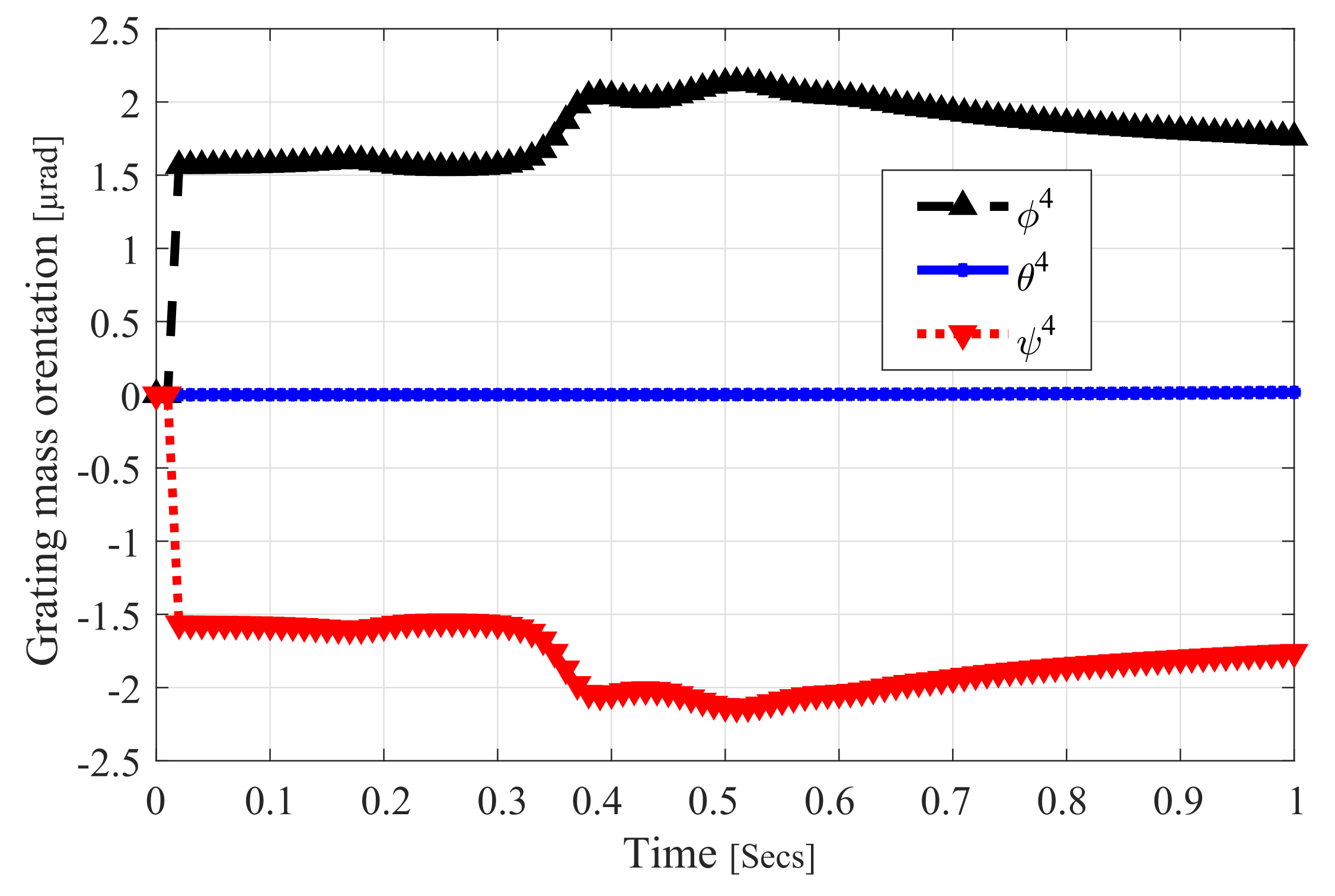
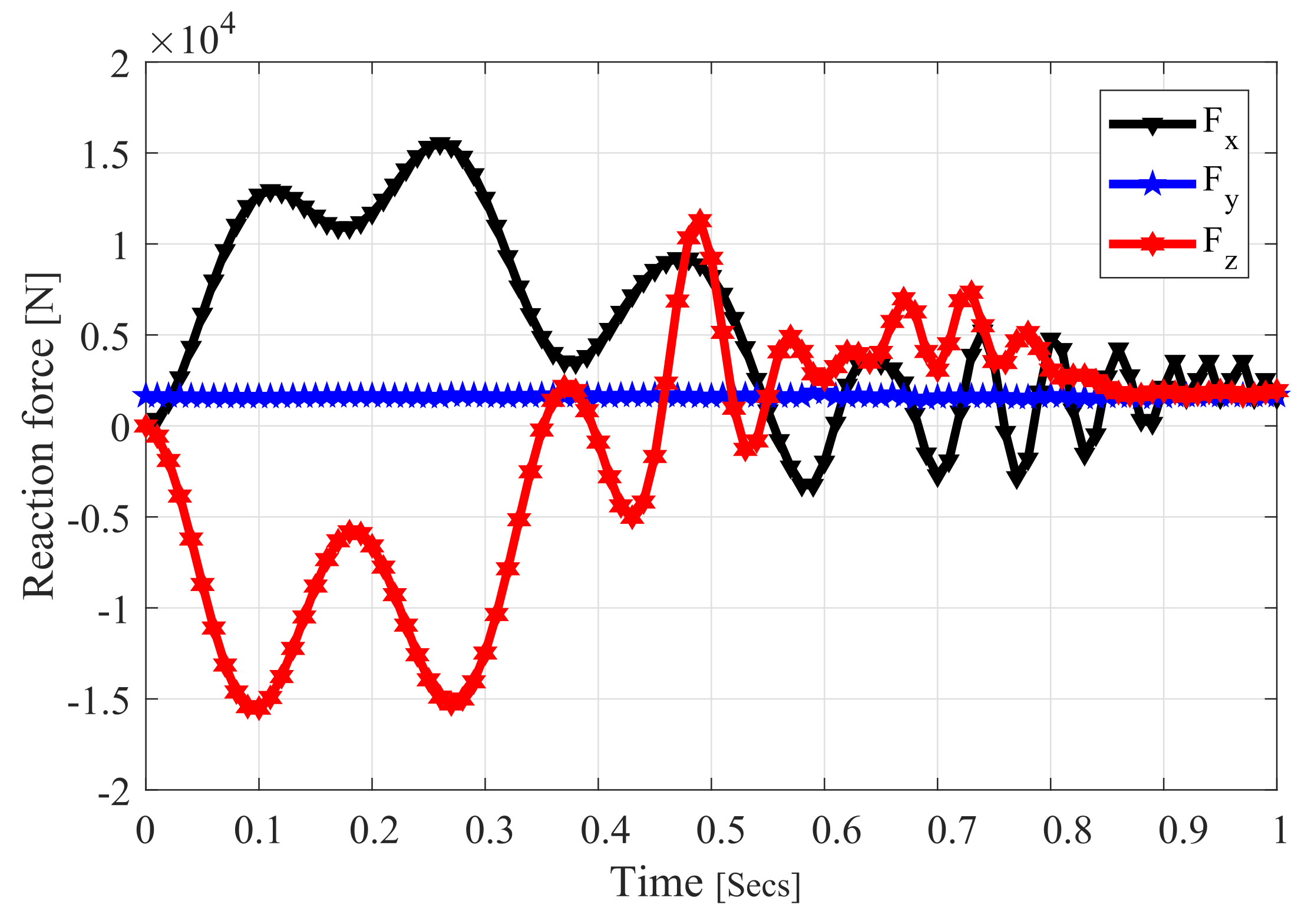
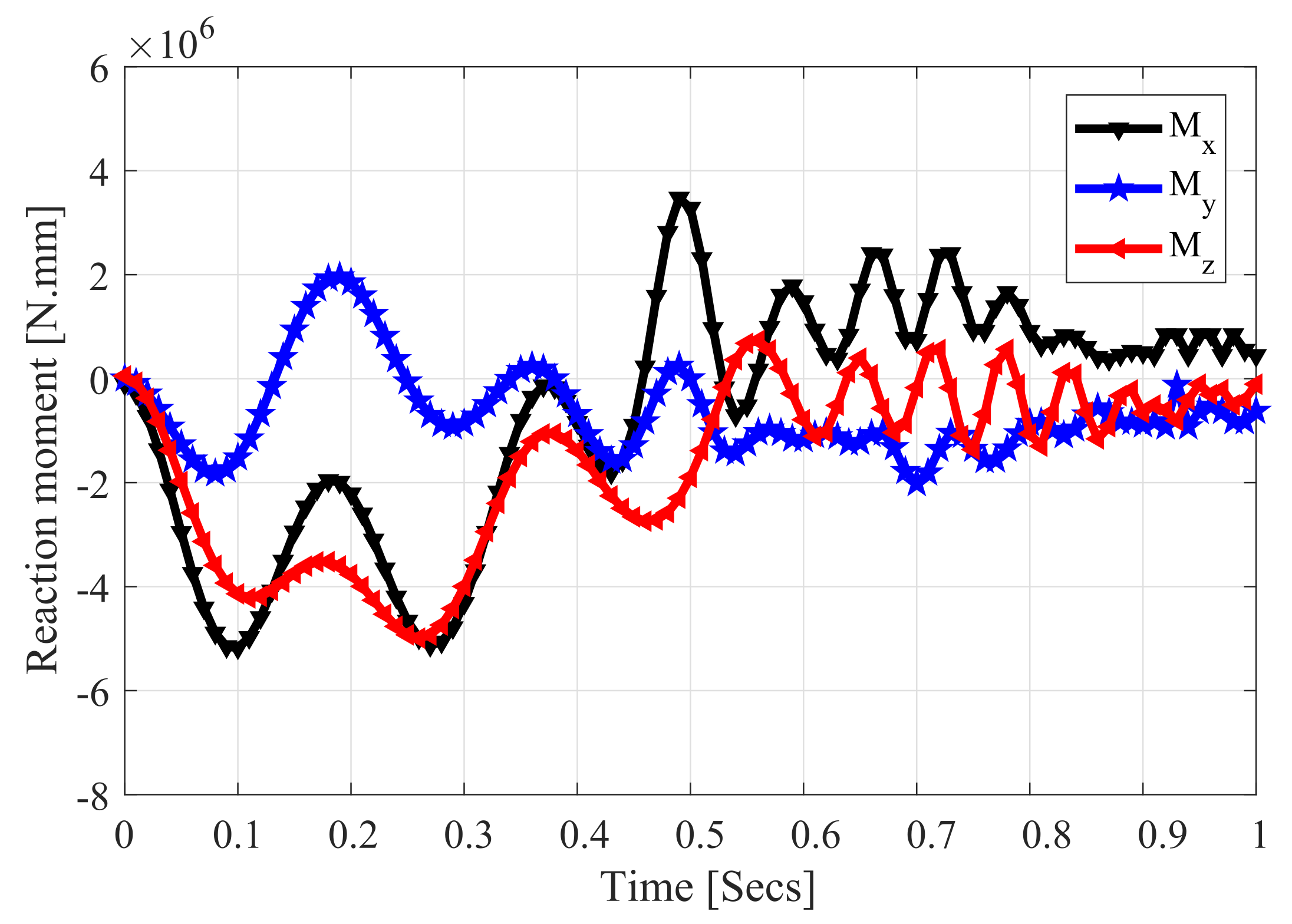



| Joint Type | Body(i) | Body(j) |
|---|---|---|
| Fixed | Grating Base | Ground |
| Prismatic(Z) | Lower plate | Grating Base |
| Prismatic(X) | Upper plate | Lower plate |
| Spherical | Grating mass | Upper plate |
| Fixed | Flexure bodies | Grating mass |
| Fixed | Flexible bodies | Flexure bodies |
| Fixed | Flexible bodies | Grating base |
| Components | Mass (kg) | I(kg.m | I(kg.m | I(kg.m |
|---|---|---|---|---|
| Grating base | 86.34 | 4.92 | 3.64 | 2.8 |
| Disk | 0.15 | 0.000035 | 0.000035 | 0.000018 |
| Disk | 0.11 | 0.000024 | 0.000013 | 0.000013 |
| Grating mass | 78.26 | 1.8 | 1.3 | 0.985 |
| Flexure part | 0.068 | 0.0001 | 0.0001 | 0.0000025 |
| Flexible part | 0.012 | 0.00001 | 0.00001 | 0.00000063 |
| DOF | X (m) | Z (m) | (rad) | (rad) | (rad) |
|---|---|---|---|---|---|
| Displacement | ±1.5 | ±3.00 | ±2.5 | ±1.5 | ±2.5 |
| Properties/Body | Flexible | Flexure |
|---|---|---|
| Mass (Kg) | 0.012 | 0.068 |
| Density (Kg/m) | 8000 | 2810 |
| Elastic Modulus (GN/m) | 193 | 72 |
| Poisson ratio | 0.27 | 0.33 |
| Tensile strength (MN/m) | 5800 | 2200 |
| Yield strength (MN/m) | 1720 | 950 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Q.; Shehata, M.; Nada, A.; Shao, Z. Development of Dynamics for Design Procedure of Novel Grating Tiling Device with Experimental Validation. Appl. Sci. 2021, 11, 11716. https://doi.org/10.3390/app112411716
Bai Q, Shehata M, Nada A, Shao Z. Development of Dynamics for Design Procedure of Novel Grating Tiling Device with Experimental Validation. Applied Sciences. 2021; 11(24):11716. https://doi.org/10.3390/app112411716
Chicago/Turabian StyleBai, Qingshun, Mohamed Shehata, Ayman Nada, and Zhongxi Shao. 2021. "Development of Dynamics for Design Procedure of Novel Grating Tiling Device with Experimental Validation" Applied Sciences 11, no. 24: 11716. https://doi.org/10.3390/app112411716
APA StyleBai, Q., Shehata, M., Nada, A., & Shao, Z. (2021). Development of Dynamics for Design Procedure of Novel Grating Tiling Device with Experimental Validation. Applied Sciences, 11(24), 11716. https://doi.org/10.3390/app112411716









