Abstract
Wind-tunnel experiments are performed to investigate the effects of trailing-edge reattachment on the flutter behaviors of spring-suspended trailing-edge-changeable section models. Different Trailing edges (TE) were fixed at the back of a body to adjust reattachment of the vortex. A laser-displacement system was used to acquire the vibration signals. The relationship between flutter characteristics and TEs that affects the wake mode was analyzed. The results show that the motion of the wake vortex has a certain correlation with the flutter stability of the bridge deck. Limit cycle flutter (LCF) occurs to a section model with a 30° TE, whose amplitude gradually increases as the wind speed increases, and the vibration develops into a hard flutter when the wind speed is 12.43 m/s. A section model with 180 TE reaches a hard flutter when the wind speed is 15.31 m/s, without the stage of LCF. As the TE becomes more and more blunt, the critical wind speed, Us, gradually increases, meaning the flutter stability gradually increases. The results reveal that LCF may still occur to the bridge section with a streamlined front edge, and, in some cases, it also may have a range of wind speeds in which LCF occurs.
1. Introduction
Flutter is a phenomenon of aerodynamic instability caused by the interaction of fluid and the vibration of structure, which was first found on thin wings. The research of wind-induced vibration of bridge decks began in 1940. Tacoma Narrows Bridge of Washington State, USA, which had just been completed and opened to traffic for 4 months, experienced severe torsional vibration under a low-speed wind of 19 m/s. After more than an hour of vibration, the bridge collapsed. Since then, the wind-induced vibration of the bridge decks has been highly reported, and a large number of research results have been obtained after 80 years of continuous in-depth research.
Bleich in 1948 [1] regarded the deck of the truss stiffening beam, commonly used in suspension bridges as a flat plate, and ignored the air force on the hollow truss. It was proposed that the Theodorsen’s unsteady aerodynamic theory [2] can be used to predict the vibration of bridge. However, the critical flutter wind speed, calculated based on Theodorsen’s unsteady aerodynamic theory, is much greater than the wind speed when the Tacoma Narrows Bridge collapsed. Kloppel et al. [3] also used Theodorsen’s function to solve the critical flutter wind speed of the bridge, but for a specific actual bridge section. A reduction factor obtained by wind tunnel tests was introduced to modify the critical flutter wind speed. Scanlan et al. [4] believed that it is difficult to obtain an aerodynamic expression similar to Theodorsen’s function for bridges with bluff-body section. Therefore, it is recommended to use aerodynamic derivatives to establish a small-amplitude, unsteady aerodynamic model of bridges in which the self-excited aerodynamic force of the main girder section of bridges is approximated by a linear function of the two-dimensional section’s motion state vector composed of flutter derivatives, and the determination of the aerodynamic derivatives requires a special wind tunnel test on segment model. The vertical and torsional self-excited aerodynamic force are obtained:
where L and M are the self-excited aerodynamic forces in the vertical and torsional directions of the main girder of the bridge, respectively; , , and 1, 2, 3, 4, are the flutter derivative of the main girder; ρ is the density of air; B is the width of the bridge; U is the average wind speed; K is the converted frequency, , where ω is the circular frequency; h and α are the displacements in the vertical and torsional directions respectively; and and are the speeds in the vertical and torsional directions respectively. Since all the motion parameters that have an influence on the self-excited aerodynamic force are considered, this method has strong universality. Therefore, Scanlan’s flutter theory has been widely used in the design of the flutter stability of bridge structures and has become a classic theory of bridge flutter. In the research of the mechanism of aerodynamic coupling of flutter, Matsumoto et al. [5,6,7] proposed the use of step-by-step analysis to analyze bridge flutter. This method divides the analysis of flutter into torsional branch and vertical branch. In each branch, the coupling effects of torsion and vertical motion are considered separately. Not only can the change in system’s damping and frequency with wind speed be obtained, but it can also reflect the role of an aerodynamic derivative in the change of vibration characteristics and the flutter derivatives’ impact on a system’s damping. Based on Scanlan’s linear flutter theory, Bartoli et al. [8] proposed an approximate method to calculate the critical wind speed and frequency of flutter by the analysis of a large number of dynamics and aerodynamics data, which only requires three flutter derivatives (, , and ) or two flutter derivatives ( and ) to perform the calculation, and greatly simplifies the approximate calculation of critical wind speed and frequency of flutter. It is suitable for bridges with the section whose bending-torsion coupling is only affected by the shape of a structural mode or a higher mode, but it cannot completely replace more accurate analysis methods. Lee et al. [9] started by simplifying the coefficients in the third and fourth degree polynomials of ω, derived from the singular condition of the frequency matrix. Under the quasi-steady assumption, they proposed an approximate formula for calculating the flutter of the aeroelastic system. The critical wind speed of flutter of long-span bridges can be estimated well within the range of bending-torsion coupling, and the calculation result fits well with the results of the wind tunnel test. The rapid and approximate calculation of bridges’ flutter stability helps to better understand the mechanism of flutter and represents the first step towards a simple engineering tool, which is also of great significance for speeding up the design process of bridges.
Researchers found in wind tunnel tests that when the model has a large wind attack angle, or the bridge’s deck cross section is a blunt-body section, there will be no obvious divergent flutter, but large-amplitude and limiting-amplitude vibration, called soft flutter, which is also known as limit cycle flutter (LCF) may occur. Correspondingly, the divergent flutter is called hard flutter [10,11,12]. Ying et al. [13] used a fluid-structure-coupling model to numerically simulate the aeroelastic response of the bridge deck and verified it with the theoretical solution of the flutter response of a thin plate. It is proposed that the increase in the wind attack angle makes the bridge deck more prone to LCF; the stable amplitude of LCF has nothing to do with the initial excitation, and the increasing the damping of structure can significantly increase the critical wind speed of LCF of the bridge, but it has little effect on the vibration frequency. Gao et al. [14] analyzed the nonlinear aeroelastic behavior of a typical passivated bridge section (that is, the bridge deck with double-sided guardrails opened) through a series of LCF tests of the Spring-Suspended Sectional Model (SSSM). A model of self-excited nonlinear force suitable for large-amplitude vibration is proposed, and its forecast results are compared with experimental results. The identified aerodynamic parameters further indicate that the mechanism of LCF is due to the negative aerodynamic damping provided by the linear term as the energy source to drive the increase in vibration amplitude and the nonlinear positive aerodynamic damping provided by the third-order angular velocity. In the tested wind speed range, the observed stable LCF amplitude increased linearly with the decrease in wind speed. Zhang et al. in 2017 [15] researched the flutter characteristics of streamlined bridge decks by using a comprehensive wind tunnel test and introduced a nonlinear mathematical model to simulate the aeroelastic behavior of nonlinear torsional flutter. It was found that nonlinear aerodynamics are the main source of nonlinear vibration. Based on the instantaneous amplitude and instantaneous frequency calculated by the normalized Hilbert transform, a system identification method was developed to extract linear and nonlinear aerodynamic parameters at the same time. On this basis, Zhang et al., in 2019, [16] simulated an LCF process of the bridge based on computational fluid dynamics (CFD) and analyzed the energy input in this process. The results show that only the first-order component of the self-excited force contributes significantly to the energy input of LCF of the bridge deck, while the influence of the higher-order force component is negligible, which means considering only the first-order component of the self-excited nonlinear force can well predict the displacement response of LCF of the bridge deck.
The self-excited aerodynamic force is sensitive to the aerodynamic shape, which means a small change in the aerodynamic shape may cause a huge change in aerodynamic force. Researchers have conducted in-depth research on the influence of aerodynamic shape on the flutter performance of bridges. Larsen [17] researched in detail the influence of aerodynamic components—such as railings and wind screens—on the critical wind speed of flutter by a series of wind-tunnel tests of the Great Belt Bridge in Denmark, including tests of a section model, a taut strip model and a full bridge model. The result provides reliable advice for the design and maintenance of the Great Belt Bridge. Bruno et al. [18] investigated the influence of deck equipment of bridges—such as middle divider, edge safety barrier, and guardrail—on the aerodynamic performance of bridges. Using numerical simulations with and without barriers, such members’ noticeable effect on the analysis bridge aerodynamics is demonstrated. The simulation results are compared with each other and then compared with wind-tunnel-test results, showing that bridge deck equipment cannot be ignored in bridge aerodynamic analysis because the existence of barriers increases the overall degree of bluffness of the section. Wilde et al. [19] used control flaps attached to the edge of the bridge deck to aerodynamically control the wind-induced instability of long-span bridges. It is proposed that the control system whose flap rotation center is located at the edge of the deck is the most effective, which can provide satisfactory aerodynamic damping and has sufficient stability. Lin et al. [20] investigated the influence of cross-section geometry and oncoming turbulence on the flutter of cable-supported bridges through wind-tunnel tests on multiple section models, under different flow conditions and subsequent flutter analysis. The results show that the width-to-depth ratio of the bridge deck plays an important role in the aerodynamic performance of the bridge. Increasing the width-to-depth ratio and the flatness of the bridge deck can improve the flutter stability of the bridge deck. In addition, the greater the intensity of turbulence, the greater the flutter stability of the bridge deck, which means the turbulence tends to enhance the flutter stability of the bridge. Based on the nonlinear aerodynamic stability analysis, Zhang et al. [21] conducted parametric studies on the Runyang bridge over the Yangtze River to investigate the effects of some design parameters on the aerodynamic. It was proposed that depth of the deck has an important effect on the aerodynamic stability of the bridge.
Based on Scanlan’s flutter theory, it is difficult to obtain the aerodynamic characteristics of a specific flow pattern and the flutter behavior caused by it, which play an important role in the design of bridge sections with higher flutter stability. Based on the basic theories of fluid mechanics and fluid-structure interaction, this paper carried out wind-tunnel experiments to investigate the effect of wake flow on the flutter stability of bridge decks.
2. Experiment Setup
The tests were performed in a blow-down wind tunnel at the Joint Laboratory of Wind Tunnel and Wave Flume, Harbin Institute of Technology, China, and the panoramic view of the wind tunnel is shown in Figure 1. The test section is 1150 mm long and has a cross-sectional area of 450 mm × 450 mm. The wind speed in the test section can be adjusted within the range of 1–30 m/s, and the turbulence of the incoming flow is lower than 0.6%, which meets the test requirements.

Figure 1.
Wind tunnel.
2.1. Model Details
As is shown in Figure 2, the overall aspect ratio of the model is 1:10, the height H is 20 mm, the width B is 200 mm, and the axial length is 430 mm. In order to study the effect of wake flow on the flutter stability of the bridge, the streamlined front edge (FE), whose section is an isosceles triangle with an apex angle of 30°, is used to reduce the separation of flow at the FE of the model. For the FE, rounded corners are used in the transition section to minimize the separation here, which is illustrated in Figure 2c. For the trailing edge (TE), a different apex angle, β, is configured to construct TEs with different degrees of streamline to obtain different wake flow. In this paper, five cases of apex angle of the TE β, from 30° to 180° (β = 30°, 45°, 60°, 90°, 180°), were studied to investigate the effects of wake flow on the flutter stability of bridge decks, using β to quantify the effects of wake flow. The details of the section are shown in Figure 2b. The test model consists of three parts: one FE, five TEs, and a foundation deck. Since the mass of the FE and TE is not negligible relative to the mass of the entire model, simply designing the TE with different shapes will cause the model of bridge deck to be seriously off-center, which may cause large errors in the test results. In order to reduce this error as much as possible, masses are added at appropriate locations inside the TE, so that the mass of each TE and moment of inertia of each TE relative to the center axis of the bridge deck are nearly equal to that of the FE (±3% theoretically). The perspectives of the FE and 5 TEs are shown in Figure 2d. Each part is made of resin material through 3D printing technology. Unfortunately, due to the limitations of 3D printing technology, the error mentioned above may be magnified. The overall rigidity of the foundation bridge deck is guaranteed by a model shell with a thickness of at least 3 mm and 3 steel bars fixed inside, and the overall rigidity of the TE and FE is guaranteed by a model shell with a thickness of at least 2 mm and the internal mass block.
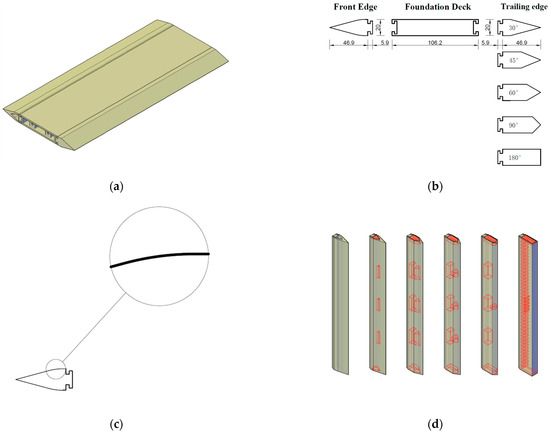
Figure 2.
Details of the test model. (a) Overview test model (case 30c-30). (b) Cross section. (c) Details about FE. (d) Details about the masses added inside TE.
A test model was installed in the test section of the wind tunnel through a spring suspension system. As shown in Figure 3, the test model is elastically supported by eight springs of equal stiffness. The tests of free vibration were performed on the five cases to obtain their natural frequency. The vertical and torsional natural frequency between each case, and , are basically equal, 2.6 Hz and 5.0 Hz, respectively. fv and ft, representing the vertical and torsional damping ratio, respectively, are both less than 0.2%, and the details of the model’s dynamic characteristics are shown in Table 1. The blockage ratio is 4.25%.
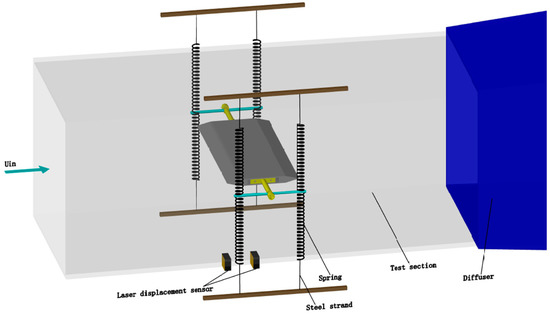
Figure 3.
The setup of the vibration system. The steel strand is tightened by bolts. The model of bridge deck is placed in the center of the test section.

Table 1.
The dynamic characteristics of model.
2.2. Measurement Details
As mentioned above, five cases of β were studied to explore the effects of wake flow on the flutter characteristics of bridge decks. The model was installed in the test section of the wind tunnel through the spring suspension system, the wind speed, Uin, was gradually increased to the model’s critical wind speed of flutter, and the laser-displacement system was used to collect the displacement response of the model. The laser-displacement system includes two IL-100 sensors produced by Keyence, USB-6288 produced by National Instruments, and a personal computer. The sampling frequency for all tests is 1000 Hz. The torsional and vertical responses are calculated as follows:
where and are the displacement signals collected by the laser-displacement system; d is the distance between two measure points; x is the vertical displacement of the deck model; and is the torsional displacement of the deck model in radians.
3. Results and Discussions
3.1. Dynamic Response of Flutter with Different Trailing Configurations
3.1.1. 30c-30 Case
Figure 4a,b, respectively, show the vertical and torsional vibration of deck model in case 30c-30, where is reduced velocity, . The blue vertical dashed line is used to distinguish several parts in the figure, each part is the continuous displacement response of the model within 10s under the corresponding .
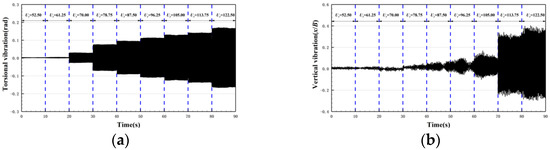
Figure 4.
Time history of displacement of the bridge deck in case 30c-30. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
When , the deck does not vibrate. As , there is an obvious single-frequency vibration in the torsional degree of freedom of the bridge deck, but it is still a multi-frequency and low-amplitude vibration in the vertical degree of freedom. Until , the vibration of the model is a torsional single-frequency LCF. When , a large and stable vibration appears in the vertical degree of freedom of the bridge deck, and its vibration frequency is equal to that of the torsional degree of freedom, which shows vertical and torsional vibrations are completely coupled. As , the vibration of the deck is a bending-torsional coupling LCF. The bridge deck in the 30c-30 case has a wide range of wind speeds in which LCF occurs. When , LCF occurs. Among them, pure torsional single-frequency vibration occurs at lower wind speeds, and when Ur is higher, it develops into bending-torsional coupling vibration.
When , stable and high-amplitude LCF occurs to the bridge deck, and as Ur is increased to 124.25, the LCF develop into hard flutter. Figure 5 shows this process. The amplitudes of the vertical and torsional degrees of freedom gradually increase to divergence.
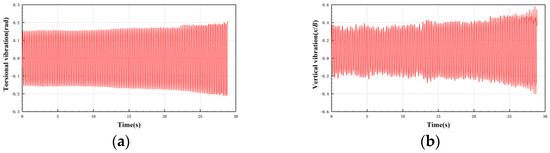
Figure 5.
Time history of vibration divergence in 30c-30 case. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.1.2. 30c-45 Case
As Figure 6 shows, in the case of 30c-45, when , the torsional and vertical vibration of the bridge deck are both multi-frequency and low-amplitude vibration. As Ur is increased to 87.50, the bridge begins to undergo torsional vibration, while the vibration is low-amplitude in the vertical degree of freedom and the effect of static wind is relatively large. When Ur is in the range of 87.50~96.25, there is stable single-frequency vibration on the torsional freedom of the bridge deck, while there are some low frequency components in the vertical degrees of freedom. In terms of vertical degrees of freedom, the effect of static wind takes a larger proportion. The coupling degree of vertical and torsional vibration is low.
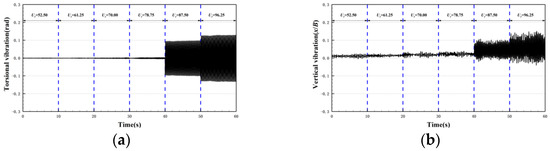
Figure 6.
Time history of displacement of the bridge deck in case 30c-45. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
Figure 7 shows the process of that vibration of bridge deck develops from LCF to hard flutter when Ur is increased from 96.25 to 97.13. There is no stable vibration in the vertical degree of freedom, which means the bridge deck’s vibration is pure torsional vibration during the process of LCF to hard flutter.
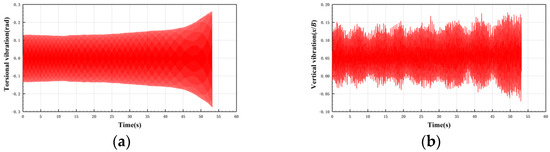
Figure 7.
Time history of vibration divergence in 30c-45 case. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.1.3. 30c-60 Case
In the 30c-60 case, as Figure 8 shows, when , there is multi-frequency and low-amplitude vibration in both vertical and torsional degree of freedom of the bridge deck. As , there is stable large-amplitude vibration in both vertical and torsional degree of freedom of the bridge deck, showing bending-torsional coupling LCF occurs.
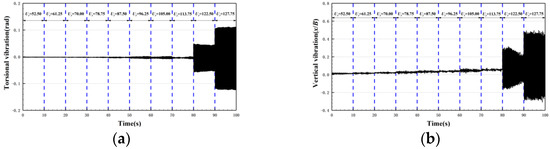
Figure 8.
Time history of displacement of the bridge deck in case 30c-60. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
As Figure 9 shows, when the Ur is increased from 127.75 to 128.63, the vibration is developed from stable LCF to hard flutter. In this process, both vertical degree of freedom and torsional degree of freedom have large amplitudes, and both have trend of divergence.
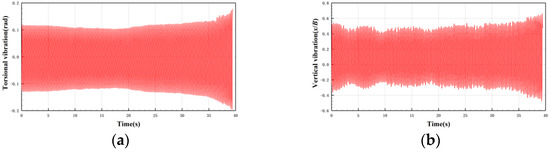
Figure 9.
Time history of vibration divergence in 30c-60 case. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.1.4. 30c-90 Case
As for the 30c-90 case, when , there is no obvious vibration observed on the bridge deck, which can be seen from Figure 10. When Ur is increased to 140.00, large-amplitude and bending-torsion coupling LCF occurs to the bridge deck. The amplitude is greatly increased compared to the case of . The vibration frequency of the vertical degrees of freedom and the torsional degrees of freedom are equal, indicating that the vibrations of the two degrees of freedom are completely coupled.
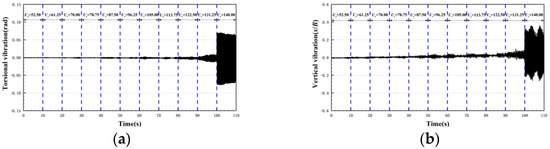
Figure 10.
Time history of displacement of the bridge deck in case 30c-90. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
As increased from 140.00 to 140.88, the amplitude of the bridge deck gradually diverged, which is shown in Figure 11. In this process, both vertical degree of freedom and torsional degree of freedom have a trend of divergence.
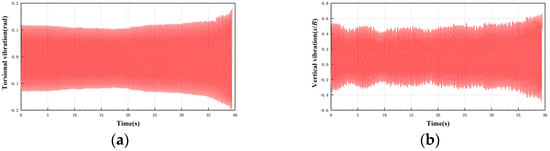
Figure 11.
Time history of vibration divergence in 30c-90 case. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.1.5. 30c-180 Case
In the 30c-180 case, as is shown in Figure 12, when , there is no obvious vibration occurring in the model. As Figure 13 shows, when is increased from 148.75 to 153.13, hard flutter occurs, instead of LCF first. Both vertical degrees of freedom and torsional degrees of freedom have obvious trends of divergence, and their vibration frequencies are equal.
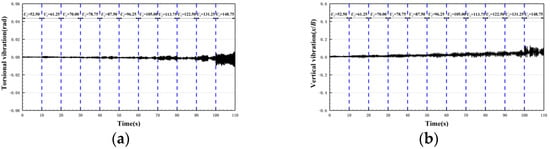
Figure 12.
Time history of displacement of the bridge deck in case 30c-180. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
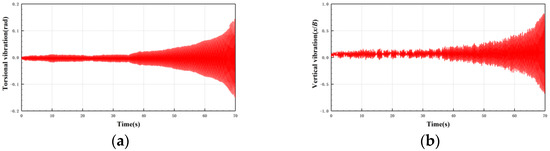
Figure 13.
Time history of vibration divergence in 30c-180 case. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.2. Frequency Domain Analysis
Figure 14 shows the vibration frequency of the model at different wind speeds in each case. It should be noted that the vibration frequency mentioned above is the frequency corresponding to the vibration mode with the highest amplitude.
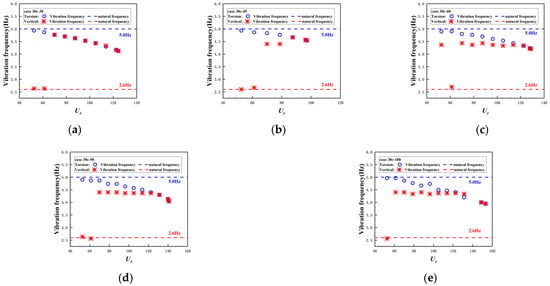
Figure 14.
Vibration frequency of each case. (a) 30c-30 case; (b) 30c-45 case; (c) 30c-60 case; (d) 30c-90 case; and (e) 30c-180 case.
As Figure 14 shows, as the wind speed increases, the vibration frequency of the vertical degree of freedom shows an upward trend, and the vibration frequency of the torsional degree of freedom shows a downward trend. It is most interesting that the torsional vibration frequency has continuous change regularities, however, the vertical vibration frequency exists as a mutation phenomenon and is attracted by the torsional vibration frequency. As the wind speed continues to increase, the main frequency of vertical vibration is equal to the torsional frequency, indicating that the vertical vibration and torsional vibration begin to couple. Since then, as the wind speed continues to increase, the vibration frequency of the model, which is the common frequency of vertical and torsional vibration, continues to decrease.
3.3. Wavelet and Hilbert Analysis
The flutter characteristics of the model are analyzed by the wavelet transform and Hilbert transform [22,23]. Since the 30c-30 case has a wide range of LCF wind speeds, and hard flutter directly takes place in the 30c-180 case when is increased from 148.75 to 153.13, the two cases are analyzed below.
The wavelet transform is performed on the vibration time history. Figure 15 shows the frequency domain distribution of the vibration of the model in case 30c-30 at each moment when . It can be seen that the frequency of vibration is mainly concentrated in the range of 4.0 to 5.0. The distribution of torsional vibration in the frequency domain is very stable, while that of vertical vibration changes more obviously with time. Figure 16 shows the distribution in the frequency domain of the vibration of the model in case 30c-180 at each moment after is increased from 148.75 to 153.13. As time passes, the frequency band of vibration in both the torsional and vertical degrees of freedom gradually widens and the amplitude gradually increases. In addition, during the period when the model vibrates obviously, the frequency band of torsional vibration is wider than that of vertical vibration.
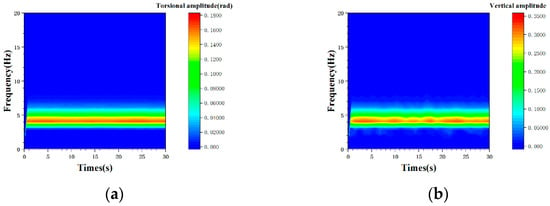
Figure 15.
Distribution of vibration in case 30c-30 when is 122.5. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
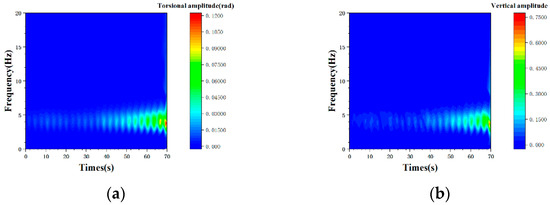
Figure 16.
Distribution of vibration in case 30c-30 when is increased from 148.75 to 153.13. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
The Hilbert transform is used to obtain the phase trajectory in phase plane. The plane composed of the vibration displacement as the abscissa and the vibration velocity as the ordinate is called the phase plane, and the curve formed by the points corresponding to the system motion state on the plane is called the phase trajectory. Figure 17 shows the phase trajectory of case 30c-30 when is 113.75 and 122.50. There are relatively stable rings in the vertical and torsional degrees of freedom, and the higher the wind speed, the larger the ring. The torsional vibration ring is thinner than that of vertical vibration, indicating that the torsional vibration is more stable. Figure 18 shows the phase trajectory of the model in different time periods in case 30c-180 when is increased from 148.75 to 153.13, where the time origin is the moment when the measurement starts. It can be seen that the phase trajectory continuously expands outwards on the counterclockwise direction. With the passage of time, the width of the phase trajectory within the same length of time gradually increases, indicating that the divergence speed of vibration gradually increases.
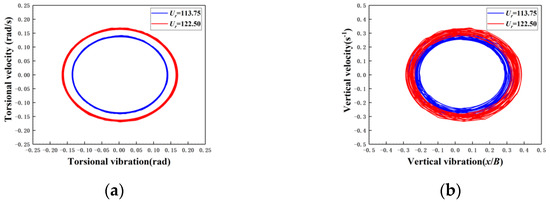
Figure 17.
Phase trajectory of case 30c-30 under different wind speeds. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
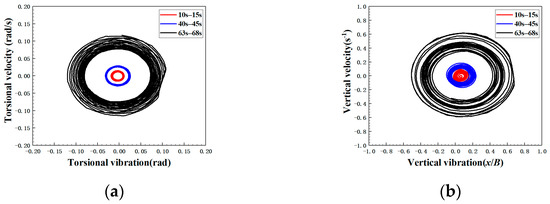
Figure 18.
Phase trajectory of case 30c-180 in different time periods when is increased from 148.75 to 153.13. (a) Torsional degree of freedom; and (b) vertical degree of freedom.
3.4. Phase Lag between Torsional and Vertcial Vibration
In order to investigate the coupling characteristics of the vertical and torsional degrees of freedom when the bridge deck vibrates, the amplitude ratio of torsional vibration to vertical vibration, and the phase difference between the torsional degrees of freedom , and the vertical degrees of freedom when bending-torsional coupling flutter occurs are analyzed.
The amplitude ratio of torsional vibration to vertical vibration is calculated as follows:
Figure 19 shows the amplitude ratio of torsional vibration to vertical vibration at various apex angles of the trailing edge. It can be found that the torsional vibration dominates the bending-torsional coupling system in case 30c-45, where the amplitude ratio of torsional vibration to vertical vibration is 5.96, and then amplitude of vertical vibration gradually increase as the trailing edge becomes blunter. At case 30c-180, the amplitude ratio of torsional vibration to vertical vibration is 0.65.
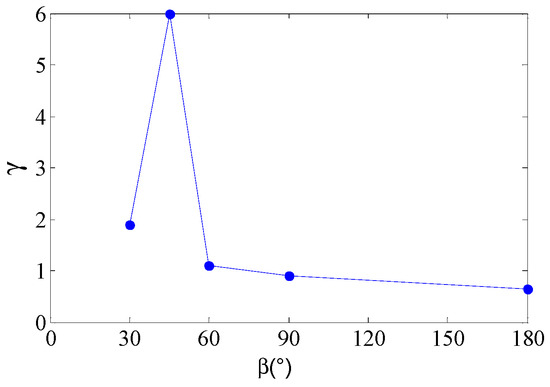
Figure 19.
The amplitude ratio of torsional vibration to vertical vibration at various apex angles of the trailing edge.
The phase difference between torsional vibration and vertical vibration is calculated as follows:
where is phase difference, is the cross-power spectrum, and is the coupling vibration frequency.
Figure 20 shows the phase difference between torsional vibration and vertical vibration at various apex angles of the trailing edge. For the 30c-30, 30c-45, 30c-60, 30c-90, and 30c-180 cases, the vertical vibration lags behind the torsional vibration by −3.8, 33.5, −7.8, −12.6, and −17.2 degrees, respectively. Except in the case 30c-45, the phase gradually decreases (gradually moves away from 0 degrees) as the trailing edge becomes blunter.
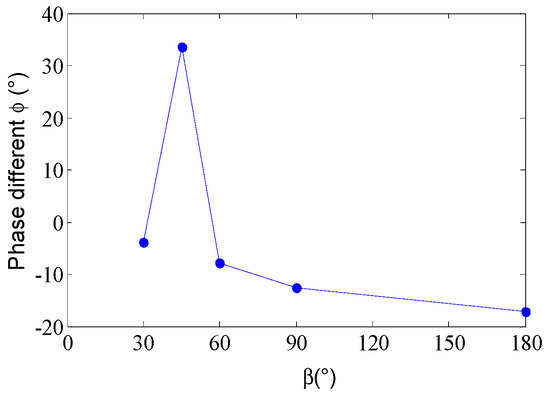
Figure 20.
The phase difference between torsional vibration and vertical vibration at various apex angles of the trailing edge.
3.5. Discussion of Effect of TE
Figure 21 and Figure 22 show the variation of deck vibration amplitude with wind speed. In order to clearly reflect the vibration characteristics of the bridge deck in each case, the amplitude of the non-divergent vibration is calculated using the average amplitude within 30 s, and the amplitude of the hard flutter is expressed by the maximum amplitude during the vibration process. The flutter stability of the bridge deck increases with the increase in the β except in case 30c-45. Similar to the torsional amplitude, except in case 30c-45, the critical flutter wind speed on the vertical degree of freedom increases gradually with the increase in the angle of the TE β.
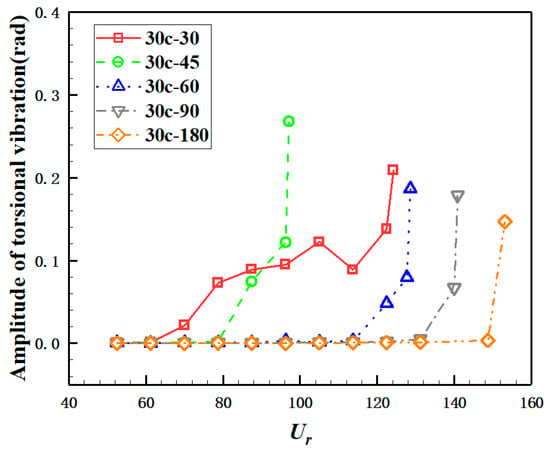
Figure 21.
Torsional amplitude changes with .
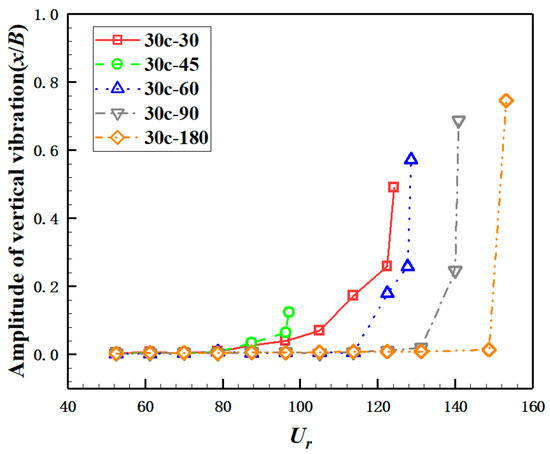
Figure 22.
Vertical amplitude changes with .
Next, this paper compares and analyzes the critical wind speed when the bridge deck starts to vibrate , the LCF wind speed range , and the critical wind speed of the hard flutter vibration . Figure 23 shows curves of , , and followed by the change in β. Among them, gradually increases with the gradual increase in β while the curve of and changing with β drops at , and then gradually increase as β increases. It shows that when , the increase in β has a significant inhibitory effect on flutter, which means the more blunt the TE of the bridge deck, the stronger the flutter stability. In this paper, the value of is used to describe the streamline performance of the TE. Figure 24 shows the change of streamline performance with β. It can be seen that the absolute value of the slope of the curve gradually decreases with the increase in the β. That means the decreasing speed of streamline performance of the TE gradually decreases, which is basically consistent with curves in Figure 23 when . The streamline performance of the TE has obvious correlation with the flutter characteristics and flutter stability of the bridge deck, while the streamline performance of the TE has a direct impact on the vortex in the wake region. The poorer the streamline performance of the TE is, the more complicated the distribution and movement of the vortex structure in the wake area will be, which means the distribution and motion law of the vortex in the wake area have an important influence on the flutter characteristics and flutter stability of the bridge deck.
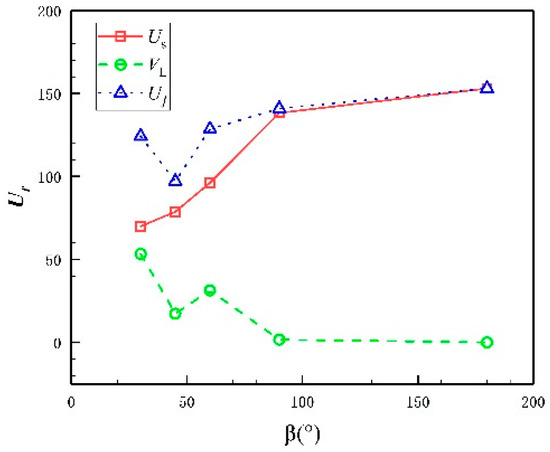
Figure 23.
The flutter characteristics of each case.
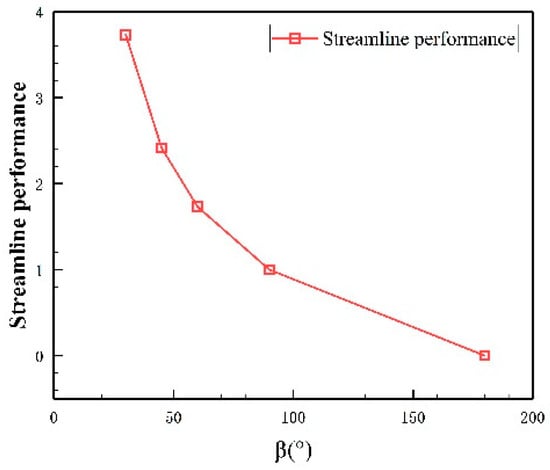
Figure 24.
The relationship between streamline performance of the TE and .
As for 30c-45 (), the flutter characteristics of the model are quite different from other conditions. First, during the process of fluttering, there is basically no vibration in the vertical degree of freedom, which indicates until hard flutter develops, the vertical and torsional vibrations of the model are still not completely coupled. Secondly, when , as β increases, will gradually increase and will gradually decrease, while and . The specific reasons need to be further experimentally studied.
4. Conclusions
In this paper, by changing the aerodynamic shape of the TE of the model, the flow pattern of the model wake is controlled, and the displacement response of the model under different wind speeds and different TEs is collected by laser displacement sensors, and then the effect of different wake flow patterns on flutter characteristics and the flutter stability of the bridge deck is studied. The vibration response of the segment model under different TEs and different incoming wind speeds is compared and analyzed, after which the flutter characteristics of the segment model with different TEs are analyzed, and the following conclusions are drawn:
- (1)
- Limit cycle flutter may still occur in the bridge section with a streamlined front edge and, in some cases, it also has a wider limit cycle flutter wind speed range.
- (2)
- When the bending-torsional coupling flutter is fully developed, the torsional degree of freedom slightly lags behind the vertical degree of freedom.
- (3)
- As the trailing edge becomes more and more blunt, the critical wind speed Us gradually increases, and the flutter stability gradually increases. The wake vortex motion has a certain correlation with the flutter stability of the bridge deck.
Author Contributions
Conceptualization, S.L.; methodology, J.F. and S.L.; experiments, B.W., J.F. and S.L.; software, J.F.; validation, J.F.; formal analysis, J.F. and S.L.; investigation, J.F., B.W. and S.L.; resources, S.L.; data curation, J.F. and S.L.; writing—original draft preparation, J.F.; writing—review & editing, J.F. and S.L.; supervision, S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study is financially supported by the NSFC under Grant No. 51878230, Natural Science Foundation of Heilongjiang Province under Grant No. YQ2021E033, Postdoctoral scientific research development fund of Heilongjiang Province under Grant No. LBH-Q20021 and supported by Heilongjiang Touyan Team and Fundamental Research Funds for the Central Universities.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bleich, F. Dynamic instability of truss-stiffened suspension bridges under wind action. Trans. Am. Soc. Civ. Eng. 1948, 114, 1177–1222. [Google Scholar] [CrossRef]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; NACA Report No. 496; National Aeronautics and Space Administration: Washington, DC, USA, 1935; pp. 291–311.
- Kloppel, K.; Thiele, F. Modellversuche im Windkanal zur Bemessung von Brucken gegen die Gefahr winderregter Schwingungen. Stahlbau 1967, 32, 353–365. [Google Scholar]
- Scanlan, R.H.; Tomko, J.J. Airfoil and Bridge Deck Flutter Derivatives. J. Eng. Mech. Div. 1971, 97, 1717–1737. [Google Scholar] [CrossRef]
- Matsumoto, M.; Kobayashi, Y.; Shirato, H. The influence of aerodynamic derivatives on flutter. J. Wind Eng. Ind. Aerodyn. 1996, 60, 227–239. [Google Scholar] [CrossRef]
- Matsumoto, M.; Daito, Y.; Yoshizumi, F.; Ichikawa, Y. Torsional flutter of bluff bodies. J. Wind Eng. Ind. Aerodyn. 1997, 69, 871–882. [Google Scholar] [CrossRef]
- Matsumoto, M.; Matsumiya, H.; Fujiwara, S.; Ito, Y. New consideration on flutter properties based on step-by-step analysis. J. Wind Eng. Ind. Aerodyn. 2010, 98, 429–437. [Google Scholar] [CrossRef] [Green Version]
- Bartoli, G.; Mannini, C. A simplified approach to bridge deck flutter. J. Wind Eng. Ind. Aerodyn. 2008, 96, 229–256. [Google Scholar] [CrossRef]
- Lee, H.; Vu, T.; Yoo, S.; Lee, H.Y. A Simplified Evaluation in Critical Frequency and Wind Speed to Bridge Deck Flutter. Procedia Eng. 2011, 14, 1784–1790. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Application of the dynamic mode decomposition to experimental data. Exp. Fluids 2011, 50, 1123–1130. [Google Scholar] [CrossRef]
- Wu, T.; Kareem, A.; Ge, Y. Linear and nonlinear aeroelastic analysis frameworks for cable-supported bridges. Nonlinear Dyn. 2013, 74, 487–516. [Google Scholar] [CrossRef]
- Amandolese, X.; Michelin, S.; Choquel, M. Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel. J. Fluids Struct. 2013, 43, 244–255. [Google Scholar] [CrossRef] [Green Version]
- Ying, X.; Xu, F.; Zhang, M.; Zhang, Z. Numerical explorations of the limit cycle flutter characteristics of a bridge deck. J. Wind Eng. Ind. Aerodyns. 2017, 169, 30–38. [Google Scholar] [CrossRef]
- Gao, G.; Zhu, L.; Han, W.; Li, J. Nonlinear post-flutter behavior and self-excited force model of a twin-side-girder bridge deck. J. Wind Eng. Ind. Aerodyn. 2018, 177, 227–241. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Ying, X. Experimental Investigations on the Nonlinear Torsional Flutter of a Bridge Deck. J. Bridge Eng. 2017, 22, 04017048. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, F.; Zhang, Z.; Ying, X. Energy budget analysis and engineering modeling of post-flutter limit cycle oscillation of a bridge deck. J. Wind Eng. Ind. Aerodyn. 2019, 188, 410–420. [Google Scholar] [CrossRef]
- Larsen, A. Aerodynamic aspects of the final design of the 1624 m suspension bridge across the great belt. J. Wind Eng. Ind. Aerodyn. 1993, 48, 261–285. [Google Scholar] [CrossRef]
- Bruno, L.; Mancini, G. Importance of Deck Details in Bridge Aerodynamics. Struct. Eng. Int. 2002, 12, 289–294. [Google Scholar] [CrossRef]
- Wilde, K.; Omenzetter, P.; Fujino, Y. Suppression of bridge flutter by active deck-flaps control system. J. Eng. Mechan. 2001, 127, 80–89. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Cheng, C.M.; Wu, J.C.; Lan, T.L.; Wu, K.T. Effects of deck shape and oncoming turbulence on bridge aerodynamics. J. Appl. Sci. Eng. 2005, 8, 43–56. [Google Scholar]
- Zhang, X.; Sun, B. Parametric study on the aerodynamic stability of a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2004, 92, 431–439. [Google Scholar] [CrossRef]
- Mariotti, A. Axisymmetric bodies with fixed and free separation: Base-pressure and near-wake fluctuations. J. Wind Eng. Ind. Aerodyn. 2018, 176, 21–31. [Google Scholar] [CrossRef]
- Rocchio, B.; Mariotti, A.; Salvetti, M.V. Flow around a 5:1 rectangular cylinder: Effects of upstream-edge rounding. J. Wind Eng. Ind. Aerodyns. 2020, 204, 104237. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).