The Effects of Aerodynamic Interference on the Aerodynamic Characteristics of a Twin-Box Girder

Abstract

To investigate the aerodynamic characteristics of a twin-box girder in turbulent incoming flow, we carried out wind tunnel tests, including two aerodynamic interferences: leading body-height grid, and leading circular cylinder. In this study, the pressure distribution and the mean and fluctuating aerodynamic forces with the two interferences are compared with bare deck in detail to investigate the relationship between aerodynamic characteristics and the incoming flow characteristics (including Reynolds number and turbulence intensity). The experimental results reveal that, owing to the body-height flow characteristics around the deck interfered with by the body-height grid, the disturbed aerodynamic characteristics of the twin-box girder differ considerably from those of the bare twin-box girder. At the upstream girder, due to the vortex emerging from the body-height grid breaking the separation bubble, pressure plateaus in the upper and lower surface are eliminated. In addition, the turbulence generated by the body-height grid reduces the Reynolds number sensitivity of the twin-box girder. At a relatively high Reynolds number, the fluctuating forces are mainly dominated by turbulence intensity, and the time-averaged forces show almost no change under high turbulence intensity. At a low Reynolds number, the time-averaged forces change significantly with the turbulence intensity. Moreover, at a low Reynolds number, the wake of the leading cylinder effectively forces the boundary layer to transition to turbulence, which reduces the Reynolds number sensitivity of the mean aerodynamic forces and breaks the separation bubbles. Additionally, the fluctuating drag force and the fluctuating lift force are insensitive to the diameter and the spacing ratio.

1. Introduction

In recent decades, super-long-span bridges have been largely designed using the sharp-edged twin-box girder, due to its superior aerodynamic stability, including the Xihoumen Bridge (main span, 1650 m), the Shanghai Yangtze River Bridge (main span, 730 m), and the Stonecutters’ Cable-Stayed Bridge (main span, 1018 m). It is generally acknowledged that the stability of super-long-span bridges is an important indicator that represents the safety of the structures. Super-long-span bridges are often built at sea, where gales often occur, and the aerodynamic forces generated by wind-induced response cannot be neglected. Moreover, the shedding vortices around the box girder induce the vibration behavior, e.g., vortex-induced vibration (VIV). Therefore, the investigation of the aerodynamic performance of the bridge structures by wind tunnel experiment [1,2,3,4] or numerical simulation [5,6,7,8] is necessary in the pre-research stage of bridge construction. However, the wind tunnel experiments usually examine the bridge section model under uniform inflow conditions, and the aerodynamic characteristics obtained under these conditions are used to represent the aerodynamic characteristics of the bridge, which cannot completely accommodate the dynamic complexity of the structures in the real engineering application environment. The bridge structure is not simply affected by uniform inflow in a natural environment, and the turbulent components usually exist in the incoming flow. For instance, the incoming flow may pass through other structures to reach the bridge deck, so the flow around the windward side of the bridge structure is in the wake of other structures, and is usually unstable, with a large fluctuation velocity component. Therefore, it is necessary to study the flow characteristics of the bridge structure under different incoming flow characteristics.

Recently, the effect of the turbulent components of incoming flow on the aerodynamic performance of bluff bridge sections has fascinated many researchers, and triggered many experimental investigations to discern the effects of the incoming flow characteristics on the bridge. Zhou et al. [9] investigated the effects of the vertical turbulence intensity of incoming flow on the aerodynamic performance of a bridge. The authors claimed that the increase in the vertical turbulence intensity of the incoming flow increases the torsional frequency, and the critical flutter wind speed decreases when the vertical turbulence intensity is 2.84%. Hunt et al. [10] and Sarwar et al. [11] pointed out that the incoming flow with the fluctuation component of long-span bridges is nonlinear with the structural motion, and the turbulence components of incoming flow (such as turbulence intensity and turbulence scale) play a vital role in controlling the aerodynamic characteristics of bridges. Scanlan and Liu [12] experimentally investigated the flutter derivatives of a bridge deck based on the turbulent components of incoming flow, and a new theory was developed, which takes the turbulent components in the incoming flow into account. Haan and Kareem [13] investigated the effects of turbulence on the aero-elastic and self-excited forces of a rectangular prism via experiments. Since turbulence is highly heterogeneous and anisotropic, the self-excited pressure fluctuation, self-excited force, and flutter derivative of a stationary prism are strongly affected by the turbulence. The authors also pointed out that the streamwise position would shift with the increase in turbulence intensity; however, the pressure amplitudes would decrease with a larger turbulence scale. Meanwhile, Matsumoto et al. [14] showed that turbulence can adversely affect the flutter performance of bridges based on experimental results. In recent years, a lot of theoretical models have been developed to evaluate the effects of turbulence on the aerodynamic characteristics of bridges. Chen et al. [15,16] proposed a time-domain approach to predict the aerodynamic response of bridges, and a nonlinear theoretical model was established to analyze the effects of turbulence on the self-excited forces and the flutter performance. Wu and Kareem [17] summarized the latest developments in aerodynamics and aero-elasticity of bluff bodies by turbulent winds. The development of theoretical models of the effects of turbulence on the aerodynamic characteristics of bluff bodies is beneficial in efforts to effectively solve the problem of aerodynamic nonlinear response induced by turbulence. However, to our best knowledge, there is still no effective theoretical model to explain the relationship between the characteristics of incoming flow and the aerodynamic performance of the twin-box girder, because the aerodynamic characteristics of the twin-box girder are highly nonlinear in turbulent flow.

The main objective of this study is to experimentally investigate the influence of different cutting-edge aerodynamic interference methods on the aerodynamic characteristics of a twin-box girder. In the present work, the Xihoumen Suspension Bridge is adopted as a prototype of a twin-box girder to investigate. The turbulence intensity I is adopted to indicate the strength of incoming flow fluctuation, and the aerodynamic characteristics of long-span bridges are generally sensitive to the Reynolds number [18]. Therefore, the comprehensive influence of turbulence intensity and the Reynolds number on the aerodynamic characteristics of the twin-box girder is investigated. The remainder of this paper is organized as follows: In Section 2, the experimental method and geometric details of the twin-box girder are presented. In Section 3, the experimental results of different aerodynamic interferences are described and discussed in detail, including the surface pressure distributions and the time-averaged and fluctuating aerodynamic forces. Finally, conclusions are presented in Section 4.

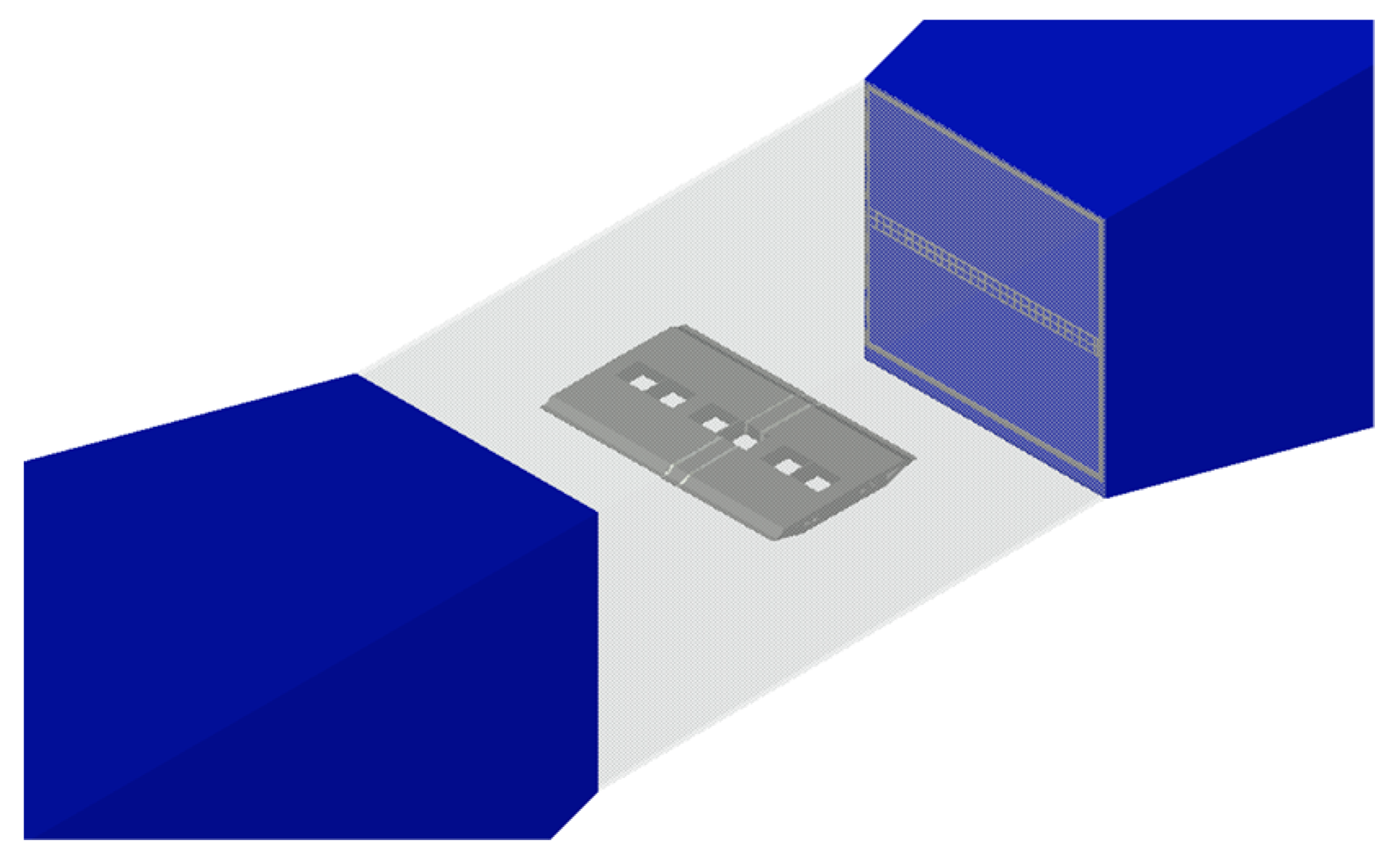
2. Experimental Setup

The experiments were conducted in a closed-loop wind tunnel (SMC-WT1, Harbin Institute of Technology, Harbin, China). With screens and honeycomb installed before the inlet of the test section, the turbulence intensity was less than 0.4% over the speed range of 4–25 m/s. In the test section, the size of the cross-section was 505 mm × 505 mm.

In this study, the Reynolds number (Re) is the ratio of inertial forces to viscous forces, which is an important dimensionless quantity in fluid mechanics, and is defined as:

$$\mathrm{Re}=\frac{\rho UH}{\mu },$$

(1)

where ρ is the density of the fluid; U is the incoming flow velocity; H is the central height of the twin-box girder, which is adopted as the characteristic length; and μ is the dynamic viscosity of the fluid. Since the present work was conducted in a conventional atmospheric boundary layer wind tunnel, the variation in the Reynolds number was achieved by adjusting the wind speed.

The turbulence intensity is an effective indicator that is associated with the turbulent kinetic energy (TKE), and it can be written as:

$$I=\frac{u^{\prime }}{\overline{U}}=\frac{\sqrt{\frac{1}{3}({u^{\prime }}_x{}^2+{u^{\prime }}_y{}^2+{u^{\prime }}_z{}^2)}}{\sqrt{{\overline{U_x}}^2+{\overline{U_y}}^2+{\overline{U_z}}^2}},$$

(2)

where ${u^{\prime }}_x{}^2$, ${u^{\prime }}_y{}^2$, and ${u^{\prime }}_z{}^2$ are the root mean square of the turbulence velocity fluctuations in the x, y, and z directions, respectively, $\overline{U_x}$, $\overline{U_y}$, and $\overline{U_z}$ are the mean velocity in the x, y, and z directions, respectively, $u^{\prime }$ is the root mean square of the turbulence velocity fluctuations, and $\overline{U}$ is the mean velocity.

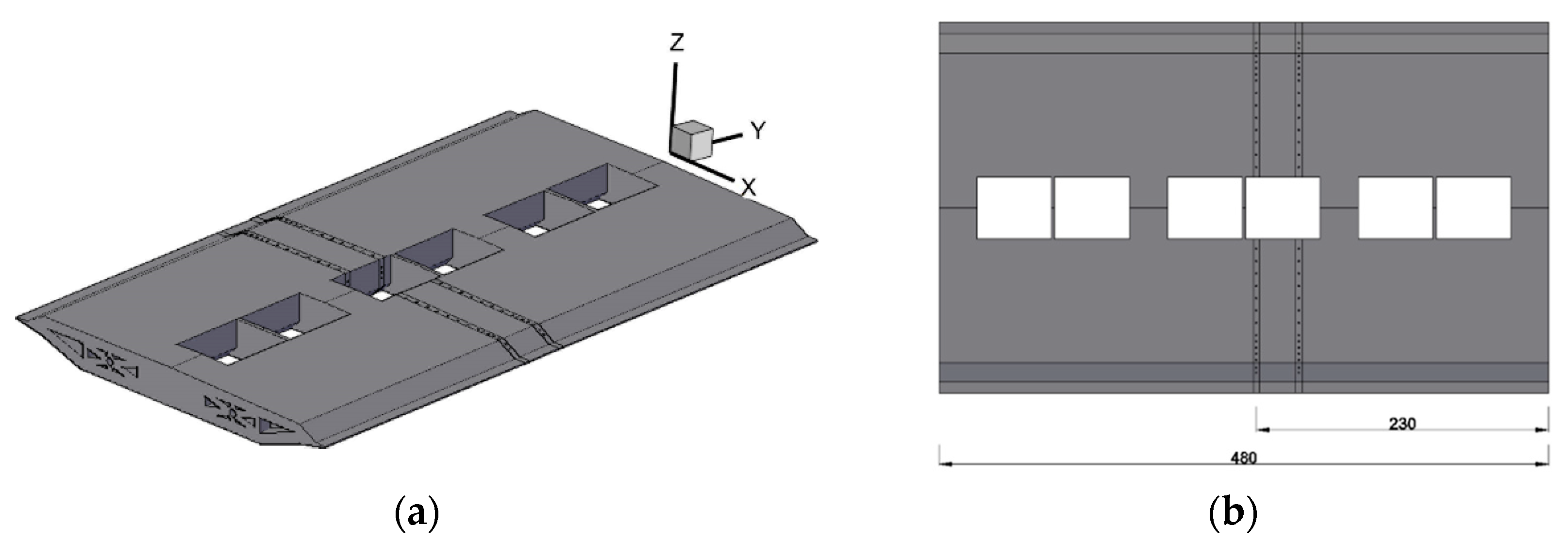
2.1. Section Model Geometrical Information and Surface Pressure Measurements

The detailed geometrical information of the prototype bridge deck is shown in Figure 1. The twin-box girder has two parallel box girders with a gap of length L = 6 m and width B = 36 m, and the center height of the deck H = 3.51 m. The spanwise length of the section model is L_s = 480 mm, and the geometric scale ratio of the section model is 1:120. Figure 2a shows a 3D sketch of the twin-box girder used in the present study. To obtain the surface pressure distributions, 46 pressure taps with a 0.5 mm radius were installed in the slice, which is 230 mm away from the right end of the bridge deck, as shown in Figure 2b. It should be noted that the experiments on the twin-box girder were stationary in this paper.

The distribution of these taps around the section circumference is illustrated in Figure 3. The pressure taps are connected to three pressure scanners (DSA3217, 16 channels for each scanner) with a measuring range of ±2.5 kPa by using connecting tubes (independent polyvinyl chloride (PVC) tubes, internal diameter of 1 mm) with a full length of 500 mm. This system is adopted to measure and record the instantaneous pressure distributions.

The Scanivalve system monitors the surface pressure data at a sampling rate of 312.5 Hz, and the time length of one sampling period is 32 s. Based on the correction algorithm [19], the distortion effects brought by the connecting tubes—such as amplification factor and phase shift [20]—are quite small and negligible in the surface pressure measurements of this study. The time-averaged pressure coefficient C_p can be calculated by nondimensionalization of the time-averaged pressure p_m, which can be written as:

$$C_p=\frac{p_m}{\frac{1}{2}{\rho }_{air}{U}_{\infty }^2},$$

(3)

$$p_m=\frac{1}{T}{\displaystyle {\int }_0^T\left(p_i-p_{\infty }\right)dt},$$

(4)

where p_i denotes the instantaneous pressure, $p_{\infty }$ is the pressure of the free stream, ${\rho }_{air}$ is the density of air, $U_{\infty }$ is the flow velocity of the free stream, and T is the sample period.

In the present study, the Reynolds number is high (Re > 5 × 10³); hence, the boundary layer around the solid structure becomes turbulent and the pressure drag force dominates the skin drag force [21]. Thus, the pressure drag force is the dominant component of total drag, and the skin friction drag can be neglected.

Once the instantaneous pressure distributions are obtained, the corresponding aerodynamic forces of the bridge girder can be calculated by standard integration, which can be expressed as follows:

$$F_D={\displaystyle \int {\mathit{P}}_{xi}\hspace{0.17em}d{s}_i},$$

(5)

$$F_L={\displaystyle \int {\mathit{P}}_{zi}\hspace{0.17em}d{s}_i},$$

(6)

$$F_m={\displaystyle \int {\mathit{P}}_i{\zeta }_i\hspace{0.17em}d{s}_i},$$

(7)

where P_i is the pressure force, P_xi and P_zi are the pressure force components along the x and z directions, respectively, ds_i denotes the element area, and ζ_i is the moment arm. It should be noted that, when the gap exists, the pressure forces at pressure taps 9–11 and 32–34 should be considered.

The drag force coefficient C_D, the lift force coefficient C_L, and the moment force coefficient C_m are defined as:

$$C_D=\frac{F_D}{\frac{1}{2}{\rho }_{air}{U}_{\infty }^{2}H{L}_s},$$

(8)

$$C_L=\frac{F_L}{\frac{1}{2}{\rho }_{air}{U}_{\infty }^{2}B{L}_s},$$

(9)

$$C_m=\frac{F_m}{\frac{1}{2}{\rho }_{air}{U}_{\infty }^2{B}^2{L}_s},$$

(10)

where F_D, F_L, and F_m are the drag, lift, and moment forces, respectively, and B is the width of the twin-box girder.

Then, the six effective indicators that represent the aerodynamic characteristics of the bridge girder can be obtained, including the mean drag force coefficients (C_{D mean}), the fluctuating drag force coefficients (C_{D rms}), the mean lift force coefficients (C_{L mean}), the fluctuating lift force coefficients (C_{L rms}), the mean moment force coefficients (C_{m mean}), and the fluctuating moment force coefficients (C_{m rms}). It should be noted that the root mean square of the specific value is adopted to represent the fluctuation.

2.2. Aerodynamic Interference Measurements

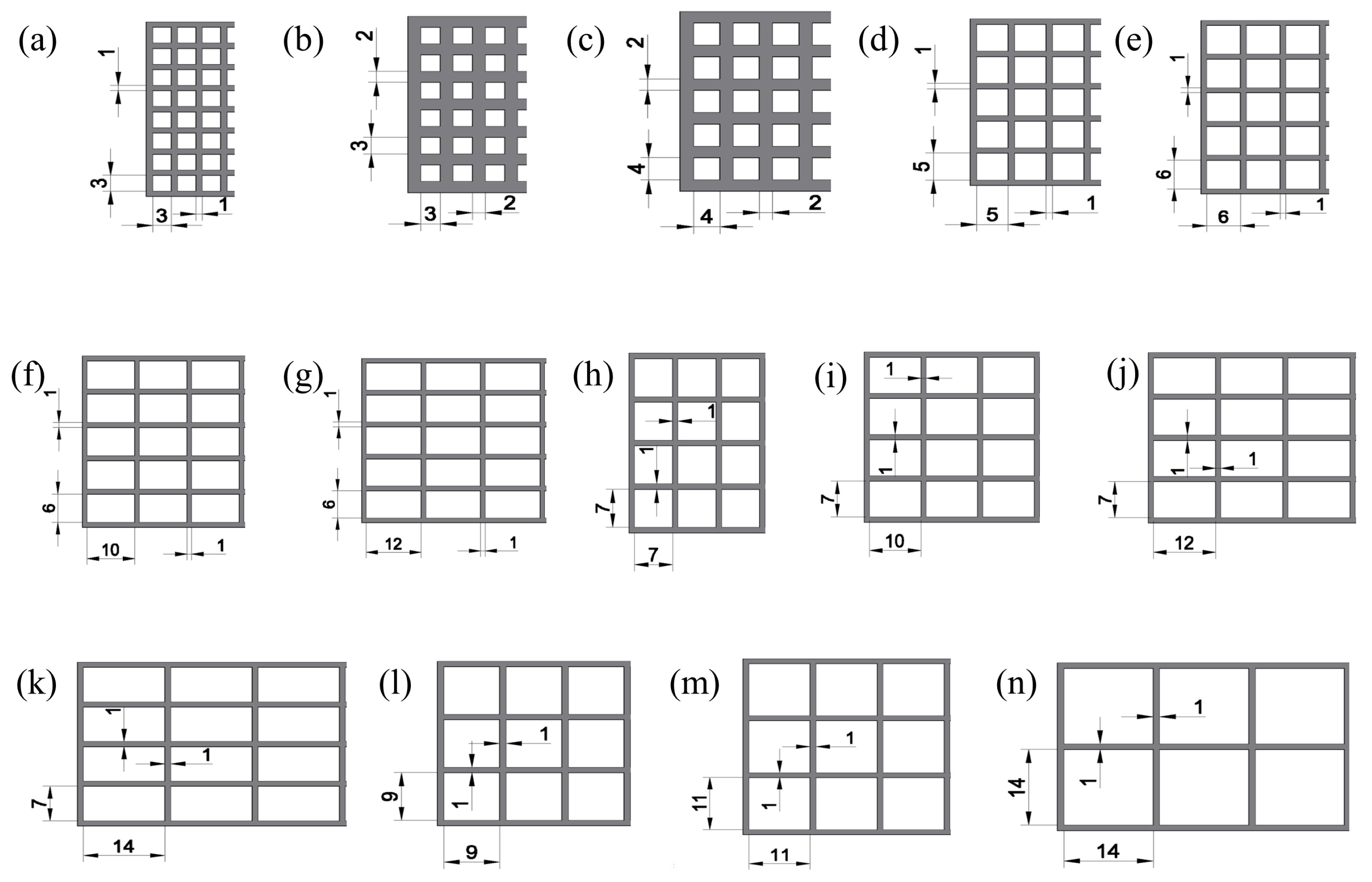
2.2.1. Leading Body-Height Grid Aerodynamic Interference

For the practical bridge structures, there exist some other structures at the upstream—for example, in the event that two bridges are close together. It is necessary to investigate the effects of the incompletely developed turbulence from the upstream body on the aerodynamic dynamic characteristics of the bridge. Based on the above consideration, for generality, the turbulence generated by the leading body-height grid is adopted to simulate the wake of the upstream body. With different body-height grids installed at the same height as the section bridge deck at the flow inlet, the turbulence intensity of the incoming flow in the model height range is affected by the geometry of the body-height grid. Therefore, the flow around the windward side of the bridge deck is changed from laminar flow to turbulent flow, with different-sized vortices generated by the interference of the body-height grid. Figure 4 shows the sketch view of the locations of the section model in the test section and the body-height grid in the flow inlet, while Figure 5 presents the detailed geometry of fourteen body-height grids (body-height grids I–XIV).

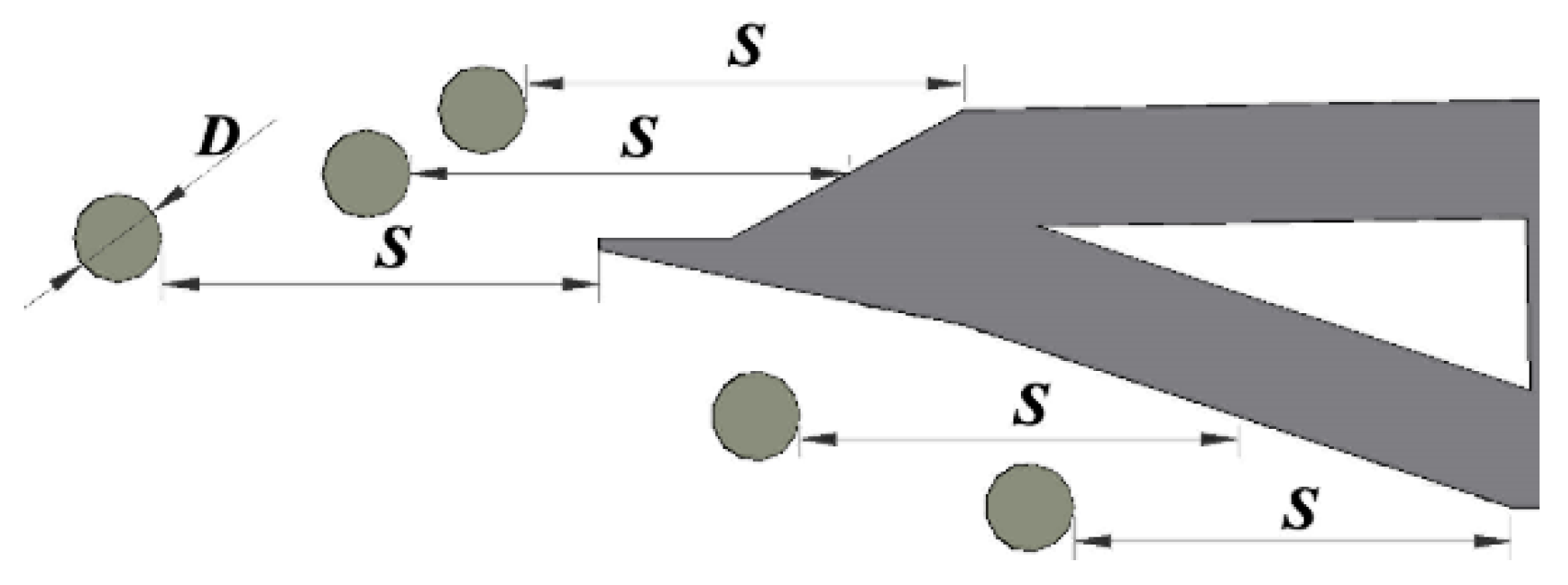
2.2.2. Leading Circular Cylinder Aerodynamic Interference

The handrail is an important accessory of the bridge structure, which is usually composed of cylinders, and the cylinders disturb the incoming flow characteristics to change the boundary layer of the box girder. Therefore, with different smooth cylinders (diameters of 3 mm, 4 mm, 5 mm, and 6 mm) installed in front of the essential flow areas of the model (upper edge, middle upper region, leading edge, middle lower region, and lower edge), the effects of different flow characteristics of essential flow regions around the section model on the surface pressure distribution and aerodynamic response of the bridge deck were investigated, and Figure 6 shows the location of cylinders in front of the bridge deck with different spacing ratios. The spacing ratio ε is defined as the ratio of the distance S between the trailing edge of the cylinder and the frontal surface of the twin-box girder to the diameter of cylinder D, ε = S/D. The spacing ratios used in this study were 2, 3, 4, and 5.

2.3. Turbulence Intensity Measurement

The turbulence intensity of incoming flow is measured by the Cobra Probe system (including Series 100 Cobra Probe, cabling, and TFI Device Control software). The Cobra Probe is composed of a multi-hole pressure probe, and is able to reconstruct the velocity components along the x, y, and z directions from pressure data. In the present work, the sampling frequency was set as 2 kHz. The Cobra Probe was placed at positions 1, 2 and 3 (see Figure 7) to measure the spread of the turbulent flow. In the present study, the turbulent properties at position 3 were adopted to characterize the incoming flow.

3. Results and Discussions

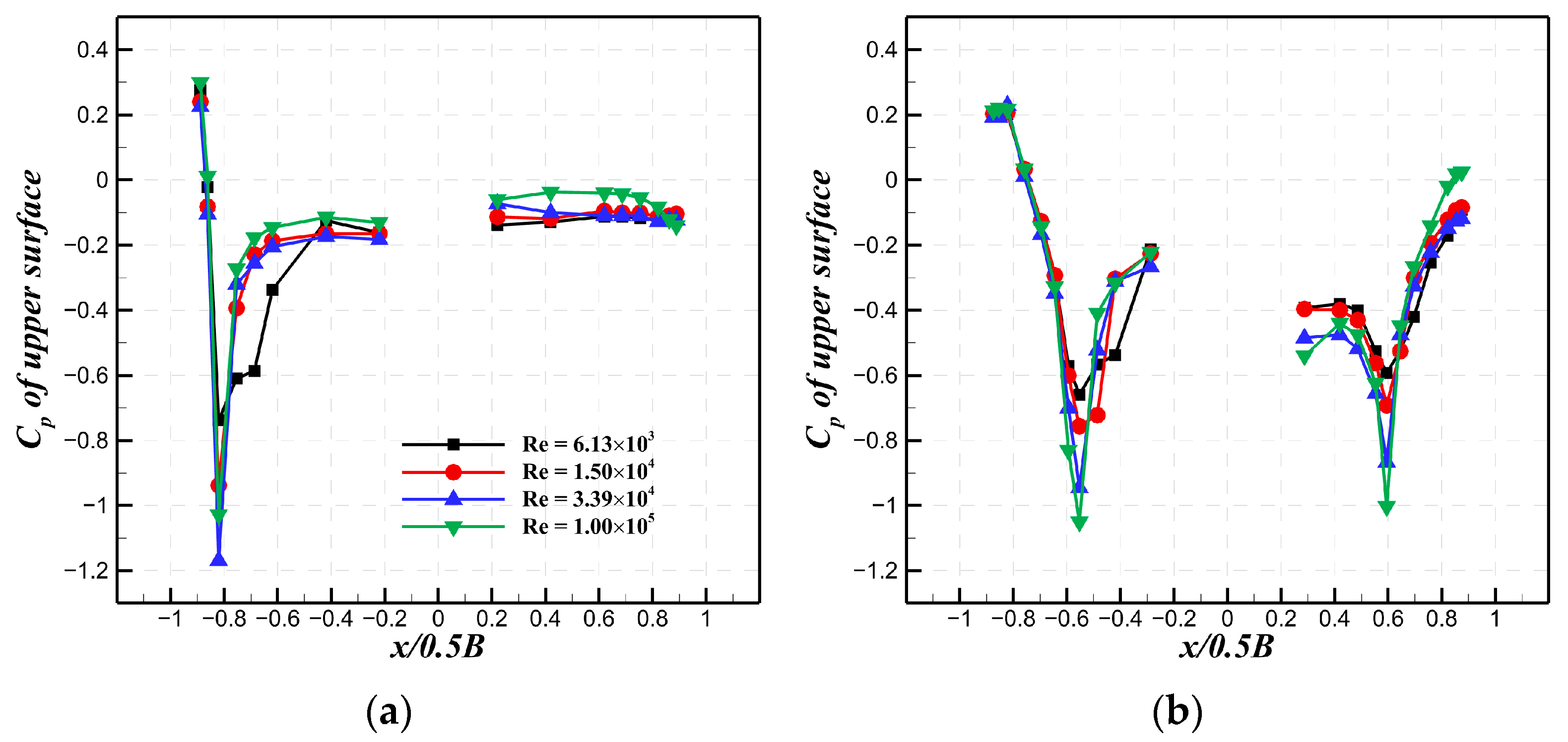
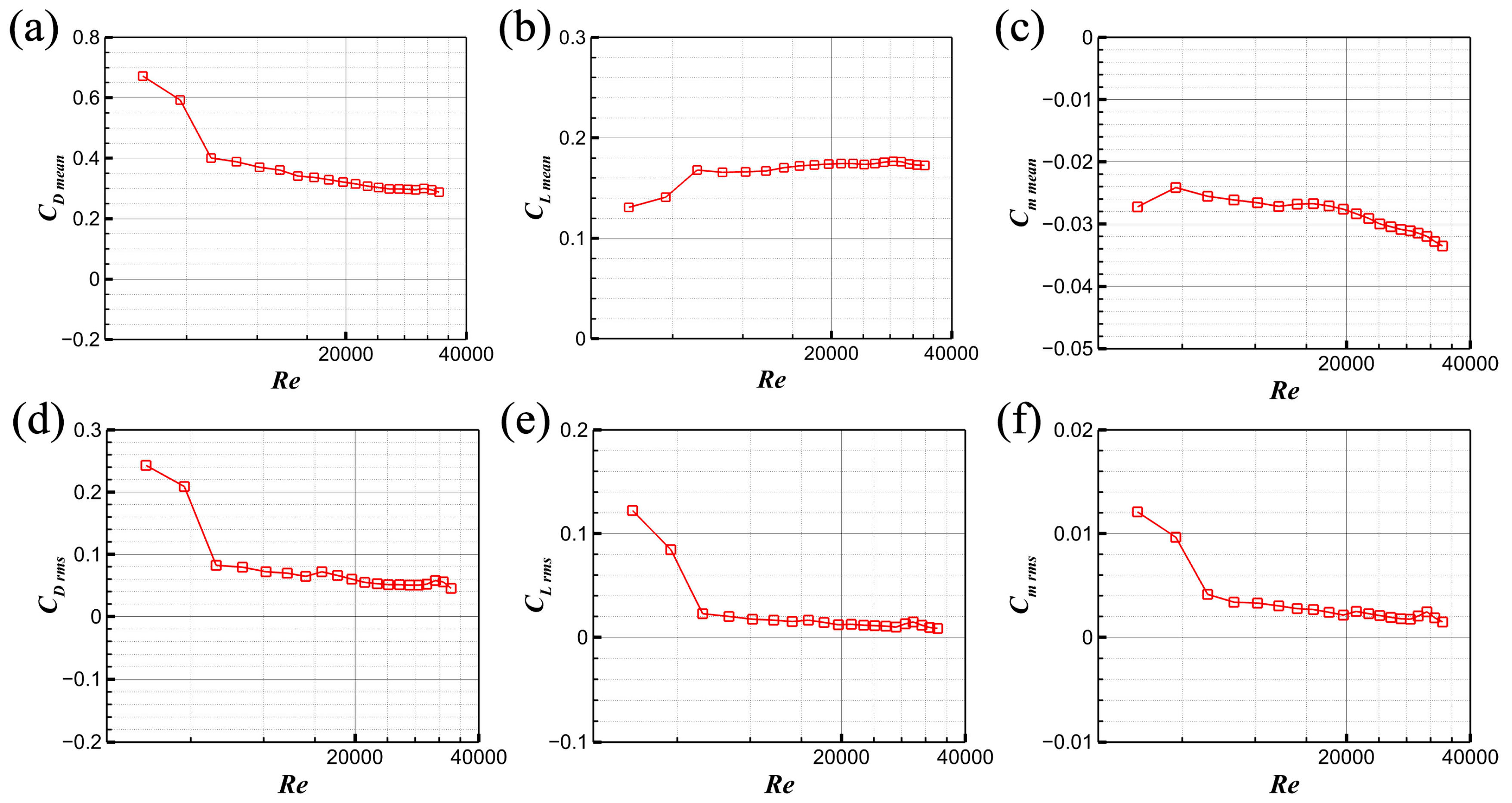
3.1. Undisturbed Surface Pressure Distribution and Aerodynamic Forces

To analyze the effects of the aerodynamic interference methods mentioned above, the aerodynamic characteristics of the bare twin-box girder were experimentally investigated, and the important aerodynamic parameters (including the surface pressure distribution and the aerodynamic forces) were obtained. Figure 8 gives the distribution of the mean pressure coefficient on the surface of the twin-box girder at different Reynolds numbers. At Re = 6.13 × 10³, the profile of the surface pressure indicates that the pressure of the upstream girder reaches a peak near the windward corner A, because the incoming flow passes through the windward slope on the upper surface and the incoming flow is affected by the forward pressure gradient, which enhances the flow speed and promotes the continuous increase in suction. After the windward corner, the flow velocity gradually decreases, and the negative pressure also decreases. It should be noted that a short-term pressure plateau is formed after the windward corner on the upper surface of the upstream girder at low Reynolds numbers (e.g., Re = 6.13 × 10³), but this pressure plateau will disappear at high Reynolds numbers. The pressure plateau is formed by the separation bubble, because the internal and external fluids of the separation bubble are relatively stable; thus, the pressure in the separation bubble is almost identical. Moreover, the endpoint of the pressure platform could be regarded as the reattachment point. Figure 8 also shows that the amplitude of the surface pressure increases with the Reynolds number, and the pressure on the lower surface of downstream girder has a common tendency to decrease first and then increase at different Reynolds numbers.

Figure 9 shows the mean and fluctuating aerodynamic force coefficients of the twin-box girder at various Reynolds numbers. The aerodynamic force coefficients show a significant change in the Reynolds number range adopted in this study. With the increase in the Reynolds number, the time-averaged drag force coefficient and the fluctuating drag force coefficient both decrease, and the rate of decrease first increases and then decreases; moreover, the maximum rate of decrease is achieved at Re = 9.21 × 10³, while the time-averaged lift force coefficient significantly increases first and then flattens with the increase in the Reynolds number. With the Re rising, the time-averaged moment force coefficient first increases rapidly, and then decreases. The fluctuating lift force coefficient and the fluctuating moment force coefficient show a similar tendency to the fluctuating drag coefficient with increasing Re.

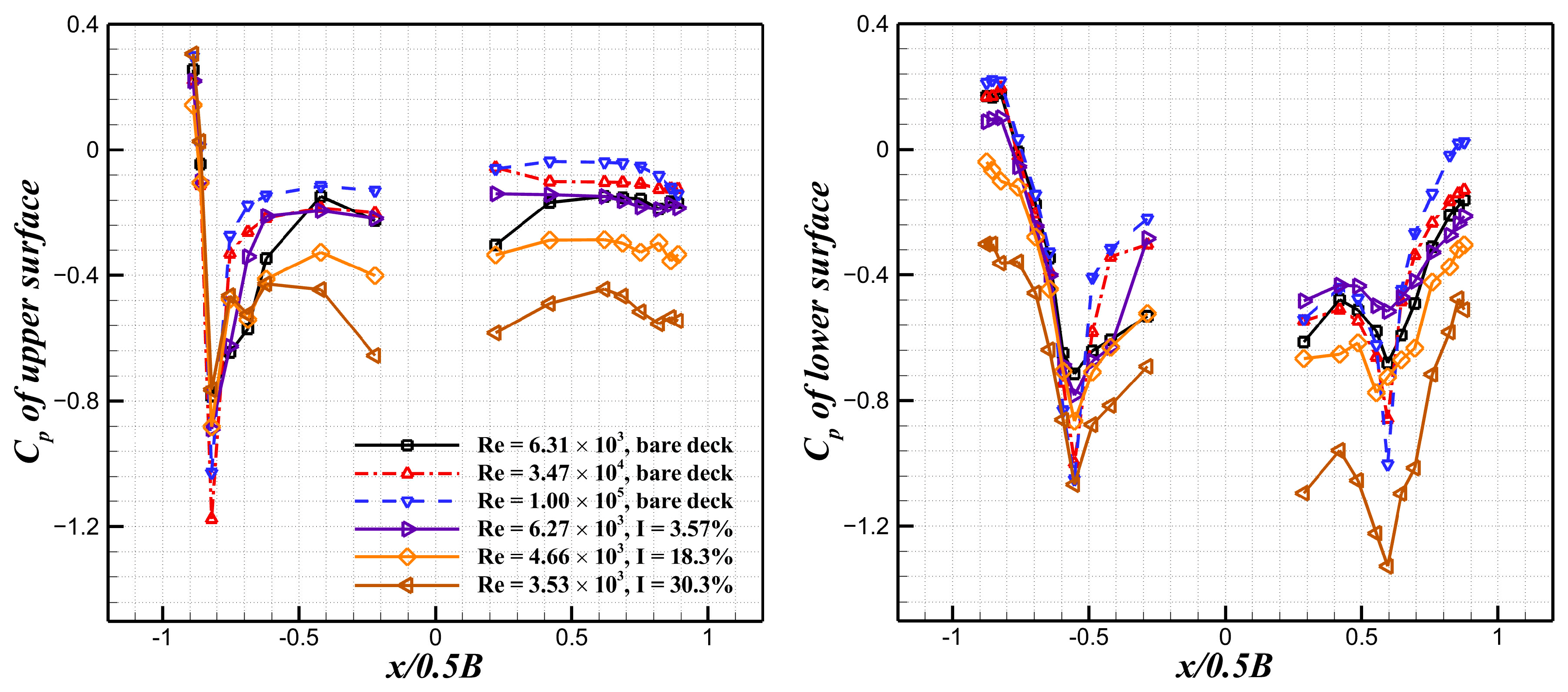
3.2. Modulation of Surface Pressure Distribution by Leading Body-Height Grids

First, the surface pressure distributions with the aerodynamic interference of the leading body-height grid were compared with those of the bare twin-box girder, as shown in Figure 10, and the effects of turbulence generated by different body-height grids on the surface pressure distribution were evaluated and analyzed.

Figure 10 clearly shows that the turbulence intensity, which is an important characteristic of incoming flow, has a significant influence on the time-averaged surface pressure distribution. Compared with the surface pressure distribution of the bare deck, the characteristic of the pressure distribution with the body-height grid aerodynamic interference changed a lot at low Reynolds numbers (Re < 1.0 × 10⁴), because the boundary layer transitioned to the turbulent boundary layer. At low turbulence intensity (I = 3.57–5.15%), the amplitude of the pressure peak was enhanced. It is also noteworthy that, at the upstream girder, the pressure plateaus (appearing in the undisturbed surface pressure distribution) in the upper and lower surfaces were eliminated, because the vortices generated by the body-height grid broke the separation bubbles, and the laminar boundary layer was transformed into turbulence, which cannot maintain a stable pressure to form the separation bubbles. At moderate turbulence intensity (I = 16.9–18.3%), the negative pressures are enhanced when x/0.5B > −0.7, indicating that the high turbulence intensity contains more energy to strengthen the flow velocity around the box girder. When the turbulence intensity is further increased (I = 27.9–31.4%), the negative pressures are also increased.

Figure 11 shows the time-averaged surface pressure distribution at different Reynolds numbers when the turbulence intensities are close. It is clearly shown that the turbulence intensity can effectively eliminate the Reynolds number sensitivity of pressure distribution, because the properties of the turbulent boundary layer are dominated by the turbulence intensity of the incoming flows.

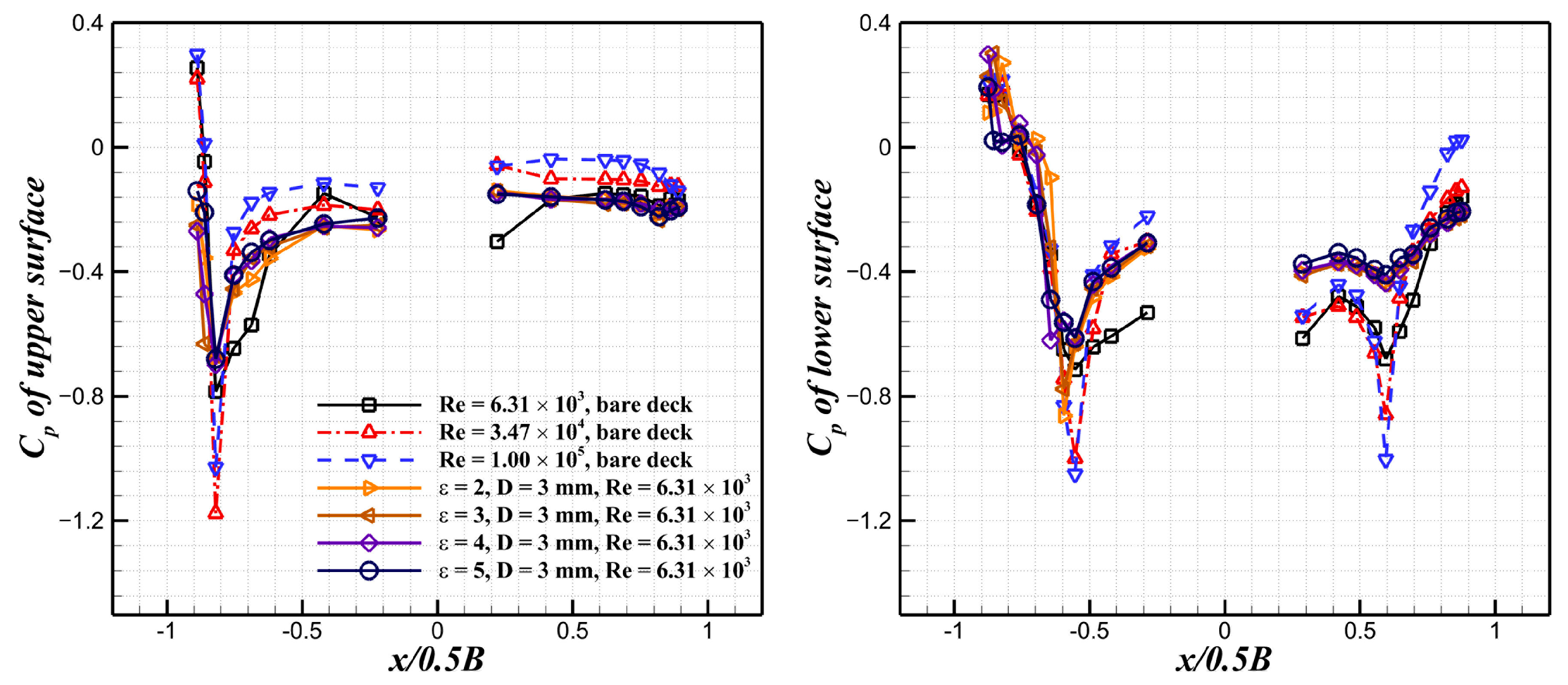
3.3. Modulation of Surface Pressure Distribution by Leading Circular Cylinders

Second, the time-averaged pressure distributions with cylinder interference were compared with the undisturbed pressure distribution. Figure 12 shows the mean surface pressure distributions with circular cylinder interference (D = 3 mm) at various spacing ratios. As shown in Figure 12, the turbulence generated by the wake of the circular cylinder significantly influences the time-averaged surface pressure distribution at the upstream girder, and the pressure plateaus formed by the separation bubbles are broken by the cylinder wake.

Moreover, Figure 12 also shows that the surface pressure on the upper and lower surfaces of the downstream girder exhibit opposite distribution characteristics. The upper surface pressure distribution shows that the negative pressure on the upper surface is lower than the undisturbed pressure at first, and then is higher than the original pressure at the same Reynolds number level. This may be because the flow velocity on the upper surface decreases after passing through the cylinder; however, continuous filling of the surrounding unaffected fluid enhances the flow velocity. The absolute value of minimum pressure on the lower surface is always less than the undisturbed pressure, which demonstrates that the cylinder located in front of the lower surface limits the velocity of the whole lower surface.

The time-averaged surface pressure distributions at different Reynolds numbers are shown in Figure 13. As shown in Figure 12 and Figure 13, it is clear that the pressure distribution at the twin-box girder is insensitive to the spacing ratio and the diameter of the cylinder. Meanwhile, it should be noted that the surface pressure distribution with circular cylinder interference on the downstream girder presents slight Reynolds number sensitivity, indicating that the vortices generated by the flow passing through the leading circular cylinders fully enforce the turbulence on the boundary layer around the twin-box girder.

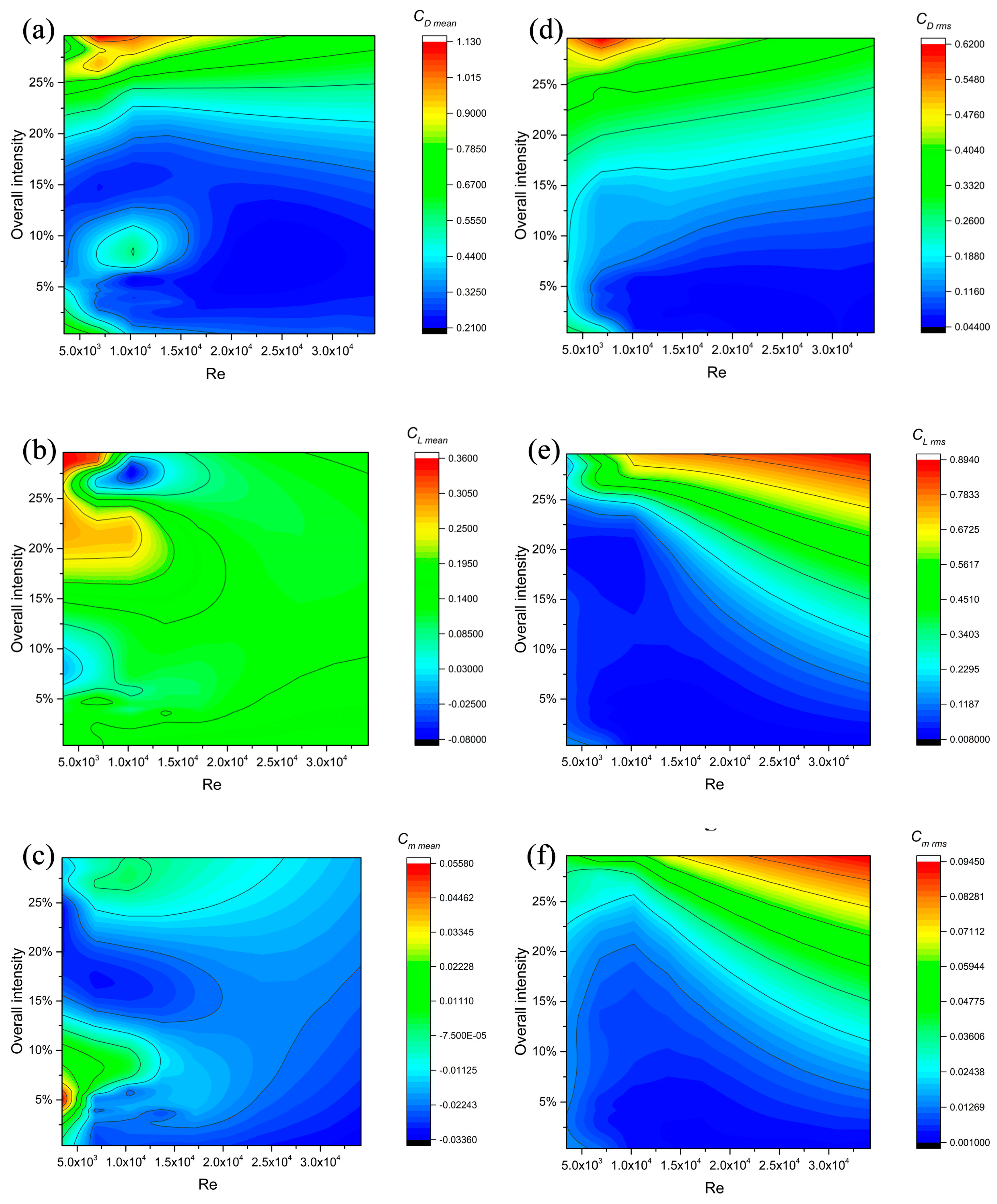
3.4. Modulation of Aerodynamic Forces by Leading Body-Height Grids

Figure 14 shows the distribution of the mean and fluctuating aerodynamic force coefficients in the phase plane of the Reynolds number and turbulence intensity, and the aerodynamic forces show strong sensitivity to the Reynolds number and turbulence intensity.

As shown in Figure 14a, the distribution of the time-averaged drag force coefficient shows different characteristics at different turbulence intensities. At low turbulence intensity (I ≤ 5%), the C_{D mean} is sensitive to the Reynolds number when Re ≤ 1.0 × 10⁴. Moreover, the hypotenuse of the contour at the corner indicates that the turbulence intensity can reduce the Reynolds number effects of C_{D mean}. When the Reynolds number is further increased, the C_{D mean} shows slight Reynolds number sensitivity, which is consistent with the bare deck (see Figure 9a). At moderate turbulence intensity (5% ≤ I ≤ 20%), the C_{D mean} is enhanced, and the C_{D mean} presents slight Reynolds number dependence. It should be noted that there exists a lock-up region of C_{D mean}. At high turbulence intensity (I > 20%), the C_{D mean} is further promoted, and is only associated with the turbulence intensity.

The time-averaged lift force coefficient shows strong sensitivity to the turbulence intensity when Re ≤ 1.0 × 10⁴ (see Figure 14b), and with the increase in turbulence intensity, the lift force is enhanced, which implies that the strength of turbulent flow can effectively promote the lift force. Meanwhile, at Re > 1e4, the lift force is insensitive to both Reynolds number and turbulence intensity, because the boundary layer transitions to full turbulence.

As for the fluctuating forces, C_{D rms} and C_{L rms} show different distribution characteristics. At low turbulence intensity (I < 2.5%), C_{D rms} shows Reynolds number dependence at low Re, i.e., Re < 1.0 × 10⁴. With the increase in turbulence intensity, the C_{D rms} is enhanced by the strong fluctuating component of incoming flow, and the Reynolds number sensitivity of the C_{D rms} is eliminated (see Figure 14d). However, the C_{L rms} depends on the Reynolds number and turbulence intensity, because the increase in Re or turbulence intensity can enhance the vertical fluctuating force.

As shown in Figure 14c,f, when Re ≤ 1.0 × 10⁴ and turbulence intensity I ≤ 12.5%, the mean moment force coefficient increases significantly with the turbulence intensity, which may be due to the increase in the vertical and horizontal fluctuating velocity of the flow field caused by the turbulence. However, in other regions, the mean moment force coefficient does not show strong turbulence intensity sensitivity, because the turbulence mainly affects and increases the horizontal and vertical velocities, but has a small impact on the moment force. The fluctuating moment force coefficient and the fluctuating lift force coefficient exhibit similar trends, indicating that the fluctuating lift force is the dominant component of the fluctuating moment force.

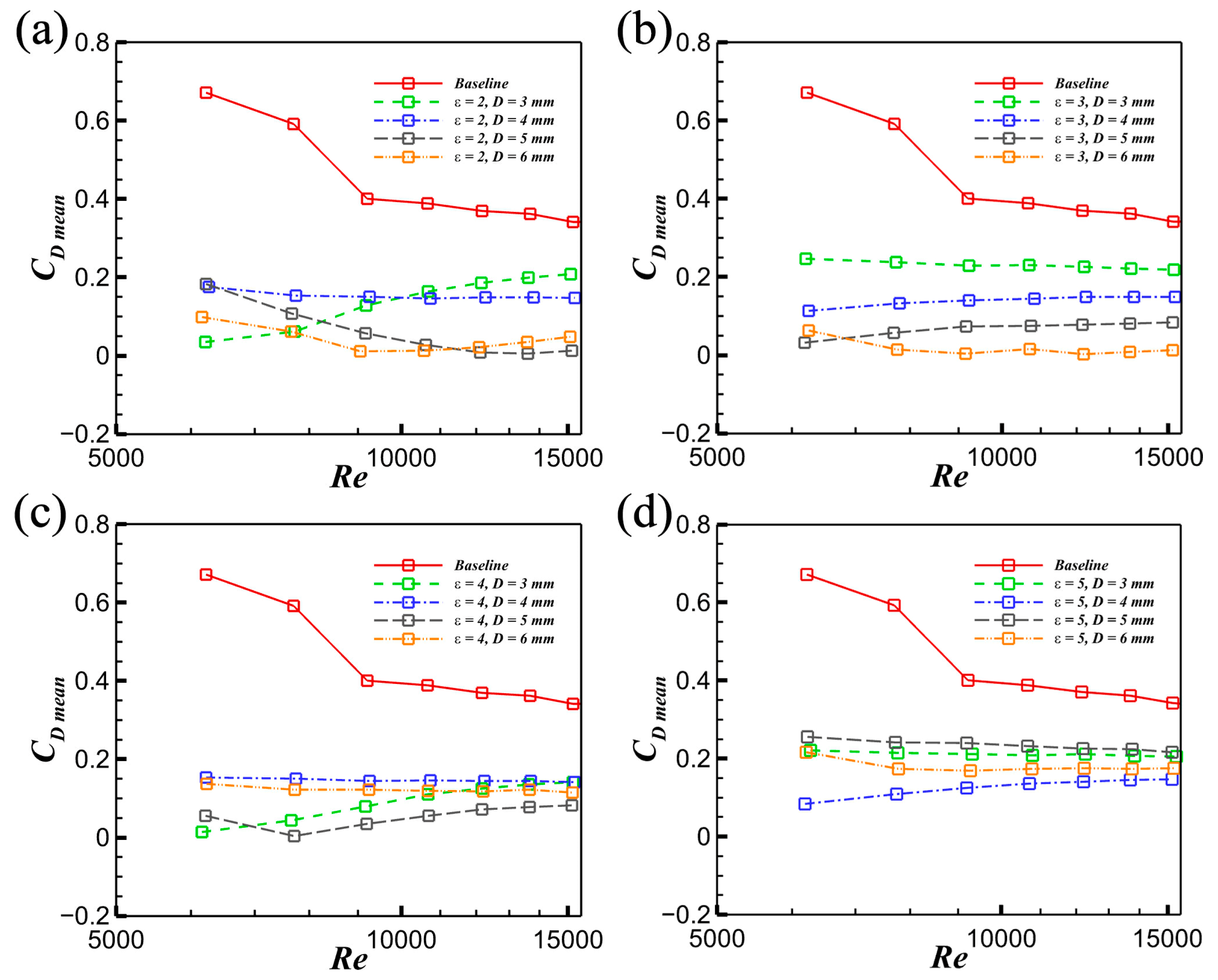
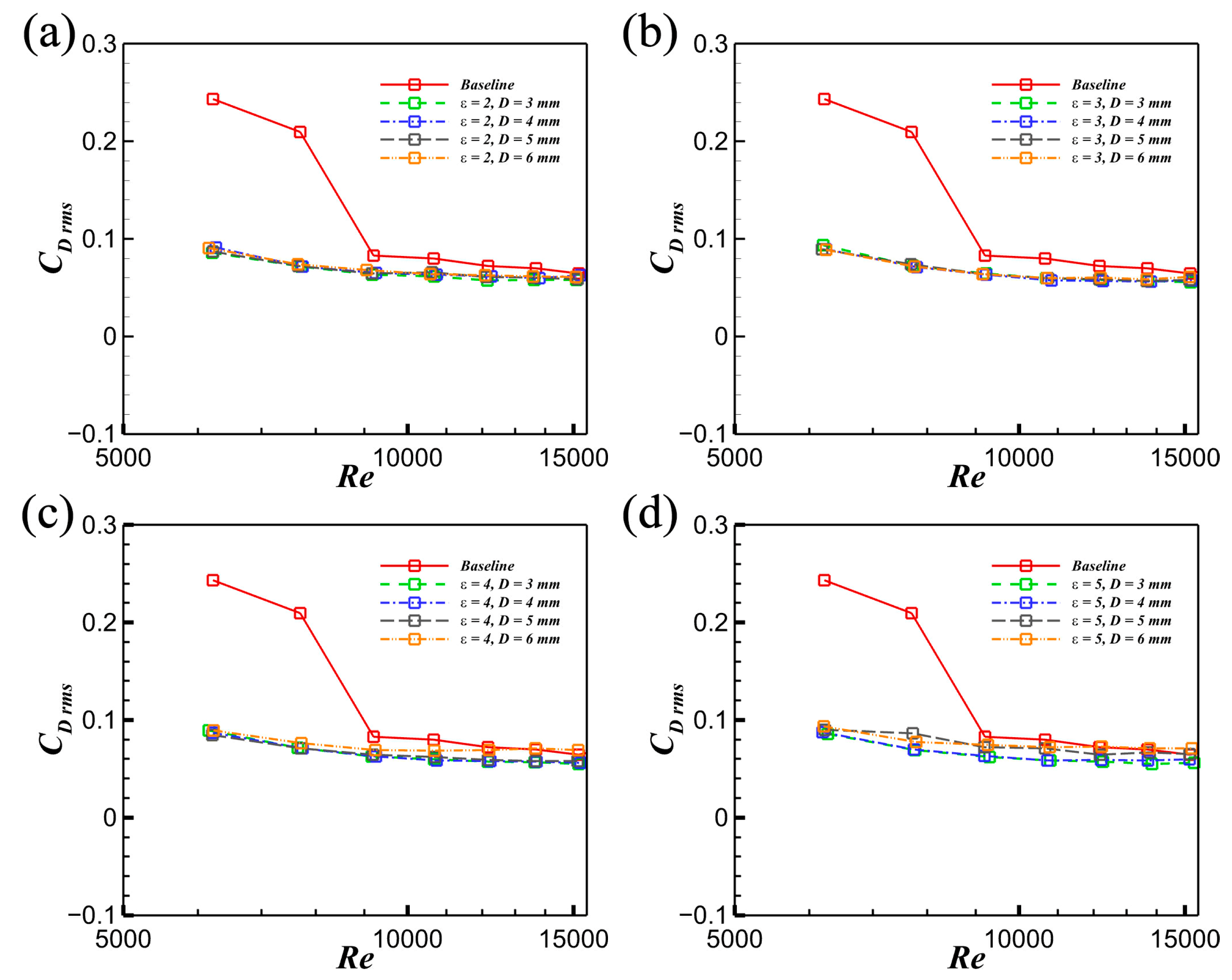
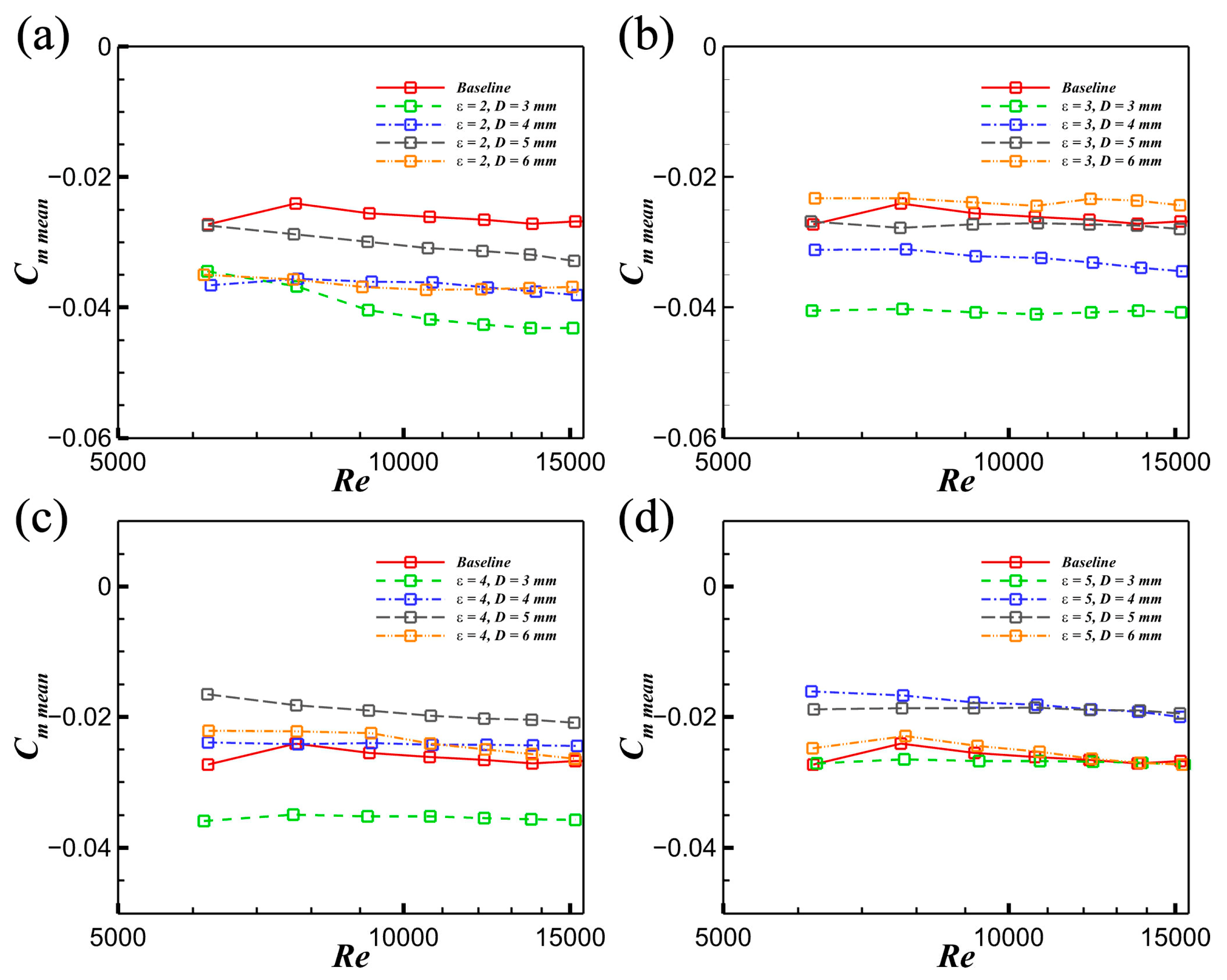
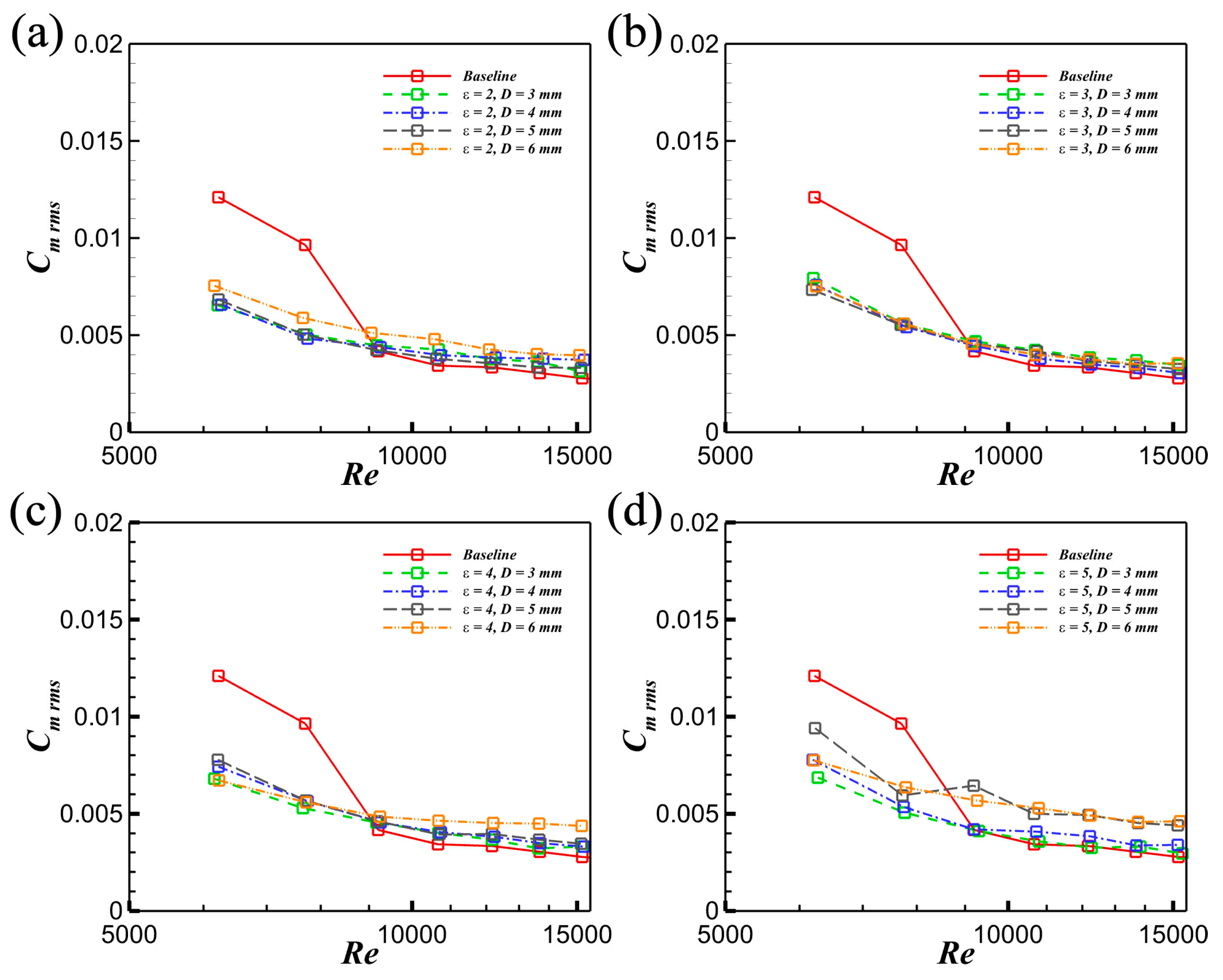
3.5. Modulation of Aerodynamic Forces by Leading Circular Cylinders

Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 show the mean and fluctuating aerodynamic force coefficients of the twin-box girder under the aerodynamic interference by leading circular cylinders at different spacing ratios. Figure 15 shows that the time-averaged drag force coefficient of the twin-box girder with cylinder interference decreased significantly compared with the original force coefficient without interference, because the shedding vortices in the wake of the circular cylinder destroyed the original laminar boundary layers; hence, the laminar boundary layers transition to turbulence at the windward corner, and the turbulent boundary layers can be maintained throughout the girder section. Thus, the boundary layer is composed of many small vortices, which effectively reduce the contact area between the fluid boundary layer and the twin-box girder, leading to a decrease in the friction between the turbulent boundary layer and the model. Meanwhile, when the vortices contact the girder, the velocity direction is generally opposite to the incoming flow. In this way, the vortices generate a force that is opposite to the streamwise direction, and the force generated by the interaction between the vortices and the girder reduces the total drag force of the bridge deck. Meanwhile, when the diameter of the cylinder is 3 mm, it clearly shows that the time-averaged drag force coefficient exhibits a periodic trend at different locations from the model, as shown in Figure 15, which indicates that the vortex scale is closer to the diameter. In addition, the time-averaged drag force with cylinder interference at low Re achieves a similar characteristic of undisturbed drag force at high Re.

Figure 16 shows that the fluctuating drag force coefficient of the twin-box girder with cylinder interference is much smaller than that of the twin-box girder without interference at Re ≤ 9.0 × 10³. Moreover, the fluctuating drag force is insensitive to the Reynolds number, and the disturbed fluctuating drag force at low Re is closer to that of the undisturbed fluctuating force at high Re. Furthermore, the fluctuating drag force is independent of the spacing ratio ε.

Figure 17 shows that the time-averaged lift force coefficient of the girder with cylinder interference also decreased sharply compared with that of the bare twin-box girder. It should be noted that with the increase in distance between the cylinder and the twin-box girder, the C_{L mean} shows less sensitivity to the Reynolds number, because the turbulence in the wake of cylinder has been fully developed, which causes the boundary layer of the body surface to transition to turbulence. When the cylinder is close to the twin-box girder, the wake of the cylinder cannot fully develop into turbulence to change the boundary layer, which explains why the Reynolds number effect still exists. In conclusion, when the spacing ratio ε > 2, the turbulence generated by the wake of the cylinder effectively eliminates the Reynolds number effects on the time-averaged lift force.

Figure 18 shows that the fluctuating lift force coefficient of the twin-box girder with cylinder interference is independent of the Reynolds number and spacing ratio ε. Moreover, the fluctuating lift force is much smaller than that of the undisturbed force at Re ≤ 9.0 × 10³. This may be because the vertical pulsation component in the cylindrical wake is very small and the turbulence generated by the cylinder suppresses the vortex shedding of the twin-box girder to reduce the fluctuation of the lift force.

Compared with the undisturbed time-averaged moment force, Figure 19 shows that the mean moment force coefficient with cylinder interference is large, and is dependent on spacing ratio and diameter. With the decrease in diameter, the time-averaged moment force coefficient C_{m mean} is slightly enhanced. Meanwhile, with the increase in the spacing ratio, the absolute value of C_{m mean} decreases gradually. When the spacing ratio ε = 5, the C_{m mean} is smaller than the undisturbed mean moment force. This indicates that the fully developed turbulence wake generated by a large spacing ratio can effectively suppress the time-averaged moment force.

Figure 20 shows the fluctuating moment force coefficient C_{m rms} of the twin-box girder with cylinder interference. At Re ≤ 9.0 × 10³, the interfered C_{m rms} is greater than the undisturbed C_{m rms}. When the spacing ratio ε ≤ 3, the C_{m rms} is insensitive to the diameter, and the C_{m rms} decreases slightly with the increase in the Reynolds number.

4. Conclusions

In the present work, the effects of two cutting-edge aerodynamic interference measures on the pressure distribution and aerodynamic force of a twin-box girder were investigated. We used the leading body-height grid and leading circular cylinder to increase the turbulence intensity of the incoming flow. The flows gained more energy before reaching the separation point, and the entrainment rate of the flow was enhanced, which not only affects the separation bubbles and reattachment points, but also changes the characteristics of the boundary layer. The conclusions are summarized as follows:

(1)

The leading body-height grid generates the turbulent incoming flow, which effectively breaks the separation bubbles and the flow reattachment, and the laminar boundary layer in the undisturbed case at low Re is forced to transition to turbulent flow. Moreover, the characteristics of surface pressure distribution with body-height grid interference are similar to those of bare deck at high Re;

(2)

The Reynolds number sensitivity of time-averaged drag force decreases with the increase in turbulence intensity, and the C_{D mean} is dominated by the turbulence intensity. While the C_{L mean} and C_{m mean} are dependent on the Re and turbulence intensity at low Re, at high Re, the C_{L mean} and C_{m mean} are insensitive to the Re and turbulence intensity. The fluctuating drag force C_{D rms} depends on the turbulence intensity, and is insensitive to the Reynolds number, while the C_{L rms} and C_{m rms} are related to both turbulence intensity and the Reynolds number. In addition, the characteristics of C_{L rms} and C_{m rms} are similar, indicating that the C_{L rms} is the dominant component of the C_{m rms};

(3)

The coherent turbulence generated by the leading circular cylinders effectively changes the boundary layer of the twin-box girder. The Reynolds number sensitivity of surface pressure distribution is reduced by the interference of cylinders, and it is insensitive to the diameter and the spacing ratio. Moreover, the separation bubbles are also broken by the wake of the cylinder;

(4)

The time-averaged drag force C_{D mean} is significantly reduced by the interference of the leading cylinder, and its Reynolds number sensitivity is diminished. Moreover, the time-averaged lift force C_{L mean} with cylinder interference is drastically decreased, and it is also insensitive to the Reynolds number. With the increase in the spacing ratio, the time-averaged moment force C_{m mean} is weakened, and its Reynolds number sensitivity is reduced. In addition, the fluctuating drag force C_{D rms} and lift force C_{L rms} are both insensitive to the Re, the spacing ratio, and the diameter, while the fluctuating moment force is closely related to these three parameters.