Dilated Filters for Edge-Detection Algorithms
Abstract
:1. Introduction
- Extend our previous analysis on first-order derivative orthogonal gradients based algorithms and Canny algorithm, that was performed in Bogdan et al. [11].
- Analyze and evaluate if the effect of dilated is maintained when using different kernels for the mentioned algorithms.
- Analyze and evaluate the effect of noise level of an input image upon the dilated filters.
- Prove the research hypothesis that dilated filters in general bring forward better results than classical or extended versions of them.
2. Dilated Filters
3. Methodology
3.1. Guo–Hall Algorithm
| Algorithm 1 Guo–Hall Algorithm. |
|
3.2. First-Order Derivative Orthogonal Gradient Operators
| Algorithm 2 First-Order Derivative Operators steps. |
Input: RGB image Output: Binary edge map Parameters: Sigma value (S), Gradient Threshold (TG)
|
3.3. First-Order Derivative Compass Gradient Operators
3.4. Frei–Chen Operator
3.5. Laplacian Edge Operator
| Algorithm 3 Laplace and LoG Operator steps. |
Input: RGB image Output: Binary edge map Parameters: [Sigma value (S) − only LoG], Gradient Threshold (TG),
|
3.6. Laplacian of Gaussian—LoG—Or Mexican Hat Operator
3.7. Marr–Hildreth Algorithm
| Algorithm 4 Marr–Hildreth Operator steps. |
Input: RGB image Output: Binary edge map Parameters: Sigma value (S), Gradient Threshold (TG), |
3.8. Canny Algorithm
| Algorithm 5 Canny Operator steps. |
Input: RGB image Output: Binary edge map Parameters: Sigma value (S), Low Threshold (TL), High Threshold (TH),
|
3.9. Shen–Castan Algorithm
| Algorithm 6 Shen–Castan Operator steps. |
Input: RGB image Output: Binary edge map Parameters: Smoothing Factor of ISEF (SF), Threshold of Laplace (TG), Zero crossing window (W), Threshold for zero crossing (R), Thinning Factor (TN)
|
3.10. Edge-Drawing Algorithm
| Algorithm 7 Edge Drawing Operator steps. |
Input: RGB image Output: Binary edge map Parameters: Gaussian Kernel (GK), Threshold of Laplace (TG), Anchor Threshold (TA), Scan Interval (SI)
|
3.11. Benchmarking the Edge Operators
- True positive points (TPs), common points of and .
- False positive points (FPs), false detected edges of .
- False negative points (FNs), missing edge points of .
- True negative points (TNs), common non-edge points.
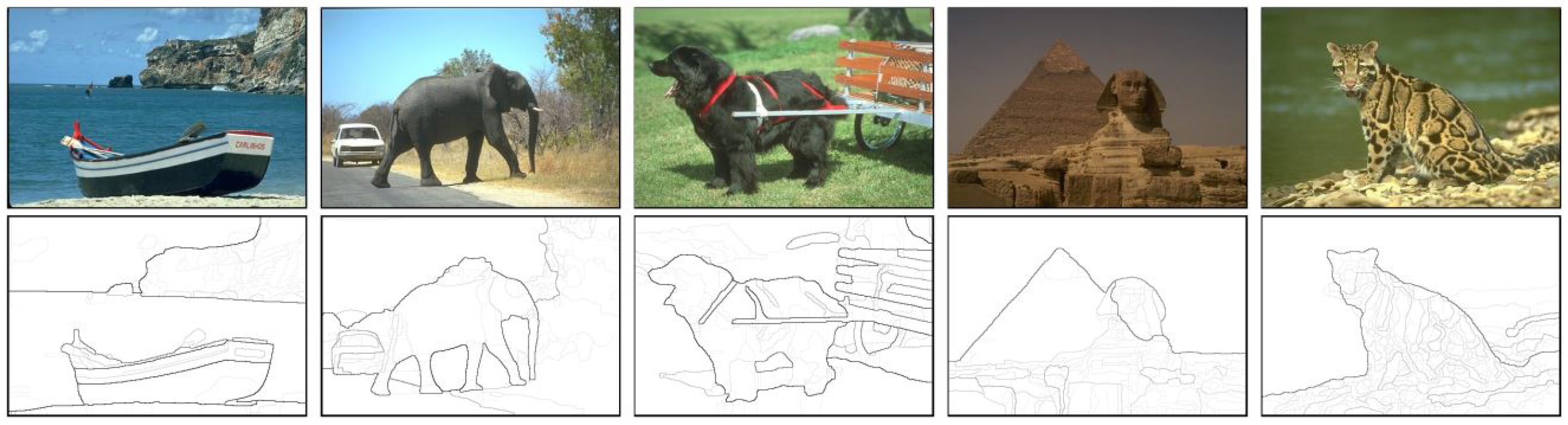
4. Experimental Results
4.1. Effect of Dilation
4.1.1. Operators Based on First-Order Discrete Kernels
4.1.2. Operators Based on Second-Order Discrete Kernels
4.1.3. Preliminary Conclusion
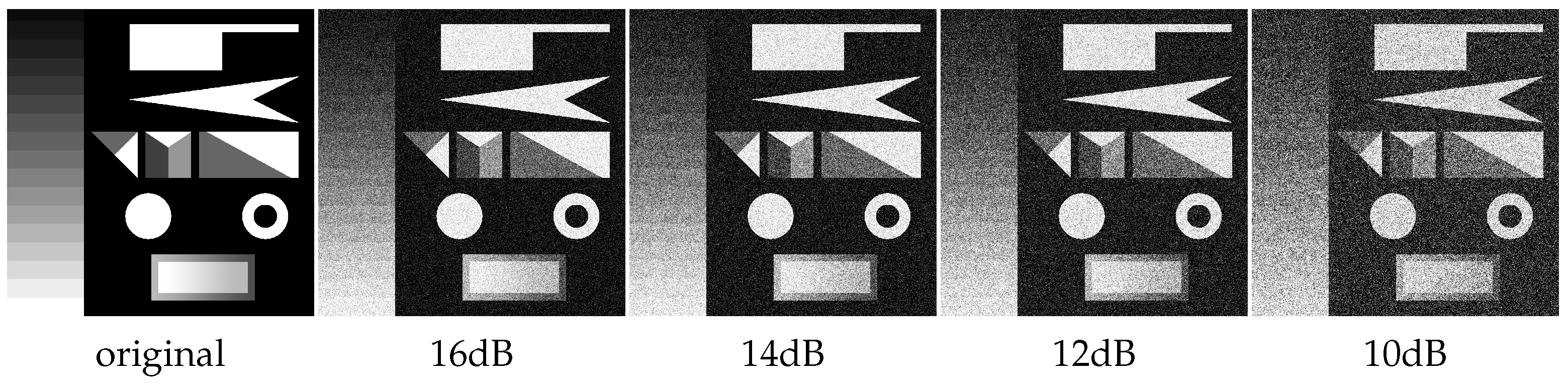
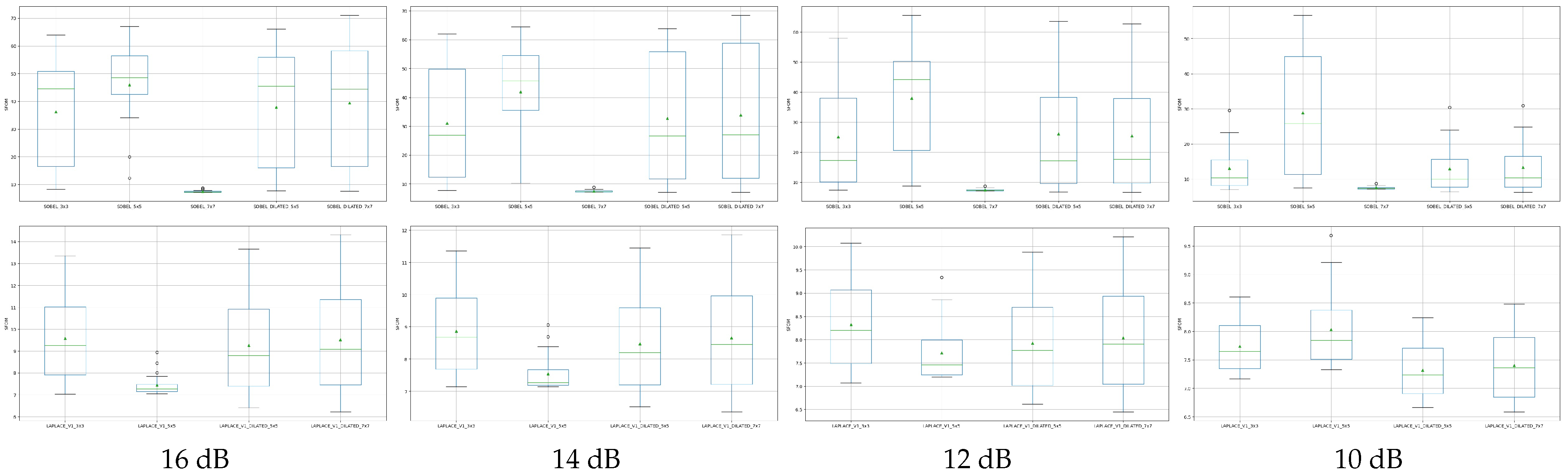
4.2. Noise Effect on Dilation
4.3. Dilation with Different Operators
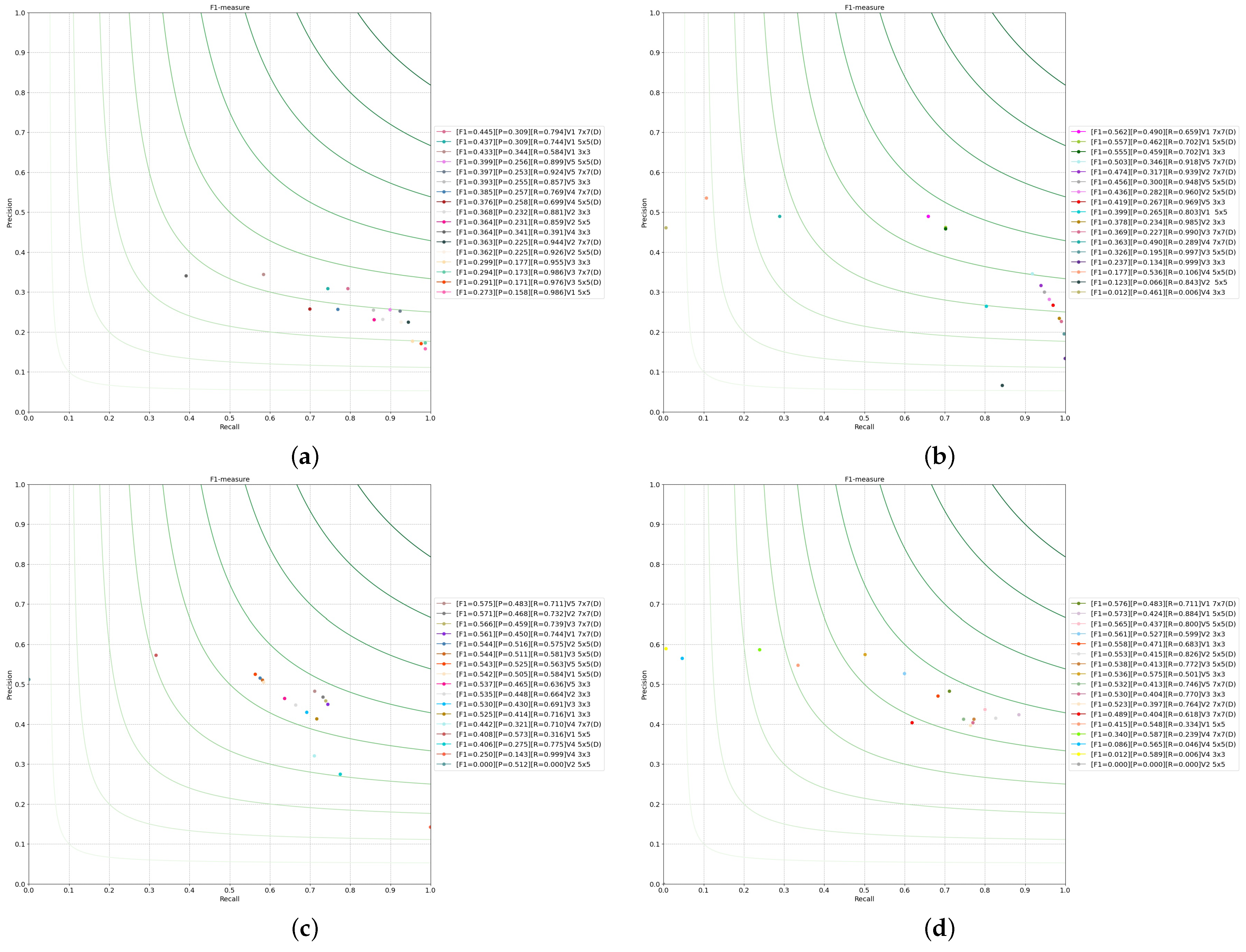
4.3.1. Operators Based on First-Order Discrete Kernels
4.3.2. Operators Based on Second-Order Discrete Kernels
4.3.3. Preliminary Conclusion
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RGB | Red-Green-Blue |
| LoG | Laplacian of Gaussian |
| ISEF | Infinite Symmetric Exponential Filter |
| ED | Edge Drawing |
| BSDS500 | Berkeley Segmentation Data Set and Benchmarks 500 |
| PCM | Pixel Corresponding Metric |
| SFoM | Symmetric Figure of Merit |
| P | Precision |
| R | Recall |
| F1 | F-measure |
| FP | False Positive |
| TP | True Positive |
| FN | False Negative |
| FoM | Pratt Figure of Merit |
| EECVF | End-to-End Computer Vision Framework |
| CV | Computer Vision |
| S | Gaussian Sigma |
| TG | Gradient Threshold |
| TL | Low Threshold |
| TH | High Threshold |
| GK | Gaussian Kernel |
| TA | Anchor Threshold |
| SI | Scan Interval |
| SF | Smoothing Factor of ISEF |
| W | Shen–Castan zero crossing window |
| R | Shen–Castan threshold for zero crossing |
| TN | Thinning Factor |
| PSNR | Peek Signal Noise Ratio |
Appendix A
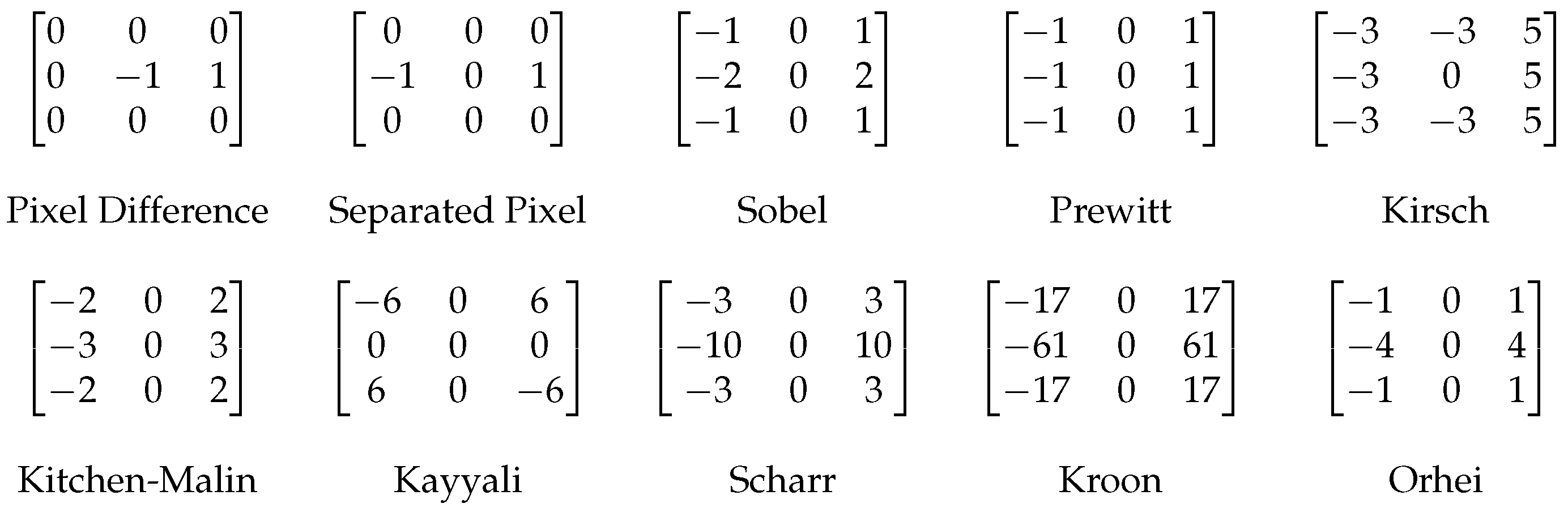
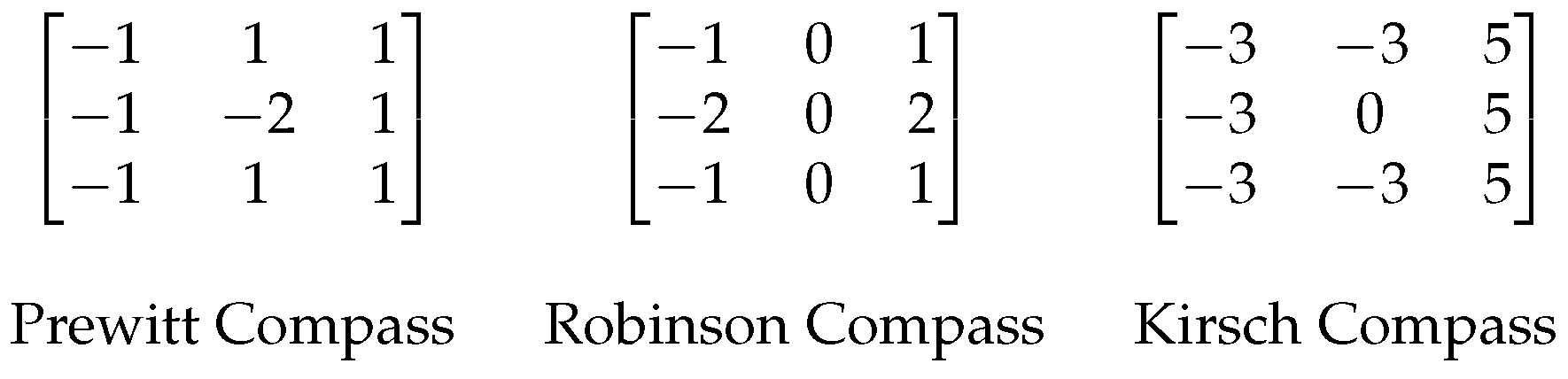


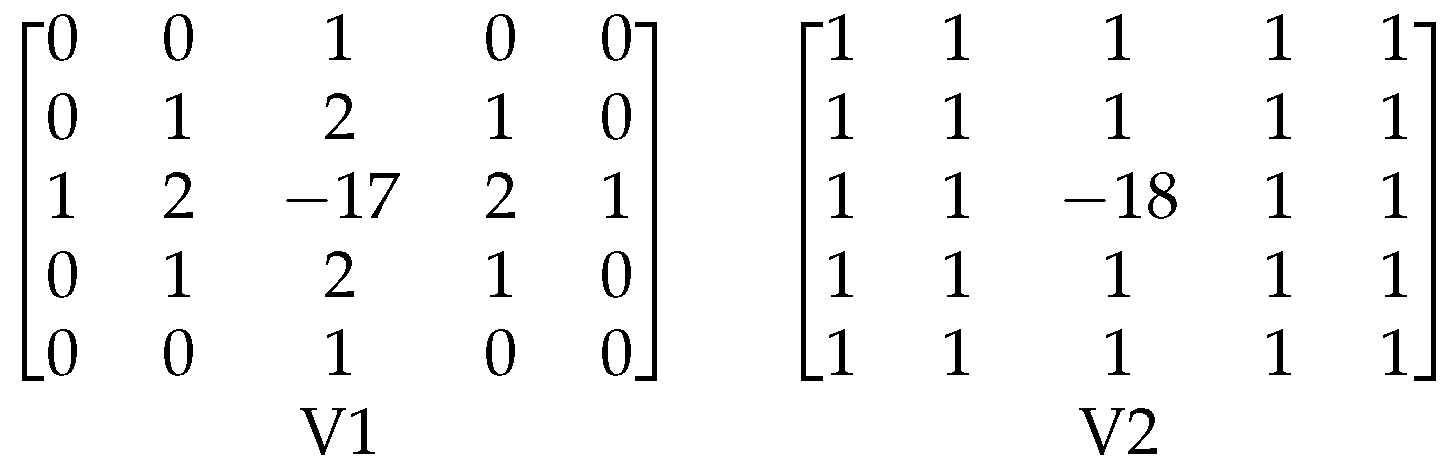

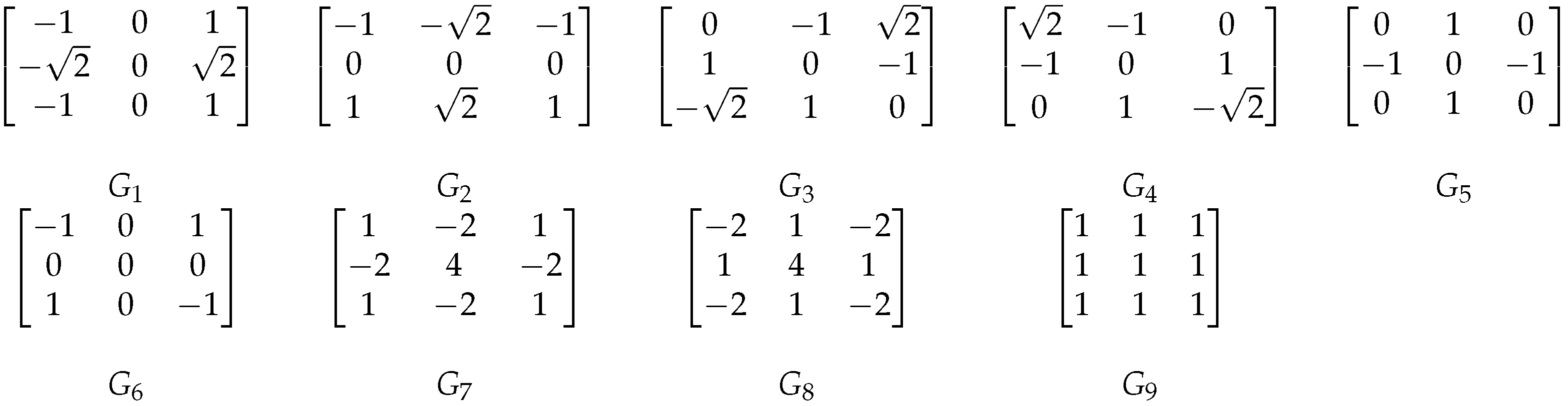
Appendix B





References
- Ziou, D.; Tabbone, S. Edge detection techniques-an overview. Pattern Recognit. Image Anal. C/C Raspoznavaniye Obraz. Anal. Izobr. 1998, 8, 537–559. [Google Scholar]
- Papari, G.; Petkov, N. Edge and line oriented contour detection: State of the art. Image Vis. Comput. 2011, 29, 79–103. [Google Scholar] [CrossRef]
- Spontón, H.; Cardelino, J. A review of classic edge detectors. Image Process. Line 2015, 5, 90–123. [Google Scholar] [CrossRef] [Green Version]
- Sen, D.; Pal, S.K. Gradient histogram: Thresholding in a region of interest for edge detection. Image Vis. Comput. 2010, 28, 677–695. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shapiro, L.; Lee, J. Morphological edge detection. IEEE J. Robot. Autom. 1987, 3, 142–155. [Google Scholar]
- Hamaguchi, R.; Fujita, A.; Nemoto, K.; Imaizumi, T.; Hikosaka, S. Effective Use of Dilated Convolutions for Segmenting Small Object Instances in Remote Sensing Imagery. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision, WACV 2018, Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1442–1450. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Yazdanbakhsh, O.; Dick, S. Multivariate Time Series Classification using Dilated Convolutional Neural Network. arXiv 2019, arXiv:1905.01697. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the 4th International Conference on Learning Representations, ICLR 2016, San Juan, PR, USA, 2–4 May 2016; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; ICLR: San Juan, PR, USA, 2016. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar] [CrossRef] [Green Version]
- Bogdan, V.; Bonchiş, C.; Orhei, C. Custom Dilated Edge Detection Filters. J. WSCG 2020, 28, 161–168. [Google Scholar] [CrossRef]
- Orhei, C.; Bogdan, V.; Bonchiş, C. Edge map response of dilated and reconstructed classical filters. In Proceedings of the 2020 22nd International Symposium on Symbolic and Numeric Algorithms for Scientific Computing (SYNASC), Timisoara, Romania, 1–4 September 2020; pp. 187–194. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 679–698. [Google Scholar] [CrossRef]
- Sobel, I.; Feldman, G. A 3 × 3 isotropic gradient operator for image processing. Pattern Classif. Scene Anal. 1973, 271–272, unpublished. [Google Scholar]
- Prewitt, J.M. Object enhancement and extraction. Pict. Process. Psychopictorics 1970, 10, 15–19. [Google Scholar]
- Scharr, H. Optimal Operators in Digital Image Processing. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2000. [Google Scholar]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. Lond. Ser. Biol. Sci. 1980, 207, 187–217. [Google Scholar]
- Castan, S.; Zhao, J.; Shen, J. New edge detection methods based on exponential filter. In Proceedings of the 10th International Conference on Pattern Recognition, Atlantic City, NJ, USA, 16–21 June 1990; Volume 1, pp. 709–711. [Google Scholar] [CrossRef]
- Chen, C.C. Fast boundary detection: A generalization and a new algorithm. IEEE Trans. Comput. 1977, 100, 988–998. [Google Scholar]
- Park, R.H. A Fourier interpretation of the Frei-Chen edge masks. Pattern Recognit. Lett. 1990, 11, 631–636. [Google Scholar] [CrossRef]
- Topal, C.; Akinlar, C. Edge drawing: A combined real-time edge and segment detector. J. Vis. Commun. Image Represent. 2012, 23, 862–872. [Google Scholar] [CrossRef]
- Jain, R.; Kasturi, R.; Schunck, B.G. Machine Vision; McGraw-hill: New York, NY, USA, 1995; Volume 5. [Google Scholar]
- Haralick, R.M.; Shapiro, L.G. Computer and Robot Vision; Addison-Wesley Reading: Boston, MA, USA, 1992; Volume 1. [Google Scholar]
- Liu, H.; Jezek, K. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Isa, N.M. Automated edge detection technique for Pap smear images using moving K-means clustering and modified seed based region growing algorithm. Int. J. Comput. Internet Manag. 2005, 13, 45–59. [Google Scholar]
- Orhei, C.; Mocofan, M.; Vert, S.; Vasiu, R. An automated threshold Edge Drawing algorithm. In Proceedings of the 2021 44th International Conference on Telecommunications and Signal Processing (TSP), Brno, Czech Republic, 26–28 July 2021; pp. 292–295. [Google Scholar] [CrossRef]
- Jie, G.; Ning, L. An improved adaptive threshold canny edge detection algorithm. In Proceedings of the 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; Volume 1, pp. 164–168. [Google Scholar]
- Azeroual, A.; Afdel, K. Fast image edge detection based on faber schauder wavelet and otsu threshold. Heliyon 2017, 3, e00485. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Chakrabarti, C.; Karam, L.J. A distributed Canny edge detector and its implementation on FPGA. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 500–505. [Google Scholar]
- Sezgin, M.; Sankur, B. Survey over image thresholding techniques and quantitative performance evaluation. J. Electron. Imaging 2004, 13, 146–165. [Google Scholar]
- Guo, Z.; Hall, R.W. Parallel thinning with two-subiteration algorithms. Commun. ACM 1989, 32, 359–373. [Google Scholar] [CrossRef]
- Mlsna, P.A.; Rodriguez, J.J. Gradient and Laplacian edge detection. In The Essential Guide to Image Processing; Elsevier: Amsterdam, The Netherlands, 2009; pp. 495–524. [Google Scholar]
- Bandai, N.; Sanada, S.; Ueki, K.; Funabasama, S.; Tsuduki, S.; Matsui, T. Morphological analysis for kinetic X-ray images of the temporomandibular joint. Nihon Hoshasen Gijutsu Gakkai Zasshi 2003, 59, 951. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lateef, R.A.R. Expansion and Implementation of a 3 × 3 Sobel and Prewitt Edge Detection Filter to a 5 × 5 Dimension Filter. J. Baghdad Coll. Econ. Sci. Univ. 2008, 1, 336–348. [Google Scholar]
- Kekre, H.; Gharge, S. Image Segmentation using Extended Edge Operator for Mammographic Images. Int. J. Comput. Sci. Eng. 2010, 2, 1086–1091. [Google Scholar]
- Levkine, G. Prewitt, Sobel and Scharr gradient 5 × 5 convolution matrices. Image Process. Artic. Second. Draft 2012. Available online: http://www.hlevkin.com/articles/SobelScharrGradients5x5.pdf (accessed on 9 November 2021).
- Gupta, S.; Mazumdar, S.G. Sobel edge detection algorithm. Int. J. Comput. Sci. Manag. Res. 2013, 2, 1578–1583. [Google Scholar]
- Kirsch, R.A. Computer determination of the constituent structure of biological images. Comput. Biomed. Res. 1971, 4, 315–328. [Google Scholar] [CrossRef]
- Kitchen, L.; Malin, J. The effect of spatial discretization on the magnitude and direction response of simple differential edge operators on a step edge. Comput. Vis. Graph. Image Process. 1989, 47, 243–258. [Google Scholar] [CrossRef]
- Chen, J.; Chen, D.; Meng, S. A Novel Region Selection Algorithm for Auto-focusing Method Based on Depth from Focus. In Proceedings of the Euro-China Conference on Intelligent Data Analysis and Applications, Málaga, Spain, 9–11 October 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 101–108. [Google Scholar]
- Kroon, D. Numerical Optimization of Kernel Based Image Derivatives; Short Paper University Twente: Enschede, The Netherlands, 2009. [Google Scholar]
- Orhei, C.; Vert, S.; Vasiu, R. A Novel Edge Detection Operator for Identifying Buildings in Augmented Reality Applications. In Proceedings of the International Conference on Information and Software Technologies, Kaunas, Lithuania, 15–17 October 2020; pp. 208–219. [Google Scholar] [CrossRef]
- Woods, J.W. Multidimensional Signal, Image, and Video Processing and Coding, Second Edition, 2nd ed.; Academic Press, Inc.: Orlando, FL, USA, 2011. [Google Scholar]
- Gonzalez, C.; Woods, E. Digital Image Processing; Addison-Wesley Publishing Company: Boston, MA, USA, 1991. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Robinson, G.S. Edge detection by compass gradient masks. Comput. Graph. Image Process. 1977, 6, 492–501. [Google Scholar] [CrossRef]
- Davies, E. A skimming technique for fast accurate edge detection. Signal Process. 1992, 26, 1–16. [Google Scholar] [CrossRef]
- Torre, V.; Poggio, T.A. On edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, PAMI-8, 147–163. [Google Scholar] [CrossRef]
- Haralick, R.M. Digital Step Edges from Zero Crossing of Second Directional Derivatives. In Readings in Computer Vision; Fischler, M.A., Firschein, O., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1987; pp. 216–226. [Google Scholar] [CrossRef]
- Grimson, W.E.L.; Hildreth, E.C. Comments on Digital Step Edges from Zero Crossings of Second Directional Derivatives. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.R. Algorithms for Image Processing and Computer Vision; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Li, Z.; Aberkane, A.; Magnier, B. Shen-Castan Based Edge Detection Methods for Bayer CFA Images. In Proceedings of the 2021 9th European Workshop on Visual Information Processing (EUVIP), Paris, France, 23–25 June 2021; pp. 1–6. [Google Scholar]
- Shen, J.; Castan, S. An optimal linear operator for step edge detection. CVGIP Graph. Model. Image Process. 1992, 54, 112–133. [Google Scholar] [CrossRef]
- Aurich, V.; Weule, J. Non-linear gaussian filters performing edge preserving diffusion. In Mustererkennung 1995; Springer: Berlin/Heidelberg, Germany, 1995; pp. 538–545. [Google Scholar]
- Wang, S.; Ge, F.; Liu, T. Evaluating edge detection through boundary detection. EURASIP J. Adv. Signal Process. 2006, 2006, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Kitchen, L.; Rosenfeld, A. Edge evaluation using local edge coherence. IEEE Trans. Syst. Man Cybern. 1981, 11, 597–605. [Google Scholar] [CrossRef]
- Heath, M.D.; Sarkar, S.; Sanocki, T.; Bowyer, K.W. A robust visual method for assessing the relative performance of edge-detection algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1338–1359. [Google Scholar] [CrossRef] [Green Version]
- Magnier, B. Edge detection: A review of dissimilarity evaluations and a proposed normalized measure. Multimed. Tools Appl. 2018, 77, 9489–9533. [Google Scholar] [CrossRef] [Green Version]
- Magnier, B.; Abdulrahman, H.; Montesinos, P. A review of supervised edge detection evaluation methods and an objective comparison of filtering gradient computations using hysteresis thresholds. J. Imaging 2018, 4, 74. [Google Scholar] [CrossRef] [Green Version]
- Yitzhaky, Y.; Peli, E. A method for objective edge detection evaluation and detector parameter selection. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1027–1033. [Google Scholar] [CrossRef]
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; You, S.; Walker, J.; Li, K.; Barnes, N. Structural Edge Detection: A Dataset and Benchmark. In Proceedings of the 2018 Digital Image Computing: Techniques and Applications (DICTA), Canberra, Australia, 10–13 December 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Mély, D.A.; Kim, J.; McGill, M.; Guo, Y.; Serre, T. A systematic comparison between visual cues for boundary detection. Vis. Res. 2016, 120, 93–107. [Google Scholar] [CrossRef]
- Silberman, N.; Hoiem, D.; Kohli, P.; Fergus, R. Indoor Segmentation and Support Inference from RGBD Images. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar] [CrossRef]
- Soria, X.; Riba, E.; Sappa, A. Dense Extreme Inception Network: Towards a Robust CNN Model for Edge Detection. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020. [Google Scholar]
- Orhei, C.; Vert, S.; Mocofan, M.; Vasiu, R. TMBuD: A dataset for urban scene building detection. In Proceedings of the International Conference on Information and Software Technologies, Kaunas, Lithuania, 14–16 October 2021; pp. 251–262. [Google Scholar] [CrossRef]
- Orhei, C.; Mocofan, M.; Vert, S.; Vasiu, R. An analysis of ED line algorithm in urban street-view dataset. In Proceedings of the International Conference on Information and Software Technologies, Kaunas, Lithuania, 14–16 October 2021; pp. 123–135. [Google Scholar] [CrossRef]
- Guizhen, M.; Zongliang, F.; Zongzhong, Y. Performance analysis and comparison of susan edge detector. Mod. Electron. Tech. 2007, 8, 189–191. [Google Scholar]
- Prieto, M.; Allen, A. A similarity metric for edge images. Pattern Anal. Mach. Intell. IEEE Trans. 2003, 25, 1265–1273. [Google Scholar] [CrossRef]
- Sasaki, Y. The Truth of the F-Measure; Technical Report; School of Computer Science, University of Manchester: Oxford, UK, 2007. [Google Scholar]
- Abdou, I.; Pratt, W. Quantitative design and evaluation of enhancement/thresholding edge detectors. Proc. IEEE 1979, 67, 753–763. [Google Scholar] [CrossRef]
- Dubuisson, M.P.; Jain, A.K. A modified Hausdorff distance for object matching. In Proceedings of the 12th International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; Volume 1, pp. 566–568. [Google Scholar]
- Orhei, C.; Mocofan, M.; Vert, S.; Vasiu, R. End-to-End Computer Vision Framework. In Proceedings of the 2020 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 5–6 November 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Orhei, C.; Vert, S.; Mocofan, M.; Vasiu, R. End-To-End Computer Vision Framework: An Open-Source Platform for Research and Education. Sensors 2021, 21, 3691. [Google Scholar] [CrossRef] [PubMed]
- Isar, A.; Nafornita, C.; Magu, G. Hyperanalytic Wavelet-Based Robust Edge Detection. Remote Sens. 2021, 13, 2888. [Google Scholar] [CrossRef]


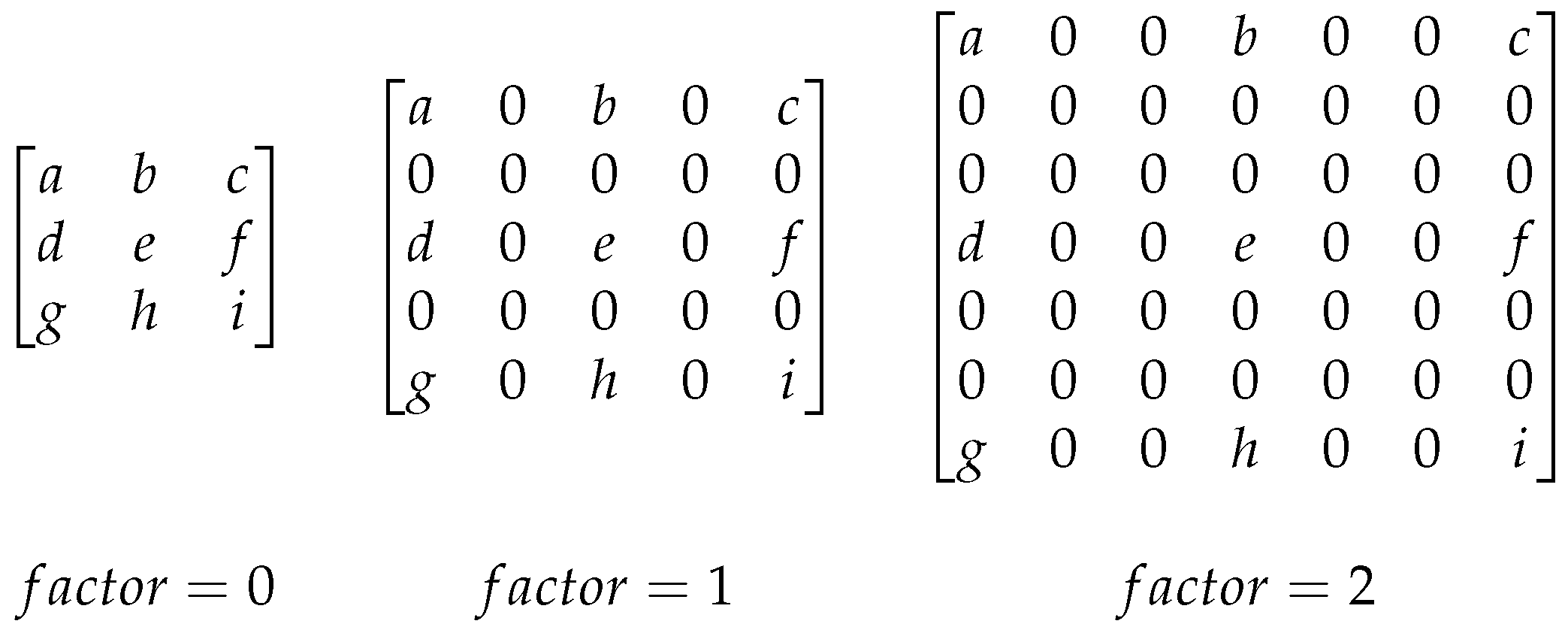
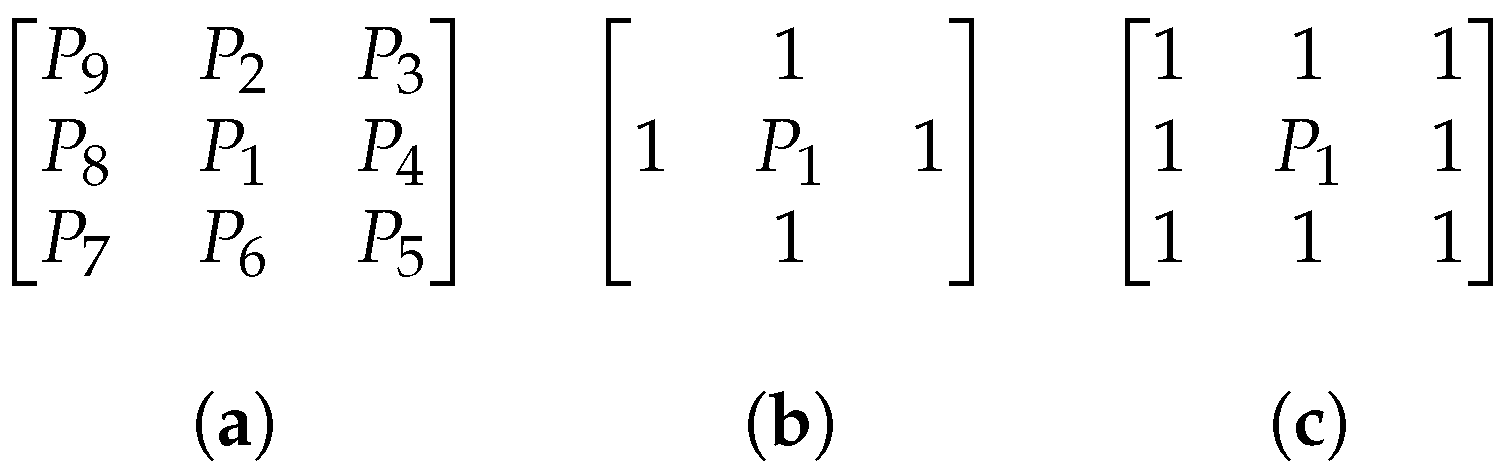

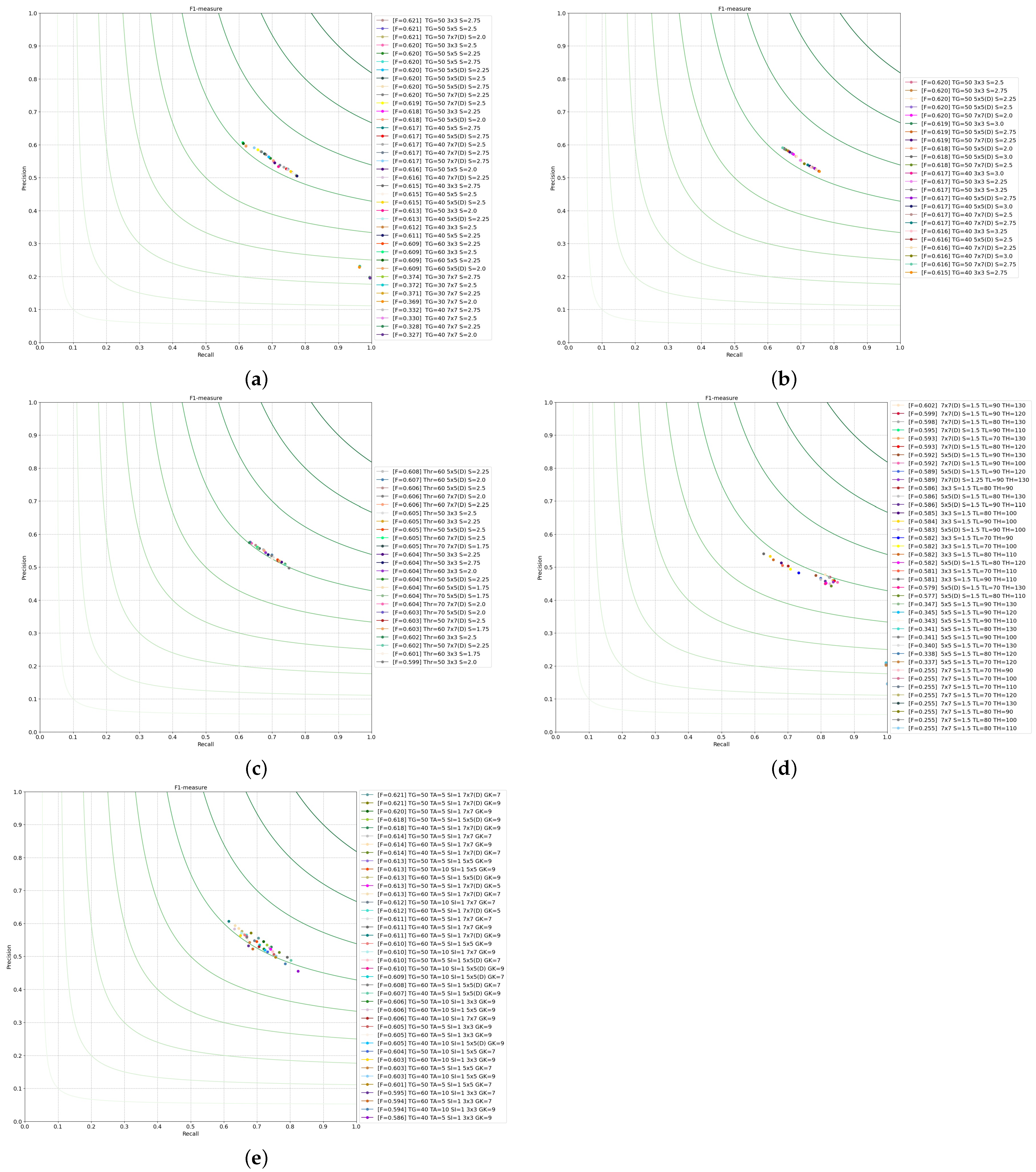
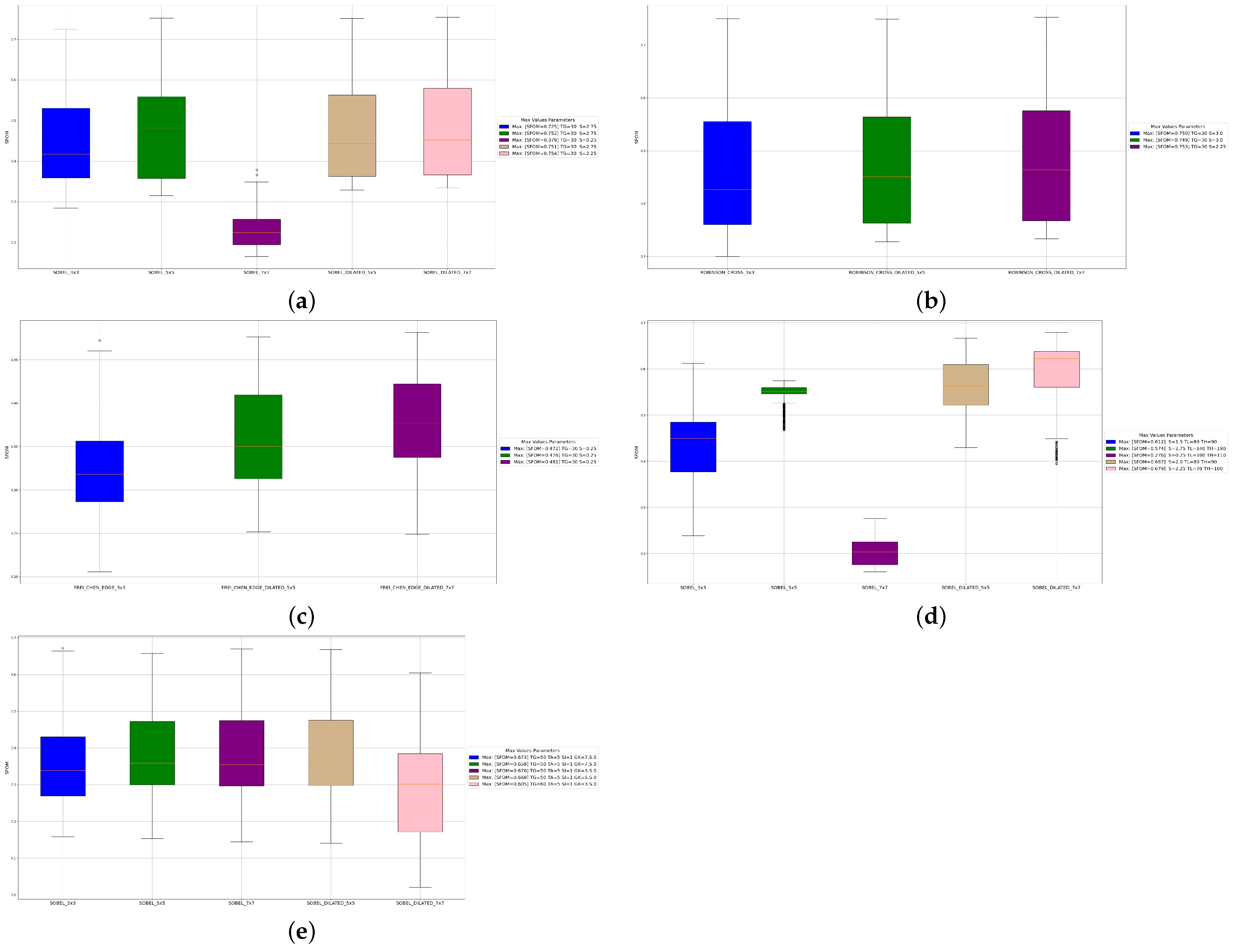
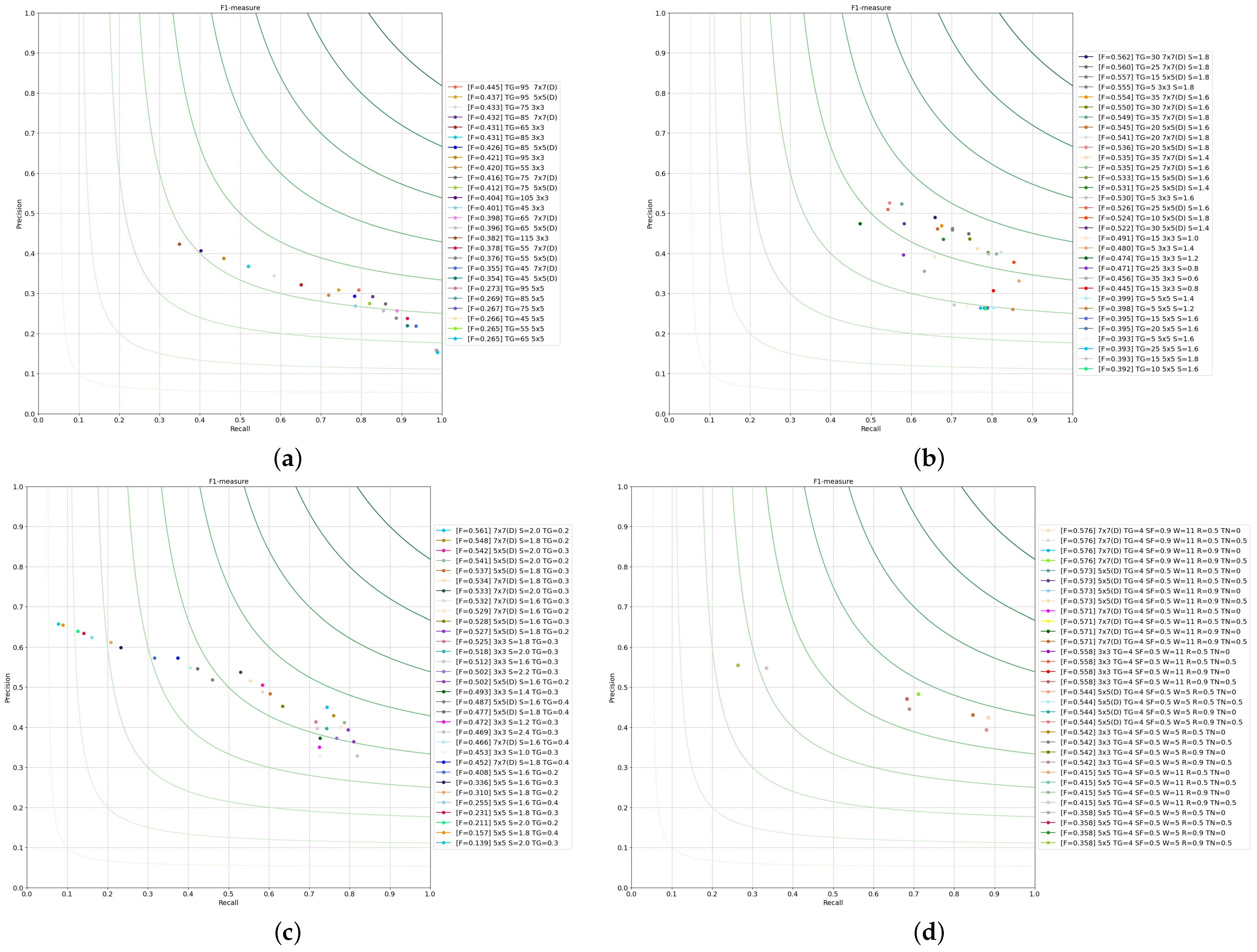


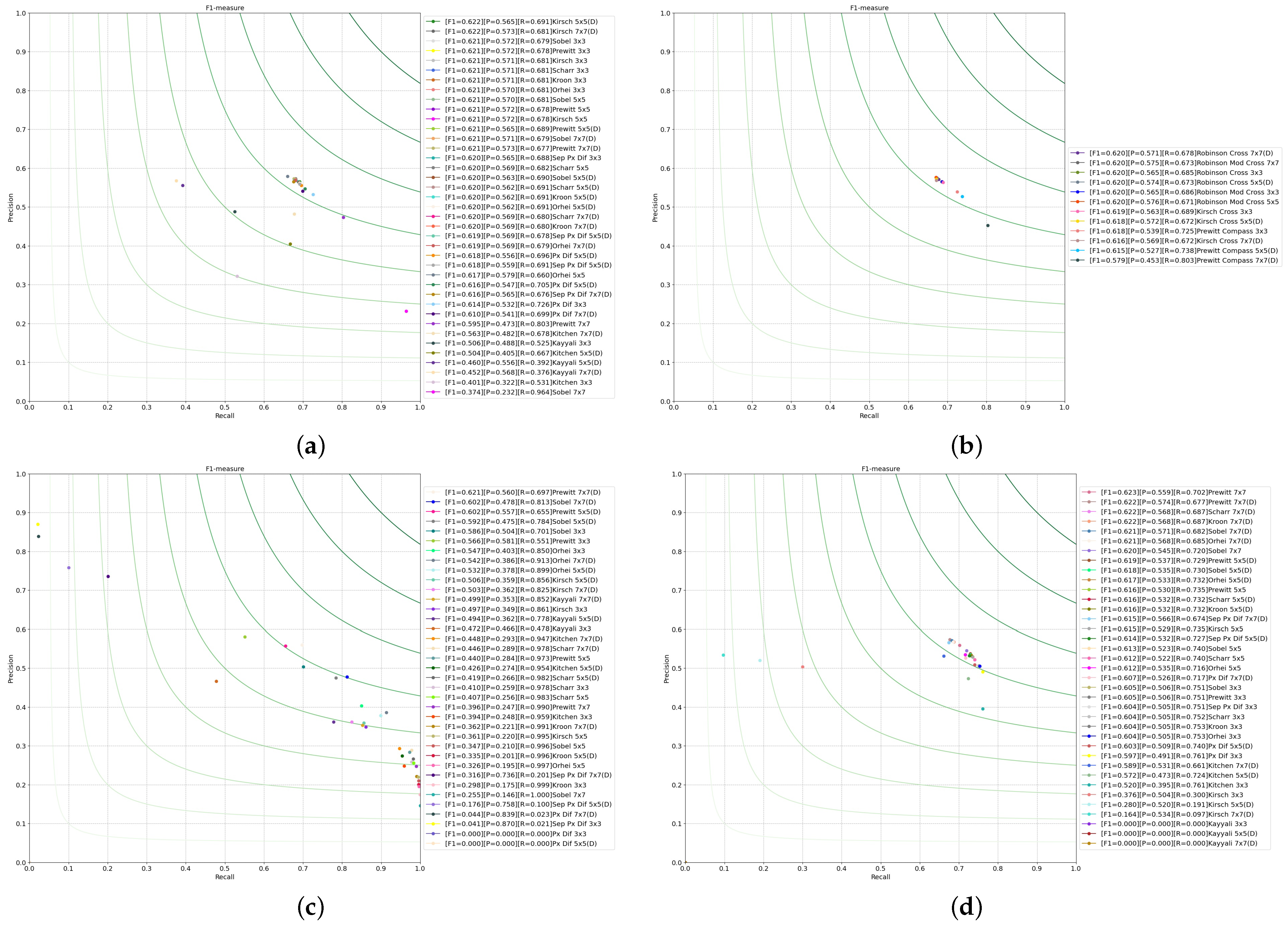
| Operator | PCM [69] | SFOM [58] | ||||||
|---|---|---|---|---|---|---|---|---|
| Kernel | P | R | F1 | Parameters | Kernel | SFoM | Parameters | |
| First Order Orthogonal | 7 × 7(D) | 0.571 | 0.679 | 0.621 | TG = 50, S = 2.75 | 7 × 7(D) | 0.754 | TG = 30, S = 2.25 |
| First Order Compass | 5 × 5(D) | 0.565 | 0.687 | 0.620 | TG = 50, S = 2.25 | 7 × 7(D) | 0.753 | TG = 30, S = 2.25 |
| Frei–Chen | 5 × 5(D) | 0.554 | 0.673 | 0.608 | TG = 60, S = 2.25 | 7 × 7(D) | 0.481 | TG = 30, S = 0.25 |
| Laplace | 7 × 7(D) | 0.309 | 0.794 | 0.445 | TG = 95 | 5 × 5(D) | 0.478 | TG = 15 |
| LoG | 7 × 7(D) | 0.490 | 0.659 | 0.562 | TG = 30, S = 1.8 | 7 × 7(D) | 0.491 | TG = 5, S = 1.0 |
| Marr–Hildreth | 7 × 7(D) | 0.450 | 0.744 | 0.561 | TG = 0.2, S = 2.0 | 5 × 5(D) | 0.411 | TG = 0.2, S = 1.6 |
| Canny | 7 × 7(D) | 0.478 | 0.813 | 0.602 | S = 1.5, TL = 90, TH = 130 | 7 × 7(D) | 0.679 | S = 2.25, TL = 70, TH = 100 |
| Shen–Castan | 7 × 7(D) | 0.483 | 0.711 | 0.576 | TG = 4, SF = 0.9, W = 11, TN = 0 | 5 × 5(D) | 0.442 | TG = 4, SF = 0.9, W = 11, TN = 0.5 |
| ED | 7 × 7(D) | 0.556 | 0.704 | 0.621 | TG = 50, TA = 5, SI = 1, GK = 7 | 3 × 3 | 0.673 | TG = 50, TA = 5, SI = 1, GK = 7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orhei, C.; Bogdan, V.; Bonchis, C.; Vasiu, R. Dilated Filters for Edge-Detection Algorithms. Appl. Sci. 2021, 11, 10716. https://doi.org/10.3390/app112210716
Orhei C, Bogdan V, Bonchis C, Vasiu R. Dilated Filters for Edge-Detection Algorithms. Applied Sciences. 2021; 11(22):10716. https://doi.org/10.3390/app112210716
Chicago/Turabian StyleOrhei, Ciprian, Victor Bogdan, Cosmin Bonchis, and Radu Vasiu. 2021. "Dilated Filters for Edge-Detection Algorithms" Applied Sciences 11, no. 22: 10716. https://doi.org/10.3390/app112210716
APA StyleOrhei, C., Bogdan, V., Bonchis, C., & Vasiu, R. (2021). Dilated Filters for Edge-Detection Algorithms. Applied Sciences, 11(22), 10716. https://doi.org/10.3390/app112210716







