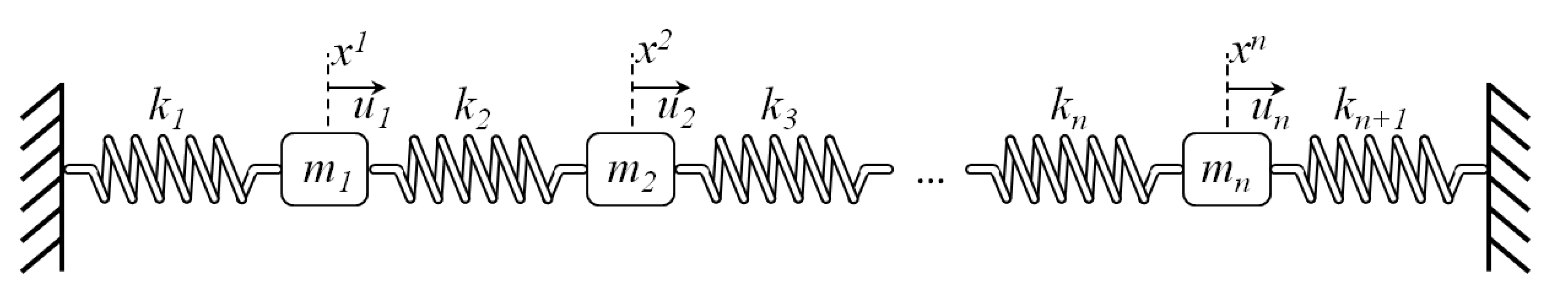A Mechanical Feedback Classification of Linear Mechanical Control Systems

Abstract

We give a classification of linear nondissipative mechanical control system under mechanical change of coordinates and feedback. First, we consider a controllable case that is somehow a mechanical counterpart of Brunovský classification, then we extend the result to all linear nondissipative mechanical systems (not necessarily controllable) which leads to a mechanical canonical decomposition. The classification of Lagrangian systems is given afterwards. Next, we show an application of the classification results to the stability and stabilization problem and illustrate them with several examples. All presented results in this paper are expressed in terms of objects on the configuration space ${\mathbb{R}}^n$ only, while the state-space of a mechanical control system is ${\mathbb{R}}^n\times {\mathbb{R}}^n$ consisting of configurations and velocities.

1. Introduction

In this paper we consider the problem of classification of linear mechanical control systems under mechanical feedback transformations. Therefore, by providing a solution to the classification problem, we answer several questions:

(a)

Given two linear mechanical systems, how to determine whether they are equivalent?

(b)

Is there a set of complete invariants that are computable in terms of objects on the configuration space only?

(c)

Is there a distinguished normal (or canonical) form?

We consider the above-defined classification problem in three important cases, namely for controllable and uncontrollable mechanical systems, and for the subclass of Lagrangian systems. A classification of controllable linear (first-order) systems $\dot{x}=Ax+Bu$ under general linear transformations and general linear feedback has been solved in the celebrated Brunovský classification [1], see also [2]. A general classification (including not necessarily controllable systems) leads to the canonical decomposition [3,4] and a short yet concise note [5]. Here, we consider the novel problem of classification of linear mechanical systems under linear transformations that respect splitting into configurations and velocities, and linear mechanical feedback. It turns out that the special form of considered (second-order) systems and the special form of (mechanical) transformations yield the counterpart of the above-mentioned classical results. In other words, we deal with a smaller class of control systems (than general linear systems) and we use more subtle mechanical feedback transformations (than general feedback transformations) and yet the invariants are perfectly analogous to those of the general case. Moreover, they can be computed on a half of the state space, namely using objects defined on the configurations space only. What is more, we show that mechanical feedback transformations are perfectly adapted to the class of mechanical systems, namely the classification of mechanical systems is the same if, instead of mechanical feedback transformations, we use all linear feedback transformations. Our analysis of the classification problem implies a series of results for stability and stabilization of linear mechanical systems that we present in Section 6. The problem of stability of motion of linear mechanical systems has been studied extensively, see e.g., [6,7], Section 5.2 in [8] and the reference therein. In those papers, certain structural assumptions (symmetry, positive definiteness, etc.) on matrices of the system are assumed, and what is crucial, dissipative forces are allowed an thus asymptotic stability is concerned. We present new results in this field. We do not assume, a priori, any structure on the mechanical system (see Section 2). Moreover, we consider mechanical systems without dissipative terms. This leads to important conclusions that, first, such systems are never asymptotically stable nor can be asymptotically stabilized by feedback. Second, only the Lagrangian subclass of mechanical control systems can be stable, therefore the problem of stabilization of (general) mechanical system reduces, actually, to the problem of finding mechanical transformations that make the system Lagrangian, which fits well to our classification problem.

The paper is organized as follows. In Section 2, we define the class of linear mechanical control systems and its special subclass, namely Lagrangian control systems, and we introduce linear mechanical feedback transformations. In Section 3 and Section 4, the complete classification under mechanical feedback transformations of, respectively, controllable (Theorem 1) and uncontrollable (Theorem 2) linear mechanical control systems is presented. Then, the classification of linear Lagrangian control systems is given in Section 5. In Section 6, we formulate results about stability and stabilization and show in Theorem 3 that, within the class of linear mechanical non-dissipative control systems, only Lagrangian ones can be stabilized (not asymptotically). Finally, we illustrate our theory by two multibody mass-spring systems. We conclude the paper in Section 8, where we summarize our results.

2. Problem Statement

2.1. Linear Mechanical Control Systems

In this subsection, we introduce the object of our study, namely linear mechanical control systems. This class is larger than linear Lagrangian control systems that will also be introduced in this subsection and form an important subclass in our study.

Consider the linear mechanical control system with n degrees of freedom and m controls

$$\begin{array}{c}\hfill \ddot{x}=Ex+Bu,\end{array}$$

(1)

where $x\in {\mathbb{R}}^n$ are the configurations (the generalized coordinates). The matrix E is an $n\times n$ constant real matrix corresponding to an uncontrolled (depending on configurations only but, possibly, non potential) force in the system and the input matrix B is an $n\times m$ constant real matrix describing external forces controlled by the controls $u\in {\mathbb{R}}^m$.

Equivalently, system (1) can be represented as a first-order system on the state-space ${\mathbb{R}}^n\times {\mathbb{R}}^n$, equipped with coordinates $(x,y)$ denoting, respectively, configurations and velocities

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{LMS}\dot{x}& =y\hfill \\ \hfill \dot{y}& =Ex+Bu,\hfill \end{array}\end{array}$$

(2)

or as a linear control system of dimension $2n$, with coordinates $z=\left(x,y\right)\in {\mathbb{R}}^n\times {\mathbb{R}}^n$ (to be precise z is a “stacked” vector $z={(x^T,y^T)}^T$, however we decide to skip this notation for a clarity sake), given by, compare [9]

$$\dot{z}=\widehat{A}z+\widehat{B}u,$$

(3)

where

$$\widehat{A}=\left(\begin{array}{cc}0& I_n\\ E& 0\end{array}\right),\widehat{B}=\left(\begin{array}{c}0\\ B\end{array}\right).$$

(4)

Notice that the equation $\dot{y}=Ex+Bu$ is not of the more general form $\dot{y}=Ex+Ly+Bu$, that is, contains neither gyroscopic nor dissipative terms $Ly$, see e.g., [6,7,9,10] for a discussion of both classes.

Our obvious inspiration are linear Lagrangian (conservative) systems which constitute a subclass of (2) whose configuration space is the real vector space ${\mathbb{R}}^n$, equipped with an inner product on the space ${\mathbb{R}}^n$ of velocities given by a real valued quadratic form $\frac{1}{2}{\dot{x}}^{T}M\dot{x}$ (describing the kinetic energy of the system), where M is a constant real symmetric and positive definite matrix $(M^T=M>0)$. Moreover, we consider the potential energy given by a quadratic form $V=\frac{1}{2}{x}^{T}Px$, where P is a symmetric potential matrix $(P^T=P)$.

The corresponding quadratic Lagrangian reads $\mathcal{L}=\frac{1}{2}{\dot{x}}^{T}M\dot{x}-\frac{1}{2}{x}^{T}Px$. The derivation of the Euler-Lagrange equations yields the second-order system:

$$M\ddot{x}+Px=Ku,$$

(5)

where K is an $n\times m$ real matrix whose columns are vectors corresponding to the external controlled forces. Straightforward calculations show that any Lagrangian linear mechanical control system can be represented by a particular form of (2), namely

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{LLS}\dot{x}& =y\hfill \\ \hfill \dot{y}& =E^{L}x+Bu,\hfill \end{array}\mathrm{where}{E}^L=-M^{-1}P\mathrm{and}B=M^{-1}K.\end{array}$$

(6)

Notice that for Lagrangian systems (6) the matrix B can be any (since K is arbitrary) but the matrix $E^L$ is special, namely the product of two symmetric matrices (the first being invertible), which we call the Lagrangian structure.

Another characterization of (6) can be formulated as follows [11].

Proposition 1.

The linear mechanical control system (2) is a Lagrangian system of the form (6) if and only if there exists a real invertible map $T:{\mathbb{R}}^n\to {\mathbb{R}}^n$ that diagonalizes the matrix E, that is, $TE{T}^{-1}=\mathrm{diag}({\lambda }_1,\dots ,{\lambda }_n)$.

For a proof see [11]. The above proposition can be rephrased as follows. All distinct eigenvalues ${\lambda }_j$ of the matrix E, $1\le j\le q$, where q is the number of distinct eigenvalues, are real, i.e., ${\lambda }_j\in \mathbb{R}$, and there are no Jordan blocks. More precisely, the algebraic multiplicity ${\mu }_j$ of ${\lambda }_j$ (indicating how many times ${\lambda }_j$ appears as a root of the characteristic polynomial of E) is equal to its geometric multiplicity ${\gamma }_j=dimker({\lambda }_i{I}_n-E)$, i.e., the dimension of the eigenspace associated with ${\lambda }_j$.

Remark 1.

Obviously, Lagrangian control systems can be represented using the Hamiltonian formulation, as Hamiltonian control systems. There exists a widely studied branch of control theory for this class of systems. For a relation between Lagrangian systems and Hamiltonian systems, including nonlinear case, see [12]. For a survey of port-Hamiltonian systems see [13].

2.2. Linear Mechanical Feedback Transformations

In this subsection, we introduce mechanical feedback transformations under which we classify linear mechanical systems, namely mechanical changes of coordinates and mechanical feedback.

A linear mechanical transformation is given by a linear transformation of the following form $\tilde{z}=\mathcal{T}z$, where $\mathcal{T}=\left(\begin{array}{cc}T& 0\\ 0& T\end{array}\right)$, $z=(x,y)$ and $\tilde{z}=(\tilde{x},\tilde{y})$, i.e.,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \tilde{x}=Tx,\tilde{y}=Ty,\end{array}\end{array}$$

(7)

where T is an invertible $n\times n$ real matrix. This linear transformation preserves configurations, i.e., maps x-coordinates into $\tilde{x}$-coordinates. Moreover, since the derivatives of configurations are velocities, it induces the linear transformation $\tilde{y}=Ty$ (given by the same T) on velocities that maps the equation $\dot{x}=y$ into $\dot{\tilde{x}}=\tilde{y}$.

The linear mechanical feedback is

$$u=Fx+G\tilde{u},$$

(8)

where F is an $m\times n$ matrix and G is an $m\times m$ invertible matrix. The linear mechanical system (2) transformed by the transformations (7) and (8) reads

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{\tilde{x}}& =Ty=\tilde{y}\hfill \\ \hfill \dot{\tilde{y}}& =T\left(E+BF\right)T^{-1}\tilde{x}+TBG\tilde{u}=\tilde{E}\tilde{x}+\tilde{B}\tilde{u}.\hfill \end{array}\end{array}$$

(9)

Definition 1.

Two systems (2), given by $\dot{x}=y$, $\dot{y}=Ex+Bu$, and $\left(\widetilde{\mathcal{LMS}}\right)$, given by $\dot{\tilde{x}}=\tilde{y}$, $\dot{\tilde{y}}=\tilde{E}\tilde{x}+\tilde{B}\tilde{u}$, are called linear mechanical feedback equivalent, briefly LMF-equivalent, if there exist mechanical transformations (7) and (8) such that $\tilde{E}=T(E+BF)T^{-1}$ and $\tilde{B}=TBG$.

It is natural to consider mechanical transformations (7) and (8), since the class of linear mechanical control systems (2) is closed under those transformations, i.e., the transformed system (9) is linear and mechanical. However, in case of the subclass of Lagrangian systems (6), the mechanical transformations need not preserve the Lagrangian structure (see Section 5 for a detailed analysis).

The group of linear mechanical transformations $LMF$, consisting of triplets $\left(\mathcal{T},F,G\right)$, preserves trajectories, that is, any element $\left(\mathcal{T},F,G\right)$ of that group maps the trajectories of (2) into those of its LMF-equivalent system $\left(\widetilde{\mathcal{LMS}}\right)$, given by (9). Indeed, if $z\left(t,z_0,u\left(t\right)\right)$ is a trajectory of (2), passing through $z_0 = (x_0,y_0)$ and corresponding to a control $u\left(t\right)$, then $\tilde{z}\left(t,{\tilde{z}}_0,\tilde{u}\left(t\right)\right)=\mathcal{T}z\left(t,z_0,u\left(t\right)\right)$ is a trajectory of (9), passing through ${\tilde{z}}_0=\mathcal{T}{z}_0=(T{x}_0,T{y}_0)$ and corresponding to $\tilde{u}\left(t\right)$, where $u\left(t\right)=Fx\left(t\right)+G\tilde{u}\left(t\right)$. Moreover, via $T:{\mathbb{R}}^n\to {\mathbb{R}}^n$, it establishes a correspondence between trajectories in the configuration space ${\mathbb{R}}^n$, i.e., $\tilde{x}\left(t,{\tilde{z}}_0,\tilde{u}\left(t\right)\right) = Tx(t,z_0,u\left(t\right))$, making the following diagram commutative (notice, however, that $\pi \left(z(t,z_0,u)\right) = x(t,z_0,u)$ depends on $z_0=(x_0,y_0)$ consisting of an initial configuration $x_0$ and initial velocity $y_0$):

$$\begin{array}{ccc}\begin{array}{c}\hfill z(t,z_0,u)\\ \begin{array}{cc}\hfill \downarrow & \pi \hfill \end{array}\end{array}& \stackrel{\left(\mathcal{T},F,G\right)}{\to }& \begin{array}{c}\hfill \tilde{z}(t,{\tilde{z}}_0,\tilde{u})\\ \begin{array}{cc}\hfill \downarrow & \pi \hfill \end{array}\end{array}\\ \hfill x(t,z_0,u)& \stackrel{\left(T,F,G\right)}{\to }& \tilde{x}(t,{\tilde{z}}_0,\tilde{u})\end{array}$$

where $\pi :{\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ is the canonical projection $\pi (x,y)=x$, which assigns to the pair $(x,y)$ the point x at which the velocity y is attached.

3. Classification of Controllable Systems (2)

A linear mechanical control system (2) is controllable if for any $t_0$, any initial state $z_0=(x_0,y_0)$, and any final state $z_f=(x_f,y_f)$ there exist $t_f>t_0$ and a control $u:[t_0,t_f]\to {\mathbb{R}}^m$, such that $z\left(t_0\right)=(x_0,y_0)$ and $z\left(t_f\right)=(x_f,y_f)$. The following result is a straightforward generalization of [10], see also [9] and cf. a classical work on modal controllability for Lagrangian class including dissipative forces [7,14].

Lemma 1 

(Controllability of (2)). For (2) the following statements are equivalent:

(i) 

$\left(\mathcal{LMS}\right)$ is controllable

(ii) 

$\mathrm{rank}\left(\widehat{B},\widehat{A}\widehat{B},\dots ,{\widehat{A}}^{2n-1}\widehat{B}\right)=2n$ (Kalman Rank Condition)

(iii) 

$\mathrm{rank}\left(\widehat{B},{\widehat{A}}^2\widehat{B},\dots ,{\widehat{A}}^{2(n-1)}\widehat{B}\right)=n$

(iv) 

$\mathrm{rank}\left(B,EB,\dots ,E^{n-1}B\right)=n$ (Mechanical Kalman Rank Condition)

Proof. 

From the Kalman controllability result, we have $\left(i\right)$⇔$\left(ii\right)$. The rest of the proof follows from a direct computation of the Kalman controllability matrix

$$\begin{array}{c}\hfill \left(\widehat{B},\widehat{A}\widehat{B},\dots ,{\widehat{A}}^{2n-1}\widehat{B}\right)=\left(\begin{array}{ccccccc}0& B& 0& EB& \dots & 0& E^{n-1}B\\ B& 0& EB& 0& \dots & E^{n-1}B& 0\end{array}\right).\end{array}$$

(10)

Therefore we see that we can take only even powers ${\widehat{A}}^{2i}\widehat{B}$ in $\left(iii\right)$ or the lower part of the matrix (10) as in $\left(iv\right)$. □

Remark 2.

Note that the Machanical Kalman Rank Condition, i.e., item $\left(iv\right)$ of Lemma 1, uses objects on the configuration space ${\mathbb{R}}^n$ only, while the state-space of (2) is ${\mathbb{R}}^n\times {\mathbb{R}}^n$. Apart of a pure mathematical value, that sort of reduction is practically motivated since computations are simpler. All of our further results share that property.

Now attach to the system (2) an n-tuple of indices $({\overline{r}}_0,\dots ,{\overline{r}}_{n-1})$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{r}}_0& =\mathrm{rank}\left(B\right),\hfill \\ \hfill {\overline{r}}_i& =\mathrm{rank}\left(B,EB,...,E^{i}B\right)-\mathrm{rank}\left(B,EB,...,E^{i-1}B\right),\hfill \end{array}\end{array}$$

(11)

for $1\le i\le n-1$. Furthermore, define the dual indices

$$\begin{array}{c}\hfill {\overline{\rho }}_j=\mathrm{card}\left({\overline{r}}_i\ge j:0\le i\le n-1\right)\mathrm{for}1\le j\le m.\end{array}$$

(12)

These integers, which we will call mechanical half-indices, are mechanical analogues of the controllability (Brunovský, Kronecker) indices $r_i$’s and ${\rho }_j$’s of system (3) defined by (11) and (12), respectively, with E replaced by $\widehat{A}$ and B by $\widehat{B}$. Note that the indices ${\overline{\rho }}_i$ are invariant under (7) and (8), therefore they form a set of invariants attached to (2). Actually, they form a set of complete invariants, as we will show in Theorem 1 below. We denote the above sequences as $\overline{\mathcal{R}}\left(E,B\right)=\left({\overline{r}}_0,\dots ,{\overline{r}}_{n-1}\right)$ and $\overline{\mathcal{P}}\left(E,B\right)=\left({\overline{\rho }}_1,\dots ,{\overline{\rho }}_m\right)$.

Proposition 2.

For the mechanical control system $\left(\mathcal{LMS}\right)$

(i) 

the sequence of indices $\mathcal{R}\left(\widehat{A},\widehat{B}\right)=\left(r_0,r_1,\dots ,r_{2n-1}\right)$ is the doubled sequence of $\overline{\mathcal{R}}\left(E,B\right)$, i.e., $\left(r_0,r_1,\dots ,r_{2n-1}\right)=\left({\overline{r}}_0,{\overline{r}}_0,{\overline{r}}_1,{\overline{r}}_1,\dots ,{\overline{r}}_{n-1},{\overline{r}}_{n-1}\right)$;

(ii) 

the mechanical half-indices are half of the controllability indices, i.e., ${\rho }_j=2{\overline{\rho }}_j$, for $1\le j\le m$.

Proof. 

Let us invoke the controllability matrix of $\left(\mathcal{LMS}\right)$ given by (10) and calculate $r_0=\mathrm{rank}\widehat{B}$ and $r_i=\mathrm{rank}\left(\widehat{B},\dots ,{\widehat{A}}^i\widehat{B}\right)-\mathrm{rank}\left(\widehat{B},\dots ,{\widehat{A}}^{i-1}\widehat{B}\right)$, and compare them with ${\overline{r}}_i$ given by (11). The crucial observation is that we can calculate the ranks of the lower and upper submatrices separately and then add them.

$$\begin{array}{cc}\hfill r_0=& \mathrm{rank}\widehat{B}=\mathrm{rank}B={\overline{r}}_0\hfill \\ \hfill r_1=& \mathrm{rank}\left(\widehat{B},\widehat{A}\widehat{B}\right)-\mathrm{rank}\widehat{B}=\left(\mathrm{rank}B+\mathrm{rank}B\right)-\mathrm{rank}B={\overline{r}}_0.\hfill \end{array}$$

Assume that $(r_0,r_1,\dots ,r_{2i-2},r_{2i-1})=\left({\overline{r}}_0,{\overline{r}}_0,\dots ,{\overline{r}}_{i-1},{\overline{r}}_{i-1}\right)$. Then

$$\begin{array}{cc}\hfill r_{2i}& =\mathrm{rank}\left(\widehat{B},\cdots ,{\widehat{A}}^{2i}\widehat{B}\right)-\mathrm{rank}\left(\widehat{B},\cdots ,{\widehat{A}}^{2i-1}\widehat{B}\right)\hfill \\ \hfill & =\mathrm{rank}\left(B,\dots ,E^{i}B\right)+\mathrm{rank}\left(B,\dots ,E^{i-1}B\right)-2\mathrm{rank}\left(B,\dots ,E^{i-1}B\right)\hfill \\ & =\mathrm{rank}\left(B,\dots ,E^{i}B\right)-\mathrm{rank}\left(B,\dots ,E^{i-1}B\right)={\overline{r}}_i,\hfill \\ \hfill r_{2i+1}& =\mathrm{rank}\left(\widehat{B},\cdots ,{\widehat{A}}^{2i+1}\widehat{B}\right)-\mathrm{rank}\left(\widehat{B},\cdots ,{\widehat{A}}^{2i}\widehat{B}\right)\hfill \\ & =2\mathrm{rank}\left(B,\dots ,E^{i}B\right)-\left(\mathrm{rank}\left(B,\dots ,E^{i}B\right)+\mathrm{rank}\left(B,\dots ,E^{i-1}B\right)\right)\hfill \\ & =\mathrm{rank}\left(B,\dots ,E^{i}B\right)-\mathrm{rank}\left(B,\dots ,E^{i-1}B\right)={\overline{r}}_i.\hfill \end{array}$$

By an induction argument, the sequence of n integers $\overline{\mathcal{R}}\left(E,B\right)=\left({\overline{r}}_0,{\overline{r}}_1,\dots ,{\overline{r}}_{n-1}\right)$ and that of $2n$ integers $\mathcal{R}\left(\widehat{A},\widehat{B}\right)=\left(r_0,\dots ,r_{2n-1}\right)$ satisfy the desired relation $\left(i\right)$. Using (12) and $\left(i\right)$, calculate, for $1\le j\le m$,

$$\begin{array}{c}\hfill {\rho }_j=\mathrm{card}\left(r_i\ge j:0\le i\le 2n-1\right)=2\mathrm{card}\left({\overline{r}}_i\ge j:0\le i\le n-1\right)=2{\overline{\rho }}_j,\end{array}$$

which proves $\left(ii\right)$. □

The following theorem asserts that mechanical half-indices form a set of complete invariants ${\overline{\rho }}_j$ of linear controllable mechanical systems (2), as do controllability indices ${\rho }_j$ and indices ${\overline{r}}_i$.

Theorem 1.

The following statements are equivalent, for fixed n and m:

(i) 

Two controllable systems (2) and $\left(\widetilde{\mathcal{LMS}}\right)$, represented by pairs $(E,B)$ and $(\tilde{E},\tilde{B})$, respectively, are LMF-equivalent,

(ii) 

$\overline{\mathcal{R}}(E,B)=\overline{\mathcal{R}}(\tilde{E},\tilde{B})$,

(iii) 

$\overline{\mathcal{P}}(E,B)=\overline{\mathcal{P}}(\tilde{E},\tilde{B})$, i.e., the mechanical half-indices coincide,

(iv) 

$\mathcal{P}(\widehat{A},\widehat{B})=\mathcal{P}(\widehat{\tilde{A}},\widehat{\tilde{B}})$, i.e., the controllability indices coincide,

where $\widehat{A},\widehat{B}$ and $\widehat{\tilde{A}},\widehat{\tilde{B}}$ are of the form (4).

Proof. 

Equivalence of $\left(ii\right)$ and $\left(iii\right)$ follows from the definition.

$\left(i\right)\iff \left(iii\right)$. We associate with (2), given by the pair $(E,B)$, a virtual linear (first-order) control system

$$\begin{array}{c}\hfill \dot{x}=Ex+Bv,\end{array}$$

(13)

and similarly with $\left(\widetilde{\mathcal{LMS}}\right)$, given by $(\tilde{E},\tilde{B})$, we associate

$$\begin{array}{c}\hfill \dot{\tilde{x}}=\tilde{E}\tilde{x}+\tilde{B}\tilde{v}.\end{array}$$

(14)

Now we directly use the Brunovský classification theorem [1] to prove that (13) and (14) are equivalent under a transformation $\tilde{x}=Tx$ and feedback $v=Fx+G\tilde{v}$, if and only if their controllability indices coincide. Note that the controllability indices of (13), respectively of (14), coincide with the mechanical half-indices of associated (2) (respectively $\left(\widetilde{\mathcal{LMS}}\right)$). Now notice that $\tilde{x}=Tx$ and $v=Fx+G\tilde{v}$ establish feedback equivalence between (13) and (14) if and only if $\tilde{x}=Tx$, $\tilde{y}=Ty$, and $u=Fx+G\tilde{u}$ establish LMF-equivalence between (2) and $\left(\widetilde{\mathcal{LMS}}\right)$. Therefore $\left(i\right)$ is equivalent to $\left(iii\right)$. Equivalence of $\left(iii\right)$ and $\left(iv\right)$ follows immediately from Proposition 2. □

Remark 3.

Notice that the general feedback group acting on systems of the form (3) by $\widehat{A}\mapsto S\left(\widehat{A}+\widehat{B}\widehat{F}\right)S^{-1}$, $\widehat{B}\mapsto S\widehat{B}\widehat{G}$ (where $S:{\mathbb{R}}^{2n}\to {\mathbb{R}}^{2n}$ is any, not necessarily of the form (7)) is much bigger than the mechanical feedback group (7) and (8). Nevertheless both group actions have exactly the same orbits when acting on linear mechanical systems (2) and thus, the same sets of complete invariants implying that if two linear mechanical systems are feedback equivalent they are also mechanical feedback equivalent.

We can formulate the following important corollary.

Corollary 1.

Any linear mechanical controllable system (2) is LMF-equivalent to the mechanical canonical form

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_i^j& =y_i^j\hfill \\ \hfill {\dot{y}}_i^j& =x_i^{j+1}\hfill \\ \hfill {\dot{y}}_i^{{\overline{\rho }}_i}& =u_i,\hfill \end{array},1\le i\le m,1\le j\le {\overline{\rho }}_i,\end{array}$$

(15)

where $({\overline{\rho }}_1,\dots ,{\overline{\rho }}_m)$ are mechanical half-indices.

The above corollary follows from the fact (see the proof of the equivalence $\left(i\right)\iff \left(iii\right)$ of Theorem 1) that if a transformation $\tilde{x}=Tx$, $v=Fx+G\tilde{v}$ brings (13) into the Brunovský form, then $\tilde{x}=Tx$, $\tilde{y}=Ty$, and $u=Fx+G\tilde{u}$ brings (2) into the above mechanical canonical form (15).

The mechanical canonical form (15) consists of m chains of even number $2{\overline{\rho }}_i$ of integrators and can also be represented in the matrix form:

$$\begin{array}{cc}\hfill \dot{x}& =y\hfill \\ \hfill \dot{y}& =E_{F}x+B_{F}u,\hfill \end{array}$$

where the pair $(E_F,B_F)$ is in the Brunovský form, i.e., $E_F$, $B_F$, are block diagonal matrices, of dimension $n\times n$ and $n\times m$, respectively, of the following forms:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill E_F=\left(\begin{array}{cccc}{N}_1& & & \\ & N_2& & \\ & & \ddots & \\ & & & N_m\end{array}\right),B_F=\left(\begin{array}{cccc}{b}_1& & & \\ & b_2& & \\ & & \ddots & \\ & & & b_m\end{array}\right),\end{array}\end{array}$$

(16)

where $N_i$, $1\le i\le m$, is a superdiagonal nilpotent matrix of dimension ${\overline{\rho }}_i$ (mechanical half-index) and $b_i$ is a ${\overline{\rho }}_i\times 1$ vector:

$$\begin{array}{c}\hfill N_i=\left(\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ & & \ddots & \\ 0& 0& 0& \dots & 1\\ 0& 0& 0& \dots & 0\end{array}\right),b_i=\left(\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right).\end{array}$$

(17)

4. Classification of Uncontrollable Systems (2)

In this section, we assume that (2) is not controllable (cf. Lemma 1), i.e.,

$$\begin{array}{c}\hfill \mathrm{rank}\left(B,EB,\dots ,E^{n-1}B\right)=k<n.\end{array}$$

We will use the same class of mechanical transformations (7) and (8) to establish a canonical form for systems (2) that are not controllable and thus we will classify them (for the controllable case, Theorem 1 and form (15) provide a complete classification).

Theorem 2.

For given $n,m,k$, the linear mechanical system (2) is LMF-equivalent to the following canonical form:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_c& =y_c\hfill \\ \hfill {\dot{y}}_c& =E_F{x}_c+B_{F}u\hfill \end{array}\begin{array}{cc}\hfill {\dot{x}}_d& =y_d\hfill \\ \hfill {\dot{y}}_d& =E_d^J{x}_d,\hfill \end{array}\end{array}$$

(18)

where $dim{x}_c=k$, and $E_F$, $B_F$ are block-diagonal matrices of dimension $k\times k$, $k\times m$, respectively, of the form (16) and (17), given by the mechanical half-indices ${\overline{\rho }}_1,\dots ,{\overline{\rho }}_m$ satisfying ${\sum }_{j=1}^m{\overline{\rho }}_j=k$, while $E_d^J$ is in the Jordan form, that is, a block-diagonal $(n-k)\times (n-k)$ matrix whose diagonal blocks are of four possible forms:

(i)

for a real eigenvalue ${\lambda }_j$ of $E_d^J$

$$\begin{array}{c}\hfill \mathrm{either}\begin{array}{c}\hfill D_j^{\mathbb{R}}=\left(\begin{array}{ccccc}{\lambda }_j& & & & \\ & \ddots & & \\ & & {\lambda }_j& \\ & & & {\lambda }_j\end{array}\right)\end{array}\mathrm{or}\begin{array}{c}\hfill J_j^{\mathbb{R}}=\left(\begin{array}{ccccc}{\lambda }_j& 1& & & \\ & \ddots & \ddots & \\ & & {\lambda }_j& 1\\ & & & {\lambda }_j\end{array}\right),\end{array}\end{array}$$

(ii)

for a complex eigenvalue ${\lambda }_j={\alpha }_j\pm \mathtt{i}{\beta }_j$ of $E_d^J$

$$\begin{array}{c}\hfill \mathrm{either}\begin{array}{c}\hfill D_j^{\mathbb{C}}=\left(\begin{array}{ccccc}{C}_j& & & & \\ & \ddots & & \\ & & C_j& \\ & & & C_j\end{array}\right)\end{array}\mathrm{or}\begin{array}{c}\hfill J_j^{\mathbb{C}}=\left(\begin{array}{ccccc}{C}_j& I_2& & & \\ & \ddots & \ddots & \\ & & C_j& I_2\\ & & & C_j\end{array}\right),\end{array}\end{array}$$

where $C_j=\left(\begin{array}{cc}{\alpha }_j& {\beta }_j\\ -{\beta }_j& {\alpha }_j\end{array}\right)$ and $I_2=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$.

Therefore any mechanical system (2) can be decomposed under LMF into two independent mechanical subsystems:

(i)

a $2k$-dimensional controllable mechanical system (2) represented in $(x_c,y_c)$-coordinates by the pair $(E_F,B_F)$, which is in the canonical form (15), with mechanical half-indices ${\overline{\rho }}_1,\dots ,{\overline{\rho }}_m$; the subindex “c” stands for controllable,

(ii)

a dynamical linear mechanical system (a system without controls) represented in $(x_d,y_d)$-coordinates by the second-order differential equation $\ddot{x}=E_d{x}_d$, where the matrix $E_d$ can always be transformed into the Jordan form $E_d^J$; the subindex “d” stands for dynamical.

Proof. 

The system (2) is uniquely defined by the pair $(E,B)$ on which an element $\left(\mathcal{T},F,G\right)$ of the group $LMF$ acts according to the rule:

$$\begin{array}{c}\hfill \left(E,B\right)\stackrel{(T,F,G)}{⟼}\left(T(E+BF)T^{-1},TBG\right),\end{array}$$

which is the same equivalence transformation as in [5], where a slightly different notation $(A=E,P=T^{-1},K=F{T}^{-1},Q=G)$ is used. By the result of [5], we bring the pair $(E,B)$ into the form:

$$\begin{array}{c}\hfill E=\left(\begin{array}{cc}{E}_F& 0\\ 0& E_d\end{array}\right),B=\left(\begin{array}{c}{B}_F\\ 0\end{array}\right),\end{array}$$

where $E_d$ is an $(n-k)\times (n-k)$ matrix and $(E_F,B_F)$ is in Brunovský form. What remains to prove is to bring $E_d$ into its canonical form $E_d^J$. In order to do that, we use a change of coordinates $x_d\mapsto T_d{x}_d$, $y_d\mapsto T_d{y}_d$, where $T_d:{\mathbb{R}}^{n-k}\to {\mathbb{R}}^{n-k}$ brings $E_d$ into its real Jordan form $E_d^J$, see e.g., [15], and apply $T=\left(\begin{array}{cc}{I}_k& 0\\ 0& T_d\end{array}\right)$. □

Denote $\mathcal{B}=\mathrm{Im}B$ and ${\mathcal{X}}_c=\mathcal{B}+E\mathcal{B}+\dots +E^{k-1}\mathcal{B}$. We have $E{\mathcal{X}}_c\subset {\mathcal{X}}_c$ (since $\mathrm{rank}(B,EB,\dots ,E^{k-1}B)=k$), so E gives rise to a well defined map $\widehat{E}:{\mathbb{R}}^n/{\mathcal{X}}_c\to {\mathbb{R}}^n/{\mathcal{X}}_c$ between the quotient spaces (i.e., factor spaces). Choose a subspace ${\mathcal{X}}_d\subset {\mathbb{R}}^n$ such that ${\mathcal{X}}_c\oplus {\mathcal{X}}_d={\mathbb{R}}^n$ and any linear coordinates $(x_c,x_d)$ on ${\mathbb{R}}^n$ such that ${\mathcal{X}}_c=\left\{\left(\begin{array}{c}{x}_c\\ 0\end{array}\right):x_c\in {\mathbb{R}}^k\right\}$ and ${\mathcal{X}}_d=\left\{\left(\begin{array}{c}0\\ x_d\end{array}\right):x_d\in {\mathbb{R}}^{n-k}\right\}$. Thus the matrix E takes in the $(x_c,x_d)$-coordinates the block-triangular form $E=\left(\begin{array}{cc}{E}_c^1& E_c^2\\ 0& E_d\end{array}\right)$ and the map $\widehat{E}$ in these coordinates is given by the matrix $E_d$. Choosing another subspace ${\tilde{\mathcal{X}}}_d$ (completing ${\mathcal{X}}_c$ to ${\mathbb{R}}^n$) will lead to another system of coordinates $({\tilde{x}}_c,{\tilde{x}}_d)$ and a matrix ${\tilde{E}}_d$ related to $E_d$ by ${\tilde{E}}_d=T{E}_d{T}^{-1}$. So the eigenvalues of $\widehat{E}$ are well defined as those of $E_d$ (being, obviously, the same as those of ${\tilde{E}}_d$).

Let ${\lambda }_1,\dots ,{\lambda }_q$ be q mutually distinct eigenvalues of the matrix $E_d$. For each ${\lambda }_j$, $1\le j\le q$, let ${\delta }_j$ be the dimension of the diagonal block of ${\lambda }_j$ and let ${\kappa }_j$ be the number of Jordan blocks of ${\lambda }_j$, whose dimensions are ${\epsilon }_j^1,\dots ,{\epsilon }_j^{{\kappa }_j}$, respectively. We define the eigenstructure ${\Lambda }_j$ of ${\lambda }_j$ by ${\Lambda }_j=({\lambda }_j,{\delta }_j,{\epsilon }_j^1,\dots ,{\epsilon }_j^{{\kappa }_j})$. Clearly, the same eigenvalue ${\lambda }_j$ may appear in more than one block and the algebraic multiplicity of ${\lambda }_j$ is ${\mu }_j={\delta }_j+{\epsilon }_j^1+\dots +{\epsilon }_j^{{\kappa }_j}$.

Proposition 3.

Two mechanical control systems (2) and $\left(\widetilde{\mathcal{LMS}}\right)$ given by $(E,B)$ and $(\tilde{E},\tilde{B})$, respectively, are LMF-equivalent if and only if their mechanical half-indices coincide, that is $\overline{\mathcal{P}}(E,B)=\overline{\mathcal{P}}(\tilde{E},\tilde{B})$, and the eigenstructures of $E_d$ and ${\tilde{E}}_d$ coincide $({\Lambda }_1,\dots ,{\Lambda }_q)=({\tilde{\Lambda }}_1,\dots ,{\tilde{\Lambda }}_q)$, up to a permutation of ${\Lambda }_j$’s, where q, the number of distinct eigenvalues, is the same for both systems.

Proof. 

By Theorem 2, both systems can be brought, by LMF-transformations, into their canonical form (18). Then, both controllable subsystems are LMF-equivalent if and only if their mechanical half-indices coincide (see Theorem 1). Finally, if the eigenstructures of $E_d^J$ and ${\tilde{E}}_d^J$ coincide, then they are the same matrices up to a permutation of blocks (note that both are in the Jordan form) and vice versa. Thus the composition of both LMF-transformations converts (2) into $\left(\widetilde{\mathcal{LMS}}\right)$. □

Example 1.

Consider two systems (2) and $\left(\widetilde{\mathcal{LMS}}\right)$, with $n=3$, $m=1$ represented, respectively, by the following pairs $(E,B)$ and $(\tilde{E},\tilde{B})$:

$$\begin{array}{c}\hfill E=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),\tilde{E}=\left(\begin{array}{ccc}1& 1& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right),B=\tilde{B}=\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right).\end{array}$$

It can be easily checked that the two systems are not LMF-equivalent. For both systems $k=1$ and the mechanical half-indices are ${\overline{\rho }}_1=1$. The dynamical (uncontrolled) part of both systems has $\lambda =1$ as an eigenvalue of algebraic multiplicity 2 but the eigenstructure of the first system is $\Lambda =(\lambda ,\delta ,\epsilon )=(1,2,0)$, meaning that $\lambda =1$ defines a diagonal block of dimension 2, and that of the second system is $\Lambda =(\tilde{\lambda },\tilde{\delta },\tilde{\epsilon })=(1,0,2)$, meaning that there is a single Jordan block of dimension 2.

5. Classification of Lagrangian Systems (6)

We start with a counterpart of Proposition 3. To formulate it, recall that the matrix $E^L=M^{-1}P$, associated with the Lagrangian system (6), has real eigenvalues and is diagonalizable. It follows that, each eigenvalue ${\lambda }_j$ of $E_d^L$ is real and its eigenstructure is ${\Lambda }_j=({\lambda }_j,{\delta }_j,0)$, for $1\le j\le q$, where q is the number of mutually distinct eigenvalues of $E_d^L$ and ${\mu }_j={\delta }_j$ are their algebraic multiplicities. In this case, we will simply denote ${\Lambda }_j=({\lambda }_j,{\mu }_j)$. Recall that, see Section 4, the matrix $E_d$ represents the quotient map $\widehat{E}:{\mathbb{R}}^n/{\mathcal{X}}_c\to {\mathbb{R}}^n/{\mathcal{X}}_c$, induced by $E:{\mathbb{R}}^n\to {\mathbb{R}}^n$, where ${\mathcal{X}}_c=\mathcal{B}+\dots +E^{k-1}\mathcal{B}$.

Proposition 4.

Two Lagrangian systems (6) and $\left(\widetilde{\mathcal{LLS}}\right)$, given by $(E^L,B)$ and $({\tilde{E}}^L,\tilde{B})$, respectively, are LMF-equivalent if and only if their mechanical half-indices coincide, that is $\overline{\mathcal{P}}(E^L,B)=\overline{\mathcal{P}}({\tilde{E}}^L,\tilde{B})$ and, up to permutations, $({\lambda }_j,{\mu }_j)=({\tilde{\lambda }}_j,{\tilde{\mu }}_j)$, for $1\le j\le q$, where ${\lambda }_j$’s and ${\tilde{\lambda }}_j$’s are distinct eigenvalues of $E_d^L$ and ${\tilde{E}}_d^L$, respectively, and q is their number (the same for both systems).

A proof follows directly from Proposition 3 applied to two Lagrangian systems. The statements of Propositions 3 and 4 are formally the same; the only difference is that the eigenstructure of $E_d$ of (2) can have any elements ${\Lambda }_j$ (real or complex eigenvalues ${\lambda }_j$ and diagonal or Jordan blocks), while ${\Lambda }_j$ of $E_d^L$ of (6) consists of real eigenvalues ${\lambda }_j$ and diagonal blocks only. Contrary to Proposition 4, that is a Lagrangian counterpart of Proposition 3, the classification Theorem 2 does not apply to the Lagrangian systems (6) because, in general, the feedback transformation $u=Fx+G\tilde{u}$ does not perserve the Lagrangian structure. Actually, the mechanical canonical form, given by $(E_F,B_F)$, is never Lagrangian because $E_F$ has all eigenvalues ${\lambda }_j=0$, and thus never can be written as a product of two symmetric matrices $E_F=-M^{-1}P$, for M being invertible. Indeed, a symmetric matrix, whose all eigenvalues are zero, is $P=0$ but then $-M^{-1}P=0\ne E_F$.

Instead of Theorem 2, we have the following result.

Proposition 5.

(i)

Any Lagrangian mechanical system (6) is LMF-equivalent to the following Lagrangian system:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_c& =y_c\hfill \\ \hfill {\dot{y}}_c& =E_F^L{x}_c+B_{F}u\hfill \end{array}\begin{array}{cc}\hfill {\dot{x}}_d& =y_d\hfill \\ \hfill {\dot{y}}_d& =E_d^L{x}_d,\hfill \end{array}\end{array}$$

(19)

where $E_d^L=\mathrm{diag}({\lambda }_1^d,\dots ,{\lambda }_l^d)$, $l=n-k$, with ${\lambda }_j^d$ arbitrary real, and $E_F^L$ is of the same form as $E_F$, given by (16) and (17), with $N_i$ replaced by $L_i=\left(\begin{array}{cccc}0& 1& \dots & 0\\ & & \ddots & \\ 0& 0& \dots & 1\\ a_1^i& a_2^i& \dots & a_{{\overline{\rho }}_i}^i\end{array}\right)$, such that the eigenvalues of $L_i$ are all real and mutually distinct.

(ii)

Any two Lagrangian systems of the form (19), with the same $E_d^L$ but arbitrary terms $a_j^i$ and ${\tilde{a}}_j^i$ (such that, for each block $1\le i\le m$, the eigenvalues ${\lambda }_j^i$ of $L_i$ are mutually distinct and so are ${\tilde{\lambda }}_j^i$ of ${\tilde{L}}_i$), are LMF-equivalent.

Proof. 

$\left(i\right)$. By Theorem 2, any (6) is LMF-equivalent to (18), whose $x_c$-subsystem is not Lagrangian, for which $E_d^J$ is $E_d^L$ (since all eigenvalues of (6) are real). Then we change $N_i$ into $L_i$ using the feedback transformation that replaces $u_i$ by ${\sum }_{j=1}^{{\overline{\rho }}_i}{a}_j^i{x}_c^j+u_i$, such that the eigenvalues of $L_i$ are real and mutually distinct, and obtain a Lagrangian system of the form (19). To prove $\left(ii\right)$, take any system of the form (19) and using the feedback transformation that replaces $u_i$ by ${\sum }_{j=1}^{{\overline{\rho }}_i}({\tilde{a}}_j^i-a_j^i)x_c^j+u_i$, we get a system of the form (19) in which ${\tilde{a}}_j^i$ take place of $a_j^i$. □

The above proposition suggests that there is no a Brunovský-like canonical form for Lagrangian systems. On one hand, the matrix $L_i$ with all $a_j^i=0$ does not give a Lagrangian system, on the other hand, there is no a privileged choice of non-zero eigenvalues, and all of them are feedback equivalent as asserted by item $\left(ii\right)$. This suggests not to change the original eigenvalues and to apply a change of coordinates $\tilde{x}=Tx$, $\tilde{y}=Ty$ only, which we treat in the next proposition.

Proposition 6.

Consider a single-input, $m=1$, Lagrangian mechanical system. It is equivalent via $\tilde{x}=Tx$, $\tilde{y}=Ty$ to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\dot{x}}_c^i& =y_c^i\hfill \\ \hfill {\dot{y}}_c^i& ={\lambda }_i^c{x}_c^i+u\hfill \end{array}1\le i\le k\begin{array}{cc}\hfill {\dot{x}}_d^i& =y_d^i\hfill \\ \hfill {\dot{y}}_d^i& ={\lambda }_i^d{x}_d^i,\hfill \end{array}1\le i\le l=n-k\end{array}$$

(20)

where all ${\lambda }_i^c,{\lambda }_i^d\in \mathbb{R}$ and, moreover, ${\lambda }_i^c$ are mutually distinct.

The above form is clear. The matrix E is diagonal and the system (6) decouples into two independent subsystems: the uncontrollable one consisting of $l=n-k$ independent second order dynamical systems ${\ddot{x}}_d^i={\lambda }_i^d{x}_d^i$ (with real eigenvalues ${\lambda }_i^d$ that can be any) and a completely controllable one consisting of k second order control systems ${\ddot{x}}_c^i={\lambda }_i^c{x}_c^i+u$, whose eigenvalues ${\lambda }_i^c$ are distinct, all controlled by the same control u. A similar form can be obtained for the multi-input case $m>1$ (with a more complicated form of the matrix B) but we will not present it here because of lack of space.

6. Stability and Stabilization

Now we come back to (not necessarily Lagrangian) mechanical systems (2) and we turn our attention to the relation between the eigenvalues of E, denoted ${\lambda }_j$, and the eigenvalues of $\widehat{A}$, denoted ${\sigma }_j$, since the latter are responsible for the stability of the system.

Lemma 2.

Let $\widehat{A}=\left(\begin{array}{cc}0& I_n\\ E& 0\end{array}\right)$. If λ is an eigenvalue of E, then $\sigma =\pm \sqrt{\lambda }$ are eigenvalues of $\widehat{A}$.

Proof. 

By a direct calculation, we see that the characteristic polynomial of $\widehat{A}$ is

$$\begin{array}{cc}\hfill det(\sigma I_{2n}-\widehat{A})=& det\left(\left(\begin{array}{cc}\sigma I_n& 0\\ 0& \sigma I_n\end{array}\right)-\left(\begin{array}{cc}0& I_n\\ E& 0\end{array}\right)\right)=det({\sigma }^2{I}_n-E)\hfill \\ & =({\sigma }^2-{\lambda }_1)({\sigma }^2-{\lambda }_2)\dots ({\sigma }^2-{\lambda }_n),\hfill \end{array}$$

since all blocks of $\widehat{A}$ commute, and where ${\lambda }_1\dots {\lambda }_n$ are the eigenvalues of E. The above polynomial has the roots ${\sigma }_j=\pm \sqrt{{\lambda }_j}$. □

If $\lambda \in \mathbb{R}$, then $\sigma =\pm a$ or $\sigma =\pm a\mathtt{i}$, where $a=\sqrt{\left|\lambda \right|}\in {\mathbb{R}}_{+}$. If $\lambda =\alpha +\beta \mathtt{i}\in \mathbb{C}$ (and its conjugate $\alpha -\beta \mathtt{i}\in \mathbb{C}$), then $\sigma =\pm (a+b\mathtt{i})$ and $\pm (a-b\mathtt{i})$, where $\alpha =a^2-b^2$ and $\beta =2ab$. Denote ${\mathbb{R}}_{\le 0}=\left\{\lambda \in \mathbb{R}:\lambda \le 0\right\}$. 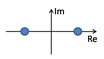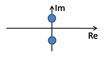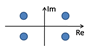Let us visualize the relation between the eigenvalues with the following table.

$\mathbf{\lambda }\left(\mathbf{E}\right)$	$\mathbf{\sigma }\left(\widehat{\mathbf{A}}\right)$	Sketch
${\mathbb{R}}_{+}$	$\pm a$
${\mathbb{R}}_{\le 0}$	$\pm a\mathtt{i}$
$\mathbb{C}$	$\pm (a+b\mathtt{i})$ and $\pm (a-b\mathtt{i})$

The above analysis of the eigenvalues leads to the following simple but important observation. We will say that a dynamical system $\dot{z}=\widehat{A}z$, for $\widehat{A}$ given by (4) and $z=(x,y)$, is stable if all its equilibrium points are stable. Recall that ${\mu }_j$ denotes the algebraic multiplicity of an eigenvalue ${\lambda }_j$ and ${\gamma }_j=dimker({\lambda }_j{I}_n-E)$ its geometric multiplicity.

Proposition 7.

Consider the dynamical system $\dot{z}=\widehat{A}z$, where $\widehat{A}=\left(\begin{array}{cc}0& I_n\\ E& 0\end{array}\right)$ or, equivalently, $\ddot{x}=Ex$.

(AS) 

The system $\dot{z}=\widehat{A}z$ is never asymptotically stable.

(S) 

The following conditions are equivalent:

(i) 

the system $\dot{z}=\widehat{A}z$ is stable,

(ii) 

all eigenvalues ${\lambda }_j$ of E satisfy ${\lambda }_j\in {\mathbb{R}}_{\le 0}$ and, moreover, their algebraic and geometric multiplicities coincide, i.e., ${\mu }_j={\gamma }_j$, for $1\le j\le q$, where q is the number of distinct eigenvalues of E_d,

(iii) 

E has a Lagrangian structure, i.e., $E=M^{-1}P$ for some symmetric matrices M (invertible) and P and the eigenvalues of E satisfy ${\lambda }_j\in {\mathbb{R}}_{\le 0}$.

Proof. 

It is immediate to see $\left(AS\right)$, since at least for one eigenvalue ${\sigma }_j$ of $\widehat{A}$ we have $\mathrm{Re}{\sigma }_j\ge 0$. Equivalence of $\left(i\right)\iff \left(ii\right)$ follows immediately from Lemma 2 and the table above. For a proof of necessity of ${\mu }_j={\gamma }_j$ (which is equivalent to $\mathrm{rank}({\lambda }_j{I}_n-E)=n-{\mu }_j$), see the proof of Theorem 4.5 in [16]. Equivalence $\left(ii\right)\iff \left(iii\right)$ is given by Proposition 1 and the comments below it. □

Of course, the class of second-order differential equations (or dynamical systems) $\ddot{x}=Ex$ is bigger than the class of Lagrangian systems $\ddot{x}=E^{L}x$ because the matrix E can be any, while $E^L$ has to be $\mathbb{R}$-diagonalizable. It is obvious that $\ddot{x}=E^{L}x$ cannot be asymptotically stable because it preserves the energy $\frac{1}{2}{\dot{x}}^{T}M\dot{x}+\frac{1}{2}{x}^{T}Px$. It turns out that $\ddot{x}=Ex$ is never asymptotically stable either (although it may have, contrary to $\ddot{x}=E^{L}x$, complex eigenvalues with non-zero real part) and, moreover, it is stable if and only if it is Lagrangian. So there are no stable second order differential equations (in other words, dynamical systems) $\ddot{x}=Ex$ others than Lagrangian ones.

A mechanical control system (2) is called asymptotically stabilizable if there exists a mechanical feedback of the form $u=Fx$ such that the closed loop

$$\begin{array}{cc}\hfill \dot{x}& =y\hfill \\ \hfill \dot{y}& =(E+BF)x\hfill \end{array}$$

is asymptotically stable and is called stabilizable if all equilibria of the above closed loop system are stable. Recall that the map $E:{\mathbb{R}}^n\to {\mathbb{R}}^n$ induces the map $\widehat{E}:{\mathbb{R}}^n/{\mathcal{X}}_c\to {\mathbb{R}}^n/{\mathcal{X}}_c$, where ${\mathcal{X}}_c\cong {\mathbb{R}}^k$, that is represented by the matrix $E_d\in {\mathbb{R}}^{l\times l}$, where $l=n-k$.

Proposition 7, applied to the uncontrolled system ${\dot{x}}_d=y_d$, ${\dot{y}}_d=E_d{x}_d$, leads to the following result describing stabizability of mechanical control systems (2).

Theorem 3.

Consider a mechanical control system (2).

(AS) 

The system (2) is never asymptotically stabilizable.

(S) 

The following conditions are equivalent:

(i) 

(2) is stabilizable,

(ii) 

the matrix $E_d$ has all eigenvalues ${\lambda }_j\in {\mathbb{R}}_{\le 0}$ and, moreover, is diagonalizable, i.e., its Jordan form $E_d^J$ consists of diagonal blocks $D_j^{\mathbb{R}}$ only, corresponding to ${\lambda }_j\in {\mathbb{R}}_{\le 0}$,

(iii) 

all eigenvalues ${\lambda }_j$ of $E_d$ satisfy ${\lambda }_j\in {\mathbb{R}}_{\le 0}$ and, moreover, their algebraic and geometric multiplicities coincide, i.e., ${\mu }_j={\gamma }_j$, for $1\le j\le q$, where q is the number of distinct eigenvalues of $E_d$,

(iv) 

the uncontrolled subsystem ${\dot{x}}_d=y_d$, ${\dot{y}}_d=E_d{x}_d$ is T-equivalent to a Lagrangian system,

(v) 

(2) is LMF-equivalent to (6) and, moreover, the matrix $E_d$ satisfies the conditions of item $\left(ii\right)$ above (or of the equivalent items $\left(iii\right)$ or $\left(iv\right)$).

Proof. 

Item $\left(AS\right)$ follows directly from Proposition 7. For $\left(S\right)$, the crucial observation is that the controllable system is stabilizable, thus we deal with the uncontrollable system only, which must already be stable for the whole system to be stabilizable. Therefore, the equivalence $\left(i\right)\iff \left(iii\right)$ follows directly from Proposition 7. Equivalence of $\left(ii\right)\iff \left(iii\right)$ is given by Proposition 1 and the comments below it. For $\left(ii\right)\iff \left(iv\right)$, note that the matrix $E_d^J$ of $\left(ii\right)$ coincides with $E_d^L$ of (19), so the transformation T that diagonalizes $E_d$ renders the uncontrolled subsystem Lagrangian. Finally, assume that (2) is LMF-equivalent to (6) and $E_d$ satisfies $\left(ii\right)$, or equivalent conditions $\left(iii\right)$ or $\left(iv\right)$, i.e., it is stable. Then, by Proposition 5 $\left(ii\right)$ it is also LMF-equivalent to a Lagrangian system that is stable. Hence, LMF-transformation stabilizes the system (2). The inverse follows from the previous arguments. □

Corollary 2.

Any stabilizing feedback $u=Fx$, for a mechanical control system (2), renders the system $\dot{x}=y$, $\dot{y}=(E+BF)x$ Lagrangian.

In other words, for (2) to be stabilizable, all unstable modes ${\ddot{x}}_j={\lambda }_j{x}_j$, where $\mathrm{Re}{\lambda }_j>0$ must be controllable, i.e., must be contained in the controllable $x_c$-subsystem, or, equivalently, all uncontrollable modes must be stable. Checking that requires, however, a decomposition of (2) into controllable and uncontrollable subsystems. Therefore we provide below invariant conditions that can be verified for any (2). This is analogous to [7], where Lagrangian systems with dissipative forces were considered.

Proposition 8.

The system (2), given by $(E,B)$, is stabilizable if and only if for any eigenvalue ${\lambda }_j$ of E such that $\mathrm{rank}({\lambda }_j{I}_n-E,B)<n$, we have ${\lambda }_j\in {\mathbb{R}}_{\le 0}$ and ${\mu }_j={\gamma }_j$, where ${\mu }_j$ and ${\gamma }_j$ are, respectively, the algebraic and geometric multiplicity of ${\lambda }_j$.

Proof. 

Note that $\mathrm{rank}({\lambda }_j{I}_n-E)<n$ if and only if ${\lambda }_j$ is an eigenvalue of E. By Hautus lemma (see e.g., [7,15,17]), if $\mathrm{rank}({\lambda }_j{I}_n-E,B)=n$, then the mode ${\ddot{x}}_j={\lambda }_j{x}_j$ is controllable. Thus, by assuming $\mathrm{rank}({\lambda }_j{I}_n-E,B)<n$ we identify all uncontrollable modes so the corresponding subsystems have to be stable, i.e., ${\lambda }_j\in {\mathbb{R}}_{\le 0}$ and ${\mu }_j={\gamma }_j$, see Theorem 3 $\left(ii\right)$. □

7. Examples

Classical examples of linear mechanical control systems are mass-spring systems. We present the equations of motions of n-coupled mass-spring system, which consists of n bodies, where the position of i-th body is denoted $x^i$, and $m_i$ is the mass of i-th body. The bodies are connected by $n+1$ springs with $k_i$ being the spring constant of i-th spring, as depicted in Figure 1. The external forces (controls) $u_i$ may, á priori, be applied to each body.

The dynamics of i-th body is given by the balance of forces acting on the body

$$\begin{array}{c}\hfill m_i{\ddot{x}}^i=-k_i\left(x^i-x^{i-1}\right)+k_{i+1}\left(x^{i+1}-x^i\right)+u_i,\end{array}$$

(21)

where $x^0\equiv x^{n+1}\equiv 0$. The equations can be formulated in the form of (5), where -4.6cm0cm

$$\begin{array}{c}\hfill M=\left(\begin{array}{ccccc}{m}_1& 0& 0& \dots & 0\\ 0& m_2& 0& \dots & 0\\ 0& 0& m_3& \dots & 0\\ 0& 0& 0& \ddots & 0\\ 0& 0& 0& \dots & m_n\end{array}\right)P=\left(\begin{array}{ccccc}{k}_1+k_2& -k_2& 0& \dots & 0\\ -k_2& k_2+k_3& -k_3& \dots & 0\\ 0& -k_3& k_3+k_4& \dots & 0\\ 0& 0& 0& \ddots & -k_n\\ 0& 0& \dots & -k_n& k_n+k_{n+1}\end{array}\right)\end{array}$$

or as a Lagrangian system of the form (6), where

$$\begin{array}{c}\hfill E=E^L=\left(\begin{array}{ccccc}\frac{-k_1-k_2}{m_1}& \frac{k_2}{m_1}& 0& \dots & 0\\ \frac{k_2}{m_2}& \frac{-k_2-k_3}{m_2}& \frac{k_3}{m_2}& \dots & 0\\ 0& \frac{k_3}{m_3}& \frac{-k_3-k_4}{m_3}& \dots & 0\\ 0& 0& 0& \ddots & \frac{k_n}{m_{n-1}}\\ 0& 0& \dots & \frac{k_n}{m_n}& \frac{-k_n-k_{n+1}}{m_n}\end{array}\right)B=\left(\begin{array}{ccccc}\frac{1}{m_1}& 0& 0& \dots & 0\\ 0& \frac{1}{m_2}& 0& \dots & 0\\ 0& 0& \frac{1}{m_3}& \dots & 0\\ 0& 0& 0& \ddots & 0\\ 0& 0& 0& \dots & \frac{1}{m_n}\end{array}\right).\end{array}$$

(22)

If all n controls are present, then the system is fully actuated. However, it is enough to apply only the control $u_n$ in order for the system to be controllable.

Example 2

(The mass-spring system with one control). Consider the n-mass-spring system (21) with only one control $u:=u_n$, i.e $u_i=0$ for $1\le i\le n-1$. The system is (2), where E is given by (22) and $b={\left(0,\dots ,\frac{1}{m_n}\right)}^T$. It is straightforward to show that $\mathrm{rank}\left(b,Eb,\dots ,E^{n-1}b\right)=n$. What is more, introduce $c=(\frac{\overline{m}}{\overline{k}},0,0,\dots ,0)$, where $\overline{m}={\prod }_{i=1}^n{m}_i$ and $\overline{k}={\prod }_{i=2}^n{k}_i$, and apply the transformation $T={(c,cE,\dots ,c{E}^{n-1})}^T$. The transformed system is a Lagrangian system of the form (19), given by:

$$\begin{array}{c}\hfill E_F^L=TE{T}^{-1}=\left(\begin{array}{cccc}0& 1& \dots & 0\\ & & \ddots & \\ 0& 0& \dots & 1\\ a_1& a_2& \dots & a_n\end{array}\right)\mathrm{and}{b}_F=Tb=\left(\begin{array}{c}0\\ ⋮\\ 0\\ 1\end{array}\right)\end{array}$$

and $E_d^L$ is nonexistent since the system is controllable. Note that, by applying the feedback $u=-{\sum }_{i=1}^n{a}_i{\tilde{x}}^i+\tilde{u}$, we obtain the (non Lagrangian) mechanical canonical form (15) or we substitute $a_i$’s with any other ${\tilde{a}}_i$’s, and those ${\tilde{a}}_i$’s, for which the corresponding eigenvalues ${\tilde{\lambda }}_j$ satisfy ${\tilde{\lambda }}_j\in {\mathbb{R}}_{\le 0}$ and are mutually distinct, give stable Lagrangian systems.

Example 3

(The uncontrollable mass-spring system). Consider the mass-spring system with 3 equal masses m and 4 equal springs with the spring constant k. The external force is applied to the second mass only. The equations of motion are of the form (6) with:

$$\begin{array}{c}\hfill E=E^L=\left(\begin{array}{ccc}-\frac{2k}{m}& \frac{k}{m}& 0\\ \frac{k}{m}& -\frac{2k}{m}& \frac{k}{m}\\ 0& \frac{k}{m}& -\frac{2k}{m}\end{array}\right)\mathit{and}b=\left(\begin{array}{c}0\\ \frac{1}{m}\\ 0\end{array}\right).\end{array}$$

A direct calculation shows that $\mathrm{rank}(b,Eb,E^{2}b)=2<n=3$. In order to decompose the system, we take $T^{-1}=\mathrm{col}(b,Eb,v)$, where $v={(1,0,0)}^T$ and set:

$$\begin{array}{c}\hfill \tilde{E}=TE{T}^{-1}=\left(\begin{array}{ccc}0& -\frac{2k^2}{m^2}& k\\ 1& -\frac{4k}{m}& 0\\ 0& 0& -\frac{2k}{m}\end{array}\right)\mathit{and}\tilde{b}=Tb=\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right).\end{array}$$

Then, by another transformation $\overline{T}=\left(\begin{array}{ccc}1& -\frac{k}{m}(2+\sqrt{2})& -\frac{m}{\sqrt{2}}\\ 1& -\frac{k}{m}(2-\sqrt{2})& \frac{m}{\sqrt{2}}\\ 0& 0& 1\end{array}\right)$ applied to the pair $(\tilde{E},\tilde{b})$, we can establish a Lagrangian system in the form (20) with coordinates $(x_c^1,x_c^2,x_d^1)$

$$\begin{array}{c}\hfill \begin{array}{cc}{\dot{x}}_c^1\hfill & =y_c^1\hfill \\ {\dot{y}}_c^1\hfill & ={\lambda }_1^c{x}_c^1+u\hfill \\ {\dot{x}}_c^2\hfill & =y_c^2\hfill \\ {\dot{y}}_c^2\hfill & ={\lambda }_2^c{x}_c^2+u\hfill \end{array}\begin{array}{cc}\hfill \hspace{1em}{\dot{x}}_d^1& =y_d^1\hfill \\ \hfill \hspace{1em}{\dot{y}}_d^1& ={\lambda }_1^d{x}_d^1,\hfill \end{array}\end{array}$$

where ${\lambda }_1^c=-\frac{k}{m}(2+\sqrt{2})$, ${\lambda }_2^c=-\frac{k}{m}(2-\sqrt{2})$ and ${\lambda }_1^d=-\frac{2k}{m}$. It is immediate to see that the system is stable since ${\lambda }_1^d,{\lambda }_1^c,{\lambda }_2^c\in {\mathbb{R}}_{\le 0}$ and all eigenvalues ${\sigma }_j$ of $\widehat{A}$ are pure imaginary giving oscillations. Moreover, the frequency $\sqrt{|{\lambda }_1^d|}$ is invariantly related to the system, while ${\lambda }_1^c$, ${\lambda }_2^c$ can be set freely (by an appropriate choice of feedback $u=F{x}_c$).

8. Conclusions

In this paper, we have studied a classification of linear mechanical control systems (2) under mechanical change of coordinates and feedback. In Section 3, Section 4 and Section 5, which are the heart of our paper, we completely solved the classification problem for both controllable and uncontrollable cases, which enabled us to establish the corresponding canonical forms. To our best knowledge this complete solution, expressing complete invariants in terms of objects on the configuration space only, have not been publish before and constitutes a novelty of our work. Our obvious inspirations are Lagrangian control systems, which apart from applicational importance, turn out to be crucial in Section 6, where we have discussed stability and stabilization of (2) (not asymptotic stabilization). The conclusion is that there are no other stabilizable mechanical control systems (2) than Lagrangian ones. Finally, we illustrated our results by a classical representative of linear mechanical control system, i.e., by the mass-spring system, which is considered in two special cases: one that is controllable and another that is not.