Design and Analysis of the Rolling and Jumping Compound Motion Robot
Abstract
:1. Introduction
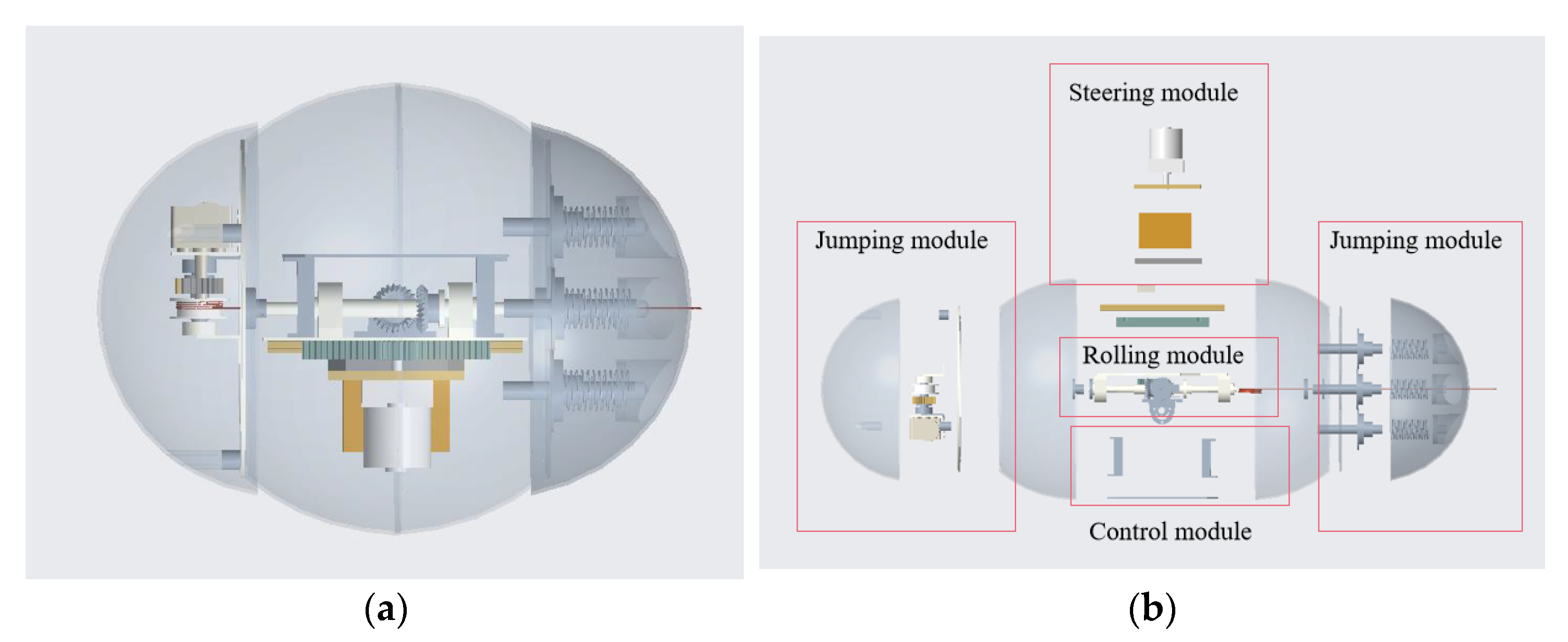
2. The Overall Design Scheme of the Rolling and Jumping Robot
2.1. Rolling Module
2.2. Steering Module
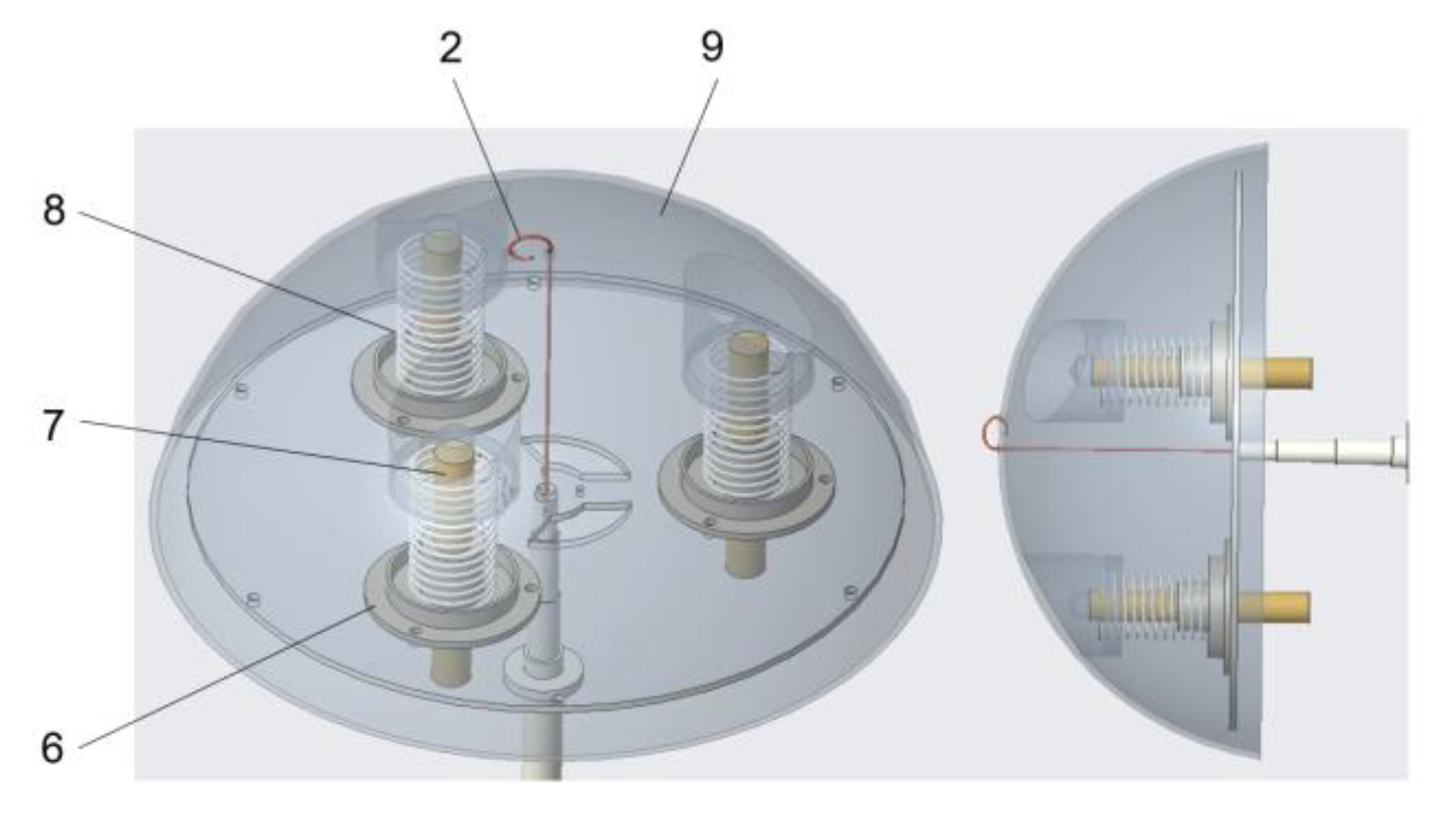
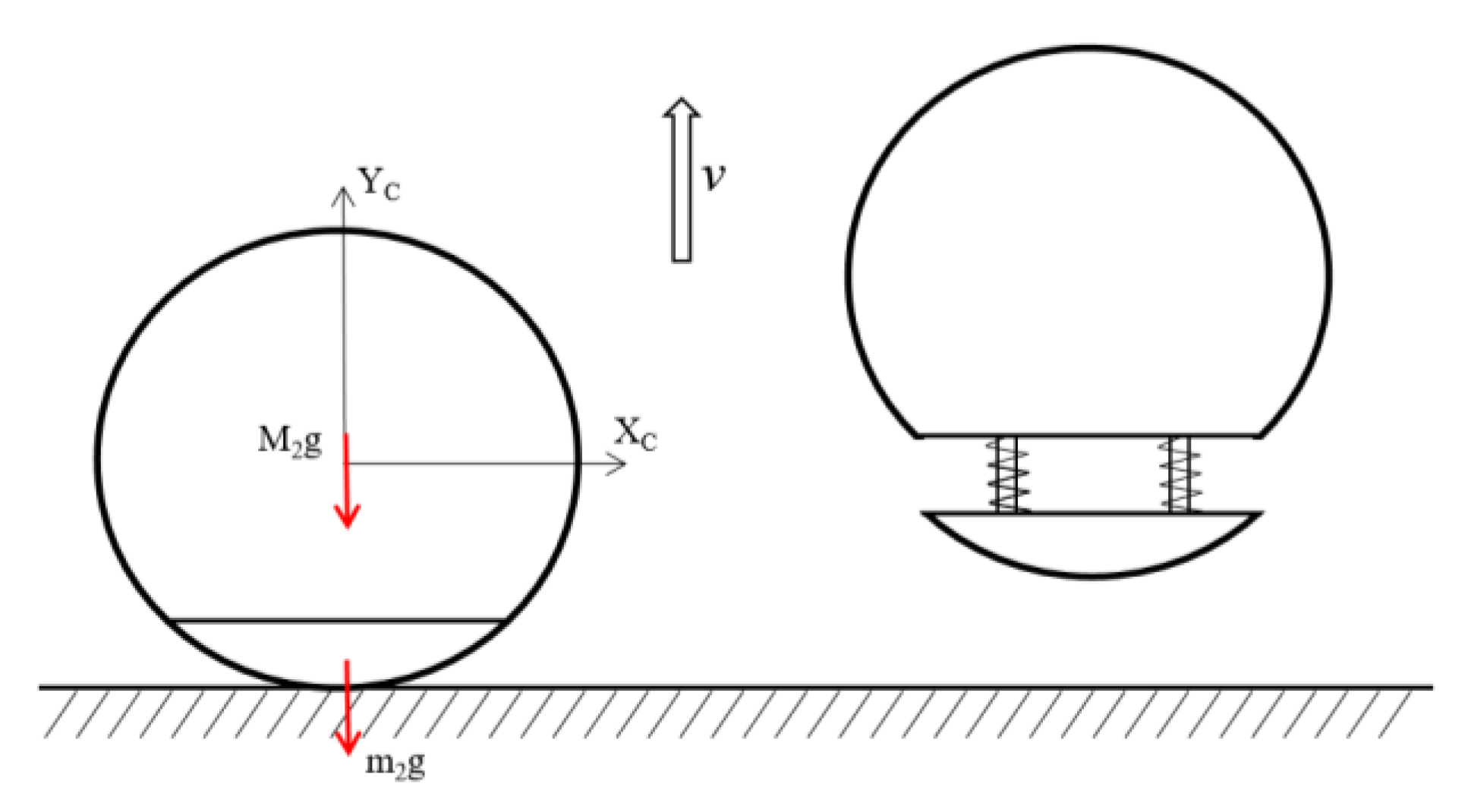
2.3. Jumping Module
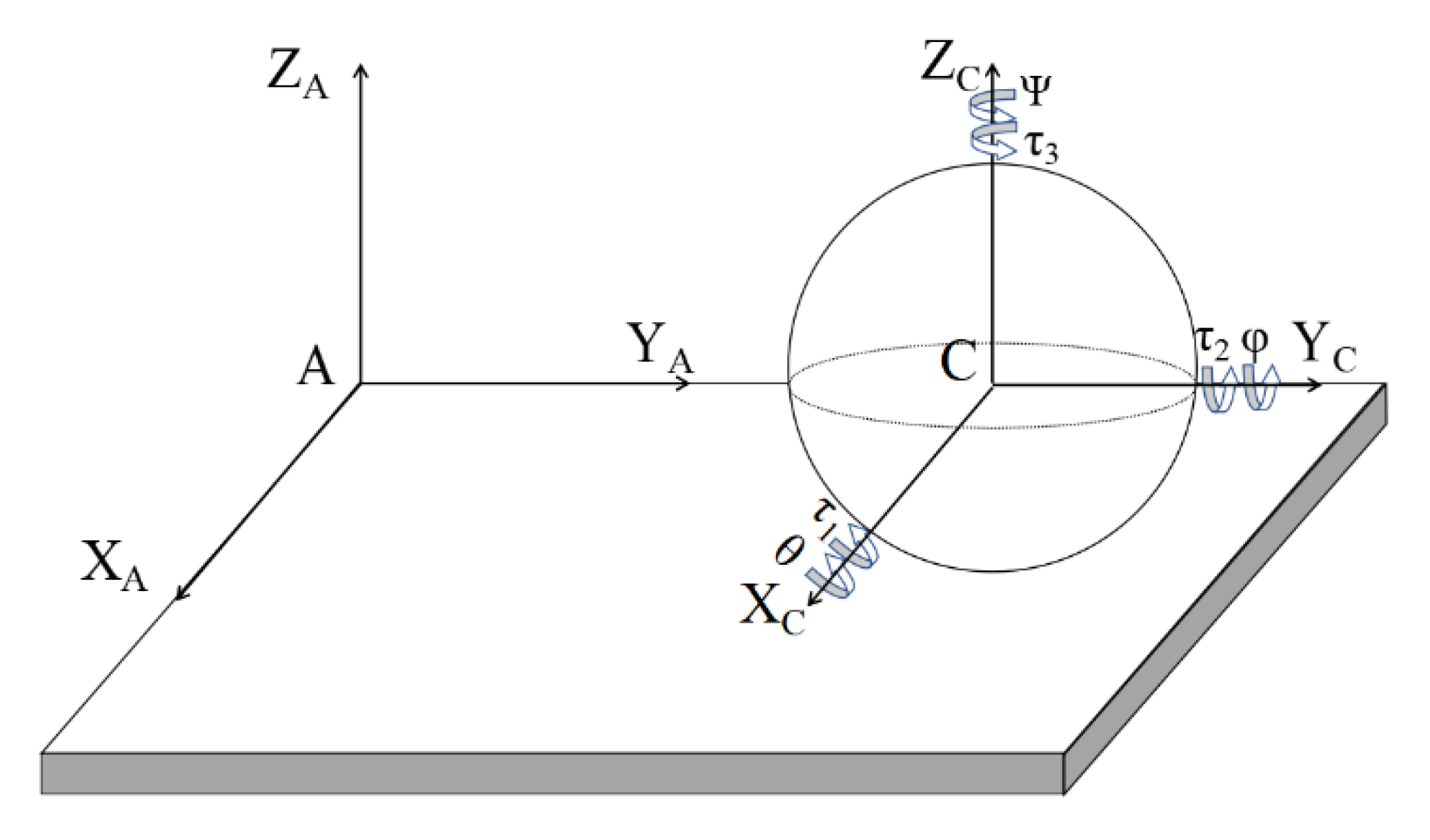
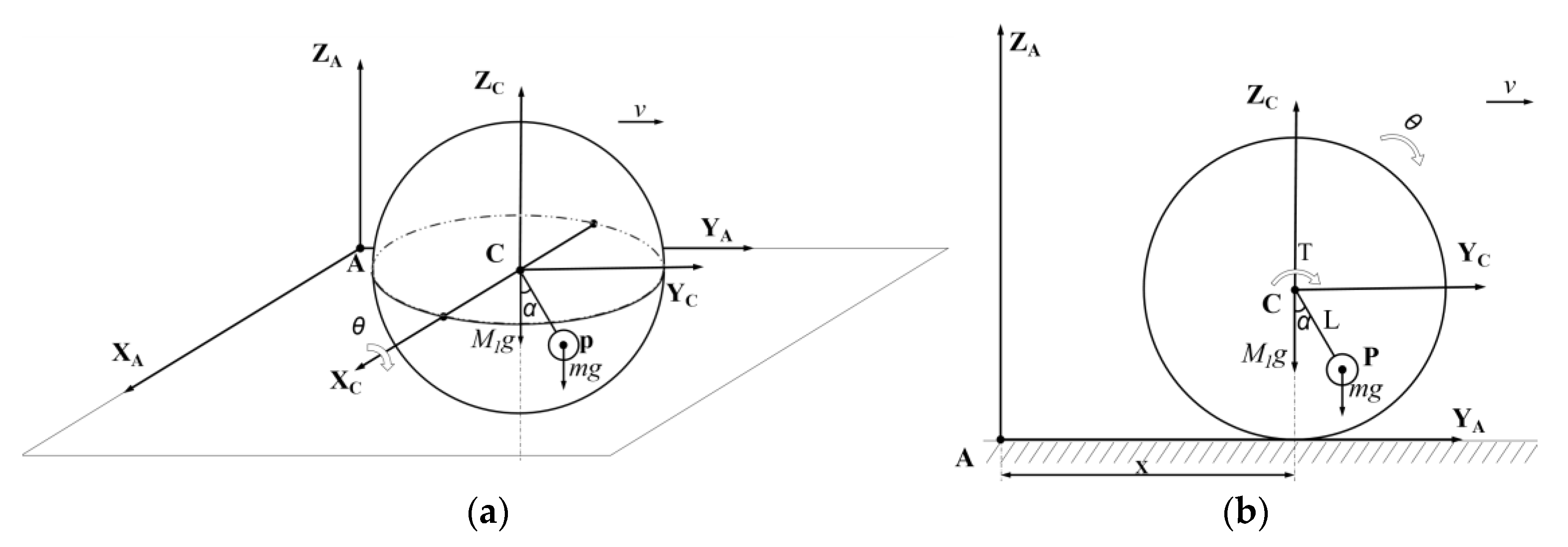
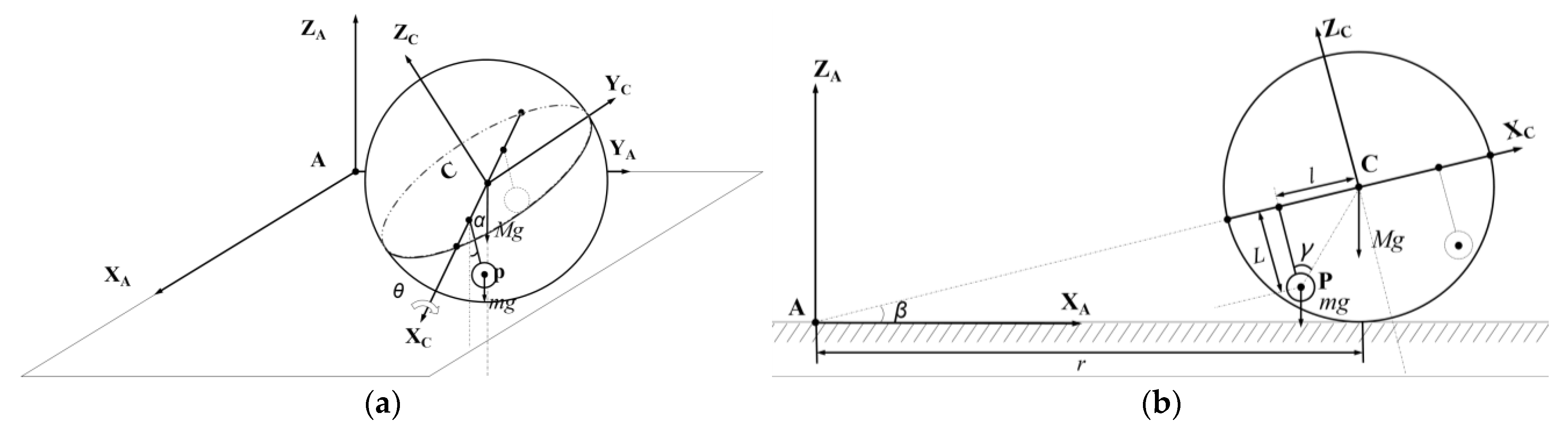
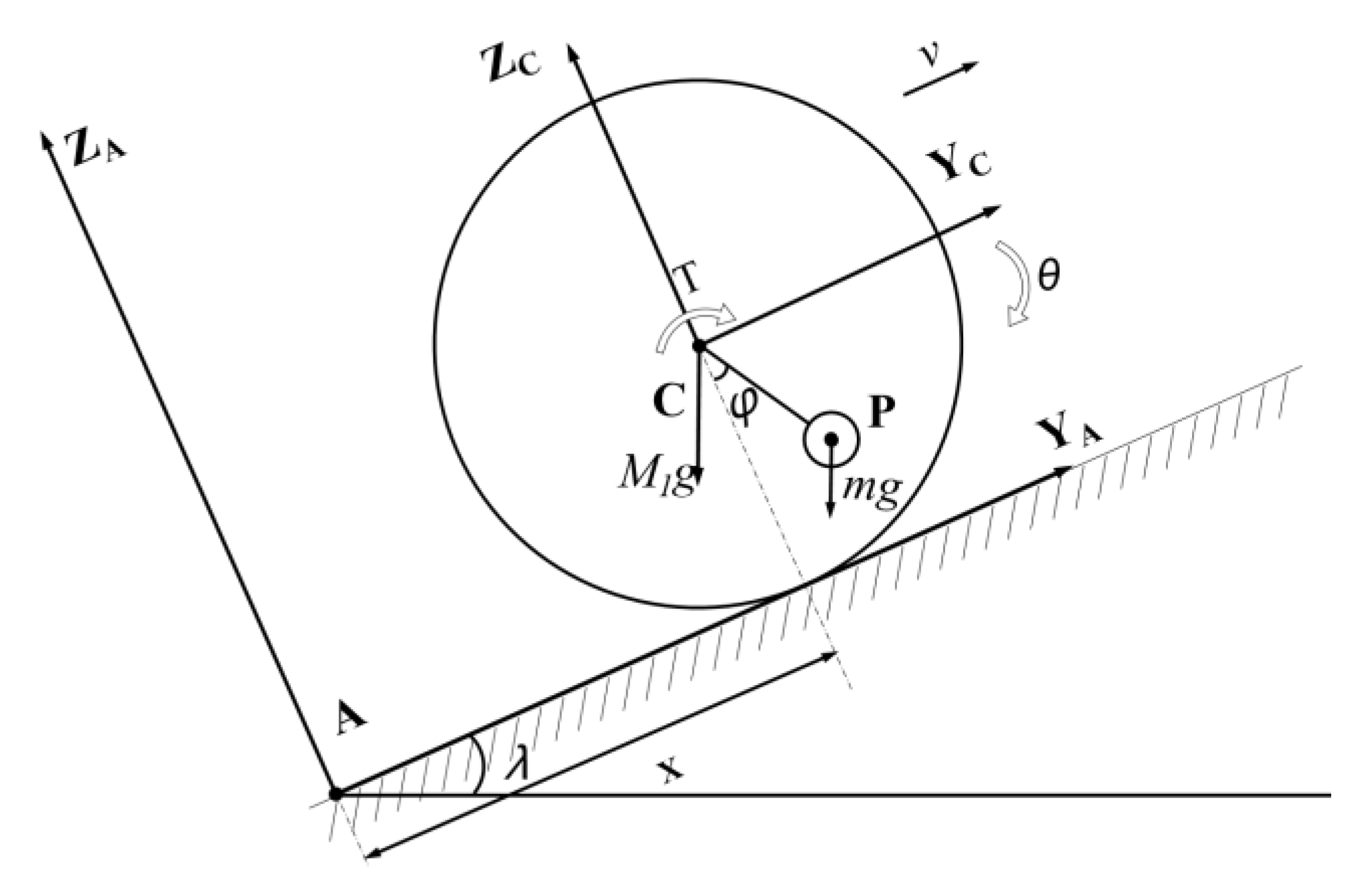
3. The Kinetic Analysis of the Rolling and Jumping Robot
- The spatial motion of the robot follows the constraint condition of rigid body sliding free rolling;
- The shell is equivalent to a homogeneous thin-walled shell with uniform mass distribution;
- In the initial state, the centroid of the robot coincides with the geometric center;
- In the moving state, only the dynamic friction between the shell and the ground is considered, and the internal friction is ignored.
3.1. Rolling Dynamic Equation
3.2. Steering Dynamics Equation
3.3. Climbing Dynamics Equation
3.4. Jumping Dynamics Equation
4. Performance Test of the Rolling and Jumping Robot
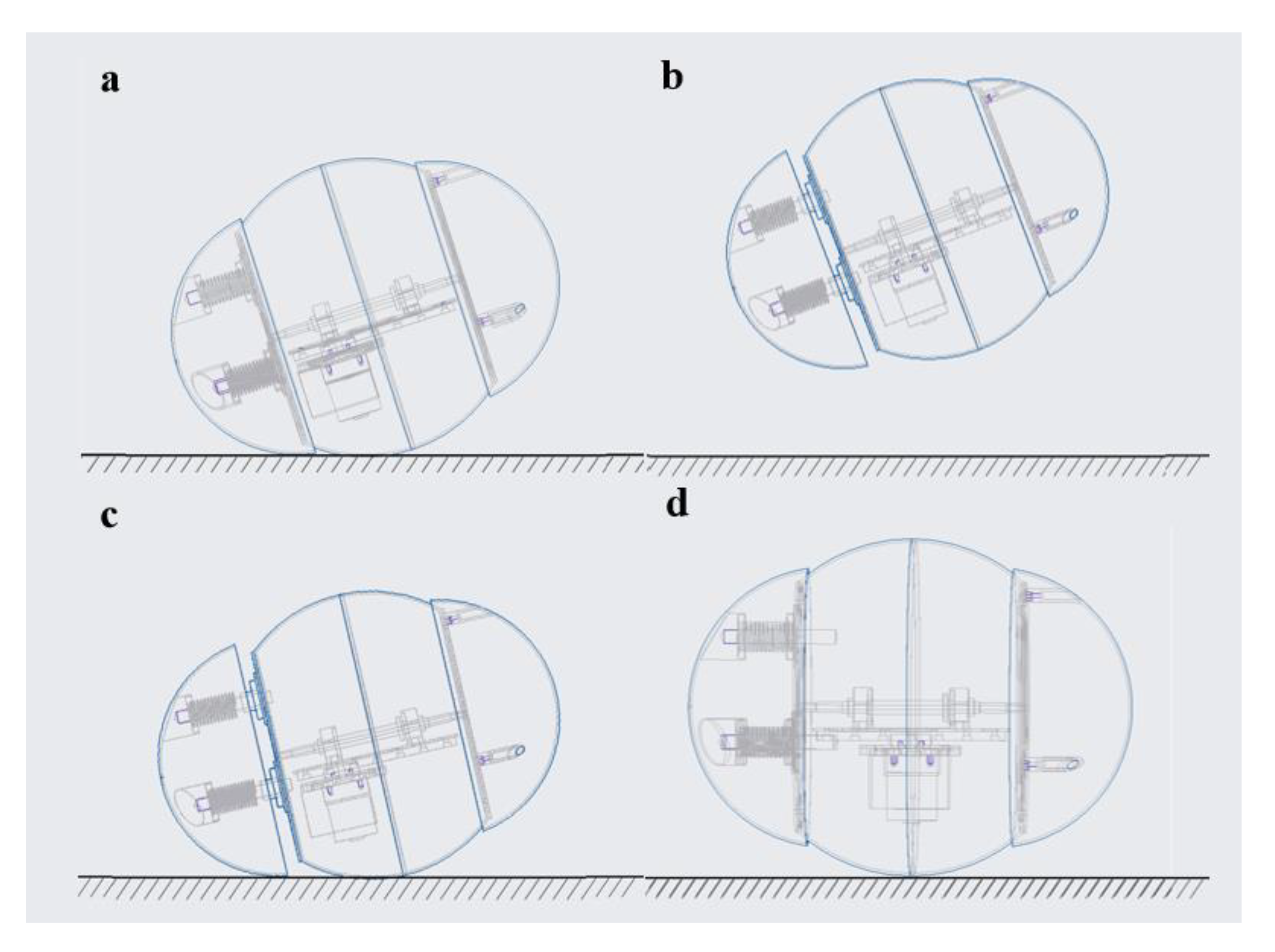
4.1. Rolling Performance
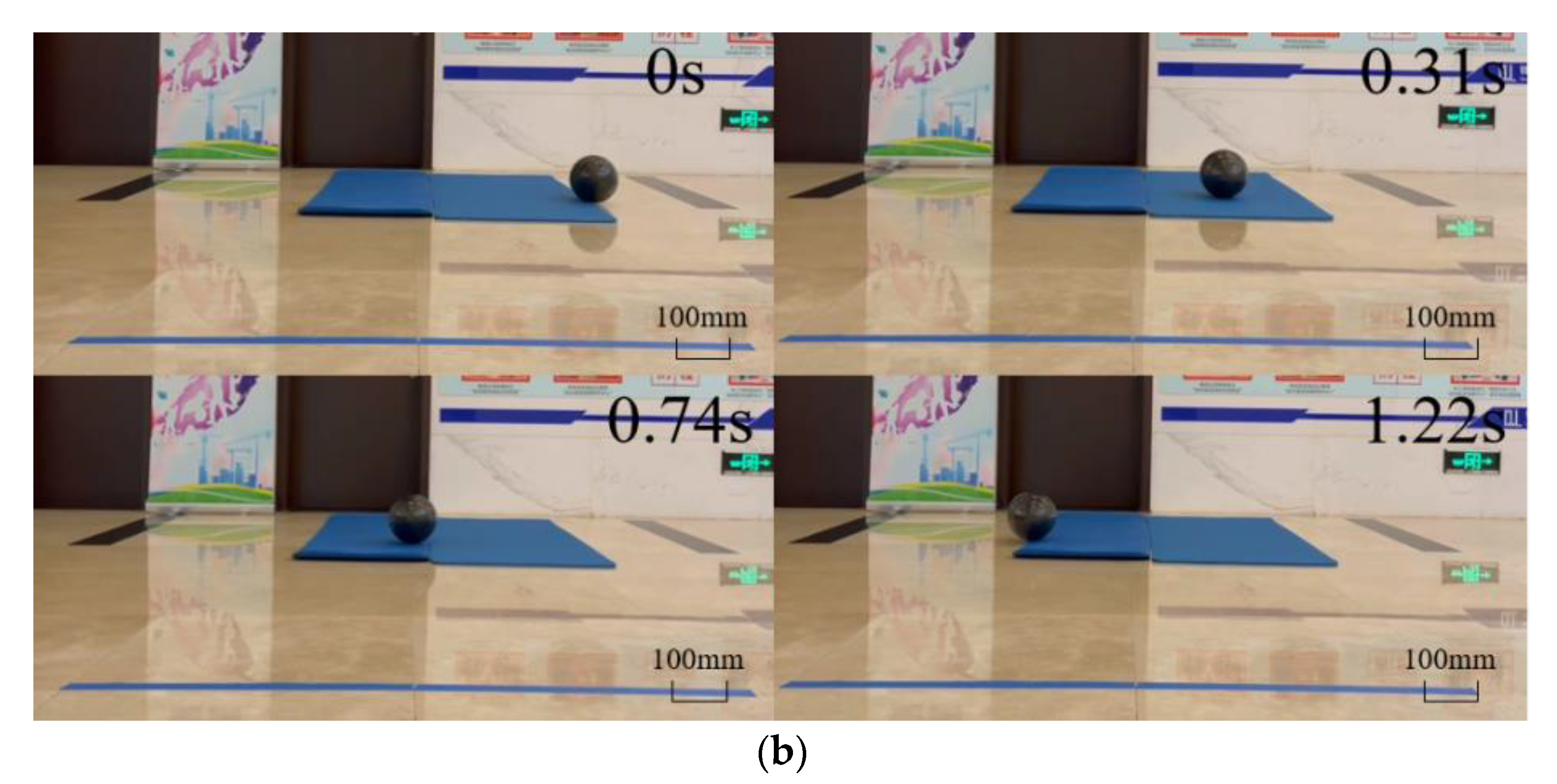
4.1.1. Rolling Speed Test
4.1.2. Turning Radius Test
4.1.3. Climbing Performance Test
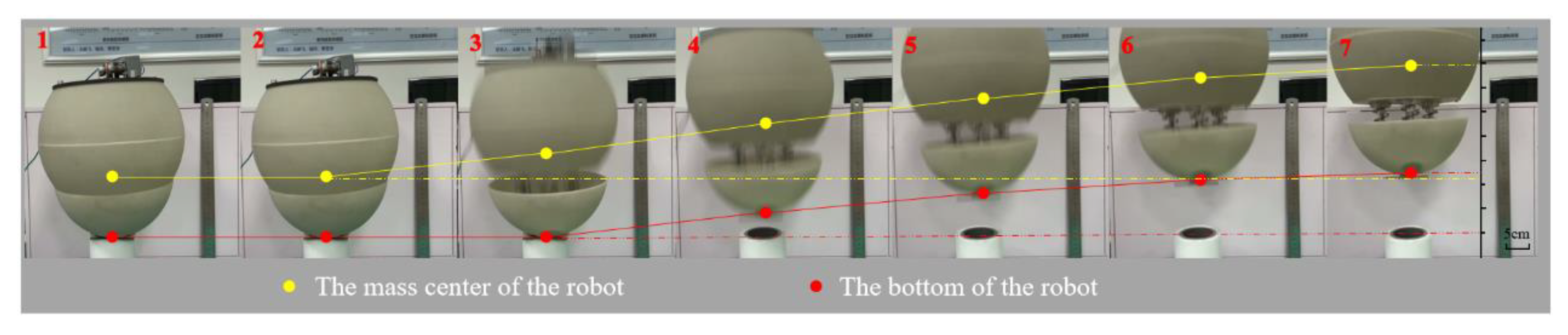
4.2. Jumping Performance
4.3. Comparison between the Theoretical Value and Test Value
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Yanagida, T.; Mohan, R.E.; Pathmakumar, T.; Elangovan, K.; Iwase, M. Design and Implementation of a Shape Shifting Rolling–Crawling–Wall-Climbing Robot. Appl. Sci. 2017, 7, 342. [Google Scholar] [CrossRef] [Green Version]
- Hayat, A.A.; Elangovan, K.; Rajesh Elara, M.; Teja, M.S. Tarantula: Design, Modeling, and Kinematic Identifucation of a Quadruped Wheeled Robot. Appl. Sci. 2019, 9, 94. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Wu, Y.; Hao, H.; Shi, H.; Huang, H. Tracked Wall-Climbing Robot for Calibration of Large Vertical Metal Tanks. Appl. Sci. 2019, 9, 2671. [Google Scholar] [CrossRef] [Green Version]
- Hwang, M.C.; Liu, F.; Yang, J.; Lin, Y. The Design and Building of a Hexapod Robot with Biomimetic Legs. Appl. Sci. 2019, 9, 2792. [Google Scholar] [CrossRef] [Green Version]
- Luo, B.; Li, B.; Yu, Y.; Yu, M.; Ma, J.; Yang, W.; Wang, P.; Jiao, Z. A Jumping Robot Driven by a Dielectric Elastomer Actuator. Appl. Sci. 2020, 10, 2241. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, R.; Minor, M.A. A simple motion planner for a spherical mobile robot. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Atlanta, GA, USA, 19–23 September 1999; pp. 896–901. [Google Scholar]
- Javadi, A.A.H.; Mojabi, P. Introducing August: A novel strategy for an omnidirectional spherical rolling robot. In Proceedings of the ICRA’02 IEEE International Conference on Robotics and Automation, Washington, DC, USA, 11–15 May 2002; pp. 3527–3533. [Google Scholar]
- Mansour, N.A.; Jang, T.; Baek, H.; Shin, B.; Ryu, B.; Kim, Y. Compliant closed-chain rolling robot using modular unidirectional SMA actuators. Sens. Actuators A Phys. 2020, 310, 112024. [Google Scholar] [CrossRef]
- Davoodi, F.; Davoudi, F. Design for the Structure and the Mechanics of Moballs; NASA Tech Briefs, 2012; Volume 36, pp. 66–68.
- Burkhardt, M.R.; Davoodi, F.; Burdick, J.W.; Davoudi, F. Energy harvesting analysis for moball, a self-propelled mobile sensor platform capable of long duration operation in harsh terrains. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2665–2672. [Google Scholar]
- Davoodi, F.; Burdick, J.W.; Rais-Zadeh, M. Moball network: A self-powered intelligent network of controllable spherical mobile sensors to explore solar planets and moons. In Proceedings of the AIAA SPACE Conference and Exposition, San Diego, CA, USA, 4–7 August 2014; pp. 1–9. [Google Scholar]
- Yoshimitsu, T.; Kubota, T.; Nakatani, I.; Adachi, T.; Saito, H. Micro-hopping robot for asteroid exploration. Acta Astronaut. 2003, 52, 441–446. [Google Scholar] [CrossRef]
- Kovač, M.; Schlegel, M.; Zufferey, J.-C.; Floreano, D. Steerable miniature jumping robot. Auton. Robot. 2009, 28, 295–306. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Song, G.; Li, Z.; Zhang, Y.; Qiao, G.; Song, A. Locomotion Performance Analysis of a Foldable Wheeled Jumping Robot: Fold Jumper. Robot 2014, 2, 250–256. [Google Scholar]
- Zhang, Y.; Huang, Z.; Han, L.; Gu, C.; Zhang, W. Design and Analysis of the Crawling and Rolling Characteristics of the Crawling and Rolling Robot for the Lunar Extreme Terrain. J. Mech. Eng. 2021, 57, 35–48. [Google Scholar]
- Wang, P.-F.; Wang, X.; Li, M.-T.; Sun, L.-N. Dynamics analysis of a micro-spherical robot. J. Harbin Inst. Technol. 2010, 9, 1398–1402. [Google Scholar]










| Physical Meaning | |
|---|---|
| M | Mass of whole robot |
| M1 | Mass of the remaining part without counterweight |
| M2 | Mass of remaining part without energy storage |
| m | Mass of counterweight |
| m0 | Mass of control module |
| m1 | Mass of energy storage |
| R | Geometric radius |
| d | Distance between the center of mass and the geometric center of the shell |
| l | Distance between the limit position on both sides of the counterweight and the shape center |
| L | Length of swing arm |
| D | Energy storage compression distance |
| β | Angle between the major shaft and the horizontal plane |
| f | Friction force |
| k | Jumping spring coefficient |
| A | Origin point of the ground coordinate system |
| C | Origin point of the moving coordinate system |
| P | Center of mass of counterweight |
| α | Deflection angle of the pendulum in rolling motion |
| r | Turning radius |
| φ | Deflection angle of the pendulum in climbing motion |
| λ | Climbing angle |
| E | Kinetic energy of the robot in rolling motion |
| V | Potential energy of the robot in rolling motion |
| EK1 | Kinetic energy of the shell in climbing motion |
| EK2 | Kinetic energy of the pendulum in climbing motion |
| EP1 | Potential energy of the shell in climbing motion |
| EP2 | Potential energy of the pendulum in climbing motion |
| T | Motion torque |
| Value | |
|---|---|
| M | 2.4 kg |
| M1 | 1.5 kg |
| M2 | 2.0 kg |
| m | 0.9 kg |
| m0 | 0.12 kg |
| m1 | 0.4 kg |
| R | 240 mm |
| d | 0 mm |
| l | 32 mm |
| L | 59 mm |
| D | 30 mm |
| β | 17.8° |
| f | 1.716 N |
| k | 2 N/mm |
| T | 1000 N/mm |
| Theoretical Value | Test Value | Relative Error | |
|---|---|---|---|
| Rolling speed | 1327 mm/s | 1229.5 mm/s | 7.34% |
| Turning radius | 263 mm | 300 mm | 14.07% |
| Maximum climbing angle | 13.67° | 11.31° | 17.26% |
| Jumping height (center of mass) | 254 mm | 210 mm | 17.32% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Li, B.; Wang, F.; Luo, B.; Jiao, Z.; Yu, Y.; Wang, P. Design and Analysis of the Rolling and Jumping Compound Motion Robot. Appl. Sci. 2021, 11, 10667. https://doi.org/10.3390/app112210667
Wu H, Li B, Wang F, Luo B, Jiao Z, Yu Y, Wang P. Design and Analysis of the Rolling and Jumping Compound Motion Robot. Applied Sciences. 2021; 11(22):10667. https://doi.org/10.3390/app112210667
Chicago/Turabian StyleWu, Huaisong, Bingyang Li, Futao Wang, Bin Luo, Zhiwei Jiao, Yuan Yu, and Pengfei Wang. 2021. "Design and Analysis of the Rolling and Jumping Compound Motion Robot" Applied Sciences 11, no. 22: 10667. https://doi.org/10.3390/app112210667
APA StyleWu, H., Li, B., Wang, F., Luo, B., Jiao, Z., Yu, Y., & Wang, P. (2021). Design and Analysis of the Rolling and Jumping Compound Motion Robot. Applied Sciences, 11(22), 10667. https://doi.org/10.3390/app112210667






